- 1Department of Mathematics, Abdul Wali Khan Uniuersity Mardan, Mardan, Pakistan
- 2Department of Mathematics, Near East University TRNC, Mersin, Turkey
- 3Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
- 4Department of Mathematics, Theoretical and Computational Science (TaCS) Center, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok, Thailand
- 5Intelligent and Nonlinear Dynamic Innovations Research Center, Department of Mathematics, Faculty of Applied Science, King Mongkut’s University of Technology North Bangkok (KMUTNB), Bangkok, Thailand
In the present work, an Elzaki transformation is combined with a decomposition technique for the solutions of fractional dynamical systems. The targeted problems are related to the systems of fractional partial differential equations. Fractional differential equations are useful for more accurate modeling of various phenomena. The Elzaki transform decomposition method is implemented in a very simple and straightforward manner to solve the suggested problems. The proposed technique requires fewer calculations and needs no discretization or parametrization. The derivative of fractional order is represented in a Caputo form. To show the conclusion, which is drawn from the results, some numerical examples are considered for their approximate analytical solution. The series solutions to the targeted problems are obtained having components with a greater rate of convergence toward the exact solutions. The new results are represented by using tables and graphs, which show the sufficient accuracy of the present method as compared to other existing techniques. It is shown through graphs and tables that the actual and approximate results are very close to each other, which shows the applicability of the presented method. The fractional-order solutions are in best agreement with the dynamics of the given problems and provide infinite choices for an optimal solution to the suggested mathematical model. The novelty of the present work is that it applies an efficient procedure with less computational cost and attains a higher degree of accuracy. Furthermore, the proposed technique can be used to solve other nonlinear fractional problems in the future, which will be a scientific contribution to research society.
1 Introduction
Fractional calculus (FC) is a subject dealing with derivatives and integrations of fractional order. The idea of FC was initiated by L’Hospital in 1965, who asked a question of Leibniz about the derivative of fractional order. In early times, the theory of FC was presented as an apparent paradox, and later on, it became the most popular area of research among researchers. Many mathematicians were attracted to FC because of its numerous applications in various areas of research. Some of the important physical phenomena in nature have been modeled more accurately by using FC than using ordinary calculus. In the literature, the applications of FC can be found in modeling of earthquake nonlinear oscillation [1], airfoil [21], fluid traffic [2], finance [22], Chaos theory [3], Zener model [23], cancer chemotherapy [6], Poisson–Nernst–Planck diffusion [24], electrodynamics [5], tuberculosis [9], hepatitis B virus [8], pine wilt disease [10], diabetes [11], hepatitis B disease model [50, 51], fractional COVID-19 model [52–54], and other applications in various areas of research [12–14].
Recently, fractional partial differential equations (FPDEs) [4] are considered the most reliable and effective technique to develop the most accurate mathematical models of various important phenomena in physics and other applied sciences. Many processes in nature are modeled accurately by using FPDEs as compared to simple PDEs such as optics [7] and tuberculosis [9]. The study related to FPDEs, the nonlinearity associated with each problem, is of greater interest because many complex phenomena in nature are modeled by using nonlinear FPDEs. In this context, Hassan et al. have presented the solutions of some nonlinear FPDEs that can be seen in studies [15–18]. Similarly, Hilfer and Ray have discussed some efficient techniques for the solution of certain nonlinear FPDEs in [19, 20], respectively.
Because of the aforementioned worthwhile applications of FC in real-world problems, researchers have made the study of this subject a compelling case for researchers. In this regard, mathematicians realized to investigate the numerical or analytical solutions of FPDEs and their systems to extend the analysis of the subject. Numerical and analytical methods are frequently used to obtain the solutions of various important mathematical models that represent some of the physical processes in nature. In this regard, mathematicians have worked hard to develop a variety of techniques for solving FPDEs and their systems. The results of the targeted problems support the actual dynamics of natural processes, making this a prominent area of research. The researchers have made their best efforts toward this topic and have established valuable techniques at regular intervals of time. In this connection, important and efficient procedures are implemented to solve FPDEs and their systems, such as the optimal homotopy asymptotic method (OHAM) [55], finite difference method (FDM) [27], Adomian decomposition method (ADM) [25, 26], extended direct algebraic method (EDAM) [58], the (G/Ǵ) expansion method [57], standard reductive perturbation method [59], the homotopy perturbation transform technique along with transformation (HPTM) [30–32], the Haar wavelet method (HWM) [33, 34], the variational iteration procedure with transformation (VITM) [38], and the differential transform method (DTM) [35–37].
Many authors have tried their best to modify the existing techniques for the solutions of FPDEs and their systems by using different transformations. The well-known transformations are the Laplace, natural, and Mohand transformations [42–44], the Mohand decomposition method [56], etc. that can be used to simplify the original problem and then utilize ADM, VIM, DTM, etc. for the solutions of the targeted problems. In the same context, the Elzaki transformation (ET) plays a vital role in solving FPDEs and their systems [48]. This transformation was introduced by Tarig Elzaki [45] to solve different kinds of DEs. First, the ET was used to solve ordinary differential equations and then extended to the solution of PDEs. Recently, many authors have combined this transformation with other existing methods and obtained solutions to higher nonlinear problems [28, 29]. Ezaki transformation is combined with the Adomian decomposition method to construct a new methodology based on ET, called the Elzaki decomposition transform method (ETDM), and is applied to the solution of FPDEs and their systems.
In this work, the analytical investigations of the linear and nonlinear systems of FPDEs are combined and solved by using the Elzaki transform decomposition method. The solutions to these systems of FPDEs were solved by Abdul Majeed Wazwaz by using the variational iteration method [39] in 2007, where he has calculated the solutions only for the integer order of the suggested system. Later on, in 2009, Jafari et al. implemented the homopotopy analysis method [40] for the proposed system related to FPDEs, wherein they investigated the fractional and integer solutions of each system simultaneously. Jafari et al. implemented the iterative Laplace transforms method [41] in 2013 to obtain solutions for the systems under consideration. In this study, we have used a very simple and straightforward technique, which is known as the Elzaki transform decomposition method (ETDM), for the solution of the previously discussed systems of FPDEs. The comparison of all the methods has confirmed that ETDM is an efficient and simple technique. Moreover, all the aforementioned techniques are analytical and therefore provide identical solutions. In this study, ETDM is further extended for the solutions of some linear and nonlinear systems of FPDEs within the Caputo operator [28, 47]. The proposed method has the novelty of expressing the nonlinear terms in the problems by using a stable and accurate procedure. The Ezaki transformation is implemented first to reduce the given problem to its simple form.
For this purpose, several nonlinear examples of FPDEs are first converted into a simpler form by using the Elzaki transformation and Adomian polynomials because the Elzaki transformation [49] cannot be implemented directly into the nonlinear terms of the targeted problems. At the end of the proposed procedure, an iterative technique is used to investigate the highly convergent components of the desired series form solution. The obtained solutions to various problems are represented through graphs and tables. The 2D and 3D plots have confirmed the greater contact between the ETDM solutions and the actual dynamics of the problems. Moreover, the present method is massive while producing the solutions at different fractional orders of the derivatives. The suggested method requires no linearization and discretization and provides suitable results by using small calculations. The accuracy of the current method is shown in terms of absolute error, which confirms the sufficient accuracy of ETDM. It is concluded that the present work will support researchers in solving high nonlinear problems in other fields of basic sciences.
2 Definitions
Here, some important definitions and literature related to the present research work are discussed. These definitions and other preliminary concepts are necessary to complete the present research task.
2.1 Riemann–Liouville Integral Operator
The fractional partial Riemann–Liouville integral, denoted by
where Γ represents the gamma function.
2.2 Caputo Operator
The Caputo operator of order α for fractional derivatives is expressed as follows [28]:
where
2.3 Lemma
For ℵ − 1 < α, β ≤ ℵ with
where ζ > 0, ℵ − 1 < α ≤ ℵ.
2.4 Definition
The Laplace transform (LT) for g(ϑ) is given as follows [43]:
2.5 Definition
The LT of fractional derivative is given as follows [43]:
where G(s) is the LT of g(ϑ).
2.6 Definition
The Mittag-Leffler function is expressed as follows [28]:
2.7 Adomian Polynomials
The Adomian polynomial to express the nonlinear term in a given problem is given as follows [28]:
where
is called Adomian polynomials.
2.8 Elzaki Transform
ET is the generalized form of Sumudu transformation, which can be define as follows [28, 46]:
The following are the results of ET for certain partial differential equations:
2.9 Elzaki Transform Fractional Derivative in Term of Caputo Sense
Theorem 1. Let the LT of the function f(ϑ) is denoted by G(s) and then ET F(q) of f(ϑ) is define as follows [47]:
Theorem 2. The ET of the fractional derivatives defined as follows:
3 Elzaki Transform Decomposition Method Procedure
Here, the ETDM procedure is [28] presented to solve the system of FPDEs:
with initial sources
where
Using the differential property of ET, we get
The decomposition solution for μ(ζ, ϑ) and ν(ζ, ϑ) is as follows:
The Adomian polynomials represent for
The nonlinearities in Eq. 6 can be represented as
Substituting Eqs 10, 12 into Eq. 9 gives
Using inverse ET to Eq. 13, we have
We describe the following terms:
In general for ℵ≥ 1, is given by
which is the generalized ETDM algorithm for the solutions of the system of FPDEs in two variables.
4 Numerical Examples
Problem 1
Here, we take the following FPDE [39–41]:
with initial source
The exact solution at α = β = 1 is
Using ET, Eq. 16 can be written as
After simplification, we obtain
Using the ET inverse to Eq. 18, we have
The assume decomposition solutions for variables μ(ζ, ϑ) and ν(ζ, ϑ) in Eq. 19 can be written as follows:
Furthermore,
The component comparison in Eq. 22 provides the following recursive ETDM algorithm:
For ℵ = 0,
For ℵ = 1,
For ℵ = 2,
Similarly for (ℵ > 2), the remaining terms of μm and νm can be calculated easily by using ETDM.In general, the solution of ETDM is given as follows:
Substituting Eqs 23, 24, 25, and 26 in Eq. 27, we get
Substituting α = β = 1 in Eq. 29, we get:
Thus,
which is the ETDM solution in closed form, when α = β = γ = 1.
Problem 2
Here, we take the following FPDE [39–41]:
with initial sources
The exact solution at α = β = γ = 1 is
Using ET, Eq. 29 can be written as follows:
After simplification, we have
Taking inverse ET of Eq. 30, we obtain
The decomposition solutions for variables μ(ζ, ς, ϑ), ν(ζ, ς, ϑ), and ω(ζ, ς, ϑ) can be written as follows:
Here,
Using Eq. 31, the nonlinearity in the given problem can be expressed as follows:
The component comparison in Eq. 32 provides the following recursive ETDM algorithm:
Using the ETDM algorithm, we get the following results:
For ℵ = 0,
For ℵ = 1,
For ℵ = 2,
In the same manner, the remaining terms of μℵ, νℵ, and ωℵ for (ℵ > 3) can be calculated easily by using ETDM. In general, solution of ETDM is given by
Substituting Eqs 34, 35, 36, and 37 in Eq. 38, we get
Substituting α = β = γ = 1 in Eq. 39, we get
which is the ETDM solution in closed form of Eq. 40, when α = β = γ = 1.
5 Results and Discussion
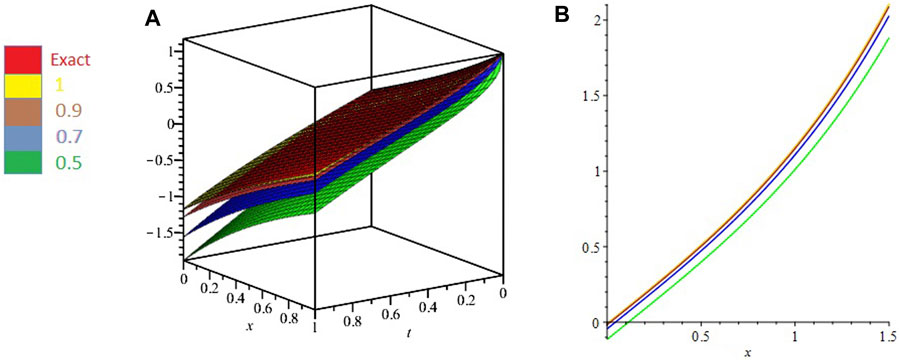
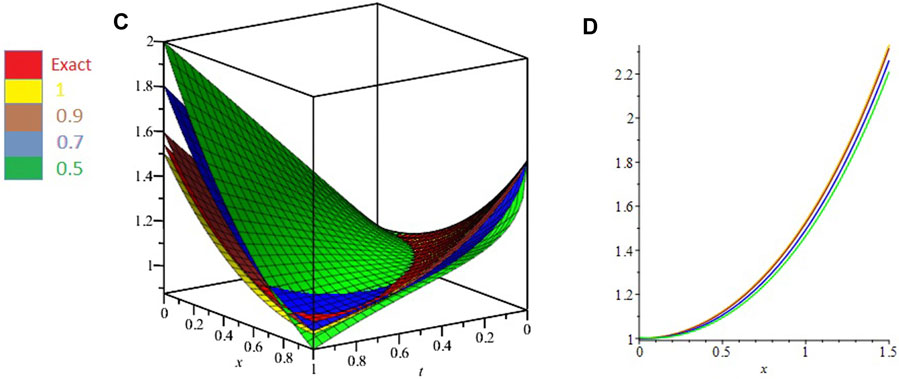
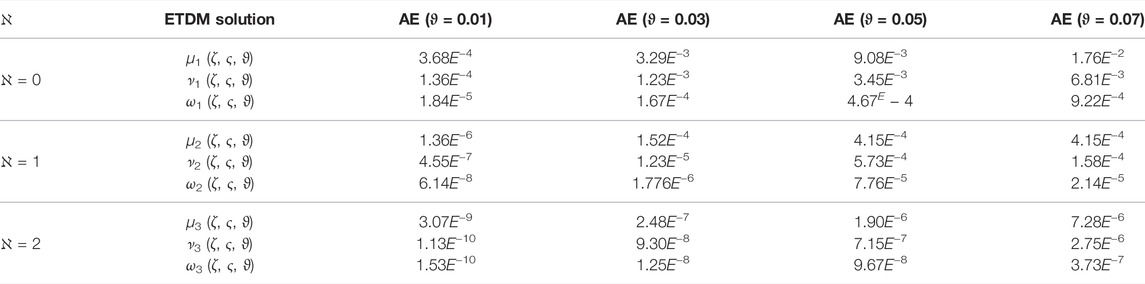
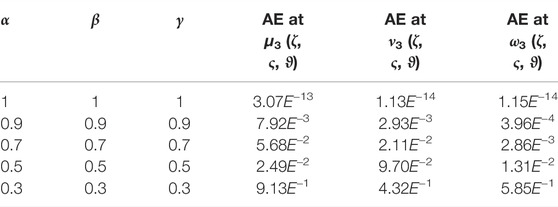
In Figure 1, 2D and 3D plots of u-solution for Problem 1 are presented at different fractional-orders of the derivatives. The sub-graphs A and B have shown the 3D and 2D plots of u-solution of Problem 1 respectively. The fractional solutions have displayed the consistent plots and therefore confirm the validity of the proposed method. Similarly, Figure 2, express the 2D and 3D plots of v-solutions at various fractional orders of the derivatives of Problem 1. The sub-graphs C and D displayed the 3D and 2D plots at differential orders of Problem 1 respectively. Figure 3, display the 3D plots fractional valued plots of variables u, v and w of Problem 2. The sub-graphs A, B and C have shown the 3D-solutions for variable u, v and w variables of Problem 2. Similarly, Figure 4, have the sub-graphs D, E and F which represent the 2D plots for variable u, v and w variables of Problem 2 respectively. Table 1, is concerned with absolute error associated with ETDM for u variable at different time level and degree of the polynomials of Problem 1. Table 2, describe the absolute error of ETDM at different fractional orders and along with third degree of the approximated polynomials. Similarly, Table 3, represents the ETDM absolute error for variables u,v and w at different time level and degree of polynomials of Problem 2. Table 4, express the absolute error of ETDM for variable u,v and w variables at different fractional orders of Problem 2. The graphs and table have shown that ETDM and Exact solutions are in closed contact with each other and possess the higher degree of accuracy.
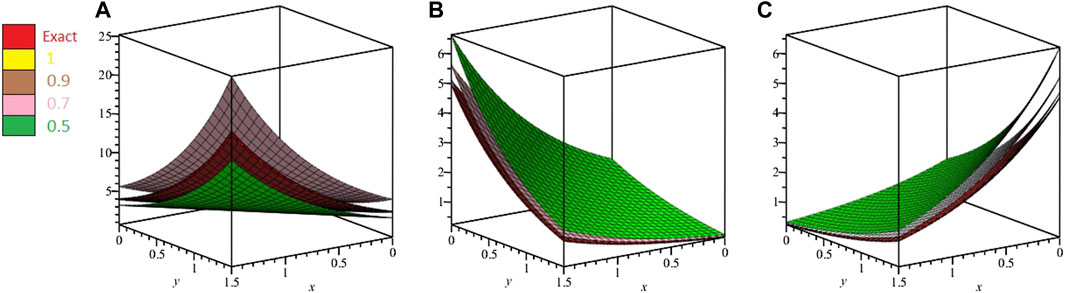
FIGURE 3. ETDM (A) 3D μ-solution, (B) 3D v-solution, and (C) 3D ω-solution graph, respectively, at various values of α, β and γ of Problem 2.
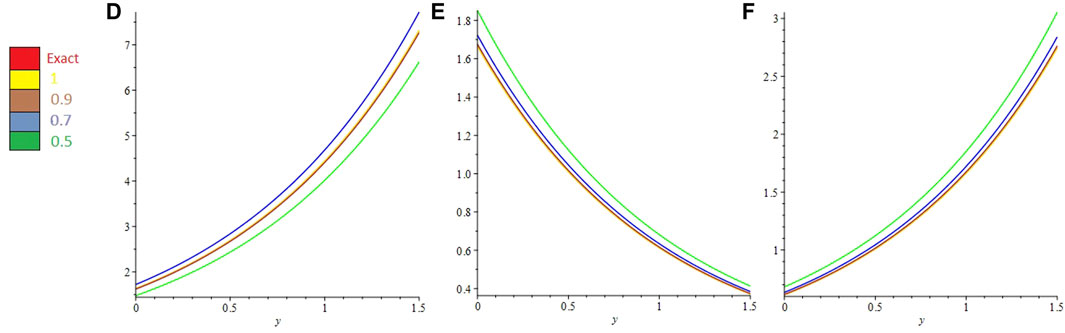
FIGURE 4. ETDM (D) 2D μ-solution, (E) 2D v-solution, and (F) 2D ω-solution graph respectively at various values of α, β and γ of Problem.
6 Conclusion
In this study, the important systems of FPDEs are considered for their analytical solutions using the ETDM. The numerical solutions are completed in two steps. In the first step, the Elzaki transformation is used to convert the targeted problems into simpler forms, and then the decomposition method is applied to obtain the resultant solutions. It is observed from the tables and figures that the current technique has a higher capability to evaluate the results of the targeted problems. The problem’s solutions at various time levels and m are investigated, which cover the different aspects of the modeling of the targeted problems and suggested technique. The solutions at various fractional orders are presented, and a very fast convergence of fractional solutions is shown toward an integer-order solution. The graphical representation has shown a very consistent relationship between the fractional- and integer-order solutions. It should be noted that the ETDM procedure is simple and straightforward, and thus, it can be extended to solve high nonlinear FPDEs and their systems.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
Qasim khan: methodology; HK: supervision; PK: funding and draft writing; and H: draft writing. KS: Funding and Investigation.
Funding
This research was funded by National Science, Research and Innovation Fund (NSRF), and King Mongkut’s University of Technology North Bangkok with Contract no. KMUTNB-FF-65-24.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank our research group for their collective efforts. The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.
References
1. He JH. August. Nonlinear Oscillation with Fractional Derivative and its Applications. Int Conf vibrating Eng (1998) 98:288–91.
2. He JH. Homotopy Perturbation Technique. Computer Methods Appl Mech Eng (1999) 178(3-4):257–62. doi:10.1016/s0045-7825(99)00018-3
3. Wu X, Lai D, Lu H. Generalized Synchronization of the Fractional-Order Chaos in Weighted Complex Dynamical Networks with Nonidentical Nodes. Nonlinear Dyn (2012) 69(1):667–83. doi:10.1007/s11071-011-0295-9
4. Sheng H, Chen Y, Qiu T. Fractional Processes and Fractional-Order Signal Processing: Techniques and Applications. Berlin, Germany: Springer Science and Business Media (2011).
5. Nasrolahpour H. A Note on Fractional Electrodynamics. Commun Nonlinear Sci Numer Simulation (2013) 18(9):2589–93. doi:10.1016/j.cnsns.2013.01.005
6. Veeresha P, Prakasha DG, Baskonus HM. New Numerical Surfaces to the Mathematical Model of Cancer Chemotherapy Effect in Caputo Fractional Derivatives. Chaos (2019) 29(1):013119. doi:10.1063/1.5074099
7. Longhi S. Fractional Schrödinger Equation in Optics. Opt Lett (2015) 40(6):1117–20. doi:10.1364/ol.40.001117
8. Ullah S, Khan MA, Farooq M. A New Fractional Model for the Dynamics of the Hepatitis B Virus Using the Caputo-Fabrizio Derivative. The Eur Phys J Plus (2018) 133(6):1–14. doi:10.1140/epjp/i2018-12072-4
9. Altaf Khan M, Ullah S, Farooq M. A New Fractional Model for Tuberculosis with Relapse via Atangana-Baleanu Derivative. Chaos, Solitons & Fractals (2018) 116:227–38. doi:10.1016/j.chaos.2018.09.039
10. Khan MA, Ullah S, Okosun KO, Shah K. A Fractional Order pine Wilt Disease Model with Caputo–Fabrizio Derivative. Adv Difference Equations (2018) 2018(1):1–18. doi:10.1186/s13662-018-1868-4
11. Singh J, Kumar D, Baleanu D. On the Analysis of Fractional Diabetes Model with Exponential Law. Adv Difference Equations (2018) 2018(1):1–15. doi:10.1186/s13662-018-1680-1
12. Hilfer R. Applications of Fractional Calculus in Physics. Orlando: Universität Mainz & Universität Stuttgart (1999).
13. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Stud (2006) 204:1–523.
14. Das S. A Note on Fractional Diffusion Equations. Chaos, Solitons & Fractals (2009) 42(4):2074–9. doi:10.1016/j.chaos.2009.03.163
15. Khan H, Shah R, Kumam P, Baleanu D, Arif M. Laplace Decomposition for Solving Nonlinear System of Fractional Order Partial Differential Equations. Adv Difference Equations (2020) 2020(1):1–18. doi:10.1186/s13662-020-02839-y
16. Alderremy AA, Khan H, Shah R, Aly S, Baleanu D. The Analytical Analysis of Time-Fractional Fornberg-Whitham Equations. Mathematics (2020) 8(6):987. doi:10.3390/math8060987
17. Shah R, Khan H, Baleanu D, Kumam P, Arif M. A Novel Method for the Analytical Solution of Fractional Zakharov–Kuznetsov Equations. Adv Difference Equations (2019) 2019(1):1–14. doi:10.1186/s13662-019-2441-5
18. Srivastava HM, Shah R, Khan H, Arif M. Some Analytical and Numerical Investigation of a Family of Fractional‐order Helmholtz Equations in Two Space Dimensions. Math Meth Appl Sci (2020) 43(1):199–212. doi:10.1002/mma.5846
19. Hilfer R. Fractional Calculus and Regular Variation in Thermodynamics. In: Applications of Fractional Calculus in Physics (2000). p. 429–63. doi:10.1142/9789812817747_0009
20. Ray SS. Exact Solutions for Time-Fractional Diffusion-Wave Equations by Decomposition Method. Phys Scr (2006) 75(1):53–61. doi:10.1088/0031-8949/75/1/008
21. Mahmood S, Shah R, khan H, Arif M. Laplace Adomian Decomposition Method for Multi Dimensional Time Fractional Model of Navier-Stokes Equation. Symmetry (2019) 1111(22):149149. doi:10.3390/sym11020149
22. Momani S, Odibat Z. Analytical Solution of a Time-Fractional Navier-Stokes Equation by Adomian Decomposition Method. Appl Mathematics Comput (2006) 177(2):488–94. doi:10.1016/j.amc.2005.11.025
23. Birajdar GA. Numerical Solution of Time Fractional Navier-Stokes Equation by Discrete Adomian Decomposition Method. Nonlinear Eng (2014) 3(1):21–6. doi:10.1515/nleng-2012-0004
24. Chaurasia VBL, Kumar D. Solution of the Time-Fractional Navier–Stokes Equation. Gen Math Notes (2011) 4(2):49–59.
25. Wang Q. Numerical Solutions for Fractional KdV-Burgers Equation by Adomian Decomposition Method. Appl Mathematics Comput (2006) 182(2):1048–55. doi:10.1016/j.amc.2006.05.004
26. Daftardar-Gejji V, Bhalekar S. Solving Multi-Term Linear and Non-linear Diffusion-Wave Equations of Fractional Order by Adomian Decomposition Method. Appl Mathematics Comput (2008) 202(1):113–20. doi:10.1016/j.amc.2008.01.027
27. Chamekh M, Elzaki TM. Explicit Solution for Some Generalized Fluids in Laminar Flow with Slip Boundary Conditions. J Math Computer Sci. (2018) 18:272–81. doi:10.22436/jmcs.018.03.03
28. Khan H, Khan A, Kumam P, Baleanu D, Arif M. An Approximate Analytical Solution of the Navier–Stokes Equations within Caputo Operator and Elzaki Transform Decomposition Method. Adv Difference Equations (2020) 2020(1):1–23. doi:10.1186/s13662-020-02839-y
29. Zhou S-S, Areshi M, Agarwal P, Shah NA, Chung JD, Nonlaopon K. Analytical Analysis of Fractional-Order Multi-Dimensional Dispersive Partial Differential Equations. Symmetry (2021) 13(6):939. doi:10.3390/sym13060939
30. Wang Q. Homotopy Perturbation Method for Fractional KdV Equation. Appl Mathematics Comput (2007) 190(2):1795–802. doi:10.1016/j.amc.2007.02.065
31. Liu H, Khan H, Shah R, Alderremy AA, Aly S, Baleanu D. On the Fractional View Analysis of Keller–Segel Equations with Sensitivity Functions. Complexity (2020) 2020:2371019. doi:10.1155/2020/2371019
32. Abdulaziz O, Hashim I, Ismail ES. Approximate Analytical Solution to Fractional Modified KdV Equations. Math Computer Model (2009) 49(1-2):136–45. doi:10.1016/j.mcm.2008.01.005
33. Rehman Mu., Khan RA. Numerical Solutions to Initial and Boundary Value Problems for Linear Fractional Partial Differential Equations. Appl Math Model (2013) 37(7):5233–44. doi:10.1016/j.apm.2012.10.045
34. Akinlar MA, Secer A, Bayram M. Numerical Solution of Fractional Benney Equation. Appl Math Inf Sci (2014) 8(4):1633–7. doi:10.12785/amis/080418
35. Secer A, Akinlar MA, Cevikel A. Similarity Solutions for Multiterm Time-Fractional Diffusion Equation. Adv Differ Equ (2012).
36. Kurulay M, Bayram M. Approximate Analytical Solution for the Fractional Modified KdV by Differential Transform Method. Commun nonlinear Sci Numer simulation (2010) 15(7):1777–82. doi:10.1016/j.cnsns.2009.07.014
37. Kurulay M, Akinlar MA, Ibragimov R. Computational Solution of a Fractional Integro-Differential Equation. Abstract Appl Anal (2013) 2013:865952. doi:10.1155/2013/865952
38. Shah R, Khan H, Baleanu D, Kumam P, Arif M. A Semi-analytical Method to Solve Family of Kuramoto-Sivashinsky Equations. J Taibah Univ Sci (2020) 14(1):402–11. doi:10.1080/16583655.2020.1741920
39. Wazwaz AM. The Variational Iteration Method for Solving Linear and Nonlinear Systems of PDEs. Comput Mathematics Appl (2007) 54(7-8):895–902. doi:10.1016/j.camwa.2006.12.059
40. Jafari H, Seifi S. Solving a System of Nonlinear Fractional Partial Differential Equations Using Homotopy Analysis Method. Commun Nonlinear Sci Numer Simulation (2009) 14(5):1962–9. doi:10.1016/j.cnsns.2008.06.019
41. Jafari H, Nazari M, Baleanu D, Khalique CM. A New Approach for Solving a System of Fractional Partial Differential Equations. Comput Mathematics Appl (2013) 66(5):838–43. doi:10.1016/j.camwa.2012.11.014
42. Shah R, Khan H, Arif M, Kumam P. Application of Laplace-Adomian Decomposition Method for the Analytical Solution of Third-Order Dispersive Fractional Partial Differential Equations. Entropy (2019) 21(4):335. doi:10.3390/e21040335
43. Khan H, Shah R, Kumam P, Arif M. Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method. Entropy (2019) 21(6):597. doi:10.3390/e21060597
44. Shah R, Khan H, Farooq U, Baleanu D, Kumam P, Arif M. A New Analytical Technique to Solve System of Fractional-Order Partial Differential Equations. IEEE Access (2019) 7:150037–50. doi:10.1109/access.2019.2946946
45. Elzaki TM. The New Integral Transform Elzaki Transform. Glob J Pure Appl Math (2011) 7(1):57–64.
46. Khalid M, Sultana M, Zaidi F, Arshad U. Application of Elzaki Transform Method on Some Fractional Differential Equations. Math Theor Model (2015) 5(1):89–96.
47. Elzaki TM. Elzaki and Sumudu Transforms for Solving Some Differential Equations. Glob J Pure Appl Mathematics (2012) 8(2).
48. He W, Chen N, Dassios I, Shah NA, Chung JD. Fractional System of Korteweg-De Vries Equations via Elzaki Transform. Mathematics (2021) 9(6):673. doi:10.3390/math9060673
49. Kalavathi A, Kohila T, Upadhyaya LM. On the Degenerate Elzaki Transform*. Bull Pure Appl Sci Sect E Math Stat E (2021) 40e:99–107. doi:10.5958/2320-3226.2021.00010.2
50. Din A, Li Y, Khan FM, Khan ZU, Liu P. On Analysis of Fractional Order Mathematical Model of Hepatitis B Using Atangana–Baleanu Caputo (ABC) Derivative. Fractals (2022) 30(01):2240017. doi:10.1142/s0218348x22400175
51. Din A, Li Y, Yusuf A, Ali AI. Caputo Type Fractional Operator Applied to Hepatitis B System. Fractals (2021) 30:2240023. doi:10.1142/S0218348X22400230
52. Din A, Khan A, Zeb A, Sidi Ammi MR, Tilioua M, Torres DFM. Hybrid Method for Simulation of a Fractional COVID-19 Model with Real Case Application. Axioms (2021) 10(4):290. doi:10.3390/axioms10040290
53. Liu P, Rahman Mu., Din A. Fractal Fractional Based Transmission Dynamics of COVID-19 Epidemic Model. Computer Methods Biomech Biomed Eng (2022) 1–18. doi:10.1080/10255842.2022.2040489
54. Liu P, Rahman Mu., Din A. Fractal Fractional Based Transmission Dynamics of COVID-19 Epidemic Model. Computer Methods Biomech Biomed Eng (2022) 1–18. doi:10.1080/10255842.2022.2040489
55. Mustahsan M, Younas HM, Iqbal S, Rathore S, Nisar KS, Singh J. An Efficient Analytical Technique for Time-Fractional Parabolic Partial Differential Equations. Front Phys (2020) 8:131. doi:10.3389/fphy.2020.00131
56. Shah R, Farooq U, Khan H, Baleanu D, Kumam P, Arif M. Fractional View Analysis of Third Order Kortewege-De Vries Equations, Using a New Analytical Technique. Front Phys (2020) 7:244. Mohand decomposition method. doi:10.3389/fphy.2019.00244
57. Ali KK, Dutta H, Yilmazer R, Noeiaghdam S. On the New Wave Behaviors of the Gilson-Pickering Equation. Front Phys (2020) 8:54. doi:10.3389/fphy.2020.00054
58. Korpinar Z, Tchier F, Inc M. On Optical Solitons of the Fractional (3+1)-Dimensional NLSE with Conformable Derivatives. Front Phys (2020) 8:87. doi:10.3389/fphy.2020.00087
Keywords: Elzaki transformation, decomposition method, nonlinear fractional partial differential equations, analytical method, nonlinear systems, absolute error, Adomian polynomials
Citation: Khan Q, Khan H, Kumam P, Hajira and Sitthithakerngkiet K (2022) The Fractional Investigation of Some Dynamical Systems With Caputo Operator. Front. Phys. 10:895451. doi: 10.3389/fphy.2022.895451
Received: 13 March 2022; Accepted: 04 April 2022;
Published: 30 May 2022.
Edited by:
Vasilios Zarikas, University of Thessaly, GreeceReviewed by:
Anwarud Din, Sun Yat-sen University, ChinaHaci Mehmet Baskonus, Harran University, Turkey
Copyright © 2022 Khan, Khan, Kumam, Hajira and Sitthithakerngkiet. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Poom Kumam, cG9vbS5rdW1Aa211dHQuYWMudGg=
 Qasim Khan1
Qasim Khan1 Hassan Khan
Hassan Khan Poom Kumam
Poom Kumam