The Qubit Fidelity Under Different Error Mechanisms Based on Error Correction Threshold

Quantum error correction is a crucial step to realize large-scale universal quantum computing, and the condition for realizing quantum error correction is that the error probability of each operation step must below some threshold. This requires that the qubits’ quality and the quantum gates precision can reach a certain level experimentally. We firstly discuss the mechanism of quantum errors: the precision of quantum gates corresponds to unitary operator errors, and the quality of qubits is attributed to decoherence. Then, according to the threshold of the surface code error correction, we proved the minimum of quantum gate fidelity should not be less than 1 − p with the error probability p, and found the natural decoherence time of qubits that can be used for error correction. This provides some kind of theoretical supports for qubits preparation and performing quantum operations experimentally.

1 Introduction

As one of the Frontier fields in the post-Moore’s Law era, quantum computing has received extensive attention from physicists, information scientists, and cryptographers. There are two main reasons. First, The spatial scale of classical computer chips has approached the scale of quantum physics. The classical laws are no longer applicable in such scale, which requiring the support of quantum theory. Second, quantum algorithms based on quantum systems can reduce the computing complexity of difficult problems, to achieve computational acceleration even exponentially, such as Shor’s algorithm [1,2], Grover’s algorithm [3,4], etc.

However, the main difficulty in the current quantum computing experiments is that it is hard to achieve large-scale qubits integration, because of the decoherence, noise in channels, and crosstalk between qubits, and so on [5,6]. Since practical universal quantum algorithms require large-scale fault-tolerant quantum computing platforms, the current stage in the field of quantum computing is to demonstrate and practicalize the quantum superiority of Noisy Intermediate Scale Qubits quantum computing [7,8]. Quantum error correction is still the most technical step that needs to be overcome and improved. If error correction is not carried out, quantum circuit will accumulate errors until the correct result cannot be obtained. The commonly used error correction scheme that can be implemented at present includes surface code (two-dimensional topological quantum error correction) [9,10]. Gidney et al. estimated that the time to crack 2048-bit RSA by executing the Shor’s algorithm on the superconducting circuits platform using the surface code is about 8 h [11], however the qubits overhead reaches 20 millions. Gouzien et al. took advantage of a 3D-guage color code and the ion trap quantum computing to reduce the qubits overhead to 13,436 at the cost of a slight increase in execution time to 177 days [12].

It can be seen that different quantum error correction schemes will have a certain impact on the overhead of quantum circuits, and will also produce different error probability thresholds p_th. This threshold p_th will further impose a constraint on the fidelity of qubits and quantum operations, which is also the focus of our work. If we want to go further in the development of quantum error correction, we need a more accurate understanding and deeper exploration of the error mechanism of qubits.

Although error correction schemes based on error syndrome detection don’t require us to identify the source of errors for each qubit, but only need the statistical probability of errors. However, during the preparation of required qubits and quantum gates, their fidelity and decoherence characteristic time should be used as reference standard. Therefore, according to the error probability threshold required by error correction schemes, after clarifying the error generation mechanism, the theoretical calibration of the corresponding standard is also an important part of overcoming the bottleneck in quantum error correction experiments.

In this work, we explore the different sources of single-qubit errors, and calculate the fidelity of quantum operations and decoherence respectively according to the surface code probability threshold p_th. For the single-qubit error correction model, the probability of detecting an error should be a comprehensive characterization of the two error sources. The conclusions of this work provide a theoretical basis for the fidelity criteria of the qubits preparation and quantum operations in experiments.

2 The Source of Qubit Errors

As a quantum system existing in the environment, qubits will inevitably interact with the surrounding environment to exchange information. This is a loss of information for qubits, and it will also bring errors to the result of quantum circuits.

We can use the fidelity between the initial and final states of a quantum system to measure the degree of information retention. But since the measurement of fidelity requires ensemble-based measurement methods such as quantum state tomography, it is not suitable to do the fidelity measurement in quantum circuits. Therefore, error correction schemes usually directly use a parity-like error characterization method to monitor errors and avoid destroying data qubits.

Specifically, the model of the interaction between a quantum system and the environment can be described by the operation-sum representation. First, the total state of the quantum system and the environment ρ = ρ₀ ⊗ ρ_env, ρ₀ represents the initial state density matrix of the quantum system, and ρ_env represents the density matrix of the environment. According to the Schmidt purification, the initial state ρ_env of the environment can always be written as a pure state, which means ${\rho }_{\text{env}}=\left|e_0\right.⟩\left.⟨e_0\right|$. Wherein $\{\left|e_k\right.⟩\}$ is a set of basis for the environment, and $\left|e_0\right.⟩$ is the initial state. Then after the whole system experiences evolution U, the final state of the quantum system $\epsilon (\rho )={\mathrm{Tr}}_{\text{env}}\left[U\left({\rho }_0\otimes \left|e_0\right.⟩\left.⟨e_0\right|\right)U^{†}\right]$, that is, ρ experiences the evolution of U, and then the environment is traced to obtain the reduced density matrix of the quantum system,

$\epsilon \left(\rho \right)=\sum _k\left|e_k\right.⟩\left.⟨e_k\right|\cdot \left[U\left({\rho }_0\otimes \left|e_0\right.⟩\left.⟨e_0\right|\right)U^{†}\right]=\sum _k{E}_k{\rho }_0{E}_k^{†},(1)$

where $E_k=\left.⟨e_k\right|U\left|e_0\right.⟩$, represents the matrix element of the U under the environmental representation, and acts on the quantum system [13].

For the quantum system, the fidelity F after the evolution is

$F\left({\rho }_0,\epsilon \left(\rho \right)\right)={\mathrm{Tr}}^2\left(\sqrt{\sqrt{\epsilon \left(\rho \right)}{\rho }_0\sqrt{\epsilon \left(\rho \right)}}\right).(2)$

In fact, after the partial tracing of the environment Tr_env, all we care about is the difference between the initial and final states of the quantum system, that is, what kind of errors will be caused. The details of the evolution process don’t need us to care about. The operator E has also become a reduced operator that only acts on the quantum system.

Next, we can judge whether E is unitary or not to classify the errors occurred from the quantum system. For the sake of simplicity, we take one qubit as the quantum system in quantum computing. Specifically, it is divided into two categories:

Unitary operator E. The operator E is unitary and can preserve the trace of the quantum state density matrix. This type of error can keep the qubit still in pure state. We know that under ideal conditions, the quantum state required for quantum computing should be a pure state, and the quantum operation should be a unitary operation¹. If the introduced error is also a unitary operator, this means that the effect of the error did not decoherent the quantum state. From the perspective of the Bloch sphere, it’s just that the state vector produces some unexpected rotations on the spherical surface.

Considering the actual operation, this kind of error mainly comes from the quantum gate. Whether it’s because the operator’s approximation can’t reach 100% accuracy, or because of environmental influences that make the quantum gates behave inaccurately, such kind of errors can be translated into single-qubit rotations on the Bloch sphere.

Non-unitary operator E. The operator E evolves the qubit from a pure state to a mixed state. This type of error can be understood as what we usually say, decoherence. Compared to the first type of error, the effects of decoherence are more common. The damping of amplitude and phase is usually due to the contact of the qubit with the environment (various types of noise). Since the qubit has become a mixed state, part of the information contained in it has changed from the form of quantum superposition to a classical mixture, which has irreversibly leaked into the environment.

From the perspective of the Bloch sphere, the decayed state vector shrinks from the surface to the inside of the sphere. The decay of the state vector can be decomposed into transverse relaxation and longitudinal relaxation [14,15]. For detailed discussion and calculation, please refer to Section 3.2.

Although from the perspective of error correction, it seems that we do not need to care about the cause of the errors, but only need to monitor the errors and take corresponding error correction operations to ensure the reliability of the circuit. However, in experiments, various quantum computing platforms using different materials and principles may have very different qubit properties and types of quantum operations. Our research conclusions can provide a unified theoretical standard for different platforms, and can obtain more precise qubit decoherence fidelity and quantum operation fidelity according to different error correction schemes and error correction standards. Therefore, the research on the error mechanism of qubits is of certain significance.

For the widely used surface code, since the error correction circuit increases the circuit depth and the number of qubits, its error threshold can also be divided into different classes [9]. Specifically, according to the surface code error correction circuit (Figure 1A), Fowler et al. divides the error thresholds into p_th,0, p_th,1, and p_th,2. These three levels of thresholds have different degrees of sensitivity to the logic error rate of the error correction circuit, and we will select the appropriate class of threshold as constraint according to the expression of fidelity.

FIGURE 1

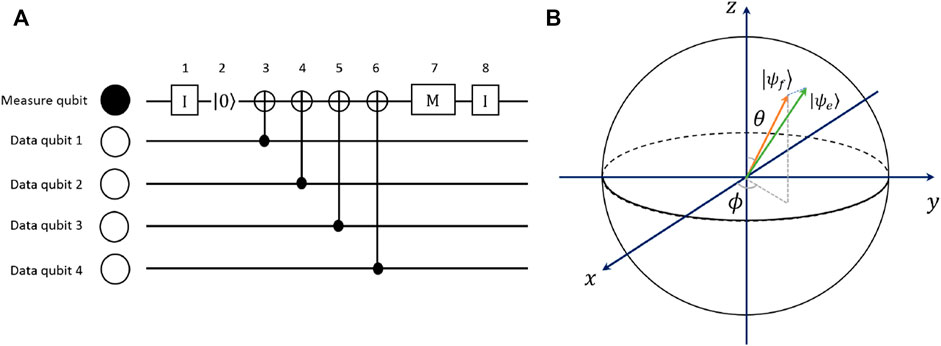
FIGURE 1. (A) Single cycle logical circuit that detects X errors in the surface code. The solid circles in the circuit represent auxiliary qubits, and the open circles represent data qubits. A single cycle contains 8 steps, including single-qubit gate, initialization, C-NOT gate, and measurement; (B) Bloch sphere representation of a single qubit. |ψ_f⟩ represents the quantum state after the ideal quantum operation, |ψ_e⟩ is the final state after the error occurs. The angle between the projection of the x − y plane and the x-axis is the phase angle ϕ, and the angle between the state vector and the z-axis is the polar angle θ.

Next, we will show the correlation between different quantum superposition initial states, error probability and fidelity for single qubit. And then theoretically deduce and calculate the qubit fidelity and quantum operation fidelity of the above two error-generating mechanisms, and find the corresponding theoretical limit under the error probability threshold.

3 Error Probability and Fidelity of Single Qubit

For any single-qubit pure state, we denote an arbitrary superposition state of |0⟩ and |1⟩ as |ψ⟩ = α|0⟩ + β|1⟩, where the normalization condition is |α|² + |β|² = 1. In a Bloch sphere with the radius of 1, |ψ⟩ is the radial vector on the sphere, taking $\alpha =\cos \frac{\theta }{2}$, $\beta =e^{i\varphi }\sin \frac{\theta }{2}$, and |ψ⟩ is expressed as

$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle =\cos \frac{\theta }{2}|0\rangle +e^{i\varphi }\sin \frac{\theta }{2}|1\rangle ,(3)$

where θ is the polar angle and ϕ is the azimuth angle. We usually use the density matrix of state ρ = |ψ⟩⟨ψ| to calculate [13].

$\rho =\left(\begin{array}{cc}\hfill |\alpha {|}^2\hfill & \hfill \alpha {\beta }^{*}\hfill \\ \hfill {\alpha }^{*}\beta \hfill & \hfill |\beta {|}^2\hfill \end{array}\right)=\frac{1}{2}\left(\begin{array}{cc}\hfill 1+\cos \theta \hfill & \hfill e^{-i\varphi }\sin \theta \hfill \\ \hfill e^{i\varphi }\sin \theta \hfill & \hfill 1-\cos \theta \hfill \end{array}\right).(4)$

For a error correction process, we need to perform error detection and correction for the result after each step. Without loss of generality, we assume that after each unitary operation of quantum computing, the final state |ψ_f⟩ = α|0⟩ + β|1⟩, where f means ‘final’. But due to the error of quantum operation or decoherence caused by noise, the final state becomes |ψ_e⟩, where e means ‘errors’. Compared with |ψ_f⟩, the difference generated by |ψ_e⟩ may originate from one or more reasons, and we will analyze them one by one below.

3.1 The Error of Unitary Operation

The quantum gate operation in the quantum circuit is usually to apply a specific controllable external field to the qubit to control it. There are different type of external field according to the different qubit systems, such as the microwave pulse [16] in the superconducting circuit system, the laser pulse [17] in the ion trap system, and so on. Here we consider the errors that such quantum operations bring to qubits because they cannot be 100% accurate.

For example, a beam of X_π-pulse can rotate the qubit by an angle of π around the x-axis, but due to the insufficient precision, the quantum state actually rotates around the x-axis by π ± δ. Such an error can be understood as an unexpected unitary operation, and equivalent to a rotation of an unknown angle. In fact this unexpectedly angle can be a rotation around any axis, not necessarily the same as the operation rotation. (Figure 1B).

According to the above operations, the single-qubit state can be written as the following process:

1. The initial state undergoes an error-free unitary operation, |ψ_f⟩ = U|ψ₀⟩;

2. The initial state undergoes an unitary operation with errors, |ψ_e⟩ = U′|ψ₀⟩ = U_eU|ψ₀⟩ = U_e|ψ_f⟩.

The qubit undergoes the quantum operation U′ with errors, which is equivalent to the qubit first undergoes the precise operation U, and then undergoes an error operation U_e, and finally becomes the quantum state with error |ψ_e⟩. U_e is also essentially a rotation operation on the Bloch sphere, so it can be decomposed into rotation around x-axis and z-axis, corresponding to the types of X and Z errors that occur in qubits respectively. Besides, the error probability is described by the rotation angle ɛ.

3.1.1 X Errors

$U_x=e^{i\epsilon \cdot {\sigma }_x}=\cos \epsilon \cdot I+i\sin \epsilon \cdot {\sigma }_x$, the probability of error $p_{U_x}={\sin }^2\epsilon$.

After the state |ψ_f⟩ is affected by U_x,

$\begin{array}{cc}\hfill {|{\psi }_e\rangle }_x& =U_x|{\psi }_f\rangle =\left(\cos \epsilon \cdot I+i\sin \epsilon \cdot {\sigma }_x\right)\left(\alpha |0\rangle +\beta |1\rangle \right)\hfill \\ \hfill & =\left(\alpha \cos \epsilon +i\beta \sin \epsilon \right)|0\rangle +\left(\beta \cos \epsilon +i\alpha \sin \epsilon \right)|1\rangle ,\hfill \end{array}(5)$

Since |ψ_f⟩ and |ψ_e⟩_x are pure states, their density matrices are ρ_f = |ψ_f⟩⟨ψ_f|, ρ_e,x = |ψ_e⟩_x⟨ψ_e| respectively. And the fidelity F_x under the X error of probability p is

$F_x\left({\rho }_f,{\rho }_{e,x}\right)={\mathrm{Tr}}^2\left(\sqrt{\sqrt{{\rho }_{e,x}}{\rho }_f\sqrt{{\rho }_{e,x}}}\right)=\mid {{\left.\right|}_x⟨{\psi }_e\mid {\psi }_f⟩|}^2.(6)$

Bringing in the |ψ_f⟩ and |ψ_e⟩, we can get

$\begin{array}{cc}\hfill F_x\left({\rho }_f,{\rho }_{e,x}\right)& ={\left(|\alpha {|}^2+|\beta {|}^2\right)}^2{\cos }^2\epsilon +{\left(\alpha {\beta }^{*}+{\alpha }^{*}\beta \right)}^2{\sin }^2\epsilon \hfill \\ \hfill & ={\cos }^2\epsilon +{\sin }^2\theta \cdot {\cos }^2\varphi \cdot {\sin }^2\epsilon .\hfill \end{array}(7)$

We can see that the fidelity $F_x\left({\rho }_f,{\rho }_{e,x}\right)$ is not only related to the error rotation angle ɛ, but also to the θ and ϕ angles of the quantum state |ψ_f⟩. This means that even the same error will have different effects on different quantum states. Figure 2A plots the relationship between $F_x\left({\rho }_f,{\rho }_{e,x}\right)$ and ɛ, θ (For the convenience of drawing, we take ϕ = 0.)

FIGURE 2

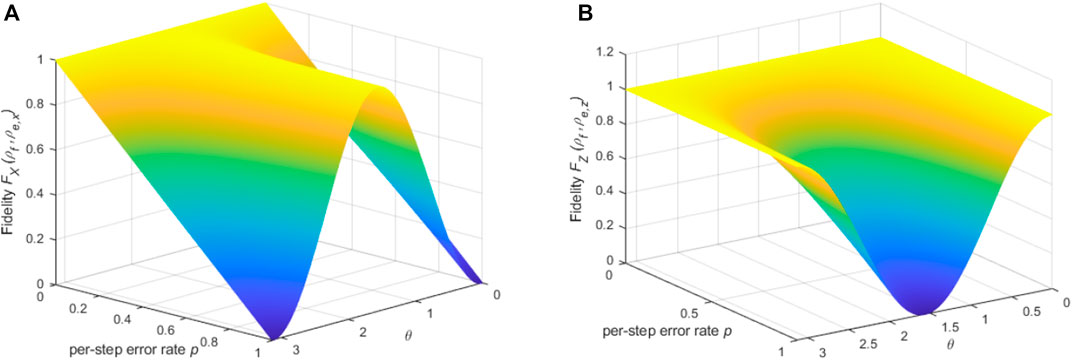
FIGURE 2. (A) For U_x errors, the qubit fidelity $F_x\left({\rho }_f,{\rho }_{e,x}\right)$ is a function of the error probability p and the polar angle θ (ϕ is set to be 0); (B) For U_z errors, the qubit fidelity $F_z\left({\rho }_f,{\rho }_{e,z}\right)$ is a function of the error probability p and the polar angle θ.

3.1.2 Z Errors

$U_z=e^{i\epsilon \cdot {\sigma }_z}=\cos \epsilon \cdot I+i\sin \epsilon \cdot {\sigma }_z$, the probability of error $p_{U_z}={\sin }^2\epsilon$.

The same process as X errors,

$\begin{array}{cc}\hfill {|{\psi }_e\rangle }_z& =U_z|{\psi }_f\rangle =\left(\cos \epsilon \cdot I+i\sin \epsilon \cdot {\sigma }_z\right)\left(\alpha |0\rangle +\beta |1\rangle \right)\hfill \\ \hfill & =\left(\cos \epsilon +i\sin \epsilon \right)\alpha |0\rangle +\left(\cos \epsilon -i\sin \epsilon \right)\beta |1\rangle .\hfill \end{array}(8)$

After the Z error for probability p, the density matrix becomes ρ_e,z = |ψ_e⟩_z⟨ψ_e|, and the fidelity

$F_z\left({\rho }_f,{\rho }_{e,z}\right)=\mid {{\left.\right|}_z⟨{\psi }_e\mid {\psi }_f⟩|}^2=\frac{1}{2}\left(1+{\cos }^2\theta +{\sin }^2\theta \cdot \cos 2\epsilon \right).(9)$

It can be found that for Z errors, the fidelity ρ_e,z = |ψ_e⟩_z⟨ψ_e| is not affected by the phase angle ϕ, but is still affected by the polar angle θ, see Figure 2B.

3.2 Natural Decoherence

We analyzed the case where the error is a unitary operator above, which ensures that the qubit is still pure. And because of the unitarity of the operator, unitary errors are in principle completely reversible. But if the error causes the qubit to evolve from a pure state to a mixed state, its information will be irreversibly lost, usually described as decoherence caused by the environment.

Under the conditions of Born approximation (weak coupling between quantum system and environment) and Markovian approximation (each noise is temporally uncorrelated), the decoherence problem of quantum system is usually described by the master equation of density matrix (quantum Liouville equation) [18].

${\partial }_t\rho =-\frac{i}{\hslash }\left[H,\rho \right]+\sum _k{\mathrm{\Gamma }}_k{\mathcal{L}}_k\left[\rho \right],(10)$

where H represents the coherent dynamic evolution Hamiltonian, and ${\mathcal{L}}_k[\rho ]=\left(\left[{\mathcal{L}}_k,\rho {\mathcal{L}}_k^{†}\right]+\left[{\mathcal{L}}_k\rho ,{\mathcal{L}}_k^{†}\right]\right)/2$ represents the incoherent evolution. ${\mathcal{L}}_k$ is the Lindblad quantum transition operator, which is used to describe the effect of different decoherence effects on the quantum state ρ, and Γ_k represents the rate (influence degree) of the corresponding ${\mathcal{L}}_k$.

The research on the master equation and multi-body quantum system is complicated, and we can refer to [19,20] for details. In universal quantum computing, any quantum operation can be decomposed into a combination of single-qubit gates and two-qubit gates. So theoretically only the decoherence of at most two bodies need to be considered in quantum computing. In this subsection, we first consider the single-qubit decoherence problem.

In theory, decoherence occurs in the entire process of quantum computing, that is, the entire process from initialization, quantum gate operation, to measurement and memory. In the stage without quantum operations, we can set the Hamiltonian H of the coherent evolution part to 0. It means that in such stage the qubit will undergo natural decoherent decay. Although such model is relatively naive, it can also correspond to the process of qubit storage and preparation, which is of great significance to quantum computing.

For the natural decoherence model of single qubit, we also categorize the types of errors [15]:

Amplitude damping. The conversion between |0⟩⇌|1⟩ is called amplitude damping. This includes the transition of |0⟩ → |1⟩ and the decay of |1⟩ → |0⟩. However, the probability of a spontaneous transition in a quantum system in equilibrium is negligible compared to the probability of decay [21]. During longitudinal relaxation, single qubit exchange energy with the environment, resulting in irreversible information leakage.

Dephasing. The decay of the phase angle ϕ is called pure dephasing. Pure dephasing does not exchange energy with the environment, so it is in principle reversible. In theory, the dynamic decoupling method can completely eliminate the pure dephase decay [22], and in practice scientists are trying to achieve it.

For the master equation solution of the above decoherence model, it can be described by a simplified form of the Bloch-Redfield density matrix [15,23,24],

${\rho }_{\text{B\hspace{0.17em}R}}=\left(\begin{array}{cc}\hfill 1+\left(|\alpha {|}^2-1\right)e^{-{\mathrm{\Gamma }}_{1}t}\hfill & \hfill \alpha {\beta }^{*}{e}^{-{\mathrm{\Gamma }}_{2}t}\hfill \\ \hfill {\alpha }^{*}\beta e^{-{\mathrm{\Gamma }}_{2}t}\hfill & \hfill |\beta {|}^2{e}^{-{\mathrm{\Gamma }}_{1}t}\hfill \end{array}\right),(11)$

The operator interaction strength Γ_k represents the decay rate, the amplitude damping rate is Γ₁, and the transverse decoherence rate is Γ₂ = Γ₁/2 + Γ_ϕ, which includes both amplitude damping and pure dephasing effects. The probability amplitude of |1⟩ is attenuated from |β|² to $|\beta {|}^2{e}^{-{\mathrm{\Gamma }}_{1}t}$, and the probability amplitude of |0⟩ is $1+\left(|\alpha {|}^2-1\right)e^{-{\mathrm{\Gamma }}_{1}t}$; the decay rate of the off-diagonal term is $e^{-{\mathrm{\Gamma }}_{2}t}$.

In the standard Bloch-Redfield model, the off-diagonal term also has a frequency detuning attenuation term e^−iδωt, which represents the attenuation caused by the frequency detuning between the qubit and the control system. The Hamiltonian H is set to 0, so the detuning term doesn’t need to be considered.

In addition, the standard Bloch-Redfield model cannot still accurately describe the decoherence of superconducting qubits. The off-diagonal term in the density matrix should also normally contain the non-exponential decay term $e^{-{\chi }_N\left(t\right)}$, which can describe 1/f-type noise. For the sake of simplicity, we do not consider the non-exponential decay term here.

With the decoherent density matrix, we compute the fidelity $F_{\text{dec}}\left({\rho }_f,{\rho }_{BR}\right)$

$\begin{array}{cc}\hfill F_{\text{dec}}\left({\rho }_f,{\rho }_{\text{B\hspace{0.17em}R}}\right)& ={\mathrm{Tr}}^2\left(\sqrt{\sqrt{{\rho }_{\text{B\hspace{0.17em}R}}}{\rho }_f\sqrt{{\rho }_{\text{B\hspace{0.17em}R}}}}\right)\hfill \\ \hfill & ={\left(\sqrt{|\alpha {|}^2\left[e^{-{\mathrm{\Gamma }}_{1}t}\left(|\alpha {|}^2-1\right)+1\right]}+|\beta {|}^2\sqrt{e^{-{\mathrm{\Gamma }}_{1}t}}\right)}^2,\hfill \end{array}(12)$

Bring $\alpha =\cos \frac{\theta }{2}$ and $\beta =e^{i\varphi }\sin \frac{\theta }{2}$ in, we can get

$\begin{array}{cc}\hfill F_{\text{dec}}\left({\rho }_f,{\rho }_{\text{B\hspace{0.17em}R}}\right)=& {\cos }^2\frac{\theta }{2}-{\sin }^2\frac{\theta }{2}\cdot \cos \theta \cdot e^{-{\mathrm{\Gamma }}_{1}t}\hfill \\ \hfill & +2{\sin }^2\frac{\theta }{2}\cdot \left|\cos \frac{\theta }{2}\right|\cdot \sqrt{e^{-{\mathrm{\Gamma }}_{1}t}-{\sin }^2\frac{\theta }{2}\cdot e^{-2{\mathrm{\Gamma }}_{1}t}}.\hfill \end{array}(13)$

It can be found that there is no related term of $e^{-{\mathrm{\Gamma }}_{2}t}$ in the fidelity $F_{\text{dec}}\left({\rho }_f,{\rho }_{\text{B\hspace{0.17em}R}}\right)$. Since Γ₂ = Γ₁/2 + Γ_ϕ, it means that $F_{\text{dec}}\left({\rho }_f,{\rho }_{\text{B\hspace{0.17em}R}}\right)$ is not affected by pure dephasing, which also reflects the reversibility of pure dephasing in the decoherence process. The relationship between $F_{\text{dec}}\left({\rho }_f,{\rho }_{\text{B\hspace{0.17em}R}}\right)$ and the polar angle θ, the amplitude damping probability $1-e^{-{\mathrm{\Gamma }}_{1}t}$ is shown in Figure 3.

FIGURE 3

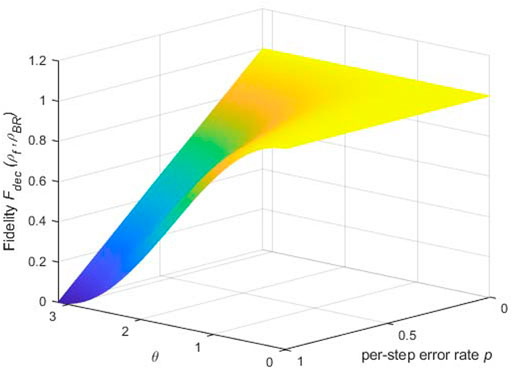
FIGURE 3. For natural decoherence, the quantum state fidelity $F_{\text{dec}}\left({\rho }_f,{\rho }_{\text{B\hspace{0.17em}R}}\right)$ as a function of decay probability p and the polar angle θ.

For different quantum states ρ_f, the effect of natural decoherence on fidelity is also different. The larger the polar angle θ, the greater the effect of amplitude damping decoherence on fidelity, and vice versa.

4 Surface Code Error Probability Threshold and the Minimum Fidelity

Surface codes have become widely used error correction schemes in various experimental platforms due to their neighbor interactions and the lattice structure that is easy to expand. In the field of error correction, the threshold theorem is the basic principle that guarantees the effectiveness of error correction schemes. Error corrections need additional auxiliary qubits and gates, which will introduce new errors. If there are too many additional errors introduced by the error correction circuits, the errors will continue to accumulate during the error correction cycle. Therefore, we need to require the error probability of the qubits and operations to be lower than a certain threshold p_th, so that the error probability of the final result of the circuit can be reduced by continuously implementing the error correction cycle [13].

For the X error correction circuit of the surface code (see Figure 1A), there are a total of 8 basic steps, including single-qubit gates, two-qubit gates, measurement and other operations. Considering these 8 steps comprehensively, error probability threshold is p_th = 0.0057 for each step [9].

The author also divided the errors into three classes, and studied the sensitivity of each type of errors to the threshold: Class0 represents the single-qubit error of the data qubit, p_th,0≅0.043; Class1 represents the initialization of the auxiliary qubit, H gate and measurement errors, p_th,1≅0.12; Class3 represents two-qubit gate errors, p_th,2≅0.0125. However, since these types of error threshold are larger than the overall threshold p_th when considered separately, we take p_th = 0.0057 for calculation.

4.1 Unitary Errors

4.1.1 X Errors

Assuming that only X errors occur, the error probability threshold p_th = sin²ɛ, $\epsilon =\arcsin \sqrt{p_{\text{th}}}\cong 0.0756$. According to Eq. 8, we can get the fidelity when the error probability p is between 0 ∼ 0.0057,

$F_x\left({\rho }_f,{\rho }_{e,x}\right)=1-\left(1-{\sin }^2\theta \cdot \cos \varphi \right)p.(14)$

Still taking ϕ = 0, the function curve is shown in Figure 4A.

FIGURE 4

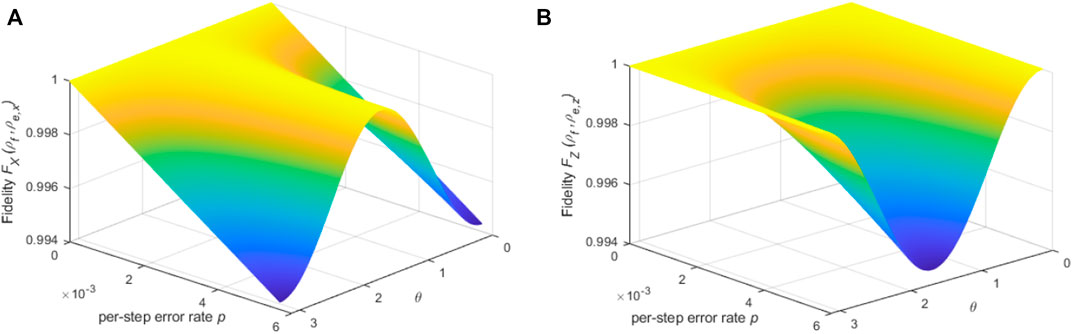
FIGURE 4. (A) The value range of fidelity $F_x\left({\rho }_f,{\rho }_{e,x}\right)$ after limiting the error probability p to the surface code error threshold range; (B) Under the same error probability value range, the value range and the gradient trend of $F_z\left({\rho }_f,{\rho }_{e,z}\right)$.

It is easy to know that the minimum value of $F_x\left({\rho }_f,{\rho }_{e,x}\right)$ is obtained at θ = 0, π. At this time, the quantum state is at the two poles of the Bloch sphere, and the X error will completely flip the qubit. If p = p_th, then for |ψ_f⟩ = |0⟩ or |ψ_f⟩ = |1⟩, the minimum fidelity $F_x{\left({\rho }_f,{\rho }_{e,x}\right)}_{\text{min}}=1-p_{\text{th}}=0.9943$. That is, the minimum fidelity of unitary operation under X error is 99.43%.

4.1.2 Z Errors

On the other hand, assuming that only Z errors occur, we bring in $\epsilon =\arcsin \sqrt{p}$,

$\begin{array}{cc}\hfill F_z\left({\rho }_f,{\rho }_{e,z}\right)& =\frac{1}{2}\left(1+{\cos }^2\theta +{\sin }^2\theta \cdot \cos 2\epsilon \right)\hfill \\ \hfill & =1-{\sin }^2\theta \cdot p,\hfill \end{array}(15)$

We can also get the function curve of $\left({\rho }_f,{\rho }_{e,z}\right)$ when 0 < p ≤ 0.0057, as shown in Figure 4B.

From Eq. 15, if θ = 0 or π, we have sin θ = 0, $F_z\left({\rho }_f,{\rho }_{e,z}\right)$ is independent of p, and Z error will not affect the fidelity. In fact, θ = 0, π corresponds to |0⟩ and |1⟩, and the Z error is to rotate the quantum state around the z axis, which naturally does not change these two quantum states. If 0 < θ < π, the minimum fidelity value when θ = π/2 is $F_z{\left({\rho }_f,{\rho }_{e,z}\right)}_{\text{min}}=1-p_{\text{th}}$, which is also 99.43%.

4.1.3 Rotation Errors Around an Arbitrary Axis m by an Angle of ɛ

Through the discussion of X and Z errors, we find that the minimum values of their fidelity are the same, although the quantum states when taking the minimum value are different. In fact, we can show that the minimum value of fidelity is 1 − p (or 1 − sin²ɛ) for the error when the state is unexpectedly rotated by ɛ around any axis m.

Proof: From Section 3.1, it can be seen that the final state with error |ψ_m⟩ = U_m|ψ_f⟩, then let $U_m=e^{i\epsilon \cdot {\sigma }_m}$, U_m represents the rotation of ɛ around the m-axis operation, σ_m is the operation of rotating π around the m-axis. ${{\sigma }_m}^2$ means 2π rotation around the m-axis, so there is ${{\sigma }_m}^2=I$. Then the fidelity

$\begin{array}{cc}\hfill F\left(|{\psi }_f\rangle ,\left|{\psi }_m\right.⟩\right)& ={\left|⟨{\psi }_f\left|U_e\right|{\psi }_f⟩\right|}^2\hfill \\ \hfill & ={\left|⟨{\psi }_f\left|\left(\cos \epsilon \cdot I+i\sin \epsilon \cdot {\sigma }_m\right)\right|{\psi }_f⟩\right|}^2\hfill \\ \hfill & ={\cos }^2\epsilon +{\sin }^2\epsilon {\left|⟨{\psi }_f\left|{\sigma }_m\right|{\psi }_f⟩\right|}^2\hfill \\ \hfill & =1-p+p{\left|⟨{\psi }_f\left|{\sigma }_m\right|{\psi }_f⟩\right|}^2.\hfill \end{array}(16)$

When $⟨{\psi }_f\left|{\sigma }_m\right|{\psi }_f⟩=0$, we have $F{\left(\left|{\psi }_f\right.⟩,\left|{\psi }_m\right.⟩\right)}_{\text{min}}=1-p$; and when $⟨{\psi }_f\left|{\sigma }_m\right|{\psi }_f⟩=1$, $F{\left(\left|{\psi }_f\right.⟩,\left|{\psi }_m\right.⟩\right)}_{\text{max}}=1$. From the perspective of the Bloch sphere, when the fidelity gets the maximum, the qubit state vectors just falls on the m-axis and we marked them as |0⟩_m and |1⟩_m. At this point, the operation of rotating around the m-axis cannot change the quantum state. When the fidelity gets the minimum, the state vector falls on the normal plane n of the m-axis, and we marked them as |ψ_m⟩_max, see Figure 5.

FIGURE 5

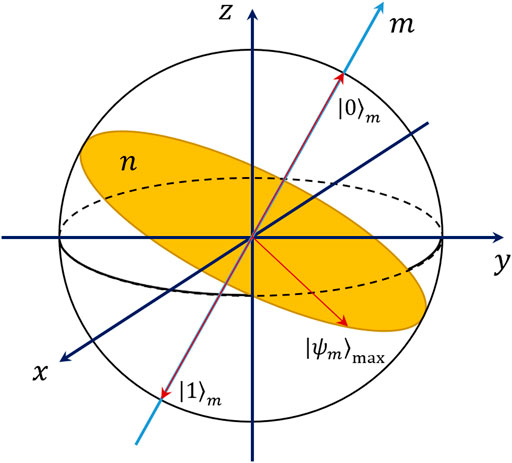
FIGURE 5. For the rotation operation of any axis m, its error operator is U_m. The maximum of fidelity $F\left(\left|{\psi }_f\right.⟩,\left|{\psi }_m\right.⟩\right)$ is obtained when the quantum state vector coincides with the m-axis, and we mark the states as $\left|0_m\right.⟩$ and $\left|1_m\right.⟩$; And the minimum of $F\left(\left|{\psi }_f\right.⟩,\left|{\psi }_m\right.⟩\right)$ is obtained when the state falls on the normal plane n of the m-axis, we mark it as ${\left|{\psi }_m\right.⟩}_{\text{max}}$.

The m-axis is also easy to determine if we know |ψ_f⟩ and |ψ_m⟩. Take the two points which are the intersection of |ψ_f⟩ and |ψ_m⟩ with the Bloch sphere respectively and connect them. The midpoint of the above line segment and the center of the sphere, these two points can determine the m-axis, which is perpendicular to the above line segment.

Moreover, U_m can be decomposed into rotating ɛ₁ around the x-axis first, and then rotating ɛ₂ around the z-axis, that is $e^{i\epsilon \cdot {\sigma }_m}=e^{i{\epsilon }_2\cdot {\sigma }_z}\cdot e^{i{\epsilon }_1\cdot {\sigma }_x}$. If $|{\psi }_f\rangle =\cos \frac{{\theta }_1}{2}|0\rangle +e^{i{\varphi }_1}\sin \frac{{\theta }_1}{2}|1\rangle$, and $|{\psi }_m\rangle =\cos \frac{{\theta }_2}{2}|0\rangle +e^{i{\varphi }_2}\sin \frac{{\theta }_2}{2}|1\rangle$, we can have

$\begin{array}{cc}\hfill |{\psi }_m\rangle =e^{i\epsilon \cdot {\sigma }_m}|{\psi }_f\rangle & =e^{i{\epsilon }_2\cdot {\sigma }_z}\cdot e^{i{\epsilon }_1\cdot {\sigma }_x}|{\psi }_f\rangle \hfill \\ \hfill & =e^{i\left({\varphi }_2-{\varphi }_1\right)\cdot {\sigma }_z}\cdot e^{i\left({\theta }_2-{\theta }_1\right)\cdot {\sigma }_x}|{\psi }_f\rangle .\hfill \end{array}(17)$

4.2 Natural Decoherence

For the natural decoherent state ρ_BR, the amplitude damping probability $p_{\text{dec}}=1-e^{-{\mathrm{\Gamma }}_{1}t}$. If the characteristic time T₁ is fixed, according to the error probability threshold pth, we can obtain the longest lifetime τ = −T₁ ln pth that the qubit can be used for quantum computing.

According to the work of Krantz et al. [15], taking T₁ = 85 μs, we can get τ = 0.489 μs. This means that a superconducting qubit with a amplitude damping lifetime of 85 μs has 489 ns available for quantum operations before decoherence. This time seems very short, but it is undoubtedly sufficient for a superconducting system with a single operation time of 10 ∼ 100 ns.

Similarly, we take the threshold p_th = 0.0057 of the surface code scheme, then there is $0.9943<e^{-{\mathrm{\Gamma }}_{1}t}<1$, and the relationship between $F_{\text{dec}}\left({\rho }_f,{\rho }_{\text{B\hspace{0.17em}R}}\right)$ and the polar angle θ and time t is shown in Figure 6.

FIGURE 6

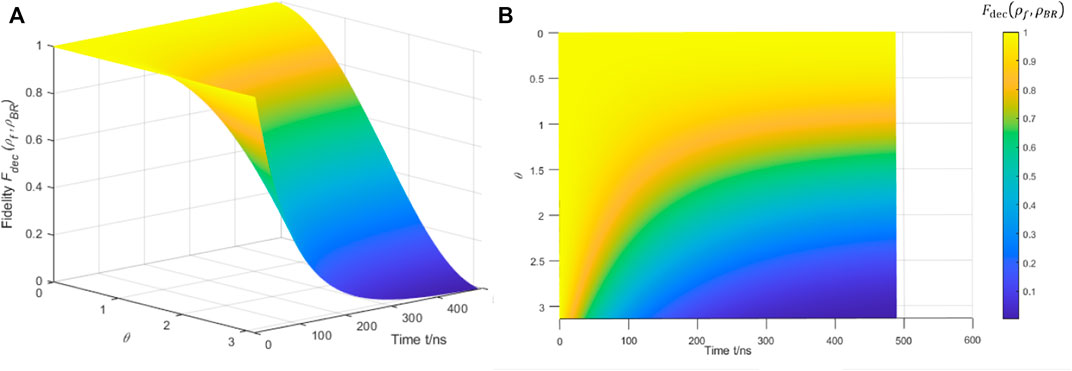
FIGURE 6. (A) The amplitude damping probability p_dec is limited in the surface code error threshold range. This figure shows the value range and gradient trend of the quantum state fidelity $F_{\text{dec}}\left({\rho }_f,{\rho }_{\text{B\hspace{0.17em}R}}\right)$; (B) The two-dimensional drawing of (A).

It can be found that the fidelity is minimized when θ = π, $F_{\text{dec}}{\left({\rho }_f,{\rho }_{\text{B\hspace{0.17em}R}}\right)}_{\text{min}}=e^{-{\mathrm{\Gamma }}_{1}t}=0.9943$.

5 Discussion

From the analysis above, we studied the fidelity of quantum unitary operations and natural decoherence under surface code threshold requirements. But in each case, we assumed that only this type of error occurs, and in practice the operation errors and decoherence would occur at the same time. Therefore, the actual error probability $p=1-\left(1-p_U\right)\left(1-p_{\text{dec}}\right)=p_U+p_{\text{dec}}-p_U\cdot p_{\text{dec}}$, since 0 < p_U, p_dec < 1, so p > p_U and also p > p_dec. Given all this, the actual quantum operation fidelity should be larger than the above calculated value of 99.43%, and the actual available decoherence time should be shorter than 489 ns.

At the same time, the threshold theorem guarantees that the circuit can correct errors by continuously increasing the number of cycles when the error probability is lower than the threshold. However, the closer the error probability is to the threshold, the more cycles are required. Due to the limited quantum resources (number of qubits, number of quantum gates), it is impossible for us to require that the actual error probability only just reaches the threshold, which will cause enormous amount of qubits. Therefore, there is a recognized fidelity standard of 99.9% (the error probability per step is 10^–3), which is assumed in some articles [9,11]. So that for the surface code, the number of physical qubits can be controlled between 10³ ∼ 10⁴ to encode a logical qubit.

For different quantum error correction codes, their error probability thresholds are different. Therefore the quantum gate fidelity and coherence time required for error correction will also be different. This will further affect the number of cycles of the error correction code, which is reflected in the required quantum resources (the corresponding amount of qubits and quantum operations). Based on our above processing method, the minimum required gate fidelity and qubit coherence time can be calculated by just obtaining the error probability threshold of the error correction code. Then according to the minimum standard, we can seek the balance between the number of quantum resources and their fidelity, which provides theoretical standards for experiments.

Two-qubit gate errors. In the previous sections, we only discussed the fidelity of single-qubit operations, but the set of general quantum gates also includes two-qubit gates, such as C-NOT gates. For a two-qubit gate, both qubit 1 and qubit 2 will have unitary errors with probability p respectively, resulting in a lower fidelity than single-qubit gate. We can regard the error of two qubits as two independent and unaffected operators’ direct product U_{qubit, 1} ⊗ U_{qubit, 2}, and the research on the fidelity of two-qubit gate is also worthy of our further study focus on.

Decoherence with driven field. In the decoherence part, we only perform the correlation calculation of natural decoherence (let the Hamiltonian H = 0). But decoherence occurs throughout the computing process, including when quantum operations are excuted. When an external field drives the quantum state evolution, decoherence occurs. And this process can be described by the master equation of the density matrix with a time-independent Hamiltonian H.

In quantum computing, single-qubit gate and two-qubit gate are usually fixed rotations rather than time-dependent continuous transformations. So for the master equation, in the part of the Heisenberg evolution ${\partial }_t\rho =-i/\hslash \left[H,\rho \right]$, the Hamiltonian H is time-independent, only ρ evolves with time. The incoherent evolution led by Lindblad operator ${\mathcal{L}}_k$ also affects the evolution of ρ in the master equation, so the qubit decoherence problem with driving field is relatively complicated, but it is also more suitable for studying the decoherence phenomenon during executing quantum operations.

6 Conclusion

In this work, we present a classification discussion about the sources of quantum errors according to the unitarity of the reduced evolutionary operators. For an unitary error, we can understand it as the precision error of the quantum operation. The effect of it is equivalent to the effect of an extra unitary rotation operation, and the quantum operation fidelity can be calculated according to the error probability threshold of the surface code. The non-unitary error can be understood as the decoherence process of qubits. We focus on the situation of natural decoherence, and calculate the qubit coherence duration that can be used for quantum error correction according to the evolution properties of decoherence.

Decoherence time and quantum gate operation fidelity are important parameters in the preparation of qubits and quantum control experimentally. Our work clarifies the mechanism of quantum error sources and provides theoretical support for laboratory technical.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

KL independently did the calculations and wrote the manuscript.

Funding

This work was supported by National Natural Science Foundation of China under Grant No. 11725524.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Yitian Wang for fruitful discussions, and Professor Qingyu Cai’s great supports.

Footnotes

¹For the two-qubit operations, we treat the two qubits together as a quantum system. If we consider one of them, it is in a mixed state, but the two-qubit state is still pure.

References

1. Shor PW. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In: Proceedings 35th annual symposium on foundations of computer science. Santa Fe, NM, USA: IEEE (1994). p. 124–34.

Google Scholar

2. Shor PW. Polynomial-time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM Rev (1999) 41:303–32. doi:10.1137/s0036144598347011

CrossRef Full Text | Google Scholar

3. Grover LK. A Fast Quantum Mechanical Algorithm for Database Search. In: Proceedings of the twenty-eighth annual ACM symposium on Theory of computing (1996). p. 212–9. doi:10.1145/237814.237866

CrossRef Full Text | Google Scholar

4. Grover LK. Quantum Mechanics Helps in Searching for a Needle in a Haystack. Phys Rev Lett (1997) 79:325–8. doi:10.1103/physrevlett.79.325

CrossRef Full Text | Google Scholar

5. Bruzewicz CD, Chiaverini J, McConnell R, Sage JM. Trapped-ion Quantum Computing: Progress and Challenges. Appl Phys Rev (2019) 6:021314. doi:10.1063/1.5088164

CrossRef Full Text | Google Scholar

6. Martinis JM, Cooper KB, McDermott R, Steffen M, Ansmann M, Osborn KD, et al. Decoherence in Josephson Qubits from Dielectric Loss. Phys Rev Lett (2005) 95:210503. doi:10.1103/physrevlett.95.210503

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Arute F, Arya K, Babbush R, Bacon D, Bardin JC, Barends R, et al. Quantum Supremacy Using a Programmable Superconducting Processor. Nature (2019) 574:505–10. doi:10.1038/s41586-019-1666-5

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wu Y, Bao W-S, Cao S, Chen F, Chen M-C, Chen X, et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys Rev Lett (2021) 127:180501. doi:10.1103/physrevlett.127.180501

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Fowler AG, Mariantoni M, Martinis JM, Cleland AN. Surface Codes: Towards Practical Large-Scale Quantum Computation. Phys Rev A (2012) 86:032324. doi:10.1103/physreva.86.032324

CrossRef Full Text | Google Scholar

10. Chen Z, Satzinger KJ, Atalaya J. Exponential Suppression of Bit or Phase Errors with Cyclic Error Correction. Nature (2021) 595:383.

PubMed Abstract | Google Scholar

11. Gidney C, Ekerå M. How to Factor 2048 Bit RSA Integers in 8 hours Using 20 Million Noisy Qubits. Quantum (2021) 5:433. doi:10.22331/q-2021-04-15-433

CrossRef Full Text | Google Scholar

12. Gouzien É, Sangouard N. Factoring 2048-bit RSA Integers in 177 Days with 13 436 Qubits and a Multimode Memory. Phys Rev Lett (2021) 127:140503. doi:10.1103/physrevlett.127.140503

PubMed Abstract | CrossRef Full Text | Google Scholar

13.[Dataset] Nielsen MA, Chuang I. Quantum Computation and Quantum Information (2002).

Google Scholar

14. Ithier G, Collin E, Joyez P, Meeson PJ, Vion D, Esteve D, et al. Decoherence in a Superconducting Quantum Bit Circuit. Phys Rev B (2005) 72:134519. doi:10.1103/physrevb.72.134519

CrossRef Full Text | Google Scholar

15. Krantz P, Kjaergaard M, Yan F, Orlando TP, Gustavsson S, Oliver WD. A Quantum Engineer's Guide to Superconducting Qubits. Appl Phys Rev (2019) 6:021318. doi:10.1063/1.5089550

CrossRef Full Text | Google Scholar

16. Ithier G. Manipulation, Readout and Analysis of the Decoherence of a Superconducting Quantum Bit. Ph.D. thesis. Paris, France: Université Pierre et Marie Curie-Paris VI (2005).

17. Olmschenk S, Younge KC, Moehring DL, Matsukevich DN, Maunz P, Monroe C. Manipulation and Detection of a Trapped Yb⁺ Hyperfine Qubit. Phys Rev A (2007) 76:052314. doi:10.1103/physreva.76.052314

CrossRef Full Text | Google Scholar

18. Devitt SJ, Munro WJ, Nemoto K. Quantum Error Correction for Beginners. Rep Prog Phys (2013) 76:076001. doi:10.1088/0034-4885/76/7/076001

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Burkard G, Koch RH, DiVincenzo DP. Multilevel Quantum Description of Decoherence in Superconducting Qubits. Phys Rev B (2004) 69:064503. doi:10.1103/physrevb.69.064503

CrossRef Full Text | Google Scholar

20. Clerk AA, Devoret MH, Girvin SM, Marquardt F, Schoelkopf RJ. Introduction to Quantum Noise, Measurement, and Amplification. Rev Mod Phys (2010) 82:1155–208. doi:10.1103/revmodphys.82.1155

CrossRef Full Text | Google Scholar

21. Berns DM, Oliver WD, Valenzuela SO, Shytov AV, Berggren KK, Levitov LS, et al. Coherent Quasiclassical Dynamics of a Persistent Current Qubit. Phys Rev Lett (2006) 97:150502. doi:10.1103/physrevlett.97.150502

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Bylander J, Gustavsson S, Yan F, Yoshihara F, Harrabi K, Fitch G, et al. Noise Spectroscopy through Dynamical Decoupling with a Superconducting Flux Qubit. Nat Phys (2011) 7:565–70. doi:10.1038/nphys1994

CrossRef Full Text | Google Scholar

23. Redfield AG. On the Theory of Relaxation Processes. IBM J Res Dev (1957) 1:19–31. doi:10.1147/rd.11.0019

CrossRef Full Text | Google Scholar

24. Bloch F. Generalized Theory of Relaxation. Phys Rev (1957) 105:1206–22. doi:10.1103/physrev.105.1206

CrossRef Full Text | Google Scholar