Observer-Based Adaptive Fuzzy Output Feedback Control of Fractional-Order Chaotic Systems With Input Quantization

This study investigates the adaptive fuzzy output feedback control of strict-feedback fractional-order chaotic systems with unmeasurable states and quantized input. First, the functional uncertainties are approximated by fuzzy logic systems (FLSs). Second, combining the FLS and the system output signal, an observer is constructed to estimate the unmeasurable states. A command filter is defined to cope with the “explosion of complexity” problem resulting from the repeated derivatives of virtual control inputs in each backstepping step. To compensate for quantization errors, a hyperbolic tangent function is introduced to transform the control signal, which can not only guarantee that the tracking error converges to an arbitrarily small region near the origin but also reduce the chattering phenomenon of the control input. In addition, the stability analysis is carried out relying on the fractional Lyapunov stability criterion such that all the signals keep bounded. Finally, a numerical simulation example is put forward to verify the effectiveness of our method.

1 Introduction

During the past few decades, fractional calculus has received increasing research interest because of its special properties that can be well used in system modeling, such as heredity and memory. After a long period of development, it has been a powerful mathematical instrument in the fields of bioengineering, physics, economics, medicine, and so on [1–4]. At the same time, many traditional calculus theories have been extended to the fractional calculus theory, especially the Mittag–Leffler stability theory [5]. As an extension of the Lyapunov stability theory, it plays an important role when designing the controller for fractional-order nonlinear systems (FONSs), including fractional-order chaotic systems (FOCSs).

Strict-feedback systems are a common form of chaotic systems, such as fractional-order Arneodo systems [6] and fractional-order Rossler systems [7]. One of the effective strategies to control these systems is the backstepping technique. However, virtual control inputs need to be repeatedly differentiated in each backstepping step, which will cause the “explosion of complexity” problem. Furthermore, different from the traditional calculus, the fractional order derivative of a composite function is a complicated infinite series that is hard to be calculated in practical engineering, which also increases the difficulty of designing controllers for strict-feedback FONSs. To this end, researchers have done special research and some interesting results have been achieved. For instance, in [8, 9], the fractional-order derivative of the virtual control input was regarded as an extra uncertain term and was approximated by fuzzy logic systems (FLSs), which can avoid the “explosion of complexity” problem; however, as the order of the system increases, the cumulative increase of fuzzy errors will affect the final control performance. To reduce the influence of fuzzy errors, an adaptive dynamic surface control was extended to FONSs in [10]. Moreover, a fractional-order command filter and an exact differentiator were introduced in [11, 12], respectively.

In addition, it is worth pointing out that in the aforementioned literature, a key assumption, i.e., the states must be measurable and should be satisfied, which is too demanding for practical engineering applications. Constrained by sensor technology or cost consumption, in most cases, only the system output signal is measurable directly, which means that the unknown states need to be estimated by developing an observer. In [13], the tracking control problem for incommensurate FONSs with input saturation was addressed via the observer-based backstepping algorithm. In [14], an observer was proposed for FONSs with unknown input gain based on the LMI technique. A sliding mode observer came up for FONSs with parameter uncertainties in [15]. However, there are still some limitations in these works: the system model of [13] is considered to be free of functional uncertainties or disturbances; the method of [14] is only applicable to system models that can be linearized; and a switch term is included in the observer structure appearing in [15], which will result in the chatting phenomenon. Some other interesting methods can be seen in [16–19]. For the observer design of the FONS, there is still a lot of work worth exploring.

On the other hand, because of limited-bandwidth communication channels and data transmission pressure, the control input signal must be quantized for some systems, such as digital control systems, hydraulic systems, and network systems [20–22]. A common type of quantizer is the sector-bounded quantizer, whose quantization errors satisfy the sector-bounded condition, including uniform quantizers, logarithmic quantizers, and hysteretic quantizers. In [23], a method that divides a sector-bounded quantizer into a linear segment and a nonlinear segment was discussed, which is the main idea of the quantized controller design. During the past few years, considerable results about quantized control for integer-order nonlinear systems have been achieved [24–27], and several important conclusions have been successfully extended to FONSs. For example, in [28], a Nussbaum function was used to study the fuzzy quantized control problem for uncertain FONSs with unknown control directions; in [29], a logarithmic quantizer was employed to achieve the synchronization control for fractional-order output-coupling neural networks; in [30], for a FONS with input quantization and actuator failures, an adaptive asymptotic tracking control strategy was proposed; in [31], an output-feedback quantized controller was designed for fractional-order neural networks described by Takagi–Sugeno fuzzy models; and in [32], the neural network-based quantized synchronization control for FOCSs was investigated. Nevertheless, it should be noted that the aforementioned literature treats the nonlinear part decomposed by the quantizer as an extra disturbance. How to better compensate for the quantization error in the design of the control input is still a matter of concern.

Inspired by the aforementioned discussion, this study investigates the adaptive fuzzy output feedback control problem for strict-feedback FOCSs subject to unmeasurable states and input quantization. The main contributions of this work are listed as follows. 1) Compared with the results presented in [13, 14], a broader class of FOCSs with functional uncertainties in each subsystem has been investigated. 2) Taking into account limited communication channels and data transmission pressure, a logarithmic quantizer is used to quantize the input signal, which has a better application value for actual engineering. 3) In comparison with the method of compensating for quantization errors in [24], a hyperbolic tangent function is introduced to transform the control signal in the controller design so that the disturbance derived from the nonlinear part of the quantizer is cleverly avoided and the chatting phenomenon is reduced. 4) Distinct from [28–32], all the states of the system model considered in this work are supposed to be unknown except the output signal.

The article is organised as follows. Some basic knowledge of fractional calculus and the problem description are provided in Section 2; Section 3 gives the details about the design of the observer and the controller; simulation results are presented in Section 4; and Section 5 summarizes the conclusion. In the following, $\mathbb{R}$ and ${\mathbb{R}}^n$ denote the spaces of real numbers and n-vectors, respectively, ${\mathbb{C}}^1$ is the space of differentiable functions, ‖ ⋅‖ stands for the Euclidean norm, and sign (⋅) represents the signum function.

2 Preliminaries and Problem Description

2.1 Preliminaries

Definition 1 [33] The Caputo’s fractional derivative is defined as

$D_t^{\vartheta }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(1-\mathit{\vartheta }\right)}{\int }_0^t{\left(t-\tau \right)}^{-\vartheta }{f}^{\prime }\left(\tau \right)d\tau ,(1)$

where 0 < ϑ < 1.

Lemma 1 [34] Suppose that $\mathit{x}(t)\in {\mathbb{R}}^n$ is Lipschitz continuous and P is a positive matrix, then

$\frac{1}{2}{D}_t^{\vartheta }{\mathit{x}}^T\left(t\right)P\mathit{x}\left(t\right)\le {\mathit{x}}^T\left(t\right)P{D}_t^{\vartheta }\mathit{x}\left(t\right).(2)$

Lemma 2 [10] Let $V(t)\in {\mathbb{C}}^1$ satisfy

$D_t^{\vartheta }V\left(t\right)\le -aV\left(t\right)+b,(3)$

where a, b > 0 are constants. Then, there exists a constant t₀ > 0 such that

$|V\left(t\right)|\le \frac{c_{0}b}{a}(4)$

holds for all t ≥ t₀, where c₀ > 1 is a constant.

Lemma 3 [11] The fractional-order command filter is defined as

$\left\{\begin{array}{cc}\hfill D_t^{\vartheta }{\gamma }_1\left(t\right)& =\beta {\gamma }_2\left(t\right),\hfill \\ \hfill D_t^{\vartheta }{\gamma }_2\left(t\right)& =-2\beta \zeta {\gamma }_2\left(t\right)-\beta \left({\gamma }_1\left(t\right)-\alpha \left(t\right)\right),\hfill \end{array}\right)(5)$

where γ₁ (0) = α(0) and γ₂ (0) = 0. The function α(t) is the input signal that satisfies $|D_t^{\vartheta }\alpha (t)|\le {\rho }_1$ and $|D_t^{2\vartheta }\alpha (t)|\le {\rho }_2$, where ρ₁, ρ₂ > 0 are constants. Then, for any μ > 0, there exist β > 0 and ζ ∈ (0, 1] so that |γ₁(t) − α(t)| ≤ μ.

2.2 Problem Description

Consider the following FOCS with a strict-feedback form:

$\left\{\begin{array}{cc}\hfill & D_t^{\vartheta }{x}_i\left(t\right)=f_i\left({\bar{\mathit{x}}}_i\right)+x_{i+1}\left(t\right),i=1,\dots ,n-1,\hfill \\ \hfill & D_t^{\vartheta }{x}_n\left(t\right)=f_n\left(\bar{\mathit{x}}\right)+q\left(u\left(t\right)\right),\hfill \\ \hfill & y\left(t\right)=x_1\left(t\right),\hfill \end{array}\right)(6)$

where ${\bar{\mathit{x}}}_i={[x_1(t),x_2(t),\dots ,x_i(t)]}^T\in {\mathbb{R}}^i$ represents the state vector, $\bar{\mathit{x}}={\bar{\mathit{x}}}_n\in {\mathbb{R}}^n$, $f_i(\cdot ):{\mathbb{R}}^i\mapsto \mathbb{R}$ is an unknown Lipschitz continuous function, y(t) and u(t) stand for the output signal and input signal, respectively, and $q(\cdot ):\mathbb{R}\mapsto \mathbb{R}$ denotes a logarithmic quantizer. It is assumed that only y(t) is measurable directly. Let y_d(t) be a referenced signal, and our objective is to design a suitable controller for the system subject to input quantization so that the output trajectory can track the referenced signal.

Assumption 1 y_d(t) and $D_t^{\vartheta }{y}_d(t)$ are continuous and known.

Assumption 2 For $\forall {\mathit{X}}_1,{\mathit{X}}_2\in {\mathbb{R}}^i$, there exists an unknown constant h_i > 0 so that

$|f_i\left({\mathit{X}}_1\right)-f_i\left({\mathit{X}}_2\right)|\le h_i\Vert {\mathit{X}}_1-{\mathit{X}}_2\Vert .(7)$

The logarithmic quantizer is characterized as follows:

$q\left(u\left(t\right)\right)=\left\{\begin{array}{cccc}\hfill & u_{j}sign\left(u\left(t\right)\right),\hfill & \hfill & \frac{u_j}{1+\varrho }<|u\left(t\right)|\le \frac{u_j}{1-\varrho },\hfill \\ \hfill & 0,\hfill & \hfill & |u\left(t\right)|\le \frac{u_{\text{min}}}{1+\varrho },\hfill \end{array}\right)(8)$

where j = 1, 2, ⋯, u_min > 0, ξ ∈ (0, 1), u_j = ξ^1−ju_min, $\varrho =\frac{1-\xi }{1+\xi }$ is the density of quantization, and $\frac{u_{\text{min}}}{1+\varrho }$ is the dead-zone of the quantizer. It is obvious that $q\left(u(t)\right)$ belongs to the set U = {0, ±u_j}, and the quantizer (8) satisfies the following properties:

$|q\left(u\left(t\right)\right)-u\left(t\right)|\le \varrho |u\left(t\right)|+u_{\text{min}}.(9)$

3 Main Results

Since all the states of the system are unmeasurable except the output signal, it is essential to design an observer first.

3.1 Observer Design

Let ${\widehat{\bar{\mathit{x}}}}_i={[{\widehat{x}}_1(t),\dots ,{\widehat{x}}_i(t)]}^T$ be the estimation of ${\bar{\mathit{x}}}_i$, then system (6) can be rewritten as

$\left\{\begin{array}{cc}\hfill & D_t^{\vartheta }\bar{\mathit{x}}=A\bar{\mathit{x}}+\sum _{i=1}^n{B}_i\left(f_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+{\tilde{f}}_i\right)+Eq\left(u\left(t\right)\right),\hfill \\ \hfill & y=C^T\bar{\mathit{x}},\hfill \end{array}\right)(10)$

where $A=\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$, $B_i={[0,\dots ,0,\underset{i-th}{\underbrace{1}},0,\dots ,0]}^T$, C = [1,0, … ,0]^T, E = [0, … ,0,1]^T, and ${\tilde{f}}_i=f_i({\bar{\mathit{x}}}_i)-f_i({\widehat{\bar{\mathit{x}}}}_i)$.

Remark 1. Since ${\bar{\mathit{x}}}_i$ is unknown, it cannot be used as the input of the FLS to approximate $f_i({\bar{\mathit{x}}}_i)$. However, the estimation ${\widehat{\bar{\mathit{x}}}}_i$ can be obtained from the observer. According to the definition of function continuity, one has

$\underset{{\widehat{\bar{\mathit{x}}}}_i\to {\bar{\mathit{x}}}_i}{\lim }{f}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)=f_i\left({\bar{\mathit{x}}}_i\right),(11)$

which means that $f_i({\widehat{\bar{\mathit{x}}}}_i)$ can be approximated as $f_i({\bar{\mathit{x}}}_i)$ when the estimation error is very small. It should be noted that $f_i({\widehat{\bar{\mathit{x}}}}_i)$ is also an unknown function, so an FLS ${\widehat{f}}_i({\widehat{\bar{\mathit{x}}}}_i)$ whose input is ${\widehat{\bar{\mathit{x}}}}_i$ will be defined to approximate $f_i({\widehat{\bar{\mathit{x}}}}_i)$ in the following analysis.Consider the following FLS [35]:

${\widehat{f}}_i\left({\widehat{\bar{\mathit{x}}}}_i,{\widehat{\mathit{W}}}_i\right)={\widehat{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right),(12)$

where ${\widehat{\mathit{W}}}_i={[{\widehat{w}}_1(t),{\widehat{w}}_2(t),\dots ,{\widehat{w}}_N(t)]}^T\in {\mathrm{\Omega }}_{c{w}_i}\subset {\mathbb{R}}^N$ is an adjustable parameter vector, ${\mathbf{\Psi }}_i({\widehat{\bar{\mathit{x}}}}_i)={[{\psi }_{i1}({\widehat{\bar{\mathit{x}}}}_i),{\psi }_{i2}({\widehat{\bar{\mathit{x}}}}_i),\dots ,{\psi }_{iN}({\widehat{\bar{\mathit{x}}}}_i)]}^T\in {\mathbb{R}}^N$ is the vector of fuzzy basis functions (this study uses the Gaussian function), and N is the number of fuzzy rules. Then, $f_i({\widehat{\bar{\mathit{x}}}}_i)$ can be approximated by the FLS (12), and the optimal approximation is

$f_i\left({\widehat{\bar{\mathit{x}}}}_i\right)={{\mathit{W}}_i^{\ast T}}^{}{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+{ϵ}_i\left({\widehat{\bar{\mathit{x}}}}_i\right),(13)$

where ${\mathit{W}}_i^{\ast }$ is the optimal parameter vector, and ${ϵ}_i({\widehat{\bar{\mathit{x}}}}_i)$ is the optimal approximation error. The optimal parameter vector ${\mathit{W}}_i^{\ast }$ is defined as

${\mathit{W}}_i^{\ast }=\arg \underset{{\widehat{\mathit{W}}}_i\in {\mathrm{\Omega }}_{cw}}{\min }\left[\underset{{\widehat{\bar{\mathit{x}}}}_i\in {\mathrm{\Omega }}_{c{\widehat{x}}_i}}{\sup }\left|f_i\left({\widehat{\bar{\mathit{x}}}}_i\right)-{\widehat{f}}_i\left({\widehat{\bar{\mathit{x}}}}_i,{\widehat{\mathit{W}}}_i\right)\right|\right],(14)$

where ${\mathrm{\Omega }}_{c{w}_i}$ and ${\mathrm{\Omega }}_{c{\widehat{x}}_i}$ represent the compact sets corresponding to ${\widehat{\mathit{W}}}_i$ and ${\widehat{\bar{\mathit{x}}}}_i$, respectively. It should be noted that ${\mathit{W}}_i^{*}$ is just considered for analysis purpose, whose value is not required. Based on [36], it is reasonable to assume that there exists an unknown constant ɛ_i > 0 such that ${ϵ}_i({\widehat{\bar{\mathit{x}}}}_i)$ meets $|{ϵ}_i({\widehat{\bar{\mathit{x}}}}_i)|\le {\epsilon }_i$.The observer is designed as

$\left\{\begin{array}{cc}\hfill & D_t^{\vartheta }\widehat{\bar{\mathit{x}}}=\bar{A}\widehat{\bar{\mathit{x}}}+\sum _{i=1}^n{B}_i{\widehat{f}}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+Eq\left(u\left(t\right)\right)+Ky\left(t\right),\hfill \\ \hfill & \widehat{y}=C^T\widehat{\bar{\mathit{x}}},\hfill \end{array}\right)(15)$

where $\bar{A}=A-K{C}^T$ and $K={[k_1,\dots ,k_n]}^T$ is a design parameter vector to ensure that $\bar{A}$ is strict Hurwitz. Consequently, for an arbitrary positive definite matrix Q, there exists a positive definite matrix P such that

$P\bar{A}+{\bar{A}}^{T}P=-Q.(16)$

Let $\tilde{\mathit{x}}=\bar{\mathit{x}}-\widehat{\bar{\mathit{x}}}={[{\tilde{x}}_1(t),\dots ,{\tilde{x}}_n(t)]}^T$ be the estimation error vector, then from Eq. 10 and Eq. 15, it can yield

$D_t^{\vartheta }\tilde{\mathit{x}}=\bar{A}\tilde{\mathit{x}}+\sum _{i=1}^n{B}_i\left({\tilde{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+{ϵ}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+{\tilde{f}}_i\right),(17)$

where ${\tilde{\mathit{W}}}_i={\mathit{W}}_i^{\ast }-{\widehat{\mathit{W}}}_i$. Then, the observer (15) can be expanded to the following form:

$\left\{\begin{array}{cc}\hfill D_t^{\vartheta }{\widehat{x}}_i\left(t\right)& =k_i{\tilde{x}}_1\left(t\right)+{\widehat{x}}_{i+1}\left(t\right)+{\widehat{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right),\hfill \\ \hfill D_t^{\vartheta }{\widehat{x}}_n\left(t\right)& =k_n{\tilde{x}}_1\left(t\right)+q\left(u\left(t\right)\right)+{\widehat{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left(\widehat{\bar{\mathit{x}}}\right).\hfill \end{array}\right.(18)$

3.2 Controller Design

Based on the information derived from the observer, the final controller will be given via the backstepping algorithm in this part. The whole design process is divided into n steps.

Step 1: let e₁(t) = x₁(t) − y_d(t), whose fractional order derivative can be expressed by

$\begin{array}{cc}\hfill D_t^{\vartheta }{e}_1\left(t\right)& =D_t^{\vartheta }{x}_1\left(t\right)-D_t^{\vartheta }{y}_d\left(t\right)\hfill \\ \hfill & =f_1\left({\bar{\mathit{x}}}_1\right)+x_2\left(t\right)-D_t^{\vartheta }{y}_d\left(t\right)\hfill \\ \hfill & =f_1\left({\widehat{\bar{\mathit{x}}}}_1\right)+{\tilde{f}}_1+x_2\left(t\right)-{\widehat{x}}_2\left(t\right)+{\widehat{x}}_2\left(t\right)-{\alpha }_1\left(t\right)+{\alpha }_1\left(t\right)-{\alpha }_1^c\left(t\right)+{\alpha }_1^c\left(t\right)-D_t^{\vartheta }{y}_d\left(t\right)\hfill \\ \hfill & =f_1\left({\widehat{\bar{\mathit{x}}}}_1\right)+{\tilde{f}}_1+{\tilde{x}}_2\left(t\right)+e_2\left(t\right)+{\alpha }_1\left(t\right)+\left({\alpha }_1^c\left(t\right)-{\alpha }_1\left(t\right)\right)-D_t^{\vartheta }{y}_d\left(t\right)\hfill \\ \hfill & ={{\mathit{W}}_1^{*}}^T{\mathbf{\Psi }}_1\left({\widehat{\bar{\mathit{x}}}}_1\right)+{ϵ}_1\left({\widehat{\bar{\mathit{x}}}}_1\right)+{\tilde{f}}_1+{\tilde{x}}_2\left(t\right)+e_2\left(t\right)+{\alpha }_1\left(t\right)+\left({\alpha }_1^c\left(t\right)-{\alpha }_1\left(t\right)\right)-D_t^{\vartheta }{y}_d\left(t\right),\hfill \end{array}(19)$

where α₁(t) is the first virtual control input, $e_2(t)={\widehat{x}}_2(t)-{\alpha }_1^c(t)$, and ${\alpha }_1^c(t)={\gamma }_{\mathrm{1,1}}(t)$ is the filter output which comes from

$\left\{\begin{array}{cc}\hfill D_t^{\vartheta }{\gamma }_{\mathrm{1,1}}\left(t\right)& ={\beta }_1{\gamma }_{\mathrm{1,2}}\left(t\right),\hfill \\ \hfill D_t^{\vartheta }{\gamma }_{\mathrm{1,2}}\left(t\right)& =-2{\beta }_1{\zeta }_1{\gamma }_{\mathrm{1,2}}\left(t\right)-{\beta }_1\left({\gamma }_{\mathrm{1,1}}\left(t\right)-{\alpha }_1\left(t\right)\right),\hfill \end{array}\right)(20)$

where γ_1,1 (0) = α₁ (0) and γ_1,2 (0) = 0. In terms of Lemma 3, for any μ₁ > 0, there exist β₁ > 0 and ζ₁ ∈ (0, 1] such that |γ_1,1(t) − α₁(t)| ≤ μ₁ for all t > 0.

Choose the virtual control input α₁(t) to be

${\alpha }_1\left(t\right)=-c_1{e}_1\left(t\right)-{{\widehat{\mathit{W}}}_1}^T{\mathbf{\Psi }}_1\left({\widehat{\bar{\mathit{x}}}}_1\right)+D_t^{\vartheta }{y}_d\left(t\right),(21)$

where c₁ > 0 is a design parameter. Substituting (21) into (19), one obtains

$D_t^{\vartheta }{e}_1\left(t\right)=-c_1{e}_1\left(t\right)+e_2\left(t\right)+{\tilde{\mathit{W}}}_1^T{\mathbf{\Psi }}_1\left({\widehat{\bar{\mathit{x}}}}_1\right)+{ϵ}_1\left({\widehat{\bar{\mathit{x}}}}_1\right)+{\tilde{f}}_1+{\tilde{x}}_2\left(t\right)+\left({\alpha }_1^c\left(t\right)-{\alpha }_1\left(t\right)\right).(22)$

Let ${\widehat{\mathit{W}}}_1$ be updated by the adaptation law

$D_t^{\vartheta }{\widehat{\mathit{W}}}_1=r_1{e}_1\left(t\right){\mathbf{\Psi }}_1\left({\widehat{\bar{\mathit{x}}}}_1\right)-a_1{\widehat{\mathit{W}}}_1,(23)$

where r₁, a₁ > 0 are design parameters.

Construct a Lyapunov function as $V_{\mathrm{1,1}}(t)=\frac{1}{2}{e}_1^2(t)+\frac{1}{2r_1}{\tilde{\mathit{W}}}_1^T{\tilde{\mathit{W}}}_1$, then one can get

$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_{\mathrm{1,1}}\left(t\right)& \le e_1\left(t\right)D_t^{\vartheta }{e}_1\left(t\right)-\frac{1}{r_1}{\tilde{\mathit{W}}}_1^T{D}_t^{\vartheta }{\widehat{\mathit{W}}}_1\hfill \\ \hfill & \le -c_1{e}_1^2\left(t\right)+e_1\left(t\right)e_2\left(t\right)+|e_1\left(t\right){\mu }_1|+|e_1\left(t\right){\epsilon }_1|+|e_1\left(t\right)|h_1\Vert \tilde{\mathit{x}}\Vert +e_1\left(t\right){\tilde{x}}_2\left(t\right)+\frac{a_1}{r_1}{\tilde{\mathit{W}}}_1^T{\widehat{\mathit{W}}}_1.\hfill \end{array}(24)$

Utilizing Young’s inequality, one has

$\begin{array}{cc}\hfill |e_1\left(t\right){\mu }_1|& \le \frac{{\eta }_1}{2}{e}_1^2\left(t\right)+\frac{{\mu }_1^2}{2{\eta }_1},\hfill \\ \hfill |e_1\left(t\right){\epsilon }_1|& \le \frac{{\eta }_1}{2}{e}_1^2\left(t\right)+\frac{{\epsilon }_1^2}{2{\eta }_1},\hfill \\ \hfill |e_1\left(t\right)|h_1\Vert \tilde{\mathit{x}}\Vert & \le \frac{{\eta }_1}{2}{e}_1^2\left(t\right)+\frac{h_1^2}{2{\eta }_1}{\tilde{\mathit{x}}}^T\tilde{\mathit{x}},\hfill \\ \hfill e_1\left(t\right){\tilde{x}}_2\left(t\right)& \le \frac{{\eta }_1}{2}{e}_1^2\left(t\right)+\frac{1}{2{\eta }_1}{\tilde{\mathit{x}}}^T\tilde{\mathit{x}},\hfill \\ \hfill \frac{a_1}{r_1}{\tilde{\mathit{W}}}_1^T{\widehat{\mathit{W}}}_1& \le -\frac{a_1}{2r_1}{\tilde{\mathit{W}}}_1^T{\tilde{\mathit{W}}}_1+\frac{a_1}{2r_1}{{\mathit{W}}_1^{\ast T}}^{}{\mathit{W}}_1^{\ast },\hfill \end{array}(25)$

where η₁ > 0 is a constant. Hence, one gets

$D_t^{\vartheta }{V}_{\mathrm{1,1}}\left(t\right)\le -\left(c_1-2{\eta }_1\right)e_1^2\left(t\right)+e_1\left(t\right)e_2\left(t\right)+\frac{h_1^2+1}{2{\eta }_1}{\tilde{\mathit{x}}}^T\tilde{\mathit{x}}+\frac{{\mu }_1^2}{2{\eta }_1}+\frac{{\epsilon }_1^2}{2{\eta }_1}-\frac{a_1}{2r_1}{\tilde{\mathit{W}}}_1^T{\tilde{\mathit{W}}}_1+\frac{a_1}{2r_1}{{\mathit{W}}_1^{\ast T}}^{}{\mathit{W}}_1^{\ast }.(26)$

Step i (i = 2, … , n − 1): similar to the previous step, the ϑ-th derivative of e_i(t) is

$\begin{array}{cc}\hfill D_t^{\vartheta }{e}_i\left(t\right)& =D_t^{\vartheta }{\widehat{x}}_i\left(t\right)-D_t^{\vartheta }{\alpha }_{i-1}^c\left(t\right)\hfill \\ \hfill & =k_i{\tilde{x}}_1\left(t\right)+{\widehat{x}}_{i+1}\left(t\right)+{\widehat{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)-D_t^{\vartheta }{\alpha }_{i-1}^c\left(t\right)\hfill \\ \hfill & =k_i{\tilde{x}}_1\left(t\right)+{\widehat{x}}_{i+1}\left(t\right)+{\alpha }_i\left(t\right)-{\alpha }_i\left(t\right)+{\alpha }_i^c\left(t\right)-{\alpha }_i^c\left(t\right)+{\widehat{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)-D_t^{\vartheta }{\alpha }_{i-1}^c\left(t\right)\hfill \\ \hfill & =k_i{\tilde{x}}_1\left(t\right)+e_{i+1}\left(t\right)+{\alpha }_i\left(t\right)+\left({\alpha }_i^c\left(t\right)-{\alpha }_i\left(t\right)\right)+{\widehat{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)-D_t^{\vartheta }{\alpha }_{i-1}^c\left(t\right),\hfill \end{array}(27)$

where α_i(t) is the ith virtual control input, $e_{i+1}(t)={\widehat{x}}_{i+1}(t)-{\alpha }_i^c(t)$, and ${\alpha }_i^c(t)={\gamma }_{i,1}(t)$ is the corresponding filter output derived from

$\left\{\begin{array}{cc}\hfill D_t^{\vartheta }{\gamma }_{i,1}\left(t\right)& ={\beta }_i{\gamma }_{i,2}\left(t\right),\hfill \\ \hfill D_t^{\vartheta }{\gamma }_{i,2}\left(t\right)& =-2{\beta }_i{\zeta }_i{\gamma }_{i,2}\left(t\right)-{\beta }_i\left({\gamma }_{i,1}\left(t\right)-{\alpha }_i\left(t\right)\right),\hfill \end{array}\right)(28)$

where γ_i,1 (0) = α_i (0) and γ_i,2 (0) = 0. Similarly, for any μ_i > 0, there exist β_i > 0 and ζ_i ∈ (0, 1] such that |γ_i,1(t) − α_i(t)| ≤ μ_i for all t > 0. We choose

${\alpha }_i\left(t\right)=-c_i{e}_i\left(t\right)-e_{i-1}\left(t\right)-{\widehat{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+D_t^{\vartheta }{\alpha }_{i-1}^c\left(t\right)-k_i{\tilde{x}}_1\left(t\right),(29)$

where c_i > 0 is a design parameter. It follows from (27) and (29) that

$D_t^{\vartheta }{e}_i\left(t\right)=-c_i{e}_i\left(t\right)-e_{i-1}\left(t\right)+e_{i+1}\left(t\right)+\left({\alpha }_i^c\left(t\right)-{\alpha }_i\left(t\right)\right).(30)$

We design the adaptation law

$D_t^{\vartheta }{\widehat{\mathit{W}}}_i=r_i{e}_i\left(t\right){\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)-a_i{\widehat{\mathit{W}}}_i,(31)$

where r_i, a_i are positive design parameters. We select the Lyapunov function as $V_{1,i}(t)=\frac{1}{2}{e}_i^2(t)+\frac{1}{2r_i}{\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i$; then,

$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_{1,i}\left(t\right)& \le e_i\left(t\right)D_t^{\vartheta }{e}_i\left(t\right)-\frac{1}{r_i}{\tilde{\mathit{W}}}_i^T{D}_t^{\vartheta }{\widehat{\mathit{W}}}_i\hfill \\ \hfill & =-c_i{e}_i^2\left(t\right)-e_{i-1}\left(t\right)e_i\left(t\right)+e_i\left(t\right)e_{i+1}\left(t\right)+e_i\left(t\right)\left({\alpha }_i^c\left(t\right)-{\alpha }_i\left(t\right)\right)-\frac{1}{r_i}{\tilde{\mathit{W}}}_i^T{D}_t^{\vartheta }{\widehat{\mathit{W}}}_i\hfill \\ \hfill & =-c_i{e}_i^2\left(t\right)-e_{i-1}\left(t\right)e_i\left(t\right)+e_i\left(t\right)e_{i+1}\left(t\right)+e_i\left(t\right)\left({\alpha }_i^c\left(t\right)-{\alpha }_i\left(t\right)\right)-e_i\left(t\right){\tilde{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+\frac{a_i}{r_i}{\tilde{\mathit{W}}}_i^T{\widehat{\mathit{W}}}_i\hfill \\ \hfill & \le -c_i{e}_i^2\left(t\right)-e_{i-1}\left(t\right)e_i\left(t\right)+e_i\left(t\right)e_{i+1}\left(t\right)+|e_i\left(t\right){\mu }_i|-e_i\left(t\right){\tilde{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+\frac{a_i}{r_i}{\tilde{\mathit{W}}}_i^T{\widehat{\mathit{W}}}_i.\hfill \end{array}(32)$

Because of the property that ${\sum }_{j=1}^N{\psi }_{ij}({\widehat{\bar{\mathit{x}}}}_i)=1$, then one has ${\mathbf{\Psi }}_i^T({\widehat{\bar{\mathit{x}}}}_i){\mathbf{\Psi }}_i({\widehat{\bar{\mathit{x}}}}_i)\le 1$. Using Young’s inequality, one has

$\begin{array}{cc}\hfill |e_i\left(t\right){\mu }_i|& \le \frac{{\eta }_i}{2}{e}_i^2\left(t\right)+\frac{{\mu }_i^2}{2{\eta }_i},\hfill \\ \hfill -e_i\left(t\right){\tilde{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)& \le \frac{{\eta }_i}{2}{e}_i^2\left(t\right)+\frac{1}{2{\eta }_i}{\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i,\hfill \\ \hfill \frac{a_i}{r_i}{\tilde{\mathit{W}}}_i^T{\widehat{\mathit{W}}}_i& \le -\frac{a_i}{2r_i}{\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+\frac{a_i}{2r_i}{{\mathit{W}}_i^{\ast T}}^{}{\mathit{W}}_i^{\ast },\hfill \end{array}(33)$

where η_i > 0 is a constant. Substituting (33) into (32), one obtains

$D_t^{\vartheta }{V}_{1,i}\left(t\right)\le -\left(c_i-{\eta }_i\right)e_i^2\left(t\right)-e_{i-1}\left(t\right)e_i\left(t\right)+e_i\left(t\right)e_{i+1}\left(t\right)+\frac{{\mu }_i^2}{2{\eta }_i}-\left(\frac{a_i}{2r_i}-\frac{1}{2{\eta }_i}\right){\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+\frac{a_i}{2r_i}{{\mathit{W}}_i^{\ast T}}^{}{\mathit{W}}_i^{\ast }.(34)$

Step n: the ϑ-th derivative of e_n(t) is given by

$\begin{array}{cc}\hfill D_t^{\vartheta }{e}_n\left(t\right)& =D_t^{\vartheta }{\widehat{x}}_n\left(t\right)-D_t^{\vartheta }{\alpha }_{n-1}^c\left(t\right)\hfill \\ \hfill & =k_n{\tilde{x}}_1\left(t\right)+q\left(u\left(t\right)\right)+{\widehat{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left(\widehat{\bar{\mathit{x}}}\right)-D_t^{\vartheta }{\alpha }_{n-1}^c\left(t\right).\hfill \end{array}.(35)$

The controller u(t) is designed as

$\left\{\begin{array}{cc}\hfill & u\left(t\right)=-\tanh \left(\frac{e_n\left(t\right)\bar{u}\left(t\right)}{\gamma }\right)\bar{u}\left(t\right),\hfill \\ \hfill & \bar{u}\left(t\right)=\frac{1}{1-\varrho }\left[-{\alpha }_n\left(t\right)+\chi \tanh \left(\frac{\chi e_n\left(t\right)}{\gamma }\right)\right],\hfill \\ \hfill & {\alpha }_n\left(t\right)=-c_n{e}_n\left(t\right)-e_{n-1}\left(t\right)-k_n{\tilde{x}}_1\left(t\right)-{\widehat{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left({\bar{\mathit{x}}}_n\right)+D_t^{\vartheta }{\alpha }_{n-1}^c\left(t\right),\hfill \end{array}\right.(36)$

where c_n, γ > 0 are two design parameters and χ > u_min is a constant. Let the adaptation law of ${\widehat{\mathit{W}}}_n$ be

$D_t^{\vartheta }{\widehat{\mathit{W}}}_n=r_n{e}_n\left(t\right){\mathbf{\Psi }}_n\left({\widehat{\bar{\mathit{x}}}}_n\right)-a_n{\widehat{\mathit{W}}}_n,(37)$

where r_n, a_n > 0 are design parameters. Defining a Lyapunov function as $V_{1,n}(t)=\frac{1}{2}{e}_n^2(t)+\frac{1}{2r_n}{\tilde{\mathit{W}}}_n^T{\tilde{\mathit{W}}}_n$ and using (35), one has

$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_{1,n}\left(t\right)\le & e_n\left(t\right)D_t^{\vartheta }{e}_n\left(t\right)-\frac{1}{r_n}{\tilde{\mathit{W}}}_n^T{D}_t^{\vartheta }{\widehat{\mathit{W}}}_n\hfill \\ \hfill =& e_n\left(t\right)k_n{\tilde{x}}_1\left(t\right)+e_n\left(t\right)q\left(u\left(t\right)\right)+e_n\left(t\right){\widehat{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left(\widehat{\bar{\mathit{x}}}\right)-e_n\left(t\right)D_t^{\vartheta }{\alpha }_{n-1}^c\left(t\right)-\frac{1}{r_n}{\tilde{\mathit{W}}}_n^T{D}_t^{\vartheta }{\widehat{\mathit{W}}}_n\hfill \\ \hfill =& e_n\left(t\right)k_n{\tilde{x}}_1\left(t\right)+e_n\left(t\right)q\left(u\left(t\right)\right)+e_n\left(t\right){\widehat{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left(\widehat{\bar{\mathit{x}}}\right)-e_n\left(t\right)D_t^{\vartheta }{\alpha }_{n-1}^c\left(t\right)-e_n\left(t\right){\tilde{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left({\widehat{\bar{\mathit{x}}}}_n\right)\hfill \\ \hfill & +\frac{a_n}{r_n}{\tilde{\mathit{W}}}_n^T{\widehat{\mathit{W}}}_n.\hfill \end{array}(38)$

Considering the term $e_n(t)q\left(u(t)\right)$, multiplying |e_n(t)| on both sides of Eq.9, invoking (36), and using the fact that |x| − x tanh (x/γ) ≤ 0.2785γ, one has

$\begin{array}{cc}\hfill e_n\left(t\right)q\left(u\left(t\right)\right)& \le e_n\left(t\right)u\left(t\right)+\varrho |e_n\left(t\right)u\left(t\right)|+u_{\text{min}}|e_n\left(t\right)|\hfill \\ \hfill & \le -e_n\left(t\right)\bar{u}\left(t\right)\tanh \left(\frac{e_n\left(t\right)\bar{u}\left(t\right)}{\gamma }\right)+\varrho \left|e_n\left(t\right)\bar{u}\left(t\right)\tanh \left(\frac{e_n\left(t\right)\bar{u}\left(t\right)}{\gamma }\right)\right|+u_{\text{min}}|e_n\left(t\right)|\hfill \\ \hfill & =-\left(1-\varrho \right)e_n\left(t\right)\bar{u}\left(t\right)\tanh \left(\frac{e_n\left(t\right)\bar{u}\left(t\right)}{\gamma }\right)+u_{\text{min}}|e_n\left(t\right)|\hfill \\ \hfill & \le -\left(1-\varrho \right)|e_n\left(t\right)\bar{u}\left(t\right)|+u_{\text{min}}|e_n\left(t\right)|+{\delta }_1\hfill \\ \hfill & \le -\left(1-\varrho \right)e_n\left(t\right)\bar{u}\left(t\right)+\chi |e_n\left(t\right)|+{\delta }_1\hfill \\ \hfill & =e_n\left(t\right){\alpha }_n\left(t\right)+\chi |e_n\left(t\right)|-\chi e_n\left(t\right)\tanh \left(\frac{\chi e_n\left(t\right)}{\gamma }\right)+{\delta }_1\hfill \\ \hfill & \le e_n\left(t\right){\alpha }_n\left(t\right)+{\delta }_2\hfill \\ \hfill & =-c_n{e}_n^2\left(t\right)-e_{n-1}\left(t\right)e_n\left(t\right)-e_n\left(t\right)k_n{\tilde{x}}_1\left(t\right)-e_n\left(t\right){\widehat{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left({\bar{\mathit{x}}}_n\right)+e_n\left(t\right)D_t^{\vartheta }{\alpha }_{n-1}^c\left(t\right)+{\delta }_2,\hfill \end{array}(39)$

where δ₁ = 0.2785γ(1 − ϱ) and δ₂ = 0.2785γ(2 − ϱ). Substituting (39) into (38), one obtains

$D_t^{\vartheta }{V}_{1,n}\left(t\right)\le -c_n{e}_n^2\left(t\right)-e_{n-1}\left(t\right)e_n\left(t\right)-e_n\left(t\right){\tilde{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left({\widehat{\bar{\mathit{x}}}}_n\right)+\frac{a_n}{r_n}{\tilde{\mathit{W}}}_n^T{\widehat{\mathit{W}}}_n+{\delta }_2.(40)$

Similar to (33), one has

$\begin{array}{cc}\hfill -e_n\left(t\right){\tilde{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left({\widehat{\bar{\mathit{x}}}}_n\right)& \le \frac{{\eta }_n}{2}{e}_n^2\left(t\right)+\frac{1}{2{\eta }_n}{\tilde{\mathit{W}}}_n^T{\tilde{\mathit{W}}}_n,\hfill \\ \hfill \frac{a_n}{r_n}{\tilde{\mathit{W}}}_n^T{\widehat{\mathit{W}}}_n& \le -\frac{a_n}{2r_n}{\tilde{\mathit{W}}}_n^T{\tilde{\mathit{W}}}_n+\frac{a_n}{2r_n}{{\mathit{W}}_n^{\ast T}}^{}{\mathit{W}}_n^{\ast },\hfill \end{array}(41)$

where η_n > 0 is a constant. Then,

$D_t^{\vartheta }{V}_{1,n}\left(t\right)\le -\left(c_n-\frac{{\eta }_n}{2}\right)e_n^2\left(t\right)-e_{n-1}\left(t\right)e_n\left(t\right)-\left(\frac{a_n}{2r_n}-\frac{1}{2{\eta }_n}\right){\tilde{\mathit{W}}}_n^T{\tilde{\mathit{W}}}_n+\frac{a_n}{2r_n}{{\mathit{W}}_n^{*}}^T{\mathit{W}}_n^{*}+{\delta }_2.(42)$

Therefore, based on the aforementioned analysis, the stability analysis can be summarized as the following theorem.

Theorem 1 Consider system (6) under Assumptions 1–2. The observer and quantizer are (15) and (8), respectively. The virtual control inputs are given by (21) and (29), and the corresponding filters are defined as (20) and (28). Consequently, the controller (36) with the parameter adaptation laws (23) (31), and (37) can guarantee that the tracking error e₁(t) and the estimation error ${\tilde{x}}_i(t)$ converge to a small region near the origin and all the signals remain bounded via selecting appropriate parameters.

Proof. Define a Lyapunov function as

$V_1\left(t\right)=\sum _{i=1}^n{V}_{1,i}\left(t\right).(43)$

By means of Eq. 26, Eq. 34, and Eq. 42, one has

$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_1\left(t\right)\le & -\left(c_1-2{\eta }_1\right)e_1^2\left(t\right)-\sum _{i=2}^{n-1}\left(c_i-{\eta }_i\right)e_i^2\left(t\right)-\left(c_n-\frac{{\eta }_n}{2}\right)e_n^2\left(t\right)-\frac{a_1}{2r_1}{\tilde{\mathit{W}}}_1^T{\tilde{\mathit{W}}}_1\hfill \\ \hfill & -\sum _{i=2}^n\left(\frac{a_i}{2r_i}-\frac{1}{2{\eta }_i}\right){\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+\frac{h_1^2+1}{2{\eta }_1}{\tilde{\mathit{x}}}^T\tilde{\mathit{x}}+\frac{{\epsilon }_1^2}{2{\eta }_1}+\sum _{i=1}^{n-1}\frac{{\mu }_i^2}{2{\eta }_i}+\sum _{i=1}^n\frac{a_i}{2r_i}{{\mathit{W}}_i^{\ast T}}^{}{\mathit{W}}_i^{\ast }+{\delta }_2\hfill \\ \hfill \le & -\sum _{i=1}^n\left(c_i-2{\eta }_i\right)e_i^2\left(t\right)-\sum _{i=1}^n\left(\frac{a_i}{2r_i}-\frac{1}{2{\eta }_i}\right){\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+\frac{h_1^2+1}{2{\eta }_1}{\tilde{\mathit{x}}}^T\tilde{\mathit{x}}+\frac{{\epsilon }_1^2}{2{\eta }_1}\hfill \\ \hfill & +\sum _{i=1}^{n-1}\frac{{\mu }_i^2}{2{\eta }_i}+\sum _{i=1}^n\frac{a_i}{2r_i}{{\mathit{W}}_i^{\ast T}}^{}{\mathit{W}}_i^{\ast }+{\delta }_2.\hfill \end{array}(44)$

We define

$V_2\left(t\right)=\frac{1}{2}{\tilde{\mathit{x}}}^{T}P\tilde{\mathit{x}}.(45)$

From Eq. 17, one has

$\begin{array}{cc}\hfill D_t^{\vartheta }{V}_2\left(t\right)& \le {\tilde{\mathit{x}}}^{T}P{D}_t^{\vartheta }\tilde{\mathit{x}}\hfill \\ \hfill & ={\tilde{\mathit{x}}}^{T}P\bar{A}\tilde{\mathit{x}}+\sum _{i=1}^n{\tilde{\mathit{x}}}^{T}P{B}_i\left({\tilde{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+{ϵ}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+{\tilde{f}}_i\right)\hfill \\ \hfill & =\frac{1}{2}{\tilde{\mathit{x}}}^{T}P\bar{A}\tilde{\mathit{x}}+\frac{1}{2}{\tilde{\mathit{x}}}^T{\bar{A}}^{T}P\tilde{\mathit{x}}+\sum _{i=1}^n{\tilde{\mathit{x}}}^{T}P{B}_i\left({\tilde{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+{ϵ}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+{\tilde{f}}_i\right)\hfill \\ \hfill & =-\frac{1}{2}{\tilde{\mathit{x}}}^{T}Q\tilde{\mathit{x}}+\sum _{i=1}^n{\tilde{\mathit{x}}}^{T}P{B}_i{\tilde{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+\sum _{i=1}^n{\tilde{\mathit{x}}}^{T}P{B}_i{ϵ}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)+\sum _{i=1}^n{\tilde{\mathit{x}}}^{T}P{B}_i{\tilde{f}}_i.\hfill \end{array}(46)$

Using Young’s inequality, one has

$\begin{array}{cc}\hfill {\tilde{\mathit{x}}}^{T}P{B}_i{\tilde{\mathit{W}}}_i^T{\mathbf{\Psi }}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)& \le \frac{\kappa }{2}{\tilde{\mathit{x}}}^T\tilde{\mathit{x}}+\frac{\Vert P{\Vert }^2}{2\kappa }{\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i,\hfill \\ \hfill {\tilde{\mathit{x}}}^{T}P{B}_i{ϵ}_i\left({\widehat{\bar{\mathit{x}}}}_i\right)& \le \frac{\kappa }{2}{\tilde{\mathit{x}}}^T\tilde{\mathit{x}}+\frac{{\epsilon }_i^2}{2\kappa }\Vert P{\Vert }^2,\hfill \\ \hfill {\tilde{\mathit{x}}}^{T}P{B}_i{\tilde{f}}_i& \le \frac{\kappa }{2}{\tilde{\mathit{x}}}^T\tilde{\mathit{x}}+\frac{h_i^2}{2\kappa }\Vert P{\Vert }^2{\tilde{\mathit{x}}}^T\tilde{\mathit{x}}.\hfill \end{array}.(47)$

It follows from Eq. 46 and Eq. 47 that

$D_t^{\vartheta }{V}_2\left(t\right)\le -\left(\frac{1}{2}{\mathrm{\lambda }}_{\text{min}}\left(Q\right)-\frac{3\kappa n}{2}-\frac{\Vert P{\Vert }^2}{2\kappa }\sum _{i=1}^n{h}_i^2\right){\tilde{\mathit{x}}}^T\tilde{\mathit{x}}+\frac{\Vert P{\Vert }^2}{2\kappa }\sum _{i=1}^n{\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+\frac{\Vert P{\Vert }^2}{2\kappa }\sum _{i=1}^n{\epsilon }_i^2.(48)$

Let V(t) = V₁(t) + V₂(t), then from Eq. 44 and Eq. 48, one has

$\begin{array}{cc}\hfill D_t^{\vartheta }V\left(t\right)=& D_t^{\vartheta }{V}_1\left(t\right)+D_t^{\vartheta }{V}_2\left(t\right)\hfill \\ \hfill \le & -\left(\frac{1}{2}{\mathrm{\lambda }}_{\text{min}}\left(Q\right)-\frac{3\kappa n}{2}-\frac{\Vert P{\Vert }^2}{2\kappa }\sum _{i=1}^n{h}_i^2-\frac{h_1^2+1}{2{\eta }_1}\right){\tilde{\mathit{x}}}^T\tilde{\mathit{x}}-\sum _{i=1}^n\left(c_i-2{\eta }_i\right)e_i^2\left(t\right)\hfill \\ \hfill & -\sum _{i=1}^n\left(\frac{a_i}{2r_i}-\frac{1}{2{\eta }_i}-\frac{\Vert P{\Vert }^2}{2\kappa }\right){\tilde{\mathit{W}}}_i^T{\tilde{\mathit{W}}}_i+\frac{\Vert P{\Vert }^2}{2\kappa }\sum _{i=1}^n{\epsilon }_i^2+\sum _{i=1}^{n-1}\frac{{\mu }_i^2}{2{\eta }_i}+\sum _{i=1}^n\frac{a_i}{2r_i}{{\mathit{W}}_i^{\ast T}}^{}{\mathit{W}}_i^{\ast }\hfill \\ \hfill & +\frac{{\epsilon }_1^2}{2{\eta }_1}+{\delta }_2\hfill \end{array}.(49)$

Setting the parameters to ensure $\frac{1}{2}{\mathrm{\lambda }}_{\text{min}}(Q)-\frac{3\kappa n}{2}-\frac{\Vert P{\Vert }^2}{2\kappa }{\sum }_{i=1}^n{h}_i^2-\frac{h_1^2+1}{2{\eta }_1}>0$, c_i − 2η_i > 0 and $\frac{a_i}{2r_i}-\frac{1}{2{\eta }_i}-\frac{\Vert P{\Vert }^2}{2\kappa }>0$, one has

$D_t^{\vartheta }V\left(t\right)\le -aV\left(t\right)+b,(50)$

in which $a=\min \left\{\left({\lambda }_{\text{min}}(Q)-3\kappa n-\frac{\Vert P{\Vert }^2}{\kappa }{\sum }_{i=1}^n{h}_i^2-\frac{h_1^2+1}{{\eta }_1}\right)/{\mathrm{\lambda }}_{\text{max}}(P),2(c_1-2{\eta }_1),\dots ,2(c_n-2{\eta }_n),a_1-\frac{r_1}{{\eta }_1}-\frac{r_1\Vert P{\Vert }^2}{\kappa },\dots ,a_n-\frac{r_n}{{\eta }_n}-\frac{r_n\Vert P{\Vert }^2}{\kappa }\right\}$, $b=\frac{\Vert P{\Vert }^2}{2\kappa }{\sum }_{i=1}^n{\epsilon }_i^2+{\sum }_{i=1}^{n-1}\frac{{\mu }_i^2}{2{\eta }_i}+{\sum }_{i=1}^n\frac{a_i}{2r_i}{{\mathit{W}}_i^{\ast T}}^{}{\mathit{W}}_i^{\ast }+\frac{{\epsilon }_1^2}{2{\eta }_1}+{\delta }_2$. According to Lemma 2, there exist a constant c₀ > 1 and a constant t₀ > 0 such that $|V(t)|\le \frac{c_{0}b}{a}$ holds for all t > t₀, which means that all the signals including the tracking error e₁(t) and the estimation error ${\tilde{x}}_i(t)$ are bounded and converge to the origin $\Vert \mathit{x}\Vert \le \sqrt{\frac{c_{0}b}{a}}$. ■

Remark 2 According to the principle of the backstepping algorithm, the role of α_i(t) is to act as the controller of the ith subsystem, and ${\alpha }_i^c(t)$ is the estimation of α_i(t) derived form the filter (28). As we all know, for the design controller of any system, the value of its control input cannot be infinite, which means that α_i(t) and its corresponding filter output ${\alpha }_i^c(t)$ are uniformly continuous.

Remark 3 The advantages of the filter (28) can not only avoid the “explosion of complexity” problem, but also release the condition of Assumption 2 in [37] (the knowledge of $D_t^{i\vartheta }{y}_d(t)$ is needed). In this study, only the information of y_d(t) and $D_t^{\vartheta }{y}_d(t)$ is required. In addition, the convergence speed of the filtered error μ_i is faster than the dynamic surface of [10]. However, it should be noted that μ_i can be decreased by increasing β_i, but the parameter drift problem will appear if β_i is too large.

Remark 4 It can be seen from the definitions of a and b in (50) that the range of ${\tilde{x}}_i(t)$ and e₁(t) can be reduced by increasing c_i and r_i, but more control energy will be consumed if c_i and r_i are too large. Moreover, when a too large r_i is selected, the parameter drift problem may also occur. For the sake of considering a trade-off between the control performance and cost consumption, it is necessary to select the proper parameters through simulation.

Remark 5 It is worth noting that the property (9) is possessed by all sector-bounded quantizers, which means that our method is valid for other forms of quantizers, such as hysteretic quantizers and uniform quantizers.

Remark 6 The scheme of designing a variable structure-quantized controller introduced in [24] can also be applied to our work. The main idea is based on the following properties of (8):

$\left\{\begin{array}{cccc}\hfill & u\left(t\right)\left(1-\varrho \right)\le q\left(u\left(t\right)\right)<u\left(t\right)\left(1+\varrho \right),\hfill & \hfill & u\left(t\right)>\frac{u_{\text{min}}}{1+\varrho },\hfill \\ \hfill & q\left(u\left(t\right)\right)=0,\hfill & \hfill & |u\left(t\right)|\le \frac{u_{\text{min}}}{1+\varrho },\hfill \\ \hfill & u\left(t\right)\left(1+\varrho \right)<q\left(u\left(t\right)\right)\le u\left(t\right)\left(1-\varrho \right),\hfill & \hfill & u\left(t\right)<-\frac{u_{\text{min}}}{1+\varrho }.\hfill \end{array}\right.(51)$

Using the method of [24], the controller u(t) can be designed as

$u\left(t\right)=sign\left(e_n\left(t\right)\right)\left[\frac{1}{1-\rho }\left(|c_n{e}_n\left(t\right)|+|k_n{\tilde{x}}_1\left(t\right)|+|{\widehat{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left(\widehat{\bar{\mathit{x}}}\right)|+|D_t^{\vartheta }{\alpha }_{n-1}^c\left(t\right)|+|e_{n-1}\left(t\right)|\right)+\frac{u_{\text{min}}}{1+\varrho }\right].(52)$

Then, according to (51), one has

$\begin{array}{cc}\hfill e_n\left(t\right)q\left(u\left(t\right)\right)& \le e_n\left(t\right)u\left(t\right)\left(1-\varrho \right)\hfill \\ \hfill & =-|e_n\left(t\right)|\left(|c_n{e}_n\left(t\right)|+|k_n{\tilde{x}}_1\left(t\right)|+|{\widehat{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left(\widehat{\bar{\mathit{x}}}\right)|+|D_t^{\vartheta }{\alpha }_{n-1}^c\left(t\right)|+|e_{n-1}\left(t\right)|+\frac{1-\varrho }{1+\varrho }{u}_{\text{min}}\right)\hfill \\ \hfill & \le -c_n{e}_n^2\left(t\right)-|e_n\left(t\right)k_n{\tilde{x}}_1\left(t\right)|-|e_n\left(t\right){\widehat{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left(\widehat{\bar{\mathit{x}}}\right)|-|e_n\left(t\right)D_t^{\vartheta }{\alpha }_{n-1}^c\left(t\right)|-|e_{n-1}\left(t\right)e_n\left(t\right)|.\hfill \end{array}(53)$

Substituting (53) into (38), one has

$D_t^{\vartheta }{V}_{1,n}\left(t\right)\le -c_n{e}_n^2\left(t\right)-|e_{n-1}\left(t\right)e_n\left(t\right)|-e_n\left(t\right){\tilde{\mathit{W}}}_n^T{\mathbf{\Psi }}_n\left({\widehat{\bar{\mathit{x}}}}_n\right)+\frac{a_n}{r_n}{\tilde{\mathit{W}}}_n\widehat{\mathit{W}}.(54)$

Then, (42) can be rewritten as

$D_t^{\vartheta }{V}_{1,n}\left(t\right)\le -\left(c_n-\frac{{\eta }_n}{2}\right)e_n^2\left(t\right)-|e_{n-1}\left(t\right)e_n\left(t\right)|-\left(\frac{a_n}{2r_n}-\frac{1}{2{\eta }_n}\right){\tilde{\mathit{W}}}_n^T{\tilde{\mathit{W}}}_n+\frac{a_n}{2r_n}{{\mathit{W}}_n^{\ast T}}^{}{\mathit{W}}_n^{\ast }.(55)$

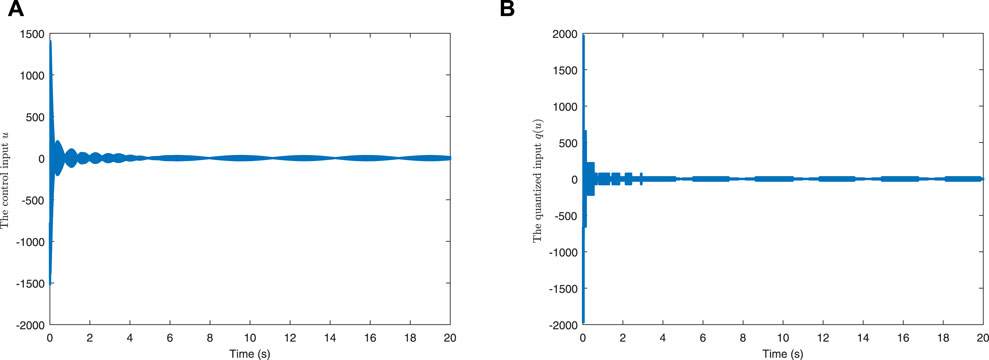
The following analysis is the same as the proof of theorem 1. The controller (52) is valid for controlling system (6), which will be demonstrated in the simulation part; however, because there is a discontinuous function sign (⋅) in (52), a serious chattering phenomenon will occur.

4 Simulation Results

In this section, a simulation example is provided to show the performance of the proposed method, and this example will show the superiority of our method in comparison with [24].

We consider the fractional-order Chua–Hartley’s chaotic system

$\left\{\begin{array}{cc}\hfill D_t^{0.98}{x}_1\left(t\right)& =\frac{10}{7}\left(x_1\left(t\right)-x_1^3\left(t\right)\right)+x_2\left(t\right),\hfill \\ \hfill D_t^{0.98}{x}_2\left(t\right)& =10x_1\left(t\right)-x_2\left(t\right)+x_3\left(t\right),\hfill \\ \hfill D_t^{0.98}{x}_3\left(t\right)& =-\frac{99}{7}{x}_2\left(t\right)+q\left(u\left(t\right)\right),\hfill \end{array}\right.(56)$

where $f_1({\bar{\mathit{x}}}_1)=\frac{10}{7}\left(x_1(t)-x_1^3(t)\right)$, $f_2({\bar{\mathit{x}}}_2)=10x_1(t)-x_2(t)$ and $f_3({\bar{\mathit{x}}}_3)=-\frac{99}{7}{x}_2(t)$. For the purpose of simulation, three FLSs are needed to approximate $f_1({\widehat{\bar{\mathit{x}}}}_1)$, $f_2({\widehat{\bar{\mathit{x}}}}_2)$, and $f_3({\widehat{\bar{\mathit{x}}}}_3)$ corresponding to $f_1({\bar{\mathit{x}}}_1)$, $f_2({\bar{\mathit{x}}}_2)$, and $f_3({\bar{\mathit{x}}}_3)$, respectively. For the first FLS, the input is x₁(t), and three Gaussian membership functions which are uniformly distributed on [ − 3, 3] are defined. Hence, three fuzzy rules are used, and the initial condition of ${\widehat{\mathit{W}}}_1$ is randomly chosen in ${\mathbb{R}}^3$. For the second FLS, the inputs are x₁(t) and ${\widehat{x}}_2(t)$, and for each input, three Gaussian membership functions which are uniformly distributed on [ − 5, 5] are used. Thus, nine fuzzy rules are used in this FLS, and the initial condition of ${\widehat{\mathit{W}}}_2$ is randomly chosen in ${\mathbb{R}}^9$. For the third FLS, the inputs are x₁(t), ${\widehat{x}}_2(t)$ and ${\widehat{x}}_3(t)$, and three Gaussian membership functions are defined which are the same as the first FLS. Twenty seven fuzzy rules are used, and the initial condition of ${\widehat{\mathit{W}}}_3$ is randomly chosen in ${\mathbb{R}}^{27}$. The initial condition of (56) is $\bar{\mathit{x}}(0)=[0.6,0.2,0.3]$, and the referenced signal is $y_d(t)=\frac{1}{2}\sin t$.

The parameter selections are chosen as follows. First, we set c₁ = 4 and c₂ = 4 for the virtual inputs in (21) and (29), respectively; second, we set c₃ = 5, χ = 0.15 and γ = 1.5 for the controller in (36); third, we set K = [k₁, k₂, k₃] = [10, 30, 200] and $\widehat{\bar{\mathit{x}}}(0)=[\mathrm{0,0,0}]$ for the observer in (15); fourth, we set r₁ = r₂ = r₃ = 0.15 and a₁ = a₂ = a₃ = 0.2 for the parameter adaptation laws in (23), (31), and (37); fifth, we set β₁ = β₂ = 5 and ζ₁ = ζ₂ = 0.5 for the filter in (20) and (28), respectively; and finally, we set u_min = 0.1 and ξ = 0.5 for the logarithmic quantizer (8).

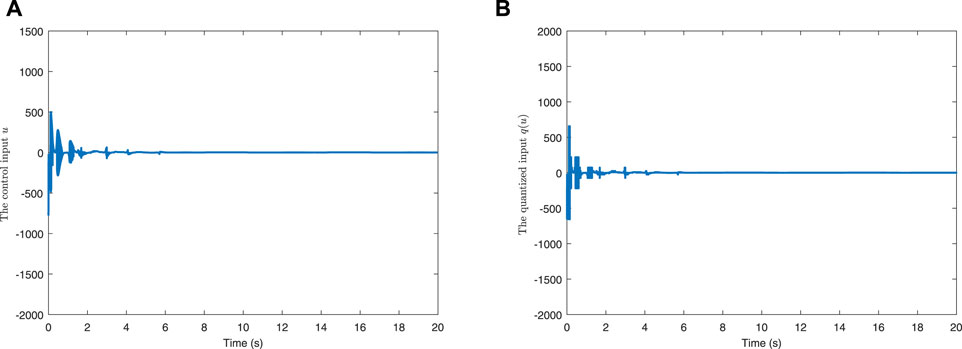
The simulation result of the tracking trajectory is presented in Figure 1A. It is clear that our method achieves a better control effect. The real states of system 56) and the estimated states are shown in Figures 1B–D. However, because of the existence of fuzzy errors, the observer curves and the real state curves cannot be completely consistent. The actual control input and the corresponding quantized input are displayed in Figure 2A and Figure 2B, respectively.

FIGURE 1

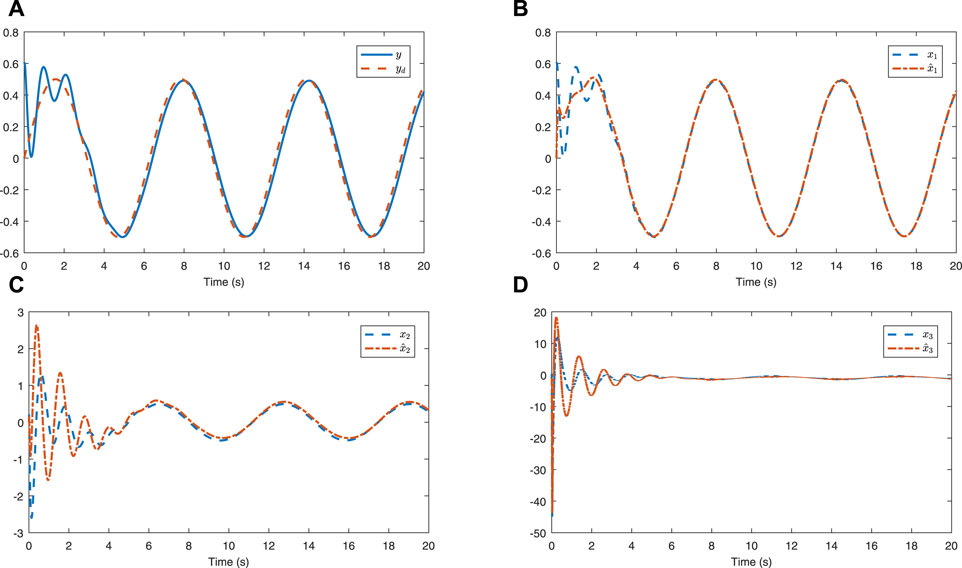
FIGURE 1. (A) Tracking performance of the output y(t). (B) x₁(t) and ${\widehat{x}}_1(t)$. (C) x₂(t) and ${\widehat{x}}_2(t)$. (D) x₃(t) and ${\widehat{x}}_3(t)$.

FIGURE 2

FIGURE 2. (A) Control input u(t). (B) Quantized input q (u(t)).

To reflect the superiority of our approach, the actual control input and the corresponding quantized input by using the method of [24] are depicted in Figure 3A and Figure 3B, respectively, and the performance comparison between the two methods is shown in Figure 4. It can be seen that under the same parameter-setting conditions, compared with [24], not only is the control effect almost the same, but also the ability to save the control energy and reduce the chattering has been greatly improved.

FIGURE 3

FIGURE 3. (A) Control input u(t). (B) Quantized input q (u(t)).

FIGURE 4

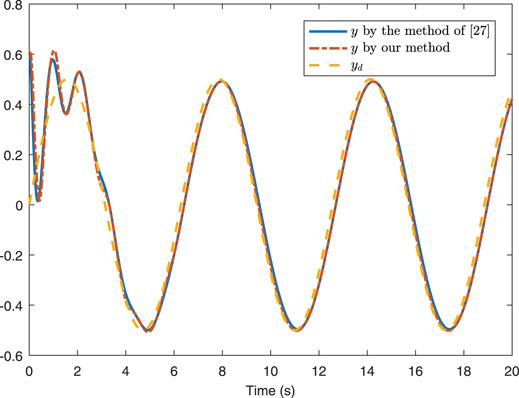
FIGURE 4. Comparative results between our approach and the method proposed by [24].

Remark 7 In this simulation, the step size is selected as h = 0.001s. In fact, since the use of the hyperbolic tangent function instead of the function sign (⋅), the input of the controller is continuous, so the chattering phenomenon does not exist theoretically. If the step size is selected as h = 0.0001s, and γ is increased, the chatting will be reduced to some extent.

5 Conclusion

The tracking control problem for strict-feedback FONSs with unknown states and functional uncertainties has been addressed in this study via the backstepping algorithm. To decrease the data transmission pressure and make use of communication channel effectively, a logarithmic quantizer is considered in the controller design. With the help of the fractional Lyapunov stability criterion, the tracking error and the estimation error converge to a small region near the origin and the boundedness of all the signals of the controlled plant is guaranteed. However, on the one hand, because of the existence of fuzzy errors, the control performance may be affected. On the other hand, the chattering phenomenon still exists. Hence, further work will focus on how to improve the recognition accuracy of FLSs and eliminate the chattering.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by the National Natural Science Foundation of China under Grant No. 12001012 and the Natural Science Foundation of Anhui Province of China under Grant No. 2008085QA10.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Magin RL. Fractional Calculus Models of Complex Dynamics in Biological Tissues. Comput Mathematics Appl (2010) 59(5):1586–93. doi:10.1016/j.camwa.2009.08.039

CrossRef Full Text | Google Scholar

2. Ali Akbar M, Ali NHM, Mohd. Ali N, Tarikul Islam M. Multiple Closed Form Solutions to Some Fractional Order Nonlinear Evolution Equations in Physics and Plasma Physics. AIMS Mathematics (2019) 4(3):397–411. doi:10.3934/math.2019.3.397

CrossRef Full Text | Google Scholar

3. Yousefpour A, Jahanshahi H, Munoz-Pacheco JM, Bekiros S, Wei Z. A Fractional-Order Hyper-Chaotic Economic System with Transient Chaos. Chaos, Solitons & Fractals (2020) 130:109400. doi:10.1016/j.chaos.2019.109400

CrossRef Full Text | Google Scholar

4. Kumar D, Singh J. Fractional Calculus in Medical and Health Science. Boca Raton, FL: CRC Press (2020).

Google Scholar

5. Li Y, Chen Y, Podlubny I. Mittag-Leffler Stability of Fractional Order Nonlinear Dynamic Systems. Automatica (2009) 45(8):1965–9. doi:10.1016/j.automatica.2009.04.003

CrossRef Full Text | Google Scholar

6. Lu JG. Chaotic Dynamics and Synchronization of Fractional-Order Arneodo's Systems. Chaos, Solitons & Fractals (2005) 26(4):1125–33. doi:10.1016/j.chaos.2005.02.023

CrossRef Full Text | Google Scholar

7. Shukla MK, Sharma BB. Backstepping Based Stabilization and Synchronization of a Class of Fractional Order Chaotic Systems. Chaos, Solitons & Fractals (2017) 102:274–84. doi:10.1016/j.chaos.2017.05.015

CrossRef Full Text | Google Scholar

8. Liu H, Pan Y, Li S, Chen Y. Adaptive Fuzzy Backstepping Control of Fractional-Order Nonlinear Systems. IEEE Trans Syst Man Cybern, Syst (2017) 47(8):2209–17. doi:10.1109/tsmc.2016.2640950

CrossRef Full Text | Google Scholar

9. Ha S, Liu H, Li S, Liu A. Backstepping-based Adaptive Fuzzy Synchronization Control for a Class of Fractional-Order Chaotic Systems with Input Saturation. Int J Fuzzy Syst (2019) 21(5):1571–84. doi:10.1007/s40815-019-00663-5

CrossRef Full Text | Google Scholar

10. Liu H, Pan Y, Cao J. Composite Learning Adaptive Dynamic Surface Control of Fractional-Order Nonlinear Systems. IEEE Trans Cybern (2020) 50(6):2557–67. doi:10.1109/TCYB.2019.2938754

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ha S, Chen L, Liu H. Command Filtered Adaptive Neural Network Synchronization Control of Fractional-Order Chaotic Systems Subject to Unknown Dead Zones. J Franklin Inst (2021) 358(7):3376–402. doi:10.1016/j.jfranklin.2021.02.012

CrossRef Full Text | Google Scholar

12. Wei Y, Du B, Cheng S, Wang Y. Fractional Order Systems Time-Optimal Control and its Application. J Optim Theor Appl (2017) 174(1):122–38. doi:10.1007/s10957-015-0851-4

CrossRef Full Text | Google Scholar

13. Sheng D, Wei Y, Cheng S, Wang Y. Observer-based Adaptive Backstepping Control for Fractional Order Systems with Input Saturation. ISA Trans (2018) 82:18–29. doi:10.1016/j.isatra.2017.06.021

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kong S, Saif M, Liu B. Observer Design for a Class of Nonlinear Fractional-Order Systems with Unknown Input. J Franklin Inst (2017) 354(13):5503–18. doi:10.1016/j.jfranklin.2017.06.011

CrossRef Full Text | Google Scholar

15. Zhong F, Li H, Zhong S. State Estimation Based on Fractional Order Sliding Mode Observer Method for a Class of Uncertain Fractional-Order Nonlinear Systems. Signal Process. (2016) 127:168–84. doi:10.1016/j.sigpro.2016.02.022

CrossRef Full Text | Google Scholar

16. Phat V, Niamsup P, Thuan MV. A New Design Method for Observer-Based Control of Nonlinear Fractional-Order Systems with Time-Variable Delay. Eur J Control (2020) 56:124–31. doi:10.1016/j.ejcon.2020.02.005

CrossRef Full Text | Google Scholar

17. Yen DTH, Huong DC. Functional Interval Observers for Nonlinear Fractional-Order Systems with Time-Varying Delays and Disturbances. Proc Inst Mech Eng J Syst Control Eng (2021) 235(4):550–62. doi:10.1177/0959651820945828

CrossRef Full Text | Google Scholar

18. Kammogne AST, Kountchou MN, Kengne R, Azar AT, Fotsin HB, Ouagni STM. Polynomial Robust Observer Implementation Based Passive Synchronization of Nonlinear Fractional-Order Systems with Structural Disturbances. Front Inform Technol Electron Eng (2020) 21(9):1369–86. doi:10.1631/fitee.1900430

CrossRef Full Text | Google Scholar

19. Zhan T, Tian J, Ma S. Full-order and Reduced-Order Observer Design for One-Sided Lipschitz Nonlinear Fractional Order Systems with Unknown Input. Int J Control Autom Syst (2018) 16(5):2146–56. doi:10.1007/s12555-017-0684-z

CrossRef Full Text | Google Scholar

20. Cittanti D, Gregorio M, Mandrile F, Bojoi R. Full Digital Control of an All-Si On-Board Charger Operating in Discontinuous Conduction Mode. Electronics (2021) 10(2):203. doi:10.3390/electronics10020203

CrossRef Full Text | Google Scholar

21. Chaker MA, Triki A. The Branching Redesign Technique Used for Upgrading Steel-Pipes-Based Hydraulic Systems: Re-examined. J Press Vessel Technology (2021) 143(3):031302. doi:10.1115/1.4047829

CrossRef Full Text | Google Scholar

22. Choi YH, Yoo SJ. Neural-networks-based Adaptive Quantized Feedback Tracking of Uncertain Nonlinear Strict-Feedback Systems with Unknown Time Delays. J Franklin Inst (2020) 357(15):10691–715. doi:10.1016/j.jfranklin.2020.08.046

CrossRef Full Text | Google Scholar

23. Zhou J, Wen C, Yang G. Adaptive Backstepping Stabilization of Nonlinear Uncertain Systems with Quantized Input Signal. IEEE Trans Automatic Control (2013) 59(2):460–4. doi:10.1109/TAC.2013.2270870

CrossRef Full Text | Google Scholar

24. Aslmostafa E, Ghaemi S, Badamchizadeh MA, Ghiasi AR. Adaptive Backstepping Quantized Control for a Class of Unknown Nonlinear Systems. ISA Trans (2021). doi:10.1016/j.isatra.2021.06.009

CrossRef Full Text | Google Scholar

25. Abdelrahim M, Dolk VS, Heemels WPMH. Event-triggered Quantized Control for Input-To-State Stabilization of Linear Systems with Distributed Output Sensors. IEEE Trans Automat Contr (2019) 64(12):4952–67. doi:10.1109/tac.2019.2900338

CrossRef Full Text | Google Scholar

26. Zhou J, Wen C, Wang W, Yang F. Adaptive Backstepping Control of Nonlinear Uncertain Systems with Quantized States. IEEE Trans Automat Contr (2019) 64(11):4756–63. doi:10.1109/tac.2019.2906931

CrossRef Full Text | Google Scholar

27. Yoo SJ, Park BS. Quantized-states-based Adaptive Control against Unknown Slippage Effects of Uncertain mobile Robots with Input and State Quantization. Nonlinear Anal Hybrid Syst (2021) 42:101077. doi:10.1016/j.nahs.2021.101077

CrossRef Full Text | Google Scholar

28. Song S, Park JH, Zhang B, Song X, Zhang Z. Adaptive Command Filtered Neuro-Fuzzy Control Design for Fractional-Order Nonlinear Systems with Unknown Control Directions and Input Quantization. IEEE Transactions on Systems, Man, and Cybernetics: Systems (2020) 51(11):7238–7249. doi:10.1109/TSMC.2020.2967425

CrossRef Full Text | Google Scholar

29. Bao H, Park JH, Cao J. Adaptive Synchronization of Fractional-Order Output-Coupling Neural Networks via Quantized Output Control. IEEE Transactions on Neural Networks and Learning Systems (2020) 32(7):3230–3239. doi:10.1109/TNNLS.2020.3013619

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Sabeti F, Shahrokhi M, Moradvandi A. Adaptive Asymptotic Tracking Control of Uncertain Fractional-Order Nonlinear Systems with Unknown Quantized Input and Control Directions Subject to Actuator Failures. J Vibration Control (2021) 10775463211017718. doi:10.1177/10775463211017718

CrossRef Full Text | Google Scholar

31. Karthick SA, Sakthivel R, Ma YK, Mohanapriya S, Leelamani A. Disturbance Rejection of Fractional-Order T-S Fuzzy Neural Networks Based on Quantized Dynamic Output Feedback Controller. Appl Mathematics Comput (2019) 361:846–57. doi:10.1016/j.amc.2019.06.029

CrossRef Full Text | Google Scholar

32. Zouari F, Boulkroune A, Ibeas A. Neural Adaptive Quantized Output-Feedback Control-Based Synchronization of Uncertain Time-Delay Incommensurate Fractional-Order Chaotic Systems with Input Nonlinearities. Neurocomputing (2017) 237:200–25. doi:10.1016/j.neucom.2016.11.036

CrossRef Full Text | Google Scholar

33. Podlubny I. Fractional Differential Equations: an Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Elsevier (1998).

Google Scholar

34. Dai H, Chen W. New Power Law Inequalities for Fractional Derivative and Stability Analysis of Fractional Order Systems. Nonlinear Dyn (2017) 87(3):1531–42. doi:10.1007/s11071-016-3131-4

CrossRef Full Text | Google Scholar

35. Wang L-X. Adaptive Fuzzy Systems and Control: Design and Stability Analysis. Upper Saddle River, NJ: Prentice-Hall (1994).

Google Scholar

36. Jiang X, Mu X, Hu Z. Decentralized Adaptive Fuzzy Tracking Control for a Class of Nonlinear Uncertain Interconnected Systems with Multiple Faults and Denial-Of-Service Attack. IEEE Trans Fuzzy Syst (2020) 29(10):3130–41. doi:10.1109/TFUZZ.2020.3013700

CrossRef Full Text | Google Scholar

37. Hua C, Ning J, Zhao G, Li Y. Output Feedback NN Tracking Control for Fractional-Order Nonlinear Systems with Time-Delay and Input Quantization. Neurocomputing (2018) 290:229–37. doi:10.1016/j.neucom.2018.02.047

CrossRef Full Text | Google Scholar