- Universities Joint Key Laboratory of Photoelectric Detection Science and Technology in Anhui Province, and School of Physics and Materials Engineering, Hefei Normal University, Hefei, China
Unlike classical correlation, quantum entanglement cannot be freely shared among many parties. This restricted shareability of entanglement among multi-party systems is known as monogamy of entanglement, which is one of the most fundamental properties of entanglement. Here, we summarize recent theoretical progress in the field of monogamy of entanglement. We firstly review the standard CKW-type monogamy inequalities in terms of various entanglement measures. In particular, the squashed entanglement and one-way distillable entanglement are monogamous for arbitrary dimensional systems. We then introduce some generalized version of monogamy inequalities which extend and sharpen the traditional ones. We also consider the dual polygamy inequalities for multi-party systems. Moreover, we present two new definitions to define monogamy of entanglement. Finally, some challenges and future directions for monogamy of entanglement are highlighted.
1 Introduction
Quantum entanglement has been recognized as the most important resource in many quantum information processing tasks [1–3]. One of the essential differences between quantum entanglement and classical correlation is that quantum entanglement cannot be freely shared among many parties. For example, in a multi-party state, if two parties are maximally entangled, then none of them can share entanglement with any part of the rest of the system. This restriction of entanglement shareability among multi-party systems is known as the monogamy of entanglement (MOE) [4, 5].
Since the MOE restricts on the amount of information that an eavesdropper could potentially obtain the secret key extraction, it is a crucial property that guarantees quantum key distribution secure [3, 4, 6]. MOE also has many fundamental applications in other areas of physics, including classification of quantum states [7–9], no-signaling theories [10], condensed-matter physics [11–13], statistical physics [14] and even black-hole physics [15].
An important basic question in the study of MOE is to determine whether a given entanglement measure is monogamous. Usually, there are several ways to define the monogamy property of entanglement measure. Originally, a monogamy relation of entanglement measure E is quantitatively displayed as an inequality of the following form
where E(ρA|BC) is an entanglement measure quantifying the degree of entanglement between subsystems A and BC, and E(ρA|B) (E(ρA|C)) is the bipartite entanglement between A and B (A and C) (See Figure 1 for a graphical representation). This inequality means that the sum of entanglement between A and each of the other parties B or C cannot exceed the entanglement between A and BC. Using squared concurrence (SC) as an entanglement measure, Coffman, Kundu and Wootters (CKW) proved the first monogamy inequality for three qubit states [16] which we shall refer to as the CKW inequality. The CKW inequality was later generalized by Osborne and Verstraete for arbitrary multi-qubit system. It should be noticed that the entanglement of formation (EOF), when not squared, does not obey the monogamy relation given by Eq. 1 [17]. Besides SC, it was further proven that similar monogamy inequality can be established for the squared entanglement of formation (SEF) [18, 19], Rényi-α entanglement (RαE) [20], the squared Rényi-α entanglement (SRαE) [21], Tsallis-q entanglement (TqE) [22], the squared Tsallis-q entanglement (STqE) [23, 24], and unified-(q, s) entanglement [25]. The establishment of these inequalities depends on monogamy inequality of SC. In this sense, these inequalities can be classified into concurrence-based monogamy relations. For high-dimensional systems, it has been shown that monogamy inequality of SC can be violated due to the existence of counterexamples [26, 27]. At present, it is still unclear whether other concurrence-based monogamy relations hold in high-dimensional systems.
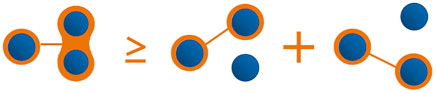
FIGURE 1. (color online). Schematic picture of the CKW-type monogamy relation described by Eq. 1.
Another way to generalize the CKW inequality is using negativity [28] or convex-roof extended negativity (CREN) [26], and CREN is a good candidate for MOE without any known example violating its CKW-type inequality even in higher-dimensional systems [26]. More recently, Gao et al [29] established a class of CKW-type monogamy inequalities based on the μ-th power of logarithmic negativity and logarithmic convex-roof extended negativity (LCREN). The CKW-type inequality was also generalized to other entanglement measures, such as squashed entanglement [30, 31], one-way distillable entanglement [30] and continuous-variable entanglement [32–34]. Among them, the squashed entanglement and one-way distillable entanglement fulfill Eq. 1 for arbitrary dimensional systems. Furthermore, other types of monogamy relations were presented in Refs. [35–51]. In particular, Regula et al [52, 53] have proposed a set of strong monogamy (SM) inequalities sharpening the conventional CKW-type inequality. For the validity of SM inequality, an extensive numerical evidence was presented for four qubit pure states together with analytical proof for some cases of multi-qubit systems.
On the other hand, the polygamous property can be regarded as another kind of entanglement constraints in multi-qubit systems, and Gour et al [54] established the first dual polygamy inequality for multi-qubit systems using concurrence of Assistance (CoA). Subsequently, polygamy inequalities was generalized into various entanglement measures [55–64].
However, the main problem with the definition of monogamy in Eq. 1 is that their validity is not universal, but depends on the specific choice of E. Moreover, several important measures of entanglement do not satisfy the relation (1). Therefore, the summation in the right-hand sides of Eq. 1 is only a convenient choice and not a necessity. To overcome this problem, one attempt is to replace Eq. 1 with a family of monogamy relations of the form E(ρA|BC) ≥ f (E (ρA|B), E (ρA|C)), where f is some function of two variables that satisfies certain conditions [65]. Another approach is based on the definition of monogamy relations without inequalities introduced in Ref. [66]. According to this definition, we can reproduce the traditional monogamy relations similar to Eq. 1 by replacing E with Eα for some α > 0.
In this review, we focus on introducing theoretical advances on monogamy of quantum entanglement but not include the topic of quantum correlations, see Ref. [67] for the summary of recent advances in monogamy of quantum correlations. In Sec.II, we firstly review the standard CKW-type monogamy inequalities in terms of various entanglement measures. In Sec.III, we then introduce some other types of monogamy inequalities which extend and sharpen the existing ones. In Sec.IV, we focus on reviewing the dual polygamy inequalities for multi-qubit systems. The new definitions of MOE are discussed in Sec.V. Finally, in Sec. VI, we give some concluding remarks.
2 CKW-Type Inequalities
In this section we briefly review the CKW-type monogamy inequality and we divide them into three categories according to different entanglement measures.
2.1 Concurrence-Based Inequalities
We start by recalling the monogamy inequality introduced by Coffman, Kundu and Wootters (CKW) [16] for three-qubit states
where C2 denote the squared concurrence for quantifying bipartite entanglement. For an arbitrary two-qubit state, concurrence is defined as [68, 69] C(ρ) = max{0, λ1 − λ2 − λ3 − λ4}, in which λ1, λ2, λ3, λ4 are the square root of the eigenvalues of the matrix ρ(σy ⊗ σy)ρ*(σy ⊗ σy)in decreasing order, σy is the Pauli spin matrix and ρ* denotes the complex conjugate of ρ. Usually, Eq. 2 is termed as CKW inequality, and it shows a tradeoff relation between the amount of entanglement shared by qubits A and B and the entanglement shared by qubits A and C. For three-qubit pure states, the difference between left and right-hand sides of Eq. 2 is interpreted as a genuine three-qubit entanglement measure, three tangle. It has been proved that three-tangle is an entanglement monotone, and the generalization of the three-tangle to mixed states can be obtained by the convex roof method [70–72]. Later, CKW inequality was generalized to the multi-qubit case,
where the Rényi-α entropy is
2.2 Negativity-Based Inequalities
Another well-known bipartite entanglement measure is negativity [76? ]. It is a rare entanglement measure which is easy to compute for pure as well for mixed bipartite states. For any bipartite state ρAB in the Hilbert space
where
where
where the minimum is taken over all possible pure state decompositions of
and Gao et al have shown that LCREN is an entanglement monotone under LOCC operations but not convex. For any n-qubit pure state
2.3 Other CKW-Type Inequalities
We now summarize other CKW-type inequalities in terms of various entanglement measure. Firstly, we consider the squashed entanglement introduced in Refs. [82, 83], which is the first additive measure with good asymptotic properties. It is defined as
where the infimum is taken over all extensions ρABE of the state ρAB and I (A: B|E) = S (ρAE) + S (ρBE) − S (ρABE) − S (ρE) is the conditional quantum mutual information. For any tripartite state ρABC, Koashi and Winter [30] have proved that squashed entanglement obeys the following CKW-type inequality:
and the above form of inequality is also true for the one-way distillable entanglement introduced in Ref. [30]. Although squashed entanglement and one-way distillable entanglement satisfies the CKW inequality for arbitrary dimensional systems, there is no analytical formula to calculate these entanglement measures.
The CKW-type inequality has also been generalized to the continuous variable systems. By introducing the continuous-variable (CV) tangle (contangle) to quantify entanglement sharing in Gaussian states, Adesso et al [32]proved the monogamy inequality for arbitrary three-mode Gaussian states and for symmetric n-mode Gaussian states. Here, contangle is defined as the convex roof of the square of the logarithmic negativity. Moreover, Hiroshima et al have generalized the monogamy inequality to all n-mode Gaussian states of in terms of squared negativity [33].
3 Strong Monogamy Inequalities
In this section we focus on reviewing some generalized version of monogamy relation. It is well known that tightening the monogamy inequalities can provide a precise characterization of the entanglement sharing and distribution in multipartite systems, thus it is important to find tight monogamy inequalities for various entanglement measure. We first consider the strong monogamy (SM) inequality introduced by Regula et al [52]. For an n-qubit pure state |ψ⟩, it was conjectured that the following inequality holds:
where the index vector
with the minimization over all possible pure state decompositions
For the validity of SM inequality, an extensive numerical evidence has been presented for four-qubit state together with analytical proof for some cases of multi-qubit state. Another generalization of SM inequality in terms of squared convex roof extended negativity (SCREN) has been presented by Choi and Kim [84], and it is shown that the superposition of the generalized W-class states and vacuum (GWV) states satisfy the SM inequality based on SCREN. In Ref. [85], Kim further proved that SM inequality holds good even in a class of higher dimensional state where the original SM inequality fails.
Next we present some other generalized version of monogamy relation. In Ref. [42], Jin et al have investigated tighter entanglement monogamy relations related to Cμ and Eμ for μ ≥ 2 and
4 Polygamy Inequalities
In previous section, we have reviewed MOE which reveals the limited shareability of multiparty quantum entanglement, the assisted entanglement was shown to have a dually monogamous property in multi-party quantum systems, i.e., polygamy of entanglement (PoE). PoE is mathematically characterized as the polygamy inequality
for a three-party quantum state and Ea (ρA|BC) denotes the bipartite assisted entanglement in the partition A|BC. In contrast to monogamy inequality, which provides an upper bound on the bipartite shareability of entanglement in multi-party systems, the polygamy inequality in Eq. 12 provides a lower bound for distribution of bipartite entanglement in multi-party systems.
The polygamy inequality in (12) was first proposed in three-qubit systems. For a three-qubit pure state |ψ⟩ABC, the following inequality holds.
where τ(|ψ⟩A|BC) is the tangle of the pure state |ψ⟩A|BC between A and BC, and τa (ρAB) = max ∑ipiτ(|ψ⟩AB) is the tangle of assistance of ρAB = TrC|ψ⟩ABC⟨ψ| with the maximum taken over all possible pure-state decomposition ρAB = ∑ipi|ψi⟩AB⟨ψi|. This inequality was generalized into multi-qubit system
For polygamy inequality beyond qubits, it was shown that von Neumann entropy can be used to establish a polygamy inequality of three-party quantum system [55]. We have E(|ψ⟩A|BC) ≤ Ea (ρA|B) + Ea (ρA|C) for any three-party pure state |ψ⟩A|BC, where E(|ψ⟩A|BC) = S (ρA) = − Tr ρA ln ρA is the von Neumann entropy of entanglement between A and BC, and Ea(ρAB) is the entanglement of assistance of ρAB defined by Ea(ρAB) = max ∑ipiE (|ψi⟩AB), where the maximization is taken over all possible pure state decompositions of ρAB. In Ref. [57], a general polygamy inequality of multipartite quantum entanglement was established for arbitrary-dimensional quantum states
5 New Definitions of MOE
In this section we present some alternative methods to define MOE. The main problem with CKW inequalities is that their validity is not universal since several important measures of entanglement do not satisfy Eq. 1. In Ref. [65], Lancien et al raise the following question: Should any entanglement measure be monogamous in a CKW-type sense? In fact, the summation in the right-hand side of Eq. 1 is only a convenient choice but not a necessity. For example, it has been shown that if E does not satisfy the CKW monogamy inequalities, it is still possible to find a positive μ such that Eμ satisfies the Eq. 1. Inspired by this idea, one attempt is to replace Eq. 1 with the following generalized monogamy relation:
where
Another approach to define MOE is given in terms of an equality, as opposed to the traditional monogamy inequality. According to the definition in Ref. [66], a measure of entanglement E is monogamous if for any ρABC ∈ SABC that satisfies
we have that E (ρAC) = 0. With respect to this definition, if the entanglement between system A and the composite system BC is as much as the entanglement that system A shares with subsystem B, then it is left with no entanglement to share with C. If E satisfies Eq.1, then any state ρA|BC that satisfies the definition (15) must E (ρAC) = 0. Therefore, the condition in Eq. 1 is stronger than the definition in Eq. 15. This new definition is consistent with Eq.1 and it has been shown that they are equivalent if and only if there exists 0 ≤ μ ≤ ∞ such that
for all ρABC ∈ SABC with fixed
6 Concluding Remarks and Outlook
The subject of MOE has attracted extensive research interest in the past two decades. In this review, we present the theoretical developments in the field of MOE, as well as some new definitions of MOE. Despite the rapid progress in recent years, there are still many challenging problems to be solved and we briefly list them as follows.
First, most previous studies of MOE are focussed on the multi-qubit systems. But our knowledge of MOE in the high-dimensional case is still very limited and there are few results on MOE for high-dimensional systems [84, 87–90]. In [91] Kim et al. proved that the n-qudit generalized W-class (GW) states satisfy the monogamy inequality in terms of the SC. Recently, Shi et al. presented in [47] new monogamy and polygamy relations for n-qudit generalized W-class states and vacuum (GWV) states in terms of the TqE. In [59, 92] the authors investigated the monogamy and polygamy relations for the GWV states in high-dimensional systems in terms of the RαE. Except for squashed entanglement and one-way distillable entanglement, monogamy relations for various entanglement measures only hold for some special high-dimensional states. The difficulties are caused by the entanglement properties in higher-dimensional systems are hardly known so far and there is no analytical formula for calculating the high-dimensional entanglement measure. Thus, it is important to explore monogamy inequality for general high-dimensional states in terms of various entanglement measures.
Second, the validity of the traditional monogamy inequality is not universal and several important measures of entanglement do not satisfy Eq. 1. However, MOE has been mathematically proven to be a valid property of entanglement in the n-shareability sense [5]. In order to solve this problem, two new definitions of MOE have been proposed. One definition is to replace the right-hand side of Eq. 1 with a universal function f independent of dimension d [65]. This definition [65] is somewhat artificial and some important entanglement measure such as EOF and relative entropy of entanglement cannot satisfy the new monogamy inequality. Another approach is to define MOE with an equality rather than inequality. It was shown that this definition is consistent with the traditional notion of MOE if the measure E is replaced by Eα for some exponent α > 0. According to this new definition, EOF are monogamous on mixed tripartite systems. It supports that monogamy is a property of entanglement and not of some particular functions quantifying entanglement. Although the second definition of MOE seems more natural in physical, there is no mathematical proof of which definition is better, and we do not know whether there are entangled states that violate the second definition. Therefore, extensive efforts are still needed to investigate the relationship between these two definitions. Moreover, by adopting these new definitions, it is necessary to explore whether many important measures of entanglement are monogamous.
Third, different attempts have been made to construct a sharper version of monogamy inequality. In particular, Regula et al [52] have proposed a set of SM inequalities in terms of concurrence. Although an extensive numerical evidence has been presented for four qubit systems, an analytical proof of SM conjecture is still desired. It would also be interesting to answer whether there are counterexamples that violate the SM inequality for more qubits. This conjecture can be further extended to negativity and SCREN for some classes of states. Future directions may include the study of SM inequalities for other entanglement monotones such as squashed entanglement.
In summary, we have reviewed the mathematical foundation of MOE but not include many problems concerning real physical phenomena, and monogamy is being considered in the study of these problems. For example, it was argued that the black hole evaporation is incompatible with our understanding of MOE [93]. Thus, it is desirable for us to have a sufficient understanding of monogamy further.
Author Contributions
XZ and WS conceived the idea. All authors contributed to the writing of the manuscript. All authors reviewed the manuscript.
Funding
This work was supported by NSF-China under Grant Nos.11904071, the Anhui Provincial Natural Science Foundation under Grant Nos.1908085QA40.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Bennett CH, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters WK. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys Rev Lett (1993) 70:1895–9. doi:10.1103/physrevlett.70.1895
2. Bennett CH, Wiesner SJ. Communication via One- and Two-Particle Operators on Einstein-Podolsky-Rosen States. Phys Rev Lett (1992) 69:2881–4. doi:10.1103/physrevlett.69.2881
3. Gisin N, Ribordy G, Tittel W, Zbinden H. Quantum Cryptography. Rev Mod Phys (2002) 74:145–95. doi:10.1103/revmodphys.74.145
5. Yang D. A Simple Proof of Monogamy of Entanglement. Phys Lett A (2006) 360:249–50. doi:10.1016/j.physleta.2006.08.027
6. Pawlowski M. Security Proof for Cryptographic Protocols Based Only on the Monogamy of Bell’s Inequality Violations. Phys Rev A (2010) 82:032313. doi:10.1103/PhysRevA.82.032313
7. Dür W, Vidal G, Cirac JI. Three Qubits Can Be Entangled in Two Inequivalent Ways. Phys Rev A (2000) 62:062314.
8. Giorgi GL. Monogamy Properties of Quantum and Classical Correlations. Phys Rev A (2011) 84:054301. doi:10.1103/physreva.84.054301
9. Prabhu R, Pati AK, Sen A, Sen U. Conditions for Monogamy of Quantum Correlations: Greenberger-Horne-Zeilinger versus W States. Phys Rev A (2012) 85:040102(R). doi:10.1103/physreva.85.040102
10. Streltsov A, Adesso G, Piani M, Bruss D. Are General Quantum Correlations Monogamous? Phys Rev Lett (2012) 109:050503. doi:10.1103/PhysRevLett.109.050503
11. Ma X-s., Dakic B, Naylor W, Zeilinger A, Walther P. Quantum Simulation of the Wavefunction to Probe Frustrated Heisenberg Spin Systems. Nat Phys (2011) 7:399–405. doi:10.1038/nphys1919
12. Brandao FGSL, Harrow AW. Proceedings of the 45th Annual ACM Symposium on Theory of Computing (2013). Available from: http://dl.acm.org/citation.cfm?doid=2488608.2488718. (June 1, 2013).
13. García-Sáez A, Latorre JI. Renormalization Group Contraction of Tensor Networks in Three Dimensions. Phys Rev B (2013) 87:085130.
14. Bennett CH. Proceedings of the FQXi 4th International Conference. Puerto Rico: Vieques Island (2014). Available from: http://fqxi.org/conference/talks/2014. (January 5-10, 2014).
15. Lloyd S, Preskill J. Unitarity of Black Hole Evaporation in Final-State Projection Models. J High Energ Phys. (2014) 2014:126. doi:10.1007/jhep08(2014)126
16. Coffman V, Kundu J, Wootters WK. Distributed Entanglement. Phys Rev A (2000) 61:052306. doi:10.1103/physreva.61.052306
17. Fanchini FF, de Oliveira MC, Castelano LK, Cornelio MF. Why Entanglement of Formation Is Not Generally Monogamous. Phys Rev A (2013) 87:032317. doi:10.1103/physreva.87.032317
18. Bai Y-K, Xu Y-F, Wang ZD. General Monogamy Relation for the Entanglement of Formation in Multiqubit Systems. Phys Rev Lett (2014) 113:100503. doi:10.1103/physrevlett.113.100503
19. Bai YK, Xu YF, Wang ZD. Hierarchical Monogamy Relations for the Squared Entanglement of Formation in Multipartite Systems. Phys Rev A (2014) 90:062343. doi:10.1103/physreva.90.062343
20. Kim JS, Sanders BC. Monogamy of Multi-Qubit Entanglement Using Rényi Entropy. J Phys A: Math Theor (2010) 43:445305. doi:10.1088/1751-8113/43/44/445305
21. Song W, Bai YK, Yang M, Cao ZL. General Monogamy Relation of Multi-Qubit System in Terms of Squared Rényi-α Entanglement. Phys Rev A (2016) 93:022306. doi:10.1103/physreva.93.022306
22. Kim JS. Tsallis Entropy and Entanglement Constraints in Multiqubit Systems. Phys Rev A (2010) 81:062328. doi:10.1103/physreva.81.062328
23. Luo Y, Tian T, Shao LH, Li YM. General Monogamy of Tsallis Q-Entropy Entanglement in Multiqubit Systems. Phys Rev A (2016) 93:062340. doi:10.1103/physreva.93.062340
24. Yuan G-M, Song W, Yang M, Li D-C, Zhao J-L, Cao Z-L. Monogamy Relation of Multi-Qubit Systems for Squared Tsallis-Q Entanglement. Sci Rep (2016) 6:28719. doi:10.1038/srep28719
25. Kim JS, Sanders BC. Unified Entropy, Entanglement Measures and Monogamy of Multi-Party Entanglement. J Phys A: Math Theor (2011) 44:295303. doi:10.1088/1751-8113/44/29/295303
26. Kim JS, Das A, Sanders BC. Entanglement Monogamy of Multipartite Higher-Dimensional Quantum Systems Using Convex-Roof Extended Negativity. Phys Rev A (2009) 79:012329. doi:10.1103/physreva.79.012329
27. Ou Y. Violation of Monogamy Inequality for Higher-Dimensional Objects. Phys Rev A (2007) 75:034305. doi:10.1103/physreva.75.034305
28. Ou YC, Fan H. Monogamy Inequality in Terms of Negativity for Three-Qubit States. Phys Rev A (2007) 75:062308. doi:10.1103/physreva.75.062308
29. Gao L-M, Yan F-L, Gao T. Monogamy of Logarithmic Negativity and Logarithmic Convex-Roof Extended Negativity. arXiv:2007.09573 (2007).
31. Yang D, Horodecki K, Horodecki M, Horodecki P, Oppenheim J, Song W. Squashed Entanglement for Multipartite States and Entanglement Measures Based on the Mixed Convex Roof. IEEE Trans Inform Theor (2009) 55:3375–87. doi:10.1109/tit.2009.2021373
32. Adesso G, Illuminati F. Continuous Variable Tangle, Monogamy Inequality, and Entanglement Sharing in Gaussian States of Continuous Variable Systems. New J Phys (2006) 8:15. doi:10.1088/1367-2630/8/1/015
33. Hiroshima T, Adesso G, Illuminati F. Monogamy Inequality for Distributed Gaussian Entanglement. Phys Rev Lett (2007) 98:050503. doi:10.1103/PhysRevLett.98.050503
34. Adesso G, Illuminati F. Strong Monogamy of Bipartite and Genuine Multipartite Entanglement: The Gaussian Case. Phys Rev Lett (2007) 99:150501. doi:10.1103/physrevlett.99.150501
35. Bandyopadhyay S, Gour G, Sanders BC. Duality for Monogamy of Entanglement. J Math Phys (2007) 48:012108.
36. Yu C-s., Song H-s. Monogamy and Entanglement in Tripartite Quantum States. Phys Lett A (2009) 373:727–30. doi:10.1016/j.physleta.2008.12.058
37. Cornelio MF. Multipartite Monogamy of the Concurrence. Phys Rev A (2013) 87:032330. doi:10.1103/physreva.87.032330
38. De Oliveira TR, Cornelio MF, Fanchini FF. Monogamy of Entanglement of Formation. Phys Rev A (2014) 89:034303. doi:10.1103/physreva.89.034303
39. Zhu X-N, Fei S-M. Entanglement Monogamy Relations of Qubit Systems. Phys Rev A (2014) 90:024304. doi:10.1103/physreva.90.024304
40. Zhu X-N, Fei S-M. Generalized Monogamy Relations of Concurrence for N-Qubit Systems. Phys Rev A (2015) 92:062345. doi:10.1103/physreva.92.062345
41. Liu F, Gao F, Wen Q-Y. Linear Monogamy of Entanglement in Three-Qubit Systems. Sci Rep (2015) 5:16745. doi:10.1038/srep16745
42. Jin Z-X, Fei S-M. Tighter Entanglement Monogamy Relations of Qubit Systems. Quan Inf Process (2017) 16:77. doi:10.1007/s11128-017-1520-3
43. Jin Z-X, Li J, Li T, Fei S-M. Tighter Monogamy Relations in Multipartite Systems. Phys Rev A (2018) 97:032336. doi:10.1103/physreva.97.032336
44. Kim JS. Hamming Weight and Tight Constraints of Multi-Qubit Entanglement in Terms of Unified Entropy. Sci Rep (2018) 8:12245. doi:10.1038/s41598-018-30766-2
45. Gao L-M, Yan F-L, Gao T. Tighter Monogamy Relations of Multiqubit Entanglement in Terms of Rényi-α Entanglement. Commun Theor Phys (2020) 72:085102. doi:10.1088/1572-9494/ab7ece
46. Char P, Dey PK, Kundu A, Chattopadhyay I, Sarkar D. Monogamy Relations for Multiqubit Systems. arXiv:2012.06429 (2012).
47. Shi X. Monogamy Relations for Generalized W Class States in Terms of Tsallis Entropy beyond Qubits. Phys Rev A (2020) 101:032344. doi:10.1103/physreva.101.032344
48. Yang X, Luo M-X. Unified Monogamy Relation of Entanglement Measures. Quan Inf Process (2021) 20:108. doi:10.1007/s11128-021-03041-z
49. Shi X, Chen L, Hu M. Multi-linear Monogamy Relations for Three Qubit States. Phys Rev A (2021) 104:012426. doi:10.1103/physreva.104.012426
50. Yang Y, Chen W, Li G, Zheng Z-J. Generalized Monogamy Inequalities of Convex-Roof Extended Negativity in N-Qubit Systems. Phys Rev A (2018) 97:012336. doi:10.1103/physreva.97.012336
51. Eltschka C, Osterloh A, Siewert J. Possibility of Generalized Monogamy Relations for Multipartite Entanglement beyond Three Qubits. Phys Rev A (2009) 80:032313. doi:10.1103/physreva.80.032313
52. Regula B, Di Martino S, Lee S, Adesso G. Strong Monogamy Conjecture for Multiqubit Entanglement: The Four-Qubit Case. Phys Rev Lett (2014) 113:110501. doi:10.1103/physrevlett.113.110501
53. Regula B, Osterloh A, Adesso G. Strong Monogamy Inequalities for Four Qubits. Phys Rev A (2016) 93:052338. doi:10.1103/physreva.93.052338
54. Gour G, Meyer DA, Sanders BC. Deterministic Entanglement of Assistance and Monogamy Constraints. Phys Rev A (2005) 72:042329. doi:10.1103/physreva.72.042329
55. Buscemi F, Gour G, Kim JS. Polygamy of Distributed Entanglement. Phys Rev A (2009) 80:012324. doi:10.1103/physreva.80.012324
56. Jin Z-X, Fei S-M. Polygamy Relations of Multipartite Entanglement beyond Qubits. J Phys A: Math Theor (2019) 52:165303. doi:10.1088/1751-8121/ab0ed9
57. Kim JS. General Polygamy Inequality of Multiparty Quantum Entanglement. Phys Rev A (2012) 85:062302. doi:10.1103/physreva.85.062302
58. Kim JS. Polygamy of Multi-Party Q-Expected Quantum Entanglement. Phys Rev A (2019) 100:062332. doi:10.1103/physreva.100.062332
59. Lai L-M, Fei S-M, Wang Z-X. Tighter Monogamy and Polygamy Relations for a Superposition of the Generalized W-Class State and Vacuum. J Phys A: Math Theor (2021) 54:425301. doi:10.1088/1751-8121/ac2475
60. Song W, Yang M, Zhao J-L, Li D-C, Cao Z-L. Polygamy Relation for the Rényi-$$\alpha $$α Entanglement of Assistance in Multi-Qubit Systems. Quan Inf Process (2019) 18:26. doi:10.1007/s11128-018-2143-z
61. Kim JS. Tsallis Entropy and General Polygamy of Multiparty Quantum Entanglement in Arbitrary Dimensions. Phys Rev A (2016) 94:062338. doi:10.1103/physreva.94.062338
62. Song W, Zhao J-L, Yu L-B, Zhang L-H. Comment on ”Unification of Multiqubit Polygamy Inequalities. Phys Rev A (2017) 95:056301. doi:10.1103/physreva.95.056301
63. Kim JS. Unification of Multiqubit Polygamy Inequalities. Phys Rev A (2012) 85:032335. doi:10.1103/physreva.85.032335
64. Kim JS. Weighted Polygamy Inequalities of Multiparty Entanglement in Arbitrary Dimensional Quantum Systems. Phys Rev A (2018) 97:042332. doi:10.1103/physreva.97.042332
65. Lancien C, Di Martino S, Huber M, Piani M, Adesso G, Winter A. Should Entanglement Measures Be Monogamous or Faithful? Phys Rev Lett (2016) 117:060501. doi:10.1103/PhysRevLett.117.060501
66. Gour G, Guo Y. Monogamy of Entanglement without Inequalities. Quantum (2018) 2:81. doi:10.22331/q-2018-08-13-81
67. Dhar HS, Pal AK, Rakshit D, Sen A, Sen U. Monogamy of Quantum Correlations - A Review. In: Lectures on General Quantum Correlations and Their Applications, Part of the Series Quantum Science and Technology. Berlin, Germany: Springer International Publishing (2017). p. 23–64. doi:10.1007/978-3-319-53412-1_3
68. Hill S, Wootters WK. Entanglement of a Pair of Quantum Bits. Phys Rev Lett (1997) 78:5022–5. doi:10.1103/physrevlett.78.5022
69. Wootters WK. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys Rev Lett (1998) 80:2245–8. doi:10.1103/physrevlett.80.2245
70. Uhlmann A. Fidelity and Concurrence of Conjugate States. Phys Rev A (2000) 62:032307. doi:10.1103/physreva.62.032307
71. Lohmayer R, Osterloh A, Siewert J, Uhlmann A. Entangled Three-Qubit States without Concurrence and Three-Tangle. Phys Rev Lett (2006) 97:260502. doi:10.1103/physrevlett.97.260502
72. Eltschka C, Osterloh A, Siewert J, Uhlmann A. Three-tangle for Mixtures of Generalized GHZ and Generalized W States. New J Phys (2008) 10:043014. doi:10.1088/1367-2630/10/4/043014
73. Kumar A. Conditions for Monogamy of Quantum Correlations in Multipartite Systems. Phys Lett A (2016) 380:3044–50. doi:10.1016/j.physleta.2016.07.032
74. Salini K, Prabhu R, Sen A, Sen U. All Multiparty Quantum States Can BeMade Monogamous. Ann Phys (2014) 348:297.
76. Plenio MB. Logarithmic Negativity: a Full Entanglement Monotone that Is Not Convex. Phys Rev Lett (2005) 95:090503. doi:10.1103/PhysRevLett.95.090503
77. He H, Vidal G. Disentangling Theorem and Monogamy for Entanglement Negativity. Phys Rev A (2015) 91:012339. doi:10.1103/physreva.91.012339
78. Peres A. Separability Criterion for Density Matrices. Phys Rev Lett (1996) 77:1413–5. doi:10.1103/physrevlett.77.1413
79. Horodecki M, Horodecki P, Horodecki R. Separability of Mixed States: Necessary and Sufficient Conditions. Phys Lett A (1996) 223:1–8. doi:10.1016/s0375-9601(96)00706-2
80. Horodecki M, Horodecki P, Horodecki R. Mixed-State Entanglement and Distillation: Is There a "Bound" Entanglement in Nature? Phys Rev Lett (1998) 80:5239–42. doi:10.1103/physrevlett.80.5239
81. Luo Y. Monogamy of αth Power Entanglement Measurement in Qubit Systems. Ann Phys (2015) 362:511–20. doi:10.1016/j.aop.2015.08.022
82. Tucci R. Entanglement of Distillation and Conditional Mutual Information. quant-ph/0202144 (2002).
83. Christandl M, Winter A. “Squashed Entanglement”: An Additive Entanglement Measure. J Math Phys (2004) 45:829–40. doi:10.1063/1.1643788
84. Choi JH, Kim JS. Negativity and strong Monogamy of Multiparty Quantum Entanglement beyond Qubits. Phys Rev A (2015) 92:042307. doi:10.1103/physreva.92.042307
85. Kim JS. Strong Monogamy of Multiparty Quantum Entanglement for Partially Coherently Superposed States. Phys Rev A (2016) 93:032331. doi:10.1103/physreva.93.032331
86. Guo Y, Gour G. Monogamy of the Entanglement of Formation. Phys Rev A (2019) 99:042305. doi:10.1103/physreva.99.042305
87. Tian T, Luo Y, Li Y. Generalised Monogamy Relation of Convex-Roof Extended Negativity in Multi-Level Systems. Sci Rep (2016) 6:36700. doi:10.1038/srep36700
88. Kim JS. Entanglement of Formation and Monogamy of Multi-Party Quantum Entanglement. Sci Rep (2021) 11:2364. doi:10.1038/s41598-021-82052-3
89. Jin Z-X, Fei S-M. Finer Distribution of Quantum Correlations Among Multiqubit Systems. Quan Inf Process (2019) 18:21. doi:10.1007/s11128-018-2137-x
90. Jin Z-X, Fei S-M. Monogamy Relations of All Quantum Correlation Measures for Multipartite Quantum Systems. Opt Commun (2019) 446:39–43. doi:10.1016/j.optcom.2019.04.062
91. Kim JS, Sanders BC. Generalized W-Class State and its Monogamy Relation. J Phys A: Math Theor (2008) 41:495301. doi:10.1088/1751-8113/41/49/495301
92. Liang YY, Zheng ZJ, Zhu CJ. Monogamy and Polygamy for Generalized W-Class States Using Rényi-α Entropy. Phys Rev A (2020) 102:062428. doi:10.1103/physreva.102.062428
Keywords: monogamy, quantum entanglement, entanglement measure, multi-party systems, polygamy
Citation: Zong X-L, Yin H-H, Song W and Cao Z-L (2022) Monogamy of Quantum Entanglement. Front. Phys. 10:880560. doi: 10.3389/fphy.2022.880560
Received: 21 February 2022; Accepted: 29 April 2022;
Published: 09 June 2022.
Edited by:
Lin Chen, Beihang University, ChinaReviewed by:
Zhixiang Jin, University of Chinese Academy of Sciences, ChinaUjjwal Sen, Harish-Chandra Research Institute, India
Copyright © 2022 Zong, Yin, Song and Cao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Song, d3NvbmczMTVAcXEuY29t
 Xiao-Lan Zong
Xiao-Lan Zong Wei Song
Wei Song