Realization of Tunable Highly-Efficient Quantum Routing in Chiral Waveguides

The chiral interaction between single photons in waveguides and quantum emitters has gained considerable attention. Here, we proposed a tunable quantum routing scheme with a chiral quantum system by coupling an emitter to two chiral waveguides. Conventional quantum routers can only be achieved with each port output probability no larger than 25%. But our scheme can transfer quantum information arbitrarily from an input port to another, and each port’s output probability is 100%. Besides, we investigated the influence of the Purcell factor in quantum routing properties. No matter how to change the size of the directionalities S_j or set a specific value to the dissipation of the emitter, we always found that the quantum routing has very high efficiency. Moreover, we also used a superconducting qubit coupled to two resonators to show the present scheme is pretty feasible for experimental implementation.

1 Introduction

To further improve the rapid-developing quantum information technology, the establishment of a global quantum network [1] is an inevitable trend in the future. The quantum network requires the realization of quantum entanglement [2–4] among multiple remote quantum memories [5], and enables multi-party quantum communication [6, 7]. Such a network can also be applied to quantum computing, distributing quantum precision measurement and fundamental tests of physics in large-scale space. Quantum internet is consisted of three basic elements, which are quantum nodes, quantum channels and quantum repeaters. Quantum nodes, which generate, process and store quantum information, are connected by long-distance quantum channels, while quantum repeaters establish and distribute entanglement. As one kind of node devices, quantum routers [8–22] are a key component of quantum network, which can transmit information continuously between remote quantum nodes. Photons play significant roles in the construction of quantum router because they are relatively free of the decoherence [23, 24]that plagues other quantum systems, and can be manipulated and detected easily. Thus, photon is an ideal candidate of the flying qubit. The waveguide is conveniently scalable so it can be easily integrated on the chip to expand the number of nodes in the quantum network. Based on these excellent characteristics, the coupled waveguide-emitter system has attracted extensive attention in the field in quantum information processing [25–33] and quantum network. In the last several years, numerous theoretical and experimental jobs have showed a variety of quantum router plans based on superconducting circuit [34], cavity-atom [35], coupled resonator [18, 39], optomechanical system [36], or quantum dot [37] for controlling the photonic transport in quantum networks. However, the expectable routing probabilities from the incident channel to the other quantum channels are limited to no more than 50% in all previous schemes. But in the paper by Li et al [38], they investigate the input-output relations of the system and analyze the effect of the atomic states on the photon transmission. They scheme can route the input signal into different output ports guided by the quantum states of a two-level atom, and they also realized 100% output. In this paper we also present a physical scheme that also achieves the output of 100%. In fact, for a complex quantum network, quantum nodes can not only be used for the localized generation, processing, and storage of quantum information, but also generate and process a single qubit. Therefore, improving the routing capabilities of quantum routers is crucial.

Here, we put forward a plan to realize quantum router, our scheme is composed of two chiral waveguides and a Λ-type three-level system. Similar model has been considered in Ref. [17] to demonstrate nonreciprocal few-photon scatterings. The single-photon scattering amplitudes are given analytically. The result shows that the quantum information incident from one waveguide can be redirected into another with 100% probability when the coupling is chiral. Compared to the previous quantum routing plans [18, 39–43] that are based on single photons, our design quantum routing can transport the quantum information deterministically from an input port to arbitrary output port with high efficiency. Such a chiral quantum system could be a genuinely compact, versatile, and powerful improvement to the development of a complex quantum network.

2 Model Setup

The physical system configuration considered in this article is shown in Figure 1. Similar model has been considered in Ref. [17] to demonstrate nonreciprocal few-photon scatterings. The hybrid system located at x = 0 is consists of two parallel waveguides and an emitter with ground states |g⟩, intermediate state |s⟩ and excited state |e⟩. The waveguides are labeled a and b respectively. In theory, we allow these couplings to be chiral and marked as λ_jL and λ_jR (j = a, b) respectively. When a single photon is incident from the left of waveguide a, it will propagate or be reflected by the atom along with the four ports of the two waveguide channels. Specifically, in this configuration, the perfect nonreciprocity of single-photon transport means when the single photon is incident from the left of a, it will be output from the right of b with a probability of 1. The Hamiltonian of the system is given by (setting ℏ = 1)

$H=H_0+H_w+H_I,(1)$

where H₀, H_w and H_I denote the free atomic Hamiltonian, the free-transport photon in the waveguide Hamiltonian and the interactions between the atom and the waveguides Hamiltonian respectively. The free atomic Hamiltonian H₀ is given by

$\begin{array}{c}\hfill H_0=\left({\omega }_s-i\gamma /2\right)|s\rangle \langle s|+\left({\omega }_e-i\mathrm{\Gamma }/2\right)|e\rangle \langle e|+\mathrm{\Omega }\left(|e\rangle \langle s|+h.c\right)\end{array}$

where ω_s (ω_e) is the frequency of the intermediate (excited)state, γ and Γ account for the spontaneous emission of the state |s⟩ and |e⟩ into other modes different from the waveguide modes, e.g., free space. Ω is the Rabi frequency of the control field that is applied to couple the atomic states |s⟩ and |e⟩. The Hamiltonian of the photon mode in the two waveguides is given by

$\begin{array}{cc}\hfill H_w& =\sum _{j=a,b}\int dx\left[C_{jR}^{†}\left(x\right)\left({\omega }_{0j}-i{\nu }_g\frac{\partial }{\partial x}\right)C_{jR}\left(x\right)\right.\hfill \\ \hfill & \left.+C_{jL}^{†}\left(x\right)\left({\omega }_{0j}+i{\nu }_g\frac{\partial }{\partial x}\right)C_{jL}\left(x\right)\right]\hfill \end{array}$

where ω_0j space is the reference frequency. Here, we set ω_0j = ω_0a = ω_0b. $C_{jR(L)}^{†}(x)$(j = a, b) is the creation operator for the right-moving (left-moving) photon along the waveguide j at position x. ν_g is the group velocity of a photon in waveguide j which is considered as equal in this work. The interaction Hamiltonian is given by

$\begin{array}{ll}\hfill H_I& =\int dx\delta \left(x\right)\left(V_{aR}{C}_{aR}^{†}\left(x\right)|g\rangle \langle e|+V_{aL}{C}_{aL}^{†}\left(x\right)|g\rangle \langle e|+h.c\right)\hfill \\ \hfill & +\int dx\delta \left(x\right)\left(V_{bR}{C}_{bR}^{†}\left(x\right)|g\rangle \langle e|+V_{bL}{C}_{bL}^{†}\left(x\right)|g\rangle \langle e|+h.c\right)\hfill \end{array}$

where δ represents the Dirac δ function. In this expression, we choose the four coupling constants [V_aR, V_aL, V_bR, V_bL] to be real numbers for simplicity. V_{aR(bR) (}V_aL(bL)) is the photon-atom coupling strength for the photon propagating along the right (left) direction, and due to the chiral interactions, V_jR ≠ V_jL (j = a, b). They are related to the final decay rates into the waveguides through ${\lambda }_{jR(L)}=V_{jR(L)}^2/{\nu }_g$. To measure the chiral coupling character, we bring in the parameter [17].

$S_j=|\frac{{\lambda }_{jR}-{\lambda }_{jL}}{{\lambda }_{jR}+{\lambda }_{jL}}|\left(j=a,b\right).(2)$

FIGURE 1

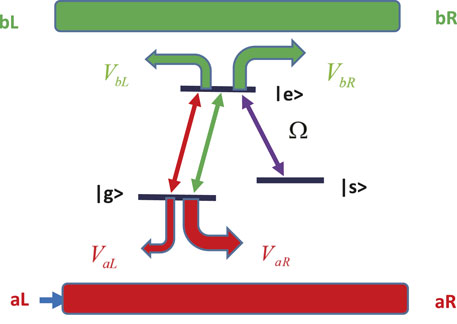
FIGURE 1. Schematic diagram of the system. Two waveguides are chirally coupled to a Λ-type three-level system, the Λ-type three-level system is located at x = 0, and the similar model has been considered in Ref. [17].

Here, S_j = 0 when λ_jR = λ_jL, which occurs in nonchiral interaction, 0 < S_j < 1 when λ_jR ≠ λ_jL, existing chiral interaction, and whereas for maximally asymmetric coupling S_j = 1. The other relevant element is the Purcell factor [44–48], which accounts for the modification of the total decay rate of an emitter placed in the vicinity of a nanostructure, $P=\frac{{\lambda }_a+{\lambda }_b}{\gamma +\mathrm{\Gamma }}$. Finally, λ_j = λ_jR + λ_jL (j = a, b), which accounts for the total decay rate of the excited state |e⟩ and intermediate state |s⟩ into each of the waveguides.

We concentrate on single-photon scattering in this system. Suppose the atom is in the ground state |g⟩ at the initial time. The wave function of the system can be expressed as

$|\psi \rangle =\sum _{j=a,b}\sum _{m=R,L}\int dx{\phi }_{jm}\left(x\right)C_{jm}^{†}\left(x\right)|0g\rangle +u_s|0s\rangle +u_e|0e\rangle (3)$

where φ_jm(x) denotes the probability amplitude of the right or left propagating photon in waveguide a or b. u_s and u_e are the amplitudes of the states |s⟩ and |e⟩, respectively, and |0g⟩ denotes the ground state, wherein there is no photon in the waveguides and the atom is at the ground state |g⟩. Suppose that the single photon is injected from the left of waveguide a, the probability that the photon propagates can be expressed as

$\begin{array}{cc}\hfill {\phi }_{aR}\left(x\right)& =e^{-ikx}\left[\theta \left(-x\right)+t^a\theta \left(x\right)\right],\hfill \\ \hfill {\phi }_{aL}\left(x\right)& =e^{-ikx}{r}^a\theta \left(-x\right),\hfill \\ \hfill {\phi }_{bR}\left(x\right)& =e^{ikx}{t}^b\theta \left(x\right),\hfill \\ \hfill {\phi }_{bL}\left(x\right)& =e^{-ikx}{r}^b\theta \left(-x\right).\hfill \end{array}(4)$

Here, t^a (t^b) denotes the single-photon transmission amplitude in waveguide a(b) and r^a (r^b) denotes the single-photon reflection amplitude in waveguide a(b). θ(x) is the Heaviside step function with θ(0) = 1/2. Using the eigenequation H|ψ⟩ = ω|ψ⟩, we obtain

$\begin{array}{cc}\hfill t^a& =\frac{\left({\lambda }_{aL}-{\lambda }_{aR}+{\lambda }_{bL}+{\lambda }_{bR}\right)\left(\omega -{\omega }_s+i\gamma /2\right)-2i\left(\omega -{\omega }_s+i\gamma /2\right)\left(\omega -{\omega }_e+i\mathrm{\Gamma }/2\right)+2i{\mathrm{\Omega }}^2}{\left({\lambda }_{aL}+{\lambda }_{aR}+{\lambda }_{bL}+{\lambda }_{bR}\right)\left(\omega -{\omega }_s+i\gamma /2\right)-2i\left(\omega -{\omega }_s+i\gamma /2\right)\left(\omega -{\omega }_e+i\mathrm{\Gamma }/2\right)+2i{\mathrm{\Omega }}^2}\hfill \\ \hfill r^a& =\frac{-2\sqrt{{\lambda }_{aL}{\lambda }_{bR}}\left(\omega -{\omega }_s+i\gamma /2\right)}{\left({\lambda }_{aL}+{\lambda }_{aR}+{\lambda }_{bL}+{\lambda }_{bR}\right)\left(\omega -{\omega }_s+i\gamma /2\right)-2i\left(\omega -{\omega }_s+i\gamma /2\right)\left(\omega -{\omega }_e+i\mathrm{\Gamma }/2\right)+2i{\mathrm{\Omega }}^2}\hfill \\ \hfill t^b& =\frac{-2\sqrt{{\lambda }_{aR}{\lambda }_{bR}}\left(\omega -{\omega }_s+i\gamma /2\right)}{\left({\lambda }_{aL}+{\lambda }_{aR}+{\lambda }_{bL}+{\lambda }_{bR}\right)\left(\omega -{\omega }_s+i\gamma /2\right)-2i\left(\omega -{\omega }_s+i\gamma /2\right)\left(\omega -{\omega }_e+i\mathrm{\Gamma }/2\right)+2i{\mathrm{\Omega }}^2}\hfill \\ \hfill r^b& =\frac{-2\sqrt{{\lambda }_{aR}{\lambda }_{bL}}\left(\omega -{\omega }_s+i\gamma /2\right)}{\left({\lambda }_{aL}+{\lambda }_{aR}+{\lambda }_{bL}+{\lambda }_{bR}\right)\left(\omega -{\omega }_s+i\gamma /2\right)-2i\left(\omega -{\omega }_s+i\gamma /2\right)\left(\omega -{\omega }_e+i\mathrm{\Gamma }/2\right)+2i{\mathrm{\Omega }}^2}\hfill \end{array}(5)$

The quantum routing properties of single photons in the four ports are characterized by the transmission coefficient T^a(b) = |t^a(b)|² and the reflection coefficient R^a(b) = |r^a(b)|². The analytic expressions above provide a complete description of the single-photon transport properties of the proposed network. Obviously, the desired quantum routing can be implemented by properly designing the relevant geometric parameter and the other physical parameters.

3 Implementing Tunable Quantum Routing Using Chiral Waveguides

In order to compare with previous research works, we first discuss the routing capability when the coupling strengths between the atom and two waveguides are equal, so the relevant photon-atom interactions are not chiral but symmetric, λ_aR = λ_aL = λ₁, λ_bR = λ_bL = λ₂. For simplicity, we assume λ₁ = λ₂, thus r^a = t^b = r^b. When Ω = 0, single photons incident from one waveguide a will be absorbed by the atom, which transits from its ground state to excited state. Since the excited state is coupled to a continuum of states, the excited two-level atom will emit a photon spontaneously into the propagating mode of either waveguide a or b. Consequently, mediated by the atom, single photons could be routed from one quantum channel to the other. In Figure 2A, we plot the image of the coefficients T^a, R^a and T^b + R^b, respectively. Here, T^b and R^b reach the maximum value of 0.25. In Figure 2B, we plot the figure of the coefficients T^a, R^a and T^b + R^b when Ω ≠ 0. The quantum routing due to the resonant tunneling process via the two dressed states is shown by the two peaks of the transfer rate in Figure 2B. When ω/λ = 0, T^a = 1. This is the conventional scheme for single-photon routing, which has an equal probability of routing the photon to either of the two waveguides, specifically, T^b = R^b = 0.25.

FIGURE 2

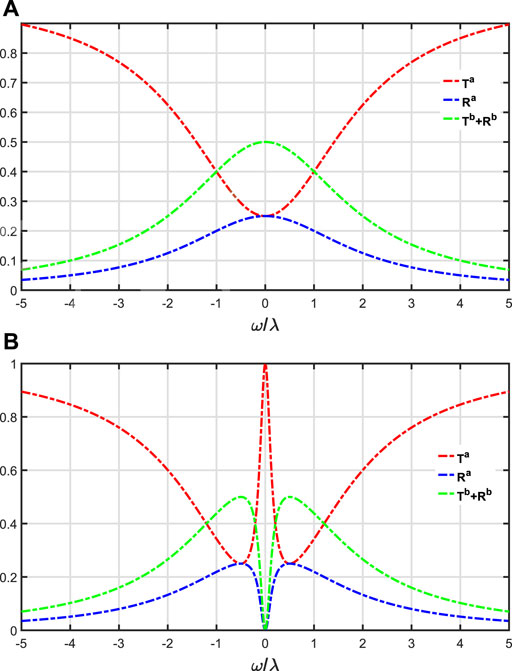
FIGURE 2. (A,B) The coefficients T^a, R^a and T^b + R^b as functions of the ω with Ω = 0 (Ω ≠ 0). Other parameters are set as follows: ω_s = ω_e = 0, λ₁ = λ₂ = λ, γ = Γ = 0.

When the coupling is chiral, λ_aR ≠ λ_aL, λ_bR ≠ λ_bL, we assume the λ_aL = λ_bL = 0, λ_aR = λ_bR = λ. In this case, we find that r^a = r^b = 0, which means that the Λ-type three-level system only couples to the right-propagating mode in the two waveguides. Figure 3 shows the probabilities of routing the incident photon to various output ports with respect to specific ω/λ. It indicates that the resonant photon incident from the left of waveguide a can output from the right of waveguide b with a probability of 100% whether Ω = 0 or Ω ≠ 0. But when Ω ≠ 0, T^b has two peaks centered at ω = ±Ω. If λ_aL = λ_bR = 0, λ_aR = λ_bL = λ, we can obtain r^a = t^b = 0, this means that the photon incident from the left of the waveguide a may output from the right of the waveguide a or the left of the waveguide b. When ω = ±Ω, R^b = 1, this means that the single photon is transferred to waveguide b and output from the left of waveguide b with a probability of 100%. In Figure 4, we show the probabilities of routing the incident photon to various output ports with respect to specific values of ω/λ, and we find that Figure 4; Figure 3 have the same physical phenomenon.

FIGURE 3

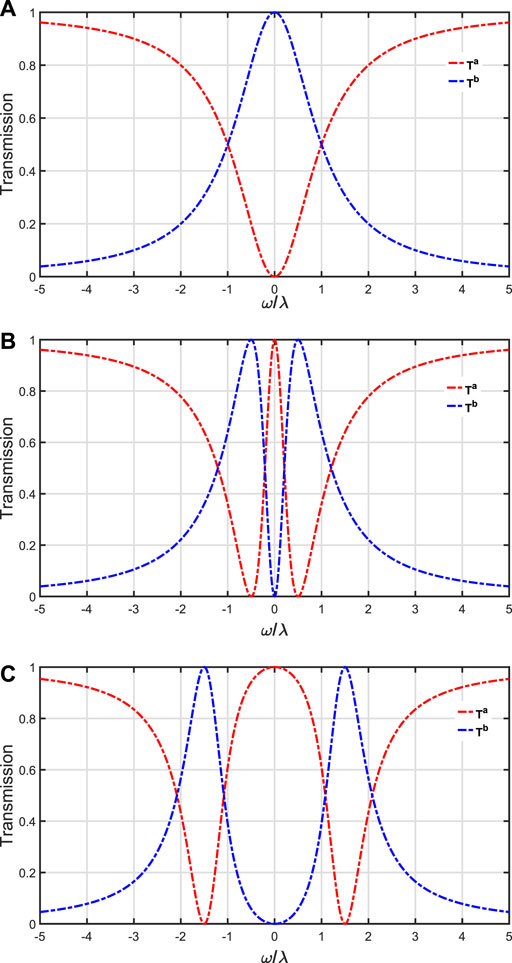
FIGURE 3. Transmission spectra of the waveguide with specific chiral photon-atom interactions, λ_aL = λ_bL = 0, λ_aR = λ_bR = λ. (A–C) T^a and T^b for different Ω = (0, 0.5, 1.5). Other parameters are set as follows: ω_s = ω_e = 0, γ = Γ = 0.

FIGURE 4

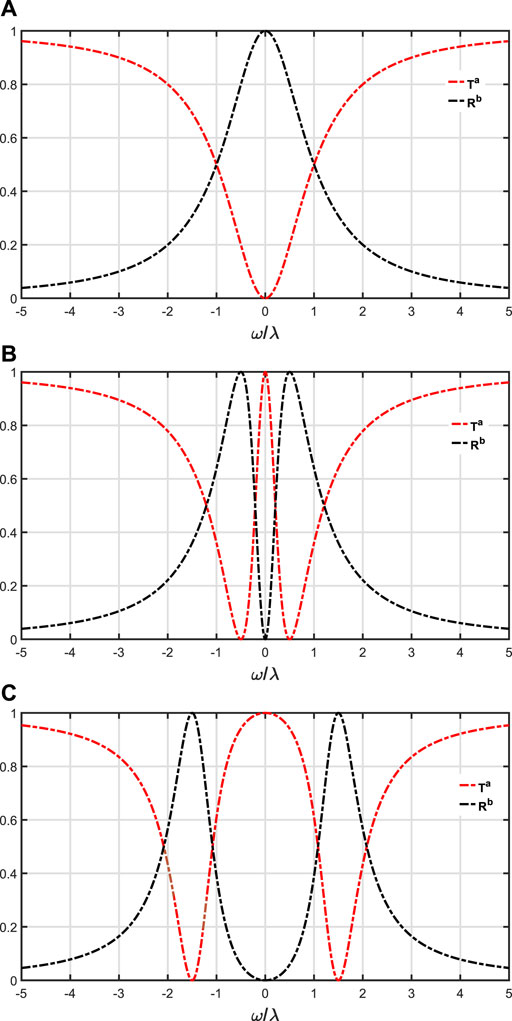
FIGURE 4. Transmission spectra and reflection spectra of the waveguide with specific chiral photon-atom interactions, λ_aL = λ_bR = 0, λ_aR = λ_bL = λ. (A–C) T^a and R^b for different Ω = (0, 0.5, 1.5). Other parameters are set as follows: ω_s = ω_e = 0, γ = Γ = 0.

4 Influence of Dissipation

In this part, we show how dissipation affects the photon routing probability. Here, we presume that λ_aL ≠ λ_aR ≠ 0 and λ_bR ≠ λ_bL ≠ 0. If t^a = 0 and an incoming photon in the resonance condition (ω = ω_s = ω_e), we can get

${\lambda }_{aR}={\lambda }_{aL}+{\lambda }_{bL}+{\lambda }_{bR}+\mathrm{\Gamma }+4\mathrm{\Omega }/\gamma (6)$

Because λ_j = λ_jR + λ_jL (j = a, b) and $P=\frac{{\lambda }_a+{\lambda }_b}{\gamma +\mathrm{\Gamma }}$

${\lambda }_b={\lambda }_{aR}-{\lambda }_{aL}-\mathrm{\Gamma }-4\mathrm{\Omega }/\gamma ={\lambda }_a\frac{2S_{a}P-1}{2P+1}-4\mathrm{\Omega }/\mathrm{\Gamma }(7)$

Here, we assume that Γ = γ. Consequently, the corresponding transmission coefficient T^b can be expressed [17].

$T_b=|t^b{|}^2=\frac{1+S_b}{1+S_a}\frac{2S_{a}P-1}{2P+1}(8)$

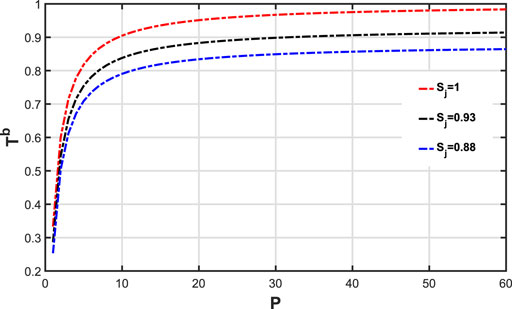
Note that in the ideal case the efficiency defined above is equal to 1, whereas in a realistic case the probability leakage into the undesired channels will reduce this value. In Figure 5, we plot the coefficients T^b with different S_j as functions of the Purcell factor P. We found that the lager Purcell factor P is, the lager coefficient T^b is, but the last T^b can reach a fixed value.

FIGURE 5

FIGURE 5. The coefficients T^b as functions of Purcell factor P. Here, S_a = S_b.

Under the resonance conditions (ω = ω_s = ω_e), in order to observe the effect of the atomic dissipation on quantum routing more explicitly, we assume γ = Γ = 0.005. The first case is the real system with λ_aR = λ_bR = λ and λ_aL = λ_bL = 0.05λ, and we investigate the performance of the single-photon transport compared with the ideal case. However, the classical optical field can still determine the locations of the peaks of T^b. Figure 6 shows T^a and T_b as a function of ω/λ. In Figure 6A, we find that when ω = ±Ω, T_b reaches the maximum, but the maxima is less than 1, since the probabilities of the photon output from the left of waveguide a and b are not zero. The other case is when λ_aR = λ_bL = λ and λ_aL = λ_bR = 0.05λ, and we plot the figure of T^a and R_b in Figure 7. At this point, we get the same physical phenomenon as Figure 6.

FIGURE 6

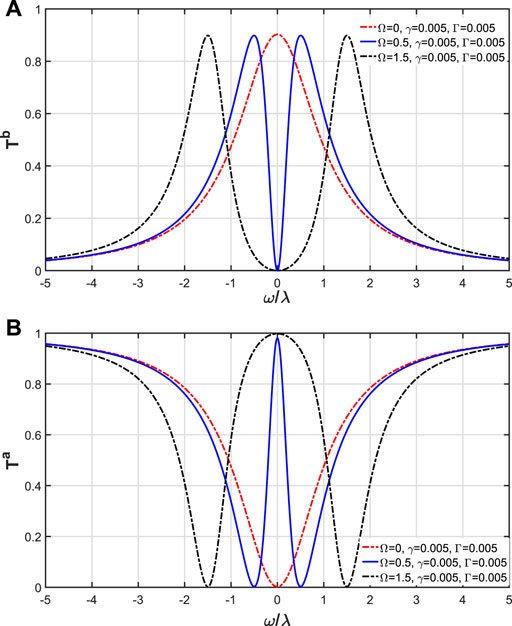
FIGURE 6. (A) T^a as a function of ω/λ and (B) T^b as a function of ω/λ, here, ω = ω_e = ω_s, γ = Γ = 0.005, λ_aR = λ_bR = λ and λ_aL = λ_bL = 0.05λ.

FIGURE 7

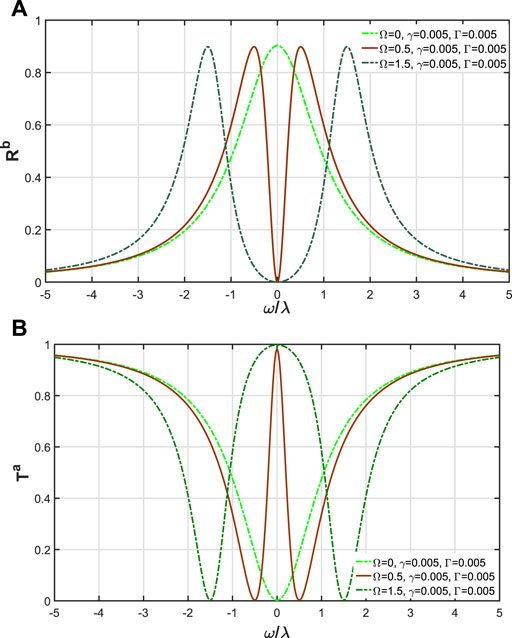
FIGURE 7. (A) T^a as a function of ω/λ and (B) R^b as a function of ω/λ, here, ω = ω_e = ω_s, γ = Γ = 0.005, λ_aR = λ_bL = λ and λ_aL = λ_bR = 0.05λ.

5 Physical Implementation

As schematically shown in Figure 8, we consider a system in which two resonators with the same fundamental mode frequencies ω_R/2π = 4.896 GHz are coupled to a superconducting qubit. The coupling frequencies between the qubit and each resonator is g/2π = 96.7 MHz. In addition to the geometric coupling g_ab/2π = 8.4 MHz there is the qubit mediated second-order dynamic coupling which depends on the magnetic flux applied to the qubit loop and on the qubit state, and the dynamical coupling on the qubit state can be used to realize switchable coupling between the two resonators [49–51]. The Hamiltonian of the whole system for the qubit coupled to the fundamental modes of the two resonators is (setting ℏ = 1) [49, 52].

$\begin{array}{cc}\hfill H& ={\omega }_{R_a}{a}^{†}a+{\omega }_{R_b}{b}^{†}b+\frac{1}{2}{\omega }_Q{\sigma }_z+g_a\left(a^{†}{\sigma }_{-}+a{\sigma }_{+}\right)\hfill \\ \hfill & +g_b\left(b^{†}{\sigma }_{-}+b{\sigma }_{+}\right)+g_{ab}\left(a^{†}b+a{b}^{†}\right)\hfill \end{array}$

where ω_Q is the qubit transition frequency, σ_z = σ₊σ₋ − σ₋σ₊ and g_a and g_b are the qubit-resonator coupling, assumed to be real for simplicity. Furthermore, we denote the annihilation (creation) operators for the two resonators A and B as a and b (a^† and b^†), respectively. Under the rotating-wave approximation, the effective Hamiltonian is [52].

$\begin{array}{cc}\hfill H_{e\mathit{ff}}& ={\omega }_{R_a}{a}^{†}a+{\omega }_{R_b}{b}^{†}b+\frac{1}{2}\left({\omega }_{R_a}+{\omega }_{R_b}\right){\sigma }_z\hfill \\ \hfill & +\frac{1}{2}{\sigma }_z\left({\mathrm{\Delta }}_a+{\mathrm{\Delta }}_b\right)+g_a\left(a^{†}{\sigma }_{-}+a{\sigma }_{+}\right)\hfill \\ \hfill & +g_b\left(b^{†}{\sigma }_{-}+b{\sigma }_{+}\right)+g_{ab}\left(a^{†}b+a{b}^{†}\right)\hfill \end{array}$

where ${\mathrm{\Delta }}_a={\omega }_Q-{\omega }_{R_a}$ and ${\mathrm{\Delta }}_b={\omega }_Q-{\omega }_{R_b}$. For the measurement, the qubit is kept in the ground state and the input power is chosen such that the mean resonator population is approximately one photon on average [50]. For coupled microwave resonators, we expect to observe two resonant modes corresponding to out-of-phase and in-phase oscillating currents in the two resonators. In this way, we can measure the transmission through the individual resonators and the transmission from the input of one resonator to the output of the second resonator [50, 51].

FIGURE 8

FIGURE 8. chematic diagram of two transmission line resonators coupled to a superconducting qubit.

6 Conclusion

In summary, we implemented a targeted single-photon router by using an effective atom-photon interface with two chiral waveguides, and no matter a classical field is turned off or turned on, it can always achieve quantum routing. Using a full quantum theory, the single-photon transmission and reflection amplitudes were analytically obtained. By the numerical method, we analyzed the relevant transport properties in detail. When the coupling between the Λ-type atom system and the waveguides is non-chiral, the maximum probability for single-photon transfer from waveguide a to waveguide b is 0.5, but at this time T^b = R^b = 0.25. In other words, we cannot directionally select quantum channels for quantum information transport in this case. When the coupling is chiral, the maximum transfer probability can achieve 100% in the ideal system. What is more, we can control single photon output from the chosen port of the waveguide b. After that, we analyzed the performance of the quantum routing. Whether we change the size of the directionalities S_j or give a certain value to the dissipation of Λ-type atom, we always found that the quantum routing has very high efficiency. Moreover, we also use the quantum circuit of the superconducting qubit coupled to two resonators verification the present scheme pretty feasible for experimental implementation. Therefore, the targeted single-photon routers we proposed here provides an effective approach to build a promising optical quantum network.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

The idea was first conceived by G-AY. G-AY was responsible for the physical modeling, the numerical calculations, and writing most of the manuscript. HL contributed to writing the manuscript.

Funding

This work are supported by the National Natural Science Foundation of China (12147146 and 12175057), and the Natural Science Foundation of Shandong Provincial (ZR2021QA046) and Shaanxi Youth Outstanding Talent Support Plan and Shaanxi Natural Science Foundation (Grant No. 2019JQ-900).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kimble HJ. The Quantum Internet. Nature (2008) 453:1023–30. doi:10.1038/nature07127

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Pittman TB, Shih YH, Strekalov DV, Sergienko AV. Optical Imaging by Means of Two-Photon Quantum Entanglement. Phys Rev A (1995) 52:R3429. doi:10.1103/physreva.52.r3429

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Deng DL, Li XP, Das Sarma S. Quantum Entanglement in Neural Network States. Phys Rev X (2017) 7:021021. doi:10.1103/physrevx.7.021021

CrossRef Full Text | Google Scholar

4. Su X, Tian C, Deng X, Li Q, Xie C, Peng K. Quantum Entanglement Swapping between Two Multipartite Entangled States. Phys Rev Lett (2016) 117:240503. doi:10.1103/physrevlett.117.240503

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Nunn J, Munns JHD, Thomas S, Kaczmarek KT, Qiu C, Feizpour A, et al. Theory of Noise Suppression in Λ-type Quantum Memories by Means of a Cavity. Phys Rev A (2017) 96:012338. doi:10.1103/physreva.96.012338

CrossRef Full Text | Google Scholar

6. Lodahl P, Mahmoodian S, Stobbe S. Interfacing Single Photons and Single Quantum Dots with Photonic Nanostructures. Rev Mod Phys (2015) 87:347–400. doi:10.1103/revmodphys.87.347

CrossRef Full Text | Google Scholar

7. Chang DE, Vuletić V, Lukin MD. Quantum Nonlinear Optics - Photon by Photon. Nat Photon (2014) 8:685–94. doi:10.1038/nphoton.2014.192

CrossRef Full Text | Google Scholar

8. Liu K, Yang J, Li XL, Li JY, Yan GA. Realization of Single-Photon Transport in One-Dimensional Coupled-Resonator Waveguides via Phase Control. Chin J Phys (2021) 72:207–13. doi:10.1016/j.cjph.2021.02.016

CrossRef Full Text | Google Scholar

9. Yan GA, Lu H. Nonreciprocal Single-Photon Router in Quantum Networks. Phys Scr (2021) 96:105102. doi:10.1088/1402-4896/ac0c5a

CrossRef Full Text | Google Scholar

10. Li JY, Li XL, Yan GA. Single-photon Quantum Router Based on Asymmetric Intercavity Couplings. Commun Theor Phys (2020) 72(5):055101. doi:10.1088/1572-9494/ab7ed5

CrossRef Full Text | Google Scholar

11. Huang JS, Zhang JH, Wei LF. Single-photon Routing with Whispering-Gallery Resonators. J Phys B: Mol Opt Phys (2018) 51:085501. doi:10.1088/1361-6455/aab5a9

CrossRef Full Text | Google Scholar

12. Yan CH, Li Y, Yuan HD, Wei LF. Targeted Photonic Routers with Chiral Photon-Atom Interactions. Phys Rev A (2018) 97:023821. doi:10.1103/physreva.97.023821

CrossRef Full Text | Google Scholar

13. Li T, Miranowicz A, Hu XD, Xia KY, Nori F. Quantum Memory and gates Using a Λ-type Quantum Emitter Coupled to a Chiral Waveguide. Phys Rev A (2018) 97:062318. doi:10.1103/physreva.97.062318

CrossRef Full Text | Google Scholar

14. Yang DC, Cheng MT, Ma XS, Xu JP, Zhu CJ, Huang XS. Phase-modulated Single-Photon Router. Phys Rev A (2018) 98:063809. doi:10.1103/physreva.98.063809

CrossRef Full Text | Google Scholar

15. Cheng MT, Ma X, Fan JW, Xu J, Zhu C. Controllable Single-Photon Nonreciprocal Propagation between Two Waveguides Chirally Coupled to a Quantum Emitter. Opt Lett (2017) 42:2914–7. doi:10.1364/OL.42.002914

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Cheng MT, Ma XS, Zhang JY, Wang B. Single Photon Transport in Two Waveguides Chirally Coupled by a Quantum Emitter. Opt Express (2016) 24:19988–93. doi:10.1364/OE.24.019988

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Gonzalez-Ballestero C, Moreno E, Garcia-Vidal FJ, Gonzalez-Tudela A. Nonreciprocal Few-Photon Routing Schemes Based on Chiral Waveguide-Emitter Couplings. Phys Rev A (2016) 94:063817. doi:10.1103/physreva.94.063817

CrossRef Full Text | Google Scholar

18. Zhou L, Yang LP, Li Y, Sun CP. Quantum Routing of Single Photons with a Cyclic Three-Level System. Phys Rev Lett (2013) 111:103604. doi:10.1103/physrevlett.111.103604

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Zhu YT, Jia WZ. Single-photon Quantum Router in the Microwave Regime Utilizing Double Superconducting Resonators with Tunable Coupling. Phys Rev A (2019) 99:063815. doi:10.1103/physreva.99.063815

CrossRef Full Text | Google Scholar

20. Witthaut D, Sørensen AS. Photon Scattering by a Three-Level Emitter in a One-Dimensional Waveguide. New J Phys (2010) 12:043052. doi:10.1088/1367-2630/12/4/043052

CrossRef Full Text | Google Scholar

21. Hoi IC, Wilson CM, Johansson G, Palomaki T, Peropadre B, Delsing P. Demonstration of a Single-Photon Router in the Microwave Regime. Phys Rev Lett (2011) 107:073601. doi:10.1103/PhysRevLett.107.073601

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yan GA, Qiao HX, Lu H, Chen AX. Quantum Information-Holding Single-Photon Router Based on Spontaneous Emission. SCIENCE CHINA Phys Mech Astron (2017) 60:9. doi:10.1007/s11433-017-9059-3

CrossRef Full Text | Google Scholar

23. Reiserer A, Kalb N, Blok MS, van Bemmelen KJM, Taminiau TH, Hanson R, et al. Robust Quantum-Network Memory Using Decoherence-Protected Subspaces of Nuclear Spins. Phys Rev X (2016) 6:021040. doi:10.1103/physrevx.6.021040

CrossRef Full Text | Google Scholar

24. Kockum AF, Johansson G, Nori F. Decoherence-free Interaction between Giant Atoms in Waveguide Quantum Electrodynamics. Phys Rev Lett (2018) 120:140404. doi:10.1103/physrevlett.120.140404

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Chen GY, Lambert N, Chou CH, Chen YN, Nor F. Surface Plasmons in a Metal Nanowire Coupled to Colloidal Quantum Dots: Scattering Properties and Quantum Entanglement. Phys Rev B (2011) 84:045310. doi:10.1103/physrevb.84.045310

CrossRef Full Text | Google Scholar

26. Zheng H, Baranger HU. Persistent Quantum Beats and Long-Distance Entanglement from Waveguide-Mediated Interactions. Phys Rev Lett (2013) 110:113601. doi:10.1103/physrevlett.110.113601

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zheng H, Gauthier DJ, Baranger HU. Waveguide-QED-based Photonic Quantum Computation. Phys Rev Lett (2013) 111:090502. doi:10.1103/PhysRevLett.111.090502

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gonzalez-Ballestero C, Moreno E, Garcia-Vidal FJ. Generation, Manipulation, and Detection of Two-Qubit Entanglement in Waveguide QED. Phys Rev A (2014) 89:042328. doi:10.1103/physreva.89.042328

CrossRef Full Text | Google Scholar

29. Facchi P, Kim MS, Pascazio S, Pepe FV, Pomarico D, Tufarelli T. Bound States and Entanglement Generation in Waveguide Quantum Electrodynamics. Phys Rev A (2016) 94:043839. doi:10.1103/physreva.94.043839

CrossRef Full Text | Google Scholar

30. Vermersch B, Guimond PO, Pichler H, Zoller P. Quantum State Transfer via Noisy Photonic and Phononic Waveguides. Phys Rev Lett (2017) 118:133601. doi:10.1103/physrevlett.118.133601

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Mahmoodian S, Lodahl P, Sørensen AS. Quantum Networks with Chiral-Light-Matter Interaction in Waveguides. Phys Rev Lett (2016) 117:240501. doi:10.1103/physrevlett.117.240501

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Shen JT, Fan S. Coherent Single Photon Transport in a One-Dimensional Waveguide Coupled with Superconducting Quantum Bits. Phys Rev Lett (2005) 95:213001. doi:10.1103/physrevlett.95.213001

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Roy D, Wilson CM, Firstenberg O Colloquium: Strongly Interacting Photons in One-Dimensional Continuum. Rev Mod Phys (2017) 89:021001. doi:10.1103/revmodphys.89.021001

CrossRef Full Text | Google Scholar

34. Kemp A, Saito S, Munro WJ, Nemoto K, Semba K. Superconducting Qubit as a Quantum Transformer Routing Entanglement between a Microscopic Quantum Memory and a Macroscopic Resonator. Phys Rev B (2011) 84:104505. doi:10.1103/physrevb.84.104505

CrossRef Full Text | Google Scholar

35. Xia K, Twamley J. All-optical Switching and Router via the Direct Quantum Control of Coupling between Cavity Modes. Phys Rev X (2013) 3:031013. doi:10.1103/physrevx.3.031013

CrossRef Full Text | Google Scholar

36. Agarwal GS, Huang S. Optomechanical Systems as Singlephoton Routers. Phys Rev A (2012) 85:021801. doi:10.1103/physreva.85.021801

CrossRef Full Text | Google Scholar

37. Bentham C, Itskevich IE, Coles RJ, Royall B, Clarke E, O'Hara J, et al. On-chip Electrically Controlled Routing of Photons from a Single Quantum Dot. Appl Phys Lett (2015) 106:221101. doi:10.1063/1.4922041

CrossRef Full Text | Google Scholar

38. Li H, Cai H, Xu J, Yakovlev VV, Yang Y, Wang DW. Quantum Photonic Transistor Controlled by an Atom in a Floquet Cavity-QED System. Opt Express (2019) 27(5):6946–57. doi:10.1364/oe.27.006946

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Lu J, Zhou L, M Kuang L, Nori F. Single-photon Router: Coherent Control of Multichannel Scattering for Single Photons with Quantum Interferences. Phys Rev A (2014) 89:013805. doi:10.1103/physreva.89.013805

CrossRef Full Text | Google Scholar

40. Gorniaczyk H, Tresp C, Schmidt J, Fedder H, Hofferberth S. Single-photon Transistor Mediated by Interstate Rydberg Interactions. Phys Rev Lett (2014) 113:053601. doi:10.1103/PhysRevLett.113.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Tiarks D, Baur S, Schneider K, Dürr S, Rempe G. Single-photon Transistor Using a Förster Resonance. Phys Rev Lett (2014) 113:053602. doi:10.1103/PhysRevLett.113.053602

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Hong FY, Xiong SJ. Single-photon Transistor Using Microtoroidal Resonators. Phys Rev A (2008) 78:013812. doi:10.1103/physreva.78.013812

CrossRef Full Text | Google Scholar

43. Neumeier L, Leib M, Hartmann MJ. Single-photon Transistor in Circuit Quantum Electrodynamics. Phys Rev Lett (2013) 111:063601. doi:10.1103/PhysRevLett.111.063601

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Muljarov EA, Langbein W. Exact Mode Volume and Purcell Factor of Open Optical Systems. Phys Rev B (2016) 94:235438. doi:10.1103/physrevb.94.235438

CrossRef Full Text | Google Scholar

45. Chebykin AV, Babicheva VE, Iorsh IV, Orlov AA, Belov PA, Zhukovsky SV. Enhancement of the Purcell Factor in Multiperiodic Hyperboliclike Metamaterials. Phys Rev A (2016) 93:033855. doi:10.1103/physreva.93.033855

CrossRef Full Text | Google Scholar

46. Rustomji K, Abdeddaim R, Martijn de Sterke C, Kuhlmey B, Enoch S. Measurement and Simulation of the Polarization-dependent Purcell Factor in a Microwave Fishnet Metamaterial. Phys Rev B (2017) 95:035156. doi:10.1103/physrevb.95.035156

CrossRef Full Text | Google Scholar

47. Pick A, Lin Z, Jin W, Rodriguez AW. Enhanced Nonlinear Frequency Conversion and Purcell Enhancement at Exceptional Points. Phys Rev B (2017) 96:224303. doi:10.1103/physrevb.96.224303

CrossRef Full Text | Google Scholar

48. Plankensteiner D, Sommer C, Reitz M, Ritsch H, Genes C. Enhanced Collective Purcell Effect of Coupled Quantum Emitter Systems. Phys Rev A (2019) 99:043843. doi:10.1103/physreva.99.043843

CrossRef Full Text | Google Scholar

49. Mariantoni M, Deppe F, Marx A, Gross R, Wilhelm FK, Solano E. Two-resonator Circuit Quantum Electrodynamics: A Superconducting Quantum Switch. Phys Rev B (2008) 78:104508. doi:10.1103/physrevb.78.104508

CrossRef Full Text | Google Scholar

50. Baust A, Hoffmann E, Haeberlein M, Schwarz MJ, Eder P, Goetz J, et al. Tunable and Switchable Coupling between Two Superconducting Resonators. Phys Rev B (2015) 91:014515. doi:10.1103/physrevb.91.014515

CrossRef Full Text | Google Scholar

51. Baust A, Hoffmann E, Haeberlein M, Schwarz MJ, Eder P, Goetz J, et al. Ultrastrong Coupling in Two-Resonator Circuit QED. Phys Rev B (2016) 93:214501. doi:10.1103/physrevb.93.214501

CrossRef Full Text | Google Scholar

52. Sete EA, Gambetta JM, Korotkov AN. Purcell Effect with Microwave Drive: Suppression of Qubit Relaxation Rate. Phys Rev B (2014) 89:104516. doi:10.1103/physrevb.89.104516

CrossRef Full Text | Google Scholar