Uncertainty Relation and Quantum Phase Transition in the Two-Dimensional Ising Model

By using quantum renormalization group (QRG) approach, we first derive the effective Hamiltonian and QRG equations of the two-dimensional (2D) Ising models with two different time-dependent transverse magnetic fields analytically. Then we examine the nonanalytic and scaling behaviors of the linear-entropy-based uncertainty relation and quantum entanglement of the models near the critical point through numerical analysis. Moreover, we investigate the relation between the quantum critical point and the external magnetic field. Our results show that both the uncertainty relation and the quantum entanglement are feasible to detect the quantum phase transition (QPT), and the uncertainty relation may be a better indicator of QPT than quantum entanglement. Our findings could shed new light on the observable of the QPTs of the solid-state system with the uncertainty relation.

1 Introduction

Quantum entanglement is one of the most astonishing notions of quantum mechanics [1, 2] and is at the centre of the large amount of applications in quantum sciences and technologies, such as quantum cryptography [3], quantum teleportation [4], superdense coding [5], and telecloning [6]. Negativity as the witness of the bipartite entanglement was introduced by Życzkowski et al [7] and then proven by Vidal and Werner [8] to be a monotone under the local operation and classical communication.

As we know, the relation between quantum entanglement and quantum phase transition (QPT) [9] is of considerable interest [10]. QPT is induced by the change of external parameters or interaction coupling constants. The divergence of the correlation length in the vicinity of the quantum critical points (QCP) indicates that the different components of the quantum system are strongly correlated. Quantum entanglement can be used as a way to measure quantum correlations and to indicate the behavior of QPT such as discontinuity close to the QCP [11, 12]. In the past few years the behavior of entanglement near QCP in different spin systems [13–15] was considered as a subject of profound significance [16–19]. Recently, A lot of work was devoted to the study of Heisenberg spin chains, particularly the one-dimensional (1D) spin chains, which can be given quantitative results and be exactly solvable [20–25]. The QPT of Heisenberg spin chains is caused by quantum fluctuations, which is essentially induced by quantum uncertainty relation of the system. Up to now, quantum uncertainty relation has gone through considerable development. Nevertheless, to our knowledge there are few studies on the relation between the uncertainty and QPT [26–29].

The quantum uncertainty relation is deemed one of the most unique and fundamental features in quantum mechanics, which states that it is impossible to simultaneously determine the definite measurement outcomes of noncommutative observables. Based on the distributions of measurement results, the uncertainty relation can be depicted in different ways [30–33]. Historically, the uncertainty principle was originally formulated by Heisenberg [34] for the coordinate and the momentum in an infinite dimensional Hilbert space. Later, Robertson generalized Heisenberg uncertainty inequality to arbitrary pairs of observables [30]. Instead of the standard deviation, the uncertainty relation can also be delicately given in terms of Shannon entropies associated with the measurement bases [35]. By considering the quantum entanglement with a memory system [36], an entropic uncertainty relation in the presence of quantum memory was proposed and attracted wide attentions [37, 38]. Taking the entangled quantum memory into account, these uncertainty relations have potential applications in quantum key distributions and entanglement witnessing [37, 39, 40]. However, all the uncertainty relations proposed above involve the measurement between only two observations and are expressed in the form of inequality. Very recently, Wang et al. [41] put forward a novel entropic uncertainty relation for bipartite systems composed of a measured subsystem A and a quantum memory B, in which projection measurements is based on a complete set of mutually unbiased bases (MUBs). By means of the complete set of MUBs, an uncertainty equality based on conditional linear entropy was derived [42, 43]. The uncertainty equality implies that the sum of uncertainties is exactly equal to the fixed quantity related to the initial bipartite state which was confirmed experimentally with optical systems [41, 44]. This uncertainty relation can be applied to quantum random number generation and quantum guessing games. On the other hand, quantum renormalization group (QRG) is one of the conceptual pillars of quantum field theory and statistical mechanics, which revolves around the idea of rescaling transformations and coarse-graining of a large-scale system [45].

The QRG method is widely used to solve exactly the 1D Ising, XXZ, XYZ and XY models [20, 46, 47]. At zero temperature, the QRG method provides insights into how the block uncertainty and entanglement change as the size of the system becomes large in 1D spin chains. On the basis of the 1D case, some further contributions on two-dimensional (2D) and higher-dimensional systems have been recently made [48–53]. In this work, we introduce two different types of the time-dependent magnetic fields into the 2D Ising models, and obtain the effective Hamiltonian of the models by employing the QRG method. Moreover, we investigate the evolution of the uncertainty in contrast to the quantum entanglement in terms of the magnetic field to characterize the QPT.

This paper is structured as follows. In Section 2, we first derive the QRG equations for the 2D models with the time-dependent magnetic fields. And in Section 3, the evolutions of the uncertainty and quantum entanglement are discussed in the 2D model. A conclusion is given in Section 4.

2 QRG for the Transverse-Field Ising Models

The QRG method can effectively process large-scale quantum spin systems [45]. The key of the QRG method is the mode thinning of the degrees of freedom followed by iterations which reduces the number of parameters step by step until reaching a fixed point. In this section, we derive the QRG equation for 2D Ising models with time-dependent magnetic fields following the method of 1D QRG.

The Hamiltonian of the 1D Ising model with N sites can be expressed as

$H_1\left(t\right)=-J_1\sum _{i=1}^N{\sigma }_i^z{\sigma }_{i+1}^z-B_p\left(t\right)\sum _i^N{\sigma }_i^x,(1)$

where J₁ > 0 is the exchange coupling constant, ${\sigma }_i^{\alpha }(\alpha =x,y,z)$ are the Pauli matrices at site i, B_p(t) (p = 1, 2) denote the time-dependent magnetic field strengths. Here, we define

$B_1\left(t\right)=kt,(2)$

$\begin{array}{c}\hfill B_2\left(t\right)=\sqrt{2}\sin \left(\omega t\right).\hfill \end{array}(3)$

Clearly, B₁(t) denotes the magnetic field strength with the linear coefficient k, while B₂(t) is the sinusoidal magnetic field strength with the frequency of ω.

Similarly, the Hamiltonian of a spin-1/2 2D Ising model with the transverse magnetic field is given by:

$H_2\left(t\right)=-J_2\sum _{⟨i,j⟩}^N{\sigma }_i^z{\sigma }_j^z-B_q\left(t\right)\sum _i^N{\sigma }_i^x,(4)$

where the coupling constant J₂ > 0, the first sum contains all the nearest-neighbor interactions, and B_q(t) (q = 3, 4) are the time-dependent linear and sinusoidal magnetic field strengths defined by

$B_3\left(t\right)=kt,(5)$

$\begin{array}{c}\hfill B_4\left(t\right)=1.8354\sqrt{2}\sin \left(\omega t\right),\hfill \end{array}(6)$

respectively. Here the coefficient $1.8354\sqrt{2}$ is chosen for easier analysis of numerical results, as 1.8354 is the critical point of the 2D Ising model described in the following text.

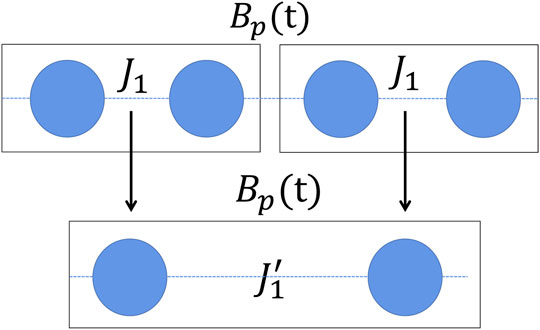
The QRG procedure of the 1D Ising model is started by decomposing the system into isolated blocks (Figure 1) and accordingly the Hamiltonian H₁(t) is divided into two parts.

$H_1\left(t\right)=H_k\left(t\right)+H_{kk}\left(t\right).(7)$

FIGURE 1

FIGURE 1. The procedure of the 1D model partitioning.

Here H_k(t) and H_kk(t) are the block and interblock Hamiltonian, respectively, which are given by

$\begin{array}{c}\hfill H_k\left(t\right)=\sum _I^{N/2}{h}_k^I\left(t\right),\hfill \\ \hfill h_k^I\left(t\right)=-J_1{\sigma }_{I,1}^z{\sigma }_{I,2}^z-B_p\left(t\right){\sigma }_{I,1}^x,\hfill \\ \hfill H_{kk}\left(t\right)=\sum _I^{N/2}{h}_{kk}^{I,I+1}\left(t\right),\hfill \\ \hfill h_{kk}^{I,I+1}\left(t\right)=-J_1{\sigma }_{I,2}^z{\sigma }_{I+\mathrm{1,1}}^z-B_p\left(t\right){\sigma }_{I,2}^x,\hfill \end{array}(8)$

where $h_k^I(t)$ and $h_{kk}^{I,I+1}(t)$ are respectively the Ith block Hamiltonian and the interblock Hamiltonian between the blocks I and I + 1.

Next we focus on the effect of magnetic field strength on QPT and do not care about the specific details of the evolution of the system. Therefore, we can make the magnetic field strength change very slowly over time, where the process coincides with the idea of quantum adiabatic approximation. The strict derivation of the quantum adiabatic theorem was first mentioned by [54]. Later, quantum adiabatic approach was extended to the degenerate case, and the quantum adiabatic condition for the degenerate case was obtained [55, 56]. The theorem states that when the time-varying rate of the Hamiltonian approaches to zero, the probability of the system leaving the instantaneous eigenstates of the Hamiltonian can be considered to be zero. In the degenerate case, the Hamiltonian $h_k^I(t)$ of the system depending on parameter t = [t₁, t₂, t₃, …, t_N] have degenerate eigenstates |n, α⟩ ≡|n, α(t)⟩(α = 1, 2, …, d_n), corresponding to the eigenvalues E_n(t) with d_n being degeneracy. The adiabatic approximation condition can be written as

$\left|\frac{⟨n,\alpha \left|\frac{d}{dt}\right|n^{\prime },{\alpha }^{\prime }⟩}{E_n-E_{n^{\prime }}}\right|\ll 1\left(n\ne n^{\prime }\right).(9)$

A detailed analysis are further performed on the left hand side (LHS) of Eq. 9 with different magnetic field parameters as shown in Figure 2. From Figure 2A, we can see that for different values of k, the LHS of the adiabatic approximation condition versus time t in linear magnetic fields B₃(t) have the similar trend, i.e., it first increases to the maximum value and then gradually decreases to 0. However, the maximum value of LHS diminishes rapidly from 0.2052 to approximately 0 (much less than 1) as k decreases from 1 to 0.01. Figure 2B shows that the maximum values of LHS appear periodically over time for the sinusoidal magnetic fields B₄(t). Our primary concern is that when the value of ω decreases to 0.01, the value of LHS is approximate to 0. As discussed above, we can set the values of magnetic field parameters k and ω as 0.01 to satisfy the adiabatic approximation condition. On the basis of the approximation condition, the transitions between energy levels of the systems can be ignored, so we can complete the subsequent QRG process by solving the stationary Schrodinger equation $h_k^I(t)\left|{\psi }_j\right.⟩=E_j\left|{\psi }_j\right.⟩(j=\mathrm{1,2})$.

FIGURE 2

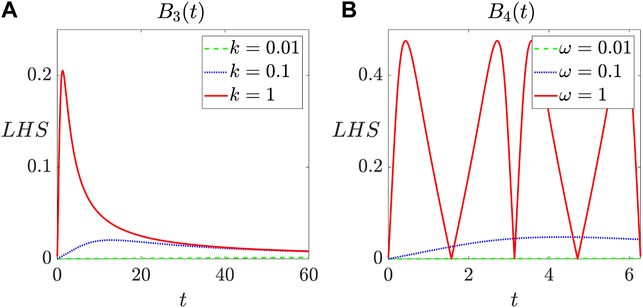
FIGURE 2. LHS of the adiabatic approximation condition versus time t for different magnetic fields: (A)B₃(t) and (B)B₄(t).

After solving the Schrodinger equation at a certain time t, we obtain two degenerate ground states |ψ₁⟩ and |ψ₂⟩, which can be used to construct the projection operator as follows

$P=\underset{I=1}{\overset{N/2}{\otimes }}{P}_I,P_I=\left|{\psi }_1\right.⟩\left.⟨\uparrow \right|+\left|{\psi }_2\right.⟩\left.⟨\downarrow \right|,(10)$

where $\left|\uparrow \right.⟩$ and $\left|\downarrow \right.⟩$ are the eigenstates of σ_z, and P_I is the projection operator of $h_k^I(t)$. Using the above formulas, we can obtain the following effective Hamiltonian H_eff given by

$\begin{array}{c}{H}_{e\mathit{ff}1}=P^{†}HP=P^{†}\left(H_k+H_{kk}\right)P\hfill \\ =J_1^{\prime }\sum _I^{N/2}{\sigma }_I^z{\sigma }_{I+1}^z-B_q^{\prime }\left(t\right)\sum _I^{N/2}{\sigma }_I^x.\hfill \end{array}(11)$

where

$\begin{array}{c}\hfill J_1^{\prime }=\frac{J_1^2}{\sqrt{J_1^2+B_q^2\left(t\right)}},\hfill \\ \hfill B^{\prime }\left(t\right)=\frac{B_q^2\left(t\right)}{\sqrt{J_1^2+B_q^2\left(t\right)}},\hfill \end{array}(12)$

which are called QRG equation. Notably, we define the effective magnetic field h₁ = B_q(t)/J₁. Then QRG equation can be written as

$h_1^{\prime }=h_1^2,(13)$

where h₁ becomes $h_1^{\prime }$ after one QRG iteration. The stable and unstable fixed points h₁ = (0, 1, ∞) of the QRG equations are obtained by solving $h_1=h_1^{\prime }=h_1^{*}$, where h₁ = 1 is an unstable fixed point and the QCP of the 1D system.

Using the similar QRG method of 1D model [48, 49, 51, 52], now we turn to investigate the related properties of the 2D square lattice. As previously discussed, the values of k and ω are theoretically set to be 0.01 in the rest of this paper. To study the ground state phases of the Hamiltonian in Eq. 4, we partition the square lattice into blocks of two sites in horizontal and vertical directions as depicted in Figure 3A.

FIGURE 3

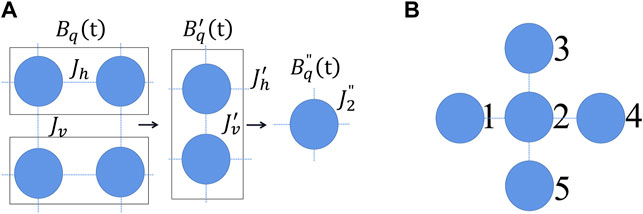
FIGURE 3. (A) The process of the 2D model partitioning, with first horizontal transformation and then vertical transformation. (B) The basic cluster with the nearest neighbor interaction in the 2D model.

In Figure 3A, J_h and J_v represent the ferromagnetic exchange coupling constants in the horizontal and vertical directions respectively, and J_h = J_v = J₂. Similar to the 1D case, we first perform the horizontal transformation

$\begin{array}{c}\hfill J_h^{\prime }=\frac{J_h^2}{\sqrt{J_h^2+B_q^2\left(t\right)}},\hfill \\ \hfill B_q^{\prime }\left(t\right)=\frac{B_q^2\left(t\right)}{\sqrt{J_h^2+B_q^2\left(t\right)}},\hfill \\ \hfill J_v^{\prime }=J_v\left(1+\frac{J_h^2}{J_h^2+B_q^2\left(t\right)}\right),\hfill \end{array}(14)$

and then the vertical transformation as follows,

$\begin{array}{c}\hfill J_h^{″}=J_h^{\prime }\left(1+\frac{J_v^{\prime 2}}{J_v^{\prime 2}+B_q^{\prime 2}\left(t\right)}\right),\hfill \\ \hfill B_q^{\prime \prime }\left(t\right)=\frac{B_q^{\prime 2}\left(t\right)}{\sqrt{J_v^{\prime 2}+B_q^{\prime 2}\left(t\right)}},\hfill \\ \hfill J_v^{″}=\frac{J_v^{\prime 2}}{\sqrt{J_v^{\prime 2}+B_q^{\prime 2}\left(t\right)}}.\hfill \end{array}(15)$

To preserve the symmetry of the system, the geometric mean idea [57] is applied to the entire transformation process $J_2^{\prime \prime }=\sqrt{J_h^{\prime \prime }{J}_v^{\prime \prime }}$. Then the effective Hamiltonian H_eff2 of the 2D model can be expressed as follows

$H_{e\mathit{ff}2}\left(t\right)=-J_2^{″}\sum _{⟨i,j⟩}^N{\sigma }_i^z{\sigma }_j^z-B_q^{″}\left(t\right)\sum _i^N{\sigma }_i^x.(16)$

The effective magnetic field is set to h₂ = B₂(t)/J₂. After the horizontal and vertical transformations, the QRG equation for the 2D model can be obtained as

$\begin{array}{c}\hfill h_2^{\prime }=\frac{h_2^4{\left({\left(1+h_2^2\right)}^3\left(4+4h_2^2+2h_2^4+h_2^6\right)\right)}^{1/4}}{\left(2+h_2^2\right){\left(8+8h_2^2+3h_2^4+h_2^6\right)}^{1/2}}\hfill \end{array},(17)$

where h₂ becomes $h_2^{\prime }$ after one QRG iteration. By solving $h_2=h_2^{\prime }=h_2^{*}$, we can get three fixed points h₂ = (0, 1.835 4, ∞), where h₂ = 1.835 4 is QCP of the ferromagnetic paramagnetic phase transition of the 2D system. Considering the symmetry of the 2D system, we select a basic cluster as the research object shown in Figure 3B, and the corresponding Hamiltonian H_c is given by

$\begin{array}{c}\hfill H_c=-J_2^{″}\left({\sigma }_2^z{\sigma }_1^z+{\sigma }_2^z{\sigma }_3^z+{\sigma }_2^z{\sigma }_4^z+{\sigma }_2^z{\sigma }_5^z\right)\hfill \\ \hfill -B_q^{″}\left(t\right)\left({\sigma }_1^x+{\sigma }_2^x+{\sigma }_3^x+{\sigma }_4^x+{\sigma }_5^x\right).\hfill \end{array}$

From the ground state $\left|{\psi }_g\right.⟩$ of H_c, we can construct the density operator ρ = |ψ_g⟩⟨ψ_g|. Then by tracing the density matrix of the subsystems 3, 4 and 5, the reduced density matrix between the sites 1 and 2 is written as

${\rho }_{12}=T{r}_{345}\rho .(18)$

As a result, after the QRG iterative process, the relation between the local and global properties of the 2D system is built. By means of the reduced density matrix ρ₁₂, we can analyze the quantum property of the 2D Ising models by calculating uncertainty relation, quantum entanglement, and so on.

3 Uncertainty Relation and Quantum Entanglement of the 2D Ising Models

In this section, we first use the quantum entanglement to gain a preliminary understanding of the long-range properties and the critical behavior in the 2D Ising model. We adopt the negativity proposed by Vidal and Werner [8] to measure quantum entanglement, which is described by

$N\left({\rho }_{12}\right)=\sum _i\left|{\lambda }_i\left({\rho }_{12}^{T_1}\right)\right|-1,(19)$

where ρ₁₂ is the reduced density matrix of subsystems 1 and 2, ${\rho }_{12}^{T_1}$ is the partial transpose matrix about particle 1, and λ_i denotes the ith eigenvalue of ${\rho }_{12}^{T_1}$. The subsystem 1 and 2 are maximally entangled for $N\left({\rho }_{12}\right)=1$, and partially entangled for $N\left({\rho }_{12}\right)<1$.

In Figure 4, we plot the properties of negativity and its first derivative for the 2D transverse-field Ising model. As seen from Figure 4A, as kt increases, N first increases gradually from zero to the maximum N_max = 0.243 7 for each QRG iteration, then decreases to zero monotonically. When kt = 1.835 4, the effective magnetic field h₂ is equal to 1.8354, which is the QPT point of the 2D system. For higher QRG iterations, the space in which N can exist gradually becomes smaller and the maximum occurring of N is closer to the QCP at kt = 1.835 4.

FIGURE 4

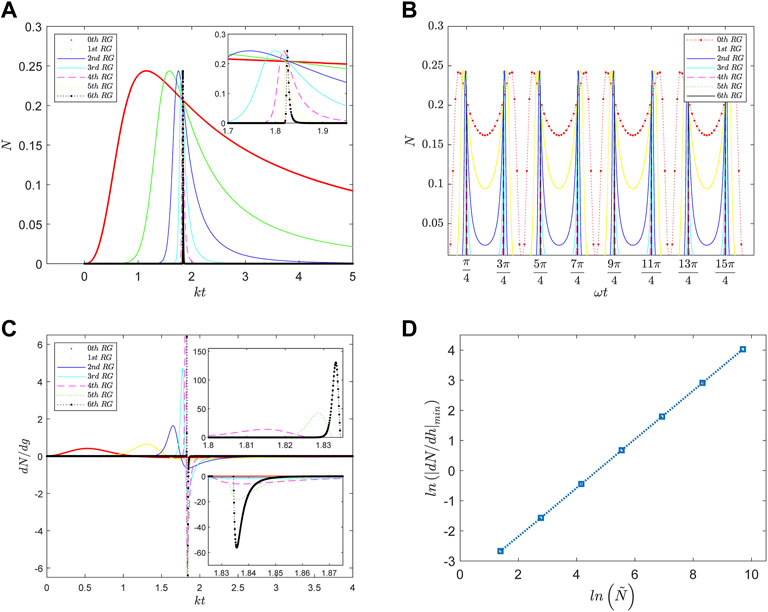
FIGURE 4. (A) The evolution of negativity of the 2D model versus kt with B₃(t), and (B) that versus ωt with B₄(t) in terms of QRG iterations. (C) The evolution of first derivative of N in terms of QRG iterations with B₃(t). The upper and lower insets show the maximum and minimum of dN/dg at the critical point respectively. (D) The scaling behavior of ln(|dN/dg|_min) with respect to the system size $\ln (\tilde{N})$.

As shown in Figure 4B, the negativity maximums N_max = 0.243 7 display periodicity versus ωt with the magnetic field B₄(t). As the size of the system increases, N_max appears approximately at $\omega t=\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4}\dots$, and herein the corresponding effective magnetic field strength satisfies h₂ = 1.835 4, which is the QCP of 2D models.

As we know, the divergence of the first derivative of N means that the system has nonanalytic behavior. From Figure 4C we can see that maxima and minima of N are almost symmetric. The maxima exhibit at the critical point of kt = 1.835 4 and become larger under the system size increasing.

We also note that the entanglement in the vicinity of the QCP shows scaling behavior [58]. Figure 4D plots the logarithm of the absolute value of minimum of dN/dh versus the system scale $\ln (\tilde{N})$, displaying a standard linear relation, where $\tilde{N}$ represents the size of the system. From the linear relation, a formula between |dN/dg|_min and $\tilde{N}$ can be obtained as $|dN/dg{|}_{\min }={\tilde{N}}^{0.7960}$, which reflects the scaling behavior of entanglement.

In general the quantum entanglement of a system is closely related to its uncertainty. To compare with quantum entanglement, in the following we investigate the uncertainty equality and inequality based on linear entropy [41]. Suppose that there is a bipartite quantum state ρ₁₂ consisting of subsystems 1 and 2 in a d₁ × d₂ (d₁ < d₂) dimensional Hilbert space. First, subsystem 1 is performed a local projection measurement with the eigenstates {|m⟩}. Then, the bipartite state can be expressed as ${\rho }_{12}^m=\left(|{m\rangle }_1\langle m|\otimes {\mathbb{I}}_2\right){\rho }_{12}\left(|{m\rangle }_1\langle m|\otimes {\mathbb{I}}_2\right)/p_m$, where ${\mathbb{I}}_2$ represents the identity operator of subsystem 2 and $p_m=\mathrm{T}\mathrm{r}\left[\left(|{m\rangle }_1\langle m|\otimes {\mathbb{I}}_2\right){\rho }_{12}\right]$ is the measurement probability. As a result, the overall state of the system after the local measurement on subsystem 1 is given by

${\rho }_{M2}=\sum _{m=1}^{d_1}{p}_m{\rho }_m=\sum _{m=1}^{d_1}|{m\rangle }_1\langle m|\otimes {⟨m\left|{\rho }_{12}\right|m⟩}_1.(20)$

To quantify the uncertainty of the composite system, we introduce conditional linear entropy S_L(M∣2) as follows,

$S_L\left(M\mid 2\right)=S_L\left({\rho }_{M\mid 2}\right)-S_L\left({\rho }_2\right)=\mathrm{T}\mathrm{r}\left({\rho }_2^2\right)-\mathrm{T}\mathrm{r}\left({\rho }_{M2}^2\right),(21)$

where ρ₂ = Tr₁(ρ₁₂) is the reduced density matrix of subsystem 2 and $S_L(\rho )=1-\mathrm{T}\mathrm{r}\left({\rho }^2\right)$ is the linear entropy. For the density matrix ρ₁₂, if a complete set of MUBs $\left\{M_{\theta }\left(\theta =\mathrm{1,2},\dots ,d_1+1\right)\right\}$ are performed, the uncertainty equality is

$\sum _{i=1}^{d_1+1}{S}_L\left(M_{\theta }\mid 2\right)=d_1\left(\mathrm{T}\mathrm{r}\left({\rho }_2^2\right)-\frac{1}{d_1}\mathrm{T}\mathrm{r}\left({\rho }_{12}^2\right)\right).(22)$

For a two-dimensional subsystem 1, the simplest complete set of MUBs is

$\begin{array}{c}\hfill M_1=\left\{|\uparrow \rangle ,|\downarrow \rangle \right\},M_2=\left\{\frac{|\uparrow \rangle +|\downarrow \rangle }{\sqrt{2}},\frac{|\uparrow \rangle -|\downarrow \rangle }{\sqrt{2}}\right\},\hfill \\ \hfill M_3=\left\{\frac{|\uparrow \rangle +i|\downarrow \rangle }{\sqrt{2}},\frac{|\uparrow \rangle -i|\downarrow \rangle }{\sqrt{2}}\right\},\hfill \end{array}(23)$

where M₁, M₂, M₃ are the eigenvectors of σ_x, σ_y, σ_z respectively. If an incomplete set of d (d < d₁ + 1) MUBs (for example, M₂ and M₃) are performed on the d₁ × d₂ dimensional Hilbert space, the uncertainty satisfies the uncertainty inequality

$\sum _{i=1}^d{S}_L\left(M_i\mid 2\right)⩾\left(d-1\right)\left[\mathrm{T}\mathrm{r}\left({\rho }_2^2\right)-\frac{1}{d}\mathrm{T}\mathrm{r}\left({\rho }_{12}^2\right)\right].(24)$

For the 2D Ising system, the uncertainty equality and inequality are plotted in Figure 5 under different magnetic fields. For each QRG iteration, the uncertainty first decreases to the minimum of 0.5 and then increases to the maximum of 1.0 with the growth of kt in Figure 5A. The change tendency of uncertainty is opposite to that of entanglement in Figure 4A, which indicates that quantum entanglement might suppress the uncertainty of the system. As the size of the system becomes larger, the uncertainty minimum occurs at kt = 1.835 4 near QCP, where the decay from maximum to minimum is very rapid and accompanied by intensive oscillations, which means that this uncertainty can precisely describe the critical behavior of the system due to the sensitivity of this uncertainty. The uncertainties shown in Figure 5B and Figure 5A have the similar evolution trend, implying that the uncertainty can characterize the QPT even without choosing the complete set of MUBs.

FIGURE 5

FIGURE 5. The evolution of the uncertainty of the 2D Ising model. The uncertainty equality (A) and inequality (B) versus kt with the magnetic field B₃(t), the uncertainty equality (C) and inequality (D) versus ωt with the magnetic field B₄(t).

From Figure 5C and Figure 5D, we can see that the behaviors of uncertainty against ωt in each half cycle are almost consistent with those against kt in Figure 5A and Figure 5B, respectively. With the system size increasing, the uncertainty minima appear nearly at $\omega t=\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4}\dots$, and the corresponding effective magnetic field h₂ = 1.835 4 is the QCP of the 2D model. Thus the application of the periodic magnetic field B₄(t) reveals the close relation between QPT and the effective magnetic field, i.e., QPT depends on the magnetic field strength rather than how the magnetic field evolves.

Through the first derivative of the uncertainty dU/dg, we can analyze its nonanalytic behavior at the QCP. For simplicity, in Figure 6 we only plot the first derivative of the uncertainty of the 2D Ising model under B₃(t) versus kt, where dU/dg denotes the first derivative of the right hand side of Eq. 22 and Eq. 24. Surprisingly, the extreme values of the first derivative of the uncertainty can reach up to about 10⁵ for each iteration, which are almost three order of magnitude larger than those of negativity. This shows that the linear-entropy-based uncertainty relation might be a better indicator of QPT than quantum entanglement. Clearly, we can see from Figure 6 that dU/dg oscillates at a high frequency between the maximum and the minimum in a very narrow range near the critical point kt = 1.835 4, which can illustrate the rapidly oscillating behavior of the uncertainty in Figure 5A and Figure 5B. Moreover, with the increase of QRG iterations, the range where the maxima and minima of dU/dg can exist becomes smaller and is approximate to the critical point. Thus, the QPT occurs very fast near the QCP for the large QRG iterations, which can also be exhibited from the rapid variation tendency of the uncertainty with respect to the magnetic field strength. These results indicate that the QRG implementation of uncertainty really captures the QPT behavior of the 2D Ising model.

FIGURE 6

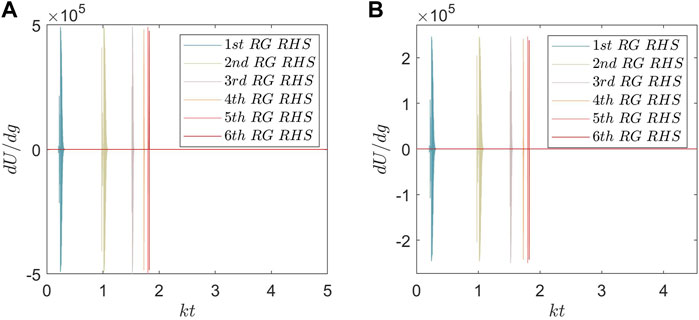
FIGURE 6. First derivative of the uncertainty equality (A) and inequality (B) versus kt with the increasing number of QRG iterations.

4 Conclusions

To summarize, we have analytically derived the effective Hamiltonian and QRG equations by employing the QRG approach. Then the behaviors of the linear-entropy-based uncertainty relation and the quantum entanglement for 2D Ising models with linear and sinusoidal transverse fields are investigated through numerical analysis. Under the linear magnetic field B₃(t), we found that the range where the maxima of entanglement and the minima of the uncertainty can exist becomes smaller and appears near the critical point as the size of the system increases. The entanglement shows an opposite evolution trend to that of the uncertainty. The evolutions of the first derivatives of the uncertainty and the entanglement in terms of QRG iterations indicate a nonanalytic behavior at the QCP. Furthermore, the absolute value of the minimum derivative of negativity against the size of the system exhibits a nice linear relationship. The uncertainty given by Eqs 22, 24 and its first derivative are more sensitive to changes of the magnetic field, resulting in oscillations at high frequency and the uncertainty derivative maxima up to 10⁵, compared with the negativity derivative maxima (∼ 10²), in the vicinity of QCP. Therefore, the uncertainty may be used as a better indicator to characterize QPT than quantum entanglement. Under the sinusoidal magnetic field B₄(t), the maxima of the entanglement and the minima of the uncertainty appear periodically versus the magnetic field, but as the system size increases, they can still gradually approach the QCP. The strong dependence of QPT on the magnetic field strength is clearly illustrated in the case of the sinusoidal magnetic field.

Our findings might be helpful to use the linear-entropy-based uncertainty relation as the indicator for the detection of the QPT, and to reveal the nature of uncertainty relation and quantum entanglement in the 2D Ising model with time-dependent transverse magnetic fields. We expect our results to be of interest for a wide range of applications in other meaningful high-dimensional spin models with the QRG method.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

Y-YF and J-ML contributed to conception and design of the study. Y-YF wrote the first draft of the manuscript. T-YJ, X-YX, and J-ML wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos. 91950112, 11174081, and 11134003, the National Key Research and Development Program of China under Grant Nos. 2016YFB0501601, 2016YFA0302103, and 2017YFF0212003, the Shanghai Municipal Science and Technology Major Project under No. 2019SHZDZX01, and the Shanghai Excellent Academic Leaders Program under No. 12XD1402400.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Einstein A, Podolsky B, Rosen N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys Rev (1935) 47:777–80. doi:10.1103/physrev.47.777

CrossRef Full Text | Google Scholar

2. Schrödinger E. Discussion of Probability Relations between Separated Systems. Math Proc Camb Phil Soc (1935) 31:555–63. doi:10.1017/s0305004100013554

CrossRef Full Text | Google Scholar

3. Ekert AK. Quantum Cryptography Based on Bell's Theorem. Phys Rev Lett (1991) 67:661–3. doi:10.1103/physrevlett.67.661

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Bennett CH, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters WK. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys Rev Lett (1993) 70:1895–9. doi:10.1103/physrevlett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bennett CH, Wiesner SJ. Communication via One- and Two-Particle Operators on Einstein-Podolsky-Rosen States. Phys Rev Lett (1992) 69:2881–4. doi:10.1103/physrevlett.69.2881

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Scarani V, Iblisdir S, Gisin N, Acín A. Quantum Cloning. Rev Mod Phys (2005) 77:1225–56. doi:10.1103/revmodphys.77.1225

CrossRef Full Text | Google Scholar

7. Życzkowski K, Horodecki P, Sanpera A, Lewenstein M. Volume of the Set of Separable States. Phys Rev A (1998) 58:883–92. doi:10.1103/physreva.58.883

CrossRef Full Text | Google Scholar

8. Vidal G, Werner RF. Computable Measure of Entanglement. Phys Rev A (2002) 65:032314. doi:10.1103/physreva.65.032314

CrossRef Full Text | Google Scholar

9. Sachdev S. Quantum Phase Transitions. Phys World (1999) 12:33–8. doi:10.1088/2058-7058/12/4/23

CrossRef Full Text | Google Scholar

10. Osterloh A, Amico L, Falci G, Fazio R. Scaling of Entanglement Close to a Quantum Phase Transition. Nature (2002) 416:608–10. doi:10.1038/416608a

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wu L-A, Sarandy MS, Lidar DA. Quantum Phase Transitions and Bipartite Entanglement. Phys Rev Lett (2004) 93:250404. doi:10.1103/physrevlett.93.250404

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Latorre JI, Lütken CA, Rico E, Vidal G. Entanglement Entropy in the Lipkin-Meshkov-Glick Model. Phys Rev A (2005) 71:034301. doi:10.1103/physreva.71.064101

CrossRef Full Text | Google Scholar

13. Gu S-J, Deng S-S, Li Y-Q, Lin H-Q. Entanglement and Quantum Phase Transition in the Extended Hubbard Model. Phys Rev Lett (2004) 93:086402. doi:10.1103/physrevlett.93.086402

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Anfossi A, Giorda P, Montorsi A. Entanglement in Extended Hubbard Models and Quantum Phase Transitions. Phys Rev B (2007) 75:165106. doi:10.1103/physrevb.75.165106

CrossRef Full Text | Google Scholar

15. Ren J, You W-L, Wang X. Entanglement and Correlations in a One-Dimensional Quantum Spin-1/2 Chain with Anisotropic Power-Law Long-Range Interactions. Phys Rev B (2020) 101:094410. doi:10.1103/physrevb.101.094410

CrossRef Full Text | Google Scholar

16. Vidal J, Palacios G, Mosseri R. Entanglement in a Second-Order Quantum Phase Transition. Phys Rev A (2004) 69:022107. doi:10.1103/physreva.69.022107

CrossRef Full Text | Google Scholar

17. Verstraete F, Popp M, Cirac JI. Entanglement versus Correlations in Spin Systems. Phys Rev Lett (2004) 92:027901. doi:10.1103/physrevlett.92.027901

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Biswas G, Biswas A. Entanglement in First Excited States of Some many-body Quantum Spin Systems: Indication of Quantum Phase Transition in Finite Size Systems. Phys Scr (2020) 96:025003. doi:10.1088/1402-4896/abce33

CrossRef Full Text | Google Scholar

19. Souza F, Veríssimo LM, Strečka J, Lyra ML, Pereira MS. Interplay between Charge and Spin thermal Entanglement in Hubbard Dimers. Phys Rev B (2020) 102:064414. doi:10.1103/physreva.102.032421

CrossRef Full Text | Google Scholar

20. Ma F-W, Liu S-X, Kong X-M. Entanglement and Quantum Phase Transition in the One-Dimensional Anisotropic XY Model. Phys Rev A (2011) 83:062309. doi:10.1103/physreva.83.062309

CrossRef Full Text | Google Scholar

21. Amico L, Fazio R, Osterloh A, Vedral V. Entanglement in many-body Systems. Rev Mod Phys (2008) 80:517–76. doi:10.1103/revmodphys.80.517

CrossRef Full Text | Google Scholar

22. Wu X, Ivanchenko MV, Jandal HA, Cicconet M, Indzhykulian AA, Corey DP. PKHD1L1 Is a Coat Protein of Hair-Cell Stereocilia and Is Required for normal Hearing. Nat Commun (2019) 10:3801. doi:10.1038/s41467-019-11712-w

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Taylor SR, Scardicchio A. Subdiffusion in a One-Dimensional Anderson Insulator with Random Dephasing: Finite-Size Scaling, Griffiths Effects, and Possible Implications for many-body Localization. Phys Rev B (2021) 103:184202. doi:10.1103/physrevb.103.184202

CrossRef Full Text | Google Scholar

24. Tutsch U, Tsyplyatyev O, Kuhnt M, Postulka L, Wolf B, Cong PT, et al. Specific Heat Study of 1D and 2D Excitations in the Layered Frustrated Quantum Antiferromagnets Cs₂CuCl_4-x Br_x. Phys Rev Lett (2019) 123:147202. doi:10.1103/PhysRevLett.123.147202

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Liu Y, Ma Y. One-Dimensional Plasmonic Sensors. Front Phys (2020) 8:260. doi:10.3389/fphy.2020.00312

CrossRef Full Text | Google Scholar

26. Coulamy IB, Warnes JH, Sarandy MS, Saguia A. Scaling of the Local Quantum Uncertainty at Quantum Phase Transitions. Phys Lett A (2016) 380:1724–8. doi:10.1016/j.physleta.2016.03.026

CrossRef Full Text | Google Scholar

27. Liu C-C, Ye L. Probing Quantum Coherence, Uncertainty, Steerability of Quantum Coherence and Quantum Phase Transition in the Spin Model. Quan Inf. Process (2017) 16:138. doi:10.1007/s11128-017-1588-9

CrossRef Full Text | Google Scholar

28. Xiong S-J, Sun Z, Liu J-M. Entropic Uncertainty Relation and Quantum Phase Transition in Spin-1/2 Heisenberg Chain. Laser Phys Lett (2020) 17:095203. doi:10.1088/1612-202x/aba2ef

CrossRef Full Text | Google Scholar

29. Karpat G, Çakmak B, Fanchini FF. Quantum Coherence and Uncertainty in the Anisotropic XY Chain. Phys Rev B (2014) 90:104431. doi:10.1103/physrevb.90.104431

CrossRef Full Text | Google Scholar

30. Robertson HP. The Uncertainty Principle. Phys Rev (1929) 34:163–4. doi:10.1103/physrev.34.163

CrossRef Full Text | Google Scholar

31. Maccone L, Pati AK. Stronger Uncertainty Relations for All Incompatible Observables. Phys Rev Lett (2014) 113:260401. doi:10.1103/physrevlett.113.260401

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Busch P, Lahti P, Werner RF. Colloquium: Quantum Root-Mean-Square Error and Measurement Uncertainty Relations. Rev Mod Phys (2014) 86:1261–81. doi:10.1103/revmodphys.86.1261

CrossRef Full Text | Google Scholar

33. Fan X-Y, Shang W-M, Zhou J, Meng H-X, Chen J-L. Studying Heisenberg-like Uncertainty Relation with Weak Values in One-Dimensional Harmonic Oscillator. Front Phys (2022) 9:803494. doi:10.3389/fphy.2021.803494

CrossRef Full Text | Google Scholar

34. Heisenberg W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. In: Original Scientific Papers Wissenschaftliche Originalarbeiten. Springer: Springer (1985). p. 478–504. doi:10.1007/978-3-642-61659-4_30

CrossRef Full Text | Google Scholar

35. Maassen H, Uffink JBM. Generalized Entropic Uncertainty Relations. Phys Rev Lett (1988) 60:1103–6. doi:10.1103/physrevlett.60.1103

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Horodecki R, Horodecki P, Horodecki M, Horodecki K. Quantum Entanglement. Rev Mod Phys (2009) 81:865–942. doi:10.1103/revmodphys.81.865

CrossRef Full Text | Google Scholar

37. Berta M, Christandl M, Colbeck R, Renes JM, Renner R. The Uncertainty Principle in the Presence of Quantum Memory. Nat Phys (2010) 6:659–62. doi:10.1038/nphys1734

CrossRef Full Text | Google Scholar

38. Wang D, Ming F, Hu ML, Ye L. Quantum‐Memory‐Assisted Entropic Uncertainty Relations. Annalen Der Physik (2019) 531:1900124. doi:10.1002/andp.201900124

CrossRef Full Text | Google Scholar

39. Tomamichel M, Lim CCW, Gisin N, Renner R. Tight Finite-Key Analysis for Quantum Cryptography. Nat Commun (2012) 3:1. doi:10.1038/ncomms1631

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Gehring T, Händchen V, Duhme J, Furrer F, Franz T, Pacher C, et al. Implementation of Continuous-Variable Quantum Key Distribution with Composable and One-sided-device-independent Security against Coherent Attacks. Nat Commun (2015) 6:1. doi:10.1038/ncomms9795

CrossRef Full Text | Google Scholar

41. Wang H, Ma Z, Wu S, Zheng W, Cao Z, Chen Z, et al. Uncertainty equality with Quantum Memory and its Experimental Verification. Npj Quan Inf (2019) 5:1. doi:10.1038/s41534-019-0153-z

CrossRef Full Text | Google Scholar

42. Wootters WK, Fields BD. Optimal State-Determination by Mutually Unbiased Measurements. Ann Phys (1989) 191:363–81. doi:10.1016/0003-4916(89)90322-9

CrossRef Full Text | Google Scholar

43. Yuan H, Zhou Z-W, Guo G-C. Quantum State Tomography via Mutually Unbiased Measurements in Driven Cavity QED Systems. New J Phys (2016) 18:043013. doi:10.1088/1367-2630/18/4/043013

CrossRef Full Text | Google Scholar

44. Ding Z-Y, Yang H, Yuan H, Wang D, Yang J, Ye L. Experimental Investigation of Entropic Uncertainty Relations and Coherence Uncertainty Relations. Phys Rev A (2020) 101:022116. doi:10.1103/physreva.101.032101

CrossRef Full Text | Google Scholar

45. Fisher ME. Renormalization Group Theory: Its Basis and Formulation in Statistical Physics. Rev Mod Phys (1998) 70:653–81. doi:10.1103/revmodphys.70.653

CrossRef Full Text | Google Scholar

46. Langari A. Quantum Renormalization Group ofXYZmodel in a Transverse Magnetic Field. Phys Rev B (2004) 69:100402. doi:10.1103/physrevb.69.100402

CrossRef Full Text | Google Scholar

47. Balazadeh L, Najarbashi G, Tavana A. Quantum Renormalization of L1-Norm and Relative Entropy of Coherence in Quantum Spin Chains Share on. Quan Inf. Process. (2020) 19:1. doi:10.1007/s11128-020-02677-7

CrossRef Full Text | Google Scholar

48. Sadiek G, Xu Q, Kais S. Tuning Entanglement and Ergodicity in Two-Dimensional Spin Systems Using Impurities and Anisotropy. Phys Rev A (2012) 85:042313. doi:10.1103/physreva.85.042313

CrossRef Full Text | Google Scholar

49. Kallin AB, Hyatt K, Singh RRP, Melko RG. Entanglement at a Two-Dimensional Quantum Critical Point: A Numerical Linked-Cluster Expansion Study. Phys Rev Lett (2013) 110:135702. doi:10.1103/physrevlett.110.135702

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Ju H, Kallin AB, Fendley P, Hastings MB, Melko RG. Entanglement Scaling in Two-Dimensional Gapless Systems. Phys Rev B (2012) 85:165121. doi:10.1103/physrevb.85.165121

CrossRef Full Text | Google Scholar

51. Gao K, Xu Y-L, Kong X-M, Liu Z-Q. Thermal Quantum Correlations and Quantum Phase Transitions in Ising-XXZ diamond Chain. Physica A: Stat Mech its Appl (2015) 429:10–6. doi:10.1016/j.physa.2015.02.007

CrossRef Full Text | Google Scholar

52. Xu Y-L, Kong X-M, Liu Z-Q, Wang C-Y. Quantum Entanglement and Quantum Phase Transition for the Ising Model on a Two-Dimension Square Lattice. Physica A: Stat Mech its Appl (2016) 446:217–23. doi:10.1016/j.physa.2015.12.002

CrossRef Full Text | Google Scholar

53. Ambjorn J, Gizbert-Studnicki J, Görlich A, Jurkiewicz J, Loll R. Renormalization in Quantum Theories of Geometry. Front Phys (2020) 8:247. doi:10.3389/fphy.2020.00247

CrossRef Full Text | Google Scholar

54. Kato T. On the Adiabatic Theorem of Quantum Mechanics. J Phys Soc Jpn (1950) 5:435–9. doi:10.1143/jpsj.5.435

CrossRef Full Text | Google Scholar

55. Wilczek F, Zee A. Appearance of Gauge Structure in Simple Dynamical Systems. Phys Rev Lett (1984) 52:2111–4. doi:10.1103/physrevlett.52.2111

CrossRef Full Text | Google Scholar

56. Sun C-P, Ge M-L. Generalizing Born-Oppenheimer Approximations and Observable Effects of an Induced Gauge Field. Phys Rev D (1990) 41:1349–52. doi:10.1103/physrevd.41.1349

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Kubica A, Yoshida B. Precise Estimation of Critical Exponents from Real-Space Renormalization Group Analysis. preprint arXiv:1402.0619. https://arxiv.53yu.com/abs/1402.0619 (2014).

Google Scholar

58. Osborne TJ, Nielsen MA. Entanglement in a Simple Quantum Phase Transition. Phys Rev A (2002) 66:032110. doi:10.1103/physreva.66.032110

CrossRef Full Text | Google Scholar