Abstract
The quantum component in uncertainty relation can be naturally characterized by the quantum coherence of a quantum state, which is of paramount importance in quantum information science. Here, we experimentally investigate quantum uncertainty relations construed with relative entropy of coherence, norm of coherence, and coherence of formation. Instead of quantum state tomographic technology, we employ the classical shadow algorithm for the detection of lower bounds in quantum uncertainty relations. With an all-optical setup, we prepare a family of quantum states whose purity can be fully controlled. We experimentally explore the tightness of various lower bounds in different reference bases on the prepared states. Our results indicate that the tightness of quantum coherence lower bounds depends on the reference bases and the purity of the quantum state.
1 Introduction
The uncertainty principle lies at the heart of quantum mechanics, which makes it different from classical theories of the physical world. It behaves as a fundamental limitation describing the precise outcomes of incompatible observables, and plays a significant role in quantum information science from quantum key distribution [1–4] to quantum random number generation [5, 6], and from quantum entanglement witness [7–9] to quantum steering [10, 11] and quantum metrology [12, 13] (also see Ref. [14] for the review of uncertainty relation and applications).
The seminal concept of uncertainty relation was proposed by Heisenberg in 1927 [15], in which he observed that the measurement of position x of an electron with error Δ(x) causes the disturbance Δ(p) on its momentum p. In particular, their product has a lower bound set by Planck constant, that is, Δ(x)Δ(p) ∼ ℏ. Later, Robertson generalized the Heisenberg’s uncertainty relation to two arbitrary observables by , with ΔA (ΔB) being the standard deviation of observable A (B), [A, B] = AB− BA being the commutator of A and B, and ⟨⋅⟩ being the expected value in a given state ρ [16]. Indeed, such an uncertainty relation has a state-dependent lower bound so that it fails to reveal the intrinsic incompatibility when A and B are noncommuting.
To address the issue of state-independence of Robertson’s uncertainty relation, the entropic uncertainty relation has been developed by Deutsch [17], Kraus [18], and Maassen and Uiffink [19]: Consider a quantum state ρ and two observables A and B; the eigenstates |ai⟩ and |bi⟩ of observable A and B constitute measurement bases and . The probability of measuring A on state ρ with ith outcome is pi = Tr[ρ|ai⟩⟨ai|], and the corresponding Shannon entropy of measurement outcomes is H(A) = −∑ipi log2pi. Then, H(A) + H(B) is lower bounded by H(A) + H(B) ≥− log2c with c = maxi,j|⟨ai|bj⟩|2 the maximal overlap between |ai⟩ and |bj⟩. According to the definition of Shannon entropy, H(A) quantifies the uncertainty or lack of information associated to a random variable, but does not indicate whether the uncertainty comes from classical or quantum parts. For instance, the measurement of Pauli observable Z on states and I/2 = (|0⟩⟨0| + |1⟩⟨1|)/2 both lead to H(Z) = 1.
It is natural to consider quantum coherence, which is one of the defining features of quantum mechanics, to quantify the quantum component in uncertainty [20–22]. Along with this, rigorous connections between quantum coherence and entropic uncertainty have been established [23, 24] based on the framework of coherence quantification [25], and the quantum uncertainty relations (QURs) have been theoretically constructed with various coherence measures [26]. On the experimental side, the QURs using relative entropy of coherence have been demonstrated to investigate the trade-off relation [27] and connection between entropic uncertainty and coherence uncertainty [28]. Still, there are several unexplored matters along the line of experimental investigations. First, although various QURs have been theoretically constructed with relative entropy of coherence, the experimental feasibility and comparison have not been tested. Second, the experimental realizations of QURs using other coherence measures beyond relative entropy of coherence are still lacking. Finally, the lower bounds in QURs are generally obtained with quantum state tomography (QST) [27, 28], which becomes a challenge when the dimension of quantum state increases.
In this study, we experimentally investigate QURs constructed with three coherence measures, relative entropy of coherence, l1 norm of coherence, and coherence of formation, on a family of single-photon states. The lower bound of the QURs is indicated with classical shadow (CS) algorithm [29]. We show that the tightness of coherence lower bounds depends on the reference bases and the purity of quantum state.
This article is organized as follows: In Section 2, we introduce the basic idea of QUR using quantum coherence measures. In Section 3, we briefly introduce the CS algorithm to detect the purity of a quantum state. In Sections 4 and 5, we present the experimental demonstration and results. Finally, we draw the conclusion in Section 6.
2 Quantum Uncertainty Relations
A functional C can be regarded as a coherence measure if it satisfies four postulates: nonnegativity, monotonicity, strong monotonicity, and convexity [25]. The different coherence measure plays different roles in quantum information processing. For instance, the relative entropy of coherence plays a crucial role in coherence distillation [30], coherence freezing [31, 32], and the secret key rate in quantum key distribution [33]. The coherence of formation represents the coherence cost, that is, the minimum rate of a maximally coherent pure state consumed to prepare the given state under incoherent and strictly incoherent operations [30]. The l1-norm of coherence is closely related to quantum multi-slit interference experiments [34] and is used to explore the superiority of quantum algorithms [35–37]. We refer to Ref. [38] for the review of resource theory of quantum coherence. In the following, we give a brief review of QURs constructed with coherence measures of relative entropy of coherence, l1-norm of coherence, and coherence of formation [26].
2.1 Quantum Uncertainty Relations Using Relative Entropy of Coherence
The relative entropy of coherence of state ρ is defined as [25]:where denotes the measurement basis of observable J, SVN(ρ) = −Tr [ρ log2ρ] is the von Neumann entropy, and ρd is the diagonal part of ρ in measurement basis . Note that . The QUR using relative entropy of coherence [26] iswhere h(x) = −x log2x − (1 − x) log2 (1 − x) is the binary entropy and is the purity of state ρ. Similarly, the entropic uncertainty relations proposed by Sánches-Ruiz [39], Berta et al. [3], and Korzekwa et al. [22] can be expressed in terms of relative entropy of coherence by (see Supplementary Material for detailed derivations)
Consider a qubit state ρ in spectral decomposition ρ = λ|ψ⟩⟨ψ| + (1 − λ)|ψ⊥⟩⟨ψ⊥| with λ(1 − λ) being the eigenvalue associated with eigenvector |ψ⟩(|ψ⊥⟩); we have SVN(ρ) = −λ log2λ − (1 − λ) log2 (1 − λ) where the purity is related to λ by .
2.2 Quantum Uncertainty Relations of the Norm of Coherence Norm of Coherence
The l1 norm of coherence in fixed measurement bases is defined in the form ofwhere the QUR using l1 norm of coherence is [26]
2.3 Quantum Uncertainty Relations Using Coherence of Formation
The coherence of formation in fixed measurement bases is defined in the form ofwhere the infimum is taken over all state decomposition of ρ = ∑ipi|φi⟩⟨φi|. The QUR using coherence of formation is [26]
3 Classical Shadow
From Section 2, it is obvious that the purity of ρ is the key ingredient in the experimental testing of various QURs. The purity can be calculated by reconstructing the density matrix of ρ with QST, which is very costly as the Hilbert space of ρ increases. Another protocol employs two copies of ρ for the detection of , that is, , with Π being the local swap operator of two copies of the state [40, 41].
Very recently, the CS algorithm has been theoretically proposed for efficient quantum state detection [29], and has been experimentally realized in the detection of purity of unknown quantum states [42, 43]. In CS algorithm, a randomly selected single-qubit Clifford unitary U is applied on ρ, and then the rotated state UρU† is measured in the Pauli-Z basis, that is, . With the outcome of |zi⟩, the estimator is constructed by . It is equivalent to measure J = U†ZU on ρ, and the measurement basis J is randomly selected from the Pauli observable basis set , with a uniform probability . The estimator can be rewritten as , where |k⟩ ∈ {|x0⟩, |x1⟩, |y0⟩, |y1⟩, |z0⟩, |z1⟩}. In particular, and are the eigenvectors of Pauli observable X and and are the eigenvectors of Pauli observable Y. It is worth noting that the construction of estimator only requires one sample. In our demonstrations, one sample is one two-photon coincidence. For a set of estimators constructed with Ns samples, the purity of state ρ can be estimated by two randomly selected independent and , that is, .
4 Experiment Realizations
To test the aforementioned QURs of various coherence measures, we consider the following single-qubit state:with 0 ≤ τ ≤ 1. Note that τ = 1 corresponds to the pure state | + ⟩ and τ = 0 corresponds to the maximally mixed state I/2. The experimental setup to generate state in Eq. 10 is shown in Figure 1A. Two photons are generated on a periodically poled potassium titanyl phosphate (PPKTP) crystal pumped by an ultraviolet CW laser diode. The generated two photons are with orthogonal polarization denoted as |HV⟩, where |H⟩ and |V⟩ denote the horizontal and vertical polarization, respectively. Two photons are separated on a polarizing beam splitter (PBS), which transmits |H⟩ and reflects |V⟩. The reflected photon is detected to herald the existence of transmitted photon in state |H⟩, which is then converted to by a half-wave plate (HWP) set at 22.5°. We sent the heralded photon into a 50:50 beam splitter (BS1), which transmits (reflects) the single photon with a probability of 50%. The photons in transmitted and reflected mode are denoted as |t⟩ and |r⟩, respectively. Two tunable attenuators are set at modes |t⟩ and |r⟩ to realize the ratio of transmission probability in |t⟩ and |r⟩ of . The photon in |r⟩ passes through an unbalanced Mach–Zehnder interferometer (MZI) consisting of two PBS and two mirrors, which acts as a completely dephasing channel in polarization degree of freedom (DOF), that is, . Finally, the two beams are incoherently mixed on BS2 to erase the information of path DOF, which leads to the state ρ(τ) in both output ports. A step-by-step calculation detailing the evolution of the single-photon state through this setup is given in Eq. 11:
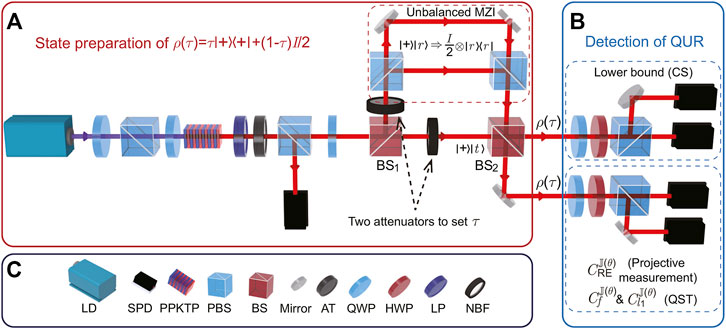
FIGURE 1
Schematic illustration of the experimental setup. (A) The setup to generate the family of states . (B) Experimental setup to implement the measurements with CS algorithm and QST. (C) Symbols used in (A) and (B). Laser diode (LD); single-photon detector (SPD); attenuator (AT); long-wave pass filter (LP); narrow-band filter (NBF).
In our experiment, we set the parameter τ = 0 to τ = 1, with an increment of 0.1, and totally generated 11 states. For each generated state, we detect the QURs with the setup shown in Figure 1B. The lower bound in QURs related to purity is measured with CS algorithm. is detected with projective measurement on basis , along with the measured purity. is calculated with reconstructed ρ(τ). All the measurement bases are realized with a HWP, a quarter-wave plate (QWP), and a PBS.
5 Experimental Results
To investigate the accuracy of estimated purity with CS algorithms, we also calculate the purity with reconstructed density matrix of ρ(τ) from QST with NS = 2000. The results of are shown in Figure 2A. The more the samples used in CS algorithm, the smaller is. We observe when Ns ≥ 600. Especially, when Ns = 2000. In Figure 2B, we show the results of and with NS = 2000 on 11 prepared ρ(τ), in which the experimental results of and have good agreements with the theoretical predictions. In the following, all the results with CS algorithm are obtained with 2000 samples. We also compare the accuracy of estimated purity from CS algorithm and QST with the same Ns (see Supplementary Material for the results).
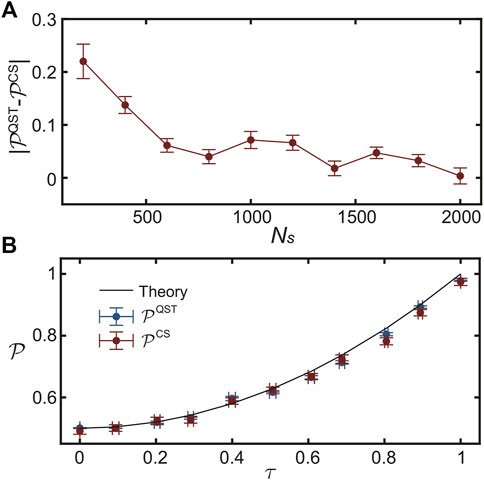
FIGURE 2
(A) Average estimated of 11 prepared states with different Ns. (B) The results of (blue dots) and (red dots). The black line is the theoretical prediction of purity of ideal ρ(τ).
We first focus on the lower bounds in QURs using relative entropy of coherence, that is, Eqs 2–5. We calculate the lower bounds in Eqs 2–5 with the estimated on ρ(τ = 1), ρ(τ = 0.894), ρ(τ = 0.688), and ρ(τ = 0.291), respectively. As shown in Figure 3A, we observe that the lower bounds in Eqs 4, 5 have the same value and outperform others when and are mutually unbiased (c = 0.5). When c becomes larger, lower bounds in Eqs 2, 3 are stricter than those in 4 and Eq. 5. However, the situation is quite different when the purity becomes smaller. As shown in Figure 3B–D, the values of lower bounds in Eqs 3, 4 are negative (we denote them as 0) when c is larger than certain values, which means that the lower bounds are loosened as for all ρ.
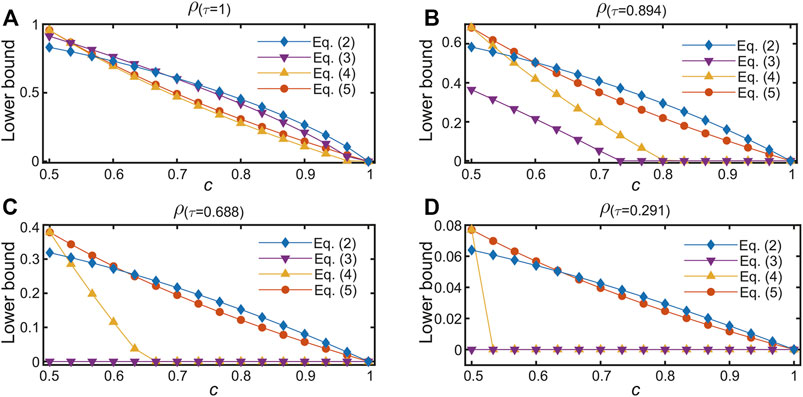
FIGURE 3
Results of estimated lower bounds in Eqs 2–5 with different c on state (A)ρ(τ = 1), (B)ρ(τ = 0.894), (C)ρ(τ = 0.688), and (D)ρ(τ = 0.291), respectively.
To investigate the tightness of various lower bounds, we measure in different reference bases. We select observables A and B from set J(θ) = cos θZ + sin θX. Specifically, we fix A = J (0°) and choose B = J (90°), J (66.42°), and J (36.86°), which correspond to c = 0.5, 0.7, and 0.9. For each observable J(θ), we perform the projective measurement on basis , and calculate the Shannon entropy of measurement outcomes H (J(θ)). Thus, we obtain , where SVN(ρ(τ)) can be calculated from . The results of QURs using relative entropy of coherence are shown in Figure 4. As shown in Figure 4A, the lower bounds in Eqs 4, 5 have the same values as is lower bounded by 1 − SVN(ρ), when c = 0.5 according to the definitions in Eqs 4, 5. When c is larger, the lower bound in Eq. 2 is stricter than others as reflected in Figure 4B and Figure 4C.
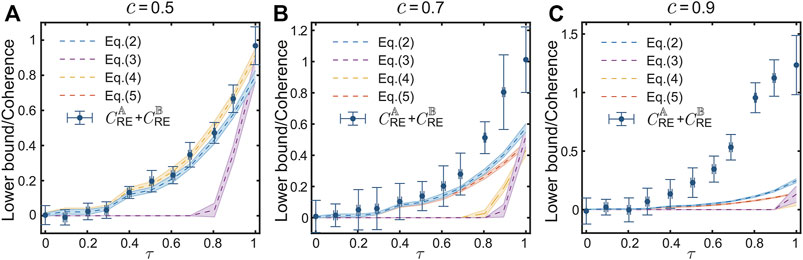
FIGURE 4
Results of QURs in Eqs 2–5 on 11 prepared states with (A)c = 0.5, (B)c = 0.7, and (C)c = 0.9. The dashed lines are the measured lower bounds and the shadow area represents the statistical error by repeating CS measurement for 20 times.
Next, we investigate the QURs using l1-norm of coherence and coherence of formation as described in Eqs 7–9. We choose observables A = J (0°) = Z and B = J (90°) = X in the coherence measure, which corresponds to c = 0.5. The and are calculated according to Eq. 7 with the reconstructed density matrix of ρ(τ). Thus, and can be calculated with and as [26]. The results of QURs using l1 norm of coherence and coherence of formation are shown in Figure 5A and Figure 5B, respectively, in which the measured coherence is well bounded by the measured lower bounds.
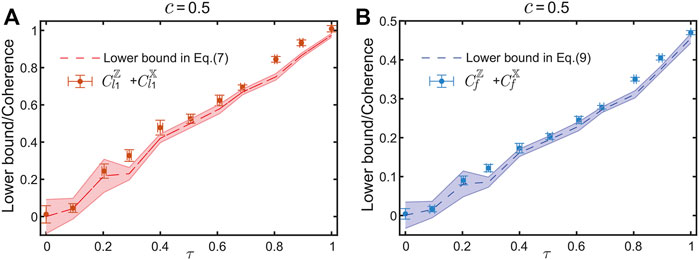
FIGURE 5
Results of (A) QUR with l1 norm of coherence and (B) QUR with coherence of formation with c = 0.5.
6 Conclusion
In this study, we experimentally investigate quantum uncertainty relations using various coherence measures. The lower bounds in quantum uncertainty relations are detected with the classical shadow algorithm, in which the measurement cost is quite small and independent of the dimension of quantum states. For the quantum uncertainty relation using relative entropy of coherence, we show that the tightness of lower bounds is highly related to the reference basis and purity of quantum state. Moreover, we test the quantum uncertainty relation using l1 norm of coherence and coherence of formation.
Our results confirm that the tightness of lower bound in quantum uncertainty relations is related to the purity of quantum states and the reference bases, which can benefit the choice of quantum uncertainty relations when considering the experimental imperfections in practice. For instance, the imperfections in state preparation and measurement apparatus correspond to the purity and reference bases in the lower bound, respectively. More importantly, our method can be generalized to multipartite states while it keeps its efficiency. The multipartite coherence could be efficiently estimated using the stabilizer theory [44, 45] and the classical shadow algorithm to detect that the purity of multipartite state is efficient as well [43].
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
XY and HL conceived the idea. TZ and HL designed the experiment. LL and TZ performed the experiment and analyzed the data. HL supervised the project. XY and HL wrote the manuscript with contributions from all authors.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No. 11974213, No. 92065112, and No. 12175003), National Key R&D Program of China (Grant No. 2019YFA0308200), Shandong Provincial Natural Science Foundation (Grant No. ZR2019MA001 and No. ZR2020JQ05), Taishan Scholar of Shandong Province (Grant No. tsqn202103013), and Shandong University Multidisciplinary Research and Innovation Team of Young Scholars (Grant No. 2020QNQT).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.873810/full#supplementary-material
References
1.
KoashiM. Unconditional Security of Quantum Key Distribution and the Uncertainty Principle. J Phys Conf Ser (2006) 36:98–102. 10.1088/1742-6596/36/1/016
2.
KoashiM. Simple Security Proof of Quantum Key Distribution Based on Complementarity. New J Phys (2009) 11:045018. 10.1088/1367-2630/11/4/045018
3.
BertaMChristandlMColbeckRRenesJMRennerR. The Uncertainty Principle in the Presence of Quantum Memory. Nat Phys (2010) 6:659–62. 10.1038/nphys1734
4.
TomamichelMRennerR. Uncertainty Relation for Smooth Entropies. Phys Rev Lett (2011) 106:110506. 10.1103/PhysRevLett.106.110506
5.
ValloneGMarangonDGTomasinMVilloresiP. Quantum Randomness Certified by the Uncertainty Principle. Phys Rev A (2014) 90:052327. 10.1103/PhysRevA.90.052327
6.
CaoZZhouHYuanXMaX. Source-independent Quantum Random Number Generation. Phys Rev X (2016) 6:011020. 10.1103/PhysRevX.6.011020
7.
PrevedelRHamelDRColbeckRFisherKReschKJ. Experimental Investigation of the Uncertainty Principle in the Presence of Quantum Memory and its Application to Witnessing Entanglement. Nat Phys (2011) 7:757–61. 10.1038/nphys2048
8.
LiC-FXuJ-SXuX-YLiKGuoG-C. Experimental Investigation of the Entanglement-Assisted Entropic Uncertainty Principle. Nat Phys (2011) 7:752–6. 10.1038/nphys2047
9.
BertaMColesPJWehnerS. Entanglement-assisted Guessing of Complementary Measurement Outcomes. Phys Rev A (2014) 90:062127. 10.1103/PhysRevA.90.062127
10.
WalbornSPSallesAGomesRMToscanoFSouto RibeiroPH. Revealing Hidden Einstein-Podolsky-Rosen Nonlocality. Phys Rev Lett (2011) 106:130402. 10.1103/PhysRevLett.106.130402
11.
SchneelochJBroadbentCJWalbornSPCavalcantiEGHowellJC. Einstein-podolsky-rosen Steering Inequalities from Entropic Uncertainty Relations. Phys Rev A (2013) 87:062103. 10.1103/PhysRevA.87.062103
12.
GiovannettiVLloydSMacconeL. Advances in Quantum Metrology. Nat Photon (2011) 5:222–9. 10.1038/nphoton.2011.35
13.
HallMJWWisemanHM. Heisenberg-style Bounds for Arbitrary Estimates of Shift Parameters Including Prior Information. New J Phys (2012) 14:033040. 10.1088/1367-2630/14/3/033040
14.
ColesPJBertaMTomamichelMWehnerS. Entropic Uncertainty Relations and Their Applications. Rev Mod Phys (2017) 89:015002. 10.1103/RevModPhys.89.015002
15.
HeisenbergW. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z Physik (1927) 43:172–98. 10.1007/BF01397280
16.
RobertsonHP. The Uncertainty Principle. Phys Rev (1929) 34:163–4. 10.1103/PhysRev.34.163
17.
DeutschD. Uncertainty in Quantum Measurements. Phys Rev Lett (1983) 50:631–3. 10.1103/PhysRevLett.50.631
18.
KrausK. Complementary Observables and Uncertainty Relations. Phys Rev D (1987) 35:3070–5. 10.1103/PhysRevD.35.3070
19.
MaassenHUffinkJBM. Generalized Entropic Uncertainty Relations. Phys Rev Lett (1988) 60:1103–6. 10.1103/PhysRevLett.60.1103
20.
ColesPJYuLGheorghiuVGriffithsRB. Information-theoretic Treatment of Tripartite Systems and Quantum Channels. Phys Rev A (2011) 83:062338. 10.1103/PhysRevA.83.062338
21.
ColesPJ. Unification of Different Views of Decoherence and Discord. Phys Rev A (2012) 85:042103. 10.1103/PhysRevA.85.042103
22.
KorzekwaKLostaglioMJenningsDRudolphT. Quantum and Classical Entropic Uncertainty Relations. Phys Rev A (2014) 89:042122. 10.1103/PhysRevA.89.042122
23.
YuanXZhouHCaoZMaX. Intrinsic Randomness as a Measure of Quantum Coherence. Phys Rev A (2015) 92:022124. 10.1103/PhysRevA.92.022124
24.
YuanXZhaoQGirolamiDMaX. Quantum Coherence and Intrinsic Randomness. Adv Quan Tech (2019) 2:1900053. 10.1002/qute.201900053
25.
BaumgratzTCramerMPlenioMB. Quantifying Coherence. Phys Rev Lett (2014) 113:140401. 10.1103/PhysRevLett.113.140401
26.
YuanXBaiGPengTMaX. Quantum Uncertainty Relation Using Coherence. Phys Rev A (2017) 96:032313. 10.1103/PhysRevA.96.032313
27.
LvW-MZhangCHuX-MCaoHWangJHuangY-Fet alExperimental Test of the Trade-Off Relation for Quantum Coherence. Phys Rev A (2018) 98:062337. 10.1103/PhysRevA.98.062337
28.
DingZ-YYangHWangDYuanHYangJYeL. Experimental Investigation of Entropic Uncertainty Relations and Coherence Uncertainty Relations. Phys Rev A (2020) 101:032101. 10.1103/PhysRevA.101.032101
29.
HuangH-YKuengRPreskillJ. Predicting many Properties of a Quantum System from Very Few Measurements. Nat Phys (2020) 16:1050–7. 10.1038/s41567-020-0932-7
30.
WinterAYangD. Operational Resource Theory of Coherence. Phys Rev Lett (2016) 116:120404. 10.1103/PhysRevLett.116.120404
31.
BromleyTRCianciarusoMAdessoG. Frozen Quantum Coherence. Phys Rev Lett (2015) 114:210401. 10.1103/PhysRevLett.114.210401
32.
YuX-DZhangD-JLiuCLTongDM. Measure-independent Freezing of Quantum Coherence. Phys Rev A (2016) 93:060303. 10.1103/PhysRevA.93.060303
33.
MaJZhouYYuanXMaX. Operational Interpretation of Coherence in Quantum Key Distribution. Phys Rev A (2019) 99:062325. 10.1103/PhysRevA.99.062325
34.
BeraMNQureshiTSiddiquiMAPatiAK. Duality of Quantum Coherence and Path Distinguishability. Phys Rev A (2015) 92:012118. 10.1103/PhysRevA.92.012118
35.
HilleryM. Coherence as a Resource in Decision Problems: The Deutsch-Jozsa Algorithm and a Variation. Phys Rev A (2016) 93:012111. 10.1103/PhysRevA.93.012111
36.
ShiH-LLiuS-YWangX-HYangW-LYangZ-YFanH. Coherence Depletion in the Grover Quantum Search Algorithm. Phys Rev A (2017) 95:032307. 10.1103/PhysRevA.95.032307
37.
LiuY-CShangJZhangX. Coherence Depletion in Quantum Algorithms. Entropy (2019) 21:260. 10.3390/e21030260
38.
StreltsovAAdessoGPlenioMB. Colloquium : Quantum Coherence as a Resource. Rev Mod Phys (2017) 89:041003. 10.1103/RevModPhys.89.041003
39.
Sánches-RuizJ. Optimal Entropic Uncertainty Relation in Two-Dimensional hilbert Space. Phys Lett A (1998) 244:189–95. 10.1016/S0375-9601(98)00292-8
40.
HorodeckiRHorodeckiPHorodeckiMHorodeckiK. Quantum Entanglement. Rev Mod Phys (2009) 81:865–942. 10.1103/RevModPhys.81.865
41.
BrydgesTElbenAJurcevicPVermerschBMaierCLanyonBPet alProbing Rényi Entanglement Entropy via Randomized Measurements. Science (2019) 364:260–3. 10.1126/science.aau4963
42.
ElbenAKuengRHuangH-Yvan BijnenRKokailCDalmonteMet alMixed-state Entanglement from Local Randomized Measurements. Phys Rev Lett (2020) 125:200501. 10.1103/PhysRevLett.125.200501
43.
ZhangTSunJFangX-XZhangX-MYuanXLuH. Experimental Quantum State Measurement with Classical Shadows. Phys Rev Lett (2021) 127:200501. 10.1103/PhysRevLett.127.200501
44.
DingQ-MFangX-XYuanXZhangTLuH. Efficient Estimation of Multipartite Quantum Coherence. Phys Rev Res (2021) 3:023228. 10.1103/PhysRevResearch.3.023228
45.
DingQ-MFangX-XLuH. The Tightness of Multipartite Coherence from Spectrum Estimation. Entropy (2021) 23:1519. 10.3390/e23111519
Summary
Keywords
quantum uncertainty relation, quantum coherence measures, classical shadow, purity of quantum states, photonic quantum information processing
Citation
Liu L, Zhang T, Yuan X and Lu H (2022) Experimental Investigation of Quantum Uncertainty Relations With Classical Shadows. Front. Phys. 10:873810. doi: 10.3389/fphy.2022.873810
Received
11 February 2022
Accepted
11 March 2022
Published
13 April 2022
Volume
10 - 2022
Edited by
Dong Wang, Anhui University, China
Reviewed by
Shao-Ming Fei, Capital Normal University, China
Xiongfeng Ma, Tsinghua University, China
Updates
Copyright
© 2022 Liu, Zhang, Yuan and Lu.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiao Yuan, xiaoyuan@pku.edu.cn; He Lu, luhe@sdu.edu.cn
This article was submitted to Quantum Engineering and Technology, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.