Microbial Adhesion on Circular Obstacles: An Optimization Study

Microbial filtration is an important process with applications in environmental, mining, and sanitary engineering. Here, we study the interplay between the motility of microswimmers and the imposed flow to determine the adhesion of bacteria at the surface of the solid obstacle. For that, we perform numerical simulations of active Brownian particles interacting with a single cylindrical obstacle when an imposed laminar flow is present. Highly and weakly persistent swimmers are studied, representing extreme cases of bacteria used in experiments and we vary the swimmers’ velocity u₀, the imposed flow velocity U_∞, and the obstacle radius R. Starting with no swimmers close to the cylinder, we inject them steadily until a constant number of swimmers are adhered to the obstacle surface. The deposition/erosion process is characterized by the number of bacteria in contact with the obstacle, quantified by the average coverage of the cylinder surface λ_trap, and the relaxation time to reach the steady state τ_trap. Two regimes are found. The Brownian deposition is attained when swimmer velocities are smaller than the imposed flow. In this case, the particles can diffuse across the streamlines and settle around the obstacle covering the whole perimeter, forming multiple layers. The direct interception is obtained when the particle’s velocities are larger, reaching the obstacle by direct swimming, in which case they form approximately one layer on the obstacle surface. It is found that λ_trap decreases with u₀ and R, but the dependence with the imposed flow U_∞ is non-monotonic, with and optimum coverage for intermediate flows, given by the crossover of the two regimes. The relaxation rate τ_trap decreases with u₀ and increases with R. The dependence of τ_trap with U_∞ is more complex, depending on the persistence of the swimmers. The existence of an optimum value of the flow velocity to reach maximum values of the number of deposited swimmers is an important design information for different applications that use microbial filtration. Finally, in general, it is found that optimal adhesion that has larger values of λ_trap and smaller values of τ_trap is obtained for more-persistent swimmers moving at small velocities interacting with small obstacles.

1 Introduction

The interaction of microorganisms with surfaces has been extensively studied in the last years [1–5], showing that active particles, in general, spend long times exploring surfaces, enhancing microbes’ first adhesion or attachment to them [6–9]. This seed or precursor of biofilm formation might be optimized if, for instance, bacteria self-organize forming stains or clusters in the space producing density gradients or, in very dense systems, orientation gradients [10, 11]. In this last case, the bacteria produce attractive fluxes on the fluid that can replenish nutrients or oxygen to the biofilm.

On the other hand, one of the principle benefits of active particle’s attraction to surfaces is microbes filtration [12]. This has been studied theoretically in the first works of Rubenstein et al. [13] and later with the work of Shimeta et al. [14]. In both cases, they analyzed the problem of microbes passing through a circular obstacle moving in a Stokes flow. By performing a dimensional analysis among different filtration parameters such as microbes activity, relative size, and relative density, they could give glances of how microbes filtration, depending on this parameters, experience different regimes where microbes’ adhesion to the surface is mediated by different physical mechanisms.

In Nature and industry, motile and non-motile microorganisms are often constrict to move on micro-channels or through porous media in the presence of external flows such as sperm in the female reproductive tract, microbes on the urine tract, soil bacteria through roots, bacteria on phytoremediation treatment, plants and bacteria on mining bioflotations [7, 15–17]. Microorganisms in all these cases are constricted to move through a series of obstacles that, recently, has been reproduced under novel laboratory conditions. It has been observed that the transport and particle’s dispersion across obstacles are strongly dependent on the external flow, obstacle radius, and bacterial strains or motility [18–21]. In this aspect, Alonso-Matilla et al. [22] studied theoretically the transport of active agents through an array of obstacles of different shapes, showing that the external flow might span different dispersion mechanisms. Recently, Secchi et al. [20] performed experiments using different strains of bacteria, whereby measuring the capture efficiency, they found that depending on their motility, the external flow, and obstacle size, the bacteria attachment was located at specific regions of the collecting surface. In recent works, the role of hydrodynamic interactions (HI) and activity, in microbe adhesion on complex surfaces, has been studied either numerically [23–27], theoretically [28–31], and experimentally [19, 20, 32–35], showing that motility define a sharp difference in particle adhesion with non-motile particles. In the case of flagellated microswimmers, their hydrodynamic interactions with the surface are crucial to understand the contact angle for particle-obstacle interactions, and therefore determine the contact time with the surface, which is a key to prop the first adhesion [6]. HI are also important to enhance predation opportunity by microbe’s entrainment on convex surfaces [28, 33] and relevant in the accumulation of active particles in the rear of an obstacle, under the effect of an external flow and due to the effect of upstream swimming for elongated microswimmers [23]. Surprisingly, the artificial microswimmers such as active colloids also explore pillar’s surfaces for long time, revealing that varying microswimmer’s activity effectively changes microswimmer’s accumulation on surfaces [32]. Sipos et al. [35] explored the role of obstacle curvature on bacterial adhesion finding that there is a characteristic radius of 140 μm, where entrapment is reduced.

Here, we present a simple model for active Brownian particles [36] to study microbe’s adhesion on convex surfaces under the effect of an external flow. The particle-obstacle hydrodynamic interactions are modeled with a short-range attractive interaction to the obstacle’s surface. Two types of active particles are studied, with different swimming persistences (low and large persistence). By adding a short-range repulsive interaction between microswimmers, we can reproduce bacterial attachment over circular obstacles of different radii [35] and the bacterial attachment on specific regions of the obstacle, depending on the relation between microswimmer’s activity and external flow [20]. Furthermore, by varying the microbe’s activity, we found a narrow velocity screen where microswimmer’s adhesion strongly changes and might determine microbes first adhesion to the surface by changing the contact time with the surface. We find that more-persistent microswimmers with low activity moving close to small obstacles, rather than big ones, in the presence of intermediate external flows optimize microbe’s adhesion on the surfaces, where the number of microswimmers attached to the surface increases and the system reaches faster the steady state. We expect that this detail study might help to improve in vitro fertilization, bio-inspired chemical treatments in industry to optimize biofilm formation, and other processes where the accumulation in surfaces is relevant.

1.1 Numerical Model

To describe the microbe’s motion, we model microswimmers as active Brownian particles (ABP) in two dimensions [37]. Here, each swimmer moves at constant speed u₀ with a persistent orientation $\widehat{e}(t)$ that undergoes rotational diffusion. That is, the orientation changes smoothly on time as compared to run-and-tumble particles (RTP), for which the director changes abruptly at discrete events. Although different, it has been shown that at large times, both models present similar dynamics and there is a direct mapping of the tumbling rate to rotational diffusion coefficient D_R [38]. The microswimmers are circular particles with diameter 2a that interact between them by excluded volume only, and no mutual alignment takes place. The ABP model, despite its simplicity, is known to reproduce many of the observed properties of microswimmers, in particular the accumulation near walls, regime where it has also been shown that the key features are equivalent to other models of active particles [39]. On the other hand, the simplicity of the ABP model, characterized by a few parameters, allows for systematic analysis and to unveil the key features of relevant phenomena for a wide range of microswimmers, without needing to model specific details of each microswimmer under study. Finally, we restrict to spherical swimmers as it has been shown that considering the ellipticity only changes quantitatively the results, with the same phenomenology as for spherical particles for the study of accumulation in surfaces [23]. The use of this model here shows how different accumulation regimes appear as a function of the self-propulsion speed compared to the imposed flow.

There is a single circular obstacle of radius R, which is impenetrable by the swimmers. At short distances, due to hydrodynamic interactions, pusher swimmers, like bacteria, are attracted to solid surfaces and they are aligned to swim parallel to them [2]. To correctly describe this interaction, for example, to get finite-induced velocities, near field hydrodynamics should be considered [40, 41], which are specific for each microbe. Instead, to mimic this effect in a more general way, without introducing hydrodynamic interactions, which are also computationally expensive, we introduce a short-range attractive force that exerts the obstacle on the swimmers and a torque that aligns them. The whole system is subject to an imposed external flow. We assume that the swimmer concentration is low enough such that the induced flow generated by them can be neglected. Hence, the form of this velocity profile is simply the one that results from the interaction of the external flow with the obstacle. Finally, the modeling is done in two spatial dimensions; the extension to three dimensions is direct.

The swimmers’ motion is completely described by the low Reynolds dynamics, i.e., inertia can be completely neglected. Hence, instead of forces and torques, it is more convenient to describe interactions by the induced linear and angular velocities they generate. Thus, the equations of motion for the position ${\vec{r}}_i$ of swimmer i are

$\frac{d{\vec{r}}_i}{dt}=u_0{\widehat{e}}_i+u\left({\vec{r}}_i\right)+{\vec{u}}_O\left({\vec{r}}_i\right)+\sum _{i\ne j}{\vec{u}}_S\left(|{\vec{r}}_i-{\vec{r}}_j|\right),(1)$

where the first term is the self-propulsion along the director, the second term is the drift produced by the external flow, and the last two terms are the induced velocities produced by the interaction with the obstacle and other swimmers, respectively. Similarly, for the director ${\widehat{e}}_i$,

$\frac{d{\widehat{e}}_i}{dt}=\left[\frac{1}{2}\nabla \times \vec{u}\left({\vec{r}}_i\right)+{\vec{\mathrm{\Omega }}}_O\left({\vec{r}}_i,{\widehat{e}}_i\right)+\sqrt{2D_R}\vec{\xi }\right]\times {\widehat{e}}_i,(2)$

where the first term describes the rotation induced by the flow vorticity, that for a spherical swimmer adopts this simple form [42, 43], the second one accounts for the reorientation of the swimmer by the interaction with the obstacle, and the last one is a stochastic term, with ξ a white noise, that produces rotational diffusion with a diffusion coefficient D_R. The cross product with the director guarantees that remains unitary. No swimmer-swimmer torques are considered.

For an ambient fluid with density ρ, viscosity η, and a small imposed flow $U_{\infty }\widehat{x}$ far from the obstacle, the presence of the obstacle centered at the origin of the coordinate system results in the velocity profile $\vec{u}(\vec{r})=U_{\infty }\left[\left(1+\frac{R^3}{2r^3}-\frac{3R}{2r}\right)\cos \theta \widehat{r}-\left(1-\frac{R^3}{4r^3}-\frac{3R}{4r}\right)\sin \theta \widehat{\theta }\right]$. Here, $r=|\vec{r}|$ is the distance to the origin, θ is measured with respect to the $\widehat{x}$ axis and $(\widehat{r},\widehat{\theta })$ is the pair of polar unit vectors.

The obstacle has radius R and the interaction is modeled with a potential U_O, such that ${\vec{u}}_O(\vec{r})=-\nabla U_O(\vec{r})$. The potential is attractive in the adhesion region, R < r_i < ɛ₀ + R, and is repulsive for r < R, describing the rigidity of the surface (see Figure 1A). This interaction mimics, in a simple way, electrostatic, hydrodynamic, or substrate effects on surfaces [16, 32, 33, 35], and allows for reversible adhesion to the surface. For simplicity, we use a Morse potential to have a simple expression valid for all distances:

$U_O\left({\vec{r}}_i\right)=U_O\left[e^{-2{\beta }_M\left(r_i-r_M\right)}-2e^{\left.-{\beta }_M\left(r_i-r_M\right)\right)}\right].(3)$

FIGURE 1

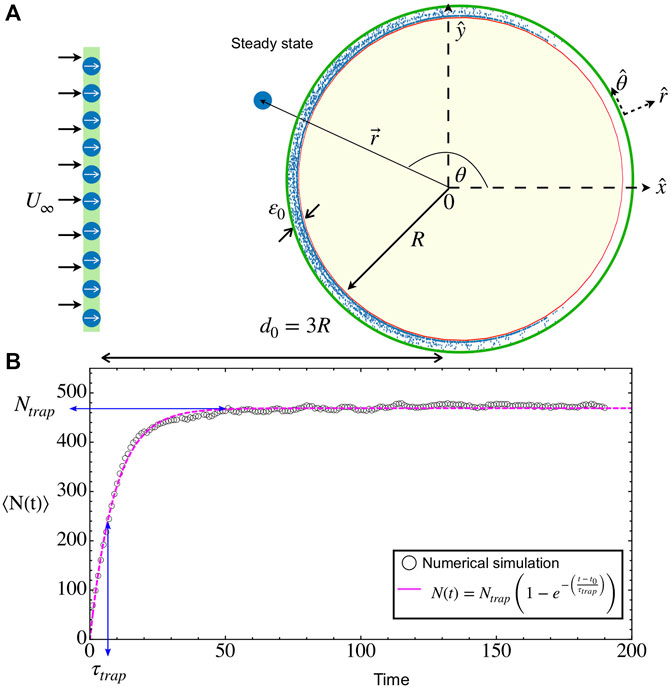
FIGURE 1. Microbial adhesion on a circular obstacle. (A) Snapshot of a transient state (Brownian deposition): Microswimmers are released in waves at a fixed distance 3R from the obstacle center while they are immersed in a constant upstream flow $U_{\infty }\widehat{x}$. When microswimmers (blue points) come into contact with the obstacle, they explore its surface forming different bacterial layers on the adhesion space, delimited by the outer green circle, at a distance ɛ₀ from the surface. (B) Characterization of the steady state: The average bacterial number on the adhesion space ⟨N(t)⟩ increases monotonically on time until it saturates. It is well fitted to the expression $⟨N(t)⟩=N_{\text{trap}}\left[1-e^{-(t-t_0)/{\tau }_{\text{trap}}}\right]$, which allows to compute two relevant observables: the steady state number of trapped particles N_trap and the growth time τ_trap which determines how fast the steady state is reached.

When the microswimmer is close to the surface of the obstacle, there is also a torque that aligns the swimmer with the surface. For simplicity, we consider that the induced angular velocity is

${\vec{\mathrm{\Omega }}}_O\left({\vec{r}}_i,{\widehat{e}}_i\right)=\left\{\begin{array}{cc}{\mathrm{\Omega }}_O{\widehat{r}}_i\times {\widehat{e}}_i\hfill & ,\text{if\hspace{0.17em}}|{\vec{r}}_i|<R+{\epsilon }_0\hfill \\ 0\hfill & ,\text{otherwise}\hfill \end{array}\right.,(4)$

with the same range as the interaction potential.

For the swimmer-swimmer interaction, we use a simple repulsive Yukawa potential

${\vec{U}}_S\left(\vec{r}\right)=U_S{e}^{-r/\left(2a\right)}/r,(5)$

which gives the induced velocity ${\vec{u}}_S(\vec{r})=-\nabla U_S(\vec{r})$.

The simulation is performed in a stripe of size L_y = 4R in the vertical direction and unbounded in the x direction. Periodic boundary conditions are used in the y direction. To generate a continuous injection of microswimmers that approach the obstacle, particles are released periodically, every τ_wave, at a distance d₀ = 3R, randomly distributed along L_y. Each wave is composed of N = 100 microswimmers, uniformly distributed in the chamber all pointing initially in the positive $\widehat{x}$ direction (see Figure 1A). The distance to the obstacle is sufficient for the swimmers to randomize and in the different observables that quantify the accumulation of swimmers in the obstacle, and there is no signature of the periodicity τ_wave.

1.2 Model Parameters and Numerical Implementation

The model has several parameters, characterizing the motion of the swimmers, their mutual interaction, and the interaction with the wall, as well as the properties of the imposed flow and obstacle size. In this study, we focus on varying the swimmer’s speed u₀, the imposed flow U_∞, and the obstacle radius R. The rest of the parameters are fixed to represent typical experimental and natural conditions.

We set the microswimmer’s diameter 2a = 1 µm in the Yukawa potential, as the length scale of the problem. The time scale of the problem is set by the rate of particle injections τ_wave = 1 s. Hence, in what follows, all lengths and times, and the derived units, are expressed as dimensionless quantities.

We define the obstacle adhesion region in ɛ₀ = 7, which accounts for the typical hydrodynamic effects in the vicinity of the obstacle [19, 20, 28]. The intensity of the interactions is rather arbitrary as it is only needed that excluded volume is accurately achieved. We use U_S = 2, U_O = 3.2, β_M = 1.44, and Ω_O = 0.28, which are sufficient to enforce the excluded volume with the integration time step Δt/τ_wave = 1 × 10^–3 and a rapid alignment with the obstacle. We consider two microswimmer types, with very different persistences, characterized by their rotational diffusion coefficient: more-persistent microswimmers with D_R = 0.16 [44, 45], and less-persistent ones with D_R = 0.6 [46]. This classification is related with different bacterial strains modified and used for medical or experimental tasks [17].

We solve the equations of motion (1) and (2) using molecular dynamics simulations with the Euler-Maruyama integration method, for a total time of 200 s. To improve the computational efficiency, we implemented cell lists for the particle-particle interactions and an effective cut-off for the particle-obstacle interaction in order to avoid unnecessary interactions when their distance is large [47].

To study how the activity u₀, obstacle radius R, and external flow U_∞ affect the first adhesion of microbes, we performed three different studies varying different parameters, for both microswimmer’s types.

i. Microswimmer activity: in this case, we will fix the obstacle radius R = 100 and the external flow U_∞ = 40, unless otherwise indicated. We study bacterial activity in the range u₀ = 14, … , 65.

ii. Obstacle radius: in this case, we will fix u₀ = 20 and U_∞ = 40, while varying R in the range 10, … , 350.

iii. External flow: in this case, we fix the obstacle radius R = 100 and the microswimmer activity u₀ = 20, while varying U_∞ = 10, … , 200.

With these set of parameters, the concentration of swimmers in the bulk of the system is dilute. Yet, still accounts a considerable accumulation of microswimmers on the obstacle surface. We performed 24 different simulations for each studied parameter combination and, for all cases, we show the average results.

2 Results

2.1 General Features and Observables

For all considered cases of velocities and obstacle radii, the temporal dynamics is rather similar. First, it takes a time t₀ ∼ 3R/(u₀ + U_∞) for the first swimmers that were injected into the system to reach the obstacle. After this time, there is a continuous income of swimmers to the obstacle. Some of them will reach the adhesion region and remain there while swimming and being advected by the flow. Interactions between swimmers create crowded environments that enhance the residence time in this zone but, also, it is possible to scatter bacteria from the surface after an encounter, helping their erosion by the external flow. As a whole, the total number of particles in the adhesion zone N(t) starts to increase steadily after t₀ until it saturates to the steady value N_trap (see Figure 1B and the Supplementary Video S1). In all cases, the average growth curves can be well fitted to the model

$⟨N\left(t\right)⟩=N_{\text{trap}}\left[1-e^{-\left(t-t_0\right)/{\tau }_{\text{trap}}}\right],(6)$

where τ_trap gives the relaxation time to reach the steady state, similar to the probability of successful interaction presented in Refs. [28, 48]. Considering that the incoming rate is constant, having Eq. 6 as solution of the balance equation implies that the desorption rate is proportional to the actual number of particles in the adhesion layer. In the steady state, the obstacle is saturated and ready for microbes to form the first adhesion [6, 8]. From the simulations, we will obtain τ_trap and N_trap, which are important parameters to characterize and optimize the microbe’s adhesion in convex surfaces.

Figure 2 presents snapshots of the system in the three regimes that are described in the text for the transient at t = τ_trap and in the steady state. In the transient, the distribution is not uniform with particles still being transported along the perimeter, except for the direct interception regime, where the distribution is uniform, although with less particles than in the steady state. In all cases, it is seen that the steady-state distribution in rather uniform in the circle, contrary to other studies where there is a larger accumulation in the back [20, 23]. The three regimes differ notably on the number of accumulated particles.

FIGURE 2

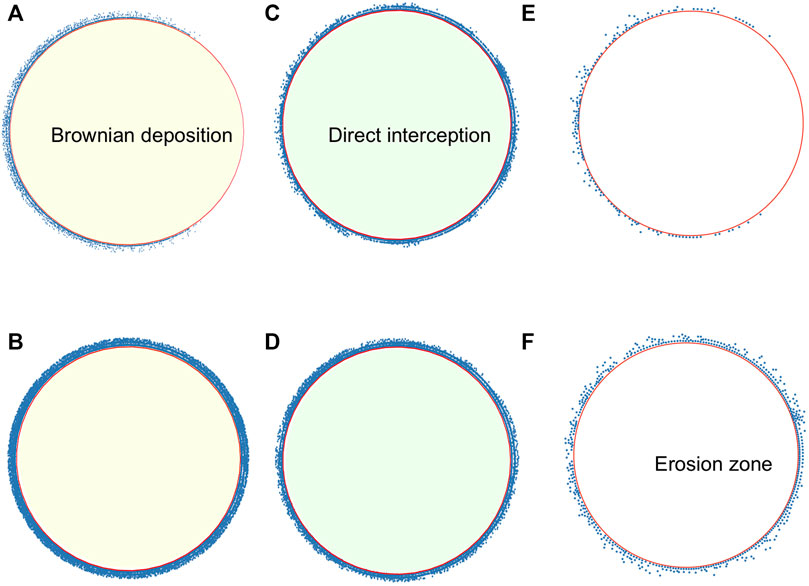
FIGURE 2. Snapshots of microswimmers on the adhesion region at different regimes. Brownian deposition for more-persistent microswimmers for u₀ = 14, U_∞ = 40, R = 100 (A) at t = τ_trap (B) at t = 200. Direct interception for less-persistent microswimmers for u₀ = 50, U_∞ = 40, R = 100 (C) at t = τ_trap, (D) at t = 200. Microswimmers, in the adhesion region, for u₀ = 20, U_∞ = 150, R = 100, (E) at t = τ_trap (F) at t = 200.

Another relevant observable is the contact time of microswimmers with obstacle’s surface, τ_contact. This parameter gives the average residency time of microbes on the surface and therefore the time available to realize an irreversible adhesion to prompt a biofilm. It is measured, for each set of parameters, as the mode considering 24 realizations of the time that particles spend inside the adhesion region.

The number of trapped particles can be compared to the maximum occupation in a monolayer, N_max ≡ 2πR/(2a), which allows us to define the dimensionless average number of deposited layers λ_trap = N_trap/N_max. Similarly, the relaxation time and the contact time can be compared to the time it takes a swimmer to travel the obstacle by its own, τ_s ≡ πR/u₀.

Using dimensional analysis, we expect that the microbial behavior depends on the Péclet number which compares advective transport with diffusion Pe = u₀/(RD_R). Then, in the limit of Pe → 0, we expect that Brownian diffusivity dominates microswimmer’s exploration of the medium, the phenomenon is known as “Brownian deposition.” While in the other limit Pe → ∞, the advection dominates and particles encounter the obstacle surface by “direct interception” [13, 14]. When varying the microswimmer’s activity, in a biological range of velocities [8], we are changing the Péclet number in a narrow window for each microswimmer’s type, and the two limiting cases are not always achieved. Furthermore, the external velocity allows to define new dimensionless parameters. Therefore, for simplicity, we present the results in terms of the control parameters, where the transition between both regimes can also be appreciated.

2.2 Varying Swimmer’s Activity

Here we keep the obstacle radius constant to R = 100 and vary the swimmer’s speed u₀. For the imposed flow, we consider three different values: U_∞ = 20, 40, and 60. We found that depending on the microswimmer’s activity and external flow there are, basically, two different regimes. In one of them, the microswimmer’s velocity is smaller compared with external flow, yet particles diffuse across the streamlines and settle around the obstacle covering the whole perimeter and forming multiple layers, this regime is known as Brownian deposition [13, 14]. In the second regime, when particle’s activity is larger than the external flow, particles scatter faster forming approximately one layer on the obstacle surface. The particle’s capture now depends only on the direct interception with the obstacle. In Figure 3, we show λ_trap, τ_trap, and the contact time τ_contact for the case U_∞ = 40, for both values of persistence. These three observables decrease with the parameter u₀/U_∞. Naturally, as the swim speed increases, the relaxation and contact times decrease accordingly. Also, the thickness of the deposited layer decreases as particles can escape more easily due to excluded volume interactions with other microswimmers.

FIGURE 3

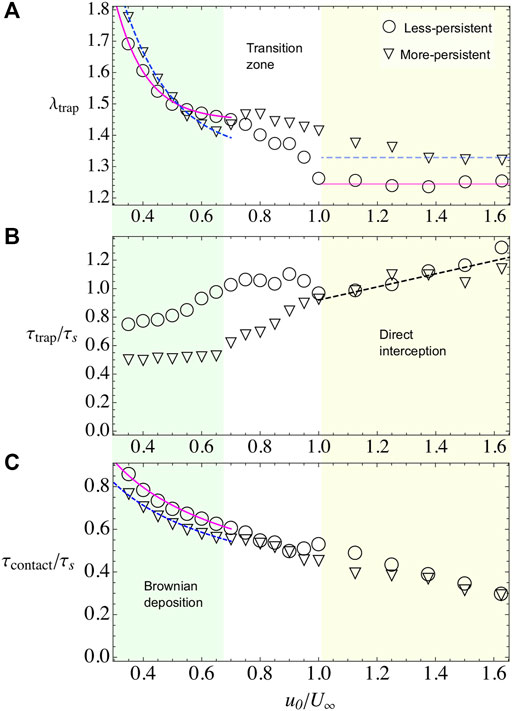
FIGURE 3. Bacterial adhesion observables when varying the microswimmer’s activity u₀ and when U_∞=40 and R =100. Different symbols represent different microswimmer’s types. For less-persistent microswimmers, we use triangles and for more-persistent circles. Two regimes are identified throughout the observables, Brownian deposition and direct interception, which are indicated by shading color and separated by a white transition zone between them. (A) λ_trap for less- and more-persistent microswimmers, respectively. The solid and dashed lines, during Brownian deposition, are phenomenological fits with the law λ_trap = A(1+ B exp(−C(u₀/U_∞))). The blurry lines represent a guide to the eye, for the tendency during the direct interception regime. (B) τ_trap for less- and more-persistent microswimmers, respectively. The dashed line in the direct interception regime is a phenomenological linear fit τ_trap/τ_s = A(1+(u₀/U_∞)). (C) The contact time decreases monotonically with the microswimmer’s activity. Less-persistent microswimmers spend slightly more time in contact with the surface during the Brownian deposition, while during the direct interception regime the residency time is the same for both microswimmer’s types.

2.2.1 First Regime: Brownian deposition

In this regime, microswimmers move slowly than the external flow. Nevertheless, the particles are not purely advected by the flow, on the contrary, they perform an exploration of the space crossing the streamlines and diffusing across the simulation area (see Supplementary Video S1). At contact with the obstacle, the flow velocity vanishes and it remains small in the adhesion region, defined as a ring of width ɛ₀ = 7 across the obstacle’s surface. Hence, the attractive potential becomes a dominant factor, increasing the contact time between microswimmers and the obstacle (Figure 3C), and also increasing the number of microbes in the adhesion region λ_trap (Figure 3A, Figure 4A,C). Moreover, the microswimmers also present a transition zone (see Figures 3,4), at $u_0^{*}\sim 30$ for all external flow’s values, where particle capture slightly increases before entering in the direct interception regime.

FIGURE 4

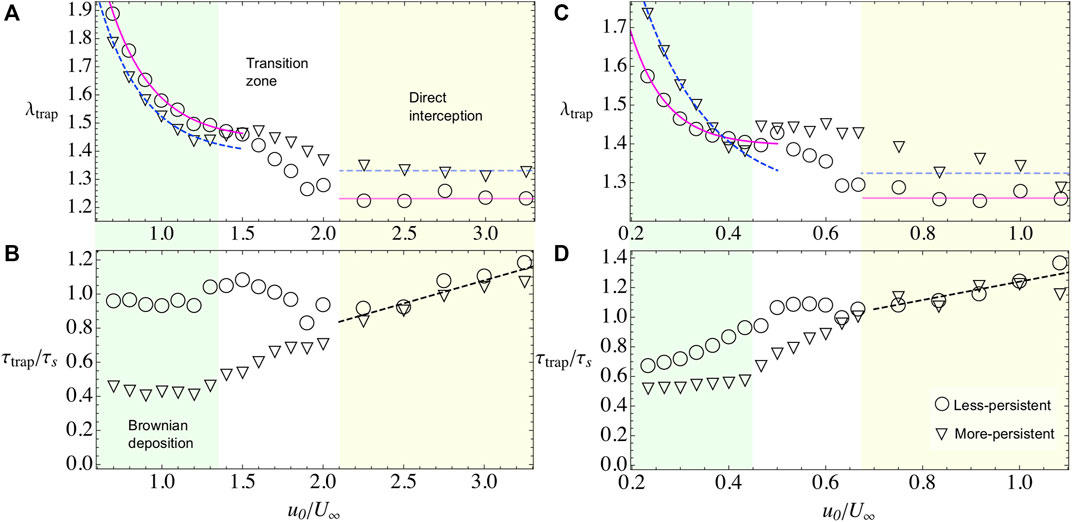
FIGURE 4. Bacterial adhesion observables when varying the microswimmer’s activity u₀ and when the external flow field is U_∞=20 (A,B) and when is U_∞=60 (C,D). In both cases, we span the two regimes by shading the area and letting the transition zone in white. Less-persistent microswimmer’s results are shown with triangles and more-persistent microswimmers in circles. (A,C) λ_trap for less- and more-persistent microswimmers, respectively. The solid and dashed lines, during Brownian deposition, are phenomenological fits with the law λ_trap = A(1+ B exp(−(u₀/U_∞)C)). The blurry lines represent a guide to the eye, for the tendency during the direct interception regime. (B,D) τ_trap for less- and more-persistent microswimmers, respectively. During the Brownian deposition, more-persistent microswimmers reach the steady state faster than the less-persistent microswimmers, being more dramatic the difference for the weak external flow case U_∞=20, where τ_trap/τ_s ∼1 showing that the steady state is reached when microswimmers travel half of the obstacle perimeter. Meanwhile, during the direct interception regime, both curves collapsed and are phenomenological described by a linear fit τ_trap/τ_s = A(1+(u₀/U_∞)).

We find that λ_trap depends on the external flow. In general, when the external flow is slower than particle’s velocity, the microswimmers can stay around the adhesion space increasing the number of trapped particles while, for stronger flows, the capture decreases. In the case of, less-persistent microswimmers (circles in Figures 3,4). For weak flows U_∞ = 20, 40 (Figures 3A,4A), respectively, the microswimmer’s disperse more enhancing the adhesion [21] and exploring for longer times the obstacle’s surface (Figure 3C), while for strong flows U_∞ = 60 (Figure 4C), since the particle trajectories are very noisy, it is highly probable to encounter another particle. As a result of the interaction, the particle can be easily kicked out from the adhesion area and dragged by the external flow, decreasing the fraction of microbes in the obstacle. We fit the fraction of microbes adhered to the obstacle, for all cases, with λ_trap(u₀/U_∞) = A+ B exp(−(u₀/U_∞)C), finding that the rate of decay C for less-persistent microswimmers increases with U_∞ being C(U_∞ = 20) = 3.68, C(U_∞ = 40) = 9.47, and C(U_∞ = 60) = 13.53 with A ≈ 1.4 and B ≈ 4.

More-persistent microswimmers are less affected by the external flow, in this regime (inverted triangles in Figures 3,4), we found a less dramatic rate of decay C with C(U_∞ = 20) = 3.57, C(U_∞ = 40) = 5.91, and C(U_∞ = 60) = 7.15, respectively, and A ≈ 1.3, B ≈ 3. Then, since the microswimmers perform less reorientations, microbe’s capture is faster as we can observe in Figure 3B, Figure 4B,D for different external flows. The relaxation time τ_trap has a similar behavior for all U_∞. We found that during this regime, more-persistent microswimmers reach the steady state before a single microswimmer performs an exploration around the obstacle’s perimeter with τ_trap/τ_s ∼ 0.5 in all cases, while less-persistent microswimmers take longer times depending on the external flow.

The contact time that in average microswimmers spent on the adhesion region decays as ${\tau }_{\text{contact}}={(A{U}_{\infty }/u_0)}^{1/2}$, with A = 0.25 and A = 0.2 for the less- and more-persistent microswimmers, respectively (Figure 6A), following a power law as [25]. According to Secchi et al. [20], non-motile particles distribute uniformly around the obstacle’s surface while motile microswimmers accumulate on the back of the obstacle [19, 20]. Here, since microswimmers are slow, we observe something similar to the case of non-motile microswimmers since they spent more time close to the surface while they diffuse around the adhesion space.

2.2.2 Second Regime: Direct Interception

In this regime, the self-propulsion is higher than the external flow, thus microswimmers move freely around the obstacle’s surface. They are scattered out from this region when they meet another microswimmer and, due to excluded volume interactions, they are deviated from their trajectory, or when they change their orientation due to rotation diffusion. Then, particle’s capture decreases as they move faster and the steady state is also reached faster (see Figure 3B, Figures 4B,D). The number of captured particles is roughly independent of U_∞ for both the more- and less-persistent microswimmers, being the number of more-persistent microswimmers in the adhesion region higher than the less-persistent. The steady state is reached at the same time for all microswimmer’s type, and varying slightly with the external flow. In Figure 3B, Figure 4B,D, the dashed line shows the best fit, which follows τ_trap(u₀/U_∞)/τ_s = A(1 + u₀/U_∞), with A(U_∞ = 20) = 0.27, A(U_∞ = 40) = 0.46, and A(U_∞ = 60) = 0.62. In average, the steady state is reached after one particle travels half of the obstacle’s perimeter, that is, τ_trap ≈ τ_s for both microswimmer’s persistences and the same happens for the contact time (see Figure 3C). Thus, since microswimmers are fast, the steady state is reached after there is a constant number of microswimmers exploring the back of the obstacle’s adhesion space [19, 20]. In this regime, the microbe’s adhesion is optimized for the more-persistent microswimmers since the obstacle captures the same number of particles, and they spent the same amount of time on the surface, yet the steady state is reached faster.

2.3 Varying the Obstacle Radius

Now, we vary the obstacle radius R, while keeping fixed the microswimmer’s activity to u₀ = 20 and the external flow to U_∞ = 40, unless otherwise indicated. The number of layers λ_trap decreases with R (Figure 5A). Small pillars are capable to adhere more than two layers of microbes and for large radii, the number of layers saturates to a value slightly larger than one. The results are well fitted to the expression λ_trap(R) = A[1 + exp(−R/R₀)], with A = 1.24 and R₀ = 65.2, independent of microswimmer’s type and external flow. With this, the total number of accumulated particles increases monotonically with R. Microbe’s capture is in agreement with some experimental results in cylindrical pillars, either for biological microswimmers such as bacteria or algae [33, 34] or artificial microswimmers [35], where there is a critical radius for constant particle’s capture located at R* ≈ 140.

FIGURE 5

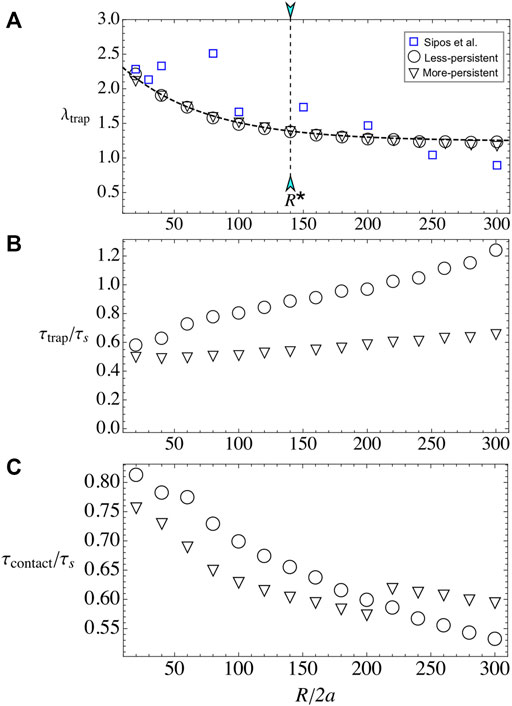
FIGURE 5. Bacterial adhesion when varying obstacle radius R. (A) λ_trap for the less- and more-persistent microswimmers. In blue squares, the experimental data for (E) E. coli adhesion around pillar obstacles by Sipos et al. [35]. The dashed line corresponds to the best fit which is independent of bacterial strain with the law λ_trap(R)= A[1+ exp(−R/R₀)]. (B) τ_trap for the less- and more-persistent microswimmers. Less-persistent microswimmers (inverted triangles) steady state is reached at a constant time τ_trap/τ_s ∼0.5, independent on the obstacle radius R. (C) The contact time increases monotonically with the obstacle radius R for u₀=20 and U_∞=40 fixed.

Regarding the relaxation time, the more-persistent microswimmers reach the steady state faster than the less-persistent ones, and in both cases τ_trap grows with the radius. The results show that for more-persistent microswimmers follows τ_trap/τ_s ∼ 0.5 for all R (see Figure 5B), while for less-persistent microswimmers the steady state increases linearly with the obstacle radius. The time that particles remain in contact with the surface τ_contact increases also with obstacle’s radius, similar to Refs. [32, 35], but it does not follow the simple law τ_contact(R) ≈ τ_s (see Figure 5C). Instead, the contact time increases with R for both microswimmer’s types, yet there is not linear dependence on its growth. Thus, the microbe’s adhesion is enhanced with small pillar radius and less-persistent microswimmers.

2.4 Varying External Flow

Here, we vary the external flow U_∞, while we keep fixed the bacterial activity to u₀ = 20 and the obstacle radius to R = 100. The number of captured layers presents a non-monotonic behavior, with a pronounced maximum for the less-persistent swimmers at U* ≈ 1, where the microswimmer and the flow velocities are similar. For the more-persistent swimmers, the maximum is less pronounced and it is located at U* ≈ 2 (see Figure 6A). For larger external velocities, microbe’s adhesion decreases due to erosion by the flow [19, 20, 49]. For the less-persistent swimmers, the erosion is well fitted to the expression λ_trap(U_∞/u₀) = 1 + 0.66 exp(−0.15U_∞/u₀), according with microbe’s erosion of the surface [20, 49]. For the more-persistent microswimmers, the decrease of λ_trap is slower and well fitted to λ_trap(U_∞/u₀) = 1.62–0.037(U_∞/u₀), similar to the experimental limit for erosion observed by Miño et al. [19].

FIGURE 6

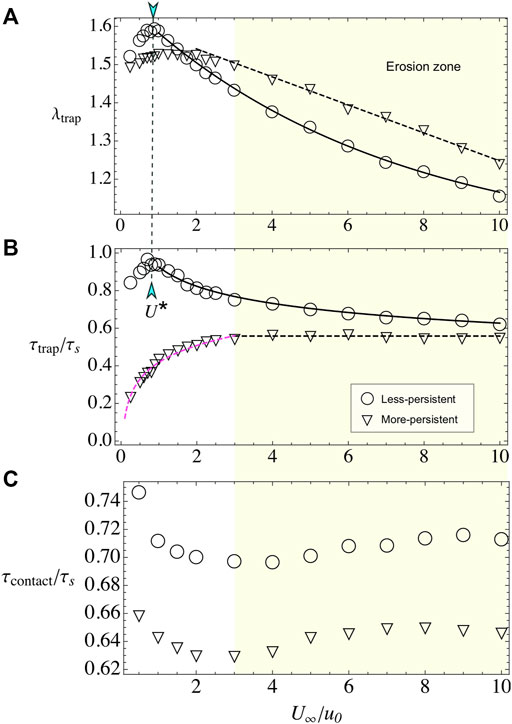
FIGURE 6. Bacterial adhesion when varying external flow U_∞. (A) λ_trap for less- and more-persistent microswimmers. In both cases, the obstacle adheres an increasing number of microswimmers on the surface for weak flows, while for U_∞> U* particles are rapidly eroded from the surface. (B) The time to reach the steady-state τ_trap has different behaviors depending on the microswimmer’s persistence. (C) When varying external flow, U_∞, keeping R =100 and u₀=20 fixed, the contact time fluctuates around a constant value, with less-persistent microswimmers spending more time at the obstacle surface.

In the case of relaxation time, we observe a very different behavior for the two analyzed persistences. For the less-persistent microswimmers, τ_trap is non-monotonic, with a maximum at U* and larger values than for the more-persistent swimmers (see Figure 6B). In the erosion phase, the time that takes to reach the steady state, for less-persistent microswimmers, decays as ${\tau }_{\text{trap}}(U_{\infty }/u_0)/{\tau }_s=0.9{(u_0/U_{\infty })}^{1/6}$. For more-persistent microswimmers, the τ_trap time increases following a law τ_trap(U_∞/u₀)/τ_s = 0.13 log(25.7U_∞/u₀) in the first phase for U_∞/u₀ < 3 and then, in the erosion zone, it is constant with τ_trap/τ_s ≈ 0.56.

Surprisingly, the contact time is constant (see Figure 6C), even in the erosion zone, with small variations around τ_contact/τ_s ≈ 0.63 for the more-persistent swimmers and τ_contact/τ_s ≈ 0.71 for the less-persistent ones. We state that the existence of this almost constant value in the contact time is related with the accumulation of microswimmers in the front and in the back of the obstacle, where there are stagnation points. The particles are expelled from these regions then by their own activity but not on by the flow [20]. Consistent with this hypothesis, the less-persistent swimmers present larger contact times. Also, in the transport of the swimmers along the adhesion zone, the imposed flow almost vanishes there, resulting in that the contact time is dominated by the travel time τ_s.

3 Discussion

We showed, with a simple ABP model, that optimizing microorganism attachment to surfaces is possible by using the right set of mechanical and biological parameters for a given problem. Our simple model proves to be in agreement with the previous quantitative and qualitative theoretical and experimental results for biological and artificial microswimmers [19, 20, 32, 35]. We found that particle’s capture around the adhesion region of a circular obstacle diminishes with the particle’s activity in all the regimes and for both studied microswimmer’s types, namely less- and more-persistent ones. In the case of active Janus particles, Simmchen et al. [32] found that increasing hydrogen peroxide concentration or activity in their experiments results in a particle’s fluorescence increase around the pillars. However, in that case, there was no external flow, and the same applies to the theoretical works for filters [13, 14]. In our model, we considered particle-particle interactions. Therefore, the scattering between particles is now very sensitive to the applied external flow showing that the limiting streamline around the obstacle determines particle’s capture [24].

We also observed that the net accumulation is larger for the more-persistent swimmers. Also, although for both microswimmer’s types the contact time increases with obstacle radius, more-persistent microswimmer’s tend to reach the steady state faster, showing that again they are good candidates for the optimization in biofilm formation. Then, by choosing the right nutrient or fuel source for microswimmers and the right microswimmer strain (less or more noisy), it is possible to enhance the chances in bacterial encounter with the obstacle’s surface. This might be also relevant for medical applications such as in vitro fertilization.

In the case of varying obstacle’s radius, we found that small obstacles can capture more particle’s layers. Larger obstacles, even though have more space to capture swimmers, are less efficient. We also found that for a limiting radius, particle’s capture becomes constant in agreement to previous results by Sipos et al. [35]. Finally, we explored the case when we vary the external flow which in the lasts years has been one of the most revisited problems in microswimmer’s filtration [21, 22, 27], particle hydrodynamic entrainment [28–30, 33, 34], and obstacle adhesion [19, 20]. We found a non-explored behavior for more-persistent microswimmers with a slower decay in particle’s capture in the erosion region and lower times for the system to reach the steady state in this case. We also could predict the velocity for the external flow passing through a circular obstacle [19] at which the erosion of the surface starts.

Our model can be straightforward applied in 3D obstacles, dense systems, porous media, or in different external flow conditions. It is also possible to extend the simple ABP model to include aligning interactions for elongated microswimmers, far-field interactions to study complex microbes, tumbling, polydispersity, or other effects. Also, different experiments show that the microbe-wall interaction is more complex than the simple attraction and alignment that we incorporated in the model, including rheotaxis [50], upstream swim [51], circular motion [52], and changes in the tumbling rate [53]. The influence of these and other effects, as well as the extension to the ABP model, must be studied in detail for quantitative predictions for specific microbes. Finally, choosing the right set of mechanical parameters such as external flow and obstacle’s radius could open new avenues in the control of bacterial deposition on roots in hydroponic crops or in mining bioflotations, opening new environmentally friendly alternatives in engineering and industrial applications.

Data Availability Statement

All simulation codes and raw data used for this paper are available from the corresponding authors upon request.

Author Contributions

FG-L and RS designed and planned research collaboratively and wrote the paper. BE and TF developed the theoretical model, and performed the numerical simulations.

Funding

This research is supported by Fondecyt Grant No. 1180791 (RS), Fondecyt Grant No. 11220683 (FG-L), and by the Millennium Science Initiative Program-NCN19 170 of ANID (Chile). Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

FG-L acknowledges Wolfram Alpha to support her with a free license for this research. We thankful to R. Di Leonardo and P. Galajda for the experimental data and the referees for their comments that improved our manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.865937/full#supplementary-material

Supplementary Video S1 | Simulation for less-persistent microswimmers for an obstacle of radius R = 100, External flow U_∞ = 40 and microswimmer’s activity u₀ = 20.

References

1. Tuson HH, Weibel DB. Bacteria-Surface Interactions. Soft Matter (2013) 9:4368–80. doi:10.1039/c3sm27705d

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Berke AP, Turner L, Berg HC, Lauga E. Hydrodynamic Attraction of Swimming Microorganisms by Surfaces. Phys Rev Lett (2008) 101:038102. doi:10.1103/PhysRevLett.101.038102

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Elgeti J, Kaupp UB, Gompper G. Hydrodynamics of Sperm Cells Near Surfaces. Biophysical J (2010) 99:1018–26. doi:10.1016/j.bpj.2010.05.015

CrossRef Full Text | Google Scholar

4. Li G, Tang JX. Accumulation of Microswimmers Near a Surface Mediated by Collision and Rotational Brownian Motion. Phys Rev Lett (2009) 103:078101. doi:10.1103/PhysRevLett.103.078101

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Smith DJ, Gaffney EA, Blake JR, Kirkman-Brown JC. Human Sperm Accumulation Near Surfaces: A Simulation Study. J Fluid Mech (2009) 621:289–320. doi:10.1017/s0022112008004953

CrossRef Full Text | Google Scholar

6. Dunne WM. Bacterial Adhesion: Seen Any Good Biofilms Lately? Clin Microbiol Rev (2002) 15:155–66. doi:10.1128/cmr.15.2.155-166.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Monteiro MP, Clerici JH, Sahoo PK, Cesar CL, de Souza AA, Cotta MA. Stiffness Signatures along Early Stages of Xylella Fastidiosa Biofilm Formation. Colloids Surf B: Biointerfaces (2017) 159:174–82. doi:10.1016/j.colsurfb.2017.07.075

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Conrad JC, Poling-Skutvik R. Confined Flow: Consequences and Implications for Bacteria and Biofilms. Annu Rev Chem Biomol Eng (2018) 9:175–200. doi:10.1146/annurev-chembioeng-060817-084006

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sahoo PK, Janissen R, Monteiro MP, Cavalli A, Murillo DM, Merfa MV, et al. Nanowire Arrays as Cell Force Sensors to Investigate Adhesin-Enhanced Holdfast of Single Cell Bacteria and Biofilm Stability. Nano Lett (2016) 16:4656–64. doi:10.1021/acs.nanolett.6b01998

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Mathijssen AJTM, Guzmán-Lastra F, Kaiser A, Löwen H. Nutrient Transport Driven by Microbial Active Carpets. Phys Rev Lett (2018) 121:248101. doi:10.1103/physrevlett.121.248101

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Martínez-García R, Nadell CD, Hartmann R, Drescher K, Bonachela JA. Cell Adhesion and Fluid Flow Jointly Initiate Genotype Spatial Distribution in Biofilms. Plos Comput Biol (2018) 14:e1006094. doi:10.1371/journal.pcbi.1006094

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Humphries S. Filter Feeders and Plankton Increase Particle Encounter Rates through Flow Regime Control. Proc Natl Acad Sci U.S.A (2009) 106:7882–7. doi:10.1073/pnas.0809063106

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Rubenstein DI, Koehl MAR. The Mechanisms of Filter Feeding: Some Theoretical Considerations. The Am Naturalist (1977) 111:981–94. doi:10.1086/283227

CrossRef Full Text | Google Scholar

14. Shimeta J, Jumars PA. Physical Mechanisms and Rates of Particle Capture by Suspension Feeders. Oceanogr Mar Biol Annu Rev (1991) 29:191–257.

Google Scholar

15. Kim G, Park K, Choi J, Gomez-Flores A, Han Y, Choi SQ, et al. Bioflotation of Malachite Using Different Growth Phases of Rhodococcus Opacus: Effect of Bacterial Shape on Detachment by Shear Flow. Int J Mineral Process (2015) 143:98–104. doi:10.1016/j.minpro.2015.09.012

CrossRef Full Text | Google Scholar

16. Dwyer R, Bruckard WJ, Rea S, Holmes RJ. Bioflotation and Bioflocculation Review: Microorganisms Relevant for mineral Beneficiation. Mineral Process. Extractive Metall (2012) 121:65–71. doi:10.1179/1743285512y.0000000005

CrossRef Full Text | Google Scholar

17. Costerton JW, Cheng KJ, Geesey GG, Ladd TI, Nickel JC, Dasgupta M, et al. Bacterial Biofilms in Nature and Disease. Annu Rev Microbiol (1987) 41:435–64. doi:10.1146/annurev.mi.41.100187.002251

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Figueroa-Morales N, Mino GL, Rivera A, Caballero R, Clément E, Altshuler E, et al. Living on the Edge: Transfer and traffic of e. coli in a confined flow. Soft Matter (2015) 11:6284–93. doi:10.1039/c5sm00939a

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Miño GL, Baabour M, Chertcoff R, Gutkind G, Clément E, Auradou H, et al. E Coli Accumulation behind an Obstacle. Adv Microbiol (2018) 8:451–64. doi:10.4236/aim.2018.86030

CrossRef Full Text | Google Scholar

20. Secchi E, Vitale A, Miño GL, Kantsler V, Eberl L, Rusconi R, et al. The Effect of Flow on Swimming Bacteria Controls the Initial Colonization of Curved Surfaces. Nat Commun (2020) 11:2851. doi:10.1038/s41467-020-16620-y

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Creppy A, Clément E, Douarche C, d’Angelo MV, Auradou H. Effect of Motility on the Transport of Bacteria Populations through a Porous Medium. Phys Rev Fluids (2019) 4:013102. doi:10.1103/physrevfluids.4.013102

CrossRef Full Text | Google Scholar

22. Alonso-Matilla R, Chakrabarti B, Saintillan D. Transport and Dispersion of Active Particles in Periodic Porous Media. Phys Rev Fluids (2019) 4:043101. doi:10.1103/physrevfluids.4.043101

CrossRef Full Text | Google Scholar

23. Lee M, Lohrmann C, Szuttor K, Auradou H, Holm C. The Influence of Motility on Bacterial Accumulation in a Microporous Channel. Soft Matter (2021) 17:893–902. doi:10.1039/d0sm01595d

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Espinosa-Gayosso A, Ghisalberti M, Ivey GN, Jones NL. Particle Capture and Low-Reynolds-Number Flow Around a Circular Cylinder. J Fluid Mech (2012) 710:362–78. doi:10.1017/jfm.2012.367

CrossRef Full Text | Google Scholar

25. Wysocki A, Elgeti J, Gompper G. Giant Adsorption of Microswimmers: Duality of Shape Asymmetry and wall Curvature. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 91:050302. doi:10.1103/PhysRevE.91.050302

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Takagi D, Palacci J, Braunschweig AB, Shelley MJ, Zhang J. Hydrodynamic Capture of Microswimmers into Sphere-Bound Orbits. Soft Matter (2014) 10:1784–9. doi:10.1039/c3sm52815d

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Sosa-Hernández JE, Santillán M, Santana-Solano J. Motility of Escherichia Coli in a Quasi-Two-Dimensional Porous Medium. Phys Rev E (2017) 95:032404. doi:10.1103/PhysRevE.95.032404

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Mathijssen AJ, Jeanneret R, Polin M. Universal Entrainment Mechanism Controls Contact Times with Motile Cells. Phys Rev Fluids (2018) 3:033103. doi:10.1103/physrevfluids.3.033103

CrossRef Full Text | Google Scholar

29. Słomka J, Alcolombri U, Secchi E, Stocker R, Fernandez VI. Encounter Rates between Bacteria and Small Sinking Particles. New J Phys (2020) 22:043016. doi:10.1088/1367-2630/ab73c9

CrossRef Full Text | Google Scholar

30. Desai N, Shaik VA, Ardekani AM. Hydrodynamic Interaction Enhances Colonization of Sinking Nutrient Sources by Motile Microorganisms. Front Microbiol (2019) 10:289. doi:10.3389/fmicb.2019.00289

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Spagnolie SE, Moreno-Flores GR, Bartolo D, Lauga E. Geometric Capture and Escape of a Microswimmer Colliding with an Obstacle. Soft Matter (2015) 11:3396–411. doi:10.1039/c4sm02785j

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Simmchen J, Katuri J, Uspal WE, Popescu MN, Tasinkevych M, Sánchez S. Topographical Pathways Guide Chemical Microswimmers. Nat Commun (2016) 7:10598. doi:10.1038/ncomms10598

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Jeanneret R, Pushkin DO, Kantsler V, Polin M. Entrainment Dominates the Interaction of Microalgae with Micron-Sized Objects. Nat Commun (2016) 7:12518. doi:10.1038/ncomms12518

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Contino M, Lushi E, Tuval I, Kantsler V, Polin M. Microalgae Scatter off Solid Surfaces by Hydrodynamic and Contact Forces. Phys Rev Lett (2015) 115:258102. doi:10.1103/physrevlett.115.258102

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Sipos O, Nagy K, Di Leonardo R, Galajda P. Hydrodynamic Trapping of Swimming Bacteria by Convex Walls. Phys Rev Lett (2015) 114:258104. doi:10.1103/physrevlett.114.258104

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Volpe G, Gigan S, Volpe G. Simulation of the Active Brownian Motion of a Microswimmer. Am J Phys (2014) 82:659–64. doi:10.1119/1.4870398

CrossRef Full Text | Google Scholar

37. Romanczuk P, Bär M, Ebeling W, Lindner B, Schimansky-Geier L. Active Brownian Particles-From Individual to Collective Stochastic Dynamics P. Eur Phys J Spec Top (2012) 202:1–162. doi:10.1140/epjst/e2012-01529-y

CrossRef Full Text | Google Scholar

38. Cates ME, Tailleur J. Motility-Induced Phase Separation. Annu Rev Condens Matter Phys (2015) 6:219–44. doi:10.1146/annurev-conmatphys-031214-014710

CrossRef Full Text | Google Scholar

39. Sepúlveda N, Soto R. Universality of Active Wetting Transitions. Phys Rev E (2018) 98:052141. doi:10.1103/PhysRevE.98.052141

CrossRef Full Text | Google Scholar

40. Dunstan J, Miño G, Clement E, Soto R. A Two-Sphere Model for Bacteria Swimming Near Solid Surfaces. Phys Fluids (2012) 24:011901. doi:10.1063/1.3676245

CrossRef Full Text | Google Scholar

41. Kantsler V, Dunkel J, Polin M, Goldstein RE. Ciliary Contact Interactions Dominate Surface Scattering of Swimming Eukaryotes. Proc Natl Acad Sci U.S.A (2013) 110:1187–92. doi:10.1073/pnas.1210548110

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Jeffery GB. The Motion of Ellipsoidal Particles Immersed in a Viscous Fluid. Proc R Soc Lond Ser A, Containing Pap a Math Phys character (1922) 102:161–79. doi:10.1098/rspa.1922.0078

CrossRef Full Text | Google Scholar

43. Bretherton FP. The Motion of Rigid Particles in a Shear Flow at Low reynolds Number. J Fluid Mech (1962) 14:284–304. doi:10.1017/s002211206200124x

CrossRef Full Text | Google Scholar

44. Miño GL, Dunstan J, Rousselet A, Clément E, Soto R. Induced Diffusion of Tracers in a Bacterial Suspension: Theory and Experiments. J Fluid Mech (2013) 729:423–44. doi:10.1017/jfm.2013.304

CrossRef Full Text | Google Scholar

45. Mathijssen AJTM, Doostmohammadi A, Yeomans JM, Shendruk TN. Hotspots of Boundary Accumulation: Dynamics and Statistics of Micro-swimmers in Flowing Films. J R Soc Interf (2016) 13:20150936. doi:10.1098/rsif.2015.0936

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Saragosti J, Silberzan P, Buguin A. Modeling E. coli tumbles by rotational diffusion. implications for chemotaxis. PloS one (2012) 7:e35412. doi:10.1371/journal.pone.0035412

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Frenkel D, Smit B, Ratner MA. Understanding Molecular Simulation: From Algorithms to Applications, 2. San Diego: Academic Press (1996).

Google Scholar

48. Gilpin W, Prakash VN, Prakash M. Vortex Arrays and Ciliary Tangles Underlie the Feeding-Swimming Trade-Off in Starfish Larvae. Nat Phys (2017) 13:380–6. doi:10.1038/nphys3981

CrossRef Full Text | Google Scholar

49. Mathijssen AJTM, Doostmohammadi A, Yeomans JM, Shendruk TN. Hydrodynamics of Micro-Swimmers in Films. J Fluid Mech (2016) 806:35–70. doi:10.1017/jfm.2016.479

CrossRef Full Text | Google Scholar

50. Marcos FHC, Fu HC, Powers TR, Stocker R. Bacterial Rheotaxis. Proc Natl Acad Sci U.S.A (2012) 109:4780–5. doi:10.1073/pnas.1120955109

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Figueroa-Morales N, Rivera A, Soto R, Lindner A, Altshuler E, Clément É. E. coli “Super-contaminates” Narrow Ducts Fostered by Broad Run-Time Distribution. Sci Adv (2020) 6:eaay0155. doi:10.1126/sciadv.aay0155

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Lauga E, DiLuzio WR, Whitesides GM, Stone HA. Swimming in Circles: Motion of Bacteria Near Solid Boundaries. Biophysical J (2006) 90:400–12. doi:10.1529/biophysj.105.069401

CrossRef Full Text | Google Scholar

53. Molaei M, Barry M, Stocker R, Sheng J. Failed Escape: Solid Surfaces Prevent Tumbling of Escherichia Coli. Phys Rev Lett (2014) 113:068103. doi:10.1103/PhysRevLett.113.068103

PubMed Abstract | CrossRef Full Text | Google Scholar