- 1School of Physical Science and Technology, Soochow University, Suzhou, China
- 2Department of Physics, Shaoxing University, Shaoxing, China
- 3Zernike Institute for Advanced Materials, University of Groningen, Groningen, Netherlands
- 4School of Physics and Electronics, Shandong Normal University, Jinan, China
- 5Shandong Provincial Engineering and Technical Center of Light Manipulation and Shandong Provincial, Key Laboratory of Optics and Photonic Devices, School of Physics and Electronics, Shandong Normal University, Jinan, China
We introduce a novel type of twisted partially coherent beams with a nonconventional correlation function, named the twisted Hermite-Gaussian correlated Schell-model (THGCSM) beam. The condition that a twist phase can be imposed on a partially coherent beam is addressed for Schell-model fields endowed with rectangular symmetry. Further, the analytical formula for the THGCSM beam propagating in free space has been derived with the help of the generalized Collins formula. The propagation properties, such as the spectral density and the spectral degree of coherence (SDOC) of the THGCSM beam, also have been studied in detail by some numerical examples. The numerical results show that the twist phase plays a role in resisting beam splitting, caused by the correlation structure, and induces the rotation of the distribution of the SDOC on propagation. Moreover, it is interesting to find that when the beam carries a twist phase, this will endow the beam the ability to maintain its distribution of the SDOC on propagation and enhance the self -reconstruction capability of the SDOC. Our results may provide new insights into nonconventional partially coherent beams with twisted phase and may be useful in some applications, such as optical communications and information recovery.
Introduction
Coherence is one of the most notable features of a laser beam. These light beams (i.e., partially coherent beam) have attracted intensive attentions due to their wide applications in inertial confinement fusion, ghost imaging, sub-Rayleigh imaging, particle trapping, free space optical communications and optical scattering [1–8]. Furthermore, Gori et al. [9, 10] proposed the sufficient conditions for designing a real genuine cross-spectral density function or matrix of a partially coherent beam. Based on the above works, a variety of partially coherent beams with nonconventional correlation functions (i.e., the correlation function doesn’t satisfy the Gaussian distribution) have been introduced theoretically and generated experimentally [11–27]. It is found that beams with nonconventional correlation functions will exhibit unique properties on propagation, such as self-splitting, self-reconstruction, locally sharpened and laterally shifted intensity maxima [13, 22, 27], which are useful in multi-particles trapping, atoms guiding, image transfer and recovery. Moreover, the beam profiles in the focal plane (or far fields) can be controlled by endowing the beam with a specific correlation function [15–19, 26], for example, dark-hollow beam profiles (or an optical cage) can be formed near the focal plane when the correlation function satisfies a Laguerre–Gaussian distribution [18]. A Multi-Gaussian correlated Schell-model beam would generate a rectangular intensity profile in the focal plane, and a ring-shaped beam and controllable intensity lattices also can be achieved with the help of the correlation functions [15, 26]. In addition, partially coherent beams with prescribed correlation functions can be applied to reduce scintillation in turbulence [28], overcome the classical Rayleigh diffraction limit [29], coherence-based optical encryption [30], robust microscopy imaging [31], robust far-field imaging [32], and optical beam shaping [33].
On the other hand, partially coherent beams with a twist phase (i.e., twisted partially coherent beam) carry orbital angular momentum (OAM) [34]. Twist phase as a “genuinely two-dimensional” phase can’t exist in a coherent beam and its value is bounded in strength. Twist phase was introduced by Simon et al. in 1993 and has been demonstrated in an experiment by Friberg [35, 36]. Due to the intrinsic chiral property of the twist phase the rotation of the beam spot on propagation is induced, and both the distribution of the SDOC, the degree of polarization and the state of polarization of the beam on propagation are affected [37, 38]. Besides, light beams with a twist phase have advantages in resisting coherence (or turbulence)-induced degeneration, depolarization and overcoming the classical Rayleigh limit [37, 39]. It is shown in [40, 41] that using a twist phase can greatly increase the amount of OAM of a partially coherent vortex beam and enhance its self-reconstruction capability.
Recently, some new ways have been introduced to generate twisted Gaussian Schell-model beams and measure their orbital angular momentum [42, 43]. The problem of when a twist phase can be imposed on a partially coherent beam, generated from a Schell-model source with axial symmetries, was explored in [44, 45]. Two approaches have been proposed to devise genuine twist beams with and without symmetry [46, 47]. In this paper, we devised a newly twisted partially coherent beam named the twisted Hermite-Gaussian correlated Schell-model (THGCSM) beam. The condition that the THGCSM beam will be bona fide is met, and the propagation properties of the THGCSM beam have been investigated in detail. Our results show that the twist phase plays a role of preventing deterioration of the intensity distribution and induces rotation of the distribution of the SDOC around the axis on propagation. Furthermore, the twist phase also will enhance the ability of the beam to maintain the distribution of the SDOC and its self-reconstruction capability, which will be useful for optical information processing and recovery.
Theory of the Twisted Hermite-Gaussian Correlated Schell-Model Beam
Twisted Schell-Model Beams With Rectangular Symmetry
Based on the unified theory of coherence and polarization, the statistical properties of a partially coherent beam can be characterized by the cross-spectral density (CSD) [48]. For Schell-model fields, endowed with rectangular symmetry, the cross-spectral density (CSD) of the beam can be expressed as
where r1 = (x1, y1), r2 = (x2, y2) are two arbitrary transverse position vectors, τ (ri) denotes the transmission function of an arbitrary (complex) amplitude filter and u (|x1-x2|)u (|y1-y2|) is the spectral degree of coherence. When the beam carries a twist phase, the CSD is defined as
where the last exponential term represents the twist phase, with μ0 being the twist factor. According to the Refs. [44, 45], the CSD will be bona fide, if and only if the corresponding uniform source, defined as
is bona fide too. Then, we find that the uniform source satisfies the following formal integral relationship
for any pair (r1, r2), ρ = (ρx, ρy) is an arbitrary transverse position vector, and
For the r. h. s of Eq. 4 we obtain:
Then, taking into account that
On letting ρ = ρ − (r2−r1), Eq. 7 can be recast as
Thus, the Equation 4 has been proved. Moreover, it has been mentioned in [45], when the Equation 4 is satisfied, the uniform source Wu defined by Eq. 3 and the twist phase Tu share the same coherent modes, defined as
with u = kμ0, k = 2π/λ is the wavenumber with wavelength λ, and j = 0, 1/2, 1, … , m = -j, j+1, … , j. Here,
If the uniform source Wu is bona fide, the sufficient condition is that the eigenvalue sequence {λj,m} should be nonnegative. These eigenvalues are defined as
On substituting equations 3 and (9) into Equation 10, and on letting
Use the Following Expression [45]
with
Eq. 13 is one of the main results of this paper, which can be used to assess the conditions when the Schell-model beams with rectangular symmetry can carry the twist phase.
Analytical Formula for a Twisted Hermite-Gaussian Correlated Schell-Model Beam
In this section, we introduce a new kind of twisted partially coherent beam with nonconventional correlation function, named the twisted Hermite-Gaussian correlated Schell-model (THGCSM) beam. As a natural extension of the Hermite-Gaussian correlated Schell-model (HGCSM) beam [22], the CSD in the source plane (z = 0) is defined as
where r1 = (x1, y1), r2 = (x2, y2) are two arbitrary transverse position vectors in the source plane, σ0 and δ0 represent the beam width and the spatial coherence width, respectively. H2m and H2n are the Hermite polynomial of order 2m and 2n, respectively. After some algebra, Equation 14 can be expressed in the following alternative form
As mentioned in section 2.1, the THGCSM beam will be bona fide, if and only if the corresponding uniform source, defined as
is bona fide too. On substituting Equation 15 into Equation 10, and after some tedious integrations and algebraic manipulations, we have
where 2F1 is a hypergeometric function. So, in order for Wu to be bona fide (i.e., λj,m should be nonnegative), the parameter u = kμ0 in Eq. 17 must be bounded by the following inequality:
Thus, the THGCSM beam will be bona fide, if and only if the Equation 18 is satisfied. Then, the propagation of the THGCSM beam through an ABCD optical system can be investigated with the help of the generalized Collins formula [38, 40].
where ρ1 = (ρx1, ρy1) and ρ2 = (ρx2, ρy2) are two arbitrary transverse position vectors in the observation plane, and A, B, C, D are the transfer matrix elements of an optical system. On substituting Equation 14 into Equation 19, we obtain the analytical formulae for the CSD of a THGCSM beam in the output plane as follows:
with
The spectral density of the THGCSM beam at point ρ in the receiver plane is defined as
The spectral degree of coherence (SDOC) of the THGCSM beam at a pair of transverse points with position vectors ρ1 and ρ2 in the output plane can be expressed by the formula
Based on the obtained formulae above, we can study the propagation properties of a THGCSM beam in a convenient way.
Numerical Simulation of a THGCSM Beam
Paraxial Propagation of the THGCSM Beam Through an ABCD Optical System.
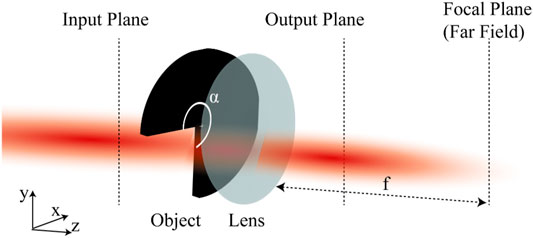
In this section, we study the paraxial propagation of the THGCSM beam through an ABCD optical system by applying the formulae derived in section 2. In the following examples, we consider the beam propagating in free space after passing through a lens with focal length f = 400mm, which is located at
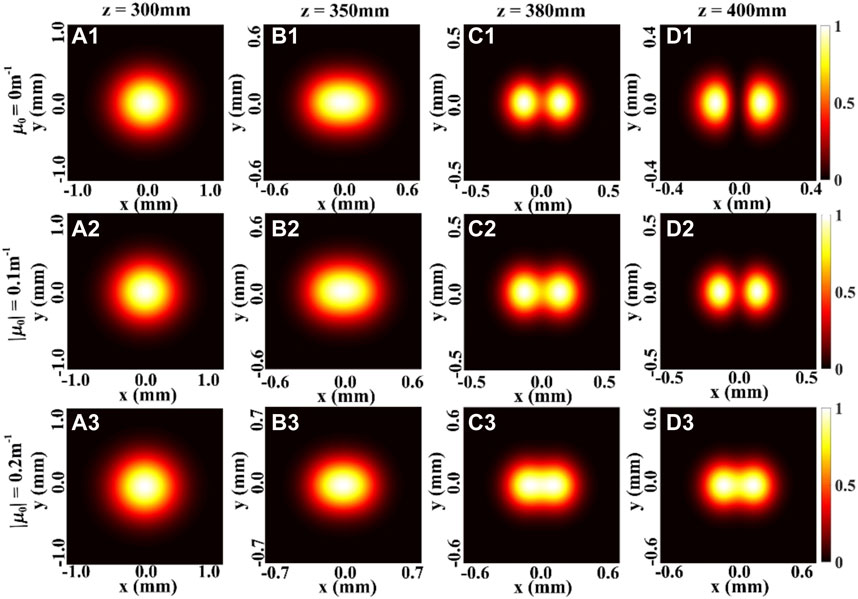
FIGURE 1. Density plot of the normalized spectral density of a focused THGCSM beam with m = 1, n = 0 for different values of the twist factor μ0 at several propagation distances.
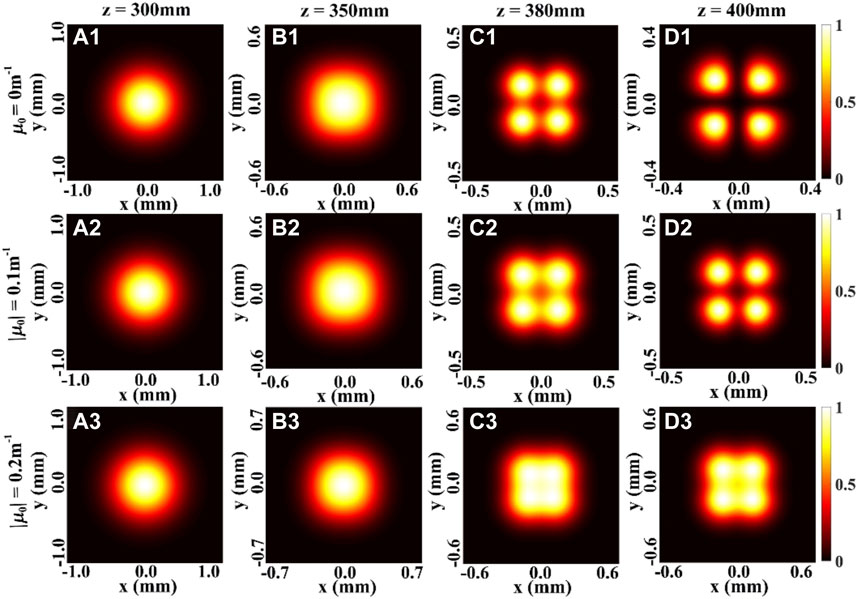
FIGURE 2. Density plot of the normalized spectral density of a focused THGCSM beam with m = 1, n = 1 for different values of the twist factor μ0 at several propagation distances.
Then, the evolution properties the SDOC of a focused THGCSM beam on propagation also have been investigated. Figures 3, 4 show the modulus of the SDOC between two points ρ and -ρ (i.e., |η(ρ,-ρ)|), at several propagation distances with different values of the twist factor μ0. The first row of the Figures 3, 4 show the variation of the SDOC of a focused HGCSM beam versus the propagation distances z. It is found that the distribution of the SDOC of the HGCSM beam exhibits an array distribution in the source plane (i.e., z = 0 mm), and the number of the beamlets increase as the values of the beam order m or n increase.
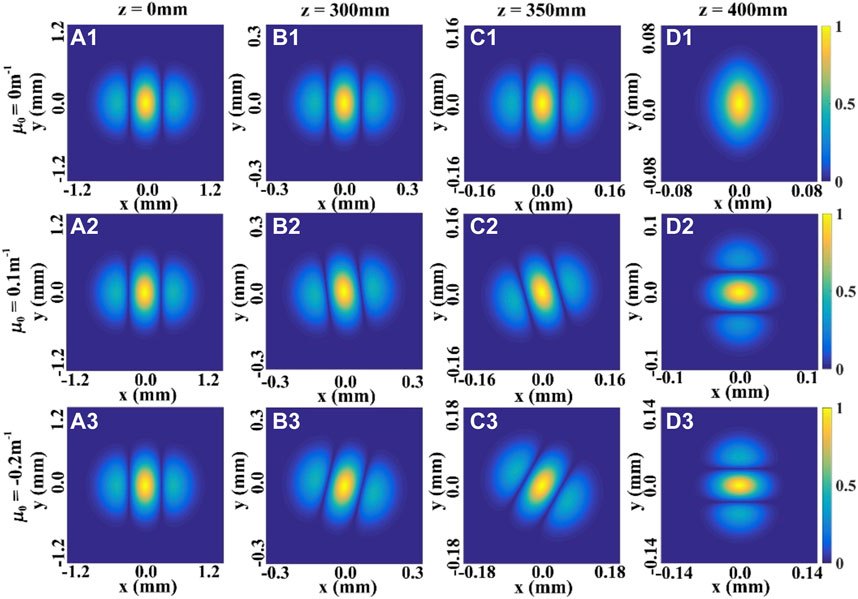
FIGURE 3. Modulus of the SDOC between two points ρ and−ρ of the THGCSM beam with m = 1, n = 0 for different values of the twist factor μ0 at several propagation distances.
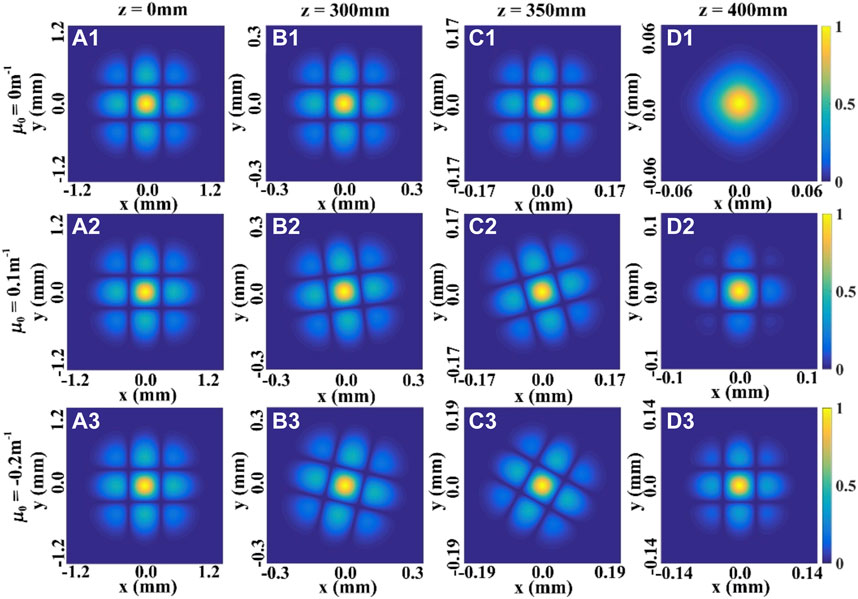
FIGURE 4. Modulus of the SDOC between two points ρ and −ρ of the THGCSM beam with m = 1, n = 1 for different values of the twist factor μ0 at several propagation distances.
When the propagation distance z increases, the profile of the SDOC firstly remains invariant, and then becomes one beam spot in the focal plane. This means that the information regarding the SDOC is increasingly lacking with increasing propagation distance. The second and the third rows of the Figures 3, 4 show the influence of the twist phase on the evolution properties of the SDOC. We find that the twist phase induces a rotation of the SDOC on propagation, such that when μ0 > 0, the distribution of the SDOC rotates anti-clockwise, and when μ0 < 0, the distribution of the SDOC rotates clockwise. The SDOC rotates faster with increasing twist factor μ0, and the rotation angle varies between −π/2 or π/2 in the focal plane. These phenomena can be explained by the fact that the twist phase imposes angular momentum on the beam. Further, one can still determine the structure of the SDOC even in the focal plane. Thus, the twist phase can be used to maintain the beam’s information of the correlation function.
In order to investigate the influence of the spatial coherence width and the twist phase on the beam propagation properties, the density plots of the normalized spectral density and the modulus of the SDOC have been studied, as shown in Figures 5, 6. In Figure 5, we calculated the density plots of the normalized spectral density and the modulus of the SDOC (|η(ρ,−ρ)|) of a focused HGCSM beam (i.e., THGCSM beam with μ0 = 0) for different values of the spatial coherence width δ0 in the focal plane. One can find that with the increase of the spatial coherence width, the beam profile of the HGCSM beam will evolve from the original array beam shape to a Gaussian beam profile (i.e., the self-splitting properties of the HGCSM beam on propagation gradually disappear) as expected in [22].
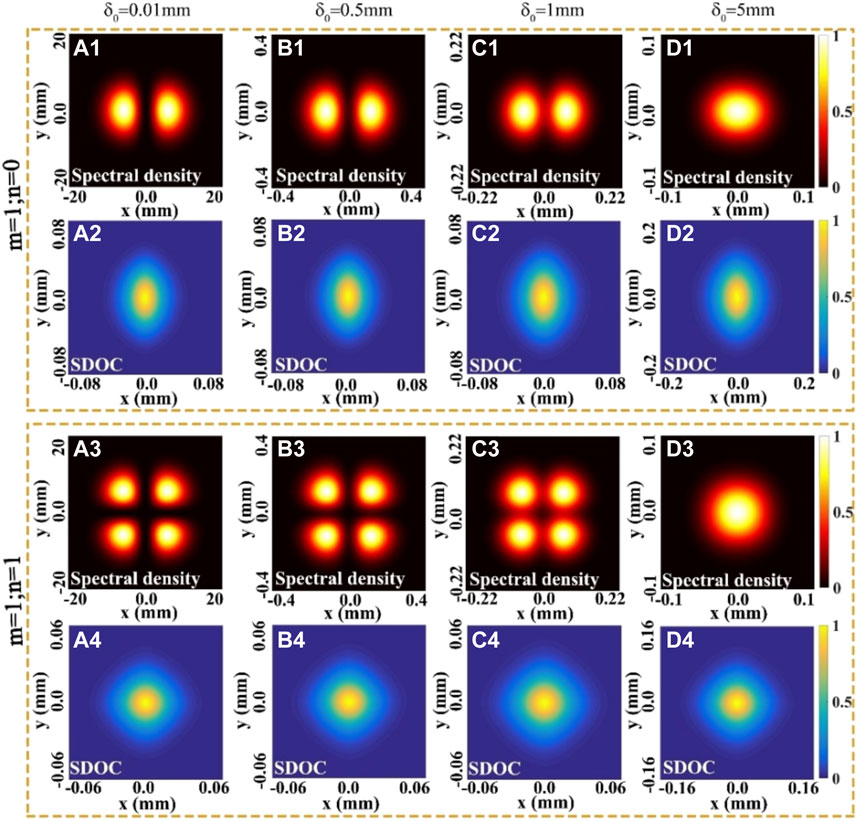
FIGURE 5. Density plots of the normalized spectral density and the modulus of the SDOC (|η(ρ,−ρ)|) of a focused HGCSM beam for different values of the spatial coherence width δ0 in the focal plane.
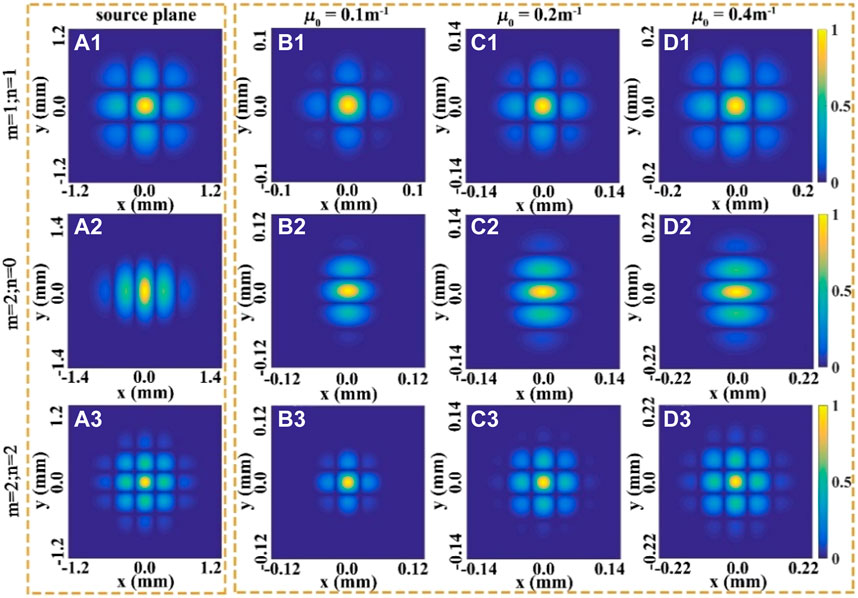
FIGURE 6. Modulus of the SDOC (|η(ρ,−ρ)|) of the THGCSM beam for different values of the twist factor μ0 in the source and focal plane, respectively.
Moreover, regardless of the value of the spatial coherence width, the distribution of the SDOC is always maintained as a beam spot. Therefore, the ability to obtain information about the correlation function of the beam in the far field (or focal plane) cannot be improved by changing the coherence length or the order m n of the beam.
Further, we calculated the modulus of the SDOC (|μ(ρ,-ρ)|) of the THGCSM beam in the source and focal plane, respectively. It is interesting to find that with the increase of the twist factor, the strength of the sidelobes of the SDOC are enhanced. This exciting new finding may help us to find a new way to improve the reliability of the correlation function.
Self-Reconstruction Characteristics of the THGCSM Beam
In this section, we focus on the Self-reconstruction behavior of the THGCSM beam when the THGCSM beam is partially blocked by a sector-shaped opaque obstacle (SSOO) in the source plane. Figure 7 shows the illustration of a THGCSM beam self-healing process. A beam in the input plane (z = 0) is disturbed by a partially opaque obstacle in the input plane and is propagating through an ABCD optical system consisting of a lens and the free space behind the lens.
Figure 8 shows the changes of the density plot of the normalized spectral density of a focused THGCSM beam obstructed by a SSOO for different values of the twist factor at several propagation distances. From the first row of the Figure 8, one can see that with the increase of the propagation distance z, due to the effect of the correlation function, the beam splits into four beamlets as expected in [22]. The second and third row of the Figure 8 show the effect of the twist phase on the normalized spectral density. By comparing the condition μ0 = 0.2 m−1 and the condition μ0 = −0.2 m−1, we can find that the twist phase would induce the rotation of the beam on propagation: the distribution of the spectral density rotates clockwise when μ0 > 0, the distribution of the spectral density rotates anti-clockwise when μ0 < 0. This phenomenon is consistent with former results [37, 38]. Therefore, the twist phase actually still causes the beam to rotate during propagation, but it is not noticeable when the beam is intact (Figures 1, 2).
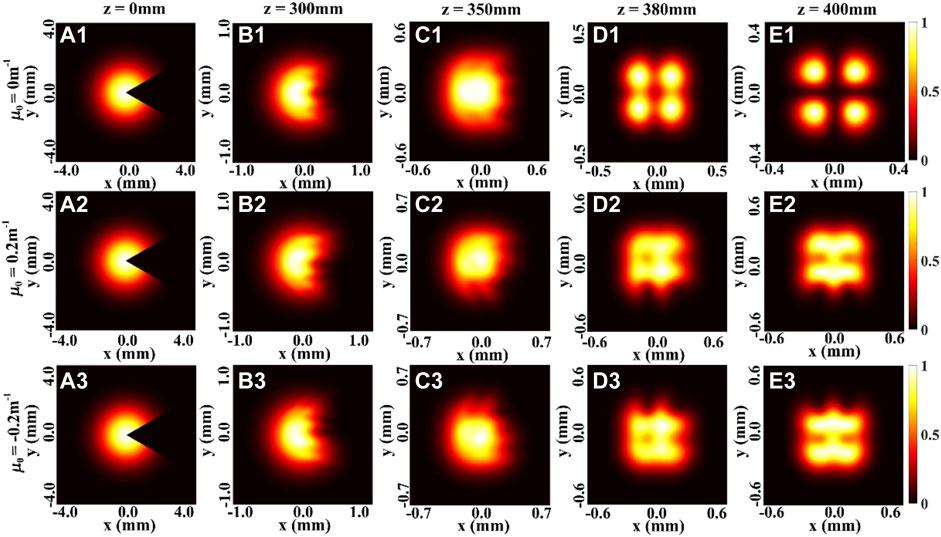
FIGURE 8. Density plot of the normalized spectral density of a focused THGCSM beam with m = 1, n = 1 obstructed by a SSOO with center angle α = π/3 for different values of the twist factor μ0 at several propagation distances.
Moreover, Figure 9 shows the Self-reconstruction characteristics of the normalized spectral density and the modulus of the SDOC (|ηρ,−ρ)|) when the beam is obstructed by a SSOO for different values of the center angle α in the focal plane. To assess the influences of the twist parameter on the self-reconstruction capability quantitatively, a parameter named the degree of self-reconstruction DP (i.e.,
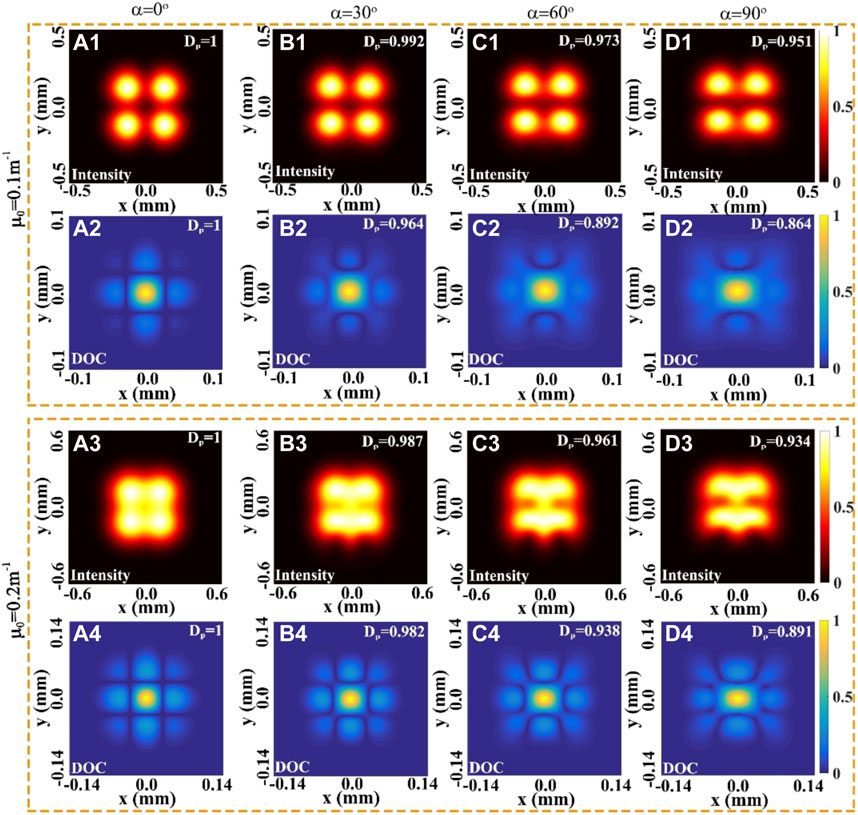
FIGURE 9. Density plot of the normalized spectral density and the modulus of the SDOC (|η(ρ,−ρ)|) of a focused THGCSM beam with m = 1, n = 1 obstructed by a SSOO for different values of twist factor μ0 and center angle α in the focal plane.
Conclusion
In summary, we have introduced a new class of partially coherent twisted beam, named twisted Hermite-Gaussian correlated Schell-model (THGCSM) beam, and investigated its propagation properties through an ABCD optical system. The problem of when a twist phase can be imposed on Schell-model source fields with rectangular symmetries was solved. Based on the derived assessment condition, the condition that the THGCSM beam will be a bona fide one, also has been explored. The analytical expression for the CSD function of the THGCSM propagation through an ABCD optical system has been derived with the help of the generalized Collins integral formula. Based on the derived formula we have examined the evolution properties of the THGCSM beam. Our simulation results indicate that the evolution properties of the beam are closely related to the twist phase, e.g., with an increasing twist phase, the self-splitting properties of the beam gradually weaken on propagation. Further, the evolution of the SDOC also has been studied. Apart from inducing the rotation of the SDOC on propagation, the twist phase can greatly enhance the ability of the SDOC to maintain its profile on propagation, even in the focal plane. This provides a way to improve the reliability of the correlation function. Moreover, the self-reconstruction characteristics of the THGCSM beam have been explored in detail, and one can find that even if the beam has been obstructed by an opaque obstacle, one still can determine the information relating to the correlation function of an obstructed THGCSM from its SDOC distribution in the focal plane. Our results are anticipated to find applications in optical communications and information recovery.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
LeL and XP proposed the idea. LeL wrote the original manuscript. HW, LiL, YD, and FW gave suggestions in numerical simulation. XP, YC, and BH supervised the project. All authors contributed to the revision of the manuscript and approved the final version.
Funding
This work was supported by the National Natural Science Foundation of China (Nos 12192254, 11774251, 11874046, 11904247, 11974218, 12104263, 12174279); National Key Research and Development Program of China (2019YFA0705000); Natural Science Foundation of Shandong Province (ZR2021QA093); Local Science and Technology Development Project of the Central Government (Grant No. YDZX20203700001766); Innovation Group of Jinan (2018GXRC010).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Kato Y, Mima K, Miyanaga N, Arinaga S, Kitagawa Y, Nakatsuka M, et al. Random Phasing of High-Power Lasers for Uniform Target Acceleration and Plasma-Instability Suppression. Phys Rev Lett (1984) 53:1057–60. doi:10.1103/PhysRevLett.53.1057
2. Ferri F, Magatti D, Gatti A, Bache M, Brambilla E, Lugiato LA. High-resolution Ghost Image and Ghost Diffraction Experiments with thermal Light. Phys Rev Lett (2005) 94:183602. doi:10.1103/PhysRevLett.94.183602
3. Oh J-E, Cho Y-W, Scarcelli G, Kim Y-H. Sub-Rayleigh Imaging via Speckle Illumination. Opt Lett (2013) 38:682–4. doi:10.1364/OL.38.000682
4. Auñón JM, Nieto-Vesperinas M. Partially Coherent Fluctuating Sources that Produce the Same Optical Force as a Laser Beam. Opt Lett (2013) 38:2869–72. doi:10.1364/OL.38.002869
5. Zhao C, Cai Y. Trapping Two Types of Particles Using a Focused Partially Coherent Elegant Laguerre-Gaussian Beam. Opt Lett (2011) 36:2251–3. doi:10.1364/OL.36.002251
6. Ricklin JC, Davidson FM. Atmospheric Optical Communication with a Gaussian Schell Beam. J Opt Soc Am A (2003) 20:856–66. doi:10.1364/josaa.20.000856
7. Beams R, Cançado LG, Oh S-H, Jorio A, Novotny L. Spatial Coherence in Near-Field Raman Scattering. Phys Rev Lett (2014) 113:186101. doi:10.1103/PhysRevLett.113.186101
8. van Dijk T, Fischer DG, Visser TD, Wolf E. Effects of Spatial Coherence on the Angular Distribution of Radiant Intensity Generated by Scattering on a Sphere. Phys Rev Lett (2010) 104:173902. doi:10.1103/PhysRevLett.104.173902
9. Gori F, Santarsiero M. Devising Genuine Spatial Correlation Functions. Opt Lett (2007) 32:3531–3. doi:10.1364/ol.32.003531
10. Gori F, Ramírez-Sánchez V, Santarsiero M, Shirai T. On Genuine Cross-Spectral Density Matrices. J Opt A: Pure Appl Opt (2009) 11:085706. doi:10.1088/1464-4258/11/8/085706
11. Cai Y, Chen Y, Yu J, Liu X, Liu L. Generation of Partially Coherent Beams. Prog Opt (2017) 62:157–223. doi:10.1016/bs.po.2016.11.001
12. Cai Y, Chen Y, Wang F. Generation and Propagation of Partially Coherent Beams with Nonconventional Correlation Functions: A Review [invited]. J Opt Soc Am A (2014) 31:2083–96. doi:10.1364/JOSAA.31.002083
13. Lajunen H, Saastamoinen T. Propagation Characteristics of Partially Coherent Beams with Spatially Varying Correlations. Opt Lett (2011) 36:4104–6. doi:10.1364/OL.36.004104
14. Wang F, Liu X, Yuan Y, Cai Y. Experimental Generation of Partially Coherent Beams with Different Complex Degrees of Coherence. Opt Lett (2013) 38:1814–6. doi:10.1364/OL.38.001814
15. Mei Z, Korotkova O. Random Sources Generating Ring-Shaped Beams. Opt Lett (2013) 38:91–3. doi:10.1364/OL.38.000091
16. Mei Z, Korotkova O. Cosine-Gaussian Schell-Model Sources. Opt Lett (2013) 38:2578–80. doi:10.1364/OL.38.002578
17. Liang C, Wang F, Liu X, Cai Y, Korotkova O. Experimental Generation of Cosine-Gaussian-Correlated Schell-Model Beams with Rectangular Symmetry. Opt Lett (2014) 39:769–72. doi:10.1364/OL.39.000769
18. Chen Y, Cai Y. Generation of a Controllable Optical Cage by Focusing a Laguerre-Gaussian Correlated Schell-Model Beam. Opt Lett (2014) 39:2549–52. doi:10.1364/OL.39.002549
19. Korotkova O. Random Sources for Rectangular Far fields. Opt Lett (2014) 39:64–7. doi:10.1364/OL.39.000064
20. Chen Y, Wang F, Liu L, Zhao C, Cai Y, Korotkova O. Generation and Propagation of a Partially Coherent Vector Beam with Special Correlation Functions. Phys Rev A (2014) 89:13801. doi:10.1103/PhysRevA.89.013801
21. Ma L, Ponomarenko SA. Free-space Propagation of Optical Coherence Lattices and Periodicity Reciprocity. Opt Express (2015) 23:1848–56. doi:10.1364/OE.23.001848
22. Chen Y, Gu J, Wang F, Cai Y. Self-splitting Properties of a Hermite-Gaussian Correlated Schell-Model Beam. Phys Rev A (2015) 91:13823. doi:10.1103/PhysRevA.91.013823
23. Zhu S, Chen Y, Wang J, Wang H, Li Z, Cai Y. Generation and Propagation of a Vector Cosine-Gaussian Correlated Beam with Radial Polarization. Opt Express (2015) 23:33099–155. doi:10.1364/OE.23.033099
24. Chen Y, Ponomarenko SA, Cai Y. Experimental Generation of Optical Coherence Lattices. Appl Phys Lett (2016) 109:061107. doi:10.1063/1.4960966
25. Liu X, Yu J, Cai Y, Ponomarenko SA. Propagation of Optical Coherence Lattices in the Turbulent Atmosphere. Opt Lett (2016) 41:4182–5. doi:10.1364/OL.41.004182
26. Liang C, Mi C, Wang F, Zhao C, Cai Y, Ponomarenko SA. Vector Optical Coherence Lattices Generating Controllable Far-Field Beam Profiles. Opt Express (2017) 25:9872–85. doi:10.1364/OE.25.009872
27. Xu Z, Liu X, Chen Y, Wang F, Liu L, Monfared YE, et al. Self-healing Properties of Hermite-Gaussian Correlated Schell-Model Beams. Opt Express (2020) 28:2828–37. doi:10.1364/OE.383805
28. Gu Y, Gbur G. Scintillation of Nonuniformly Correlated Beams in Atmospheric Turbulence. Opt Lett (2013) 38:1395–7. doi:10.1364/OL.38.001395
29. Liang C, Wu G, Wang F, Li W, Cai Y, Ponomarenko SA. Overcoming the Classical Rayleigh Diffraction Limit by Controlling Two-point Correlations of Partially Coherent Light Sources. Opt Express (2017) 25:28352–62. doi:10.1364/OE.25.028352
30. Peng D, Huang Z, Liu Y, Chen Y, Wang F, Ponomarenko SA, et al. Optical Coherence Encryption with Structured Random Light. PhotoniX (2021) 2:6–15. doi:10.1186/s43074-021-00027-z
31. Shen Y, Sun H, Peng D, Chen Y, Cai Q, Wu D, et al. Optical Image Reconstruction in 4f Imaging System: Role of Spatial Coherence Structure Engineering. Appl Phys Lett (2021) 118:181102. doi:10.1063/5.0046288
32. Liu Y, Chen Y, Chen Y, Wang F, Cai Y, Liang C, et al. Robust Far-Field Imaging by Spatial Coherence Engineering. Opto-Electron Adv (2021) 4:210027. doi:10.29026/oea.2021.210027
33. Chen Y, Wang F, Cai Y. Partially Coherent Light Beam Shaping via Complex Spatial Coherence Structure Engineering. Adv Phys X (2022) 7:2009742. doi:10.1080/23746149.2021.2009742
34. Serna J, Movilla JM. Orbital Angular Momentum of Partially Coherent Beams. Opt Lett (2001) 26:405–7. doi:10.1364/OL.26.000405
35. Simon R, Mukunda N. Twisted Gaussian Schell-Model Beams. J Opt Soc Am A (1993) 10:95. doi:10.1364/JOSAA.10.000095
36. Friberg AT, Tervonen E, Turunen J. Interpretation and Experimental Demonstration of Twisted Gaussian Schell-Model Beams. J Opt Soc Am A (1994) 11:1818–26. doi:10.1364/JOSAA.11.001818
37. Peng X, Liu L, Yu J, Liu X, Cai Y, Baykal Y, et al. Propagation of a Radially Polarized Twisted Gaussian Schell-Model Beam in Turbulent Atmosphere. J Opt (2016) 18:125601. doi:10.1088/2040-8978/18/12/125601
38. Wu G. Propagation Properties of a Radially Polarized Partially Coherent Twisted Beam in Free Space. J Opt Soc Am A (2016) 33:345–50. doi:10.1364/JOSAA.33.000345
39. Tong Z, Korotkova O. Beyond the Classical Rayleigh Limit with Twisted Light. Opt Lett (2012) 37:2595–7. doi:10.1364/OL.37.002595
40. Peng X, Liu L, Wang F, Popov S, Cai Y. Twisted Laguerre-Gaussian Schell-Model Beam and its Orbital Angular Moment. Opt Express (2018) 26:33956–69. doi:10.1364/OE.26.033956
41. Peng X, Wang H, Liu L, Wang F, Popov S, Cai Y. Self-reconstruction of Twisted Laguerre-Gaussian Schell-Model Beams Partially Blocked by an Opaque Obstacle. Opt Express (2020) 28:31510–23. doi:10.1364/OE.408357
42. Wang H, Peng X, Liu L, Wang F, Cai Y, Ponomarenko SA. Generating Bona Fide Twisted Gaussian Schell-Model Beams. Opt Lett (2019) 44:3709–12. doi:10.1364/OL.44.003709
43. Wang H, Peng X, Zhang H, Liu L, Chen Y, Wang F, et al. Experimental Synthesis of Partially Coherent Beam with Controllable Twist Phase and Measuring its Orbital Angular Momentum. Nanophotonics (2021). doi:10.1515/nanoph-2021-0432
44. Borghi R. Twisting Partially Coherent Light. Opt Lett (2018) 43:1627–30. doi:10.1364/OL.43.001627
45. Borghi R, Gori F, Guattari G, Santarsiero M. Twisted Schell-Model Beams with Axial Symmetry. Opt Lett (2015) 40:4504. doi:10.1364/OL.40.004504
46. Mei Z, Korotkova O. Random Sources for Rotating Spectral Densities. Opt Lett (2017) 42:255–8. doi:10.1364/OL.42.000255
47. Gori F, Santarsiero M. Devising Genuine Twisted Cross-Spectral Densities. Opt Lett (2018) 43:595–8. doi:10.1364/OL.43.000595
Keywords: self-reconstruction, spectral degree of coherence, twist phase, propagation properties, partially coherent
Citation: Liu L, Wang H, Liu L, Dong Y, Wang F, Hoenders BJ, Chen Y, Cai Y and Peng X (2022) Propagation Properties of a Twisted Hermite-Gaussian Correlated Schell-Model Beam in Free Space. Front. Phys. 10:847649. doi: 10.3389/fphy.2022.847649
Received: 03 January 2022; Accepted: 18 January 2022;
Published: 16 February 2022.
Edited by:
Shangran Xie, Beijing Institute of Technology, ChinaReviewed by:
Xinglin Zeng, Max Planck Institute for the Science of Light, GermanyYang Chen, Paul Scherrer Institut (PSI), Switzerland
Copyright © 2022 Liu, Wang, Liu, Dong, Wang, Hoenders, Chen, Cai and Peng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yangjian Cai, eWFuZ2ppYW5jYWlAc3VkYS5lZHUuY24=; Xiaofeng Peng, eGZwZW5nODg4QDE2My5jb20=
 Leixin Liu1
Leixin Liu1 Haiyun Wang
Haiyun Wang Yahong Chen
Yahong Chen Yangjian Cai
Yangjian Cai Xiaofeng Peng
Xiaofeng Peng