- 1Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing, China
- 2Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education, Guangxi University, Nanning, China
- 3Guangxi Key Laboratory of Disaster Prevention and Engineering Safety, Guangxi University, Nanning, China
Traditional macroscopic phenomenon constitutive model is not easy to describe in the non-linear mechanical properties of porous rock materials, since the effect of porosity does not incorporate into the strength criterion. This paper presents a simple elastoplastic damage constitutive model of porous rock material based on micromechanical theory. To consider the heterogeneities of the studied porous rock, a simplified representative volume element is introduced, and it is assumed that it is made up of randomly distributed spherical pores embedded in a solid matrix obeying Drucker-Prager yield function. Thus, a homogenized plastic criterion considering the effect of porosity is introduced to describe the macroscopic plastic mechanical properties of porous rock materials. In this model, the non-associated flow rule and isotropic strain hardening law are used, and then the degradation of elastic and plastic properties is employed by adopting a damage criterion. This criterion is related to the evolution of equivalent plastic strain. In order to verify the accuracy of the model, the corresponding numerical program was used to realize the micro-macro constitutive model, and the results were compared with the triaxial compression test results of sandstone under different confining pressures. It is observed that the numerical simulation results are in great agreement with the experimental data, indicating that the proposed model is able to predict the main mechanical behavior of porous sandstone.
Introduction
As a complex geological material, the rock mass contains various primary microstructures, including pores, cracks, inclusions, etc. The initiation and expansion of microdefects in rock mass reflect the degree of mechanical deterioration [1]. The deformation of inners pores or voids exhibits a great influence on the effective strength and mechanical behaviors on such materials, which lead to the complex plastic deformation, tension-compression asymmetry [2–5], brittle-ductile transition, and so on. In order to present the non-linear behaviors of porous medium and reflect the effects of the voids on the strength related to its plastic deformation, a numerous of previous investigations [6–8] have been proposed, which are based on the theory of kinematical limit analysis and provides the theoretical determination or numerical assessment of macroscopic yield criteria for porous materials. The present works are first to establish an appropriate effective plastic yield criterion for a porous medium. Then, an analytical effective plastic yield function is obtained by the second homogenization step. Finally, consider the effects of mineral grains to determine the macroscopic plastic behavior of porous materials.
However, most of the above theories do not consider the influence of porosity inside rock on the evolution of damage. Several previous studies have shown that the growth of internal microdefects and the local stress concentration are two main factors, leading to the damage evolution in rocks under the external loading [9–12]. Further, the construction in geotechnical engineering often changes the stress state of rock mass, aggravating the damage evolution around the excavation section [13–16]. Hence, the damage modeling remains an ongoing interest in investigating the mechanical behavior of rock-like materials. On one hand, thanks to the rapid development of various kinds of rock testing techniques, considerable experimental studies have been conducted for understanding the underlying mechanism of damage evolution in rocks [17, 18]. On the other hand, the rock damage model research also has remarkable development. So far, many researchers have established numerous rock damage constitutive models based on different theoretical frameworks from various perspectives [19–21].
At the same time, as a natural porous material, rock has many pores at different scales. The development mechanism of plasticity and damage is bound to be related to the development and evolution of porosity. For this purpose, the present study is aiming to develop a micro-mechanics based constitutive model for plastic deformation and damage evolution in sandstone containing two populations of pores and mineral based on the plasticity theory and the irreversible thermodynamic framework [22, 23]. This work will put effort into developing a simple elastoplastic damage coupled constitutive model of porous rocks considering the effect of porosity and damage degradation.
The Elastoplastic Damage Constitutive Model of Sandstone
According to the experimental data of triaxial compression and irreversible thermodynamic theory [21], a elastoplastic constitutive model describing the damage of sandstone under drainage conditions is established, which can reflect the mechanical behavior of the sandstone with different seepage conditions in the stress field.
Porous Media Model
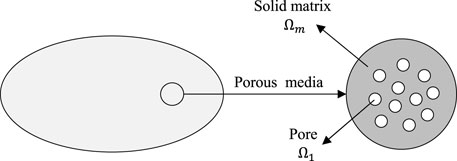
Based on the theory of porous media mechanics, the non-linear mechanical response of sandstone is described by using the plastic yield equation considering porosity. At the same time, the damage evolution criterion was established based on the existing damage theory, and independent damage variables were introduced into the plastic yield function to describe the damage evolution of rock in the process of deformation and failure, so as to determine the coupling relationship between plastic deformation and damage development. This model can simulate both pre-peak strengthening and post-peak softening behaviors at the same time. The physical model of porous media is shown in Figure 1.
As is shown in Figure 1, the porous media is considered made up of isotropic solid matrix and random pore at microscale. The volumes of solid matrix and of the void are noted as
Compared with metal materials, the pressure sensitivity and volumetric deformation are two crucial characteristics of rock materials. In order to consider these aspects, here we assumed that the solid matrix is made up of elastoplastic material subjected to Drucker-Prager yield criterion.
Based on the assumption of small deformation, in the field of traditional plastic mechanics, the total strain increment of rock can be decomposed into elastic strain (increment) and plastic strain (increment):
Referring to the previous research theory of porous media [6–8], the effective volume modulus and shear modulus of intact and non-destructive rock materials are expressed as follows:
where the parameters
Concerning the assumption of material isotropy and damage extension isotropy, the scalar
As a result, the macroscopic elastic stress-strain relation of the rock in the incremental form writes [24]:
where
Plastic Model
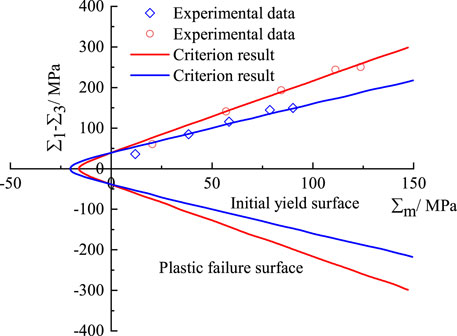
In general, the M-C yield criterion and D-P yield criterion are used for the yield function. Based on the above experimental results of triaxial compression, the yield surfaces of sandstone under seepage conditions are close to non-linear characteristic of elliptical surface, thus the typical porous plastic criterion proposed by Ref. [25] is used to describe the mechanical response of sandstone in the study. The plastic yield surface equation is defined as:
where
T is the plastic hardening function, which reflects the pre-peak strengthening and post-peak softening behavior of sandstone [26]. Based on the thermodynamic framework and the work of [27], the plastic thermodynamic potential of sandstone
Thus the expression of hardening function T is derived as:
where
In addition, the non-associated plastic potential function
where t is plastic hardening function related to damage variable and plastic shear strain of rock and can be given by:
where
where
Assuming that the change of pore volume on the microscopic scale only depends on pore plastic compression and expansion, and ignore the influence of new pore nucleation, according to function Eq. 1, we can get that:
Where
where
According to the energy-based equivalence condition provided by Ref. [28], the following relation between plastic strain rate of porous medium material and equivalent plastic strain rate of solid matrix can be derived as presented in [29]:
With the relations (Eqs 16, 17) and
Damage Evolution Criterion
In accordance with the thermodynamic theory, the effect of the damage driving force related to the free energy release rate in the elastic stage on the damage of rock change its internal structure. The internal cracks of the sandstone specimen are mostly closed based on conventional triaxial compression. Therefore, the damage of the sandstone is primarily caused by plastic shear, while the damage caused by the elastic deformation is very small. According to the previous study [21] and ignoring the effect of elasticity, the damage driving force
In addition, the damage evolution criterion of the rock is introduced by the Mazars’ research [30], and the damage evolution function
where
Plastic Damage Constitutive Relations
The plastic flow and damage evolution of sandstone are coupled processes under loading conditions [27]. To reflect the effect of pore water pressure on mechanical behavior of rock, the plasticity multiplier
In addition, based on the plastic flow rule, the increment of plastic deformation and damage variable are defined as:
According to Eqs. 6, 7, 10–13, 18–21, the plastic multiplier and the damage evolution multiplier are obtained:
The parameter A and B is written as follows:
Model Verification and Numerical Simulation
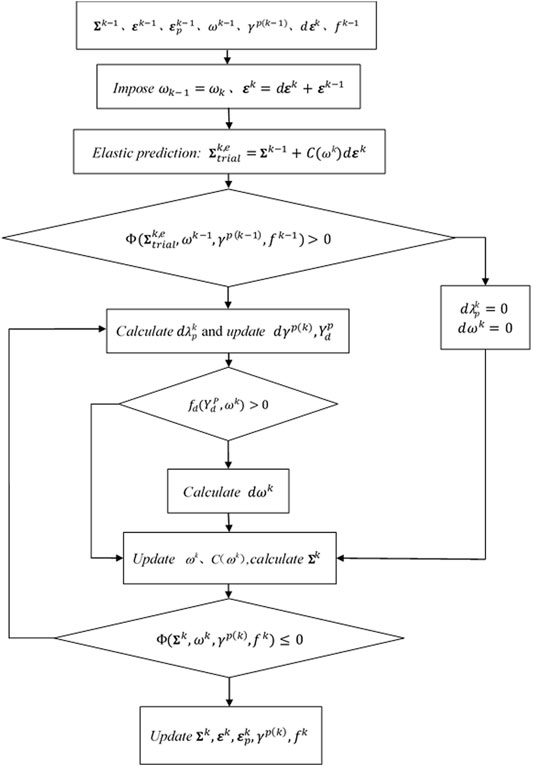
In this model, we divided the whole loading process into a limit number of steps. It is assumed that the parameters of the k-1 step loading variables including
The detailed process of calculation can be divided into the following steps:
(1) Suppose
(2) If
(3) Based on the updated
(4) Damage stiffness matrix
(5) If
First, according to the previous studies [7, 29], basic parameters of the sandstone, such as the elastic modulus
Figure 4 shows the experimental stress-strain curves of sandstone and the corresponding numerical results. As can be seen from Figure 4, it is obvious that the experimental data and numerical results are very close before the peak stress, which shows that the non-linear transition from brittleness to plasticity for the sandstone can be well fitted with increasing the strain.
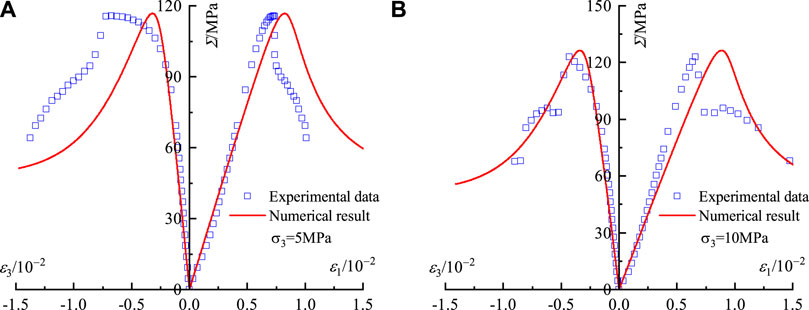
FIGURE 4. Comparison of stress-strain curves between numerical results and experimental data under triaxial compression test. (A) Confining pressure of 5 MPa. (B) Confining pressure of 10 MPa.
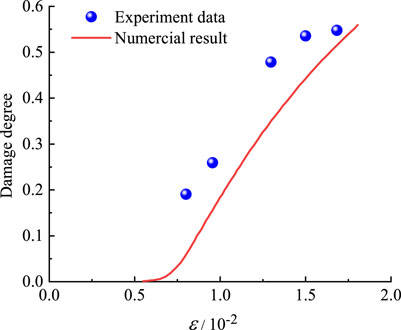
In order to further verify the rationality of the damage evolution model, a comparative analysis was made between the damage evolution value and the test results under the condition of 10 MPa confining pressure (Figure 5), in which the damage evolution test data were calculated by the acoustic emission method. As shown in Figure 5, damage development is very limited in the initial loading stage. With the increase of deviational stress, mechanical damage gradually develops and eventually leads to rock failure.
Conclusion
In this paper, an elastoplastic damage constitutive model for sandstone considering the influence of rock pores is constructed based on the previous research results and the knowledge framework of irreversible thermodynamics. In this proposed model, the plastic flow and damage evolution of sandstone are coupled and combine with non-associative plastic potential function to capture its elastoplastic behaviors.
In order to verify its prediction ability of porous rocks damage evolution, the numerical simulations of this model have been plotted and compared with experimental data of triaxial compression tests on sandstone. A good agreement between the numerical and experimental results has been observed, indicating that the proposed model is able to describe the main features of porous sandstone.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
CC: Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing—Original Draft; CY: Conceptualization, Resources, Supervision, Writing—Review and Editing.
Funding
This work was supported by National Natural Science Foundation of China (No. 12102129), open fund of Guangxi Key Laboratory of Disaster Prevention and Engineering Safety (No. 2020ZDK009), the Fundamental Research Funds for the Central Universities (No. B220202014), China Postdoctoral Science Foundation (No. 2021M690047) and the Program to Cultivate Middle-aged and Young Science Leaders of Colleges and Universities of Jiangsu Province, China.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Li P, Yvonnet J, Combescure C. An Extension of the Phase Field Method to Model Interactions between Interfacial Damage and Brittle Fracture in Elastoplastic Composites. Int J Mech Sci (2020) 179:105633. doi:10.1016/j.ijmecsci.2020.105633
2. Du Z, Guo X. Variational Principles and the Related Bounding Theorems for Bi-modulus Materials. J Mech Phys Sol (2014) 73(dec):183–211. doi:10.1016/j.jmps.2014.08.006
3. You T, Zhu Q-Z, Li P-F, Shao J-F. Incorporation of Tension-Compression Asymmetry into Plastic Damage Phase-Field Modeling of Quasi Brittle Geomaterials. Int J Plasticity (2020) 124:71–95. doi:10.1016/j.ijplas.2019.08.003
4. Du Z, Zhang Y, Zhang W, Guo X. A New Computational Framework for Materials with Different Mechanical Responses in Tension and Compression and its Applications. Int J Sol Structures (2016) 100-101:54–73. doi:10.1016/j.ijsolstr.2016.07.009
5. Guo Y, Liu G, Liu H, Huang Y. Creep Damage Model Considering Unilateral Effect Based on Bimodulus Theory. Int J Damage Mech (2021) 30(2):1558–93. doi:10.1177/10567895211017319
6. Shen WQ, Shao JF. An Incremental Micro-macro Model for Porous Geomaterials with Double Porosity and Inclusion. Int J Plasticity (2016) 83:37–54. doi:10.1016/j.ijplas.2016.04.002
7. Shen WQ, Zhang J, Shao JF, Kondo D. Approximate Macroscopic Yield Criteria for Drucker-Prager Type Solids with Spheroidal Voids. Int J Plasticity (2017) 99:221–47. doi:10.1016/j.ijplas.2017.09.008
8. Shen WQ, Shao J-F, Kondo D. Macroscopic Criteria for Green Type Porous Materials with Spheroidal Voids: Application to Double Porous Materials. Int J Numer Anal Meth Geomech (2017) 41(11):1453–73. doi:10.1002/nag.2691
9. Krajcinovic D, Fonseka GU. The Continuous Damage Theory of Brittle Materials, Part 1: General Theory. J Appl Mech (1981) 48(4):809–15. doi:10.1115/1.3157739
10. Rousselier G, Devaux JC, Mottet G. Experimental Validation of Constitutive Relations Including Ductile Fracture Damage. Fracture (1984) 1205–13. doi:10.1016/B978-1-4832-8440-8.50105-8
11. Marigo JJ. Modelling of Brittle and Fatigue Damage for Elastic Material by Growth of Microvoids. Eng Fracture Mech (1985) 21(4):861–74. doi:10.1016/0013-7944(85)90093-1
12. Shao JF. Poroelastic Behaviour of Brittle Rock Materials with Anisotropic Damage. Mech Mater (1998) 30(1):41–53. doi:10.1016/S0167-6636(98)00025-8
13. Kim K, Rutqvist J, Birkholzer J. Lattice Modeling of Excavation Damage in Argillaceous Clay Formations: Influence of Deformation and Strength Anisotropy. Tunnelling Underground Space Technol (2020) 98:103196. doi:10.1016/j.tust.2019.103196
14. Li A, Dai F, Liu Y, Du H, Jiang R. Dynamic Stability Evaluation of Underground Cavern Sidewalls against Flexural Toppling Considering Excavation-Induced Damage. Tunnelling Underground Space Technol (2021) 112(4):103903. doi:10.1016/j.tust.2021.103903
15. Shen P, Tang H, Zhang B, Ning Y, He C. Investigation on the Fracture and Mechanical Behaviors of Simulated Transversely Isotropic Rock Made of Two Interbedded Materials. Eng Geology (2021) 286(2):106058. doi:10.1016/j.enggeo.2021.106058
16. Wang C, Wei P, Wang X, Zhang S, Cui W. Blast-Resistance and Damage Evaluation of Concrete Gravity Dam Exposed to Underwater Explosion: Considering the Initial Stress Field. KSCE J Civ Eng (2021) 25:2922–35. doi:10.1007/s12205-021-1650-0
17. Carpinteri A, Lacidogna G, Accornero F, Mpalaskas AC, Matikas TE, Aggelis DG. Influence of Damage in the Acoustic Emission Parameters. Cement and Concrete Composites (2013) 44:9–16. doi:10.1016/j.cemconcomp.2013.08.001
18. Chang S-H, Lee C-I. Estimation of Cracking and Damage Mechanisms in Rock under Triaxial Compression by Moment Tensor Analysis of Acoustic Emission. Int J Rock Mech Mining Sci (2004) 41(7):1069–86. doi:10.1016/j.ijrmms.2004.04.006
19. Chen L, Shao JF, Zhu QZ, Duveau G. Induced Anisotropic Damage and Plasticity in Initially Anisotropic Sedimentary Rocks. Int J Rock Mech Mining Sci (2012) 51(none):13–23. doi:10.1016/j.ijrmms.2012.01.013
20. Wang W, Shao J, Zhu Q, Xu W. A Discrete Viscoplastic Damage Model for Time-dependent Behaviour of Quasi-Brittle Rocks. Int J Damage Mech (2015) 24(1):21–40. doi:10.1177/1056789514520801
21. Chiarelli AS, Shao JF, Hoteit N. Modeling of Elastoplastic Damage Behavior of a Claystone. Int J Plasticity (2003) 19(1):23–45. doi:10.1016/S0749-6419(01)00017-1
22. Othman MIA, Said S, Marin M. A Novel Model of Plane Waves of Two-Temperature Fiber-Reinforced Thermoelastic Medium under the Effect of Gravity with Three-Phase-Lag Model. Hff (2019) 29(12):4788–806. doi:10.1108/HFF-04-2019-0359
23. Marin M, Othman MIA, Seadawy AR, Carstea C. A Domain of Influence in the Moore-Gibson-Thompson Theory of Dipolar Bodies. J Taibah Univ Sci (2020) 14(1):653–60. doi:10.1080/16583655.2020.1763664
24. Cao YJ, Shen WQ, Shao JF, Wang W. A Multi-Scale Model of Plasticity and Damage for Rock-like Materials with Pores and Inclusions. Int J Rock Mech Mining Sci (2021) 138(4):104579. doi:10.1016/j.ijrmms.2020.104579
25. Maghous S, Dormieux L, Barthélémy JF. Micromechanical Approach to the Strength Properties of Frictional Geomaterials. Eur J Mech - A/Solids (2009) 28(1):179–88. doi:10.1016/j.euromechsol.2008.03.002
26. Liu L, Xu WY, Zhao LY, Zhu QZ, Wang RB. An Experimental and Numerical Investigation of the Mechanical Behavior of Granite Gneiss under Compression. Rock Mech Rock Eng (2016) 50(2):499–506. doi:10.1007/s00603-016-1067-0
27. Shao JF, Jia Y, Kondo D, Chiarelli AS. A Coupled Elastoplastic Damage Model for Semi-brittle Materials and Extension to Unsaturated Conditions. Mech Mater (2006) 38(3):218–32. doi:10.1016/j.mechmat.2005.07.002
28. Gurson AL. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I-Yield Criteria and Flow Rules for Porous Ductile Mediaflow Rules for Porous Ductile Media. J Eng Mater Technol (1977) 99(1):2–15. doi:10.1115/1.3443401
29. Shen WQ, Shao JF, Kondo D, Gatmiri B. A Micro-macro Model for Clayey Rocks with a Plastic Compressible Porous Matrix. Int J plasticity (2012) 36:64–85. doi:10.1016/j.ijplas.2012.03.006
Keywords: elastoplastic damage constitutive model, porous rock, non-associate flow rule, numerical analysis, damage
Citation: Chao C, Yajun C, Yanli J, Xuelei D, Shifan L and Kuan Z (2022) A Simple Elastoplastic Damage Constitutive Model of Porous Rock Materials. Front. Phys. 10:838827. doi: 10.3389/fphy.2022.838827
Received: 18 December 2021; Accepted: 21 February 2022;
Published: 27 April 2022.
Edited by:
Wanqing Shen, Université de Lille, FranceReviewed by:
Marin I. Marin, Transilvania University of Brașov, RomaniaZongliang Du, Dalian University of Technology, China
Copyright © 2022 Chao, Yajun, Yanli, Xuelei, Shifan and Kuan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Cao Yajun, Y2FveWFqdW5AaGh1LmVkdS5jbg==
 Chen Chao
Chen Chao Cao Yajun
Cao Yajun Jin Yanli2,3
Jin Yanli2,3