Statistical Analysis of Hydrodynamic Forces in Power-Law Fluid Flow in a Channel: Circular Versus Semi-Circular Cylinder

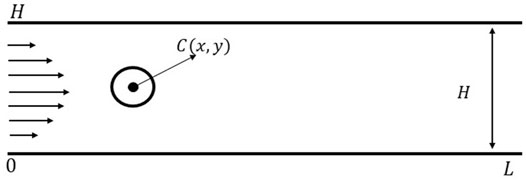
This numerical study is about the steady incompressible non-Newtonian fluid flow in a channel with static obstacles. The flow field is governed by the Generalized Navier-Stokes equations incorporating the constitutive relation of power-law fluids. Three cases are considered: 1) circular obstacle $\left(C_1\right)$, 2) semicircular obstacle $\left(C_2\right)$, and 3) both circular and semicircular obstacles. A range of values of the power-law index $0.3\le n\le 1.7$ are considered at $Re=20$ to check the impact of shear-thinning and shear-thickening viscosity on the drag and lift coefficients. The correlation between drag and lift coefficients is calculated against the power-law index. The simulated results of velocity and pressure are investigated at different sections of the channel. Benchmark results of drag and lift for the Newtonian fluid are reproduced as a special case. A strong positive correlation is observed between drag and lift coefficients in the case of a single obstacle, while in the case of dual obstacles and inverse correlation, drag and lift coefficients have been found.

Introduction

The fluid flow past solid bodies is one of the practical problems being investigated in the domain of fluid mechanics, and hence, it has attained the focus of engineers and scientists. The phenomenon has a lot of engineering and industrial applications. In the past, a lot of work has been done, and many aspects of flow have been investigated for Newtonian fluid both in experimental and numerical ways [1–7]. The investigation of flow around rigid bodies has many engineering applications such as the aerodynamics of chimney stacks, skyscrapers, suspension bridges, etc. During the last decade, the fluid past the bluff bodies of different shapes and sizes has been investigated by many researchers [8–10]. The wake produced by the separation of fluid past the bluff bodies mainly depends on the shape and size of the obstacles [11–15]. To investigate the steady and periodic wake, the effective Reynolds number is used by Dumouchel et al. [16]. The effect of different Reynolds numbers on fluid flow past non-spherical bodies was observed by Berrone [17], Liu and Kopp [18], and Schewe [19].

The medical and engineering contribution of viscous fluid has been truly recognized for the last couple of centuries. Engineers and medical scientists paid special attention to understanding the nature of fluids and more specifically to the visible fluids. As science evolved, the types of fluids, the flow characteristics, and the invisible forces involved in fluid flow are the major discoveries that are being used nowadays for the benefit of mankind. In recent times, flow geometry is one of the main focuses of attention for many researchers. Understanding the elastic and plastic characteristics of some fluids is due to such attention. The fluid flow is mainly dependent on certain factors like pressure, velocity, and viscosity. Mathematically speaking, the shear stress and shear rate of strain are the key factors to be investigated together with viscosity [20–24].

Based on generalized Newtonian fluids, this work is related to the fluid flow around the obstacles of circular and semicircular shape. The flow regime is compared for both cases. For different values of Reynolds numbers, the Newtonian fluid flow around obstacles of different shapes has been investigated by many [25,26]. The laminar flow characteristics can be observed for low values of Reynold numbers, generally for Newtonian fluids. The fluids with shear-thinning viscosity are considered the simplest version of non-Newtonian fluids, but with the advancement of computational techniques, the fluids with shear-thickening viscosity are attaining the interest of researchers [27]. For many non-Newtonian fluids, the shearing characteristics are investigated in reference [28].

Recognizing the industrial applications of flow around semi-cylinders, this work is confined to some numerical results. The comparison is made with the results of the circular cylinder. We organize the manuscript as follows. Section 2 is concerned with the mathematical modeling and numerical approach for this work. Section 3 displays the results and discussion for the involved factors. The conclusion of the present study is revealed in Section 4.

Mathematical Modeling and Numerical Scheme

The Navier Stokes equations provide the way to understand and deal with fluid engineering [29–33]. These equations are set on nonlinear partial differential equations, due to which analytical solution of such problems as well as of other problems arising as models of wave propagation [34,35] is often difficult. In order to solve them, one needs to approach a numerical solution. Among many numerical tools reported in the literature to deal with the mechanics of fluid flow, the finite element method (FEM) is the prominent one. The functionality of the finite element method and the mathematical modeling for our problem is described in references [36–42].

$\nabla \cdot \mathbf{u}=0(1)$

$\rho \left(\mathbf{u}\cdot \nabla \mathbf{u}\right)=-\nabla p+\nabla \cdot \tau ,(2)$

where the symbols have their usual meanings.

Power-Law Fluid

The power-law fluid was first suggested by W. Ostwald in 1925. Although the simplest model shows dependence upon the shear rate with the minimal number of parameters, it is representative of many non-Newtonian fluids. One of the advantages of this model is that it gives rise to analytical solutions in many cases, and hence, this model is widely used in applications. The model [25] is given by the following:

$\tau =m{\left(\dot{\gamma }\right)}^n,(3)$

where $\tau$ and $\dot{\gamma }$ are the shear stress and shear rate while $n$ and $m$ are the power-law index and consistency index, respectively.

Flow Configuration

A circular cylinder with a diameter $D=0.1$ is placed in a channel at various positions. The dimension of the given domain is $\left[\mathrm{0,2.2}\right]\times \left[\mathrm{0,0.41}\right]$. The circular obstacle $C_1$ and semi-circular $C_2$ are fixed at $\left(0.2,0.2\right)$ in the channel for two different studies. Later, $C_1$ and $C_2$ are placed in the channel simultaneously in a series at $\left(0.2,0.2\right)$ and $\left(0.5,0.2\right)$, respectively. The flow analysis is two-dimensional as there is no flow in the z-direction. The x-directional inlet is set at the left-hand side of the channel. An inflow profile is parabolic with maximum velocity $u_{\max }=0.3$ at the inlet of the channel. The y-direction explains the fully developed x-directional flow profile. A do-nothing boundary condition at the outlet is chosen. The other walls of the channel are set with no-slip conditions.

As the fluid interacts with the bluff body, the flow pressure exerts some forces on the surface of the cylinder(s) which are quantified as drag and lift. The dimensionless coefficients of these forces are as follows:

$C_D=\frac{2F_d}{\rho U_{mean}^{2}D},(4)$

$C_L=\frac{2F_l}{\rho U_{mean}^{2}D}.(5)$

Here, the average velocity is $U_{\text{mean}}$ and D is the diameter of the obstacle. Figure 1 shows the schematic diagram of the geometry used for this analysis. Figure 2 shows the computational grids at refinement level 1 for all three cases. The governing equation is discretized using FEM to approximate the important quantities like velocity and pressure. The reduced equations are solved using Newton’s method. To stop the nonlinear iterative process, we adopt the following criteria:

$\left|\frac{{\psi }^{k+1}-{\psi }^k}{{\psi }^{k+1}}\right|\le {10}^{-6}(6)$

here, $k$ displays the number of iterations and $\psi$ denotes a component of the solution. The non-Newtonian power-law fluid is used to investigate the velocity and pressure behavior. For a fixed value of $Re=20$, the power-law index is used as an input parameter.

FIGURE 1

FIGURE 1. Schematic diagram of the problem.

FIGURE 2

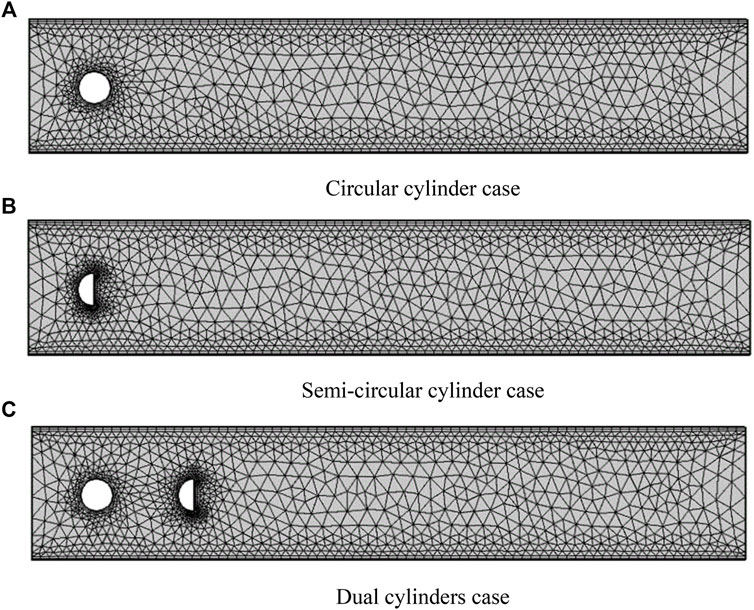
FIGURE 2. Hybrid mesh at coarse level. (A) Circular cylinder case. (B) Semi-circular cylinder case. (C) Dual cylinders case.

Results and Discussions

A) Code Validation

To validate the solution scheme, the results of Schäfer et al. [43] are reproduced for the circular cylinder case at $Re=20$ and $n=1$, which is the Newtonian case. The close correspondence is observed for the values of drag and lift between the present work and the published work [43], which gives them confidence in solution methodology. The reference values of ${\text{C}}_{\text{D}}$ and ${\text{C}}_{\text{L}}$ as given in reference [43] are as follows:

$\begin{array}{l}{C}_D=5.579535,\\ C_L=0.010618.\end{array}$

B) Correlation of Fluid Forces

In the present case, viscosity is the function of shear rate $\dot{\gamma }$ and the power law exponent $\left(n\right)$ which can give rise to different flow regimes as shear thinning, Newtonian, and shear thickening. To visualize the influence of $n$, equidistant values of the $n$ are chosen around the Newtonian case $(n=1)$ for shear thinning and shear thickening behaviors.

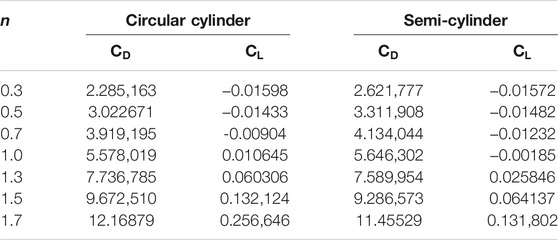
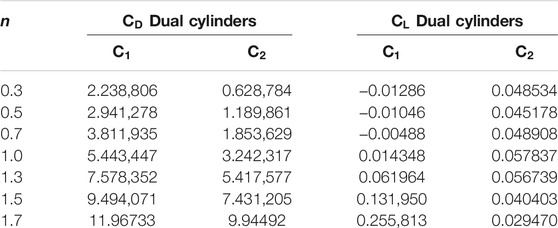
Tables (1)-(2) show the results of ${\text{C}}_{\text{D}}$ and ${\text{C}}_{\text{L}}$ calculated for 1) circular cylinder, 2) semi-circular cylinder, and 3) dual cylinder. For a steady flow, the drag is directly related to n. For the shear-thinning case $\left(n<1\right)$, the drag is a bit higher at a semi-cylinder than the drag on a circular cylinder. For the shear-thickening case $\left(n>1\right)$, the situation is reversed. In the dual cylinder case, less drag is observed than in the single cylinder.

TABLE 1

TABLE 1. Impacts of $n$ on drag and lift coefficients for single obstacles.

TABLE 2

TABLE 2. Impacts of $n$ on drag and lift coefficients for dual obstacles.

The strength of association between hydrodynamic forces using software SPSS-23 is represented in Tables (3)-(4). A strong and positive correlation is observed between drag and lift when cylinders are taken separately. However, in the case of a dual cylinder placed in a channel, an inverse association between drag and lift is observed at the semi-circular (downstream) cylinder.

TABLE 3

TABLE 3. Correlation coefficient for ${\text{C}}_{\text{D}}$ and ${\text{C}}_{\text{L}}$ (single cylinder).

TABLE 4

TABLE 4. Correlation coefficient for ${\text{C}}_{\text{D}}$ and ${\text{C}}_{\text{L}}$ (dual cylinder).

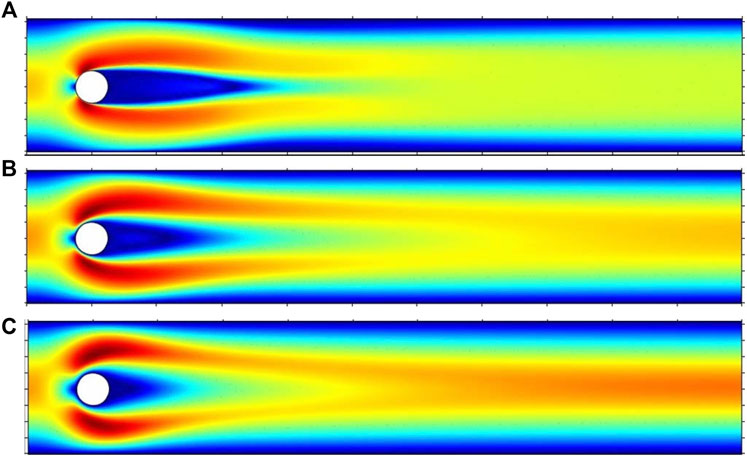
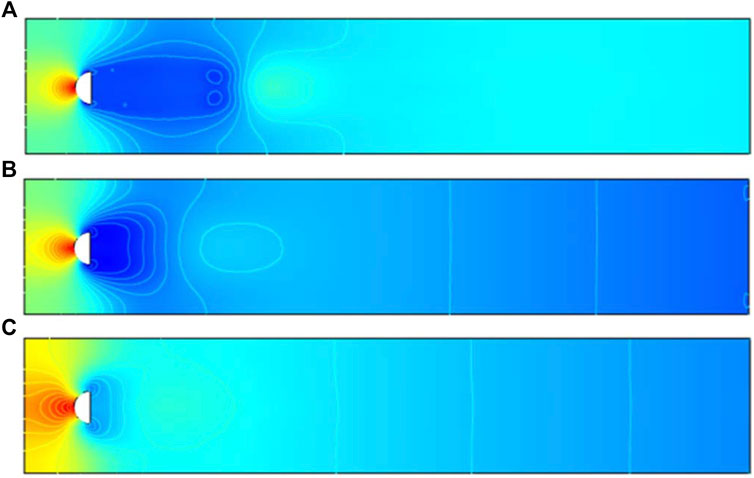
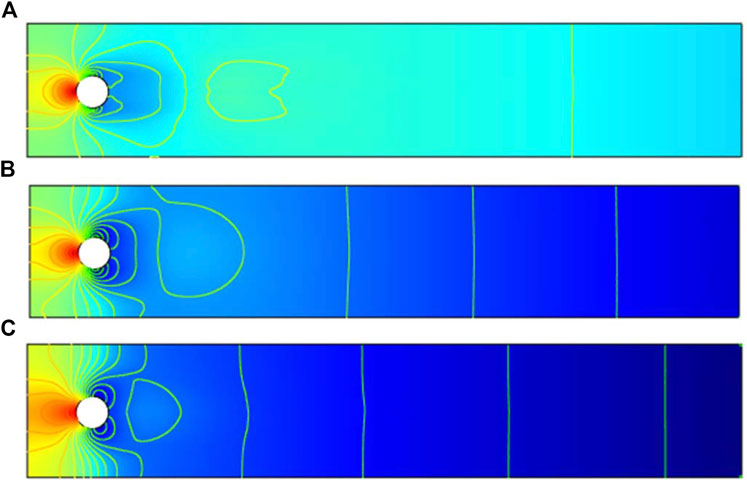
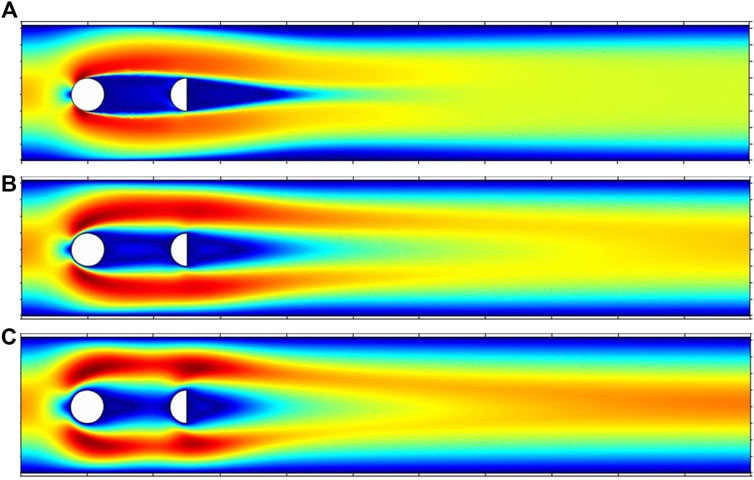
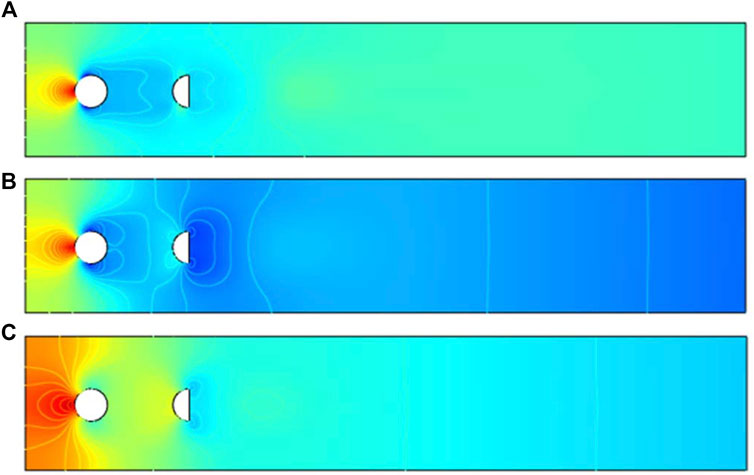
C) Impact on Velocity and Pressure

In the present work, the steady, laminar, and incompressible flow is observed using generalized power-law fluid. The dimensionless parameter n is used to observe the velocity and pressure behavior for shear-thinning $\left(n<1\right)$, shear thickening $\left(n>1\right)$, and the Newtonian case $\left(n=1\right)$ when the fluid encounters an obstacle. At the stagnation point, the fluid elements come to rest and then accelerate, bifurcating the fluid around the cylinder in the direction of velocity. The maximum velocity is observed at the corner of the cylinder for a specific region. This maximum velocity region around the cylinder increases and moves ahead with the increasing value of n (see Figures 3, 4, 5). It is also observed that the velocity increases around the central horizontal axis of the channel as fluid thickening increases. As in Figures 3, 4, 5, the flow separation is observed in the rear side of the obstacle. The flow separation gets reduced for increasing n. Moreover, in the case of a semi-circular cylinder, the flow separation gets a longer range (see Figure 4).

FIGURE 3

FIGURE 3. Effects on velocity with $Re=20$ for $n=0.3,1$ and $1.7$.

FIGURE 4

FIGURE 4. Effects on the velocity profile with $Re=20$ for $n=0.3,1$ and $1.7$.

FIGURE 5

FIGURE 5. Effects on the velocity profile with $Re=20$ for $n=0.3,1$ and $1.7$.

For all three cases, the pressure profiles can be visualized in Figures 6, 7, 8. In the free stream region, the pressure gets reduced with increasing n. In the case of the semicircular cylinder (Figure 7), an interesting pressure visualization appears for the shear-thinning case (n = 0.3). An invisible mild stagnation region appears at around $0.6\le x\le 0.9$, and then it gets evenly distributed afterward. In the dual cylinder case (Figure 8), the increasing pressure is observed up to the walls of the channel before the first obstacle (see Figure 8C), and the presence of the second obstacle has a significant impact on the pressure spread together with the increasing value of n.

FIGURE 6

FIGURE 6. Effects on pressure with $Re=20$ for $n=0.3,1$ and $1.7$.

FIGURE 7

FIGURE 7. Effects on pressure with $Re=20$ for $n=0.3,1$ and $1.7$.

FIGURE 8

FIGURE 8. Effects on pressure with $Re=20$ for $n=0.3,1$ and $1.7$.

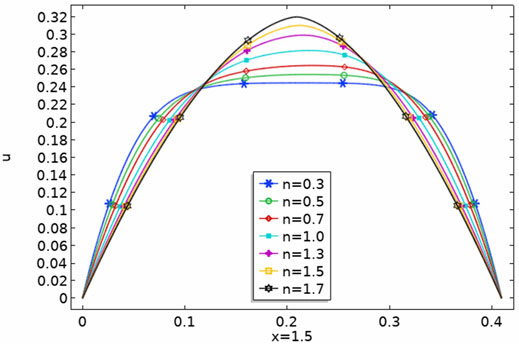
D) Line Graph Behavior

In Figure 9, we demonstrate the executed $u$-velocity at several power-law indexes. In detail, $x=0.0$ the fluid is initially injected at the inlet of the channel with a parabolic profile. The line graphs of u-velocity are drawn in the free stream region at $x=1.5$ to observe the impact of the $n$ on velocity. It is observed that shear-thinning fluid moves closer to the channel walls like in the n = 0.3 case. The distance of the fluid flow and the channel walls increases with the increasing fluid thickness like $n=1.7$ in Figure 9.

FIGURE 9

FIGURE 9. Velocity line graphs at x = 1.5.

Concluding Remarks

The influence of shape and orientation of obstacles on hydrodynamic forces has been studied in the present work. A statistical analysis is also performed by computation on the correlation coefficient for all cases. Code validation is performed as a special case, and results show excellent agreement with the reference values of the drag and lift coefficients. The main findings are mentioned below:

• High-velocity magnitude is observed for the shear-thinning cases.

• Pressure dispersion from the stagnation point is also highly associated with the power-law index.

• A strong and positive correlation is observed between drag and lift when cylinders are taken separately.

• The case of a dual cylinder placed in a channel; an inverse association between drag and lift is observed at the semi-circular cylinder.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

Conceptualization, RM, AHM, and IS; methodology, AM and IS; writing ‒original draft preparation, AHM and AM; supervision, RM and IS; writing --review and editing, NH and IK; Software, MT and NH; Validation, MT; Funding acquisition, MT, IS, NH, and IK, Formal analysis, NH. All authors have read and agreed to the published version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tritton DJ. Experiments on the Flow Past a Circular cylinder at Low Reynolds Numbers. J Fluid Mech (1959) 6(4):547–67. doi:10.1017/s0022112059000829

CrossRef Full Text | Google Scholar

2. Dennis SCR, Chang G-Z. Numerical Solutions for Steady Flow Past a Circular cylinder at Reynolds Numbers up to 100. J Fluid Mech (1970) 42(3):471–89. doi:10.1017/s0022112070001428

CrossRef Full Text | Google Scholar

3. Fornberg B. A Numerical Study of Steady Viscous Flow Past a Circular cylinder. J Fluid Mech (1980) 98(4):819–55. doi:10.1017/s0022112080000419

CrossRef Full Text | Google Scholar

4. Fornberg B. Steady Viscous Flow Past a Circular cylinder up to Reynolds Number 600. J Comput Phys (1985) 61(2):297–320. doi:10.1016/0021-9991(85)90089-0

CrossRef Full Text | Google Scholar

5. Peregrine DH. A Note on the Steady high-Reynolds-number Flow about a Circular cylinder. J Fluid Mech (1985) 157:493–500. doi:10.1017/s0022112085002464

CrossRef Full Text | Google Scholar

6. Cliff R, Grace JR, Weber ME. Bubbles, Drops and Particles. New York: Academic Press (1978).

Google Scholar

7. Zdravkovich MM. Flow Around Circular Cylinders: Volume 2: Applications, Vol. 2. Oxford, United Kingdom: Oxford University Press (2003).

Google Scholar

8. Kim T, Flynn MR. Numerical Simulation of Air Flow Around Multiple Objects Using the Discrete Vortex Method. J Wind Eng Ind Aerodyn (1995) 56(2–3):213–34. doi:10.1016/0167-6105(94)00090-z

CrossRef Full Text | Google Scholar

9. Bergstrom DJ, Wang J. Discrete Vortex Model of Flow over a Square cylinder. J Wind Eng Ind Aerodynamics (1997) 67-68:37–49. doi:10.1016/s0167-6105(97)00061-5

CrossRef Full Text | Google Scholar

10. Taylor I, Vezza M. Prediction of Unsteady Flow Around Square and Rectangular Section Cylinders Using a Discrete Vortex Method. J Wind Eng Ind Aerodyn (1999) 82(1–3):247–69. doi:10.1016/s0167-6105(99)00038-0

CrossRef Full Text | Google Scholar

11. Oertel H. Wakes behind blunt Bodies. Annu Rev Fluid Mech (1990) 22:539–62. doi:10.1146/annurev.fl.22.010190.002543

CrossRef Full Text | Google Scholar

12. Coutanceau M, Defaye J-R. Circular cylinder Wake Configurations: A Flow Visualization Survey. Appl Mech Rev (1991) 44:255–305. doi:10.1115/1.3119504

CrossRef Full Text | Google Scholar

13. Norberg C. Fluctuating Lift on a Circular cylinder: Review and New Measurements. J Fluids Structures (2003) 17(1):57–96. doi:10.1016/s0889-9746(02)00099-3

CrossRef Full Text | Google Scholar

14. Huang Y, Wu W, Zhang H. Numerical Study of Particle Dispersion in the Wake of Gas-Particle Flows Past a Circular cylinder Using Discrete Vortex Method. Powder Tech (2006) 162(1):73–81. doi:10.1016/j.powtec.2005.09.008

CrossRef Full Text | Google Scholar

15. Luo K, Fan J, Li W, Cen K. Transient, Three-Dimensional Simulation of Particle Dispersion in Flows Around a Circular cylinder Re=140-260). Fuel (2009) 88(7):1294–301. doi:10.1016/j.fuel.2008.12.026

CrossRef Full Text | Google Scholar

16. Dumouchel F, Lecordier JC, Paranthoën P. The Effective Reynolds Number of a Heated cylinder. Int J Heat Mass Transfer (1998) 41(12):1787–94. doi:10.1016/s0017-9310(97)00293-7

CrossRef Full Text | Google Scholar

17. Berrone M, Garbero V, Massimo M. Numerical Simulation of Low-Reynolds Number Flows Past Rectangular Cylinders Based on Adaptive Finite Element and Finite Volume Methods. Comput. Fluids (2011) 40(7):14. doi:10.1016/j.compfluid.2010.08.014

CrossRef Full Text | Google Scholar

18. Liu Z, Kopp GA. High-resolution Vortex Particle Simulations of Flows Around Rectangular Cylinders. Comput Fluids (2011) 40(1):2–11. doi:10.1016/j.compfluid.2010.07.011

CrossRef Full Text | Google Scholar

19. Schewe G. Reynolds-number-effects in Flow Around a Rectangular cylinder with Aspect Ratio 1:5. J Fluids Structures (2013) 39:15–26. doi:10.1016/j.jfluidstructs.2013.02.013

CrossRef Full Text | Google Scholar

20. Sivakumar P, Prakash Bharti R, Chhabra RP. Effect of Power-Law index on Critical Parameters for Power-Law Flow across an Unconfined Circular cylinder. Chem Eng Sci (2006) 61(18):6035–46. doi:10.1016/j.ces.2006.05.031

CrossRef Full Text | Google Scholar

21. Kumar B, Mittal S. Effect of Blockage on Critical Parameters for Flow Past a Circular cylinder. Int J Numer Meth Fluids (2006) 50(8):987–1001. doi:10.1002/fld.1098

CrossRef Full Text | Google Scholar

22. Rao PK, Sahu AK, Chhabra RP. Momentum and Heat Transfer from a Square cylinder in Power-Law Fluids. Int J Heat Mass Transf (2011) 54(1–3):390–403. doi:10.1016/j.ijheatmasstransfer.2010.09.032

CrossRef Full Text | Google Scholar

23. Chandra A, Chhabra RP. Flow over and Forced Convection Heat Transfer in Newtonian Fluids from a Semi-circular cylinder. Int J Heat Mass Transf (2011) 54(1–3):225–41. doi:10.1016/j.ijheatmasstransfer.2010.09.048

CrossRef Full Text | Google Scholar

24. Faruquee Z, Ting DS-K, Fartaj A, Barron RM, Carriveau R. The Effects of axis Ratio on Laminar Fluid Flow Around an Elliptical cylinder. Int J Heat Fluid Flow (2007) 28(5):1178–89. doi:10.1016/j.ijheatfluidflow.2006.11.004

CrossRef Full Text | Google Scholar

25. Rao PK, Sahu AK, Chhabra RP. Flow of Newtonian and Power-Law Fluids Past an Elliptical cylinder: a Numerical Study. Ind Eng Chem Res (2010) 49(14):6649–61. doi:10.1021/ie100251w

CrossRef Full Text | Google Scholar

26. Kumar De A, Dalal A. Numerical Simulation of Unconfined Flow Past a Triangular cylinder. Int J Numer Meth Fluids (2006) 52(7):801–21. doi:10.1002/fld.1210

CrossRef Full Text | Google Scholar

27. Bhatti MM, Riaz A, Zhang L, Sait SM, Ellahi R. Biologically Inspired thermal Transport on the Rheology of Williamson Hydromagnetic Nanofluid Flow with Convection: an Entropy Analysis. J Therm Anal Calorim (2021) 144:2187–202. doi:10.1007/s10973-020-09876-5

CrossRef Full Text | Google Scholar

28. Bhatti MM, Zeeshan A, Bashir F, Sait SM, Ellahi R. Sinusoidal Motion of Small Particles through a Darcy-Brinkman-Forchheimer Microchannel Filled with Non-newtonian Fluid under Electro-Osmotic Forces. J Taibah Uni Sci (2021) 15(1):514-529. doi:10.1080/16583655.2021.1991734

CrossRef Full Text | Google Scholar

29. Cuahutenango-Barro B, Taneco-Hernández MA, Gómez-Aguilar JF. On the Solutions of Fractional-Time Wave Equation with Memory Effect Involving Operators with Regular Kernel. Chaos, Solitons & Fractals (2018) 115:283–99. doi:10.1016/j.chaos.2018.09.002

CrossRef Full Text | Google Scholar

30. El-Ajou A, Oqielat MN, Al-Zhour Z, Kumar S, Momani S. Solitary Solutions for Time-Fractional Nonlinear Dispersive PDEs in the Sense of Conformable Fractional Derivative. Chaos (2019) 29(9):093102. doi:10.1063/1.5100234

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Kumar S, Kumar A, Momani S, Aldhaifallah M, Nisar KS. Numerical Solutions of Nonlinear Fractional Model Arising in the Appearance of the Strip Patterns in Two-Dimensional Systems. Adv Differ Equ (2019) 2019(1):413. doi:10.1186/s13662-019-2334-7

CrossRef Full Text | Google Scholar

32. Sharma B, Kumar S, Cattani C, Baleanu D. Nonlinear Dynamics of Cattaneo–Christov Heat Flux Model for Third-Grade Power-Law Fluid. J Comput Nonlinear Dyn (2020) 15(1). doi:10.1115/1.4045406

CrossRef Full Text | Google Scholar

33. Santos TF, Santos CMS, Aquino MS, Ionesi D, Medeiros JI. Influence of Silane Coupling Agent on Shear Thickening Fluids (STF) for Personal protection. J Mater Res Tech (2019) 8(5):4032–9. doi:10.1016/j.jmrt.2019.07.013

CrossRef Full Text | Google Scholar

34. Othman MIA, Said S, Marin M. A Novel Model of Plane Waves Oftwo-Temperature Fiber-Reinforced Thermoelastic Medium under the Effect of Gravity with Three-Phase-Lag Model. Int J Numer Meth Heat Fluid Flow (2019) 29. 359. doi:10.1108/hff-04-2019-0359

CrossRef Full Text | Google Scholar

35. Marin M, Othman MIA, Seadawy AR, Carstea C. A Domain of Influence in the Moore–Gibson–Thompson Theory of Dipolar Bodies. J Taibah Uni Sci (2020) 14:653. doi:10.1080/16583655.2020.1763664

CrossRef Full Text | Google Scholar

36. Mahmood R, Bilal S, Majeed AH, Khan I, Sherif E-SM. A Comparative Analysis of Flow Features of Newtonian and Power Law Material: A New Configuration. J Mater Res Technol (2019) 9(2):1978-1987. doi:10.1016/j.jmrt.2019.12.030

CrossRef Full Text | Google Scholar

37. Mahmood R, Bilal S, Majeed AH, Khan I, Nisar KS. CFD Analysis for Characterization of Non-linear Power Law Material in a Channel Driven Cavity with a Square cylinder by Measuring Variation in Drag and Lift Forces. J Mater Res Tech (2020) 9(3):3838–46. doi:10.1016/j.jmrt.2020.02.010

CrossRef Full Text | Google Scholar

38. Bilal S, Mahmood R, Majeed AH, Khan I, Nisar KS. Finite Element Method Visualization about Heat Transfer Analysis of Newtonian Material in Triangular Cavity with Square cylinder. J Mater Res Tech (2020) 9(3):4904–18. doi:10.1016/j.jmrt.2020.03.010

CrossRef Full Text | Google Scholar

39. Majeed AH, Jarad F, Mahmood R, Siddique I. Topological Characteristics of Obstacles and Nonlinear Rheological Fluid Flow in Presence of Insulated Fins: A Fluid Force Reduction Study. Mathematical Problems in Engineering (2021) 2021. 9199512. doi:10.1155/2021/9199512

CrossRef Full Text | Google Scholar

40. Majeed AH, Mahmood R, Abbasi WS, Usman K. Numerical Computation of MHD Thermal Flow of Cross Model over an Elliptic Cylinder: Reduction of Forces via Thickness Ratio. Mathematical Problems in Engineering (2021) 2021. 2550440. doi:10.1155/2021/2550440

CrossRef Full Text | Google Scholar

41. Mehmood A, Mahmood R, Majeed AH, Awan FJ. Flow of the Bingham Papanastasiou Regularized Material in a Channel in the Presence of Obstacles: Correlation between Hydrodynamic Forces and Spacing of Obstacles. Modelling and Simulation in Engineeringub (2021) 2021. 5583110. doi:10.1155/2021/5583110

CrossRef Full Text | Google Scholar

42. Ahmad H, Mahmood R, Hafeez MB, Majeed AH, Askar S, Shehzad H. Thermal Visualization of Ostwald-De Waele Liquid in Wavy Trapezoidal Cavity: Effect of Undulation and Amplitude. Case Stud Therm Eng. (2022) 29. 101698. doi:10.1016/j.csite.2021.101698

CrossRef Full Text | Google Scholar

43. Schäfer M, Turek S, Durst F, Krause E, Rannacher R. Benchmark Computations of Laminar Flow Around a cylinder In: EH Hirschel. editors Flow Simulation with High-Performance Computers II. Berlin/Heidelberg, Germany: Springer (1996). p. 547–66. doi:10.1007/978-3-322-89849-4_39

CrossRef Full Text | Google Scholar