- 1School of Electronics Engineering and Computer Science, Peking University, Beijing, China
- 2Key Laboratory of High Confidence Software Technologies, Peking University, Beijing, China
- 3China Northwest Center of Financial Research, Lanzhou University of Finance and Economics, Lanzhou, China
- 4School of Information Engineering, Lanzhou University of Finance and Economics, Lanzhou, China
- 5Key Laboratory of E-Business Technology and Application, Lanzhou, China
- 6College of Mathematics and Statistics, Northwest Normal University, Lanzhou, China
Controlling the trapping process is one of the important themes in the study of random walk in real complex systems. We studied two types of random walks that are different from the traditional random walk on a directed weighted network. The first type of random walk is the weighted random walk controlled by the weight θ, and the other is the delayed-weighted random walk affected by both delay probability p and weight θ. Furthermore, we derived analytically the average trapping time (ATT) measuring the efficiency of the two types of trapping processes; the result shows that the ATT grows sub-linearly, linearly, and super-linearly with the network order when the weight satisfies
1 Introduction
In addition to the topological structure and characteristic of complex networks, the dynamic process in the network is also worth exploring because of its wide range of applications. Random walk, as a fundamental tool to describe the dynamic process of network, has been widely used to evaluate dynamical properties of different complex networks, involving practical problems such as page searching [1], epidemic spreading [2], target searching [3, 4], and energy transporting [5, 6]. As a main sub-topic in the research of random walks, the trapping problem refers to a special random walk in which a trap is placed at a given trap. A related basic quantity is the mean first passage time (MFPT), which represents the expected time required for the walker to reach the trap from the node i for the first time. The average trapping time (ATT) is the average of MFPTs over all starting nodes except the trap; the ATT is used as an index to measure the trapping efficiency of the trapping process [7, 8].
In order to improve the trapping efficiency, it is highly desirable to seek an effective method to adjust the trapping process in complex systems, such as treelike fractals [9] and one-dimensional systems. Researchers have studied the dynamic process of several types of networks without weight and direction, such as the Sierpinski network [10, 11], Koch network [12], and fractal lattice [13]. In view of the fact that many research studies on random walks mainly focus on undirected and unweighted networks, Zhang et al. [14] discussed two types of random walks for a class of weighted and undirected networks. Dai et al. [15–18] introduced several weighted random walks on the complex network. In fact, many real networks contain the relationships between individuals with different weights in different directions. For example, the degree of understanding between individuals in social networks, the traffic flow between two places on the transportation network, and the number of vaccines put in the epidemic prevention process are all related to the direction and weight of real networks [19, 20].
There are delays existing in some complex systems; this is the result of transportation or chemical reactions that require action time. The random walks that reveal the effects of delay have been proposed and studied through a mathematical framework [21]. On the other hand, a large amount of work on the trap problem of undirected networks cannot fully describe the real complex networks. The difference between the out-degree and in-degree of the node is considered in a directed network, and the weight of network is combined; we have explored the ATT of a class of directed weighted networks, and the random walk in the directed weighted network can be made more efficient by adjusting the weight factor and delay parameter, thus achieving the purpose of adjusting the random walk process.
The main contents of this study are divided into the following sections. First, we introduced some basic concepts related to random walks. In section 3, we designed a class of directed weighted edge-iteration networks, in which each pair of nodes is connected by two edges in opposite directions, and the weight of edge is controlled by the weight parameter θ; the delay phenomenon is measured by the delay parameter p. In section 4, we derived the exact analytical expression of the ATT for a given target node and found that the ATT of this network grows sub-linearly, linearly, and super-linearly, the three ways when parameter θ goes from 0 to infinity. Also, the delay parameter p not only changes the pre-factor of the ATT but also the weight θ can modify the pre-factor and scaling of the ATT.
2 Preliminaries
We focused on two types of biased random walks with a given target node. The directed weighted network constructed in this study is abbreviated as
The mean first passage time for a walker moving from node i to the target node in the network
Furthermore, Eq. 1 can be transformed into the following matrix form;
where
The ATT is defined as the mean of
where τij is essentially the ij-th entry of matrix (I − P)−1 combining Eq.3.
The aforementioned equation shows that the calculation of the ATT can be simplified as summing all the entries of the matrix (I − P)−1. It is worth noting that the network order Nt increases exponentially with t when t → +∞; this calculation for a large t is very time-consuming. However, we can use Eq. 4 to verify the analytical solution of the ATT.
3 Design of a DWEI-Network
Many problems can be abstracted as graphs for research [22–24]. In view of the differences between the out-degree and in-degree of node in the real network, we proposed a network operator called the directed weighted edge-iteration transformation (DWEI-transformation) to construct our network by an iterative method. We set wi→j as the weight of an edge from node i to node j in our network; it satisfies
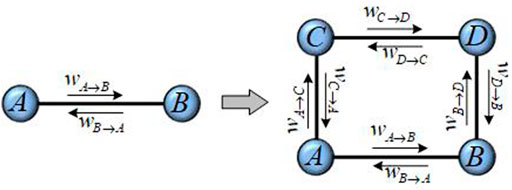
Directed weighted edge-iteration transformation (DWEI-transformation). For an edge e = AB with two end nodes A and B, the two weights of this edge are wA→B and wB→A. A new edge with end nodes C and D is added; then, two new edges are connected between A and C, and B and D, respectively; the weights of new edges are distributed according to the following rules.
(a) wA→C = θwA→B and wC→A = wB→A;
(b) wC→D = θwC→A and wD→C = wA→C;
(c) wB→D = θwB→A and wD→B = wA→B.
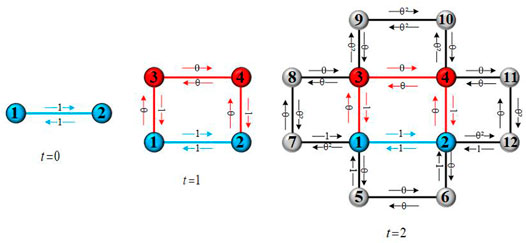
Figure 1 is a schematic diagram of the DWEI-transformation.
Let
Algorithm 1. DWEI-network construction algorithm.

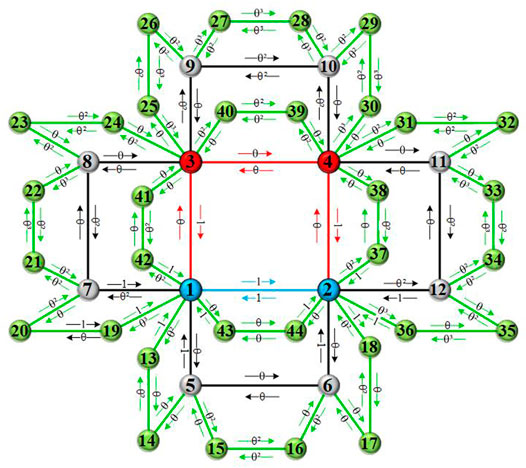
The out-strength of node i at time step t is defined as the sum of all weights of the edges starting from node i in −˗G(t), denoted as s + i (t) = PNt j=1 wi˗j (t). Meanwhile, the in-strength of node i represents the sum of the weights of all edges whose terminating nodes are i, expressed as s − i (t) = PNt j=1 wj˗i(t). The growth pattern determined by the node of network allows us to calculate the total number of nodes in −˗G(t) is Nt = 2 3 (4t + 2). Let ki(t) be the degree of a node i in network −˗G(t), the relationship between the degree of node i is ki(t) = 2ki(t − 1) in two consecutive time steps t − 1 and t. We can also get s + i (t) = (1 + Θ) t−ti+1 according to the definition of s+i(t), ti represents the time step when node i joined the network.
4 ATT for Weighted Walks
Different from the method of calculating the ATT by eigenvalues [25, 26], we derived a relationship governing the evolution for
Lemma 1. For the weighted walks of the DWEI network
Proof. : The mean first-passage time between any two nodes in the DWEI network can be divided into the following three categories, and their simplified representation is as follows. Let X be the MFPT starting from the node i to any of its ki(t − 1) old neighbors, which are directly connected to node i at the time step t − 1. Y represents the MFPT from any of ki(t − 1) new neighbors of node i to one of its ki(t − 1) old neighbors, and Z is the MFPT for starting from others new neighbors other than the aforementioned new nodes of node i to one of its ki(t − 1) old neighbors. Thus, considering two consecutive time steps, we found that X, Y, Z satisfy the following equations:
We get a solution X = 1 + 2θ by solving the aforementioned formula; it means that from the time step t to the next time t + 1, the trapping time for an arbitrary node i increases 1 + 2θ times the previous moment, that is,
and the sum of the MFPT of all new nodes at a time step τ is formulated as
Then, the average trapping time ⟨T⟩t of the DWEI network
Theorem 2. For the weighted random walks, Nt is the DWEI network order, let θ > 0 be the weight factor and t be the time step, then
(1) For
The dominating term of ⟨T⟩t is ⟨T⟩t ∼ Nt for t → ∞.
(2) When
the relationship between ⟨T⟩t and the network order Nt satisfy
Proof. It can be seen that the problem for evaluating ⟨T⟩t is reduced to determining
Obviously, once we calculated the result of
Combining the two formulas in Eq. 14, we can get
For the DWEI network corresponding to the first few time steps, since the number of nodes in the network is small, we can directly calculate the value of
Among the four nodes, the two nodes labeled 1 and 2 are called old nodes, and 3 and 4 are called new nodes; thus, the sum of MFPTs of all new nodes is equal to
Therefore, the sum of MFPTs of all nodes in the network
Considering Eq. 15 and summing this equation over all new nodes in
Similarly, the following equation about
Then, subtracting the product of Eq.19 multiplied by 2 (1 + 2θ) from Eq. 20, we have
After merging
Considering a value
1) For
We can get
2) When
With the help of a condition
Furthermore, substituting Eq.27 into Eq. 10, we get the average of all MFPTs in the network
Actually, the DWEI network can be regarded as a binary network for a special case θ = 1; based on this situation, the value of ⟨T⟩t we obtained is consistent with the result in the literature [27]. Next, we showed how to express ⟨T⟩t in terms of the network order Nt; Substituting
as t → ∞. According to Eq. 29, we found that the weight θ can not only modify the pre-factor of ⟨T⟩t but also the scaling log4 (1 + 2θ) of ⟨T⟩t. In addition, we can obtain the following conclusions in weighted random walks by analyzing Eqs 25, 29, when
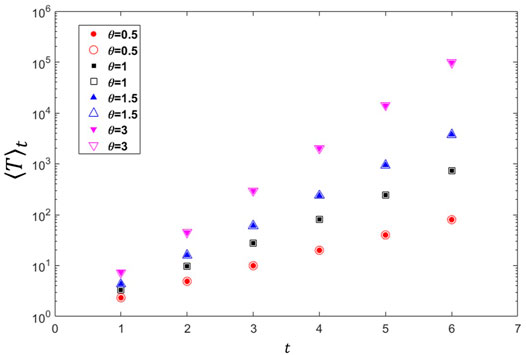
FIGURE 4. Solids indicate the numerical results, and the hollows indicate the results of our analytical results.
5 ATT for Delayed Weighted Walks
In this section, a delay probability 0 ≤ p ≤ 1 is introduced to explore its impact on the ATT of our network in the weighted random walk with delay [28]. The delayed weighted random walk is defined as follows; for delay probability 0 ≤ p ≤ 1, the walker in network
The two special cases of delayed weighted random walks are as follows:
1) When p = 0, delayed weighted random walks reduce to regular weighted random walks discussed in the previous section because the walker moves from node i to any neighboring node j with transition probability
2) When p = 1, if node i is created before the time step t, then the walker jumping from the current node i to any neighboring node j in
Lemma 3. For the delayed weighted random walks of the DWEI network
Proof. : Let
The solved X involves the delay probability p and the weight factor θ; its expression is
Therefore, we have deduced the relationship between
Theorem 4. For the delayed weighted random walks, let θ > 0 and t ≥ 0 be the weight factor and time step, Nt is the DWEI-network order; then, the exact dependence of ATT on the network order Nt is as follows:
(1) For
2) When
for t → ∞.
Proof. : We defined ⟨F⟩t as the ATT for delayed weighted random walks in the network
The sum of MFPT of all nodes in the network is composed of the sum of MFPT of old nodes and new nodes; it can be formulated as
Similar to the calculation of Eqs 13, 17, it shows that our calculation focuses on solving
We can directly get
Multiplying Eq.38 with 2 (1 + 2θ) and subtracting the result from Eq. 39, we derived the recursive connection between
where
1) When the weight factor satisfies
In this case, we can calculate the sum of MFPT of all nodes by combining Eqs 24, 37, 42:
Substituting Eq.43 into Eq. 36, we can get the expression of ⟨F⟩t. Furthermore, we deduce that the trend of ⟨F⟩t increases with Nt for a large network:
The aforementioned formula shows that ⟨F⟩t increases linearly with Nt when
Among them, three variables A, B, C equal to
Next, we gave the average of MFPT for all nodes except the trap node; substituting Eq.45 into Eq. 36, we obtain
Considering
For a large t, we have the following expression for the dominating term of ⟨F⟩t:
Therefore, Eq.49 shows that ⟨F⟩t grows sub-linearly and super-linearly with the network size, when
6 Conclusion
Based on the undirected unweighted network, we considered the weight and the out-degree and in-degree of nodes in complex systems. We proposed a network operator and a class of directed weighted edge-iteration networks and derived the closed form solution of the average trapping time of two different random walks with a given trap node; one of the random walks is based on the weight θ alone acting on the transition probability, and the other is the weight factor θ and delay parameter p impacting on the transition probability at the same time. The solution shows that the directed weighted construction has a significant effect on the trapping efficiency, and the leading scale of the ATT can be sub-linearly, linearly, and super-linearly with the network size when
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
JS provided this topic and wrote the manuscript. MM and MZ discussed and drew all figures. BY modified and guided the manuscript. All authors contributed to the manuscript and approved the submitted version.
Funding
This research was supported by the National Key Research and Development Plan under the Grant No. 2019YFA0706401 and the National Natural Science Foundation of China under Grants Nos. 61872166 and 61662066, the Technological Innovation Guidance Program of Gansu Province: Soft Science Special Project (21CX1ZA285), and the Northwest China Financial Research Center Project of Lanzhou University of Finance and Economics (JYYZ201905).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Hwang S, Lee DS, Kahng B. First Passage Time for Random Walks in Heterogeneous Networks. Phys Rev Lett (2012) 109(8):088701. doi:10.1103/PhysRevLett.109.088701
2. Bestehorn M, Riascos AP, Michelitsch TM, Collet BA. A Markovian Random Walk Model of Epidemic Spreading. Continuum Mech Thermodyn (2021) 33:1207–21. doi:10.1007/s00161-021-00970-z
3. Shirsat A, Elamvazhuthi K, Berman S. Multi-Robot Target Search Using Probabilistic Consensus on Discrete Markov Chains. In: 2020 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR). Abu Dhabi, UAE: IEEE (2020). doi:10.1109/ssrr50563.2020.9292589
4. El Hadidy MAA. Generalised Linear Search Plan for a D-Dimensional Random Walk Target. Ijmor (2019) 15(2):211. doi:10.1504/ijmor.2019.10022970
5. Blumen A, Zumofen G. Energy Transfer as a Random Walk on Regular Lattices. J Chem Phys (1981) 75:892–907. doi:10.1063/1.442086
6. Sokolov IM, Mai J, Blumen A. Paradoxal Diffusion in Chemical Space for Nearest-Neighbor Walks over Polymer Chains. Phys Rev Lett (1997) 79:857–60. doi:10.1103/physrevlett.79.857
7. Zhang Z, Julaiti A, Hou B, Zhang H, Chen G. Mean First-Passage Time for Random Walks on Undirected Networks. Eur Phys J B (2011) 84(4):691–7. doi:10.1140/epjb/e2011-20834-1
8. LinZhang YZZ, Zhang Z. Random Walks in Weighted Networks with a Perfect Trap: an Application of Laplacian Spectra. Phys Rev E Stat Nonlin Soft Matter Phys (2013) 87(6):062140. doi:10.1103/PhysRevE.87.062140
9. Wu B, Zhang Z. Controlling the Efficiency of Trapping in Treelike Fractals. J Chem Phys (2013) 139(2):024106. doi:10.1063/1.4812690
10. Bentz JL, Turner JW, Kozak JJ. Analytic Expression for the Mean Time to Absorption for a Random walker on the Sierpinski Gasket. Ii. The Eigenvalue Spectrum. Phys Rev E Stat Nonlin Soft Matter Phys (2010) 82(1):011137. doi:10.1103/PhysRevE.82.011137
11. Kozak JJ, Balakrishnan V. Analytic Expression for the Mean Time to Absorption for a Random walker on the Sierpinski Gasket. Phys Rev E Stat Nonlin Soft Matter Phys (2002) 65(1):021105. doi:10.1103/PhysRevE.65.021105
12. Zhang Z, Zhou S, Xie W, Chen L, Lin Y, Guan J. Standard Random Walks and Trapping on the Koch Network with Scale-free Behavior and Small-World Effect. Phys Rev E Stat Nonlin Soft Matter Phys (2009) 79(6):061113. doi:10.1103/PhysRevE.79.061113
13. Haynes CP, Roberts AP. Global First-Passage Times of Fractal Lattices. Phys Rev E Stat Nonlin Soft Matter Phys (2008) 78(1):041111. doi:10.1103/PhysRevE.78.041111
14. Lin Y, Zhang Z. Controlling the Efficiency of Trapping in a Scale-free Small-World Network. Sci Rep (2014) 4:6274. doi:10.1038/srep06274
15. Zhu F, Dai M, Dong Y, Liu J. Random Walk and First Passage Time on a Weighted Hierarchical Network. Int J Mod Phys C (2014) 25(9):1450037. doi:10.1142/s0129183114500375
16. Dai M, Ye D, Li X, Hou J. Average Weighted Receiving Time in Recursive Weighted Koch Networks. Pramana - J Phys (2016) 86(6):1173–82. doi:10.1007/s12043-016-1196-8
17. Chen Y, Dai M, Wang X, Sun Y, Su W. Multifractal Analysis of One-Dimensional Biased Walks. Fractals (2018) 26:1850030. doi:10.1142/s0218348x18500305
18. Dai M, Dai C, Ju T, Shen J, Sun Y, Su W. Mean First-Passage Times for Two Biased Walks on the Weighted Rose Networks. Physica A: Stat Mech its Appl (2019) 523:268–78. doi:10.1016/j.physa.2019.01.112
19. Chennubhotla C, Bahar I. Signal Propagation in Proteins and Relation to Equilibrium Fluctuations. Plos Comput Biol (2007) 3(10):1716–26. doi:10.1371/journal.pcbi.0030172
20. Wu Z, Gao Y. Average Trapping Time on Weighted Directed Koch Network. Sci Rep (2019) 9(1):14609–11. doi:10.1038/s41598-019-51229-2
21. Ohira T, Yamane T. Delayed Stochastic Systems. Phys Rev E (2000) 61(2):1247–57. doi:10.1103/physreve.61.1247
22. Zhu E, Jiang F, Liu C, Xu J. Partition Independent Set and Reduction-Based Approach for Partition Coloring Problem. IEEE Trans Cybern (2020) 99:1–10. doi:10.1109/tcyb.2020.3025819
23. Liu C. A Note on Domination Number in Maximal Outerplanar Graphs. Discrete Appl Maths (2021) 293(1):90–4. doi:10.1016/j.dam.2021.01.021
24. Liu C, Zhu E, Zhang Y, Zhang Q, Wei X. Characterization, Verification and Generation of Strategies in Games with Resource Constraints. Automatica (2022) 140:110254. doi:10.1016/j.automatica.2022.110254
25. Xie P, Zhang Z, Comellas F. The Normalized Laplacian Spectrum of Subdivisions of a Graph. Appl Maths Comput (2016) 286:250–6. doi:10.1016/j.amc.2016.04.033
26. Xie PC, Zhang ZZ, Comellas F. On the Spectrum of the Normalized Laplacian of Iterated Triangulations of Graphs. Appl Maths Comput (2015) 273:1123–9.
27. Zhang Z, Xie W, Zhou S, Li M, Guan J. Distinct Scalings for Mean First-Passage Time of Random Walks on Scale-free Networks with the Same Degree Sequence. Phys Rev E Stat Nonlin Soft Matter Phys (2009) 80(6):061111. doi:10.1103/PhysRevE.80.061111
Keywords: random walk, directed network, weight, mean first passage time, trapping efficiency
Citation: Su J, Ma M, Zhang M and Yao B (2022) Adjusting the Trapping Process of a Directed Weighted Edge-Iteration Network. Front. Phys. 10:822712. doi: 10.3389/fphy.2022.822712
Received: 26 November 2021; Accepted: 06 June 2022;
Published: 14 July 2022.
Edited by:
Nuno A. M. Araújo, University of Lisbon, PortugalReviewed by:
Yilun Shang, Northumbria University, United KingdomEnqiang Zhu, Guangzhou University, China
Copyright © 2022 Su, Ma, Zhang and Yao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mingjun Zhang, emhhbmdtamx6QDE2My5jb20=
 Jing Su
Jing Su Mingyuan Ma
Mingyuan Ma Mingjun Zhang3,4,5*
Mingjun Zhang3,4,5*