Is the Anisotropic Tilt Angle Necessary in the Turbulence Spectrum of Refractive-Index Fluctuations?

With the deepening of atmospheric turbulence research, scientists have discovered that the anisotropy of turbulence cells cannot be ignored. The anisotropic non-Kolmogorov turbulence model is more in line with the actual situation of atmospheric turbulence. However, the recent experimental results of Korotkova et al. and Beason et al. display that the turbulence cell has an anisotropic tilt angle, that is, the long axis of the turbulence cell may not be horizontal to the ground but has a certain angle with the ground. Therefore, it is urgent to analyze whether the anisotropic tilt angle is necessary in the turbulence spectrum. In this study, we develop the anisotropic non-Kolmogorov turbulence spectra for the horizontal and vertical links in the presence of the anisotropic tilt angle. Then, based on these spectra, the analytical expressions of the scintillation index for the horizontal and vertical links are derived under weak fluctuation condition. The results indicate that the anisotropic tilt angle is necessary in the vertical link but not in the horizontal link.

1 Introduction

Although the Kolmogorov turbulence model is the most widely utilized atmospheric turbulence model at present Andrews and Phillips [1], as more and more atmospheric experimental results inconsistent with the Kolmogorov turbulence model are discovered, scientists have found that the anisotropic non-Kolmogorov turbulence model is a more realistic model for atmospheric turbulence Manning [2]; Procaccia and Constantin [3]; Belen’kii et al. [4]; Toselli et al. [5]; Andrews et al. [6]; Kessar et al. [7]; Cui et al. [8]; Wang et al. [9]; Beason et al. [10]; Zhai [11]; Roşu et al. [12]; Xu and Lai [13,14]. Later, in the process of establishing the anisotropic non-Kolmogorov turbulence model and related turbulence theory, in order to simplify the modeling, a hypothesis that the long axis of the turbulence cell should be horizontal to the ground is extensively introduced Andrews et al. [6]; Cui et al. [8]. However, the recent experimental results of Korotkova et al. and Beason et al. have clearly shown that the turbulence cell has an anisotropic tilt angle, that is, the long axis of the turbulence cell may not be horizontal to the ground but has a certain angle with the ground Wang et al. [9]; Beason et al. [10]. Therefore, discussing whether it is necessary to increase the parameter anisotropic tilt angle in the turbulence spectrum has become an urgent and interesting problem to be solved. In this study, considering the anisotropic tilt angle, the anisotropic non-Kolmogorov turbulence spectra for the horizontal and vertical links are developed. Based on these spectra, we derive the analytical expressions of the scintillation index for the horizontal and vertical links under weak fluctuation condition and then, calculations are implemented to evaluate the influence of the anisotropic tilt angle on the scintillation index in the horizontal and vertical links. It is anticipated that this study will benefit the construction of the atmospheric turbulence model and understanding of optical wave transmission in anisotropic non-Kolmogorov links.

2 Formulation

As is well-known, for the horizontal link, the power spectrum model of anisotropic non-Kolmogorov turbulence, which considers the uneven distribution of the horizontal and vertical atmosphere, has the following expression Andrews et al. [6].

${\mathrm{\Phi }}_n\left({\kappa }_x,{\kappa }_y\right)=\frac{A\left(\alpha \right){\tilde{C}}_n^2{\mu }_x{\mu }_y}{{\left({\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2\right)}^{\alpha /2}},3<\alpha <4,(1)$

where μ_x and μ_y are the anisotropic factors which can describe the asymmetry of turbulence cells, κ_x and κ_y are the x and y components of the spatial wavenumber vector κ, respectively, $\kappa =\sqrt{{\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2}$, α is the spectral power law, ${\tilde{C}}_n^2$ is the structure constant for the anisotropic non-Kolmogorov horizontal link which has units of m^3−α, and $A\left(\alpha \right)=\mathrm{\Gamma }\left(\alpha -1\right)\cos \left(\alpha \pi /2\right)/4{\pi }^2$ and $\mathrm{\Gamma }\left(x\right)$ denote the Gamma function. At α = 11/3 and μ_x = μ_y = 1, Eq. 1 reduces to the conventional Kolmogorov spectrum. It is to be noted that in the field of laser atmospheric propagation, the turbulence spectrum usually refers to the spatial power spectral density of refractive-index fluctuations.

In order to introduce the anisotropic tilt angle γ into the turbulence spectrum for the horizontal link, we make a rotation with the same angle γ in the κ-space. Hence, the spatial wavenumbers become κ_x = κ_rx  cos γ − κ_ry  sin γ and κ_y = κ_rx  sin γ + κ_ry  cos γ in place of κ_x and κ_y in Eq. 1, respectively. Here, κ_rx and κ_ry are the newly introduced coordinates after rotating the coordinate system in κ-space through angle γ, and the power spectrum model for the anisotropic non-Kolmogorov horizontal link in the presence of the anisotropic tilt angle γ has the following expression

${\mathrm{\Phi }}_n\left({\kappa }_{rx},{\kappa }_{ry}\right)=\frac{A\left(\alpha \right){\tilde{C}}_n^2{\mu }_x{\mu }_y}{{\left(m^2{\kappa }_{rx}^2+n^2{\kappa }_{ry}^2+g{\kappa }_{rx}{\kappa }_{ry}\right)}^{\alpha /2}},3<\alpha <4,(2)$

where

$m=\sqrt{{\mu }_x^2{\cos }^2\gamma +{\mu }_y^2{\sin }^2\gamma },(3)$

$n=\sqrt{{\mu }_x^2{\sin }^2\gamma +{\mu }_y^2{\cos }^2\gamma },(4)$

$g=2\sin \gamma \cos \gamma \left({\mu }_y^2-{\mu }_x^2\right).(5)$

It is to be noted that the definition of the anisotropic tilt angle γ in the horizontal and vertical links is the same. To avoid repetition, the figure for the anisotropy model of the turbulence cell in the horizontal link is not separately given here; please refer to Figure 2 for the definition of the anisotropic tilt angle γ. As shown in Figure 2, the anisotropic tilt angle γ is the angle between the plane XON where the long axes of the ellipsoid are located and the horizontal plane XOY; counterclockwise value is positive, and the value range is 0–180°.

For the weak Kolmogorov horizontal link, the scintillation index of a plane wave is defined by Andrews and Phillips [1].

${\sigma }_I^2=8{\pi }^2{k}^{2}L{\int }_0^1{\int }_0^{\infty }\kappa {\mathrm{\Phi }}_n\left(\kappa \right)\left[1-\cos \left(\frac{L{\kappa }^2\xi }{k}\right)\right]d\kappa d\xi ,(6)$

where L is the link distance, ξ is the normalized path coordinate related to z by ξ = 1 − z/L and k = 2π/λ, and λ is the wavelength. Substituting Eq. 2 into Eq. 6 leads to

$\begin{array}{c}{\sigma }_I^2=4\pi k^{2}L{\int }_0^1{\int }_0^{\infty }{\int }_0^{\infty }{\mathrm{\Phi }}_n\left({\kappa }_{rx},{\kappa }_{ry}\right)\hfill \\ \times \left[1-\cos \left(\frac{L{\kappa }^2\xi }{k}\right)\right]d{\kappa }_{rx}d{\kappa }_{ry}d\xi .\hfill \end{array}(7)$

We can transform the stretched coordinate system for ${\mathrm{\Phi }}_n\left({\kappa }_{rx},{\kappa }_{ry}\right)$ into an isotropic coordinate system by use of the following substitutions,

${\kappa }_{rx}=\frac{q_x}{m}=\frac{q\cos \theta }{m},{\kappa }_{ry}=\frac{q_y}{n}=\frac{q\sin \theta }{n},q=\sqrt{q_x^2+q_y^2},(8)$

$\kappa =q\sqrt{\frac{{\cos }^2\theta }{m^2}+\frac{{\sin }^2\theta }{n^2}},d{\kappa }_{rx}d{\kappa }_{ry}=\frac{d{q}_{x}d{q}_y}{mn}=\frac{qdqd\theta }{mn},(9)$

${\mathrm{\Phi }}_n\left(q\right)=\frac{A\left(\alpha \right){\tilde{C}}_n^2{\mu }_x{\mu }_y}{q^{\alpha }}{\left(1+\frac{g\cos \theta \sin \theta }{mn}\right)}^{-\alpha /2}.(10)$

Substituting Eqs 8–10 into Eq. 7, we can obtain

$\begin{array}{c}{\sigma }_I^2=4\pi k^{2}L{\int }_0^1{\int }_0^{\mathrm{2}\pi }{\int }_0^{\infty }A\left(\alpha \right){\tilde{C}}_n^2{q}^{1-\alpha }\frac{{\mu }_x{\mu }_y}{mn}{\left(1+\frac{g\cos \theta \sin \theta }{mn}\right)}^{-\frac{\alpha }{2}}\hfill \\ \times \left[1-\cos \left(\frac{L{q}^2\xi }{k}\left(\frac{{\cos }^2\theta }{m^2}+\frac{{\sin }^2\theta }{n^2}\right)\right)\right]dqd\theta d\xi .\hfill \end{array}(11)$

Then, evaluating this integral, the scintillation index for a plane wave transmitting through the weak anisotropic non-Kolmogorov horizontal link in the presence of the anisotropic tilt angle γ can be obtained

$\begin{array}{c}{\sigma }_I^2=-\frac{2}{\alpha }\mathrm{\Gamma }\left(1-\frac{\alpha }{2}\right)\mathrm{\Gamma }\left(\alpha -1\right)\sin \left(\frac{\alpha \pi }{4}\right)\cos \left(\frac{\alpha \pi }{2}\right){\tilde{C}}_n^2{k}^{3-\frac{\alpha }{2}}{L}^{\frac{\alpha }{2}}\hfill \\ \times \frac{{\mu }_x{\mu }_y}{mn}\frac{1}{2\pi }{\int }_0^{2\pi }{\left(1+\frac{g\cos \theta \sin \theta }{mn}\right)}^{-\frac{\alpha }{2}}{\left(\frac{{\cos }^2\theta }{m^2}+\frac{{\sin }^2\theta }{n^2}\right)}^{\frac{\alpha }{2}-1}d\theta .\hfill \end{array}(12)$

In Figure 1, the influence of the anisotropic tilt angle γ on the scintillation index of a plane wave in the weak anisotropic non-Kolmogorov horizontal link is numerically analyzed. It is to be noted that in the calculation, we have λ = 1.55 μm, L = 5 km, and ${\tilde{C}}_n^2=1\times 10^{-14}{\mathrm{m}}^{3-\alpha }$. It can be easily seen from Figure 1 that for different values of power law α, anisotropic factors μ_x and μ_y and the variation of the anisotropic tilt angle γ has no effect on the scintillation index for the horizontal link, so the anisotropic tilt angle γ is not necessary in the horizontal link. This result can be physically explained by mentioning the change of curvature of the anisotropic turbulence cells with respect to the isotropic case, and anisotropic turbulence cells will change the focusing properties of the turbulence. When a beam propagates along the long axis of the anisotropic turbulence cells (horizontal link), the radius of curvature for the interface between the beam and anisotropic turbulence cells is small, and the beam will be more deviated from the direction of propagation because these cells act as lenses with a lower radius of curvature Toselli et al. [5]. Correspondingly, while a beam propagates along the short axis of the anisotropic turbulence cells (vertical link), the radius of curvature for the interface between the beam and anisotropic turbulence cells is large, and the beam will be less deviated from the direction of propagation because these cells act as lenses with a higher radius of curvature. Then, based on simple spatial geometry knowledge, we can easily deduce that as the anisotropic tilt angle γ changes, the radius of curvature for the interface between the propagated beam and anisotropic turbulence cells is unchanged in the horizontal link. Hence, the anisotropic tilt angle γ is not necessary in the horizontal link.

FIGURE 1

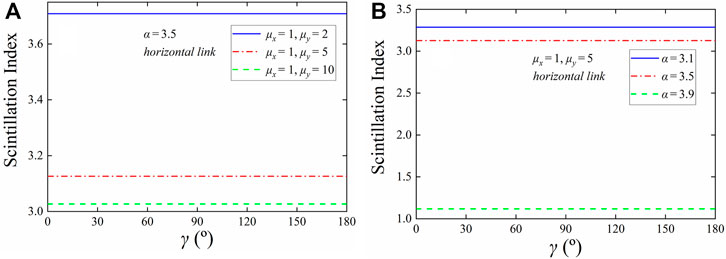
FIGURE 1. Scintillation index of a plane wave versus the anisotropic tilt angle γ for the horizontal link. (A) With various anisotropic factor μ_x and μ_y values; (B) with various power law α values.

Because the anisotropic non-Kolmogorov structure constant for the vertical link is altitude-dependent and the optical wave propagation direction in the horizontal and vertical links is different, that is, the z-axis direction of the corresponding coordinate system is different, so the turbulence spectrum for the vertical link in the presence of the anisotropic tilt angle γ cannot be obtained from the turbulence spectrum for the horizontal link Eq. 1 by coordinate transformation in κ-space. Then, we will introduce a new method to establish the turbulence spectrum for the vertical link in the presence of the anisotropic tilt angle γ.

First, in order to simplify the modeling, different from the horizontal link, we only consider the existence of an anisotropic factor μ in the vertical link, that is, assuming OX = ON = μs and OM = s. The anisotropic factor μ denotes the ratio of the horizontal axis to the vertical axis for the turbulence cell. Then, based on simple spatial geometry knowledge, we can easily deduce that when only an anisotropic factor μ is considered, the turbulence cell satisfies the ellipsoid hypothesis. In addition, an ellipsoid model in the presence of the anisotropic tilt angle γ is built to illustrate the actual turbulence cell for the vertical link, as shown in Figure 2. Obviously, the individual shape of the turbulence cell is random, not a perfect ellipsoid. However, from the perspective of ensemble average, the ellipsoid hypothesis can be made, which will not lead to a large error between the theoretical model and the actual turbulence.

FIGURE 2

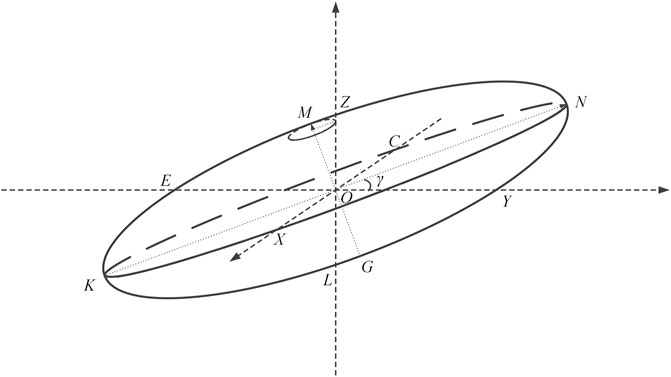
FIGURE 2. Anisotropy of the turbulence cell for the vertical link in the presence of the anisotropic tilt angle γ.

Second, as displayed in Figure 2, the plane XOY is the horizontal plane, and OZ is the plumb line, which denotes the optical wave propagation direction for the vertical link. Then, based on the ellipsoid hypothesis of the turbulence cell, we have OX = OC = ON = OK = μs and OM = OG = s. In addition, the previous assumption is consistent with many studies on the anisotropic turbulence, in which the length of the horizontal axis for the turbulence cell is usually one to several times the length of the vertical axis Cui et al. [8]; Wang et al. [9]; Beason et al. [10].

Finally, the anisotropic factors of the turbulence cell in the presence of the anisotropic tilt angle γ are evaluated It can be easily seen from Figure 2 that due to the existence of the anisotropic tilt angle γ, the turbulence cell rotates counterclockwise by angle γ around the x-axis; the y-axis and z-axis intersect the ellipsoid at points Y and Z, respectively. From the symmetry of the ellipse, OY = OE and OZ = OL. Because only the vertical link is considered in this study, the optical wave propagation direction is always the z-axis. In addition, the straight-lines XC, YE, and ZL form a rectangular coordinate system and satisfy OX = OC, OY = OE, and OZ = OL. So, we can use the ratio between OX, OY, and OZ to calculate the anisotropic factors of the turbulence cell for the vertical link, that is, μ_x = OX/OZ and μ_y = OY/OZ. Based on the standard equation of ellipse and simple trigonometric function, we can obtain that $OZ=\mu s\sqrt{\left(1+{\tan }^2\gamma \right)/\left({\tan }^2\gamma +{\mu }^2\right)}$ and $OY=\mu s\sqrt{\left(1+{\tan }^2\gamma \right)/\left(1+{\mu }^2{\tan }^2\gamma \right)}$. Then, the anisotropy model of the turbulence cell for the vertical link in the presence of the anisotropic tilt angle γ is established, and the anisotropic factors μ_x and μ_y can be expressed as

${\mu }_x=\sqrt{\frac{{\mu }^2+{\tan }^2\gamma }{1+{\tan }^2\gamma }},{\mu }_y=\sqrt{\frac{{\mu }^2+{\tan }^2\gamma }{1+{\mu }^2{\tan }^2\gamma }}.(13)$

Substituting the anisotropy model of the turbulence cell for the vertical link in the presence of the anisotropic tilt angle γ Eq. 13 into the extant anisotropic non-Kolmogorov turbulence spectrum model Andrews et al. [6] and considering that the anisotropic non-Kolmogorov structure constant will vary with the altitude, the power spectrum model for the anisotropic non-Kolmogorov vertical link in the presence of the anisotropic tilt angle γ can be obtained

${\mathrm{\Phi }}_n\left({\kappa }_x,{\kappa }_y,h\right)=\frac{A\left(\alpha \right){\tilde{C}}_n^2\left(h\right){\mu }_x{\mu }_y}{{\left({\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2\right)}^{\alpha /2}},3<\alpha <4.(14)$

As displayed in the study by Andrews et al. [15]; Zhai et al. [16], ${\tilde{C}}_n^2$ for the vertical link is altitude-dependent and provided by

$\begin{array}{c}{\tilde{C}}_n^2\left(h\right)=\frac{0.033}{A\left(\alpha \right)}{\left(k/h\right)}^{\left(\alpha /2-11/6\right)}\hfill \\ \times \left[0.00594{\left(\frac{w}{27}\right)}^2{\left({10}^{-5}h\right)}^{10}\right.\exp \left(-\frac{h}{1000}\right)\hfill \\ +2.7\times 10^{-16}\exp \left(-\frac{h}{1500}\right)\left.+C_n^2\left(0\right)\exp \left(-\frac{h}{100}\right)\right],\hfill \end{array}(15)$

where w is the rms wind speed with units of m/s, h is the altitude with units of m, and $C_n^2\left(0\right)$ is the nominal value of $C_n^2$ when h = 0 with units of m^−2/3. It is to be noted that Eq. 15 is based on non-Kolmogorov turbulence; however we suppose that it is also valid in the presence of anisotropic non-Kolmogorov turbulence, at least approximately.

In the case of a downlink, the scintillation index can be accurately modeled by a plane wave. For an uplink, where the atmospheric turbulence begins just outside the transmitting aperture, a spherical wave can be assumed. Thus, for a plane wave and vertical downlink, the scintillation index under weak fluctuation condition is given by Andrews and Phillips [1].

$\begin{array}{c}{\sigma }_{I,downlink}^2=8{\pi }^2{k}^2{\int }_{h_0}^H{\int }_0^{\infty }\kappa {\mathrm{\Phi }}_n\left(\kappa ,h\right)\hfill \\ \times \left\{1-\cos \left[\frac{L{\kappa }^2}{k}\left(\frac{h-h_0}{H-h_0}\right)\right]\right\}d\kappa dh.\hfill \end{array}(16)$

For a spherical wave and vertical uplink, the scintillation index under weak fluctuation condition is given by Andrews and Phillips [1].

$\begin{array}{c}{\sigma }_{I,uplink}^2=8{\pi }^2{k}^2{\int }_{h_0}^H{\int }_0^{\infty }\kappa {\mathrm{\Phi }}_n\left(\kappa ,h\right)\hfill \\ \times \left\{1-\cos \left[\frac{L{\kappa }^2}{k}\frac{\left(H-h\right)\left(h-h_0\right)}{{\left(H-h_0\right)}^2}\right]\right\}d\kappa dh,\hfill \end{array}(17)$

where h₀ represents the altitude with units of m for the downlink receiver or the uplink transmitter, L represents the link distance, and H = h₀ + L represents the satellite altitude with units of m. Substituting Eq. 14 into Eqs 16, 17 leads to

$\begin{array}{c}{\sigma }_{I,downlink}^2=4\pi k^2{\int }_{h_0}^H{\int }_0^{\infty }{\int }_0^{\infty }{\mathrm{\Phi }}_n\left({\kappa }_x,{\kappa }_y,h\right)\hfill \\ \times \left\{1-\cos \left[\frac{L{\kappa }^2}{k}\left(\frac{h-h_0}{H-h_0}\right)\right]\right\}d{\kappa }_{x}d{\kappa }_{y}dh,\hfill \end{array}(18)$

$\begin{array}{c}{\sigma }_{I,uplink}^2=4\pi k^2{\int }_{h_0}^H{\int }_0^{\infty }{\int }_0^{\infty }{\mathrm{\Phi }}_n\left({\kappa }_x,{\kappa }_y,h\right)\hfill \\ \times \left\{1-\cos \left[\frac{L{\kappa }^2}{k}\frac{\left(H-h\right)\left(h-h_0\right)}{{\left(H-h_0\right)}^2}\right]\right\}d{\kappa }_{x}d{\kappa }_{y}dh.\hfill \end{array}(19)$

We can transform the stretched coordinate system for ${\mathrm{\Phi }}_n\left({\kappa }_x,{\kappa }_y,h\right)$ into an isotropic coordinate system by use of the following substitutions:

${\kappa }_x=\frac{q_x}{{\mu }_x}=\frac{q\cos \theta }{{\mu }_x},{\kappa }_y=\frac{q_y}{{\mu }_y}=\frac{q\sin \theta }{{\mu }_y},q=\sqrt{q_x^2+q_y^2},(20)$

$\kappa =q\sqrt{\frac{{\cos }^2\theta }{{\mu }_x^2}+\frac{{\sin }^2\theta }{{\mu }_y^2}},d{\kappa }_{x}d{\kappa }_y=\frac{d{q}_{x}d{q}_y}{{\mu }_x{\mu }_y}=\frac{qdqd\theta }{{\mu }_x{\mu }_y},(21)$

${\mathrm{\Phi }}_n\left(q,h\right)=\frac{A\left(\alpha \right){\tilde{C}}_n^2\left(h\right){\mu }_x{\mu }_y}{q^{\alpha }}.(22)$

Substituting Eqs 20–22 into Eqs 18, 19, we can obtain

$\begin{array}{c}{\sigma }_{I,downlink}^2=4\pi k^2{\int }_{h_0}^H{\int }_0^{2\pi }{\int }_0^{\infty }A\left(\alpha \right){\tilde{C}}_n^2\left(h\right)q^{1-\alpha }\hfill \\ \times \left\{1-\cos \left[\frac{L{q}^2}{k}\left(\frac{h-h_0}{H-h_0}\right)\left(\frac{{\cos }^2\theta }{{\mu }_x^2}+\frac{{\sin }^2\theta }{{\mu }_y^2}\right)\right]\right\}dqd\theta dh,\hfill \end{array}(23)$

$\begin{array}{c}{\sigma }_{I,uplink}^2=4\pi k^2{\int }_{h_0}^H{\int }_0^{2\pi }{\int }_0^{\infty }A\left(\alpha \right){\tilde{C}}_n^2\left(h\right)q^{1-\alpha }\hfill \\ \times \left\{1-\cos \left[\frac{L{q}^2}{k}\frac{\left(H-h\right)\left(h-h_0\right)}{{\left(H-h_0\right)}^2}\left(\frac{{\cos }^2\theta }{{\mu }_x^2}+\frac{{\sin }^2\theta }{{\mu }_y^2}\right)\right]\right\}dqd\theta dh.\hfill \end{array}(24)$

Then, evaluating these integrals, the scintillation index for the plane wave vertical downlink and spherical wave vertical uplink under weak anisotropic non-Kolmogorov turbulence in the presence of the anisotropic tilt angle γ can be obtained.

$\begin{array}{c}{\sigma }_{I,downlink}^2=-4{\pi }^2{k}^{3-\frac{\alpha }{2}}{L}^{\frac{\alpha }{2}-1}\mathrm{\Gamma }\left(1-\frac{\alpha }{2}\right)\sin \left(\frac{\alpha \pi }{4}\right)\hfill \\ \times {\int }_{h_0}^{H}A\left(\alpha \right){\tilde{C}}_n^2\left(h\right){\left(\frac{h-h_0}{H-h_0}\right)}^{\frac{\alpha }{2}-1}dh\hfill \\ \times \frac{1}{2\pi }{\int }_0^{2\pi }{\left(\frac{{\cos }^2\theta }{{\mu }_x^2}+\frac{{\sin }^2\theta }{{\mu }_y^2}\right)}^{\frac{\alpha }{2}-1}d\theta ,\hfill \end{array}(25)$

$\begin{array}{c}{\sigma }_{I,uplink}^2=-4{\pi }^2{k}^{3-\frac{\alpha }{2}}{L}^{\frac{\alpha }{2}-1}\mathrm{\Gamma }\left(1-\frac{\alpha }{2}\right)\sin \left(\frac{\alpha \pi }{4}\right)\hfill \\ \times {\int }_{h_0}^{H}A\left(\alpha \right){\tilde{C}}_n^2\left(h\right){\left[\frac{\left(H-h\right)\left(h-h_0\right)}{{\left(H-h_0\right)}^2}\right]}^{\frac{\alpha }{2}-1}dh\hfill \\ \times \frac{1}{2\pi }{\int }_0^{2\pi }{\left(\frac{{\cos }^2\theta }{{\mu }_x^2}+\frac{{\sin }^2\theta }{{\mu }_y^2}\right)}^{\frac{\alpha }{2}-1}d\theta .\hfill \end{array}(26)$

Figure 3; Figure 4 present the variation of the scintillation index for the downlink and uplink against the function of the anisotropic tilt angle γ under different anisotropic factor μ and power law α values. It is to be noted that in the calculation, we have λ = 1.55 μm, L = 1,000 km, $C_n^2\left(0\right)=1\times 10^{-14}{\mathrm{m}}^{-2/3}$, h₀ = 0 m, and w = 30 m/s. As displayed in Figure 3; Figure 4, for different values of power law α and anisotropic factor μ, the scintillation index for the downlink and uplink first increase and then decay with the rising of the anisotropic tilt angle γ, and the curves are symmetric about the straight-line γ = 90°, so the anisotropic tilt angle γ is necessary in the vertical link. As mentioned before, anisotropic turbulence cells will change the focusing properties of the turbulence Toselli et al. [5]. Then, based on simple spatial geometry knowledge and the ellipsoid hypothesis of the turbulence cell, we can easily find that with the increasing of the anisotropic tilt angle γ, the radius of curvature for the interface between the propagated beam and the anisotropic turbulence cells first decays and then increases in the vertical link. In addition, with the change of the radius of curvature, the deviation effect of turbulence on the propagated beam is first strengthened and then weakened. Hence, the anisotropic tilt angle γ is necessary in the vertical link. In addition, the symmetry of the curves about the straight-line γ = 90° is consistent with the ellipsoid hypothesis of the turbulence cell, so our model is self-consistent.

FIGURE 3

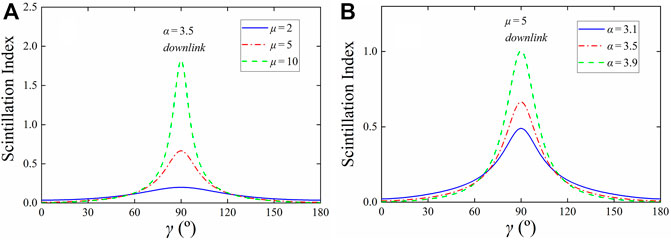
FIGURE 3. Scintillation index of the downlink versus the anisotropic tilt angle γ. (A) With various anisotropic factor μ values; (B) with various power law α values.

FIGURE 4

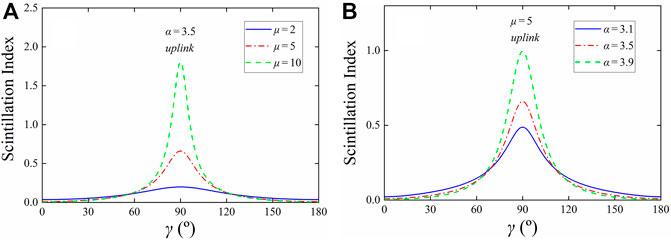
FIGURE 4. Scintillation index of the uplink versus the anisotropic tilt angle γ. (A) With various anisotropic factor μ values; (B) with various power law α values.

3 Conclusion

In this study, the anisotropic non-Kolmogorov turbulence spectra in the presence of the anisotropic tilt angle γ are developed for the horizontal and vertical links. Then, based on these spectra, the analytical expressions of the scintillation index for the weak anisotropic non-Kolmogorov horizontal and vertical links are derived. The calculation results indicate that for different values of power law α, anisotropic factors μ_x and μ_y and the variation of the anisotropic tilt angle γ has almost no effect on the scintillation index for the horizontal link. In addition, for different values of power law α and anisotropic factor μ, the scintillation index for the downlink and uplink first increase and then decay with the rising of the anisotropic tilt angle γ, and the curves are symmetric about the straight-line γ = 90°. Therefore, the anisotropic tilt angle γ is necessary in the vertical link, but not in the horizontal link. It should be noted that this study will benefit the construction of the atmospheric turbulence model and the understanding of optical wave transmission in anisotropic non-Kolmogorov links.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

CZ proposed the project. CZ conducted the equation derivation, simulation, and image processing. CZ wrote the manuscript.

Funding

This study was supported by the National Natural Science Foundation of China under Grant 61901097.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Andrews LC, Phillips RL Laser Beam Propagation through Random Media. Bellingham, WA, USA: SPIE Optical Engineering Press (2005).

Google Scholar

2. Manning R An Anisotropic Turbulence Model for Wave Propagation Near the Surface of the Earth. IEEE Trans Antennas Propagat (1986) 34:258–61. doi:10.1109/tap.1986.1143797

CrossRef Full Text | Google Scholar

3. Procaccia I, Constantin P Non-Kolmogorov Scaling Exponents and the Geometry of High Reynolds Number Turbulence. Phys Rev Lett (1993) 70:3416–9. doi:10.1103/physrevlett.70.3416

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Belen’kii MS, Barchers JD, Karis SJ, Osmon CL, Brown JM, Fugate RQ Preliminary Experimental Evidence of Anisotropy of Turbulence and the Effect of Non-kolmogorov Turbulence on Wavefront Tilt Statistics. Proc SPIE (1999) 3762:396–406.

Google Scholar

5. Toselli I, Agrawal B, Restaino S Light Propagation through Anisotropic Turbulence. J Opt Soc Am A (2011) 28:483–8. doi:10.1364/josaa.28.000483

CrossRef Full Text | Google Scholar

6. Andrews LC, Phillips RL, Crabbs R Propagation of a Gaussian-Beam Wave in General Anisotropic Turbulence. Proc SPIE (2014) 9224:922402. doi:10.1117/12.2061892

CrossRef Full Text | Google Scholar

7. Kessar M, Plunian F, Stepanov R, Balarac G. Non-Kolmogorov cascade of Helicity-Driven Turbulence. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 92:031004. doi:10.1103/PhysRevE.92.031004

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Cui L, Xue B, Zhou F Generalized Anisotropic Turbulence Spectra and Applications in the Optical Waves' Propagation through Anisotropic Turbulence. Opt Express (2015) 23:30088–103. doi:10.1364/oe.23.030088

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wang F, Toselli I, Li J, Korotkova O Measuring Anisotropy Ellipse of Atmospheric Turbulence by Intensity Correlations of Laser Light. Opt Lett (2017) 42:1129–32. doi:10.1364/ol.42.001129

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Beason M, Smith C, Coffaro J, Belichki S, Spychalsky J, Titus F, et al. Near Ground Measure and Theoretical Model of Plane Wave Covariance of Intensity in Anisotropic Turbulence. Opt Lett (2018) 43:2607–10. doi:10.1364/ol.43.002607

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zhai C Fiber-coupling Efficiency of a Gaussian-Beam in Anisotropic Non-kolmogorov Turbulence in the Presence of Random Angular Jitter. Results Phys (2020) 16:102985. doi:10.1016/j.rinp.2020.102985

CrossRef Full Text | Google Scholar

12. Roşu IA, Cazacu MM, Ghenadi AS, Bibire L, Agop M On a Multifractal Approach of Turbulent Atmosphere Dynamics. Front Earth Sci (2020) 8:216.

Google Scholar

13. Xu G, Lai J Average Capacity Analysis of the Underwater Optical Plane Wave over Anisotropic Moderate-To-strong Oceanic Turbulence Channels with the Málaga Fading Model. Opt Express (2020) 28:24056–68. doi:10.1364/oe.400988

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Xu G, Lai J Scintillation index and BER Performance for Optical Wave Propagation in Anisotropic Underwater Turbulence under the Effect of Eddy Diffusivity Ratio. Appl Opt (2020) 59:2551–8. doi:10.1364/ao.382628

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Andrews LC, Phillips RL, Crabbs R, Wayne D, Leclerc T, Sauer P Atmospheric Channel Characterization for ORCA Testing at NTTR. Proc SPIE (2010) 7588:80–91. doi:10.1117/12.842441

CrossRef Full Text | Google Scholar

16. Zhai C, Tan L, Yu S, Cao Y, Ma J Fiber Coupling Efficiency in Non-kolmogorov Satellite Links. Opt Commun (2015) 336:93–7. doi:10.1016/j.optcom.2014.09.063

CrossRef Full Text | Google Scholar