Stability and Controllability of Various Spatial Solitons in Exciton–Polariton Condensates by a Composite Pumping

We investigate the stability and controllability of one-dimensional bright and dark solitons, and two-dimensional bright solitons and vortices with the charges m = 1 and 2, respectively, in a nonresonantly incoherent pumped exciton–polariton condensates. A composite pumping, consisting of the constant part and the Bessel-type spatially modulating part, is introduced to balance the gain and loss. We demonstrate that the pumping can not only stabilize all these solitons but also modulate the profiles of these solitons. We also find that all these solitons obtained in this study are different from the ones in the previous studies. Our work may pave a way to modulate these solitons in the nonresonantly pumped exciton–polariton system.

1 Introduction

In semiconductor microcavities, exciton–polariton condensates can be formed at a few Kelvin or even at room temperature [1–5]. The strong light–matter interaction [6] observed in the exciton–polariton condensates allows it to be an ideal platform to study quantum nonequilibrium physics and exotic properties of high-orbital condensates [7]. These novel properties are also very important to form various nonlinear phenomena, such as bistability [8, 9], information processing [10–12], pattern formation [13–15], artificial polariton molecules [16], chaos [17], quantum vortices [18–25], and spatial solitons [21, 22, 26–38].

Spatial solitons are formed by balancing the diffraction and nonlinearity. There are rich nonlinear physics and important practical applications [39, 40]. The lattice solitons [41], defect solitons [42], interface kink solitons [43], and surface lattice solitons [44] had been found in the (1 + 1)-dimensional saturated nonlinear Schrödinger equation (SNLSE). And in the coherent atomic media, the (2 + 1) dimensional [(2 + 1) D ] SNLSE [45] (or cubic–quintic nonlinear Schrödinger equation [46]) was researched. The bright ground solitons, vortices [47], and double-hump solitons [48] have been found in the [(2 + 1) D] SNLSE, and lattice solitons [41] and discrete solitons [49] have also been obtained in the SNLSE in which there was a periodical modulation potential in the denominator of the saturable nonlinear term. However, except for the bright ground solitons and lattice solitons [41], all others solitons are unstable. In a recent study, a high-dimensional SNLSE including a trapping potential was constructed and various stable nonlinear modes [50] were obtained.

In the nonresonant incoherent exciton–polariton condensations with the homogeneous pumping, dark solitons are unstable, and it would disappear after evolution in a short time for one- [32] and two-dimensional [33] systems. The spatially periodic [22], ring-shaped [15, 23, 35], and Gaussian-shaped [21, 30, 31] pumping have been proposed to stabilize solitons. However, the balance between the nonlinear gain and the constant loss is not realized, so the stability of solitons is still an open question.

Under the adiabatic approximation of reservoir density, the exciton–polariton condensates can be described by SNLSE with the Kerr nonlinear term and the gain and loss terms, so the formations and stability of nonlinear modes in this system are of particular interest, and the mechanisms are also very complex. When we discuss the nonlinear excitations (such as solitons and vortices) on the basis of homogeneous condensates, it is difficult to realize the balance between the nonlinear gain and the invariable constant loss. Recently, we proposed the composite pumping including the constant part and Gaussian-type spatially modulating part to balance the gain and loss, and generate the stable nonlinear modes [38]. But the roles of constant pumping and spatial modulating pumping had not been elaborated carefully.

In this study, we construct a nonresonant composite pumping, consisting of the constant part and the Bessel-type spatially modulating part, to balance the nonlinear gain and the invariable loss. Then, the Gross–Pitaevskii equations described the dynamics of the exciton–polariton condensates are solved, and the one-dimensional bright and dark solitons and two-dimensional bright solitons and vortices with different charges are obtained. Their stability is proved by the linear stability analysis and evolution, and their controllability is discussed. And we find that the balance or near balance between gain and loss is the necessary condition for the stability of solitons with the nonzero homogeneous background. In addition, we also find that the spatial modulated pumping can be used to modulate the profiles of solitons.

The article is organized as follows. In Section 2, the model under study is introduced. In Section 3, various soliton solutions, their properties, and their stabilities are discussed. In the last section, the main results are summarized.

2 Model

Using the mean-field theory, the dynamics of two-dimensional exciton–polariton condensates are described by using a dissipative Gross–Pitaevskii equation for the polariton field Ψ and the rate equation of the density of the excitonic reservoir n_R:

$\begin{array}{ccc}\hfill & \hfill & i\hslash \frac{\partial \mathrm{\Psi }}{\partial t}=\left[-\frac{{\hslash }^2}{2m^{*}}\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)+g_C|\mathrm{\Psi }{|}^2+g_R{n}_R+i\frac{\hslash }{2}\left(R{n}_R-{\gamma }_C\right)\right]\mathrm{\Psi },\hfill \end{array}(1)$

$\begin{array}{ccc}\hfill & \hfill & \frac{\partial n_R}{\partial t}=P_u\left(\mathbf{r}\right)-\left({\gamma }_R+R|\mathrm{\Psi }{|}^2\right)n_R,\hfill \end{array}(2)$

where P_u(r) is the nonresonant optical pumping; m* is the effective polariton mass of the lower polariton branch; γ_C and γ_R are the polariton and exciton loss rates, respectively; R is the condensation rate; g_C represents the strength of the nonlinear interaction between polaritons; and g_R is the interaction strength between polaritons and reservoir excitons. The nonresonant pumping is constructed by P_u(r) = P₀ + P₁J_n(r/w₀), which consists of a cw field P₀ and Bessel-type field, respectively, J_n denotes the n-order Bessel function, r = x for one-dimensional system, and $r=\sqrt{x^2+y^2}$ for the two-dimensional system.

The dimensionless forms of Eqs 1, 2 can be written as

$\begin{array}{ccc}\hfill i\frac{\partial u}{\partial s}& =\hfill & -{\nabla }_{\perp }^{\prime 2}u-{\sigma }_1|u{|}^{2}u-{\sigma }_{2}nu+i\left({\sigma }_{3}n-{\sigma }_4\right)u,\hfill \end{array}(3)$

$\begin{array}{ccc}\hfill \frac{\partial n}{\partial s}& =\hfill & {\sigma }_{5}P\left(\mathbf{r}\right)-{\sigma }_5\left(1+{\sigma }_6|u{|}^2\right)n,\hfill \end{array}(4)$

where s = t/τ₀, (ξ, η) = (x/R_x, y/R_y), u = Ψ/ψ₀, $n=n_R/n_R^0$, w = w₀/R_x, ${\nabla }_{\perp }^{\prime 2}={\partial }^2/\partial {\xi }^2+{\delta }^2{\partial }^2/\partial {\eta }^2$, δ = R_x/R_y, and $P(\mathbf{r})={\sigma }_7+{\sigma }_8{J}_n(\frac{\sqrt{{\xi }^2+{\eta }^2/{\delta }^2}}{w})$, with ${\tau }_0(\equiv 2m^{*}{R}_x^2/\hslash )$, R_{x, y}, ${\psi }_0^2$, and $n_R^0$ being, respectively, characteristic time, the width of quantum well layers in x, y directions, the condensate density, and the reservoir density. These coefficients in Eqs 3, 4 are ${\sigma }_1=-g_C{\psi }_0^2{\tau }_0/\hslash$, ${\sigma }_2=-g_R{n}_R^0{\tau }_0/\hslash$, ${\sigma }_3=R{n}_R^0{\tau }_0/2$, σ₄ = γ_Cτ₀/2, σ₅ = γ_Rτ₀, ${\sigma }_6=R{\psi }_0^2/{\gamma }_R$, ${\sigma }_7=\frac{P_0}{n_R^0{\gamma }_R}$, and σ₈ = σ₇P₁/P₀. The characteristic time τ₀ = 5.45 × 10^{–10 s} can be obtained by the parameters in Ref. [32].

Here, if R_x = R_y, this model is (2 + 1) dimensional, that is, the quantum well layers are sandwiched between the two distributed Bragg reflectors [2]. If R_x ≪ R_y, δ ≪ 1, the effect of ∂²/∂η² can be neglected, so Eqs 3, 4 are reduced to quasi (1 + 1) dimensional, such as the nanowire system [32].

3 Soliton Solutions and Their Properties

The linear properties of Eqs 3, 4 have been discussed in Ref. [38]. To obtain the stationary soliton solutions, we substitute u(ξ, η, s) = ψ(ξ, η) exp(iβs) and n(ξ, η, s) = n′(ξ, η) into Eqs 3, 4, and obtain

$-\beta \psi +{\nabla }_{\perp }^{\prime 2}\psi +{\sigma }_1|\psi {|}^2\psi +{\sigma }_2{n}^{\prime }\psi -i\left({\sigma }_3{n}^{\prime }-{\sigma }_4\right)\psi =0,(5)$

where $n^{\prime }=\frac{P(\mathbf{r})}{1+{\sigma }_6|\psi {|}^2}$. By using the Newton conjugate gradient method [51], the profiles and power $P^{\prime }=\int {\int }_{-\infty }^{+\infty }|\psi {|}^{2}d\xi d\eta$ or the renormalized power $P^{\prime }=\int {\int }_{-\infty }^{+\infty }\Vert \psi {|}^2-|{\psi }_0{|}^2|d\xi d\eta$ (mainly for the solitons with background) of the soliton solutions are obtained, and ψ₀ is the amplitude of the background. The stability of the soliton solutions ψ can also be analyzed by introducing the perturbations $u(\xi ,\eta ,s)=\{\psi (\xi ,\eta )+ϵ[v_1(\xi ,\eta )e^{\lambda s}+v_2^{*}(\xi ,\eta )e^{{\lambda }^{*}s}]\}{e}^{i\beta s}$, $n(\xi ,\eta ,s)=n^{\prime }+ϵ[v_3(\xi ,\eta )e^{\lambda s}+v_3^{*}(\xi ,\eta )e^{{\lambda }^{*}s}]$, where v₁, v₂, and v₃ are the normal modes and λ is the corresponding eigenvalue of the perturbations, and solving the eigenvalue problem as shown in Ref. [38]. In general, we use the parameters σ₁ = −1, σ₂ = 0.3, σ₃ = 0.15, σ₄ = 0.1, σ₅ = 1, and σ₆ = 4, which are obtained by substituting the parameters in [32] into these formulas given Eq. 4.

3.1 The Soliton Solutions for One-Dimensional System

We discuss the one-dimensional soliton solutions of Eq. 5 and their stability first. The nonlinear modes are excited on a homogeneous background of the steady condensate wave function for the bright and dark solitons. The bright solitons are with a zero background, and the dark solitons are with a nonzero homogeneous background, so the physical mechanisms to generate and stabilize these bright solitons and dark solitons are different. For them, the nonlinear saturated gain term cannot be balanced by the constant loss directly, so an inhomogeneous pumping is necessary to stabilize them. For the dark solitons, the inhomogeneous pumping can not only be used as an external potential but also suppress the nonlinear saturated gain caused by the nonlinear excitation. Meanwhile, the homogeneous pumping suppresses the constant loss for the soliton. For the bright ones, the competitions between the inhomogeneous pumping, nonzero homogeneous background of the steady condensate wave function, and the gain and loss are complicated. Here, we choose the 0-order Bessel inhomogeneous pumping and w = 2.5 to find the one-dimensional bright and dark solitons.

Using the Newton conjugate gradient method [51], we first find the soliton solutions of Eq. 5, then make the linear stability analyses, and evolve the obtained solitons by Eqs 3, 4. The bright solitons with β = 0.35 and their stability are shown in Figure 1. From the profiles of bright solitons, since a dip contributes to the nonlinear saturated gain term, σ₈ > 0 is taken to compensate the loss. Figures 1A–D illustrate the power and stability curves as a function of the homogeneous pumping σ₇ (the inhomogeneous pumping σ₈). From the power curves in Figure 1B, one can find positive inhomogeneous pumping is necessary to generate the bright solitons. Although there are stable bright solitons, the stable ranges for the parameters σ_7,8 are narrow, as shown in Figures 1C,D. In Figures 1E,G, the red solid lines denote the profiles |ψ| of the steady states by solving Eq. 5, the green dashed lines denote the profiles of pumping. From them, we find the pumping can modulate the profiles of the bright solitons. In the center of Figure 1E, the highest peak of the soliton profile is fully in agreement with the highest peak of the pump, and the two side peaks of the soliton profile are also in agreement with the side peaks of pumping. And in the center of Figure 1G, the highest peaks of the soliton profile and pump are also concordant, but the second and third side peaks of pumping are coincident with the second and third side valleys of the soliton profile. Thus, the profiles of pumping can be used to reconstruct the shapes of bright solitons.

FIGURE 1

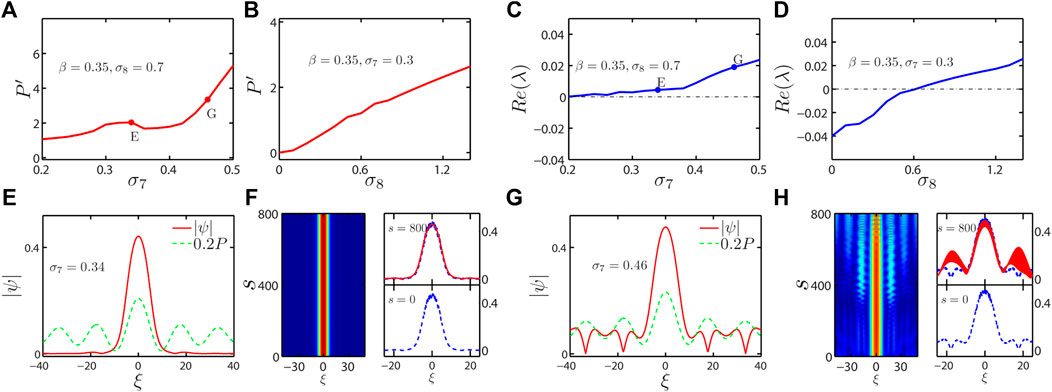
FIGURE 1. (Color online) (A–D) Power and stability curves of the bright solitons as a function of σ₇ (σ₈). (E,G) Profiles of the bright solitons with the different σ₇ marked by the dots and the letters E and G in (A,C). The red solid lines denote the profiles |ψ| of the nonlinear steady states obtained by solving Eq. 5. The green dashed lines denote one-fifth of the pumping P. (F,H) The projections and profiles of the evolution results. In the left panels, the projections are shown. The profiles of the evolution results at the special times s are shown in the right panels. The blue dashed lines are the initial profiles after adding the random perturbations.

The stability is proved further by a numerical evolution of Eqs 3, 4, and adding the random perturbations into the initial values of evolution, that is, the initial value is taken as u(s = 0, ξ, η) = ψ(ξ, η) (1 + ɛρ₁) and n(s = 0, ξ, η) = n′(ξ, η) (1 + ɛρ₂), where ɛ = 0.1, ρ_1,2 are the random variables uniformly distributed in the interval [0, 1], and s = 100 denotes 54.5 ns. In Figures 1F,H, the projections of the evolution results are shown in the left panels, and the blue dashed lines and the red solid lines denote the profiles of the evolution results at the times s = 0 and s = 800 in the right panels, respectively. The evolution results are in agreement with the results of the stability analyses. The profile of the bright soliton can conserve perfectly even after evolution 436 ns from the numerical results in Figure 1F.

There are the Kerr nonlinearity terms, saturated nonlinearity terms, and the composite pumping terms in Eqs 3, 4, so it is possible to support the bright solitons and dark solitons simultaneously in the exciton–polariton condensate system. Since a hump contributes to the nonlinear saturated gain term due to the profiles of the dark solitons, the coefficient of inhomogeneous pumping should be σ₈ < 0 for reducing the gain. Figures 2A,B illustrate the power curves as a function of the homogeneous pumping σ₇ and the inhomogeneous pumping σ₈, respectively, here, β = 0.1. Figure 2C shows the stability curves as a function of σ₇ and σ₈. For explaining the reason of soliton stability, we introduce $I={\int }_{-\infty }^{+\infty }({\sigma }_{3}n-{\sigma }_4)d\xi$ to denote the intensity of the total gain and loss. In Figure 2D, the intensity I as a function of σ₇ and σ₈ is shown. We find that the value of I is close to zero when the soliton is stable. The small value means that the balance or near balance between the nonlinear gain and constant loss is realized. From the power curves in Figure 2B, one can find that the negative inhomogeneous pumping supports the dark solitons, very narrow intervals of σ₈ > 0 also support the dark solitons. And the stable ranges of parameters σ_7,8 are both narrow. In Figures 2E,G, the red solid lines (the blue dashed dotted lines) denote the profiles |ψ| (the phases ϕ) of soliton solutions by solving Eq. 5. And the green dashed lines denote the intensity of pumping. From them, it is obvious that the profiles of dark solitons are modulated by pumping.

FIGURE 2

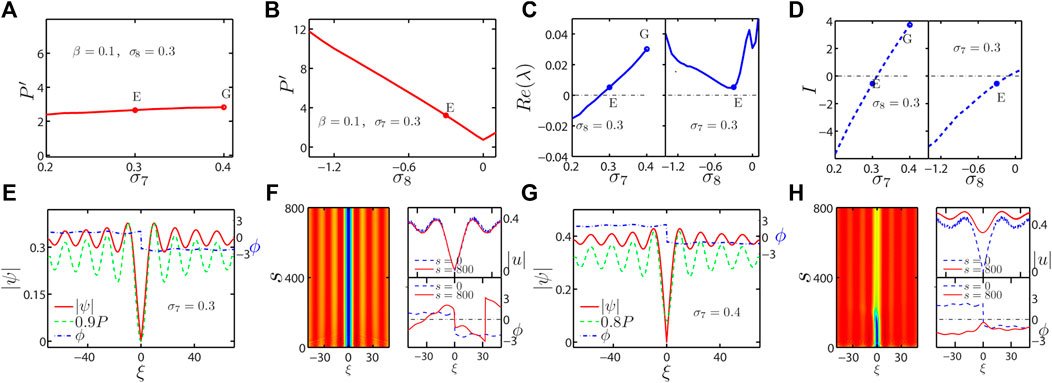
FIGURE 2. (Color online) (A,B) Power curves of the dark solitons as a function of σ₇ and σ₈, respectively. (C) Stability curves of the dark solitons as a function of σ₇ (left panel) and σ₈ (right panel). (D) The intensity I of the total gain and loss as a function of σ₇ (left panel) and σ₈ (right panel). (E,G) Profiles of the dark solitons with the different σ₇ marked by the dots and the letters E and G in (A–D). The red solid lines (the blue dashed-dotted lines) denote the profiles |ψ| (phases ϕ) of the nonlinear steady states obtained by solving Eq. 5. The green dashed lines denote the pumping P after multiplying 0.9. (F,H) The projections and profiles of the evolution results. Projections are shown in the left panels. The profiles |u| and the phases ϕ of the evolution results at the special times s are shown in the right panels. The blue dashed lines are the initial values of evolution after adding the random perturbations.

The evolution results are shown in Figures 2F,H, the projections of evolution results are shown in the left panels, the evolution results of s = 0 (s = 800) are denoted by the red solid lines (the blue dashed lines) in the right panels. From the phase ϕ of the right panels in Figure 2F, the profiles of dark solitons in s = 0 and s = 800 are in agreement very well, and the phase jump still keeps obviously after evolution 436 ns. The phase jump will disappear with the increasing evolution times when the dark solitons are unstable, as shown in Figure 2H.

From the aforementioned results, the homogeneous and inhomogeneous parts of pumping are both very important to generate and stabilize the bright and dark solitons. Furthermore, the inhomogeneous part can also be used to modulate the shapes of nonlinear solitons. And the small intensity I is very important for the stability of dark solitons, that is, the balance between the nonlinear gain and constant loss is very important to stabilize dark solitons.

3.2 The Soliton Solutions for Two-Dimensional System

It is very interesting to find stable high-dimensional solitons and control them in exciton–polariton models (3) and (4). In this subsection, we study the properties of high-dimensional spatial solitons. Here, we take the second-order Bessel-type pumping and w = 1 in the inhomogeneous pumping.

The two-dimensional bright solitons are shown in Figure 3 with β = 0.35. Figures 3A–D show the power and stability curves as a function of σ₇ (σ₈). From them, we not only obtain the parameters ranges supporting the two-dimensional bright solitons but also show the stability of these solitons. Figures 3E–H are the profiles and evolutions of the two-dimensional bright solitons, respectively. In these insets, the red solid lines, the green dashed lines, and the blue dashed lines are the cross sections of the profiles of the initial bright solitons, the profiles of the pumping, and the profiles after the evolution s, respectively. From Figure 3E, we find that there are three rings in the profile of the bright soliton, which we do not find in the previous reports about soliton solutions of the exciton–polariton system, and the positions of the rings are consistent with those of the ring of pumping by the insets. After taking the different parameters as shown in Figure 3G, many more rings appear in the profile of the bright soliton.

FIGURE 3

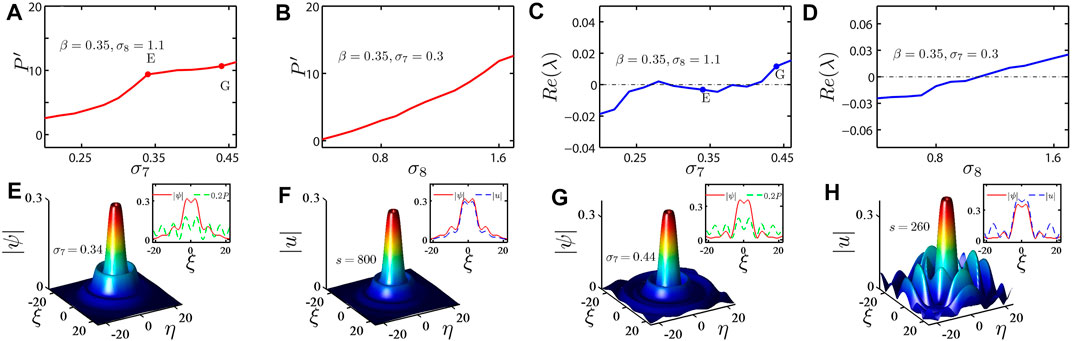
FIGURE 3. (Color online) (A–D) Power and stability curves of the two-dimensional bright solitons as a function of σ₇ (σ₈). (E,G) Profiles of the bright solitons with the different σ₇ marked by the dots and the letters E and G in (A,C). In the insets, the red solid lines denote the cross sections of the profiles by taking η = 0. The green dashed lines denote one-fifth of the pumping P. (F,H) The profiles of the evolution results. The cross sections of the profiles are shown in the insets by taking η = 0. The blue dashed lines denote the cross sections of the evolution results at the special times s. The red solid lines are the initial values of evolution after adding the random perturbations.

We also find the vortex solitons by imprinting a phase factor exp(imθ) ($\theta =\arctan \frac{\eta }{\xi }$ is the azimuthal coordinate) onto the initial trial solutions. Although there exist the vortices in the exciton–polariton system, it is still interesting to study how to enhance the stability of the vortices and control the shapes of the vortices.

In Figure 4, we show the vortices with m = 1 and their stability. The power and stability curves as a function of σ_{7, 8} are shown in Figures 4A–B. Figure 4C shows the stable intervals of the vortices with m = 1 as a function of σ₇ and σ₈; Figure 4D is the intensity I of the total gain and loss as a function of σ₇ and σ₈, and Figures 4E–H are the profiles and the evolutions, respectively. Comparing Figure 4A with Figure 4B, despite there are the wide parameter intervals of σ₇ to support the vortices, the parameter ranges to stabilize them are very narrow. However, the situation is different for parameter σ₈, we find the vortices with m = 1 are stable in the whole ranges of σ₈ < 0, as shown in Figure 4B, and unstable for σ₈ > 0. And the vortex is also stable even in the absence of the inhomogeneous pumping (in the case of σ₈ = 0). Thus, for the case of m = 1, all these vortices are stable as long as σ₈ ≤ 0. The results are also consistent with the intensity curves, as shown in Figure 4D. From the insets of Figure 4E, the top one is the phase of vortex, and in the bottom one, the red solid line and the green dashed line are the cross sections of the profiles of the initial vortex and one of the pumping. From this, we also find every fluctuation of the profile is consistent with that of the pump.

FIGURE 4

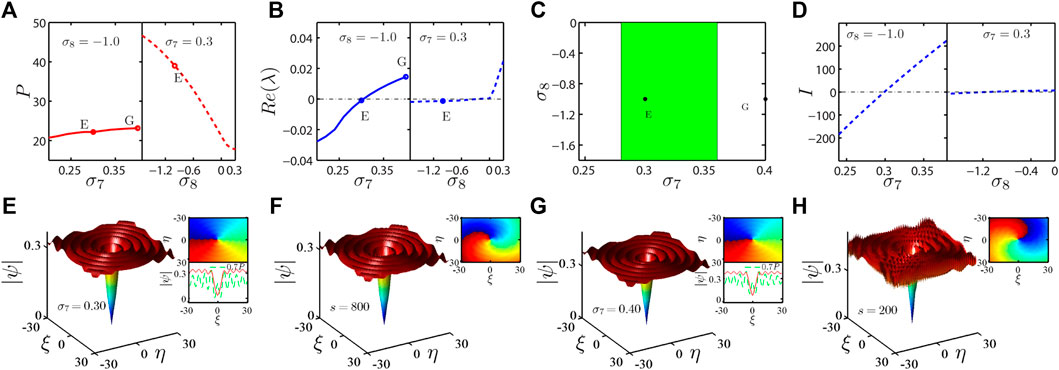
FIGURE 4. (Color online) (A) Power curves of the vortices with m = 1 as a function of σ₇ (left panel) and σ₈ (right panel). (B) Stability curves of the vortices with m = 1 as a function of σ₇ (left panel) and σ₈ (right panel). (C) Stable intervals of vortices with m = 1 as a function of σ₇ and σ₈. (D) The intensity I of the total gain and loss as a function of σ₇ (left panel) and σ₈ (right panel). (E–H) Profiles and evolution results of the vortices with the different σ₇ marked by dots and the letters E and G in (A–C). In these insets, the top ones show the phases of the vortices, the bottom ones are the cross sections of the profiles denoted by the red solid lines, and pumping after multiplying 0.7 is denoted by the green dashed lines.

Furthermore, we also investigate the vortices with m = 2 in Figure 5. The power and stability curves as a function of σ_{7, 8} are shown in Figures 5A–B. Figure 5C shows the stable intervals of the vortices with m = 2 as a function of σ₇ and σ₈, and Figure 5D shows the intensity I of the total gain and loss as a function of σ₇ and σ₈. Figures 5E–H are the profiles and the evolutions, respectively. Comparing Figure 5 with Figure 4, one can find the existence ranges of the vortices are the same, and the tendency of the stability curves is also the same, whereas the stability is different. Through the stability analyses, it is obvious that the vortices of σ₈ < − 0.3 are stable for m = 2. However, from the intensity I curves as shown in the right panel of Figure 5D, the value of I is small in the whole intervals of σ₈, but there is only the stable interval of σ₈ < − 0.3. It is obvious that the small value of I is necessary and is not a sufficient condition of soliton stability. Thus, we see that the inhomogeneous pumping is very important for stabilizing the higher charged vortices.

FIGURE 5

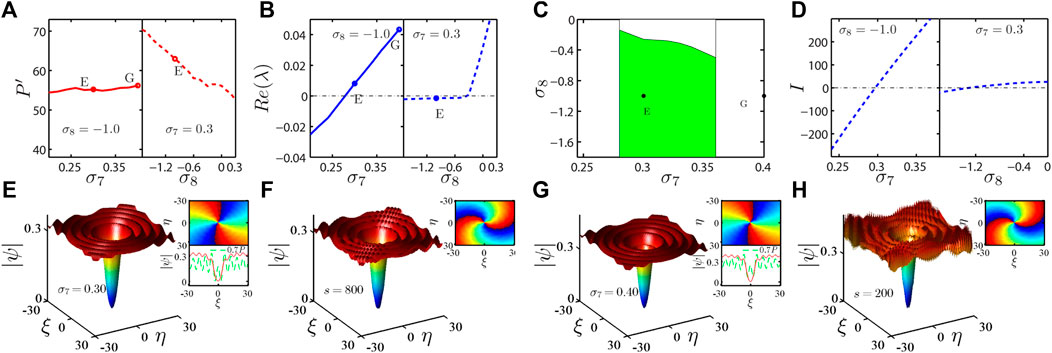
FIGURE 5. (Color online) (A) Power curves of the vortices with m = 2 as a function of σ₇ (left panel) and σ₈ (right panel). (B) Stability curves of the vortices with m = 2 as a function of σ₇ (left panel) and σ₈ (right panel). (C) Stable intervals of the vortices with m = 2 as a function of σ₇ and σ₈. (E–H) Profiles and evolution results of the vortices with the different σ₇ marked by the dots and the letters E, G in (A–C). In these insets, the top ones show the phases of the vortices, the bottom ones are the cross sections of the profiles denoted by the red solid lines, and pumping after multiplying 0.7 is denoted by the green dashed lines.

4 Summary

In conclusion, the stability and controllability of one- and two-dimensional spatial solitons have been discussed by introducing the nonresonant pumping in exciton–polariton condensates. The introduced pumping contains the homogeneous part that balances the constant loss, in addition to the inhomogeneous Bessel-type spatially modulating part that compensates the gain or loss caused by the denominator of the nonlinear saturated gain term. The bright and dark solitons in the one-dimensional system, and the bright solitons and vortices with m = 1 and m = 2 in the two-dimensional system have been found. These solitons could be stabilized by engineering the homogeneous and inhomogeneous pumping. The intensity of the total gain and loss could be used as the necessary condition of soliton stability. And in the parameter regions of the stable soliton, the bright solitons can be excited by initial Gaussian or sech functions with the similar amplitude and width to the stable bright solitons, the dark solitons can be excited by the initial tanh function with the similar background and width to the stable black solitons, or by the phase imprinting method. And the vortex solitons can be excited by imprinting a phase factor exp(imθ) onto a trial function with the similar amplitude and width to the stable vortex solitons. In addition, we have also found that the Bessel-type inhomogeneous pumping could be used to control the profiles of nonlinear modes. The results presented here may be useful for understanding the physical properties of the condensates out of equilibrium and guiding the experimental studying of the condensate solitons, which may have potential applications in polariton condensates for information storages and processing or quantum simulators.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by the National Natural Science Foundation of China (Nos. 11835011 and 12074343) and the Natural Science Foundation of Zhejiang Province of China (No. LZ22A050002).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Deng H, Weihs G, Santori C, Bloch J, Yamamoto Y. Condensation of Semiconductor Microcavity Exciton Polaritons. Science (2002) 298:199–202. doi:10.1126/science.1074464

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Kasprzak J, Richard M, Kundermann S, Baas A, Jeambrun P, Keeling JMJ, et al. Bose-Einstein Condensation of Exciton Polaritons. Nature (2006) 443:409–14. doi:10.1038/nature05131

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Balili R, Hartwell V, Snoke D, Pfeiffer L, West K. Bose-Einstein Condensation of Microcavity Polaritons in a Trap. Science (2007) 316:1007–10. doi:10.1126/science.1140990

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Deng H, Haug H, Yamamoto Y. Exciton-polariton Bose-Einstein Condensation. Rev Mod Phys (2010) 82:1489–537. doi:10.1103/RevModPhys.82.1489

CrossRef Full Text | Google Scholar

5. Christopoulos S, von Högersthal GBH, Grundy AJD, Lagoudakis PG, Kavokin AV, Baumberg JJ, et al. Room-temperature Polariton Lasing in Semiconductor Microcavities. Phys Rev Lett (2007) 98:126405. doi:10.1103/PhysRevLett.98.126405

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Carusotto I, Ciuti C. Quantum Fluids of Light. Rev Mod Phys (2013) 85:299–366. doi:10.1103/RevModPhys.85.299

CrossRef Full Text | Google Scholar

7. Kim NY, Kusudo K, Wu C, Masumoto N, Löffler A, Höfling S, et al. Dynamical D-Wave Condensation of Exciton-Polaritons in a Two-Dimensional Square-Lattice Potential. Nat Phys (2011) 7:681–6. doi:10.1038/NPHYS2012

CrossRef Full Text | Google Scholar

8. Bajoni D, Semenova E, Lemaître A, Bouchoule S, Wertz E, Senellart P, et al. Optical Bistability in a GaAs-Based Polariton Diode. Phys Rev Lett (2008) 101:266402. doi:10.1103/PhysRevLett.101.266402

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Goblot V, Nguyen HS, Carusotto I, Galopin E, Lemaître A, Sagnes I, et al. Phase-controlled Bistability of a Dark Soliton Train in a Polariton Fluid. Phys Rev Lett (2016) 117:217401. doi:10.1103/PhysRevLett.117.217401

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Liew TCH, Kavokin AV, Shelykh IA. Optical Circuits Based on Polariton Neurons in Semiconductor Microcavities. Phys Rev Lett (2008) 101:016402. doi:10.1103/PhysRevLett.101.016402

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Adrados C, Liew TCH, Amo A, Martín MD, Sanvitto D, Antón C, et al. Motion of Spin Polariton Bullets in Semiconductor Microcavities. Phys Rev Lett (2011) 107:146402. doi:10.1103/PhysRevLett.107.146402

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Ballarini D, De Giorgi M, Cancellieri E, Houdré R, Giacobino E, Cingolani R, et al. All-optical Polariton Transistor. Nat Commun (2013) 4:1778. doi:10.1038/ncomms2734

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Borgh MO, Keeling J, Berloff NG. Spatial Pattern Formation and Polarization Dynamics of a Nonequilibrium Spinor Polariton Condensate. Phys Rev B (2010) 81:235302. doi:10.1103/PhysRevB.81.235302

CrossRef Full Text | Google Scholar

14. Luk MH, Tse YC, Kwong NH, Leung PT, Lewandowski P, Binder R, et al. Transverse Optical Instability Patterns in Semiconductor Microcavities: Polariton Scattering and Low-Intensity All-Optical Switching. Phys Rev B (2013) 87:205307. doi:10.1103/PhysRevB.87.205307

CrossRef Full Text | Google Scholar

15. Li G. Azimuthons and Pattern Formation in Annularly Confined Exciton-Polariton Bose-Einstein Condensates. Phys Rev A (2016) 93:013837. doi:10.1103/PhysRevA.93.013837

CrossRef Full Text | Google Scholar

16. Johnston A, Kalinin KP, Berloff NG. Artificial Polariton Molecules. Phys Rev B (2021) 103:L060507. doi:10.1103/PhysRevB.103.L060507

CrossRef Full Text | Google Scholar

17. Ruiz-Sánchez R, Rechtman R, Rubo YG. Autonomous Chaos of Exciton-Polariton Condensates. Phys Rev B (2020) 101:155305. doi:10.1103/PhysRevB.101.155305

CrossRef Full Text | Google Scholar

18. Liew TCH, Kavokin AV, Shelykh IA. Excitation of Vortices in Semiconductor Microcavities. Phys Rev B (2007) 75:241301. doi:10.1103/PhysRevB.75.241301

CrossRef Full Text | Google Scholar

19. Rubo YG. Half Vortices in Exciton Polariton Condensates. Phys Rev Lett (2007) 99:106401. doi:10.1103/PhysRevLett.99.106401

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Voronova NS, Lozovik YE. Excitons in Cores of Exciton-Polariton Vortices. Phys Rev B (2012) 86:195305. doi:10.1103/PhysRevB.86.195305

CrossRef Full Text | Google Scholar

21. Ostrovskaya EA, Abdullaev J, Desyatnikov AS, Fraser MD, Kivshar YS. Dissipative Solitons and Vortices in Polariton Bose-Einstein Condensates. Phys Rev A (2012) 86:013636. doi:10.1103/PhysRevA.86.013636

CrossRef Full Text | Google Scholar

22. Ma X, Egorov OA, Schumacher S. Creation and Manipulation of Stable Dark Solitons and Vortices in Microcavity Polariton Condensates. Phys Rev Lett (2017) 118:157401. doi:10.1103/PhysRevLett.118.157401

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Ma X, Schumacher S. Vortex-vortex Control in Exciton-Polariton Condensates. Phys Rev B (2017) 95:235301. doi:10.1103/PhysRevB.95.235301

CrossRef Full Text | Google Scholar

24. Dominici L, Carretero-González R, Gianfrate A, Cuevas-Maraver J, Rodrigues AS, Frantzeskakis DJ, et al. Interactions and Scattering of Quantum Vortices in a Polariton Fluid. Nat Commun (2018) 9:1467. doi:10.1038/s41467-018-03736-5

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Alperin SN, Berloff NG. Multiply Charged Vortex States of Polariton Condensates. Optica (2021) 8:301–7. doi:10.1364/OPTICA.418377

CrossRef Full Text | Google Scholar

26. Yulin AV, Egorov OA, Lederer F, Skryabin DV. Dark Polariton Solitons in Semiconductor Microcavities. Phys Rev A (2008) 78:061801. doi:10.1103/PhysRevA.78.061801

CrossRef Full Text | Google Scholar

27. Egorov OA, Skryabin DV, Yulin AV, Lederer F. Bright Cavity Polariton Solitons. Phys Rev Lett (2009) 102:153904. doi:10.1103/PhysRevLett.102.153904

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Sich M, Krizhanovskii DN, Skolnick MS, Gorbach AV, Hartley R, Skryabin DV, et al. Observation of Bright Polariton Solitons in a Semiconductor Microcavity. Nat Photon (2012) 6:50–5. doi:10.1038/nphoton.2011.267

CrossRef Full Text | Google Scholar

29. Grosso G, Nardin G, Morier-Genoud F, Léger Y, Deveaud-Plédran B. Dynamics of Dark-Soliton Formation in a Polariton Quantum Fluid. Phys Rev B (2012) 86:020509. doi:10.1103/PhysRevB.86.020509

CrossRef Full Text | Google Scholar

30. Ostrovskaya EA, Abdullaev J, Fraser MD, Desyatnikov AS, Kivshar YS. Self-localization of Polariton Condensates in Periodic Potentials. Phys Rev Lett (2013) 110:170407. doi:10.1103/PhysRevLett.110.170407

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Tanese D, Flayac H, Solnyshkov D, Amo A, Lemaître A, Galopin E, et al. Polariton Condensation in Solitonic gap States in a One-Dimensional Periodic Potential. Nat Commun (2013) 4:1749. doi:10.1038/ncomms2760

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Xue Y, Matuszewski M. Creation and Abrupt Decay of a Quasistationary Dark Soliton in a Polariton Condensate. Phys Rev Lett (2014) 112:216401. doi:10.1103/PhysRevLett.112.216401

CrossRef Full Text | Google Scholar

33. Smirnov LA, Smirnova DA, Ostrovskaya EA, Kivshar YS. Dynamics and Stability of Dark Solitons in Exciton-Polariton Condensates. Phys Rev B (2014) 89:235310. doi:10.1103/PhysRevB.89.235310

CrossRef Full Text | Google Scholar

34. Cilibrizzi P, Ohadi H, Ostatnicky T, Askitopoulos A, Langbein W, Lagoudakis P. Linear Wave Dynamics Explains Observations Attributed to Dark Solitons in a Polariton Quantum Fluid. Phys Rev Lett (2014) 113:103901. doi:10.1103/PhysRevLett.113.103901

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Kulczykowski M, Bobrovska N, Matuszewski M. Bright Sink-type Localized States in Exciton-Polariton Condensates. Phys Rev B (2015) 91:245310. doi:10.1103/PhysRevB.91.245310

CrossRef Full Text | Google Scholar

36. Kol GR. Breather-type Solitons in Exciton-Polariton Microcavities. Eur Phys J Plus (2017) 132:530. doi:10.1140/epjp/i2017-11802-4

CrossRef Full Text | Google Scholar

37. Hivet R, Flayac H, Solnyshkov DD, Tanese D, Boulier T, Andreoli D, et al. Half-solitons in a Polariton Quantum Fluid Behave like Magnetic Monopoles. Nat Phys (2012) 8:724–8. doi:10.1038/NPHYS2406

CrossRef Full Text | Google Scholar

38. Zhang K, Wen W, Lin J, Li H-j. Generation and Stability of Diversiform Nonlinear Localized Modes in Exciton-Polariton Condensates. New J Phys (2021) 23:033011. doi:10.1088/1367-2630/abe79f

CrossRef Full Text | Google Scholar

39. Stegeman GI, Segev M. Optical Spatial Solitons and Their Interactions: Universality and Diversity. Science (1999) 286:1518–23. doi:10.1126/science.286.5444.1518

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Paz-Alonso MJ, Michinel H. Superfluidlike Motion of Vortices in Light Condensates. Phys Rev Lett (2005) 94:093901. doi:10.1103/PhysRevLett.94.093901

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Efremidis NK, Hudock J, Christodoulides DN, Fleischer JW, Cohen O, Segev M. Two-dimensional Optical Lattice Solitons. Phys Rev Lett (2003) 91:213906. doi:10.1103/PhysRevLett.91.213906

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Yang J, Chen Z. Defect Solitons in Photonic Lattices. Phys Rev E (2006) 73:026609. doi:10.1103/PhysRevE.73.026609

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Huang C, Zheng J, Zhong S, Dong L. Interface Kink Solitons in Defocusing Saturable Nonlinear media. Opt Commun (2011) 284:4225–8. doi:10.1016/j.optcom.2011.04.062

CrossRef Full Text | Google Scholar

44. Zhan K, Li X. Surface Lattice Solitons in Saturable Nonlinear media Driven by the Quadratic Electro-Optic Effect. Opt Commun (2013) 307:80–5. doi:10.1016/j.optcom.2013.06.010

CrossRef Full Text | Google Scholar

45. Li H-j., Dong L, Hang C, Huang G. Gain-assisted High-Dimensional Self-Trapped Laser Beams at Very Low Light Levels. Phys Rev A (2011) 83:023816. doi:10.1103/PhysRevA.83.023816

CrossRef Full Text | Google Scholar

46. Michinel H, Paz-Alonso MJ, Pérez-García VM. Turning Light into a Liquid via Atomic Coherence. Phys Rev Lett (2006) 96:023903. doi:10.1103/PhysRevLett.96.023903

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Dreischuh A, Paulus GG, Zacher F, Grasbon F, Walther H. Generation of Multiple-Charged Optical Vortex Solitons in a Saturable Nonlinear Medium. Phys Rev E (1999) 60:6111–7. doi:10.1103/PhysRevE.60.6111

CrossRef Full Text | Google Scholar

48. Yang J. Internal Oscillations and Instability Characteristics Of(2+1)-Dimensional Solitons in a Saturable Nonlinear Medium. Phys Rev E (2002) 66:026601. doi:10.1103/PhysRevE.66.026601

CrossRef Full Text | Google Scholar

49. Fleischer JW, Segev M, Efremidis NK, Christodoulides DN. Observation of Two-Dimensional Discrete Solitons in Optically Induced Nonlinear Photonic Lattices. Nature (2003) 422:147–50. doi:10.1038/nature01452

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Zhang K, Liang Y-z., Lin J, Li H-j. Controlling the Stability of Nonlinear Optical Modes via Electromagnetically Induced Transparency. Phys Rev A (2018) 97:023844. doi:10.1103/PhysRevA.97.023844

CrossRef Full Text | Google Scholar

51. Yang J. Numerical Methods for Nonlinear Wave Equations. In: R Haberman, editor. Nonlinear Waves in Integrable and Nonintegrable Systems. Philadephia: SIAM (2011). p. 327–403.

Google Scholar