Correlation Between Avalanches and Emitted Energies During Fracture With a Variable Stress Release Range

We observe the failure process of a fiber bundle model with a variable stress release range, γ, and higher the value of γ, lower the stress release range. By tuning γ from low to high, it is possible to go from the mean-field (MF) limit of the model to the local load-sharing (LLS) limit where local stress concentration plays a crucial role. In the MF limit, individual avalanches (number of fibers breaking in going from one stable state to the next, s) and the corresponding energies E emitted during those avalanches have one-to-one linear correlation. This results in the same size distributions for both avalanches (P(s)) and energy bursts (Q(E)): a scale-free distribution with a universal exponent value of −5/2. With increasing γ, the model enters the LLS limit beyond some γ_c. In this limit, due to the presence of local stress concentrations around a damaged region, such correlation C(γ) between s and E decreases, i.e., a smaller avalanche can emit a large amount of energy or a large avalanche may emit a small amount of energy. The nature of the decrease in the correlation between s and E depends highly on the dimension of the bundle. In this work, we study the decrease in the correlation between avalanche size and the corresponding energy bursts with an increase in the load redistribution localization in the fiber bundle model in one and two dimensions. Additionally, we note that the energy size distribution remains scale-free for all values of γ, whereas the avalanche size distribution becomes exponential for γ > γ_c.

1 Introduction

Disordered materials, when subjected to external stress, go through local damages that eventually emerge as a catastrophic fracture when the load exceeds a critical value. These breaking events, called avalanches, are usually detected as acoustic emissions [1]. Systematic statistical analysis of the time series of these events has led to a considerable insight into the failure dynamics of disordered samples across scales. In particular, the scale-free nature of the size distribution of these avalanches has motivated a “critical phenomenal” description of fracture processes. From laboratory-scale experiments to earthquake statistics, the Guttenberg–Richter-like law is widely and accurately verified [2, 3]. The statistics of damage avalanches and the corresponding emitted energies are studied also in other systems such as dislocation dynamics and magnetic systems. both theoretically and experimentally [4–7].

The advantage of having a critical phenomenal description is that the dynamics are expected to be independent of the microscopic details of the individual systems studied and will depend on a few parameters such as the dimensionality of the system, the interaction range, and order parameter definition (see, for e.g., [8]). This means simplified models with very few parameters should be able to reproduce the “critical description” of these avalanching phenomena. Indeed, there have been many such attempts. Some well-explored models in this regard include the fiber bundle model [9], the random fuse model [10], and Burridge–Knopoff model for earthquakes [11]. There are also multiple efforts in molecular dynamics simulations to obtain scale-free avalanche statistics (see, for e.g., [12] for a review).

The two quantities, avalanche size and the corresponding energy bursts, are generally distinct. While the former gives a measure of the area opened up during a fracture event (or the number of spins changing orientation in a disordered magnetic system under an external field), the latter gives a measure of the (strain) energy released due to such events. Depending on how the avalanche size is defined in a system, a generally nonlinear relationship can be obtained between avalanche size and energy burst. This relationship has been studied analytically using mean-field models, numerically using lattice models or discrete elements models, and also experimentally in rupture cascades in laboratories and earthquakes for crackling noise in magnetic domains [7]. While the average values of energy bursts (⟨E⟩) and avalanche sizes or damage (⟨s⟩) are known in those systems, in this work, we focus on how does the individual correspondence between the avalanche size and energy of a particular event vary with localization of load redistribution in the context of the fiber bundle model in one and two dimensions. It was noted earlier [13] that in the extreme limit of the nearest neighbor load sharing, those avalanches of large sizes can have small energy release and vice versa. In terms of the size distribution functions, the avalanche size distribution is exponential, but the energy distribution is a power law. It was also shown recently in a rock deformation experiment through a combination of acoustic energy measurement and an in situ x-ray imaging of the microstructure that local strain and the corresponding acoustic emission amplitudes can be uncorrelated [14]. This can be attributed to changes in the local stiffness in a damaged region in the experiment. As for the theoretical modeling is concerned, tuning the range of load redistribution in the fiber bundle model can shed light on this phenomenon. Therefore, in this work, we systematically explore the intermediate ranges between the nearest neighbor and the equal load-sharing limits and study the correspondence of avalanche size and energy bursts and their size distributions.

In the fiber bundle model, the mode of failure depends mainly on two factors: the strength of disorder in the individual failure threshold of the fibers and the range of stress release [15–18] when one such fiber is broken. Such interplay between disorder and damage nucleation not only affects the failure mode but also influences the spatial correlation during the failure process [17–20]. The range of stress release has two extreme limits, viz. the equal and nearest neighborhood load sharing. However, in most disordered materials, the effective mechanisms are in between these two extreme cases. Therefore, it is crucial to know to what extent one can infer the magnitude of one of these quantities when the other quantity is known. In this work, we study the fiber bundle model in one and two dimensions with variable ranges of load sharing. We look at the distributions of the avalanche size and energy. We also look at the correlation measures for the time series of avalanche sizes and the corresponding energy bursts as a function of the range of stress release. We show that as soon as localization in the load redistribution is introduced, the one-to-one linear correspondence between the avalanche size and the corresponding energy bursts decreases. The nature of decreases and the size distribution of the two quantities depend strongly on the dimensionality of the model.

2 Description of the Fiber Bundle Model

The fiber bundle model has been proven to be a very useful yet very simple model to study failure processes in disordered systems. It has gained a lot of attention among engineers, material scientists, and physicists after its introduction by Pierce in 1926 [9]. A conventional fiber bundle model of size L consists of L parallel Hookean fibers for 1d and L × L fibers in 2d, placed vertically between two supporting clamps (1d) or plates (2d). The clamps/plates are pulled apart by a force F, creating stress f = F/N per fiber. Here, N is the total number of fibers. For 1d, N = L, and for 2d, N = L². The disorder is introduced within the model as fluctuation of failure strength values in the individual fibers. In the present work, such strength values (h) are chosen from a uniform distribution between (0, 1). A certain fiber i will break irreversibly if the applied stress σ(i) on that fiber crosses its threshold value h(i). The load carried by the broken fibers is then redistributed to the other surviving fibers. As mentioned earlier, the two extreme limits of such redistribution schemes are the global or equal load sharing (all surviving fibers get an equal fraction of the redistributed load [9, 21]) and the nearest neighbor load sharing (only the nearest neighbors share the redistributed load) [22–28].

Here, we have adopted an intermediate load-sharing scheme that interpolates continuously between these two extreme limits [17, 29]. If σ_i is the stress of the ith broken fiber, then for a certain fiber j, the local stress profile after redistribution will obey the following rule:

${\sigma }_j\to {\sigma }_j+\frac{r_{ij}^{-\gamma }}{Z}{\sigma }_i(1)$

where r_ij is the distance between the fibers i and j. Z is the normalization factor given by

$Z=\sum _k{r}_{ik}^{-\gamma }(2)$

where k runs over all surviving fibers. With the present rule, a high γ stands for a low-stress release range and hence closer to the LLS scheme. On the other hand, for low γ, the model enters the ELS or mean-field limit. Earlier studies pointed out a critical γ_c for both one- [17] and two-dimensional [29] fiber bundle model around which this transition from LLS to ELS limit takes place. The values of γ_c for one and two dimensions are 4/3 and 2.15 ± 0.05, respectively [17]. After such redistribution, other fibers can break due to the elevated local stress profile, and the stress is again redistributed. This starts an avalanche at the same external stress. The size s of an avalanche is the number of fibers broken until the system reaches the next stable configuration (loads on all surviving fibers are lower than their respective failure thresholds). The energy emitted during an avalanche of size s is represented as follows:

$E\left(s\right)=\sum _1^s\frac{1}{2}{h}_i^2(3)$

where h_i’s are the threshold values of the s broken fibers during the avalanche. An average energy ⟨E⟩ can be calculated then by averaging overall E values corresponding to a certain avalanche size s. The total bundle might break through a single avalanche, or it can come to a stable state after an avalanche. In the latter case, we increase the applied stress just to break the next weakest fiber and start a new avalanche. This process goes on until all fibers are broken.

3 Numerical Results

Numerically, we have studied both one- and two-dimensional fiber bundle models with a variable stress release range, characterized by γ (Eq. 1). The system sizes vary from 10³ to 10⁵ for one dimension and from 50 × 50 to 300 × 300 for two dimensions. The failure threshold distribution for the fibers is kept uniform in (0, 1). The value of γ was increased from 0 to 8, which allows us to explore the whole region between ELS to LLS, during the failure process.

We start by observing the relation between s and ⟨E⟩ with variation in γ. This will give us an idea about the correlation that the avalanche size and the energy has in between. Such correlation is then explored explicitly through a correlation function C(γ) and compared with s vs. ⟨E⟩ behavior. Finally, the distribution of avalanches and emitted energies are shown, and a connection between them is established through the correlation function.

3.1 Relation Between s and E

As mentioned earlier, in experiments and theory, the relationship between s and E are well studied (see, for e.g., [4, 7]). Here, we study this relation and also the correlations between an avalanche and the corresponding energy in the fiber bundle models.

Figure 1 shows the scatter plot of the avalanche size s and the corresponding energy emission E for each avalanche event. The emitted energy for a certain avalanche is defined by Eq. 3. We have explored this s vs. E behavior for the low-stress (γ = 4 for 1d and γ = 8 for 2d) as well as high-stress release range (γ = 0.1 for both 1d and 2d). For the lower value of γ, the model is in the mean-field limit while for the higher γ value, the model is close to the LLS scheme. The upper panel of Figure 1 shows the results for one dimension and the lower one for the two dimensions.

FIGURE 1

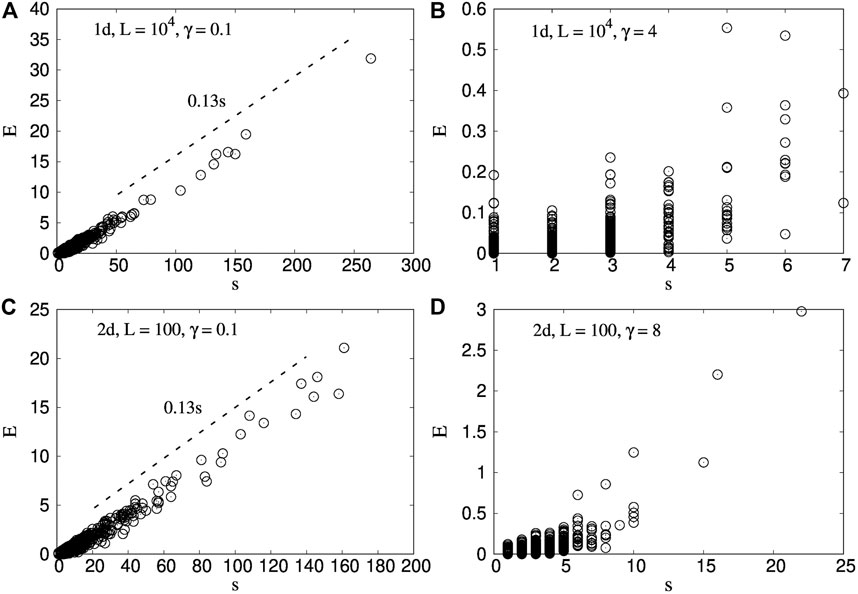
FIGURE 1. Variation of avalanche size s with corresponding emitted energy E for (A) γ = 0.1 and (B) 4.0 in case of a 1d bundle and for (C) γ = 0.1 and (D) 8.0 in case of a 2d bundle. There is a high correlation between s and E for low γ (ELS limit). The plot is rather scattered with a relatively low correlation when γ is high (LLS limit). Though this trend is same for both dimensions, the scatter seems less as we go to the higher dimension.

We observe that when γ is low, E increases with s linearly. A recent article [13] has already discussed such correlation between avalanche size and emitted energy in the mean-field limit of the model, which we obtain here by keeping a high range (hence low γ) of load redistribution. On the other hand, when γ is high, the plot of s vs. E shows a scatter with a relatively lower correlation between the two quantities. Such a decrease in the correlation with γ is observed for both one and two dimensions of the model. This is in line with recent experimental observations in rock deformation, where local strain and acoustic emissions were measured contemporaneously [14] and found to be uncorrelated i.e., larger avalanches can emit low energies and vice versa. A more quantitative analysis of the correlation measures observed here is discussed later on.

Figure 2 shows the distributions Q_s(E) of E for a given value of s for two values of γ (0 and 4) in the one dimension. The distributions are skewed (can be fitted with the Weibull form in some cases), but the averages are well defined. The skewness is high for high γ, where the local stress concentration is prominent. In this limit, Q_s(E) fits well with a Weibull distribution. At low γ, on the other hand, Q_s(E) is fitted with both the Gaussian and Weibull distribution for high s, while the distribution is more like a Weibull when s is low.

FIGURE 2

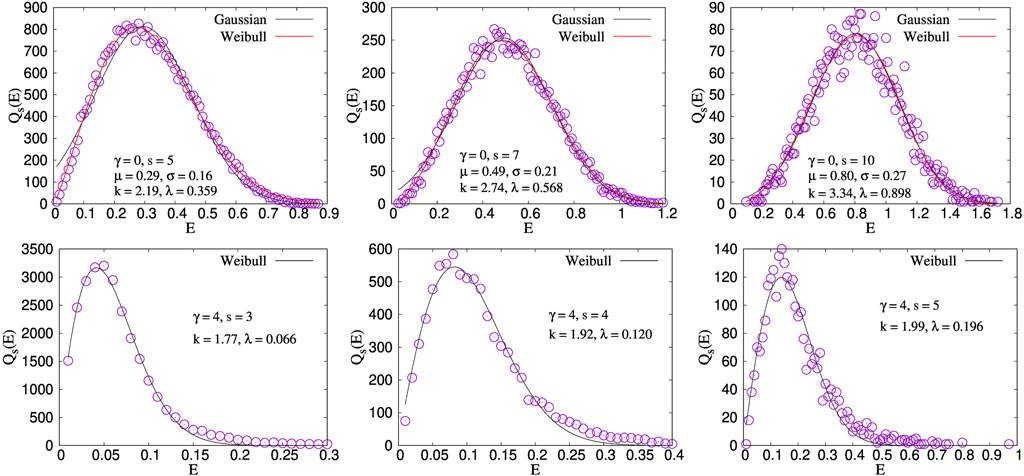
FIGURE 2. Distributions of the energies emitted for a given avalanche size for two values of γ (0 and 4) are shown for the simulations in one dimension. The distributions are fitted with both the Gaussian $\left(Q_s(E)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{1}{2}{(\frac{E-\mu }{\sigma })}^2}\right)$ as well as Weibull $\left(Q_s(E)=(k/\lambda ){(E/\lambda )}^{k-1}{e}^{-{(E/\lambda )}^k}\right)$ distribution. The fitting is better with Weibull distribution, unless the value of s is very high where Q_s(E) can be fitted with both distributions. While the distributions are skewed, the averages (⟨E⟩) are well defined, which is what we used for the subsequent results.

Figure 3 shows the variation of the avalanche size s with an average energy ⟨E⟩ corresponding to s. ⟨E⟩ is calculated by averaging overall energy values that are associated with a certain avalanche size s. The difference between this figure and Figure 1 is that in the former all energy values for a particular avalanche are shown, while here only the average of those values is shown. When the γ value is low, we observe ⟨E⟩∼ s for large values of ⟨E⟩, and a nonlinear part corresponding to low ⟨E⟩. The linearity for low γ exists because the model is in the mean-field limit where s and E are highly correlated (as can be seen qualitatively in Figure 1). On the other hand, for high γ, the bundle breaks long before we observe any linear behavior between s and ⟨E⟩. Only the initial nonlinear part is observed in this case. The fact that ⟨E⟩ is not linear with s for high γ is also reflected by the scattered behavior of E with s. For this nonlinear part, the variation of s and ⟨E⟩ is ⟨E⟩∼ s^β, with an exponent, which is dependent on γ, β ≡ β(γ). For large values of γ, β = 2.5, which was also seen in [13] for the LLS scheme, i.e., γ → ∞. We will again come back to this linear and nonlinear relationship between s and ⟨E⟩ while discussing the distributions of avalanche sizes and emitted energies.

FIGURE 3

FIGURE 3. Variation of ln s with ln ⟨E⟩ for the (A) 1d and (B) 2d FBM with different values of γ as indicated. For low values of γ, a linear relation is observed. For γ > γ_c, there is a nonlinear relationship, viz. ⟨E⟩∼ s^β, with an exponent, which is dependent on γ, β ≡ β(γ). For high values of γ, β ≈ 2.5, as also seen in Ref. [13].

3.2 Study of the Distributions P(s) and Q(E)

In this section, we will discuss how the distribution of avalanche sizes and energies behaves as the stress release range γ is varied. The upper panel of Figure 4 shows the results for one dimension while the results in the lower panel correspond to two dimensions. We denote distribution of avalanche sizes by P(s) and distribution of energies by Q(E).

FIGURE 4

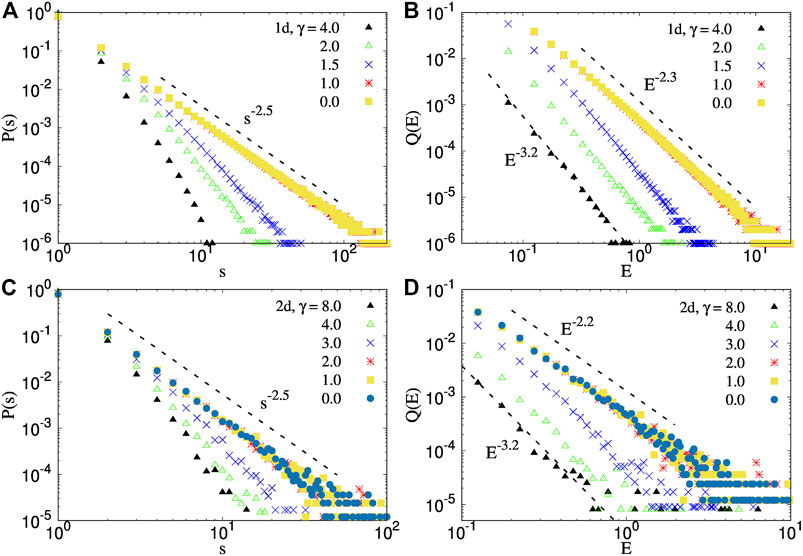
FIGURE 4. Distribution of the avalanche sizes P(s) and energies Q(E) with s and E, respectively, when γ is varied between 0.1 and 8.0. (A,B) show the distributions P(s) and Q(E) in 1d, respectively. The same for 2d is shown in (C,D). L = 10⁵ for 1d, and a bundle of size 300 × 300 is used for 2d. For both 1d and 2d, P(s) is a power-law distribution below γ_c and an exponential distribution above γ_c. Q(E), on the other hand, remains scale-free for both dimensions irrespective of the value of γ, though the value of the exponent changes with γ when γ > γ_c.

We observe the following behavior for P(s) and Q(E) with a variation in γ in the model:

• For low γ (ELS limit), both P(s) and Q(E) are scale-free distributions with a universal exponent of −5/2, as predicted in the mean-field calculations. This is shown in Figures 4A,B for 1d and in Figures 4C,D for 2d. This is due to the fact that in this limit, ⟨E⟩∼ s, and the distribution of E should be exactly similar to the distribution of s which is a scale-free distribution with an exponent −5/2 in the ELS limit [30].

• When γ is very high, Q(E) is a scale-free distribution in spite of the fact that the distribution P(s) is an exponential [31] here. This is due to the lack of correlation between s and E which is presented in Figures 1, 3.

• Throughout the entire range of γ, the energy distribution is a power law ($Q(E)$∼$E^{-{\tau }_E}$), while the avalanche size distribution is a power law ($P(s)$∼$s^{-{\tau }_s}$) for γ < γ_c and exponential for γ > γ_c.

• It is possible to show that τ_E = β(γ) + 1 [13], assuming the aforementioned nonlinear relation between s and ⟨E⟩ and P(s) to be an exponential distribution. We see here that this scaling form is in fact generally valid for γ > γ_c (see Figure 5). β is a continuously varying function of γ which makes τ_E also vary with γ.

FIGURE 5

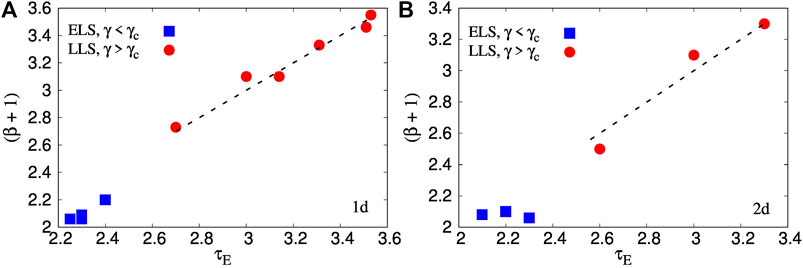
FIGURE 5. Plot of τ_E and β(γ) + 1 showing a numerical validation of the scaling form τ_E = β(γ) + 1 for γ > γ_c. This is a more general form of the particular case seen in Ref. [13], where β(γ → ∞) = 2.5. γ_c = 4/3 for 1d [18] and 2.15 for 2d [18].

3.3 Correlation Function

Finally, we reach a point where we can discuss the correlation between the individual avalanches s and the corresponding energy emitted E, quantitatively. For this, we have calculated the Pearson correlation function and defined a correlation coefficient C(γ) as

$C\left(\gamma \right)=\frac{n\left(\sum s_n.E_n\right)-\left(\sum s_n\right)\left(\sum E_n\right)}{\sqrt{\left[n\sum \underset{n}{\overset{2}{s}}-{\left(\sum s_n\right)}^2\right]\left[n\sum \underset{n}{\overset{2}{E}}-{\left(\sum E_n\right)}^2\right]}}(4)$

where n is total number of avalanches excluding the final one during the failure of the bundle. s₁, s₂, … , s_n are burst sizes of 1st, 2nd, … , nth avalanche and the corresponding emitted energies are given as E₁, E₂, … , E_n, respectively.

Figure 6 shows how the correlation function C(γ) behaves as γ increases. The left and the right figures show the results for one- and two-dimensional FBM, respectively. When γ is low, C(γ) has a value closer to 1.0. This supports our earlier claim that s and E have a high correlation at low γ, which corresponds to the ELS or mean-field limit of the model. Similarly, at high γ, where the model is in the LLS limit, a relatively smaller value of C(γ) suggests a lesser correlation between s and E. This decrease of C(γ) takes place around the critical value of γ_c around which the ELS to LLS transition is observed. When the size of the bundle is increased, C(γ) shifts to a higher value at low γ and a lower value at high γ, suggesting a sharper decay of C(γ) around γ_c. Such effect of the system size is more visible in the one-dimensional case due to the higher range of sizes accessible here. Doing the same for two dimensions will computationally be much more costly. Also, notice that the value of C(γ) in the LLS limit is higher for two dimensions as the increase in the dimension brings the model closer to the mean-field limit.

FIGURE 6

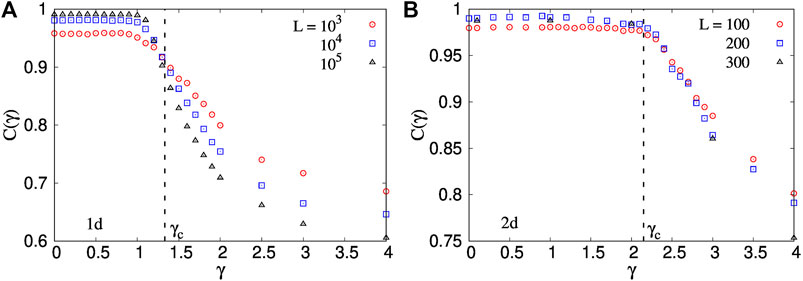
FIGURE 6. Variation of the correlation function C(γ) is shown with γ for the (A) 1d and (B) 2d fiber bundle model. For γ < γ_c, s and E have high correlation among themselves which is visible in Figure 1 as well. For γ > γ_c, C(γ) falls to a lower value suggesting low s − E correlation. γ_c = 4/3 for 1d [18] and 2.15 for 2d [18]. The results for 1d is shown for L = 10³, 10⁴, and 10⁵ while the results for 2d are shown for L = 100, 200, and 300.

4 Discussion and Conclusion

In driven disordered systems in general and fracture propagation in particular, an avalanche of size s corresponds to the opening up of a fractured surface (or reorientation of magnetic spins in a disordered magnetic system), while the corresponding energy burst E is the strain energy released, usually in the form of acoustic emission. In experiments and theory, the usually nonlinear relationship between these two quantities has been extensively studied (see, for e.g., [4, 7]). In this work, we have studied the changes in this relationship with the variation in the range of stress release following a local failure, using the fiber bundle model as a prototypical example. In particular, we assess the correlation between the individual avalanches and the corresponding energy bursts, as a function of this stress release range (parameterized by γ in Eq. 1). We show that the correlation decreases from a value close to 1.0 (fully correlated) in the mean-field limit (γ → 0) to a significantly lower value in the nearest neighbor load-sharing limit, for both one and two dimensions. This is in line with recent experimental observations [14] in rock deformations, where an in situ measurement of a large change in the local strains (through x-ray imaging) did not always correspond with a large acoustic emission and vice versa.

In the fiber bundle model, the failure mode depends on the range of stress release, once the disorder distribution is fixed in a moderate range (uniform in (0, 1) here). The reason for the different modes of failure is the competition of damage progression due to stress localization near an already damaged region and vulnerable spots at some distance from the damaged region. While the first mechanism promotes a nucleation-driven failure, the latter leads toward percolative damage. The critical range that separates these two limits has been studied elsewhere [17, 18]. The underlying mechanism is not only valid for the fiber bundle model [17–20] but also seen in the random fuse model [32, 33] and in molecular dynamics simulations [34]. The present study is a manifestation of these two competing effects. Indeed, for a wide range of stress release, load increases on almost all elements, and hence the weaker among those elements break first. Given that there is no spatial correlation between the failure thresholds of the fibers, the damage is percolative. When the load redistribution range is more localized (for higher γ values), the correspondence between an avalanche size and the corresponding energy burst decreases. Indeed, we see that beyond a critical value γ_c, which depends on the dimension of the model, the correlation between avalanche and energy drops drastically. Incidentally, this is also where the size distribution of avalanches becomes exponential from the power-law behavior for γ < γ_c.

Specifically, we have plotted s vs. E in Figure 1, where a clear linearity is observed for a wide range of stress redistribution. But for localized ranges, the linearity is not present. The correlation between the two quantities drops from one as the stress release is localized. However, a positive correlation always remains, which is anyway expected. But, there could be individual events that are of larger sizes which still can emit relatively less energy. In the distribution functions, the differences are more apparent. For very high values of γ, the avalanche size distribution always remains exponential, but the energy distribution always shows a power-law behavior with a higher value of the exponent (see Figure 4) in both one and two dimensions. This highlights the fact that in the localized load sharing, one can see power-law distributions in energy, which is what is usually measured in the experiments, while the size distributions can already shift to exponential.

In conclusion, the interchangeability of the avalanche size and energy in the fiber bundle model is only valid when the stress release range is very wide. Specifically, this equivalence is not valid in the nucleation failure mode. However, not only that the correlations between the two quantities are less, but also the size distribution of the energy still shows a scale-free behavior where the avalanche size distribution may not, in both one and dimensions. Given that in real materials that the stress release range is always somewhat local, the observations here can explain the simultaneous existence of damage localization and scale-free distributions of emitted energies.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

NB has carried out numerical simulations in the 1d and 2d FBM and performed the data analysis. SB and SR formulated the problem. SR wrote the first draft of the manuscript and helped with the 1d simulation as well as data analysis. SB helped with simulation and data analysis as well as carried out the final edit of the manuscript to bring it to its present form. All authors have read and approved the manuscript.

Funding

SR was supported by the Research Council of Norway through its Centres of Excellence funding scheme, project number 262644.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bonamy D, Bouchaud E. Failure of Heterogeneous Materials: A Dynamic Phase Transition? Phys Rep (2011) 498:1–44. doi:10.1016/j.physrep.2010.07.006

CrossRef Full Text | Google Scholar

2. Kawamura H, Hatano T, Kato N, Biswas S, Chakrabarti BK. Statistical Physics of Fracture, Friction, and Earthquakes. Rev Mod Phys (2012) 84:839–84. doi:10.1103/revmodphys.84.839

CrossRef Full Text | Google Scholar

3. de Arcangelis L, Godano C, Grasso JR, Lippiello E. Statistical Physics Approach to Earthquake Occurrence and Forecasting. Phys Rep (2016) 628:1–91. doi:10.1016/j.physrep.2016.03.002

CrossRef Full Text | Google Scholar

4. Kun F, Varga I, Lennartz-Sassinek S, Main IG. Rupture Cascades in a Discrete Element Model of a Porous Sedimentary Rock. Phys Rev Lett (2014) 112:065501. doi:10.1103/PhysRevLett.112.065501

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Halton CG, Main IG, Meredith PG. A Comparison of Seismic and Structural Measurements of Scaling Exponents during Tensile Subcritical Crack Growth. J Struct Geology (1993) 15:1485.

Google Scholar

6. Minozzi M, Caldarelli G, Pietronero L, Zapperi S. Dynamic Fracture Model for Acoustic Emission. The Eur Phys J B - Condensed Matter (2003) 36:203–7. doi:10.1140/epjb/e2003-00336-7

CrossRef Full Text | Google Scholar

7. Salije EKH, Dahmen KA. Crackling Noise in Disordered Materials. Annu Rev Condens Matter Phys (2014) 5:233. doi:10.1146/annurev-conmatphys-031113-133838

CrossRef Full Text | Google Scholar

8. Bonamy D, Santucci S, Ponson L. Crackling Dynamics in Material Failure as the Signature of a Self-Organized Dynamic Phase Transition. Phys Rev Lett (2008) 101:045501. doi:10.1103/PhysRevLett.101.045501

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Pierce FT. Tensile Tests for Cotton Yarns, “The Weakest Link” Theorems on the Strength of Long and Composite Specimens. J Text Inst (1926) 17:355.

Google Scholar

10. de Arcangelis L, Redner S, Herrmann HJ. A Random Fuse Model for Breaking Processes. J Physique Lett (1985) 46:L585. doi:10.1051/jphyslet:019850046013058500

CrossRef Full Text | Google Scholar

11. Burridge R, Knopoff L. Model and Theoretical Seismicity. Bull Seismol Soc Am (1967) 57:341–71. doi:10.1785/bssa0570030341

CrossRef Full Text | Google Scholar

12. Bitzek E, Kermode JR, Gumbsch P. Atomistic Aspects of Fracture. Int J Fract (2015) 191:13–30. doi:10.1007/s10704-015-9988-2

CrossRef Full Text | Google Scholar

13. Roy S, Biswas S. Size Distribution of Emitted Energies in Local Load Sharing Fiber Bundles. Front Phys (2021) 9:643602. doi:10.3389/fphy.2021.643602

CrossRef Full Text | Google Scholar

14. Cartwright-Taylor A, Mangriotis M-D, Main I, Butler IB, Fusseis F, Ling M, et al. Seismic Events Miss Important Grain-Scale Mechanisms Governed by Kinematics during Shear Failure of Porous Rock (2021). doi:10.21203/rs.3.rs-1034813/v1

CrossRef Full Text | Google Scholar

15. Roy S, Ray P. Critical Behavior in Fiber Bundle Model: A Study on Brittle to Quasi-Brittle Transition. Europhysics Lett (2015) 112:26004. doi:10.1209/0295-5075/112/26004

CrossRef Full Text | Google Scholar

16. Roy S. Predictability and Strength of a Heterogeneous System: The Role of System Size and Disorder. Phys Rev E (2017) 96:042142. doi:10.1103/PhysRevE.96.042142

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Biswas S, Roy S, Ray P. Nucleation versus Percolation: Scaling Criterion for Failure in Disordered Solids. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 91:050105. doi:10.1103/PhysRevE.91.050105

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Roy S, Biswas S, Ray P. Modes of Failure in Disordered Solids. Phys Rev E (2017) 96:063003. doi:10.1103/PhysRevE.96.063003

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sinha S, Roy S, Hansen A. Phase Transitions and Correlations in Fracture Processes where Disorder and Stress Compete. Phys Rev Res (2020) 2:043108. doi:10.1103/physrevresearch.2.043108

CrossRef Full Text | Google Scholar

20. Roy S. From Nucleation to Percolation: The Effect of System Size when Disorder and Stress Localization Compete. Front Phys (2021) 9:752086. doi:10.3389/fphy.2021.752086

CrossRef Full Text | Google Scholar

21. Daniels HE. The Statistical Theory of Strength of Bundles of Threads. Proc R Soc London, Ser A (1945) 183:405.

Google Scholar

22. Phoenix SL. The Asymptotic Distribution for the Time to Failure of a Fiber Bundle. Adv Appl Probab (1979) 11:153–87. doi:10.1017/s0001867800031748

CrossRef Full Text | Google Scholar

23. Smith RL, Phoenix SL. Asymptotic Distributions for the Failure of Fibrous Materials under Series-Parallel Structure and Equal Load-Sharing. J Appl Mech (1981) 48:75–82. doi:10.1115/1.3157595

CrossRef Full Text | Google Scholar

24. Newman WI, Phoenix SL. Time-dependent Fiber Bundles with Local Load Sharing. Phys Rev E Stat Nonlin Soft Matter Phys (2001) 63:021507. doi:10.1103/PhysRevE.63.021507

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Harlow DG, Phoenix SL. The Chain-Of-Bundles Probability Model for the Strength of Fibrous Materials II: A Numerical Study of Convergence. J Compos Mater (1978) 12:314–34. doi:10.1177/002199837801200308

CrossRef Full Text | Google Scholar

26. Harlow DG, Phoenix SL. Probability Distributions for the Strength of Fibrous Materials under Local Load Sharing I: Two-Level Failure and Edge Effects. Adv Appl Probab (1982) 14:68–94. doi:10.1017/s0001867800036715

CrossRef Full Text | Google Scholar

27. Smith RL. Proc R Soc London, Ser A (1982) 382:179.

28. Sinha S, Kjellstadli JT, Hansen A. Local Load-Sharing Fiber Bundle Model in Higher Dimensions. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 92:020401. doi:10.1103/PhysRevE.92.020401

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Hidalgo RC, Moreno Y, Kun F, Herrmann HJ. Fracture Model with Variable Range of Interaction. Phys Rev E Stat Nonlin Soft Matter Phys (2002) 65:046148. doi:10.1103/PhysRevE.65.046148

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Hammer PC, Hansen A. The Distribution of Simultaneous Fiber Failures in Fiber Bundles. ASME J Appl Mech (1992) 59:909.

Google Scholar

31. Kloster M, Hansen A, Hemmer PC. Burst Avalanches in Solvable Models of Fibrous Materials. Phys Rev E (1997) 56:2615–25. doi:10.1103/physreve.56.2615

CrossRef Full Text | Google Scholar

32. Moreira AA, Oliveira CLN, Hansen A, Araújo NAM, Herrmann HJ, Andrade JS Fracturing Highly Disordered Materials. Phys Rev Lett (2012) 109:255701. doi:10.1103/physrevlett.109.255701

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Shekhawat A, Zapperi S, Sethna JP. From Damage Percolation to Crack Nucleation through Finite Size Criticality. Phys Rev Lett (2013) 110:185505. doi:10.1103/physrevlett.110.185505

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Yamaguchi Y, Biswas S, Hatano T, Goehring L. Failure Processes of Cemented Granular Materials. Phys Rev E (2020) 102:052903. doi:10.1103/PhysRevE.102.052903

PubMed Abstract | CrossRef Full Text | Google Scholar