Network Structures for Asset Return Co-Movement: Evidence From the Chinese Stock Market

This article focuses on the detailed network structure of the co-movement for asset returns. Based on the Chinese sector indices and Fama-French five factors, we conducted return decomposition and constructed a minimum spanning tree (MST) in terms of the rank correlation among raw return, idiosyncratic return, and factor premium. With the adoption of a rolling window analysis, we examined the static and time-varying characteristics associated with the MST(s). We obtained the following findings: 1) A star-like structure is presented for the whole sample period, in which market factor MKT acts as the hub node; 2) the star-like structure changes during the periods for major market cycles. The idiosyncratic returns for some sector indices would be disjointed from MKT and connected with their counterparts and other pricing factors; and 3) the effectiveness of pricing factors are time-varying, and investment factor CMA seems redundant in the Chinese market. Our work provides a new perspective for the research of asset co-movement, and the test of the effectiveness of empirical pricing factors.

1 Introduction

Co-movement refers to the correlated or similar movement of two or more entities. In finance, the co-movement of asset returns is crucial to the cross-sectional diversification and management of systematic risk. It also affects the way shocks are transmitted and thus the level of systemic risk [1]. Understanding the co-movement for asset returns is essential and beneficial in the academic field and practical investment. According to the seminal work by Ref. [2], asset co-movement could be decomposed into two parts. One part is “reasonable” co-movement, which is related to the fundamentals of assets. And the other part is “excess” co-movement, or “friction-based” co-movement, which is linked to investor sentiment and is beyond the explanation of fundamental change with respect to the assets. Motivated by Ref. [2], a strand of ensuing studies have been carried out in the literature, with the adoption of the indicators in terms of R² or its variants derived from the regression on the market performance [1, 3–5].

However, most literature has concentrated more on the co-movement between individual assets and market performance rather than that among the assets themselves. In practice, people may be more concerned with the co-dependency or cross-correlation for various assets. It was virtually realized via the indirect evaluation of the co-movement between each asset and market performance [6], because of computational complexity in early years. The overall market performance serves as the “intermediary” during the process.

Along with the sharp drop in computing costs, an increasing number of researchers have turned their attention to more direct and accurate metrics of the co-movement among the assets. In particular, based upon the network theory, a surge of literature is coming out to unveil the co-movement structures within or across asset classes. The network-based approach typically consists of the following two steps: 1) constructing the matrix in terms of cross-correlation coefficients for given assets, and thereby 2) mapping it to a graph, in which the nodes refer to the assets with links or edges connecting them.¹ Therefore, the topological properties associated with the graph or network can be further obtained to describe the structure of the co-movement.

For the first step, Pearson correlation is one of the most popular methods, especially in the early literature, in which it is simple to capture the linear correlations between the assets. Some similar alternatives include partial correlation [7], co-integration [8], and lead–lag relation [9–11]. Although these approaches function well in featuring the linear correlation among assets, they fail to capture the non-linear correlation that is more prevalent in financial markets. In response, more approaches have been employed, such as copula [12], mutual information [13], and rank correlation [14]. For the second step, it is easy to build a complete graph or network based on the raw correlation matrix, containing rich and even redundant information. An information filter is necessary, and a number of network-based methods have been developed to this end. For instance, minimum spanning tree (MST, hereafter) is one of the most popular methods [15–17]. Assuming that there are a total of N nodes in the original network, N − 1 most important edges would be retained in the MST. Planar maximally filtered graph (PMFG, hereafter) has also been frequently adopted in the literature [18]. The PMFG retains more information and exhibits more robustness than the MST. It is mainly realized by the fact that the nodes have no cross-linkage on the planar. In comparison, the most intuitive way is to conduct the threshold method [19, 20], which is able to filter out all the nodes with linkage weights greater than a specific critical value.

In this work, we concentrate on the detailed co-movement of the assets proxied by industrial sector indices in China. China has witnessed rapid development in its financial market in recent decades, while some phenomena still characterize the Chinese market, including the less transparent information environment at the market and firm levels, and a more significant proportion of irrational individual investors [21]. These result in remarkably distinct performance in the stock market from other mature markets [22], which necessitates further study. Furthermore, despite rich research on the co-movement for the assets in China, insufficient attention has been paid to a more detailed co-movement structure, which plays an increasingly important role in portfolio selection and risk management. On the other hand, with the rapid development of “factor zoo” [23], the performance of assets can be attributed to the compensation for various kinds of risks or the premium for investing styles. In this vein, it pays to perform an anatomy of the co-movement structure for the asset, which is the focus of our work.

Given that the network-based approach is more informative about detailed co-movement structures than those traditional methods with respect to the linear regression model (i.e., R² and its variants), we constructed the MST with layered structures in terms of correlations among systematic, idiosyncratic, and raw returns of assets. Based on the network theory, topological properties associated with the MST can be derived to describe the co-movement structure. For the whole sample period, we found that the MST presented a star-like connection, with the hub node being market factor MKT, and all sector nodes were connected to market factor MKT. Size factor SMB was directly linked to the sector composite (Cps), while the other three factors were connected through SMB. Our plot of the MST also implied the effectiveness of Fama-French pricing factors in China: market factor MKT played an important role, while investment factor CMA seemed redundant. These findings are consistent with the prior literature [24, 25].

With the adoption of the rolling window analysis, we observed that the topological properties associated with the network structure are time-varying. In particular, in major market cycles, the star-like structure would be accordingly changing. This is featured by the fact that a few idiosyncratic returns for sector indices would be disjointed from market factor MKT and then connected to their counterparts, which is consistent with the findings from Ref. [14]. Meanwhile, pricing factors would generally exhibit more favorable pricing efficacy.

The contributions of our work are as follows:

Our first contribution is to probe into the detailed co-movement structures of asset returns in China, to which scarce attention has been paid. In fact, to the best of our knowledge, our work is the first which is aimed for this purpose. A mounting of the literature has focused on the individual stock co-movement in China as well as the driving factors of change in the co-movement structure [11, 26], while another strand of the literature has examined the co-movement structure across the asset classes, such as that for the individual stocks in the Chinese market and other mature markets [27], and that between global oil prices and China’s commodity sectors [28]. In comparison, our focus on detailed co-movement structures of asset returns differentiates our work from the literature mentioned previously. Specifically, we conduct the return decomposition based on the Fama-French five-factor model for China and further construct the MST with layered structures. Based on this, we probe into the inter-structure for the co-movement between asset raw return and price premium, and the intra-structures for the factor premiums and idiosyncratic returns.

Our second contribution is to extend Ref. [14] by considering the weighted schemes for the co-movement structure in asset returns. The authors of Ref. [14] adopt the network-based approach to examine the asset returns’ co-movement in the US market. Based on the Fama-French three-factor model, they decompose the returns of industrial sector indices into systematic and idiosyncratic parts. They further examine the properties associated with time-varying MSTs with unweighted edges between the returns. Their results suggest that unexpected industries connect idiosyncratically through the dot-com bust. Different from their work, we focus on unweighted as well as weighted schemes in our work. Our results based on weighted schemes reveal more explicit and remarkable fluctuations in the measures for the co-movement structure for the period of major cycles in China than the results based on unweighted schemes, including the period around 2007, 2015, and 2018, corresponding to three major bursts of stock bubbles in China. In comparison, the results based on unweighted schemes convey less information, especially highlighted by our results for the intra-structure of returns’ co-movement.²

Last but more importantly, our work adds to the literature on empirical asset pricing by providing evidence of the time-varying effectiveness of pricing factors in the Chinese stock market. By conducting the rolling window analysis, our work lends support to the importance of market factor MKT but the redundancy of the investment factor CMA, which is also consistent with empirical findings in previous literature. In fact, the majority of research works focusing on asset co-movement are conducted based on cross-sectional and time-series regressions. In contrast, we employ the network-based approaches to fulfill the goal. In this regard, our research also provides a new perspective on the effectiveness evaluation of empirical pricing factors.

The article proceeds as follows: Section 2 and Section 3 introduce the method and data employed in the study; Section 4 presents empirical findings; Section 5 introduces the results of robustness check; and Section 6 concludes.

2 Methodology

2.1 Decomposition of Asset Return

Our interest is on the detailed co-movement structures for asset prices. We examine it by focusing on the inter- and intra-structures of the co-movement among raw, systematic, and idiosyncratic asset returns. Therefore, our first step is to conduct the decomposition of raw asset returns. According to the theoretical backgrounds of the macro-economy and empirical asset pricing, asset return can be explained by several common risk factors regarding fundamentals, plus the compensation for the idiosyncratic shocks whose expected value is zero [29]. In light of this, we can base on a specific popular pricing model to do the return decomposition [21, 30]. We resort to one of the most popular pricing models, that is, Fama-French five-factor model (FF5, hereafter) for the Chinese stock market [31]. More importantly, five factors from FF5 can function more favorably to describe the systematic risks and deliver better explanation power to the performance regarding individual assets and asset portfolios than Fama-French three-factor [32] and CAPM models [33–35] for China [24, 25]. Specifically, we regress the return time-series for each of the 28 sector indices against the Fama-French five factors. In this way, the idiosyncratic return for each sector indices can be captured by the residuals plus the intercept.³ The process mentioned previously can be described as follows:

$E{R}_i={\alpha }_i+{\beta }_{\text{MKT},i}{R}_{\mathrm{M}\mathrm{K}\mathrm{T}}+{\beta }_{\text{SMB},i}{R}_{\mathrm{S}\mathrm{M}\mathrm{B}}+{\beta }_{\text{HML},i}{R}_{\mathrm{H}\mathrm{M}\mathrm{L}}+{\beta }_{\text{RMW},i}{R}_{\mathrm{R}\mathrm{M}\mathrm{W}}+{\beta }_{\text{CMA},i}{R}_{\mathrm{C}\mathrm{M}\mathrm{A}}+{\epsilon }_i,{\epsilon }_i\sim N\left(0,{\sigma }_{\epsilon }^2\right),(1)$

where ER_t denotes daily log return for stock index i, and R_MKT denotes value-weighted market portfolio returns, both in excess of the risk-free rate; R_SMB, R_HML, R_RMW, and R_CMA constructed following Refs. [31, 36, 37] represent size, value, profitability, and investment factors, respectively. ɛ_i denotes the idiosyncratic return of asset i. Accordingly, the raw asset return can be split into systematic component that is captured by β_MKT,iR_MKT + β_SMB,iR_SMB + β_HML,iR_HML + β_RMW,iR_RMW + β_CMA,iR_CMA, and the idiosyncratic return that is captured by α_i + ɛ_i.

2.2 Measurement of Co-Movement

As alternatives, we gauge the co-movement between each pair of return series with rank correlation, namely, Spearman’s ρ and Kendall’s τ, which are able to describe the non-linear relationship among various components based on return decomposition.⁴

Spearman’s ρ is equivalent to Pearson’s linear correlation applied to the rankings of each return series. Assume two return series $A={\{A_i\}}_1^n$ and $B={\{B_i\}}_1^n$, if all the ranks are distinct; then the equation could be simplified to

${\rho }_{A,B}^{Spearman}=1-\frac{6\sum \underset{i}{\overset{2}{d}}}{n\left(n^2-1\right)},(2)$

where d_i = rg (A_i) − rg (B_i) is the difference between the two ranks of each observation in A and B, and n is the length of each series [38].

Kendall’s τ coefficient can be defined as

${\tau }_{A,B}=\frac{2K}{n\left(n-1\right)},(3)$

where $K={\sum }_{i=1}^{n-1}{\sum }_{j=i+1}^{n}f(A_i,A_j,B_i,B_j)$, and

$f\left(A_i,A_j,B_i,B_j\right)=\left\{\begin{array}{cc}\hfill 1,& if\left(A_i-A_j\right)\left(B_i-B_j\right)>0\hfill \\ \hfill 0,& if\left(A_i-A_j\right)\left(B_i-B_j\right)=0,\hfill \\ \hfill -1,& if\left(A_i-A_j\right)\left(B_i-B_j\right)<0\hfill \end{array}\right.(4)$

According to Eq. 4, the Kendall correlation between two variables will be high when observations have similar ranks and low when observations have dissimilar ranks. Specifically, the value of τ ranges from −1 to +1. A value of −1 indicates that one’s ranking is the reverse of the other, while a value of +1 indicates that the two rankings are the same. A value of 0 indicates no relationship between them [39].

Both of the aforementioned correlation coefficients measure monotonicity relationships. Strictly speaking, the Kendall correlation is preferred over the Spearman correlation because of a smaller gross error sensitivity and a smaller asymptotic variance [40], which nevertheless makes no difference in our study. Unless noted otherwise, Spearman’s ρ is adopted as the measurement of correlation, and we leave out the superscript Spearman in the left hand of Eq. 2 in the remainder of the article.

In light of Ref. [14], we introduce a special correlation structure for the purpose of this work. In particular, we set the correlation coefficient between raw and idiosyncratic returns as one. In other words, raw return Y and its idiosyncratic component I is perfectly correlated, and together, they can be further viewed as a new type of node labeled as Z. The correlation coefficient of special nodes pair Z ∼ Z is, in fact, the correlation coefficient of their idiosyncratic components I ∼ I, and the correlation coefficient of special node and factor premium Z ∼ F equals that of its raw return and factor premium Y ∼ F. Assuming there are a total of N assets and M risk factors, that is, the size of the network is N + M, we thus obtain the correlation matrix C as follows:

$C=\left(\begin{array}{cccccc}\hfill {\rho }_{I_1,I_1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{I_1,I_N}\hfill & \hfill {\rho }_{Y_1,F_1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{Y_1,F_M}\hfill \\ \hfill \cdots \hfill & \hfill \ddots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill {\rho }_{I_N,I_1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{I_N,I_N}\hfill & \hfill {\rho }_{Y_N,F_1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{Y_N,F_M}\hfill \\ \hfill {\rho }_{F_1,Y_1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{F_1,Y_N}\hfill & \hfill {\rho }_{F_1,F_1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{F_1,F_M}\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \ddots \hfill & \hfill \cdots \hfill \\ \hfill {\rho }_{F_M,Y_1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{F_M,Y_N}\hfill & \hfill {\rho }_{F_M,F_1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{F_M,F_M}\hfill \end{array}\right),(5)$

2.3 Construction of the Network

We can construct an undirected network as follows: First, correlation matrix C formed according to Eq. 5 needs to be transformed to a distance matrix before constructing the network. We follow Ref. [41] to construct the distance measurement for nodes pair (A, B) in the network:

$D_{A,B}=\sqrt{1-|{\rho }_{A,B}|},(6)$

which is also proven to satisfy the properties of distance norm: 1) $D_{A,B}^{(.)}=0$ if and only if A = B, 2) $D_{A,B}^{(.)}=D_{B,A}^{(.)}$, and 3) $D_{A,B}^{(.)}<=D_{A,K}^{(.)}+D_{K,B}^{(.)}$.⁵

Second, distance matrix D constructed previously still contains rich information regarding co-movement structures. It can map to a complete graph, in which each pair of vertices is connected by an edge. However, our purpose is to conduct the study based on a more concise structure containing the most important links or edges. Accordingly, the MST is employed to filter the original network. We follow the process similar to that under Kruskal’s algorithm [42]. Specifically, the lower-diagonal elements of C are sorted in order. We then rely on the sorted values to screen out the most significant links, so as to construct an MST. The links with lower values are preferred, and all nodes are connected sequentially through the shortest distance. As a result, N + M − 1 links are retained, through which all of the N + M nodes are connected in the network, compared to a total of $\frac{(N+M)(N+M-1)}{2}$ edges in its complete graph.

2.4 Topological Properties of the Network

We investigate both static and dynamic co-movement structures by examining the network’s topological properties. In order to capture the detailed structure of the co-movement, the properties are required to characterize the tightness as well as the shape of the network structure. It is stressed that the results of all metrics based on both unweighted and distance-weighted (see Eq. 6) networks are presented in our work, and the comparison of the results would be conducive to detecting the effectiveness of pricing factors.

For the tightness of the entire network, we consider node distance as a proxy, dis_A,B, for node pair (A, B) [43–45], which acts as an intuitive but favorable measurement for the level of co-movement.⁶ The unweighted distance between A and B is defined as the shortest path length between them. According to Eq. 6, the weighted distance between A and B can be defined as the length of the shortest D-weighted path between them. It is noted that the weighted node distance functions better in capturing the dynamics of network tightness, given that the unweighted node distance may remain unchanged over time. To gauge the tightness of the network more accurately, we employ the indicator in terms of nodes’ distance, which is similar with network efficiency [46]:

$NT=\frac{{\sum }_{A\ne B}\frac{1}{di{s}_{A,B}}}{\left(N+M\right)\left(N+M-1\right)},(7)$

where dis_A,B represents the unweighted or weighted distance between A and B, and N + M denotes the network size. Specifically, the network structure is tight (loose), when NT is larger (smaller), thus indicating the higher (lower) level of co-movement.

In addition, we attempt to devote more attention to the sub-networks, or detailed structures of co-movement, including the inter-structure of co-movement across raw return and factor premium, and the intra-structures for idiosyncratic returns and factor premiums. As for the sub-network based on given node types, NT fails to measure the network tightness, since the nodes may be connected by other nodes outside the sub-network of our interest. We thus consider the average link size of a given sub-network as an alternative. It is defined by the following:

${\bar{l}}_S=\frac{{\sum }_{e\in S}{l}_e}{{\sum }_{e\in G}{l}_e}.(8)$

where l_e represents the length of link e in the network. S refers to the sub-network of our interest, while the entire network is denoted as G. It is noted that the change of link size for the entire network is controlled for in Eq. 8. By doing so, we can obtain more accurate results for the co-movement structure.⁷ In the case of an unweighted network, the length of link e equals one, if it exists in network S, and zero otherwise. In this regard, ∑_e∈Sl_e is given by the total link size for all the links of network S, and ∑_e∈Gl_e equals N + M − 1. In this vein, a larger (smaller) value of ${\bar{l}}_S$ implies the higher (lower) level of tightness, and thereby the lower (higher) level of co-movement for a given network S. In the case of a weighted network, l_e refers to distance measurement d depicted by Eq. 6. Thus, ∑_e∈Sl_e and ∑_e∈Gl_e equal the sum of d in the network S and G, respectively. When the absolute link size is fixed, a larger (smaller) value of ${\bar{l}}_S$ implies the lower (higher) level of the co-movement across the returns in given network S.

As for the shape of the network structure, we consider the node degree, node strength, and their variants as the major measurements. Node degree is defined as the number of links connecting a given node to the rest of the network. Its weighted version, or node strength, is defined as the sum of weights (or distances) of links connected to the node. Here we focus on the maximum and the standard deviation of the node degree (strength). The maximum degree of the network is defined as the degree of the node with the greatest number of edges incident to it. We define the maximum strength of the network as the strength of the node with the greatest weight of edges incident to it. Intuitively, the evolution of maximum degree (strength) indicates a time-varying network shape. The standard deviation of node degree (strength) measures the amount of dispersion of nodes’ degree (strength), which plays a more critical role in characterizing the shape of the network. Specifically, a larger (smaller) standard deviation of degree (strength) implies that the shape of the network is more inclined to be the star-like (chain-like) connection.

3 Data

Obviously, individual stocks within the same industry or sector, or more broadly, some style of “portfolio,” share the co-movement to a large extent [2]. Therefore, we adopt the sector indices as our data sample, instead of individual stocks. By doing this, the industry effects are controlled for in our work so that a more precise co-movement structure can be further evaluated. Specifically, our work is conducted based on 28 sector indices, issued by Shenyin and Wanguo Securities Co., Ltd (http://www.swsresearch.com), and the period spans from 5 January, 2000 to 29 March, 2019. With the closing price of sector indices on a daily basis, we can further obtain their daily log returns, that is, r_t = log (p_t) − log (p_t−1). Summary statistics associated with daily log returns for different indices are reported in Panel A of Table 1. It is noted that price limit trading rules implemented currently in China became effective since December 1996, requiring that the maximum daily price fluctuation in terms of the last closing price is ±10% for risk stocks, as highlighted by the results in the columns of Max and Min. It is also evident that each sector produces a time-series average positive profit, and the most outperformed is F&D with the return of 0.05% per day, or around 12.6% $(\approx 0.05\%\times 252)$ per year. The standard deviation (std) of daily returns ranges from 1.7% to 2.3%; thus, the annualized standard deviation ranges from about 27% to 37%, which is remarkably higher than those of major assets around the world.⁸ In addition to these, we can observe that a majority of sector returns are negatively skewed, indicating the relatively higher possibility of a flash crash. The kurtosis is beyond five for all sector indices, accompanied with the evidence of negatively skewed distribution, which suggests that the sector indices are not normally distributed. Accordingly, this can be further confirmed by the significant statistics of Jarbe–Barque tests at the 1% level.

TABLE 1

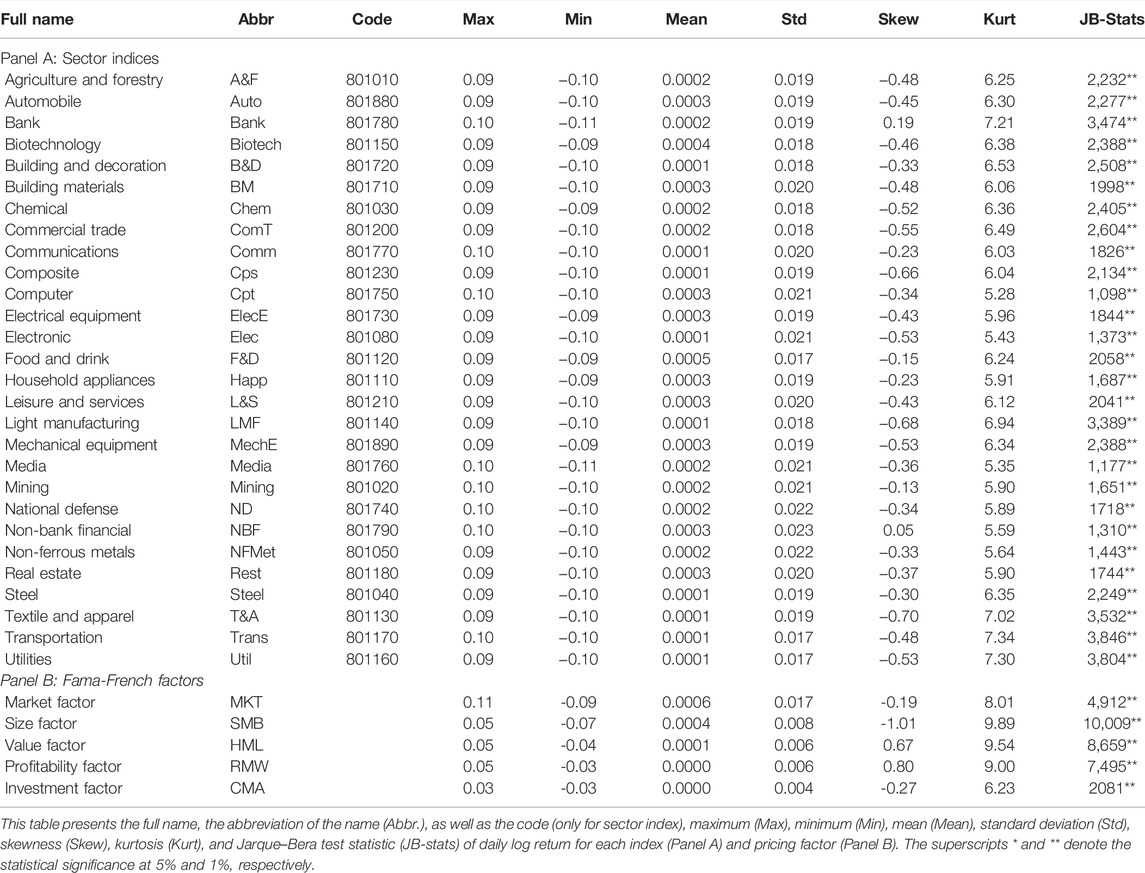
TABLE 1. Descriptive statistics of log returns for 28 sector indices and the premiums for Fama-French five factors.

Additionally, for the decomposition of the asset return, we also retrieve a risk-free interest rate as well as Fama-French five factors for China on a daily basis from the China Stock Market and Accounting Research (CSMAR) database, which is the comprehensive database for Chinese business research, covering data on the Chinese stock market.⁹ Specifically, the risk-free interest rate is proxied by the 3 month fixed deposit benchmark interest rate published by the China Central Bank. Pricing factors are constructed strictly following Ref. [31]. Summary statistics associated with Fama-French pricing factors are also presented in Panel B of Table 1. Apparently, the market factor, MKT, outperforms other four factors and even 28 sector indices, with an annual return of 15% $(\approx 0.06\%\times 252)$. MKT has larger magnitudes of maximum (11%) and minimum (9%), thus implying the higher volatility, which can also be confirmed by its daily standard deviation of 1.7%, or around 27% per year, at least twice than those for other four factors. It is noted that although MKT is the most volatile among the factors, it is still located within the lower range of the standard deviation for sector indices. Accompanied with its highest profits, MKT produces the highest Sharpe ratio and acts as the best “asset” within the framework of portfolio theory [47]. Except for MKT, the maximum and minimum magnitudes for the other four factors are lower than 5% and 7% per day, respectively. Relatively speaking, SMB and HML are more profitable than the others, with the annual return of 10% $(\approx 0.04\%\times 252)$ and 2.5% ($\approx 0.01\%\times 252$), respectively, while RMW and CMA produce the profits approaching zero per day. SMB and HML are more volatile, with the annual standard deviation of 12.7% and 9.5%, respectively, than 6.3% for CMA. Similarly, five factors are not normally distributed, as suggested by the results of their skewness, kurtosis, and the statistics under the Jarbe–Barque test.

4 Empirical Results

4.1 Network Connectedness Over the Whole Sample Period

To begin with, we examine the results over the whole sample period. With a daily log return for 28 stock indices, we first retrieve their idiosyncratic returns by performing the regression of their raw returns on Fama-French five-factor premiums, as described by Eq. 1. Factor premium, raw return, and its corresponding idiosyncratic return are employed to calculate the correlation matrix C in terms of Spearman’s ρ. With the adoption of the distance measurement in Eq. 6, C is transformed to D, and its MST can further be obtained, as presented in Figure 1. The network comprises 33 nodes with 32 most significant linkages connecting them. The white circles in the figure represent different sector indices, while the gray ones represent pricing factors. The width of edges between nodes denotes the reciprocal of the distance between them. The edges in bold imply that the shorter the distance the closer the relationship between the connecting nodes.

FIGURE 1

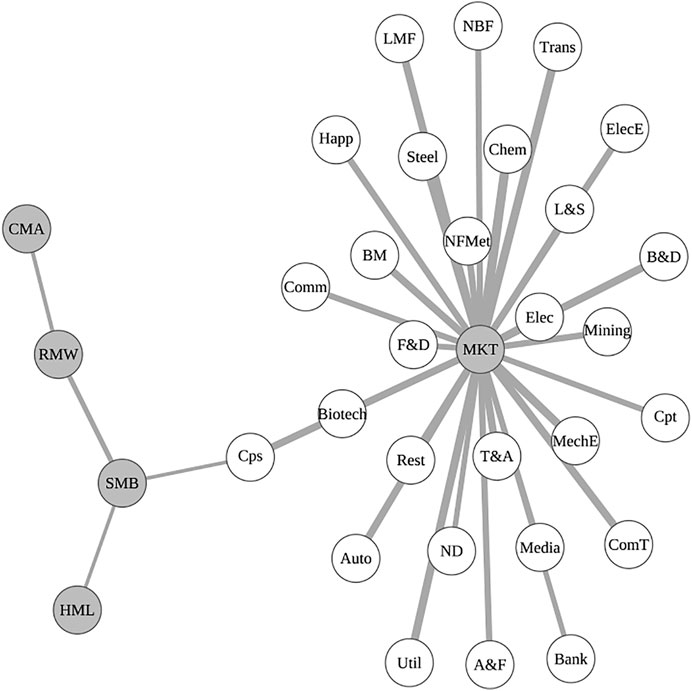
FIGURE 1. MST for the whole sample period from 1 July 2000 to 29 March 2019. White circles denote 28 sector indices, while gray circles denote five pricing factors.

It is evident that all sector indices are connected to factor MKT, as shown in the plot of the MST, which suggests that sector indices exhibit a high degree of co-movement with market factor MKT compared to other risk factors. Apparently, market factor MKT has the maximum degree, while the other four factors are connected with other sector nodes through sector Cps. Specifically, size factor SMB is directly linked to sector Cps, while the other three factors are connected through SMB. In comparison, investment factor CMA lies in the most periphery of the MST structure.

We also notice that it is more distant between pricing factors than that between MKT and sector indices. That is, the links connecting MKT with sector indices are more preferred during the construction of the MST. In some sense, the results aforementioned also unveil the relative strength of the pricing effectiveness of risk factors in the Chinese stock market, which are in accordance with empirical findings from the literature on asset pricing. As documented in previous research works, Fama-French five factors in emerging markets behave differently from other mature markets. It is widely acknowledged that market factor MKT is not enough to capture the common risks associated with assets, and thus, “factor zoo” has been developed to fulfill this end [23]. Furthermore, new pricing factors that have been proven in mature markets are applied to emerging markets, including China. As for the Chinese market, size factor SMB and profitability factor RMW are found to function well [24], while investment factor CMA seems redundant [24, 25], and the results regarding value factor HML are mixed [24, 48, 49], which is consistent with our findings in Figure 1.

4.2 Dynamics of Network Connectedness

In order to probe into the dynamics for the co-movement among raw returns, factor premiums, and their idiosyncratic returns, rolling or moving window analysis is conducted [50–53]. It is noted that the rolling window analysis has been frequently adopted in the literature. Researchers record the behavior regarding the variable of interest in each moving window, thereby obtaining its dynamics over time. In the fields of finance, the authors of Ref. [54] put forward the famous Fama-MacBeth regression to process the panel data by evaluating the time-series estimates of slopes based on cross-sectional regression in each moving window, which has been widely employed in financial studies; recent research works include Refs. [55–58] among others. The authors of Ref. [59] propose variance decomposition based on the VAR model to detect the spillover effect of variables of interest, whose dynamics are also obtained by re-estimating the model for each moving window [60, 61]. There is a body of literature proposing the econophysics-based methods to process financial data, with the adoption of the rolling window analysis as well [62]. It is noted that the rolling window analysis has also been applied to other fields, including particle-in-cell simulation [63], recurrence plot-based complexity measurement [64], mutual information estimation [65], and the study of the dynamical response of a population [66].

As for our work, the most intuitive and efficient way is to evaluate the properties associated with the MST in each moving window and further examine their dynamic behaviors. The observations in each time window should be sufficient to guarantee a precise estimation. Following Ref. [14], the sizes of the rolling window and the step are set as 120 trading days and 1 day, respectively. As such, we follow the process similar to what is illustrated in the previous subsection, except that at each trading day t during the sample period, we construct the MST based on the data derived from the decomposition of the index return over the past period from t − 1 to t − 120. To capture the changing structure of co-movement, we examine the evolution of the topological properties of the MSTs.

We also wonder whether the topological characteristics of the network are related to market performance. To this end, we perform a rough division in terms of market performance proxied by the Shanghai Component Index (SHCI, hereafter). As shown in Figure 2, market trends over the period from January 2000 to March 2019 are roughly divided into five market cycles, which are typically composed of the phases of accumulation, mark-up, distribution, and mark-down. In the figure, the red curve represents the rising phase of the market, while the black curve represents the downward or adjusting phase. We focus on the network structures over three time periods corresponding to the three most important market cycles, namely, the periods around 2007, 2015, and 2018.

FIGURE 2

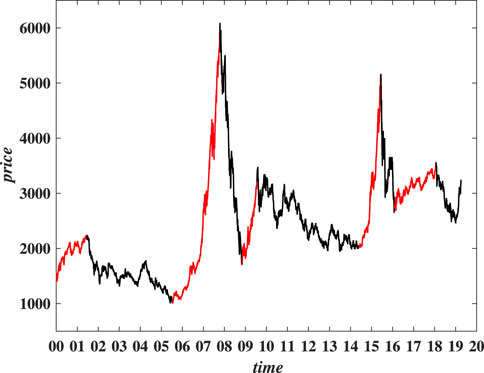
FIGURE 2. (Color line) Rough partition of market cycles in terms of the daily closing price of the SHCI.

The results are presented in Figures 3, 4. On the whole, our results unveil the strong correlation between the evolution of topological properties of the network structure and market cycles, regardless of which topological properties are considered.

FIGURE 3

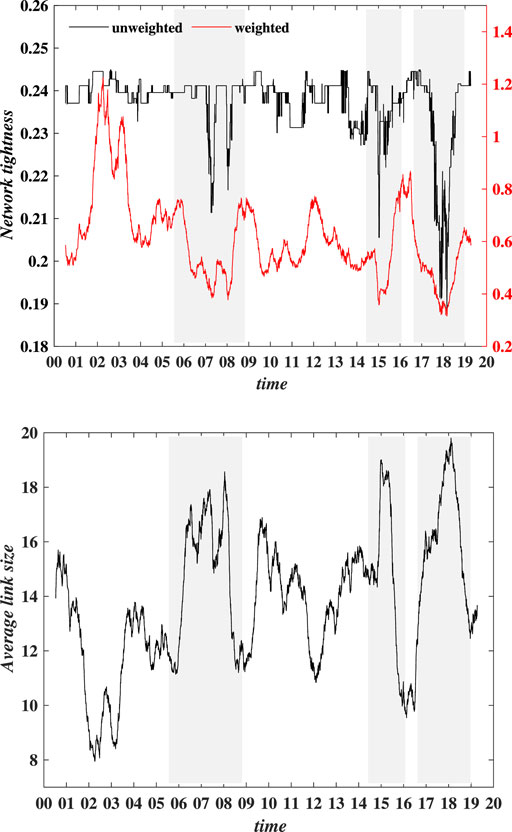
FIGURE 3. (Color line) Evolution of network tightness indicator NT and weighted link size for the entire network, presented in the top and bottom panels, respectively. The sample period is from 1 July 2001 to 29 March 2019. The shaded parts in each plot correspond to the three major market cycles.

FIGURE 4

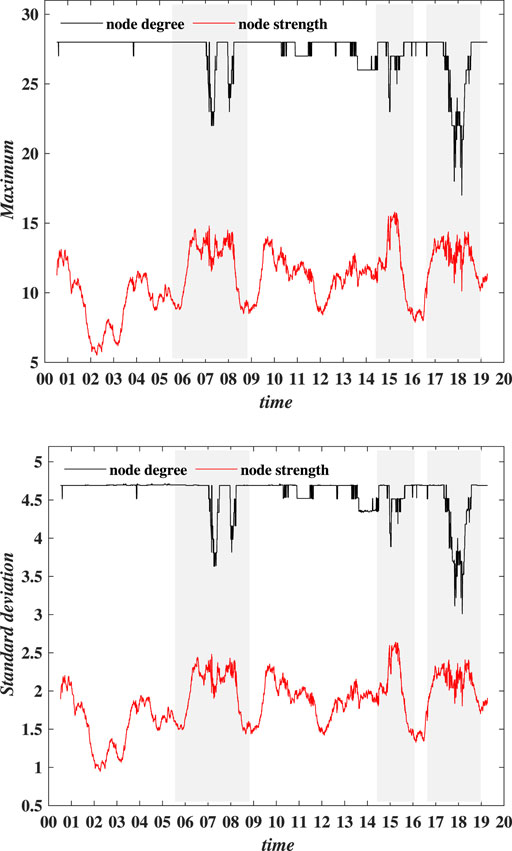
FIGURE 4. (Color line) Evolution of maximum and standard deviation of node degree (strength), presented in the top and bottom panels, respectively. The sample period is from 1 July 2001 to 29 March 2019. The shaded parts in each plot correspond to the three major market cycles.

According to Eq. 7, NT plays an important role in characterizing the level of network tightness. In the top panel of Figure 3, we can readily observe that both unweighted and weighted results vary over time and are closely related to the major market cycles, represented by the shaded parts in the plot. NT experiences a sharp decrease during all three major periods, thus indicating the lower level of co-movement. It is more pronounced in the unweighted case, since NT remains relatively stable with slight fluctuations most of the time, except for the three periods of our interest. It is also worth noting that the evolution of the average distance is not exactly coherent with the market trend. The Chinese market has witnessed the most significant bubble formation and bursting during the period around 2007, while the market cycle around 2018 is relatively insignificant. However, Figure 3 presents a seemingly more pronounced increase of the average distance realized for the period around 2018, rather than 2007. This finding can also be observed in the following results with respect to other properties. In addition, we also measure the network tightness by the link size for the entire network, as described by ∑_e∈Gl_e according to Eq. 8. Here we focus on the results for the weighted case, as shown in the bottom panel of Figure 3. It is noted that the unweighted link size for the entire network remains the value of 32 all the time, while the result for the weighted case is obviously time-varying. Also, consistent with findings based upon the results of NT, link size exhibits a significant increase during three major periods, indicating the lower level of co-movement.

On the other hand, the node degree (strength) of the network can be employed to depict the shape of the network. The results for maximum and standard deviation of the node degree (strength) are presented in the top and bottom panels of Figure 4, respectively. The maximum degree (strength) shows the importance of the most connected node in the network, while the standard deviation of the node degree (strength) denotes the dispersion of node degree (strength) across the network. As shown in the figure, node strength is more volatile over time, while node degree remains stable, with the value being around 28 at most times.¹⁰ This implies that the degree of the remaining nodes fluctuates within a small range; accompanied with the results in the previous section, market factor MKT is supposed to be the hub node over the rolling time windows, which needs further validation. In addition, we can observe that maximum degree experiences a sharp decrease in all three market cycles, which indicates that some edges of the hub node are disjointed. Meanwhile, a pronounced increase in node strength suggests that the level of co-movement between the hub node and its connected nodes is weakening. As for the standard deviation of degree (strength), the results are basically the same as that for the maximum degree (strength). The results above imply a star-like connection in the network structure, which is also time-varying, especially over the period corresponding to major market cycles.

In order to provide more evidence about the existence of star-like connection, we further resort to the assortativity coefficient [14], and the results are shown in Figure 5. Obviously, the assortativity coefficient is changing over time and exhibits more significant fluctuations in three major cycles. It is noted that all results over the rolling windows are negative, which confirms that nodes with an extremely high degree tend to connect with nodes with very low degrees. This is also consistent with our previous findings as well as those from the prior literature [14].

FIGURE 5

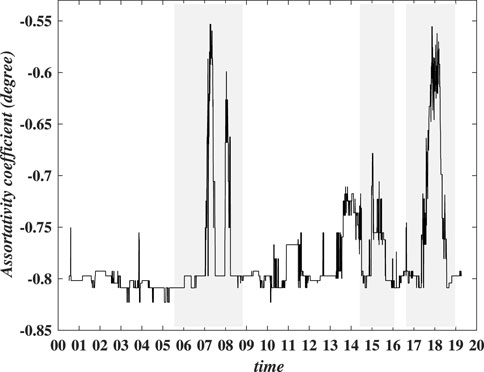
FIGURE 5. Evolution of assortativity coefficient in terms of node strength. The sample period is from 1 July 2001 to 29 March 2019. The shaded parts in each plot correspond to the three major market cycles.

It is noted that our results are similar to those from Ref. [14] that adopts a network-based approach to examine the asset returns’ co-movement in the US market. Based on the Fama-French three-factor model, the authors decompose the returns of industrial sector indices into systematic and idiosyncratic parts. Their results also suggest the time-varying co-movement structures over the period from 1970 to 2015 (see Figures 2, 3 from Ref. [14]). However, they observe large fluctuations of measures for co-movement structures over the period around the dot-com bubble only. It is somewhat out of surprise that no large fluctuations are observed for the period around 2008, corresponding to the Global Financial Crisis (GFC). This is partly due to their adoption of unweighted schemes, which may be insensitive to small changes in co-movement structures. Our results in the following text would further highlight this.

In addition, to further understand the MST structures in the three market cycles of our interest, we plot the MSTs for three moments that are randomly chosen out in each of the periods for three market cycles. The results are shown in Supplementary Figure S1 through Supplementary Figure S3. It is evident that compared with the results for the whole sample period in Figure 1, Supplementary Figure S1 presents a perfect star-like network, though some sector indices are disjointed from market factor MKT, and instead, they are connected to their counterparts. A similar finding is obtained by Ref. [14]. The authors also observe that MKT acts as a hub node that connects the majority of idiosyncratic returns most of the time, implying the critical role in pricing the assets, while some of the industrial sectors would be disjointed from MKT and connect with themselves through the risky periods (see Figure 6 from Ref. [14]).

The structure for pricing factors is also slightly different. Among them, value factor HML is connected with sector Steel, through which it is connected with market factor MKT. The other three factors are connected in sequence and connected with market factor MKT through sector Bank. In comparison, in the plots for 2015 and 2018, as shown in Supplementary Figures S2,3, respectively, the MST structures are remarkably different from what is suggested in Figure 1, and the nodes of sector indices are more inclined to connect with their counterparts and also with other pricing factors. Additionally, we observe that value factor HML and profitability factor RMW take up more important positions in the MST, and size factor SMB acts as the bridge for other factors. However, investment factor CMA seems less important than the other factors in the plots.

4.3 Detailed Structure of Co-Movement

With the rolling window analysis, we further attempt to acquire more information regarding the detailed structure for different node pairs. In doing so, we divide the entire network structure into three parts, that is, intra-structures for both factor premiums and idiosyncratic returns, and the inter-structure for raw return and factor premium. We will evaluate the characteristics with respect to each sub-network. Here, we employ the average link size as the main measurement of the network structure, as described in Eq. 8, instead of average distance that only captures the characteristics associated with the entire network structure.

4.3.1 Inter-Structure for Raw Return and Factor Premium

Figure 6 presents the results with respect to the inter-structure of co-movement between raw return and factor premium. Similar to previous results, the unweighted result of the link size is less volatile. Specifically, in the result of the unweighted case, its fluctuation is around 0.95 over most periods, which suggests that about 95% of connected edges in the network exist between the sector indices and pricing factors. In comparison, the weighted results fluctuate more frequently and range between 0.7 and 0.96. As to the results for the three market cycles, we can observe much more pronounced fluctuations in both cases, indicating a sudden change in the MST structure.

FIGURE 6

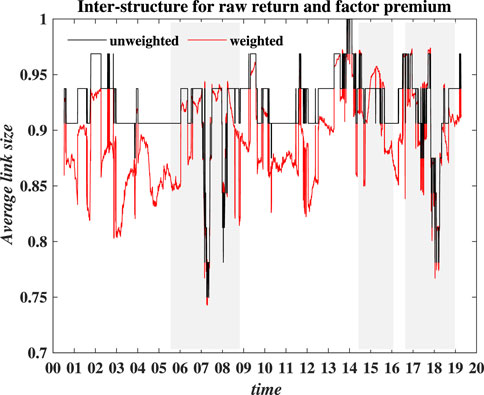
FIGURE 6. (Color line) Evolution of the average link size of intra-structure for idiosyncratic returns of sector indices. The sample period is from 1 July 2001 to 29 March 2019. The shaded parts in each plot correspond to the three major market cycles.

It is noted that the results for three major market cycles are mixed. For the periods around 2007 and 2018, both unweighted and weighted values exhibited a sharp decline with wild fluctuation, implying a loose network structure. In comparison, the results over the period around 2015 were different. The unweighted value remains stable, while the weighted value peaks instead of slumping down, suggesting the lower level of co-movement.

4.3.2 Intra-Structure for Idiosyncratic Returns

The results in Figure 7 reveal important changes in the network structures for major market cycles. The average link size in the figure remains zero most of the time, which indicates no connection exists between idiosyncratic returns in the network. We have already obtained the results for the whole sample period in Figure 1 that sector indices are all connected through market factor MKT. However, in some time windows, such as three major cycles, the connectivity for idiosyncratic returns is significantly enhanced, regardless of whether it is in the weighted or unweighted case. This may be caused by the characteristics embedded in the MST. As the correlation between sector nodes and common risk factors is weakened, they have to connect to other nodes instead. On the other hand, this also implies the possibility of potential pricing factors hiding in idiosyncratic returns, which requires further investigation.

FIGURE 7

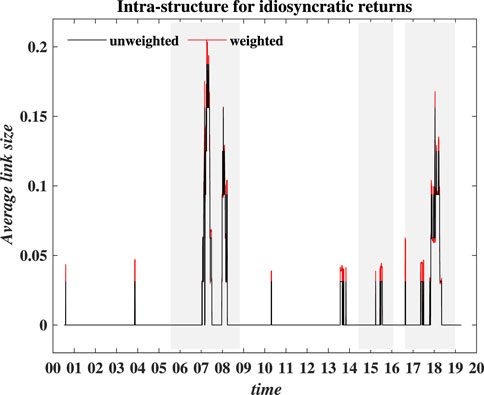
FIGURE 7. (Color line) Evolution of the average link size of intra-structure for the idiosyncratic returns of sector indices. The sample period is from 1 July 2001 to 29 March 2019. The shaded parts in each plot correspond to the three major market cycles.

4.3.3 Intra-Structure for Factor Premiums

Finally, we move to the results for intra-structures of co-movement for factor premiums. The results are presented in Figure 8. Unweighted results fluctuate slightly, ranging from 0% to 10%, while weighted results fluctuate frequently, but they are all within a range from 0% to 20%, and weighted average link size has a downward trend in fluctuations over time. For three major market cycles, both the weighted and unweighted results exhibit different decrease degrees. In fact, the link size for pricing factors is expected to be as small as possible. This is in line with the intention of asset pricing theory, which is to explore irrelevant but economically meaningful risk factors. As such, the co-movement between factors and assets is expected to be as strong as possible, demonstrating factor pricing effectiveness. Our results provide evidence that Fama-French five factors are not suitable for the Chinese stock market on the ground that some risk factors play their roles only in major market cycles, which is consistent with our previous finding.

FIGURE 8

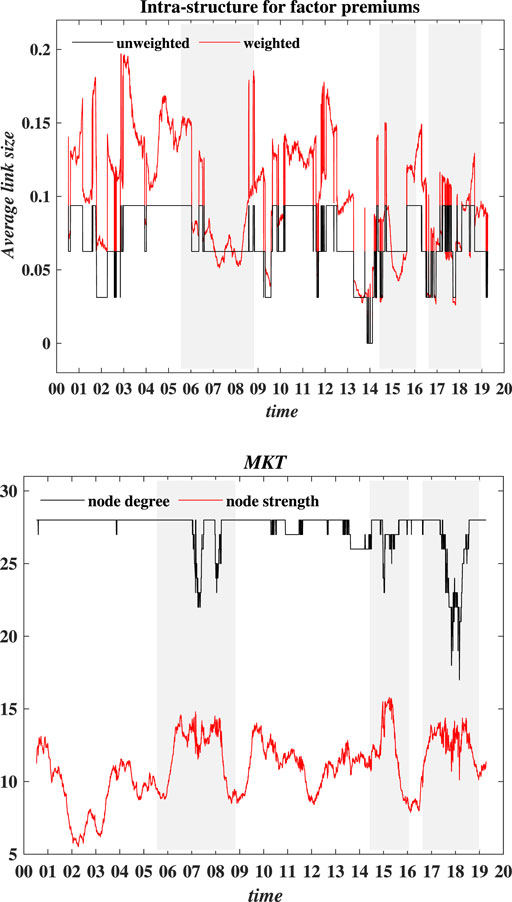
FIGURE 8. (Color line) Evolution of the average link size of intra-structure for factor premiums and the node degree (strength) of market factor MKT, presented in top and bottom plots, respectively. The sample period is from 1 July 2001 to 29 March 2019. The shaded parts in each plot correspond to the three major market cycles.

We attempt to explore further how Fama-French five factors are connected. We examine the evolution of node degree (strength) for each factor. Here, we report the results on the market factor MKT only, whose degree remains at a high level for most time windows. As shown in the bottom panel of Figure 8, node degree of MKT only fluctuates slightly, with the value being around 28 in the plot. This also provides evidence of a close relationship between the MKT and other sector indices. The dynamic changes of node strength over time seem to be irregular. However, for major market cycles, node strength of MKT factor would be increasing, which implies the weakening of the relationship with its connected nodes. In comparison, node degree (strength) for the other four factors fluctuates more frequently and exhibited a significant upward trend only in the major cycle around 2018, as shown in Supplementary Figure S4 through Supplementary Figure S7.

5 Robustness Check

We employ alternative correlation metrics to conduct the robustness check, including Pearson’s ρ and Kendall’s τ. It is noted that similar results are obtained based on different measurements, and our main findings still hold. In addition, we also examine the sensitivity of the results when the size of the rolling step and window varies. The results also indicate that our findings are not sensitive to the settings associated with the rolling window analysis.¹¹

6 Discussion and Summary

In this work, we probe into the detailed structure of co-movement for the asset price. Specifically, using the data of Chinese sector indices and Fama-French five factors, we perform the return decomposition and construct a minimum spanning tree (MST) in terms of the rank correlation coefficients among raw return, idiosyncratic return, and factor premium.

For the whole sample period, the MST presents a star-like connection with the hub node being market factor MKT, and all sector nodes are connected to market factor MKT. We find that the topological properties associated with the network structure are time-varying in the rolling window analysis. In particular, in major market cycles, the star-like structure would be changing. This is featured by the fact that a few idiosyncratic returns for sector indices would be disjointed from market factor MKT and then connected to their counterparts. Also, pricing factors will generally exhibit more favorable effectiveness of pricing assets.

Our results imply the importance of monitoring assets’ co-movement in practice. Regulators should be alert to the structural changes in assets’ co-movement and take measures to avoid further risk spillovers. Specifically, given that strengthened co-movement of idiosyncratic returns may lead to continued amplification of risk, much more attention should be paid to industrial sectors that are disjointed from crucial risk factors. In addition, our work also provides a new perspective for the research on the co-movement structure for the asset price. The effectiveness of new pricing factors can also be evaluated within this framework. It is also noted that this work’s focus is to describe characteristics associated with the time-varying co-movement structure, whose driving forces will be left in our future work.

Data Availability Statement

The data analyzed in this study are subject to the following licenses/restrictions: The data for Chinese stock indices used in this study are openly available. Access to the data can be obtained from SWS research. The data for pricing factors and interest rate are owned by CSMAR, and there are fees associated with the database. Requests to access these datasets should be directed to SWS research: http://www.swsresearch.com/EN/default.aspx; CSMAR: http://www.gtarsc.com/#/index.

Author Contributions

HLS: data curation, conceptualization, investigation, methodology, funding acquisition, and project administration; HC: software, validation, visualization, and writing—original draft.

Funding

This work was partly supported by Humanities and Social Sciences Fund of Ministry of Education of China (20YJC790113), the Project of Philosophy and Social Science Research in Colleges and Universities in Jiangsu Province (2019SJA0156), and the Startup Foundation for Introducing Talent of NUIST.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to acknowledge the reviewers for their constructive comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.593493/full#supplementary-material

Footnotes

¹The edge exists between the nodes for assets if they have a higher pairwise correlation, which will be detailed in the following sections. Note that “edge” and “link” are interchangeable in our work.

²Similarly, results from Ref. [14] suggest that large fluctuations of measures of co-movement structures coincide with the burst of the dot-com bubble, while they remain relatively stable for other periods with major risk events (from Figure 4 through Figure 5 in Ref. [14]). We argue that this may be, to a large extent, due to the unweighted scheme adopted by the authors.

³The efficacy of the Fama-French five-factor models for the Chinese stock market is not our focus in this work. We consider pricing factors possibly regarding fundamentals in the study to serve more favorably for our purpose of return decomposition.

⁴It is noted that although we report main results based on rank correlation, our findings still hold and are even more significant when Pearson’s ρ is adopted.

⁵It is noted that conventional method of mapping the correlation to the distance relies on $D_{A,B}=\sqrt{2(1-{\rho }_{A,B})}$ [15, 16]. In this vein, positive (negative) correlation gives rise to the short (long) distance. However, this is not what is required in our work. High magnitudes of pairwise correlations, irrespective of their directions, would imply the close relationship between the assets, on which the high level of co-movement is based. Thus, Eq. 6 serves the purposes of our work better.

⁶Thanks for the comment offered by one of the anonymous reviewers, and we notice that tightness of the network in our study is similar to the conception of network robustness [46]. Despite this, our work concentrates on evaluating network connectivity for assets and pricing factors. Therefore, we adopt “tightness” rather than “robustness” to highlight this focus.

⁷We argue that it is necessary to consider the weight changes for the edges in the network. For the inter-structure for raw return and factor premium, we observe a significant increase in the weighted link size, but a decrease in the unweighted link size. This is mainly due to the increase in distance measurement for the entire network. Unsurprisingly, the results are consistent after allowing for weight changes.

⁸For the recent decade, global commodities have achieved the highest annualized standard deviation of about 17%, which is obviously lower than those for sector indices in China. In the Chinese market, the majority of investors are retail investors, causing larger irrational and speculative behaviors and thereby higher volatility [22]. For more information regarding the historical volatility of worldwide assets, refer to https://advisor.visualcapitalist.com/asset-class-risk-and-return/.

⁹As for the detailed construction of Fama-French five factors, we refer interested readers to Ref. [31] as well as the documents by the CSMAR (https://www.gtadata.com/), which is not the focus in our study.

¹⁰It is noted that the theoretical maximum is 32, which is the number of edges in the network.

¹¹The results mentioned previously could be provided upon the requests.

References

1. Malceniece L, Malcenieks K, Putniņš TJ. High Frequency Trading and Comovement in Financial Markets. J Financial Econ (2019) 134:381–99. doi:10.1016/j.jfineco.2018.02.015

CrossRef Full Text | Google Scholar

2. Barberis N, Shleifer A, Wurgler J. Comovement. J Financial Econ (2005) 75:283–317. doi:10.1016/j.jfineco.2004.04.003

CrossRef Full Text | Google Scholar

3. Morck R, Yeung B, Yu W. The Information Content of Stock Markets: Why Do Emerging Markets Have Synchronous Stock price Movements? J Financial Econ (2000) 58:215–60. doi:10.1016/S0304-405X(00)00071-4

CrossRef Full Text | Google Scholar

4. Hameed A, Kang W, Viswanathan S. Stock Market Declines and Liquidity. J Financ (2010) 65:257–93. doi:10.1111/j.1540-6261.2009.01529.x

CrossRef Full Text | Google Scholar

5. Karolyi GA, Lee K-H, Van Dijk MA. Understanding Commonality in Liquidity Around the World. J Financial Econ (2012) 105:82–112. doi:10.1016/j.jfineco.2011.12.008

CrossRef Full Text | Google Scholar

6. Markowitz H. Portfolio Selection. J Finance (1952) 7:77–91. doi:10.2307/2975974

CrossRef Full Text | Google Scholar

7. Kenett DY, Huang X, Vodenska I, Havlin S, Stanley HE. Partial Correlation Analysis: Applications for Financial Markets. Quantitative Finance (2015) 15:569–78. doi:10.1080/14697688.2014.946660

CrossRef Full Text | Google Scholar

8. Tu C. Cointegration-based Financial Networks Study in Chinese Stock Market. Physica A: Stat Mech its Appl (2014) 402:245–54. doi:10.1016/j.physa.2014.01.071

CrossRef Full Text | Google Scholar

9. Billio M, Getmansky M, Lo AW, Pelizzon L. Econometric Measures of Connectedness and Systemic Risk in the Finance and Insurance Sectors. J Financial Econ (2012) 104:535–59. doi:10.1016/j.jfineco.2011.12.010

CrossRef Full Text | Google Scholar

10. Curme C, Tumminello M, Mantegna RN, Stanley HE, Kenett DY. Emergence of Statistically Validated Financial Intraday lead-lag Relationships. Quantitative Finance (2015) 15:1375–86. doi:10.1080/14697688.2015.1032545

CrossRef Full Text | Google Scholar

11. Bu H, Tang W, Wu J. Time-varying Comovement and Changes of Comovement Structure in the Chinese Stock Market: A Causal Network Method. Econ Model (2019) 81:181–204. doi:10.1016/j.econmod.2019.03.002

CrossRef Full Text | Google Scholar

12. Liu B-Y, Ji Q, Fan Y. A New Time-Varying Optimal Copula Model Identifying the Dependence across Markets. Quantitative Finance (2017) 17:437–53. doi:10.1080/14697688.2016.1205208

CrossRef Full Text | Google Scholar

13. Guo X, Zhang H, Tian T. Development of Stock Correlation Networks Using Mutual Information and Financial Big Data. PloS one (2018) 13:e0195941. doi:10.1371/journal.pone.0195941

PubMed Abstract | CrossRef Full Text | Google Scholar

14. de Carvalho PJC, Gupta A. A Network Approach to Unravel Asset price Comovement Using Minimal Dependence Structure. J Banking Finance (2018) 91:119–32. doi:10.1016/j.jbankfin.2018.04.012

CrossRef Full Text | Google Scholar

15. Mantegna RN. Hierarchical Structure in Financial Markets. Eur Phys J B (1999) 11:193–7. doi:10.1007/s100510050929

CrossRef Full Text | Google Scholar

16. Bonanno G, Caldarelli G, Lillo F, Mantegna RN. Topology of Correlation-Based Minimal Spanning Trees in Real and Model Markets. Phys Rev E (2003) 68:046130. doi:10.1103/PhysRevE.68.046130

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Oh G. Grouping Characteristics of Industry Sectors in Financial Markets. Physica A: Stat Mech its Appl (2014) 395:261–8. doi:10.1016/j.physa.2013.09.031

CrossRef Full Text | Google Scholar

18. Tumminello M, Aste T, Di Matteo T, Mantegna RN. A Tool for Filtering Information in Complex Systems. Proc Natl Acad Sci U.S.A (2005) 102:10421–6. doi:10.1073/pnas.0500298102

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Onnela J-P, Kaski K, Kertész J. Clustering and Information in Correlation Based Financial Networks. The Eur Phys J B - Condensed Matter (2004) 38:353–62. doi:10.1140/epjb/e2004-00128-7

CrossRef Full Text | Google Scholar

20. Tse CK, Liu J, Lau FCM. A Network Perspective of the Stock Market. J Empirical Finance (2010) 17:659–67. doi:10.1016/j.jempfin.2010.04.008

CrossRef Full Text | Google Scholar

21. Shi H-L, Zhou W-X. Horse Race of Weekly Idiosyncratic Momentum Strategies with Respect to Various Risk Metrics: Evidence from the Chinese Stock Market. North Am J Econ Finance (2021) 58:101478. doi:10.1016/j.najef.2021.101478

CrossRef Full Text | Google Scholar

22. Shi H-L, Jiang Z-Q, Zhou W-X. Profitability of Contrarian Strategies in the Chinese Stock Market. PLOS ONE (2015) 10:e0137892. doi:10.1371/journal.pone.0137892

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Cochrane JH. Presidential Address: Discount Rates. J Financ (2011) 66:1047–108. doi:10.1111/j.1540-6261.2011.01671.x

CrossRef Full Text | Google Scholar

24. Guo B, Zhang W, Zhang Y, Zhang H. The Five-Factor Asset Pricing Model Tests for the Chinese Stock Market. Pacific-Basin Finance J (2017) 43:84–106. doi:10.1016/j.pacfin.2017.02.001

CrossRef Full Text | Google Scholar

25. Lin Q. Noisy Prices and the Fama-French Five-Factor Asset Pricing Model in China. Emerging Markets Rev (2017) 31:141–63. doi:10.1016/j.ememar.2017.04.002

CrossRef Full Text | Google Scholar

26. Huang C, Deng Y, Yang X, Cao J, Yang X. A Network Perspective of Comovement and Structural Change: Evidence from the Chinese Stock Market. Int Rev Financial Anal (2021) 76:101782. doi:10.1016/j.irfa.2021.101782

CrossRef Full Text | Google Scholar

27. Chiang TC, Lao L, Xue Q. Comovements between Chinese and Global Stock Markets: Evidence from Aggregate and Sectoral Data. Rev Quant Finan Acc (2016) 47:1003–42. doi:10.1007/s11156-015-0529-x

CrossRef Full Text | Google Scholar

28. Chen P. Global Oil Prices, Macroeconomic Fundamentals and China's Commodity Sector Comovements. Energy Policy (2015) 87:284–94. doi:10.1016/j.enpol.2015.09.024

CrossRef Full Text | Google Scholar

29. Ross SA. The Arbitrage Theory of Capital Asset Pricing. J Econ Theor (1976) 13:341–60. doi:10.1016/0022-0531(76)90046-6

CrossRef Full Text | Google Scholar

30. Blitz D, Hanauer MX, Vidojevic M. The Idiosyncratic Momentum Anomaly. Int Rev Econ Finance (2020) 69:932–57. doi:10.1016/j.iref.2020.05.008

CrossRef Full Text | Google Scholar

31. Fama EF, French KR. A Five-Factor Asset Pricing Model. J Financial Econ (2015) 116:1–22. doi:10.1016/j.jfineco.2014.10.010

CrossRef Full Text | Google Scholar

32. Fama EF, French KR. Common Risk Factors in the Returns on Stocks and Bonds. J Financial Econ (1993) 33:3–56. doi:10.1016/0304-405X(93)90023-5

CrossRef Full Text | Google Scholar

33. Sharpe WF. Capital Asset Prices: a Theory of Market Equilibrium under Conditions of Risk*. J Finance (1964) 19:425–42. doi:10.1111/j.1540-6261.1964.tb02865.x

CrossRef Full Text | Google Scholar

34. Lintner J. The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets. Rev Econ Stat (1965) 47:13–37. doi:10.2307/1924119

CrossRef Full Text | Google Scholar

35. Mossin J. Equilibrium in a Capital Asset Market. Econometrica (1966) 34:768–83. doi:10.2307/1910098

CrossRef Full Text | Google Scholar

36. Fama EF, French KR. Dissecting Anomalies with a Five-Factor Model. Rev Financ Stud (2016) 29:69–103. doi:10.1093/rfs/hhv043

CrossRef Full Text | Google Scholar

37. Fama EF, French KR. International Tests of a Five-Factor Asset Pricing Model. J Financial Econ (2017) 123:441–63. doi:10.1016/j.jfineco.2016.11.004

CrossRef Full Text | Google Scholar

38. Spearman C. The Proof and Measurement of Association between Two Things. Am J Psychol (1904) 15:72–101. doi:10.2307/1412159

CrossRef Full Text | Google Scholar

39. Kendall MG. A New Measure of Rank Correlation. Biometrika (1938) 30:81–93. doi:10.1093/biomet/30.1-2.81

CrossRef Full Text | Google Scholar

40. Croux C, Dehon C. Influence Functions of the Spearman and Kendall Correlation Measures. Stat Methods Appl (2010) 19:497–515. doi:10.1007/s10260-010-0142-z

CrossRef Full Text | Google Scholar

41. Zheng Z, Yamasaki K, Tenenbaum JN, Stanley HE. Carbon-dioxide Emissions Trading and Hierarchical Structure in Worldwide Finance and Commodities Markets. Phys Rev E (2013) 87:012814. doi:10.1103/PhysRevE.87.012814

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Kruskal JB. On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem. Proc Amer Math Soc (1956) 7:48–50. doi:10.1090/s0002-9939-1956-0078686-7

CrossRef Full Text | Google Scholar

43. Newman MEJ. Scientific Collaboration Networks. I. Network Construction and Fundamental Results. Phys Rev E (2001) 64:016131. doi:10.1103/PhysRevE.64.016131

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Newman MEJ. Scientific Collaboration Networks. II. Shortest Paths, Weighted Networks, and Centrality. Phys Rev E (2001) 64:016132. doi:10.1103/PhysRevE.64.016132

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Opsahl T, Agneessens F, Skvoretz J. Node Centrality in Weighted Networks: Generalizing Degree and Shortest Paths. Social Networks (2010) 32:245–51. doi:10.1016/j.socnet.2010.03.006

CrossRef Full Text | Google Scholar

46. Bellingeri M, Bevacqua D, Scotognella F, Alfieri R, Nguyen Q, Montepietra D, et al. Link and Node Removal in Real Social Networks: A Review. Front Phys (2020) 8:228. doi:10.3389/fphy.2020.00228

CrossRef Full Text | Google Scholar

47. Markowitz H. Portfolio Selection*. J Finance (1952) 7:77–91. doi:10.2307/297597410.1111/j.1540-6261.1952.tb01525.x

CrossRef Full Text | Google Scholar

48. Hu GX, Chen C, Shao Y, Wang J. Fama-French in China: Size and Value Factors in Chinese Stock Returns. Int Rev Finance (2019) 19:3–44. doi:10.1111/irfi.12177

CrossRef Full Text | Google Scholar

49. Liu J, Stambaugh RF, Yuan Y. Size and Value in China. J Financial Econ (2019) 134:48–69. doi:10.1016/j.jfineco.2019.03.008

CrossRef Full Text | Google Scholar

50. Fenn DJ, Porter MA, Williams S, McDonald M, Johnson NF, Jones NS. Temporal Evolution of Financial-Market Correlations. Phys Rev E (2011) 84:026109. doi:10.1103/PhysRevE.84.026109

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Ross GJ. Dynamic Multifactor Clustering of Financial Networks. Phys Rev E (2014) 89:022809. doi:10.1103/PhysRevE.89.022809

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Shi H-L, Jiang Z-Q, Zhou W-X. Time-varying Return Predictability in the Chinese Stock Market. Rep Adv Phys Sci (2017) 01:1740002. doi:10.1142/S2424942417400023

CrossRef Full Text | Google Scholar

53. Shi H-L, Zhou W-X. Wax and Wane of the Cross-Sectional Momentum and Contrarian Effects: Evidence from the Chinese Stock Markets. Physica A: Stat Mech its Appl (2017) 486:397–407. doi:10.1016/j.physa.2017.05.078

CrossRef Full Text | Google Scholar

54. Fama EF, MacBeth JD. Risk, Return, and Equilibrium: Empirical Tests. J Polit Economy (1973) 81:607–36. doi:10.1086/260061

CrossRef Full Text | Google Scholar

55. Atilgan Y, Bali TG, Demirtas KO, Gunaydin AD. Left-tail Momentum: Underreaction to Bad News, Costly Arbitrage and Equity Returns. J Financial Econ (2020) 135:725–53. doi:10.1016/j.jfineco.2019.07.006

CrossRef Full Text | Google Scholar

56. Hou K, Xue C, Zhang L. Replicating Anomalies. Rev Financ Stud (2020) 33:2019–133. doi:10.1093/rfs/hhy131

CrossRef Full Text | Google Scholar

57. Ali U, Hirshleifer D. Shared Analyst Coverage: Unifying Momentum Spillover Effects. J Financial Econ (2020) 136:649–75. doi:10.1016/j.jfineco.2019.10.007

CrossRef Full Text | Google Scholar

58. Parsons CA, Sabbatucci R, Titman S. Geographic lead-lag Effects. Rev Financ Stud (2020) 33:4721–70. doi:10.1093/rfs/hhz145

CrossRef Full Text | Google Scholar

59. Diebold FX, Yılmaz K. On the Network Topology of Variance Decompositions: Measuring the Connectedness of Financial Firms. J Econom (2014) 182:119–34. doi:10.1016/j.jeconom.2014.04.012

CrossRef Full Text | Google Scholar

60. Diebold FX, Yilmaz K. Trans-Atlantic Equity Volatility Connectedness: U.S. And European Financial Institutions, 2004-2014. J Financial Econom (2015) 14:nbv021–127. doi:10.1093/jjfinec/nbv021

CrossRef Full Text | Google Scholar

61. Bostanci G, Yilmaz K. How Connected Is the Global Sovereign Credit Risk Network? J Banking Finance (2020) 113:105761. doi:10.1016/j.jbankfin.2020.105761

CrossRef Full Text | Google Scholar

62. Plerou V, Gopikrishnan P, Rosenow B, Amaral LAN, Guhr T, Stanley HE. Random Matrix Approach to Cross Correlations in Financial Data. Phys Rev E (2002) 65:066126. doi:10.1103/PhysRevE.65.066126

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Yoffe SR, Lehe R, Ersfeld B, Brunetti E, Vieux G, Noble A, et al. Particle-in-cell Simulation of Plasma-Based Amplification Using a Moving Window. Phys Rev Res (2020) 2:013227. doi:10.1103/PhysRevResearch.2.013227

CrossRef Full Text | Google Scholar

64. Marwan N, Wessel N, Meyerfeldt U, Schirdewan A, Kurths J. Recurrence-plot-based Measures of Complexity and Their Application to Heart-Rate-Variability Data. Phys Rev E (2002) 66:026702. doi:10.1103/PhysRevE.66.026702

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Moon Y-I, Rajagopalan B, Lall U. Estimation of Mutual Information Using Kernel Density Estimators. Phys Rev E (1995) 52:2318–21. doi:10.1103/PhysRevE.52.2318

CrossRef Full Text | Google Scholar

66. McDonald M, Suleman O, Williams S, Howison S, Johnson NF. Impact of Unexpected Events, Shocking News, and Rumors on Foreign Exchange Market Dynamics. Phys Rev E (2008) 77:046110. doi:10.1103/PhysRevE.77.046110

PubMed Abstract | CrossRef Full Text | Google Scholar