Ideal nodal net phonons in Pn3¯m type Ag2O

The topological phonon state is a new field that has sparked much interest. Weyl phonons in FeSi, for example, have been theoretically proposed and experimentally identified. In this work, via the first-principle calculation, we prove the ideal nodal net phonons exist in a realistic material Ag₂O with $Pn\overline{3}m$ type structure. With the help of the Berry phase calculations, we find that the nodal net phonons in Ag₂O are topologically non-trivial. The phononic surface states are visible, which benefits the experimental detections. The results in this work contribute to the material realization of topological nodal net phonons. The author hopes the experimental verification of the novel topological phonons can be performed in the following investigations.

Introduction

Topological semimetals [1–10] with symmetry-protected bands crossing around the Fermi level have inspired enormous interest in condensed matter physics. As a typical family of topological semimetals, node-line semimetals [11–20] have high band degeneracy along a certain line in the Brillouin zone (BZ), and the resultant drumhead surface states at the boundary. Suppose more than one nodal line/ring appears in momentum space. In that case, these nodal lines/rings may form complex topological nodal structures in the three-dimensional (3D) Brillouin zone (BZ), such as nodal-chain [21–28], nodal-box [29], nodal-link [30–35], and nodal-net [36, 37] structures.

Topological state research has recently been extended to bosonic systems, such as photons in photonic crystals, phonon systems in 3D solids, and classical elastic waves in macroscopic artificial phononic crystals. In realistic materials, topological phonons [38–45] could play an essential role in thermal transports, electron-phonon coupling, and other phonon-related processes. Thus far, researchers have predicted some realistic materials [46–65] to host nodal net phonons. For example, using first-principles calculations, [66] discovered a nodal net state in the semiconductor copper chloride (CuCl). CuCl has a cubic crystal structure with the space group Pa3 (No. 205). In momentum space, the nodal net has a hexahedral shape and is made up of interconnected quadruple degenerate straight nodal lines. Moreover, with the help of first-principle calculations and symmetry analysis, [67] proposed the coexistence of the three-nodal surface and nodal net phonons in space groups with numbers 61 and 205. Some realistic materials, such as ZnSb with SG No. 61 and RuS₂, P₂Pt, and OsS₂ with SG No. 205, hosting three-nodal surface and nodal net phonons have also been identified by [67].

In this paper, based on first-principles calculations, we contribute to one more realistic material with ideal nodal net phonons. Ag₂O is Cuprite structured and crystallizes in the cubic $Pn\overline{3}m$ space group. Ag¹⁺ is bonded in a linear geometry to two equivalent O²⁻ atoms. O²⁻ is bonded to four equivalent Ag¹⁺ atoms to form corner-sharing OAg₄ tetrahedra. The lattice constants for the cubic Ag₂O are optimized via first-principle calculations. The obtained results from the calculations for the lattice constants are a = b = c = 4.81 Å, which are in good agreement with the experimental data [68], i.e., a = b = c = 4.73 Å. The crystal structure of the relaxed Ag₂O is shown in Figure 1A, where the Ag atoms and O atoms occupy the 2a, and 4c Wyckoff positions, respectively.

FIGURE 1

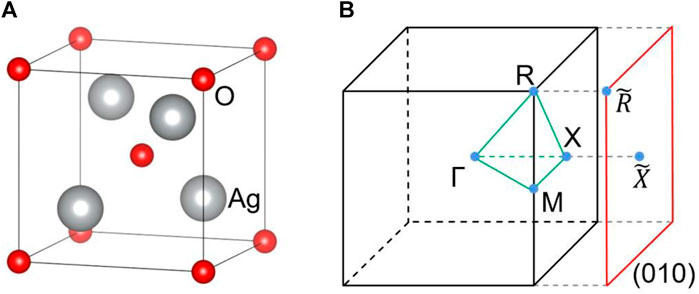
FIGURE 1. (A) The crystal structure of Ag₂O, (B) 3D bulk Brillouin zone (BZ), and the two-dimensional (2D) surface BZ.

Methods

The calculations for the realistic material Ag₂O were performed using the Vienna ab initio Simulation Package [69] and the framework of density functional theory. The calculation’s energy and force convergence criteria were set to 10⁻⁶ eV and −0.01 eV/A, respectively. The plane-wave expansion was truncated at 500 eV, and the entire BZ was sampled by a 7 × 7 × 7 Monkhorst-Pack grid. We used the PHONOPY code to generate the symmetry information and construct the constant force matrices for phonon spectra calculations. To calculate the phonon surface states, we used the WannierTools package [70] in conjunction with the iterative Green function method to construct the tight-binding model Hamiltonian.

Weyl nodal net phonons

Based on the determined lattice constants, the phonon dispersion for a 2 × 2 × 2 supercell of Ag₂O is shown in Figure 2A. Note that the phonon-related properties in this work are calculated based on the density functional perturbation theory (DFPT). According to Figure 2A, there is no imaginary frequency in the phonon spectrum, indicating the dynamical stability of cubic Ag₂O. Around the frequency of five THz, two phonon bands along X-R-Γ-M and Γ-X merged into one twofold degenerate phonon bands along the X-M path. We want to point out that a similar case can also be found around the frequency of 14 THz. Here, we only focus on the twofold degenerate phonon bands along the X-M path. The three-dimensional plot of the twofold degenerate phonon bands along the X-M is shown in Figure 2B, and one can see a cross-shaped nodal structure appears (see the dotted lines) in Figure 2B.

FIGURE 2

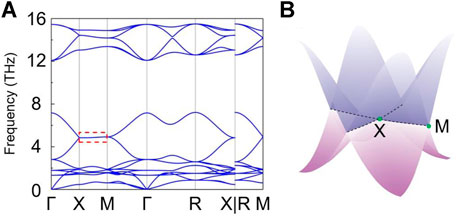
FIGURE 2. (A) Phonon dispersion of Ag₂O along the Γ-X-M-Γ-R-X|R-M paths. (B) The 3D plot of the cross-shaped nodal structure.

To better view the cross-shaped nodal structure in the phonon dispersion of Ag₂O, we plot the phonon band structure of the crossing branches in ky = π plane (See Figure 3A). The cross-shaped nodal structure in the k_y = π plane is formed from crossing two straight Weyl nodal lines. We select some symmetry points along the X-M path and show the phonon dispersions for Ag₂O along the a-b-a’, c-d-c’, e-f-e’, and g-h-g’ in Figure 3C. All the crossing points are doubly degenerate points with a linear phonon band dispersion (see Figure 3C). Note that the cross-shaped nodal structures can also exist in k_y = -π, k_x = ± π, k_z = ± π plane. That is, these straight nodal lines are perpendicular to each other in different planes, forming a Weyl nodal net in the 3D BZ, as illustrated in Figure 3B.

FIGURE 3

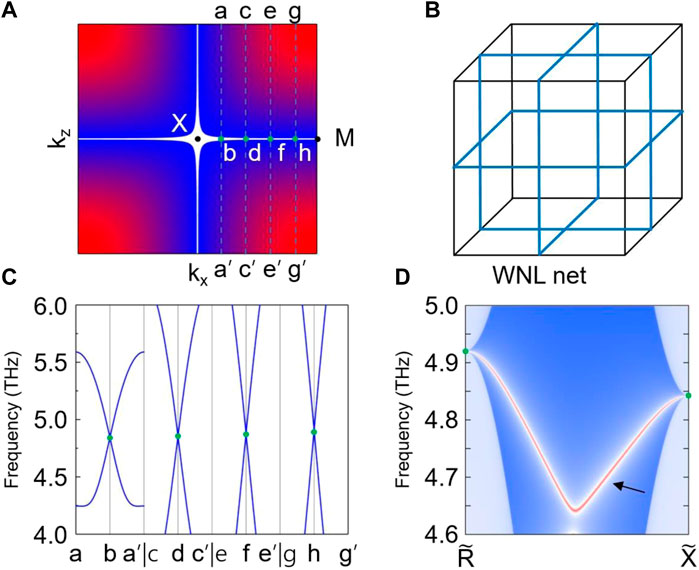
FIGURE 3. (A) A map of energy gaps between the two crossing branches around 5 THz in the ky = π plane. (B) A schematic diagram of Weyl nodal net in 3D BZ. (C) Phonon dispersions of Ag₂O along the a-b-a’, c-d-c’, e-f-e’, and g-h-g’ paths. (D) Phononic drumhead-like surface states in (010) surface.

Phononic surface states

To examine the topological nature of the Weyl nodal net phonons in Ag₂O, we calculate its Berry phase using the following formula: ${\gamma }_n={\oint }_C{A}_n\left(\mathbf{k}\right)\cdot d\mathbf{l}$, where $A_n\left(\mathbf{k}\right)=-i{{\displaystyle \sum }}_n〈u_n\left(\mathbf{k}\right)\left|{\nabla }_{\mathbf{k}}\right|u_n\left(\mathbf{k}\right)〉$ is the Berry connection. Calculated results show that the Weyl nodal net phonons host a π Berry phase, indicating topologically non-trivial behaviors. The non-trivial nodal net phonons will lead to phononic drumhead-like surface states. As shown in Figure 3D, we project the two Weyl points (belong to the Weyl net) into $\stackrel{\sim }{R}$ and $\stackrel{\sim }{X}$ surface points to the (010) surface (see Figure 2B). The phonon LDOS projected on the (010) surface BZ along $\stackrel{\sim }{R}$-$\stackrel{\sim }{X}$. Obviously, a clear drumhead-like surface state, connected by the projections of the Weyl points, is visible and marked by the black arrow. The bulk stats do not cover such a phononic surface state and would benefit the experimental detections shortly.

Summary and remarks

We show that nodal net phonons exist in Ag₂O using first-principles calculations. Straight lines constrained in the high-symmetry line X-M at the BZ boundary represent the nodal net. Because there is no spin in phononic systems, the nodal net phonons in Ag₂O are resistant to time-reversal symmetry breaking. Before closing the paper, we would like to point out that our results can also guide the investigations of the Weyl nodal net in spinless electronic systems (such as topological semimetals without the consideration of spin-orbital coupling). We present a spinless lattice model to demonstrate the existence of Weyl nodal net states in spinless materials with SG 224. A unit cell with one site (0,0,0) was considered in this spinless lattice model, and s orbital was placed on this site. The four-band tight-binding (TB) Hamiltonian is shown as follows: $\mathcal{H}=\left(\begin{array}{cccc}\mathrm{e}& \mathrm{A}& \mathrm{B}& \mathrm{C}\\ \mathrm{A}& \mathrm{e}& \mathrm{D}& \mathrm{E}\\ \mathrm{B}& \mathrm{D}& \mathrm{e}& \mathrm{F}\\ \mathrm{C}& \mathrm{E}& \mathrm{F}& \mathrm{e}\end{array}\right)$, where $A=4s\mathrm{Cos}\left(k_x\right)\mathrm{Cos}\left[\left(k_y+k_z\right)/2\right]$, $B=4s\cos \left(k_y\right)\mathrm{Cos}\left[\left(k_x+k_z\right)/2\right]$, $C=4s\mathrm{Cos}\left[\left(k_x+k_y\right)/2\right]\mathrm{Cos}\left(k_z\right)$, $D=4s\mathrm{Cos}\left[\left(k_x-k_y\right)/2\right]\mathrm{Cos}\left(k_z\right)$, $E=4s\mathrm{Cos}\left(k_y\right)\mathrm{Cos}\left[\left(k_x-k_z\right)/2\right]$, $\mathrm{F}=4\mathrm{s}\mathrm{C}\mathrm{o}\mathrm{s}\left({\mathrm{k}}_{\mathrm{x}}\right)\mathrm{Cos}\left[\left({\mathrm{k}}_{\mathrm{y}}-{\mathrm{k}}_{\mathrm{z}}\right)/2\right]$. When we set e = 0.4 and s = 0.1, the band structure of this spinless lattice model is shown in Figure 4. From Figure 4, one finds that the appearance of the Weyl nodal line along the X-M path further reflects the occurrence of the Weyl nodal net in 3D BZ.

FIGURE 4

FIGURE 4. Band structure of the spinless lattice model with SG 224.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Calculating, writing, and researching are done by YL.

Funding

This work is supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJZD-K202104101 and No. KJQN202204104) and the school-level Scientific Research Project of Chongqing Youth Vocational and Technical College (Grant No. CQY2021KYZ03).

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer HZ declared a shared affiliation with the author(s) add initials here unless all authors are concerned to the handling editor at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Burkov AA. Topological semimetals. Nat Mater (2016) 15(11):1145–8. doi:10.1038/nmat4788

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Gao H, Venderbos JW, Kim Y, Rappe AM. Topological semimetals from first principles. Annu Rev Mater Res (2019) 49:153–83. doi:10.1146/annurev-matsci-070218-010049

CrossRef Full Text | Google Scholar

3. Weng H, Dai X, Fang Z. Topological semimetals predicted from first-principles calculations. J Phys Condensed Matter (2016) 28(30):303rrrrrrrrrrr001. doi:10.1088/0953-8984/28/30/303001

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Bernevig A, Weng H, Fang Z, Dai X. Recent progress in the study of topological semimetals. J Phys Soc Jpn (2018) 87(4):041001. doi:10.7566/jpsj.87.041001

CrossRef Full Text | Google Scholar

5. Zhang X, Jin L, Dai X, Liu G. Topological type-II nodal line semimetal and Dirac semimetal state in stable kagome compound Mg₃Bi₂. J Phys Chem Lett (2017) 8(19):4814–9. doi:10.1021/acs.jpclett.7b02129

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Tian L, Liu Y, Meng W, Zhang X, Dai X, Liu G. Spin–orbit coupling-determined topological phase: Topological insulator and quadratic Dirac semimetals. J Phys Chem Lett (2020) 11(24):10340–7. doi:10.1021/acs.jpclett.0c03103

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Xu G, Wang W, Zhang X, Du Y, Liu E, Wang S, et al. Weak antilocalization effect and noncentrosymmetric superconductivity in a topologically nontrivial semimetal LuPdBi. Scientific Rep (2014) 4(1):5709–7. doi:10.1038/srep05709

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Meng W, Zhang X, He T, Jin L, Dai X, Liu Y, et al. Ternary compound HfCuP: An excellent Weyl semimetal with the coexistence of type-I and type-II Weyl nodes. J Adv Res (2020) 24:523–8. doi:10.1016/j.jare.2020.05.026r

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Chen DY, Wu Y, Jin L, Li Y, Wang X, Duan J, et al. Superconducting properties in a candidate topological nodal line semimetal SnTaS₂ with a centrosymmetric crystal structure. Phys Rev B (2019) 100(6):064516. doi:10.1103/physrevb.100.064516

CrossRef Full Text | Google Scholar

10. Wang X, Ding G, Cheng Z, Surucu G, Wang XL, Yang T. Rich topological nodal line bulk states together with drum-head-like surface states in NaAlGe with anti-PbFCl type structure. J Adv Res (2020) 23:95–100. doi:10.1016/j.jare.2020.01.017

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang X, Ding G, Khandy SA, Cheng Z, Zhang G, Wang XL, et al. Unique topological nodal line states and associated exceptional thermoelectric power factor platform in Nb₃GeTe₆ monolayer and bulk. Nanoscale (2020) 12(32):16910–6. doi:10.1039/d0nr03704d

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wang X, Ding G, Cheng Z, Surucu G, Wang XL, Yang T. Novel topological nodal lines and exotic drum-head-like surface states in synthesized CsCl-type binary alloy TiOs. J Adv Res (2020) 22:137–44. doi:10.1016/j.jare.2019.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang X, Cheng Z, Zhang G, Kuang M, Wang XL, Chen H. Strain tuning of closed topological nodal lines and opposite pockets in quasi-two-dimensional α-phase FeSi₂. Phys Chem Chem Phys (2020) 22(24):13650–8. doi:10.1039/d0cp02334e

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zhou F, Liu Y, Kuang M, Wang P, Wang J, Yang T, et al. Time-reversal-breaking Weyl nodal lines in two-dimensional A₃C₂ (A= Ti, Zr, and Hf) intrinsically ferromagnetic materials with high Curie temperature. Nanoscale (2021) 13(17):8235–41. doi:10.1039/d1nr00139f

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhou F, Cui C, Wang J, Kuang M, Yang T, Yu ZM, et al. Perovskite-type YRh₃B with multiple types of nodal point and nodal line states. Phys Rev B (2021) 103(24):245126. doi:10.1103/physrevb.103.245126

CrossRef Full Text | Google Scholar

16. Jin L, Zhang X, He T, Meng W, Dai X, Liu G. Topological nodal line state in superconducting NaAlSi compound. J Mater Chem C (2019) 7(34):10694–9. doi:10.1039/c9tc03464a

CrossRef Full Text | Google Scholar

17. He T, Zhang X, Wang L, Liu Y, Dai X, Wang L, et al. Ideal fully spin-polarized type-II nodal line state in half-metals X₂YZ₄ (X= K, Cs, Rb, YCr, Cu, Z= Cl, F). Mater Today Phys (2021) 17:100360. doi:10.1016/j.mtphys.2021.100360

CrossRef Full Text | Google Scholar

18. He T, Zhang X, Liu Y, Dai X, Wang L, Liu G. Potential antiferromagnetic Weyl nodal line state in LiTi₂O₄ material. Phys Rev B (2021) 104(4):045143. doi:10.1103/physrevb.104.045143

CrossRef Full Text | Google Scholar

19. Yang Z, Hu J. Non-Hermitian Hopf-link exceptional line semimetals. Phys Rev B (2019) 99(8):081102. doi:10.1103/physrevb.99.081102

CrossRef Full Text | Google Scholar

20. Li Y, Xia J. Cubic hafnium nitride: A novel topological semimetal hosting a 0-dimensional (0-D) nodal point and a 1-D topological nodal ring. Front Chem (2020) 8:727. doi:10.3389/fchem.2020.00727

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yu R, Wu Q, Fang Z, Weng H. From nodal chain semimetal to Weyl semimetal in HfC. Phys Rev Lett (2017) 119(3):036401. doi:10.1103/physrevlett.119.036401

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yan Q, Liu R, Yan Z, Liu B, Chen H, Wang Z, et al. Experimental discovery of nodal chains. Nat Phys (2018) 14(5):461–4. doi:10.1038/s41567-017-0041-4

CrossRef Full Text | Google Scholar

23. Zhang X, Jin L, Dai X, Chen G, Liu G. Ideal inner nodal chain semimetals in Li₂XY (X= Ca, Ba; Y= Si, Ge) materials. J Phys Chem Lett (2018) 9(18):5358–63. doi:10.1021/acs.jpclett.8b02204

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Chang G, Xu SY, Zhou X, Huang SM, Singh B, Wang B, et al. Topological Hopf and chain link semimetal states and their application to Co₂MnGa. Phys Rev Lett (2017) 119(15):156401. doi:10.1103/physrevlett.119.156401

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Fu B, Fan X, Ma D, Liu CC, Yao Y. Hourglasslike nodal net semimetal in Ag₂BiO₃. Phys Rev B (2018) 98(7):075146. doi:10.1103/physrevb.98.075146

CrossRef Full Text | Google Scholar

26. Chen C, Su Z, Zhang X, Chen Z, Sheng XL. From multiple nodal chain to Dirac/Weyl semimetal and topological insulator in ternary hexagonal materials. The J Phys Chem C (2017) 121(51):28587–93. doi:10.1021/acs.jpcc.7b11075

CrossRef Full Text | Google Scholar

27. Bzdušek T, Wu Q, Rüegg A, Sigrist M, Soluyanov AA. Nodal-chain metals. Nature (2016) 538(7623):75–8. doi:10.1038/nature19099

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gao Y, Xie Y, Chen Y, Gu J, Chen Z. Spindle nodal chain in three-dimensional α′ boron. Phys Chem Chem Phys (2018) 20(36):23500–6. doi:10.1039/c8cp03874k

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Sheng XL, Yu ZM, Yu R, Weng H, Yang SA. d orbital topological insulator and semimetal in the antifluorite Cu₂S family: Contrasting spin Helicities, nodal box, and hybrid surface states. J Phys Chem Lett (2017) 8(15):3506–11. doi:10.1021/acs.jpclett.7b01390

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yan Z, Bi R, Shen H, Lu L, Zhang SC, Wang Z. Nodal-link semimetals. Phys Rev B (2017) 96(4):041103. doi:10.1103/physrevb.96.041103

CrossRef Full Text | Google Scholar

31. Chang PY, Yee CH. Weyl-link semimetals. Phys Rev B (2017) 96(8):081114. doi:10.1103/physrevb.96.081114

CrossRef Full Text | Google Scholar

32. Zhou Y, Xiong F, Wan X, An J. Hopf-link topological nodal-loop semimetals. Phys Rev B (2018) 97(15):155140. doi:10.1103/physrevb.97.155140

CrossRef Full Text | Google Scholar

33. Liu Z, Lou R, Guo P, Wang Q, Sun S, Li C, et al. Experimental observation of Dirac nodal links in centrosymmetric semimetal TiB₂. Phys Rev X (2018) 8(3):031044. doi:10.1103/physrevx.8.031044

CrossRef Full Text | Google Scholar

34. Chen W, Lu HZ, Hou JM. Topological semimetals with a double-helix nodal link. Phys Rev B (2017) 96(4):041102. doi:10.1103/physrevb.96.041102

CrossRef Full Text | Google Scholar

35. Tan X, Li M, Li D, Dai K, Yu H, Yu Y. Demonstration of Hopf-link semimetal bands with superconducting circuits. Appl Phys Lett (2018) 112(17):172601. doi:10.1063/1.5029439

CrossRef Full Text | Google Scholar

36. Wang JT, Nie S, Weng H, Kawazoe Y, Chen C. Topological nodal-net semimetal in a graphene network structure. Phys Rev Lett (2018) 120(2):026402. doi:10.1103/physrevlett.120.026402

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Feng X, Yue C, Song Z, Wu Q, Wen B. Topological Dirac nodal-net fermions in AlB₂-type TiB₂ and ZrB₂. Phys Rev Mater (2018) 2(1):014202. doi:10.1103/physrevmaterials.2.014202

CrossRef Full Text | Google Scholar

38. Wang X, Zhou F, Yang T, Kuang M, Yu ZM, Zhang G. Symmetry-enforced ideal lanternlike phonons in the ternary nitride Li6WN4. Phys Rev B (2021) 104(4):L041104. doi:10.1103/physrevb.104.l041104

CrossRef Full Text | Google Scholar

39. Zhou F, Chen H, Yu ZM, Zhang Z, Wang X. Realistic cesium fluogermanate: An ideal platform to realize the topologically nodal-box and nodal-chain phonons. Phys Rev B (2021) 104(21):214310. doi:10.1103/physrevb.104.214310

CrossRef Full Text | Google Scholar

40. Xie C, Liu Y, Zhang Z, Zhou F, Yang T, Kuang M, et al. Sixfold degenerate nodal-point phonons: Symmetry analysis and materials realization. Phys Rev B (2021) 104(4):045148. doi:10.1103/physrevb.104.045148

CrossRef Full Text | Google Scholar

41. Wang X, Yang T, Cheng Z, Surucu G, Wang J, Zhou F, et al. Topological nodal line phonons: Recent advances in materials realization. Appl Phys Rev (2022) 9(4):041304. doi:10.1063/5.0095281

CrossRef Full Text | Google Scholar

42. Ding G, Zhou F, Zhang Z, Yu ZM, Wang X. Charge-two Weyl phonons with type-III dispersion. Phys Rev B (2022) 105(13):134303. doi:10.1103/physrevb.105.134303

CrossRef Full Text | Google Scholar

43. Liu Y, Chen X, Xu Y. Topological phononics: From fundamental models to real materials. Adv Funct Mater (2020) 30(8):1904784. doi:10.1002/adfm.201904784

CrossRef Full Text | Google Scholar

44. Liu Y, Lian CS, Li Y, Xu Y, Duan W. Pseudospins and topological effects of phonons in a kekulé lattice. Phys Rev Lett (2017) 119(25):255901. doi:10.1103/physrevlett.119.255901

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Liu Y, Zou N, Zhao S, Chen X, Xu Y, Duan W. Ubiquitous topological states of phonons in solids: Silicon as a model material. Nano Lett (2022) 22(5):2120–6. doi:10.1021/acs.nanolett.1c04299

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Wang J, Yuan H, Kuang M, Yang T, Yu ZM, Zhang Z, et al. Coexistence of zero-one-and two-dimensional degeneracy in tetragonal SnO₂ phonons. Phys Rev B (2021) 104(4):L041107. doi:10.1103/physrevb.104.l041107

CrossRef Full Text | Google Scholar

47. Zhong M, Han Y, Wang J, Liu Y, Wang X, Zhang G. Material realization of double-Weyl phonons and phononic double-helicoid surface arcs with P213 space group. Phys Rev Mater (2022) 6(8):084201. doi:10.1103/physrevmaterials.6.084201

CrossRef Full Text | Google Scholar

48. Xie C, Yuan H, Liu Y, Wang X, Zhang G. Three-nodal surface phonons in solid-state materials: Theory and material realization. Phys Rev B (2021) 104(13):134303. doi:10.1103/physrevb.104.134303

CrossRef Full Text | Google Scholar

49. Feng Y, Xie C, Chen H, Liu Y, Wang X. Dirac point phonons at high-symmetry points: Towards materials realization. Phys Rev B (2022) 106(13):134307. doi:10.1103/physrevb.106.134307

CrossRef Full Text | Google Scholar

50. Chen J, He J, Pan D, Wang X, Yang N, Zhu J, et al. Emerging theory and phenomena in thermal conduction: A selective review. Sci China Phys Mech Astron (2022) 65(11):117002–16. doi:10.1007/s11433-022-1952-3

CrossRef Full Text | Google Scholar

51. Yang T, Xie C, Chen H, Wang X, Zhang G. Phononic nodal points with quadratic dispersion and multifold degeneracy in the cubic compound Ta₃Sn. Phys Rev B (2022) 105(9):094310. doi:10.1103/physrevb.105.094310

CrossRef Full Text | Google Scholar

52. Wang X, Zhou F, Zhang Z, Wu W, Yu ZM, Yang SA. Single pair of multi-Weyl points in nonmagnetic crystals. Phys Rev B (2022) 106(19):195129. doi:10.1103/physrevb.106.195129

CrossRef Full Text | Google Scholar

53. Li J, Wang L, Liu J, Li R, Zhang Z, Chen XQ. Topological phonons in graphene. Phys Rev B (2020) 101(8):081403. doi:10.1103/physrevb.101.081403

CrossRef Full Text | Google Scholar

54. Singh S, Wu Q, Yue C, Romero AH, Soluyanov AA. Topological phonons and thermoelectricity in triple-point metals. Phys Rev Mater (2018) 2(11):114204. doi:10.1103/physrevmaterials.2.114204

CrossRef Full Text | Google Scholar

55. Süsstrunk R, Huber SD. Classification of topological phonons in linear mechanical metamaterials. Proc Natl Acad Sci (2016) 113(33):E4767–75. doi:10.1073/pnas.1605462113

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Sreeparvathy PC, Mondal C, Barman CK, Alam A. Coexistence of multifold and multidimensional topological phonons in KMgBO₃. Phys Rev B (2022) 106(8):085102. doi:10.1103/physrevb.106.085102

CrossRef Full Text | Google Scholar

57. You JY, Sheng XL, Su G. Topological gimbal phonons in T-carbon. Phys Rev B (2021) 103(16):165143. doi:10.1103/physrevb.103.165143

CrossRef Full Text | Google Scholar

58. Liu QB, Wang ZQ, Fu HH. Ideal topological nodal-surface phonons in RbTeAu-family materials. Phys Rev B (2021) 104(4):L041405. doi:10.1103/physrevb.104.l041405

CrossRef Full Text | Google Scholar

59. Chen XQ, Liu J, Li J. Topological phononic materials: Computation and data. The Innovation (2021) 2(3):100134. doi:10.1016/j.xinn.2021.100134

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Zhang T, Song Z, Alexandradinata A, Weng H, Fang C, Lu L, et al. Double-Weyl phonons in transition-metal monosilicides. Phys Rev Lett (2018) 120(1):016401. doi:10.1103/physrevlett.120.016401

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Liu QB, Wang ZQ, Fu HH. Topological phonons in allotropes of carbon. Mater Today Phys (2022) 24:100694. doi:10.1016/j.mtphys.2022.100694

CrossRef Full Text | Google Scholar

62. Jin YJ, Chen ZJ, Xia BW, Zhao YJ, Wang R, Xu H. Ideal intersecting nodal-ring phonons in bcc C₈. Phys Rev B (2018) 98(22):220103. doi:10.1103/physrevb.98.220103

CrossRef Full Text | Google Scholar

63. Miao H, Zhang TT, Wang L, Meyers D, Said AH, Wang YL, et al. Observation of double Weyl phonons in parity-breaking FeSi. Phys Rev Lett (2018) 121(3):035302. doi:10.1103/physrevlett.121.035302

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Liu Y, Xu Y, Duan W, 2019. Research (2019). p. 1–8. doi:10.34133/2019/5173580Three-dimensional topological states of phonons with tunable pseudospin physicsResearch

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Wang Z, Zhou W, Rudenko AN, Yuan S. Lattice dynamics and topological surface phonon states in cuprous oxide Cu₂O. Phys Rev B (2021) 103(19):195137. doi:10.1103/physrevb.103.195137

CrossRef Full Text | Google Scholar

66. Liu QB, Fu HH, Wu R. Topological phononic nodal hexahedron net and nodal links in the high-pressure phase of the semiconductor CuCl. Phys Rev B (2021) 104(4):045409. doi:10.1103/physrevb.104.045409

CrossRef Full Text | Google Scholar

67. Wang J, Yuan H, Yu ZM, Zhang Z, Wang X. Coexistence of symmetry-enforced phononic Dirac nodal-line net and three-nodal surfaces phonons in solid-state materials: Theory and materials realization. Phys Rev Mater (2021) 5(12):124203. doi:10.1103/physrevmaterials.5.124203

CrossRef Full Text | Google Scholar

68. Norby P, Dinnebier R, Fitch AN. Decomposition of silver carbonate; the crystal structure of two high-temperature modifications of Ag₂CO₃. Inorg Chem (2002) 41(14):3628–37. doi:10.1021/ic0111177

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Sun G, Kürti J, Rajczy P, Kertesz M, Hafner J, Kresse G. Performance of the Vienna ab initio simulation package (VASP) in chemical applications. J Mol Struct THEOCHEM (2003) 624(1-3):37–45. doi:10.1016/s0166-1280(02)00733-9

CrossRef Full Text | Google Scholar

70. Wu Q, Zhang S, Song HF, Troyer M, Soluyanov AA. WannierTools: An open-source software package for novel topological materials. Comp Phys Commun (2018) 224:405–16. doi:10.1016/j.cpc.2017.09.033

CrossRef Full Text | Google Scholar