Multiple-symmetry-protected lantern-like nodal walls in lithium-rich compound LiRuO2

Topological semimetals have attracted wide attention due to their potential applications, such as electronic devices and electrocatalysis. Herein, based on the first-principles calculations and symmetry analysis, we first report that ternary compound pnnm-type LiRuO₂ is a typical lantern-like nodal wall semimetal. Specifically, without considering spin-orbit coupling (SOC), one-dimensional (1D) two-fold degenerate bands on the k_i = ±π (i = x, y) planes form the two-dimensional (2D) topological state (namely, nodal surface) under the constraint of multiple symmetry operations. In addition, the symmetry-enforced nodal network is formed on the k_z = ±π planes. Finally, these nodal networks and nodal surfaces are coupled together to form lantern-like nodal walls. Remarkably, these topological states are protected by multiple symmetries, namely, nonsymmorphic two-fold screw-rotational symmetry [S_2i (i = x, y)], time-reversal symmetry (T), inversion symmetry (I), glide plane symmetry (σ_z), and two-fold rotational symmetry (C_2x/y). In addition, we further discuss the effect of spin-orbit coupling on the lantern-like nodal walls. We find that even if LiRuO₂ contains S_2z and T symmetries, these nodal surfaces and nodal networks are still broken. Then, due to the existence of I and T symmetries, Dirac nodal lines and Dirac points are formed in the low-energy region. Therefore, our work indicates that LiRuO₂ is an excellent material platform for researching multiple topological states.

1 Introduction

Topological insulators (TIs) have attracted extensive attention in condensed matter physics due to the fact that they possess the Dirac cone feature on some specific surfaces [1–3]. Inspired by TIs, the researchers found that there exist multiple types of crossing points near the Fermi level in some electronic band structures with a metal feature. Under some symmetry operations, such as mirror plane symmetry, glide plane symmetry, and inversion/time-reversal symmetries, these crossing points generate topological states of different dimensions. It is well known that the high-dimensional fermions usually originate from topological states of a lower dimension. Among them, the most typical example is that the one-dimensional Weyl/Dirac nodal line [4–10] is actually formed by countless zero-dimensional Weyl/Dirac points [11–20]. In other words, a two-dimensional nodal surface [21–25] is made up of countless one-dimensional nodal lines. In this case, the classification of topological semimetals is greatly expanded. Thus, topological states with different dimensions exhibit a variety of interesting properties, such as opposite chirality [11–15], Fermi arc or drumhead-like surface states [4–10], and high surface density of states [26–29]. These properties make topological semimetals have important application prospects in electronic devices or electrocatalysis [e.g., hydrogen evolution reaction (HER) and N₂ cleavage] [26–31].

It is well known that with the increase of dimensions, topological fermions usually require higher symmetry operations. So far, the topological fermion with the highest dimension has been theoretically proved to be a two-dimensional nodal surface. Wu et al. [21] and Yu et al. [32] analyzed that there exist only three possible for nodal surfaces, namely one (a), two (b), or three (c) nodal surfaces, as shown in Figures 1A–C. At present, in electronic systems, a large number of topological nodal surface semimetals have been reported [21–35], such as hexagonal compounds XTiO₂ (X = Li, Na, and K Rb) [22], Ti₃Al family [23], quasi-one-dimensional half-metals XYZ₃ (X = Ca, Rb, Y = Cr, Cu, and Z = Cl, I) [24], electride Ba₄Al₅ [25], and Sr₅X₃ (X = As, Sb, and Bi) [33]. We can find that more nodal surface semimetals only exist in one nodal surface, while reported two and three nodal surfaces are mainly concentrated in phonon systems [36–38]. Interestingly, in these phonon systems, Wang et al. [38] found that P42/nmc-type Li₆WN₄ material possesses a novel topological phase, namely ideal lantern-like phonons. This lantern-like phonon is composed of two nodal surfaces and two symmetry-enforced nodal networks, as shown in Figure 1D. To the best of our knowledge, this novel topological phase may not have been reported in electronic systems. Therefore, it is urgent to find the real materials with this topological state in the electronic system.

FIGURE 1

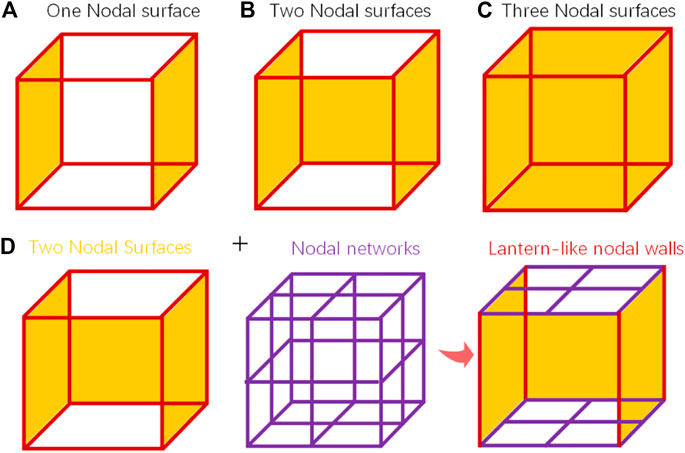
FIGURE 1. (A) Schematic diagrams of (A) one nodal surface, (B) two nodal surfaces, (C) three nodal surfaces, and (D) lantern-like nodal walls.

In this work, we first report that the synthesized ternary compound LiRuO₂ possesses this novel type of topological state, namely lantern-like nodal wall. Specifically, in compound LiRuO₂, there exist two-fold degenerate bands along k-paths X-S-R-U (k_x = π) and Y-S-R-T (k_y = π). Under the combined operation of S_2x/y and T symmetries, these degenerate bands form two-dimensional nodal surfaces on k_x = π and k_y = π planes. In addition, a symmetry-enforced nodal network is formed on the k_z = π surface due to the existence of a two-fold rotational symmetry (C_2x/y) along the k_x/y directions, glide plane (σ_z), inversion-reversal (I), and T symmetry. Finally, two nodal networks and two nodal surfaces form the lantern-like nodal wall. However, when spin-orbit coupling (SOC) is considered, the lantern-like nodal wall is broken and transformed into Dirac points (located at Z point) and Dirac nodal lines (on k_z = 0 and k_y = π planes) under IT symmetries.

2 Calculations and results

2.1 Crystal and electronic structures

Figures 2A,B show the crystal structure and the Brillouin zone (BZ) of LiRuO₂. It possesses a typical orthorhombic structure and belongs to the space group Pnnm (No. 58). The primitive cell of LiRuO₂ contains eight atoms [see 3) of Figure 2A], namely, two Li atoms at the 2c Wyckoff position (0,0, and 1/2), two Ru atoms at the 2a Wyckoff position (1/2, 1/2, and 1/2), and four O atoms at the 4 g Wyckoff position (0, 0.67, and 0.75). From the crystal structure, we can find that six O atoms form a tilted octahedron, and Ru atoms are contained in the body center, while Li atoms form a one-dimensional chain along the c-axis [see (I and 2) of Figure 2A]. In fact, LiRuO₂ is the final configuration in which the abundant lithium ions are inserted into the anodic material RuO₂. Specifically, researchers [39] have proved that RuO₂ with a hexagonal structure is an excellent anode material. Then, RuO₂ was ground into powder, mixed with Li in proportion, and placed in acetone and dibutyl phthalate to form the final lithium-ion battery LiRuO₂ with an orthorhombic structure [see Figure 2C]. Interestingly, we find that LiRuO₂ shows abundant degenerate bands near the Fermi level from its electronic band structure. As shown in Figure 2D, the k-paths Y-S-R-T-Y (k_x = π), X-S-R-U-X (k_y = π), and Z-U-R-T-Z (k_z = π) are all two-fold degenerate bands, and these bands are mainly contributed by O atoms of octahedron and Ru atoms of body center, as shown in Figure 2E. Finally, these degenerate bands form a new type of lantern-like nodal wall under multiple symmetric operations.

FIGURE 2

FIGURE 2. Crystal structure (A) and Brillouin zone (B) of LiRuO₂. Among them, the primitive cell (iii) of LiRuO₂ is formed by countless O atoms with a tilted octahedron, Ru atoms with a body center, and Li atoms with a one-dimensional chain (ii). (C) Anode material RuO₂ with a tetragonal structure forms the final LiRuO₂ with an orthorhombic structure by inserting lithium ions. The electronic band structure without SOC (D) and the density of states (E) of LiRuO₂, where the arrows point the two-fold degenerate bands of all k-paths.

2.2 Lantern-like nodal wall

Since the lantern-like nodal wall is composed of two nodal networks and two nodal surfaces, we will analyze the two topological states one by one from two aspects of symmetry operations and DFT calculations.

2.2.1 Analysis of symmetry

In space group (SG) 58, the symmetry operations contain: two-fold screw symmetries: $S_{2y}=\left\{x,y,z\right\}\to \left\{-x+\frac{1}{2},y+\frac{1}{2},-z+\frac{1}{2}\right\}$, $S_{2x}=\left\{x,y,z\right\}\to \left\{x+\frac{1}{2},-y+\frac{1}{2}-z+\frac{1}{2}\right\}$, inversion symmetry: $I=\left\{x,y,z\right\}\to \left\{-x,-y,-z\right\}$, rotation symmetries: $C_{2y}=\left\{x,y,z\right\}\to \left\{x+\frac{1}{2},-y+\frac{1}{2},z\right\}$, $C_{2x}=\left\{x,y,z\right\}\to \left\{-x+\frac{1}{2},y+\frac{1}{2},z\right\}$, $C_{2z}=\left\{x,y,z\right\}\to \left\{-x,-y,z\right\}$, mirror symmetry: $M_x=\left\{x,y,z\right\}\to \left\{-x,y,z\right\}$, $M_y=\left\{x,y,z\right\}\to \left\{x,-y,z\right\}$, $M_z=\left\{x,y,z\right\}\to \left\{x,y,-z\right\}$, glide symmetries: ${\sigma }_z=\left\{x,y,z\right\}\to \left\{x,y,-z+\frac{1}{2}\right\}$, ${\sigma }_x=\left\{x,y,z\right\}\to \left\{x+\frac{1}{2},-y+\frac{1}{2},z+\frac{1}{2}\right\}$, ${\sigma }_x=\left\{x,y,z\right\}\to \left\{-x+\frac{1}{2},y+\frac{1}{2},z+\frac{1}{2}\right\}$, and T symmetry. Based on Yu et al.‘s report [32], when rotation [C_i (i = x, y, z)], glide plane (σ_i), I, and T symmetries are organized together, causing the formation of symmetry-enforced two-fold degenerate bands along high-symmetry-paths. According to the aforementioned symmetry operations, we can find that SG 58 can form symmetry-enforced nodal networks on k_x/k_y/k_z = ±π planes. In addition, based on the work of Wu et al. [21], when the two-fold screw symmetry [S_2i (i = x, y, z)] is combined with the T symmetry [namely, ${\left({TS}_{2i}\right)}^2=e^{-i{k}_i}=-1,$ where $k_i$ is $k_i=\pi$ surface], 2D nodal surfaces can be formed in momentum space. Remarkably, SG 58 contains S_2x and S_2y and T symmetries, indicating a Kramer-like degeneracy can be formed on k_x and k_y = ±π planes. In other words, the nodal networks on k_x/k_y planes also belong to a part of the nodal surfaces are protected by [S_2x/2yT].

2.2.2 Nodal networks

By DFT calculation, we find that the calculated results in LiRuO₂ compound are consistent with the symmetry analysis. Specifically, as shown in Figure 3A, we can find that these bands along k-paths Г-Y, Г-X, Г-Z are single band. Based on group theoretic analysis, the irreducible representations of these single bands are {R₁, R₂, R₃, and R₄}. Finally, these single bands form symmetry-enforced two-fold degenerate bands [namely open nodal line] along k-paths Y-S-R-T-Y (k_x = π), X-S-R-U-X (k_y = π), and Z-U-R-T-Z (k_z = π) [See Figure 3B]. In addition, the irreducible representations of these nodal lines on k_x = π, k_y = π, and k_z = π are {R₂, R₄}, {R₆, R₈}, and R₅, respectively. Due to the existence of M_x/y/z symmetries, these nodal lines finally form the nodal network on different surfaces, as shown in Figure 3C. Remarkably, based on the symmetry analysis and the following DFT verification, the nodal network on the k_x/y planes actually belongs to part of the two nodal surfaces. It is well known that a pair of Weyl points of opposite chirality are connected by a one-dimensional Fermi arc, as shown in 1) of Figure 3D. For LiRuO₂ compound, these nodal lines on k_z = π are composed of countless zero-dimensional Weyl points. Thus, the surface state of nodal line is connected by countless one-dimensional Fermi arcs, namely drumhead-like surface state, as shown in 2) of Figure 3D. In this case, compared with the Weyl semimetals, the surfaces of nodal line semimetals possess higher density of states (DOSs), as shown in 3) of Figure 3D. Based on some reports of topological catalysis [26–31], high surface DOS [namely (001) surface] may possess potential application prospects for the catalytic performance.

FIGURE 3

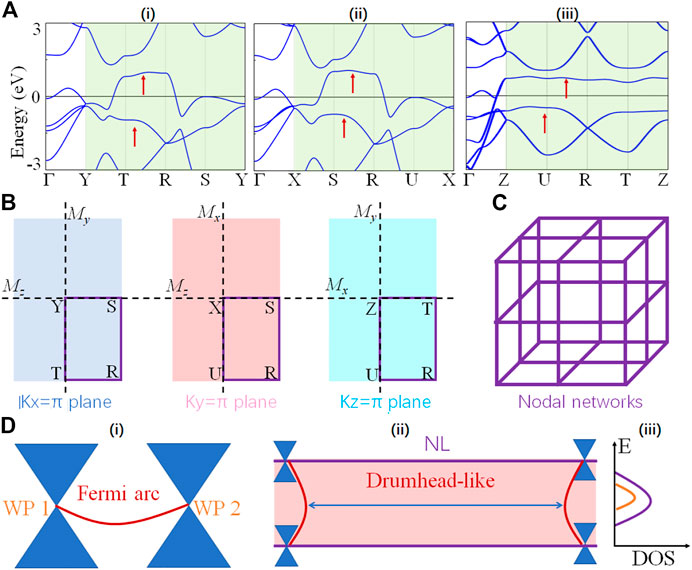
FIGURE 3. (A) Electronic band structures along k-paths (i) Y-S-R-T-Y (k_x = π), (ii) X-S-R-U-X (k_y = π), and (iii) Z-U-R-T-Z (k_z = π) (B) Different surfaces of LiRuO₂ in momentum space, where these purple lines represent the node lines. These nodal lines finally form the nodal networks on different surfaces (C). (D) Schematic diagram of the surface states for (i) Wey point (WP) and (ii) nodal line (NL).

2.2.3 Two nodal surfaces

By symmetry analysis, the nodal lines on the k_x = π/k_y = π planes should belong to a part of two nodal surfaces. In this section, we verify the existence of two nodal surfaces by DFT calculation. Figure 4A shows the electronic band structure along the highly symmetric paths on the k_x = π/k_y = π planes. Then, we denote the midpoints of the T-S (R-Y) and X-R (U-S) paths as B and D [See Figure 4B]. Obviously, we can clearly observe that the two linear single bands cross at B and D points, as shown in Figure 4C. In other words, the whole surfaces of k_x = π/k_y = π are double degenerate bands. Furthermore, the three-dimensional dispersion bands on k_x = π and k_x = 0.8π planes are calculated, as shown in Figure 4D. We find that when on the k_x = π plane, the two single bands are combined to form a curved double degenerate surface. On the contrary, the bands on the k_x = 0.8π plane evolves into four curved single bands due to the absence of S_2x symmetry. Therefore, the aforementioned DFT calculations fully confirm that the k_x = π/k_y = π planes are the double degenerate surfaces, which agree well with the results of the symmetry analysis. In addition, the surface states of zero-dimensional nodal points and one-dimensional nodal lines are one-dimensional Fermi arcs and two-dimensional drumhead-like, respectively. In other words, the dimension of the surface state is one dimension higher than that of the topological fermion. Since the highest dimension of the projected surface in three-dimensional materials is a two-dimensional surface, there is no surface state for nodal surface.

FIGURE 4

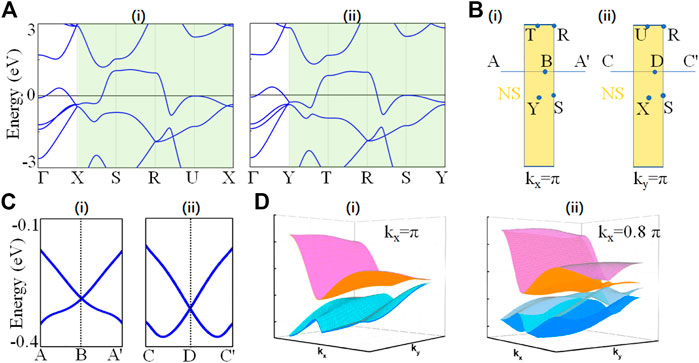
FIGURE 4. (A) Electronic band structures along k-paths (i) Y-S-R-T-Y (k_x = π) and (ii) X-S-R-U-X (k_y = π) (B) Some symmetry points of (i) k_x = π/(ii) k_y = π planes for LiRuO₂ in momentum space. (C) Electronic band structure along k-paths (i) A-B-A′ and (ii) C-D-C’. (D) Three-dimensional dispersion bands on k_x = π and k_x = 0.8π planes.

3 Discussions and conclusion

Before concluding the discussion, we also discuss the effect of SOC on the lantern-like nodal wall. As reported by Wu et al. [21], all types of topological nodal surfaces may be destroyed after considering SOC but may be retained in containing the combined nonsymmorphic two-fold screw-rotational and T symmetries. For LiRuO₂ compound, we find that even if this material contains S_2z and T symmetries, the two nodal surfaces and two nodal networks are broken, as shown in Figure 5A. Due to the existence of IT symmetries, Dirac points and Dirac nodal lines are finally formed on the high symmetric point Z and the k-paths X-S-Y (k_z = 0), S-R (k_y = π), respectively [See Figures 5B,C]. It is worth noting that these Dirac points and Dirac nodal lines are composed of a pair of Weyl points with opposite chirality (C = ±1). In other words, the Chern number of these Dirac states are 0 (C = 0). That is, these Dirac states do not have topologically protected Fermi arc and drumhead surface states.

FIGURE 5

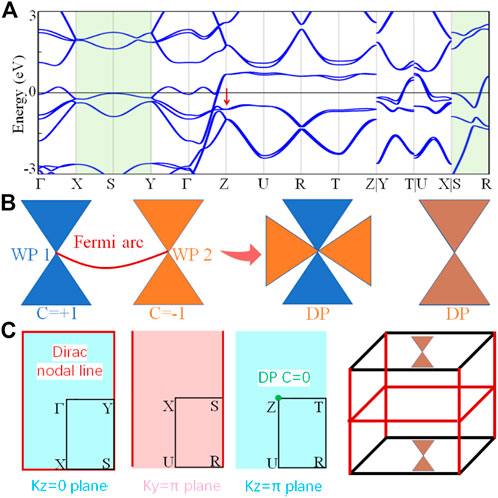
FIGURE 5. (A) Electronic band structures with SOC for LiRuO₂ compound. (B) Schematic diagram of a pair of Weyl points with opposite chirality and Dirac point. Among them, the two Dirac points are formed by four single bands and two double degenerate bands. (C) Different surfaces of LiRuO₂ in momentum space, where these red lines and green dot represent the node lines and Dirac point, respectively.

In conclusion, we find that two nodal surfaces exist on the k_x = ±π and k_y = ±π planes of LiRuO₂. These nodal surfaces are protected by nonsymmorphic two-fold screw-rotational (S_2x/S_2y) and T symmetries and are classified to the second class (class-II) of nodal surfaces. In addition, the symmetry-enforced nodal network is formed on the k_z = ±π surfaces due to the existence of a two-fold rotational symmetry (C_2x/y), glide plane (σ_z), inversion-reversal (I), and T symmetries. Finally, the two nodal networks and two nodal surfaces form the lantern-like nodal wall.

4 Calculation methods

In this work, the first-principles calculations were performed in the framework of density functional theory (DFT) by using the Vienna ab initio simulation package (VASP) [40, 41]. For ionic potentials, the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) method is used [42]. The cutoff energy was adopted as 550 eV, and the Brillouin zone was sampled with Γ-centered k-point mesh of 9 × 9×11 for both structural optimization and self-consistent calculations. The energy convergence criteria were chosen as 10⁻⁵ eV. In addition, the DFT + U method was used to calculate the band structures of compound LiRuO₂ (U_Ru = 3eV) [43]. We find that the change of the electronic band structure is weak at different U values, which is similar to some of the previous reports [13, 44].

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

HG and WM: manuscript writing, data computing, and data analysis LW: band analysis. JD: modifying the article.

Funding

This study was funded by the Beijing Nova Program (Beijing Municipal Science and Technology Commission, Grant No. Z211100002121079) and Post-graduate’s Innovation Fund Project of Hebei Province (Department of Education of Hebei Province, Grant No. CXZZBS2022036).

Acknowledgments

The authors acknowledge the computational support from the Texas Advanced Computing Center.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hasan MZ, Kane CL. Colloquium: Topological insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/revmodphys.82.3045

CrossRef Full Text | Google Scholar

2. Qi X-L, Zhang S-C. Topological insulators and superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/revmodphys.83.1057

CrossRef Full Text | Google Scholar

3. Bansil A, Lin H, Das T. Colloquium: Topological band theory. Rev Mod Phys (2016) 88:021004. doi:10.1103/revmodphys.88.021004

CrossRef Full Text | Google Scholar

4. Wang XT, Yang T, Cheng ZX, Surucu G, Wang J, Zhou F, et al. Topological nodal line phonons: Recent advances in materials realization. Appl Phys Rev (2022) 9:041304. doi:10.1063/5.0095281

CrossRef Full Text | Google Scholar

5. Jin L, Zhang X, Liu Y, DaiShen XX, Wang L, Liu G, et al. Two-dimensional Weyl nodal-line semimetal in a d⁰ ferromagnetic K₂N monolayer with a high Curie temperature. Phys Rev B (2020) 102:125118. doi:10.1103/physrevb.102.125118

CrossRef Full Text | Google Scholar

6. Yang SA, Pan H, Zhang F. Dirac and Weyl superconductors in three dimensions. Phys Rev Lett (2014) 113:046401. doi:10.1103/physrevlett.113.046401

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yu R, Weng H, Fang Z, Dai X, Hu X. Topological node-line semimetal and Dirac semimetal state in antiperovskite Cu₃PdN. Phys Rev Lett (2015) 115:036807. doi:10.1103/physrevlett.115.036807

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kim Y, Wieder BJ, Kane CL, Rappe AM. Dirac line nodes in inversion-symmetric crystals. Phys Rev Lett (2015) 115:036806. doi:10.1103/physrevlett.115.036806

PubMed Abstract | CrossRef Full Text | Google Scholar

9. He T, Zhang X, Wang L, Liu Y, Dai X, Wang L, et al. Ideal fully spin-polarized type-II nodal line state in half-metals X₂YZ₄ (X=K, Cs, Rb, Y=Cr, Cu, Z=Cl, F). Mater Today Phys (2021) 17:100360. doi:10.1016/j.mtphys.2021.100360

CrossRef Full Text | Google Scholar

10. Li S, Yu ZM, Liu Y, Guan S, Wang SS, Zhang X, et al. Type-II nodal loops: Theory and material realization. Phys Rev B (2017) 96:081106. doi:10.1103/physrevb.96.081106

CrossRef Full Text | Google Scholar

11. Armitage N, Mele E, Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev Mod Phys (2018) 90:015001. doi:10.1103/revmodphys.90.015001

CrossRef Full Text | Google Scholar

12. Wan X, Turner AM, Vishwanath A, Savrasov SY. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys Rev B (2011) 83:205101. doi:10.1103/physrevb.83.205101

CrossRef Full Text | Google Scholar

13. Meng WZ, Zhang XM, Liu Y, Dai XF, Liu GD. Lorentz-violating type-II Dirac fermions in full-Heusler compounds XMg₂Ag (X = Pr, Nd, Sm). New J Phys (2020) 22:073061. doi:10.1088/1367-2630/ab9d55

CrossRef Full Text | Google Scholar

14. Young SM, Zaheer S, Teo JCY, Kane CL, Mele EJ, Rappe AM. Dirac semimetal in three dimensions. Phys Rev Lett (2012) 108:140405. doi:10.1103/physrevlett.108.140405

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Ding GQ, Zhou F, Zhang ZY, Yu ZM, Wang XT. Charge-two Weyl phonons with type-III dispersion. Phys Rev B (2022) 105:134303. doi:10.1103/physrevb.105.134303

CrossRef Full Text | Google Scholar

16. Soluyanov AA, Gresch D, Wang ZJ, Wu QS, Troyer M, Dai X, et al. Type-II Weyl semimetals. Nature (2015) 527:495–8. doi:10.1038/nature15768

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Liu ZK, Zhou B, Wang ZJ, Weng HM, Prabhakaran D, et al. Discovery of a three-dimensional topological Dirac semimetal, Na ₃ Bi. Na₃bi Sci (2014) 343:864–7. doi:10.1126/science.1245085

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Gibson Q, Evtushinsky D, Zabolotnyy V, Buchner B, Cava RJ. Experimental realization of a three-dimensional Dirac semimetal. Phys Rev Lett (2014) 113:027603. doi:10.1103/physrevlett.113.027603

PubMed Abstract | CrossRef Full Text | Google Scholar

19. He TL, Zhang XM, Liu Y, Yu ZM, et al. Ferromagnetic hybrid nodal loop and switchable type-I and type-II Weyl fermions in two dimensions. Phys Rev B (2020) 102:075133. doi:10.1103/physrevb.102.075133

CrossRef Full Text | Google Scholar

20. Young SM, Kane CL. Dirac semimetals in two dimensions. Phys Rev Lett (2015) 115:126803. doi:10.1103/physrevlett.115.126803

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wu WK, Liu Y, LiZhong SC, Yu ZM, Sheng XL et al Nodal surface semimetals: Theory and material realization. Phys Rev B (2018) 97:115125. doi:10.1103/physrevb.97.115125

CrossRef Full Text | Google Scholar

22. Yang T, Jin L, Liu Y, Zhang XM, Wang XT. Spin-polarized type-II nodal loop and nodal surface states in hexagonal compounds XTiO₂ (X= Li, Na, K, Rb). Phys Rev B (2021) 103:235140. doi:10.1103/physrevb.103.235140

CrossRef Full Text | Google Scholar

23. Zhang XMYZM, Wu WK, Wang SS, Sheng XL, Sheng XL et al Nodal loop and nodal surface states in the Ti₃Al family of materials. Phys Rev B (2018) 97:235150. doi:10.1103/physrevb.97.235150

CrossRef Full Text | Google Scholar

24. He TL, Liu Y, Tian L, Zhang XM, Meng WZ, Dai XF, et al. Coexistence of fully spin-polarized Weyl nodal loop, nodal surface, and Dirac point in a family of quasi-one-dimensional half-metals. Phys Rev B (2021) 103:085135. doi:10.1103/physrevb.103.085135

CrossRef Full Text | Google Scholar

25. Meng WZ, Zhang XM, Liu Y, Dai XF, Liu GD. Antiferromagnetism caused by excess electrons and multiple topological electronic states in the electride Ba₄Al₅·e^-. Phys Rev B (2021) 104:195145. doi:10.1103/physrevb.104.195145

CrossRef Full Text | Google Scholar

26. Wang LR, Zhang XM, Meng WZ, Liu Y, Dai XF, Liu GD. A topological quantum catalyst: The case of two-dimensional traversing nodal line states associated with high catalytic performance for the hydrogen evolution reaction. J Mater Chem A Mater (2021) 9:22453–61. doi:10.1039/d1ta06553j

CrossRef Full Text | Google Scholar

27. Li G, Felser C. Heterogeneous catalysis at the surface of topological materials. Appl Phys Lett (2020) 116:070501. doi:10.1063/1.5143800

CrossRef Full Text | Google Scholar

28. Li JX, Ma H, Xie Q, Feng SB, Ullah S, Li R et al Topological quantum catalyst: Dirac nodal line states and a potential electrocatalyst of hydrogen evolution in the TiSi family. Sci China Mater (2018) 61:23–9. doi:10.1007/s40843-017-9178-4

CrossRef Full Text | Google Scholar

29. Rajamathi CR, Gupta U, Kumar N, Yang H, Sun Y, SuB V et al Weyl semimetals as hydrogen evolution catalysts. Adv Mater (2017) 29:1606202. doi:10.1002/adma.201606202

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yang Q, Li GW, Manna K, Fan FR, Felser C, Sun Y. Topological engineering of Pt-Group-Metal-Based chiral crystals toward high-efficiency hydrogen evolution catalysts. Adv Mater (2020) 32:1908518. doi:10.1002/adma.201908518

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Liu W, Zhang XM, Meng WZ, Liu Y, Dai XF, Liu GD. Theoretical realization of hybrid Weyl state and associated high catalytic performance for hydrogen evolution in NiSi. iScience (2022) 25:103543. doi:10.1016/j.isci.2021.103543

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Yu ZM, Zhang ZY, Liu GB, Wu WK, Li XP, Zhang RW, et al. Encyclopedia of emergent particles in three-dimensional crystals. Sci Bull (2022) 67:375–80. doi:10.1016/j.scib.2021.10.023

CrossRef Full Text | Google Scholar

33. Khan MR, Bu K, Wang JT, Chen CF. Topological nodal surface semimetal states in Sr₅X₃ compounds (X=As, Sb, Bi). Phys Rev B (2022) 105:245152. doi:10.1103/physrevb.105.245152

CrossRef Full Text | Google Scholar

34. Zhong CY, Chen YP, Xie Y, Yang SA, Cohen ML, Zhang SB. Towards three-dimensional Weyl-surface semimetals in graphene networks. Nanoscale (2016) 8:7232–9. doi:10.1039/c6nr00882h

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Liang QF, Zhou J, Yu R, Wang Z, Weng HM. Node-surface and node-line fermions from nonsymmorphic lattice symmetries. Phys Rev B (2016) 93:085427. doi:10.1103/physrevb.93.085427

CrossRef Full Text | Google Scholar

36. Xie CW, Yuan HK, Liu Y, Wang XT, Zhang G. Three-nodal surface phonons in solid-state materials: Theory and material realization. Phys Rev B (2021) 104:134303. doi:10.1103/physrevb.104.134303

CrossRef Full Text | Google Scholar

37. Xie CW, Yuan HK, Liu Y, Wang XT. Two-nodal surface phonons in solid-state materials. Phys Rev B (2022) 105:054307. doi:10.1103/physrevb.105.054307

CrossRef Full Text | Google Scholar

38. Wang XT, Zhou F, Yang T, Kuang MQ, Yu ZM, Zhang G, et al. Symmetry-enforced ideal lantern-like phonons in ternary nitride Li₆WN₄. Phys Rev B (2021) 104:L041104. doi:10.1103/physrevb.104.l041104

CrossRef Full Text | Google Scholar

39. Hu YY, Liu ZG, Nam KW, Borkiewicz OJ, Cheng J, Hua X, et al. Origin of additional capacities in metal oxide lithium-ion battery electrodes. Nat Mater (2013) 12:1130–6. doi:10.1038/nmat3784

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B (1999) 59:1758–75. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

41. Blochl PE. Projector augmented-wave method. Phys Rev B (1994) 50:17953–79. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

42. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Anisimov VI, Zaanen J, Andersen OK. Band theory and mott insulators: Hubbard U instead of stoner I. Phys Rev B (1991) 44:943–54. doi:10.1103/physrevb.44.943

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Meng WZ, Zhang XM, He TL, Jin L, Dai X, Liu Y Ternary compound HfCuP: An excellent Weyl semimetal with the coexistence of type-I and type-II Weyl nodes. J Adv Res (2020) 24:523–8. doi:10.1016/j.jare.2020.05.026

PubMed Abstract | CrossRef Full Text | Google Scholar