ABC energies and spectral radii of some graph operations

The present article presents some new results relating to Atomic Bond Connectivity energies and Spectral radii of generalized splitting and generalized shadow graphs constructed on the basis of some fundamental families of cycle graph C_n, complete graph K_n and complete bipartite graph K_n,n referred as base graphs. In fact we relate the energies and Spectral radii of splitting and shadow graphs with the energies and Spectral radii of original graphs.

1 Introduction

Let G be a simple, finite and undirected graph having vertex set V(G) and edge set E(G). The order and the size of the graph G are n and m, respectively. The term “degree of vertex” (abbreviated as d_i) refers to the number of edges that terminate at a vertex i in the graph G. When the vertices i and j of the graph G are adjacent, then ij entry of the ABC matrix of G is equal to $\sqrt{\frac{d_i+d_j-2}{d_i{d}_j}}$, otherwise it is equal to 0. Recently, Estrada introduced this matrix, closely related to the atom-bond connectivity abbreviated as ABC index, as a matrix representation of the probability of visiting a nearest neighbor edge from one side or the other of a given edge in a graph, which in the context of molecular graphs can be related to the polarizing capacity of the bond under consideration. The heat of production of alkanes and the ABC index were shown to be closely connected in [1]. On the basis of the proportion of 1,3-interactions to the total number of 1,2-,1,3-, and 1,4-interactions in alkanes, Estrada later offered a quantum-chemical explanation for this descriptive ability of the ABC index in [2]. Gutman further demonstrated that the ABC index is capable of reproducing the heat of formation with precision comparable to that of advanced ab initio and DFT (MP2, B3LYP) quantum chemical calculations in [3]. These chemical applications have stimulated extensive mathematical research on the ABC index [4–8]. Estrada in [9] recently gave the generalization ABC_α a probabilistic meaning and referred it as the label generalized ABC index, suggesting that the term $\frac{d_i+d_j-2}{d_i{d}_j}$ stands for the likelihood of visiting a closest neighbor edge from either the left or the right side of a certain edge in a graph. This justification is comprehensive enough to cover the case of polarizing bonds in a molecular context. He then provided a matrix representation of these probabilities in the form of generalized ABC matrix. Adjacency matrix of the graph G is denoted by A(G), where

$A\left(G\right)=\left\{\begin{array}{ccc}\hfill 1\hfill & \hfill \hfill & \hfill i\sim j,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill otherwise.\hfill \end{array}\right\}$

When the vertices i and j are adjacent we use the notation i ∼ j. It is obvious that the generalized ABC matrix of G can be thought of as a particular kind of weighted adjacency matrix of G. Eigenvalues of the Adjacency matrix A(G) are basically the eigenvalues of the graph G. If the eigenvalues of the graph G are denoted as α₁, α₂⋯α_n, then energy of the graph G is denoted by ɛ(G) and is defined as sum of absolute values of all eigenvalues of the graph G. Quantum chemistry served as an inspiration for the energy of the graph G. Idea of energy of the graph was initiated by Ivan Gutman in 1978 [10]. Initially it was an strange idea so very few scientist were compelled to notice the idea of energy of the graph G. Over the recent years different variants of energies have been introduced with a variety of applications in diverse areas. One such energy is the ABC energy introduced taking into account the fruitful applications of the ABC index.

A logical query is raised, what connection can be made between the ABC energy of a given graph G and the graph that was created from G using various graph operations? We have taken into consideration two graphs operations, the splitting graph and the shadow graph, in order to respond to this query. A lot of work is done in this field in last few years. J. B. Liu et al. discussed Distance and Adjacency Energies of Multi-Level Wheel Networks in [11]. Largest eigenvalue of the graph G is called Spectral radius of the graph G and it is denoted by ρ(G). Zhang et al. in [12], recently established new results using two well-known operations, splitting and shadow graphs on a given regular graph that relates the Spectral radius of the original graph and the newly created graph. Z. Q. Chu et al. discussed Laplacian and signless Laplacian spectra and energies of multi-step wheels in [13]. Chen hypothesized in [14] that the star graph S_n has the lowest ABC energy of any tree of order n, while Gao et al. demonstrated this hypotheses in [15]. Ghorbani et al. discussed certain bounds for the ABC Spectral radius and ABC energy of general graphs as well as various ABC eigenvalue features in [16]. Yalcin et al. discussed several upper and lower bounds for the skew ABC energy of digraphs in [17]. R. Singh et al. discussed Sombor energy of m-splitting and m-shadow graphs constructed on the basis of any regular graph in [18]. In [19] Vaidya et al. established new results $E(Sp{l}_1(G))=\sqrt{5}E(G)$, E (Sh₂G)) = 2E(G) for 1-splitting and 2-shadow graph using adjacency energy. In [20] Vaidya and Popat arrived at fairly general conclusions for adjacency energy $E(Sp{l}_m(G))=\sqrt{1+4m}E(G)$, E (Sh_m(G)) = mE(G) by taking into account two graph operations namely m-splitting and m-shadow graphs [ABC(G)] = a_ij referred as atom-bond connectivity matrix of the graph G defined in [16] having entries,

$a_{ij}=\left\{\begin{array}{cccccccc}\hfill \sqrt{\frac{d_i+d_j-2}{d_i{d}_j}},\hfill & \hfill \hfill & \hfill if\hfill & \hfill v_i\hfill & \hfill and\hfill & \hfill v_j\hfill & \hfill are\hfill & \hfill adjacent,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}$

Eigenvalues of ABC matrix of the graph G are denoted as η₁, η₂, ⋯η_n. ABC spectrum of the graph G is a multiset consisting of the ABC eigenvalues of the graph G denoted by specABC. If distinct ABC eigenvalues of the graph G are η₁, η₂, ⋯η_n with multiplicities m₁, m₂, ⋯m_n respectively, then

$specABC=\left(\begin{array}{cccc}\hfill {\eta }_1\hfill & \hfill {\eta }_2\hfill & \hfill \cdots \hfill & \hfill {\eta }_n\hfill \\ \hfill m_1\hfill & \hfill m_2\hfill & \hfill \cdots \hfill & \hfill m_n\hfill \end{array}\right).$(1.1)

Then ABC energy is defined aspt

$ABC\epsilon \left(G\right)=\sum _{i=1}^n|{\eta }_i|,$

where η₁, η₂, … , η_n are the eigenvalues of ABC matrix.

ABC Spectral radius is defined as

$\rho ABC\left(G\right)=\underset{i=1}{\overset{n}{\max }}|{\eta }_i|,$

where η₁, η₂, … , η_n are the eigenvalues of ABC matrix.

2 Preliminaries

In this part we outline main ideas and preliminary facts related to our main results. Let C_n and K_n, respectively, stand for the cycle and the complete graph on n vertices, as usual. Let K_m,nbe a complete bipartite graph with two partite sets that each have m and n vertices. When all of the vertices in the graph G have the same degree then the graph G is said to be regular graph. C_n is two regular graph, K_n is n − 1 regular and complete bipartite K_n,n is n regular graph.

We actually generate new graph from a given graph refereed as base graph. Sampath Kumar and Walikar first introduced the splitting graph in [21]. The splitting graph Spl(G) of the graph G can be obtained by adding to every vertex a new vertex a′, such that a′ is adjacent to every vertex that is adjacent to a in G. The shadow graph Sh(G) of the graph G is obtained by taking two copies of G, say G′ and G′′. Join every vertex b′ in G′ to the neighbors of the corresponding vertex b′′ in G′′. These two notions of producing new graphs have natural generalizations. The above given definitions can be treated as 1-splitting and 2-shadow graph of a given graph whereas a general idea of producing s - splitting or s - shadow graphs where we take s new vertices or s new copies of G. Following definition is central to our results. The s-splitting graph Spl_s(G) of G is obtained by adding to every vertex a of G new s vertices, say v₁, v₂, v₃, …., v_s such that v_i (1 ≤ i ≤ s), is adjacent to every vertex that is adjacent to v in G.

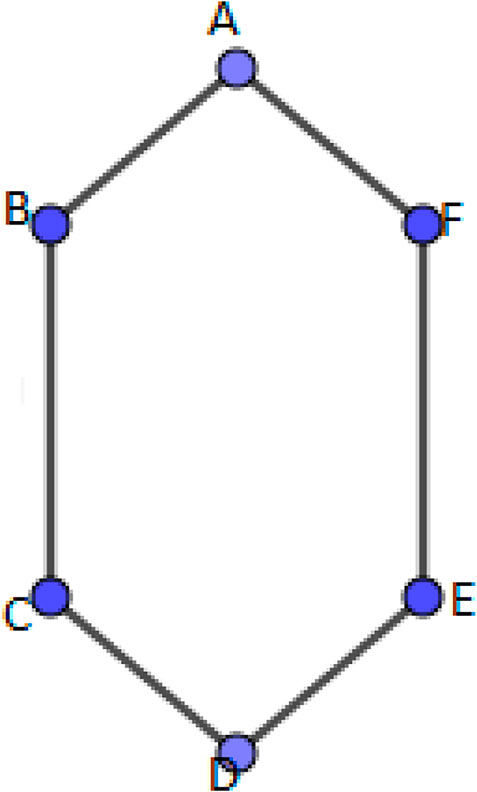
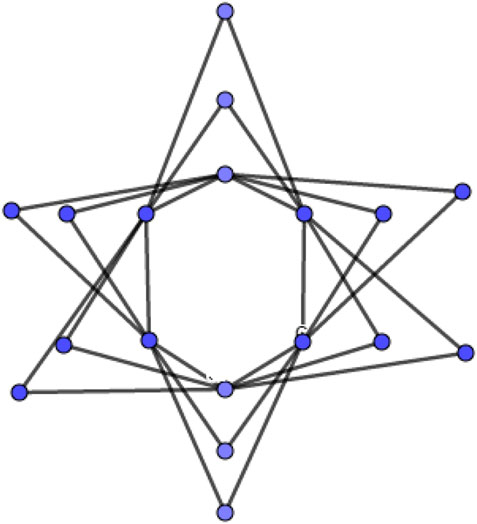
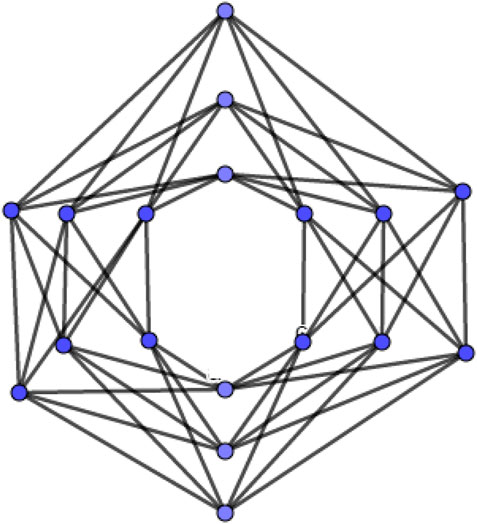
The s-shadow graph Sh_s(G) of a connected graph G is constructed by taking s copies of G, say G₁, G₂, G₃, …., G_s then join each vertex u in G_i to the neighbors of the corresponding vertex v in G_j such that v_i (1 ≤ i ≤ s). Figure 1 is an example of base graph C₆, and Figure 2 is 2-splitting graph of C₆ and Figure 3 is 3-shadow graph of C₆.

FIGURE 1

FIGURE 1. Example of base graph C6.

FIGURE 2

FIGURE 2. Spl₂(B₁), the 2-splitting graph of B₁.

FIGURE 3

FIGURE 3. Sh₃(B₁), the 3-shadow graph of B₁.

[19] Let PϵR^m×n, QϵR^p×q. The Tensor or kronecker product of P and Q is the matrix defined by.

$P\otimes Q=\left(\begin{array}{cccc}\hfill a_{11}Q\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .a_{1n}Q\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill a_{m1}Q\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .a_{mn}Q\hfill \end{array}\right).$

Lemma 1.1 [19]. Let PϵM^m, QϵMⁿ, λ be an eigenvalue of P related to eigenvector y, and μ be an eigenvalue of Q related to eigenvector x. Then λμ is an eigenvalue of P⊗Q related to eigenvector y⊗x.In the present article we produce new results about ABC energies and ABC Spectral radii of s-splitting and s-shadow graphs. In fact we relate these energies and Spectral radii of new graph operations with the energies and Spectral radii of original graphs. The article is organized as follows. In section 3, we derive ABC energies and ABC Spectral radii of generalized splitting graph constructed on cycle graph, complete graph and complete bipartite graph. In section 4 we proceed to find similar results but for generalized shadow graph of the given graph.

3 ABC energies and spectral radii of generalized splitting graph

In this part we relate ABC energies and ABC Spectral radii of generalized Splitting graph of C_n, K_n and K_n,n with original graph of C_n, K_n and K_n,n respectively.The following result relates the ABC energy of s-splitting graph of C_n with the ABC energy of C_n.

Theorem 1. Let C_n be a cycle graph and ABCɛ(Spl_s(C_n)) be the ABC energy of s-splitting graph of C_n, then $ABC\epsilon (Sp{l}_s(C_n))=\frac{\sqrt{(4s^3+8s^2+6s+1)}}{s+1}ABC\epsilon (C_n)$.

Proof. Let v₁, v₂, v₃, …., v_n be the vertices of C_n. The ABC matrix of C_n has entries given by

$ABC\left(C_n\right)=\left[\begin{array}{cccccccc}\hfill 0\hfill & \hfill \sqrt{\frac{2}{4}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \sqrt{\frac{2}{4}}\hfill \\ \hfill \sqrt{\frac{2}{4}}\hfill & \hfill 0\hfill & \hfill \sqrt{\frac{2}{4}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{\frac{2}{4}}\hfill & \hfill 0\hfill & \hfill \sqrt{\frac{2}{4}}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \sqrt{\frac{2}{4}}\hfill \\ \hfill \sqrt{\frac{2}{4}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \sqrt{\frac{2}{4}}\hfill & \hfill 0\hfill \end{array}\right].$

Let $v_i^1,v_i^2,v_i^3,\dots ,v_i^s$ be the vertices related to each v_i, which are added in C_n to obtain Spl_s (C_n) such that $N(v_i^1)=N(v_i^2)=N(v_i^3)=\dots ,N(v_i^s)=N(v_i)$. Then ABC(Spl_s (C_n)) can be written as follows

$ABC\left(Sp{l}_s\left(C_n\right)\right)=\left[\begin{array}{cccc}\hfill {\aleph }_1\hfill & \hfill {\aleph }_2\hfill & \hfill \dots \hfill & \hfill {\aleph }_2\hfill \\ \hfill {\aleph }_2\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\aleph }_2\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right].$

Matrix ℵ₁ has entries given by

$d_{ij}=\left\{\begin{array}{c}\hfill \sqrt{\frac{4s+2}{4{\left(s+1\right)}^2}}\text{if}{v}_i\text{is\hspace{0.17em}adjacent\hspace{0.17em}to}{v}_j,\hfill \\ \hfill 0\text{elsewhere}.\hfill \end{array}\right\}.$

Entries of matrix ℵ₂ are given below

$e_{ij}=\left\{\begin{array}{c}\sqrt{\frac{2\left(s+1\right)}{4\left(s+1\right)}}\text{if}{v}_i\text{\hspace{0.17em}is\hspace{0.17em}adjacent\hspace{0.17em}to}{v}_j,\hfill \\ 0\text{elsewhere}.\hfill \end{array}\right..$

${\aleph }_1=\sqrt{\frac{2s+1}{{(s+1)}^2}}ABC(C_n)$,andℵ₂ = ABC(C_n).Now ABC(Spl_s (C_n)) can be written in block matrix as follows

$\begin{array}{l}\hfill ABC\left(Sp{l}_s\left(C_n\right)\right)\\ =\left\{\begin{array}{cccc}\hfill \sqrt{\frac{2s+1}{{\left(s+1\right)}^2}}ABC\left(C_n\right)\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill ABC\left(C_n\right)\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}\hfill \\ =ABC\left(C_n\right)\otimes \left\{\begin{array}{cccc}\hfill \sqrt{\frac{2s+1}{{\left(s+1\right)}^2}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}.\hfill \end{array}$

Let

$A={\left\{\begin{array}{cccc}\hfill \sqrt{\frac{2s+1}{{\left(s+1\right)}^2}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}}_{s+1}$

Now we compute the eigenvalues of A. Since matrix A is of rank two, A has two non-zero eigenvalues, say α₁ and α₂. Obviously,

${\alpha }_1+{\alpha }_2=tr\left(A\right)=\sqrt{\frac{2s+1}{{\left(s+1\right)}^2}}.$(3.1)

Consider,

$A^2={\left\{\begin{array}{cccc}\hfill \frac{2s+1}{{\left(s+1\right)}^2}+s\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill \sqrt{\frac{2s+1}{{\left(s+1\right)}^2}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 1\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}}_{s+1}$

Then

${\alpha }_1^2+{\alpha }_2^2=tr\left(A^2\right)=\frac{2s+1}{{\left(s+1\right)}^2}+2s.$(3.2)

Solving Equation 3.1 and Equation 3.2, we have

${\alpha }_1=\frac{\sqrt{2s+1}+\sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)},$(3.3)

and

${\alpha }_2=\frac{\sqrt{2s+1}-\sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)}.$(3.4)

So,

$specA=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill \frac{\sqrt{2s+1}+\sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)}\hfill & \hfill \frac{\sqrt{2s+1}-\sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right).$(3.5)

Since ABC(Spl_s (C_n)) = ABC(C_n)⊗A, it follows that if λ₁, λ₂, … λ_n are the eigenvalues of ABC(C_n), then by Lemma 1.1, we have

$\begin{array}{ll}\hfill ABC\epsilon \left(Sp{l}_s\left(C_n\right)\right)& =\sum _{i=1}^n|\frac{\sqrt{2s+1}\pm \sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)}{\lambda }_i|\hfill \\ \hfill & =\sum _{i=1}^n|{\lambda }_i|\left[\frac{\sqrt{2s+1}+\sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)}\right.\hfill \\ \hfill & \left.+\frac{\sqrt{4s^3+8s^2+6s+1}-\sqrt{2s+1}}{2\left(s+1\right)}\right]\hfill \\ \hfill & =\frac{\sqrt{\left(4s^3+8s^2+6s+1\right)}}{s+1}ABC\epsilon \left(C_n\right).\hfill \end{array}$

The following result relates the ABC Spectral radius of s-splitting graph of C_n with the ABC Spectral radius of C_n.

Corollary 2. Let C_n be a cycle graph and ρABC(Spl_s(C_n)) be the ABC Spectral radius of s-splitting graph C_n, then $\rho ABC(Sp{l}_s(C_n))=\rho ABC(C_n)(\frac{\sqrt{2s+1}+\sqrt{4s^3+8s^2+6s+1}}{2(s+1)})$.

Proof. By similar arguments as formula (3.5) in Theorem 1,

$specA=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill \frac{\sqrt{2s+1}+\sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)}\hfill & \hfill \frac{\sqrt{2s+1}-\sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right).$

Since ABC(Spl_s (C_n)) = ABC(C_n)⊗A, it follows that if η₁, η₂, η₃, … η_n are eigenvalues of ABC(C_n) then by Lemma 1.1, we have

$\begin{array}{ll}\hfill \rho ABC\left(Sp{l}_s\left(C_n\right)\right)& =ma{x}_{i=1}^n\left|\left(specA\right)\left.\right){\eta }_i\right|\hfill \\ \hfill & =ma{x}_{i=1}^n|{\eta }_i|\left[\frac{\sqrt{2s+1}+\sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)}\right]\hfill \\ \hfill & =\rho ABC\left(C_n\right)\left(\frac{\sqrt{2s+1}+\sqrt{4s^3+8s^2+6s+1}}{2\left(s+1\right)}\right).\hfill \end{array}$

The following result relates the ABC energy of s-splitting graph of K_n with the ABC energy of K_n.

Theorem 3. Let K_n be a complete graph on n vertices and ABCɛ(Spl_s(K_n)) be the ABC energy of s-splitting graph of K_n, then

$ABC\epsilon (Sp{l}_s(K_n))=\frac{\sqrt{4s^3(n-1)+s^2(12n-20)+s(10n-18)+2n-4}}{(s+1)(\sqrt{2n-4})}ABC\epsilon (K_n).$

Proof. Let v₁, v₂, v₃, …., v_n be the vertices of K_n. The ABC matrix of K_n has entries given by

$ABC\left(K_n\right)=\left\{\begin{array}{cccccccc}\hfill \sqrt{\frac{2n-4}{{\left(n-1\right)}^2}},\hfill & \hfill \hfill & \hfill if\hfill & \hfill v_i\hfill & \hfill and\hfill & \hfill v_j\hfill & \hfill are\hfill & \hfill adjacent,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}$

Let $v_i^1,v_i^2,v_i^3,\dots ,v_i^s$ be the vertices related to each v_i, which are added in K_n to obtain Spl_s (K_n) such that $N(v_i^1)=N(v_i^2)=N(v_i^3)=\dots ,N(v_i^s)=N(v_i)$. Then ABC(Spl_s (K_n)) can be written in block matrix as follows

$\begin{array}{l}ABC\left(Sp{l}_s\left(K_n\right)\right)\hfill \\ =\left\{\begin{array}{cccc}\hfill \sqrt{\frac{1+\frac{s\left(n-1\right)}{n-2}}{{\left(s+1\right)}^2}}*ABC\left(K_n\right)\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill \sqrt{\frac{1+\frac{s\left(n-1\right)}{2n-4}}{\left(s+1\right)}}*ABC\left(K_n\right)\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}\hfill \\ =ABC\left(K_n\right)\otimes \left\{\begin{array}{cccc}\hfill \sqrt{\frac{1+\frac{s\left(n-1\right)}{n-2}}{{\left(s+1\right)}^2}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill \sqrt{\frac{1+\frac{s\left(n-1\right)}{2n-4}}{\left(s+1\right)}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}.\hfill \end{array}$

Let

$A={\left\{\begin{array}{cccc}\hfill \sqrt{\frac{1+\frac{s\left(n-1\right)}{n-2}}{{\left(s+1\right)}^2}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill \sqrt{\frac{1+\frac{s\left(n-1\right)}{2n-4}}{\left(s+1\right)}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}}_{s+1}$

Now we compute the eigenvalues of A. Since matrix A is of rank two, A has two non-zero eigenvalues, say α₁ and α₂. Obviously,

${\alpha }_1+{\alpha }_2=tr\left(A\right)=\sqrt{\frac{1+\frac{s\left(n-1\right)}{n-2}}{{\left(s+1\right)}^2}}.$(3.6)

Consider,

$A^2={\left\{\begin{array}{cccc}\hfill \frac{1+\frac{s\left(n-1\right)}{n-2}}{{\left(s+1\right)}^2}+s\left(\frac{1+\frac{s\left(n-1\right)}{2n-4}}{\left(s+1\right)}\right)\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill \sqrt{\frac{1+\frac{s\left(n-1\right)}{2n-4}}{\left(s+1\right)}}*\sqrt{\frac{1+\frac{s\left(n-1\right)}{n-2}}{{\left(s+1\right)}^2}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill \frac{1+\frac{s\left(n-1\right)}{2n-4}}{\left(s+1\right)}\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}}_{s+1}$

Then

${\alpha }_1^2+{\alpha }_2^2=tr\left(A^2\right)=\frac{1+\frac{s\left(n-1\right)}{n-2}}{{\left(s+1\right)}^2}+2s\left.\right(\frac{1+\frac{s\left(n-1\right)}{2n-4}}{\left(s+1\right)}\left.\right).$(3.7)

Solving Equation 3.6 and (3.7), we have

${\alpha }_1=\frac{\sqrt{2n+2sn-2s-4}+\sqrt{4s^3\left(n-1\right)+s^2\left(12n-20\right)+s\left(10n-18\right)+2n-4}}{2\left(s+1\right)\sqrt{2n-4}},$(3.8)

and

${\alpha }_2=\frac{\sqrt{2n+2sn-2s-4}-\sqrt{4s^3\left(n-1\right)+s^2\left(12n-20\right)+s\left(10n-18\right)+2n-4}}{2\left(s+1\right)\sqrt{2n-4}}.$(3.9)

So,

$specA=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill T_1\hfill & \hfill T_1\hfill \\ \hfill s-1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right),$(3.10)

where $T_1=\frac{\sqrt{2n+2sn-2s-4}+\sqrt{4s^3(n-1)+s^2(12n-20)+s(10n-18)+2n-4}}{2(s+1)\sqrt{2n-4}}$.and$T_2=\frac{\sqrt{2n+2sn-2s-4}-\sqrt{4s^3(n-1)+s^2(12n-20)+s(10n-18)+2n-4}}{2(s+1)\sqrt{2n-4}}$.Since ABC(Spl_s (K_n)) = ABC(K_n)⊗A, it follows that if λ₁, λ₂, … λ_n are the eigenvalues of ABC(K_n) then by Lemma 1.1, we have

$\begin{array}{l}\hfill ABC\epsilon \left(Sp{l}_s\left(K_n\right)\right)\\ =\sum _{i=1}^n|\frac{\sqrt{2n+2sn-2s-4}\pm \sqrt{4s^3\left(n-1\right)+s^2\left(12n-20\right)+s\left(10n-18\right)+2n-4}}{2\left(s+1\right)\sqrt{2n-4}}{\lambda }_i|\hfill \\ =\sum _{i=1}^n|{\lambda }_i|\left[\frac{\sqrt{2n+2sn-2s-4}+\sqrt{4s^3\left(n-1\right)+s^2\left(12n-20\right)+s\left(10n-18\right)+2n-4}}{2\left(s+1\right)\sqrt{2n-4}}\right.\hfill \\ \left.+\frac{\sqrt{4s^3\left(n-1\right)+s^2\left(12n-20\right)+s\left(10n-18\right)+2n-4}-\sqrt{2n+2sn-2s-4}}{2\left(s+1\right)\sqrt{2n-4}}\right]\hfill \\ =\frac{\sqrt{4s^3\left(n-1\right)+s^2\left(12n-20\right)+s\left(10n-18\right)+2n-4}}{\left(s+1\right)\left(\sqrt{2n-4}\right)}ABC\epsilon \left(K_n\right).\hfill \end{array}$

The following result relates the ABC Spectral radius of s-splitting graph of K_n with the ABC Spectral radius of K_n.

Corollary 4. Let K_n be a graph and ρABC(Spl_s(K_n)) be the ABC Spectral radius of s-splitting graph K_n, then $\rho ABC(Sp{l}_s(K_n))=\rho ABC(K_n)(\frac{\sqrt{2n+2sn-2s-4}+\sqrt{4s^3(n-1)+s^2(12n-20)+s(10n-18)+2n-4}}{2(s+1)\sqrt{2n-4}})$.

Proof. By similar arguments as formula (3.10) in Theorem 3,

$specA=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill T_1\hfill & \hfill T_2\hfill \\ \hfill s-1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right),$

where $T_1=\frac{\sqrt{2n+2sn-2s-4}+\sqrt{4s^3(n-1)+s^2(12n-20)+s(10n-18)+2n-4}}{2(s+1)\sqrt{2n-4}}$,and $T_2=\frac{\sqrt{2n+2sn-2s-4}-\sqrt{4s^3(n-1)+s^2(12n-20)+s(10n-18)+2n-4}}{2(s+1)\sqrt{2n-4}}$.Since ABC(Spl_s (K_n)) = ABC(K_n)⊗A, it follows that if η₁, η₂, η₃, … η_n are the eigenvalues of ABC(K_n) then by Lemma 1.1, we have

$\begin{array}{l}\hfill \rho ABC\left(Sp{l}_s\left(K_n\right)\right)\\ =ma{x}_{i=1}^n\left|\left(specA\right)\left.\right){\eta }_i\right|\hfill \\ =ma{x}_{i=1}^n|{\eta }_i|\left[\frac{\sqrt{2n+2sn-2s-4}+\sqrt{4s^3\left(n-1\right)+s^2\left(12n-20\right)+s\left(10n-18\right)+2n-4}}{2\left(s+1\right)\sqrt{2n-4}}\right]\hfill \\ =\rho ABC\left(K_n\right)\left.\right(\frac{\sqrt{2n+2sn-2s-4}+\sqrt{4s^3\left(n-1\right)+s^2\left(12n-20\right)+s\left(10n-18\right)+2n-4}}{2\left(s+1\right)\sqrt{2n-4}}\left.\right).\hfill \end{array}$

The following result relates the ABC energy of s-splitting graph of K_n,n with the ABC energy of K_n,n.

Theorem 5. Let K_n,n be a complete bipartite graph and ABCɛ(Spl_s(K_n,n)) be the ABC energy of s-splitting graph of K_n,n, then

$ABC\epsilon \left(Sp{l}_s\left(K_{n,n}\right)\right)=\frac{\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{\left(s+1\right)\left(\sqrt{2n-2}\right)}ABC\epsilon \left(K_{n,n}\right).$

Proof. Let v₁, v₂, v₃, …., v_n be the vertices of K_n,n. The ABC matrix of K_n,n has entries given by

$ABC\left(K_{n,n}\right)=\left\{\begin{array}{cccccccc}\hfill \sqrt{\frac{2n-2}{{\left(n\right)}^2}},\hfill & \hfill \hfill & \hfill if\hfill & \hfill v_i\hfill & \hfill and\hfill & \hfill v_j\hfill & \hfill are\hfill & \hfill adjacent,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}$

Let $v_i^1,v_i^2,v_i^3,\dots ,v_i^s$ be the vertices related to each v_i, which are added in K_n,n to obtain Spl_s (K_n,n) such that $N(v_i^1)=N(v_i^2)=N(v_i^3)=\dots ,N(v_i^s)=N(v_i)$. Then ABC(Spl_s (K_n,n)) can be written in block matrix as follows

$\begin{array}{ll}\hfill ABC\left(Sp{l}_s\left(K_{n,n}\right)\right)& =\left\{\begin{array}{cccc}\hfill \sqrt{\frac{1+\frac{2sn}{2n-2}}{{\left(s+1\right)}^2}}*ABC\left(K_{n,n}\right)\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill \sqrt{\frac{1+\frac{\mathrm{sn}}{2n-2}}{\left(s+1\right)}}*ABC\left(K_{n,n}\right)\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}\hfill \\ \hfill & =ABC\left(K_{n,n}\right)\otimes \left\{\begin{array}{cccc}\hfill \sqrt{\frac{1+\frac{2sn}{2n-2}}{{\left(s+1\right)}^2}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill \sqrt{\frac{1+\frac{\mathrm{sn}}{2n-2}}{\left(s+1\right)}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}.\hfill \end{array}$

Let

$A={\left\{\begin{array}{cccc}\hfill \sqrt{\frac{1+\frac{2sn}{2n-2}}{{\left(s+1\right)}^2}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill \sqrt{\frac{1+\frac{\mathrm{sn}}{2n-2}}{\left(s+1\right)}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}}_{s+1}.$

Now we compute the eigenvalues of A. Since matrix A is of rank two, A has two non-zero eigenvalues, say α₁ and α₂. Obviously,

${\alpha }_1+{\alpha }_2=tr\left(A\right)=\sqrt{\frac{1+\frac{2sn}{2n-2}}{{\left(s+1\right)}^2}}.$(3.11)

Consider,

$A^2={\left\{\begin{array}{cccc}\hfill \frac{1+\frac{2sn}{2n-2}}{{\left(s+1\right)}^2}+s\left(\frac{1+\frac{\mathrm{sn}}{2n-2}}{\left(s+1\right)}\right)\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=j=1,\hfill \\ \hfill \sqrt{\frac{1+\frac{2sn\left.\right)}{2n-2}}{{\left(s+1\right)}^2}}*\sqrt{\frac{1+\frac{\mathrm{sn}}{2n-2}}{\left(s+1\right)}}\hfill & \hfill \hfill & \hfill if\hfill & \hfill i=1,j\ge 2\hfill & \hfill and\hfill & \hfill j=1,i\ge 2,\hfill \\ \hfill \frac{1+\frac{\mathrm{sn}}{2n-2}}{\left(s+1\right)}\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}}_{s+1}.$

Then

${\alpha }_1^2+{\alpha }_2^2=tr\left(A^2\right)=\frac{1+\frac{2sn\left.\right)}{2n-2}}{{\left(s+1\right)}^2}+2s\left(\frac{1+\frac{\mathrm{sn}}{2n-2}}{\left(s+1\right)}\right).$(3.12)

Solving Equation 3.11 and Equation 3.12, we have ${\alpha }_1=\frac{\sqrt{2n+2sn-2}+\sqrt{4s^{3}n+s^2(12n-8)+s(10n-8)+2n-2}}{2(s+1)\sqrt{2n-2}}$, and ${\alpha }_2=\frac{\sqrt{2n+2sn-2}-\sqrt{4s^{3}n+s^2(12n-8)+s(10n-8)+2n-2}}{2(s+1)\sqrt{2n-2}}$. So,

$specA=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill \frac{\sqrt{2n+2sn-2}+\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{2\left(s+1\right)\sqrt{2n-2}}\hfill & \hfill \frac{\sqrt{2n+2sn-2}-\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{2\left(s+1\right)\sqrt{2n-2}}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right).$(3.13)

Since ABC(Spl_s (K_n,n)) = ABC(K_n,n)⊗A, it follows that if λ₁, λ₂, … λ_n are the eigenvalues of ABC(K_n,n) then by Lemma 1.1, we have

$\begin{array}{ll}\hfill ABC\epsilon \left(Sp{l}_s\left(K_{n,n}\right)\right)& =\sum _{i=1}^n|\frac{\sqrt{2n+2sn-2}\pm \sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{2\left(s+1\right)\sqrt{2n-2}}{\lambda }_i|\hfill \\ \hfill & =\sum _{i=1}^n|{\lambda }_i|[\frac{\sqrt{2n+2sn-2}+\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{2\left(s+1\right)\sqrt{2n-2}}\hfill \\ \hfill & +\frac{\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}-\sqrt{2n+2sn-2}}{2\left(s+1\right)\sqrt{2n-2}}]\hfill \\ \hfill & =\frac{\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{\left(s+1\right)\left(\sqrt{2n-2}\right)}ABC\epsilon \left(K_{n,n}\right).\hfill \end{array}$

The following result relates the ABC Spectral radius of s-splitting graph of K_n,n with the ABC Spectral radius of K_n,n.

Corollary 6. Let K_n,n be a graph and ρABC(Spl_s(K_n,n)) be the ABC Spectral radius of s-splitting graph K_n,n, then$\rho ABC(Sp{l}_s(K_{n,n}))=\rho ABC(K_{n,n})(\frac{\sqrt{2n+2sn-2}+\sqrt{4s^{3}n+s^2(12n-8)+s(10n-8)+2n-2}}{2(s+1)\sqrt{2n-2}})$.

Proof. By similar arguments as formula (3.13) in Theorem 5,

$specA=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill \frac{\sqrt{2n+2sn-2}+\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{2\left(s+1\right)\sqrt{2n-2}}\hfill & \hfill \frac{\sqrt{2n+2sn-2}-\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{2\left(s+1\right)\sqrt{2n-2}}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right).$

Since ABC(Spl_s (K_n,n)) = ABC(K_n,n)⊗A, it follows that if η₁, η₂, η₃, … η_n are eigenvalues of ABC(K_n,n) then by Lemma 1.1, we have

$\begin{array}{ll}\hfill \rho ABC\left(Sp{l}_s\left(K_{n,n}\right)\right)& =ma{x}_{i=1}^n\left|\left(specA\right)\left.\right){\eta }_i\right|\hfill \\ \hfill & =ma{x}_{i=1}^n|{\eta }_i|\left[\frac{\sqrt{2n+2sn-2}+\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{2\left(s+1\right)\sqrt{2n-2}}\right]\hfill \\ \hfill & =\rho ABC\left(K_{n,n}\right)\left(\frac{\sqrt{2n+2sn-2}+\sqrt{4s^{3}n+s^2\left(12n-8\right)+s\left(10n-8\right)+2n-2}}{2\left(s+1\right)\sqrt{2n-2}}\right).\hfill \end{array}$

4 ABC energies and spectral radii of generalized shadow graph

In this part we relate ABC energies and ABC Spectral radii of generalized Shadow graph of K_n, C_n and K_n,n with original graph of K_n, C_n and K_n,n, respectively.

The following result relates the ABC energy of s-shadow graph of K_n with the ABC energy of K_n.

Theorem 7. Let K_n be a complete graph and ABCɛ(Sh_s(K_n)) be the ABC energy of s-shadow graph of K_n, then$ABC\epsilon (S{h}_s(K_n))=\sqrt{\frac{s(n-1)-1}{n-2}}ABC\epsilon (K_n)$.

Proof. Let v₁, v₂, v₃, …., v_n be the vertices of K_n. The ABC matrix of K_n has entries given by

$ABC\left(K_n\right)=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill & \hfill \cdots \hfill & \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill & \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill \\ \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill & \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill & \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill \\ \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill & \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill & \hfill \cdots \hfill & \hfill \sqrt{\frac{2\left(n-2\right)}{{\left(n-1\right)}^2}}\hfill & \hfill 0\hfill \end{array}\right].$

Let G₁, G₂, G₃, …., G_s be the s copies of the graph K_n which we take to construct Sh_s(K_n). Then ABC(Spl_s (K_n)) can be written as follows

$ABC\left(S{h}_s\left(K_n\right)\right)=\left[\begin{array}{cccc}\hfill {\hslash }_1\hfill & \hfill {\hslash }_1\hfill & \hfill \dots \hfill & \hfill {\hslash }_1\hfill \\ \hfill {\hslash }_1\hfill & \hfill {\hslash }_1\hfill & \hfill \dots \hfill & \hfill {\hslash }_1\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\hslash }_1\hfill & \hfill {\hslash }_1\hfill & \hfill \cdots \hfill & \hfill {\hslash }_1\hfill \end{array}\right].$

Matrix ℏ₁ has entries given by

$f_{ij}=\left\{\begin{array}{c}\hfill \sqrt{\frac{2sn-2s-2}{s^2{\left(n-1\right)}^2}}\text{if}{v}_i\text{is\hspace{0.17em}adjacent\hspace{0.17em}to}{v}_j,\hfill \\ \hfill 0\text{elsewhere}.\hfill \end{array}\right\}.$

${\hslash }_1=\sqrt{\frac{\frac{s(n-1)-1}{n-2}}{s^2}}ABC(K_n)$.Then ABC(Sh_s(K_n)) can be written in block matrix as follows

$\begin{array}{ll}\hfill ABC\left(S{h}_s\left(K_n\right)\right)& =\left\{\begin{array}{ccccccc}\hfill \sqrt{\frac{\frac{s\left(n-1\right)-1}{n-2}}{s^2}}*ABC\left(K_n\right)\hfill & \hfill \hfill & \hfill for\hfill & \hfill all\hfill & \hfill i\hfill & \hfill and\hfill & \hfill j\hfill \end{array}\right\}\hfill \\ \hfill & =ABC\left(K_{n,n}\right)\otimes \left\{\begin{array}{ccccccc}\hfill \sqrt{\frac{\frac{s\left(n-1\right)-1}{n-2}}{s^2}}\hfill & \hfill \hfill & \hfill for\hfill & \hfill all\hfill & \hfill i\hfill & \hfill and\hfill & \hfill j\hfill \end{array}\right\}.\hfill \end{array}$

Let

$A={\left\{\begin{array}{ccccccc}\hfill \sqrt{\frac{\frac{s\left(n-1\right)-1}{n-2}}{s^2}}\hfill & \hfill \hfill & \hfill for\hfill & \hfill all\hfill & \hfill i\hfill & \hfill and\hfill & \hfill j.\hfill \end{array}\right\}}_s$

Now we compute the eigenvalues of A. Since matrix A is of rank one, so A has only one non-zero eigenvalue, say α₁. We have${\alpha }_1=tr(A)=s(\sqrt{\frac{\frac{s(n-1)-1}{n-2}}{s^2}})=\sqrt{\frac{s(n-1)-1}{n-2}}$.So,

$specA=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \sqrt{\frac{s\left(n-1\right)-1}{n-2}}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill \end{array}\right).$(4.1)

Since ABC(Sh_s(K_n)) = ABC(K_n)⊗A, it follows that if λ₁, λ₂, … λ_n are the eigenvalues of ABC(K_n) then by Lemma 1.1, we have

$\begin{array}{ll}\hfill ABC\epsilon \left(S{h}_s\left(K_n\right)\right)& =\sum _{i=1}^n|\sqrt{\frac{s\left(n-1\right)-1}{n-2}}{\lambda }_i|\hfill \\ \hfill & =\sum _{i=1}^n|{\lambda }_i|\left[\sqrt{\frac{s\left(n-1\right)-1}{n-2}}\right]\hfill \\ \hfill & =\sqrt{\frac{s\left(n-1\right)-1}{n-2}}ABC\epsilon \left(K_n\right).\hfill \end{array}$

The following result relates the ABC Spectral radius of s-shadow graph of K_n with the ABC Spectral radius of K_n.

Corollary 8. Let K_n be a graph and ρABC(Sh_s(K_n)) be the ABC Spectral radius of s-shadow graph of K_n, then $\rho ABC(S{h}_s(K_n))=\rho ABC(K_n)(\sqrt{\frac{s(n-1)-1}{n-2}})$.

Proof. By similar arguments as formula (4.1) in Theorem 7,

$specA=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \sqrt{\frac{s\left(n-1\right)-1}{n-2}}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill \end{array}\right).$

So ABC(Sh_s(K_n)) = ABC(K_n)⊗A, it follows that if η₁, η₂, η₃, … η_n are eigenvalues of ABC(K_n) then by Lemma 1.1, we have

$\begin{array}{ll}\hfill \rho ABC\left(S{h}_s\left(K_n\right)\right)& =ma{x}_{i=1}^n\left|\left(specA\right)\left.\right){\eta }_i\right|\hfill \\ \hfill & =\rho ABC\left(K_n\right)\left(\sqrt{\frac{s\left(n-1\right)-1}{n-2}}\right).\hfill \end{array}$

The following result relates the ABC energy of s-shadow graph of C_n with the ABC energy of C_n.

Theorem 9. Let C_n be a cycle graph and ABCɛ(Sh_s(C_n)) be the ABC energy of s-shadow graph of C_n, then $ABC\epsilon (S{h}_s(C_n))=\sqrt{2s-1}ABC\epsilon (C_n)$.

Proof. Let v₁, v₂, v₃, …., v_n be the vertices of C_n. The ABC matrix of C_n has entries given by

$ABC\left(C_n\right)=\left\{\begin{array}{cccccccc}\hfill \sqrt{\frac{2}{4}},\hfill & \hfill \hfill & \hfill if\hfill & \hfill v_i\hfill & \hfill and\hfill & \hfill v_j\hfill & \hfill are\hfill & \hfill adjacent,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}$

Let G₁, G₂, G₃, …., G_s be the s copies of the graph C_n which we take to construct Sh_s(C_n). Then ABC(Sh_s(C_n)) can be written in block matrix as follows

$\begin{array}{ll}\hfill ABC\left(S{h}_s\left(C_n\right)\right)& =\left\{\begin{array}{ccccccc}\hfill \sqrt{\frac{2s-1}{s^2}}*ABC\left(C_n\right)\hfill & \hfill \hfill & \hfill for\hfill & \hfill all\hfill & \hfill i\hfill & \hfill and\hfill & \hfill j\hfill \end{array}\right\}\hfill \\ \hfill & =ABC\left(C_n\right)\otimes \left\{\begin{array}{ccccccc}\hfill \sqrt{\frac{2s-1}{s^2}}\hfill & \hfill \hfill & \hfill for\hfill & \hfill all\hfill & \hfill i\hfill & \hfill and\hfill & \hfill j\hfill \end{array}\right\}.\hfill \end{array}$

Let

$A={\left\{\begin{array}{ccccccc}\hfill \sqrt{\frac{2s-1}{s^2}}\hfill & \hfill \hfill & \hfill for\hfill & \hfill all\hfill & \hfill i\hfill & \hfill and\hfill & \hfill j.\hfill \end{array}\right\}}_s$

Now we compute the eigenvalues of A. Since matrix A is of rank one, so A has only one non-zero eigenvalue, say α₁. We have

${\alpha }_1=tr\left(A\right)=s\left(\sqrt{\frac{2s-1}{s^2}}\right)=\sqrt{2s-1}.$

So,

$specA=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \sqrt{2s-1}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill \end{array}\right).$(4.2)

Since ABC(Sh_s(C_n)) = ABC(C_n)⊗A, it follows that if λ₁, λ₂, … λ_n are the eigenvalues of ABC(C_n) then by Lemma 1.1, we have

$\begin{array}{ll}\hfill ABC\epsilon \left(S{h}_s\left(C_n\right)\right)& =\sum _{i=1}^n|\sqrt{2s-1}{\lambda }_i|\hfill \\ \hfill & =\sum _{i=1}^n|{\lambda }_i|\left[\sqrt{2s-1}\right]\hfill \\ \hfill & =\sqrt{2s-1}ABC\epsilon \left(C_n\right).\hfill \end{array}$

The following result relates the ABC Spectral radius of s-shadow graph of C_n with the ABC Spectral radius of C_n.

Corollary 10. Let C_n be a graph and ρABC(Sh_s(C_n)) be the ABC Spectral radius of s-shadow graph of C_n, then $\rho ABC(S{h}_s(C_n))=\rho ABC(C_n)(\sqrt{2s-1})$.

Proof. By similar arguments as formula (4.2) in Theorem 9,

$specA=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \sqrt{2s-1}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill \end{array}\right).$

Since ABC(Sh_s(C_n)) = ABC(C_n)⊗A, it follows that if η₁, η₂, η₃, … η_n are eigenvalues of ABC(C_n) then by Lemma 1.1 we have

$\begin{array}{ll}\hfill \rho ABC\left(S{h}_s\left(C_n\right)\right)& =ma{x}_{i=1}^n\left|\left(specA\right)\left.\right){\eta }_i\right|\hfill \\ \hfill & =ma{x}_{i=1}^n|{\eta }_i|\left[\sqrt{2s-1}\right]\hfill \\ \hfill & =\rho ABC\left(C_n\right)\left(\sqrt{2s-1}\right).\hfill \end{array}$

The following result relates the ABC energy of s-shadow graph of K_n,n with the ABC energy of K_n,n.

Theorem 11. Let K_n,n be a complete bipartite graph and ABCɛ(Sh_s(K_n,n)) be the ABC energy of s-shadow graph of K_n,n, then $ABC\epsilon (S{h}_s(K_{n,n}))=\sqrt{\frac{\mathrm{sn}-1}{n-1}}ABC\epsilon (K_{n,n})$.

Proof. Let v₁, v₂, v₃, …., v_n be the vertices of K_n,n. The ABC matrix of K_n,n has entries given by

$ABC\left(K_{n,n}\right)=\left\{\begin{array}{cccccccc}\hfill \sqrt{\frac{2n-2}{{\left(n\right)}^2}},\hfill & \hfill \hfill & \hfill if\hfill & \hfill v_i\hfill & \hfill and\hfill & \hfill v_j\hfill & \hfill are\hfill & \hfill adjacent,\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill elsewhere.\hfill \end{array}\right\}$

Let G₁, G₂, G₃, …., G_s be the s copies of the graph K_n,n which we take to construct Sh_s(K_n,n). Then ABC(Sh_s(K_n,n)) can be written in block matrix as follows

$\begin{array}{ll}\hfill ABC\left(S{h}_s\left(K_{n,n}\right)\right)& =\left\{\begin{array}{ccccccc}\hfill \sqrt{\frac{\frac{\mathrm{sn}-1}{n-1}}{s^2}}*ABC\left(K_{n,n}\right)\hfill & \hfill \hfill & \hfill for\hfill & \hfill all\hfill & \hfill i\hfill & \hfill and\hfill & \hfill j\hfill \end{array}\right\}\hfill \\ \hfill & =ABC\left(K_{n,n}\right)\otimes \left\{\begin{array}{ccccccc}\hfill \sqrt{\frac{\frac{\mathrm{sn}-1}{n-1}}{s^2}}\hfill & \hfill \hfill & \hfill for\hfill & \hfill all\hfill & \hfill i\hfill & \hfill and\hfill & \hfill j\hfill \end{array}\right\}.\hfill \end{array}$

Let

$A={\left\{\begin{array}{ccccccc}\hfill \sqrt{\frac{\frac{\mathrm{sn}-1}{n-1}}{s^2}}\hfill & \hfill \hfill & \hfill for\hfill & \hfill all\hfill & \hfill i\hfill & \hfill and\hfill & \hfill j.\hfill \end{array}\right\}}_s$

Now we compute the eigenvalues of A. Since matrix A is of rank one, so A has only one non-zero eigenvalue, say α₁. We have${\alpha }_1=tr(A)=s\sqrt{\frac{\frac{\mathrm{sn}-1}{n-1}}{s^2}}=\sqrt{\frac{\mathrm{sn}-1}{n-1}}$.So,

$specA=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \sqrt{\frac{\mathrm{sn}-1}{n-1}}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill \end{array}\right).$(4.3)

Since ABC(Sh_s(K_n,n)) = ABC(K_n,n)⊗A, it follows that if λ₁, λ₂, … λ_n are the eigenvalues of ABC(K_n,n) then by Lemma 1.1, we have

$\begin{array}{ll}\hfill ABC\epsilon \left(S{h}_s\left(K_{n,n}\right)\right)& =\sum _{i=1}^n|\sqrt{\frac{\mathrm{sn}-1}{n-1}}{\lambda }_i|\hfill \\ \hfill & =\sum _{i=1}^n|{\lambda }_i|\left[\sqrt{\frac{\mathrm{sn}-1}{n-1}}\right]\hfill \\ \hfill & =\sqrt{\frac{\mathrm{sn}-1}{n-1}}ABC\epsilon \left(K_{n,n}\right).\hfill \end{array}$

The following result relates the ABC Spectral radius of s-shadow graph of K_n,n with the ABC Spectral radius of K_n,n.

Corollary 12. Let K_n,n be a complete bipartite graph and ρABC(Sh_s(K_n,n)) be the ABC Spectral radius of s-shadow graph of K_n,n, then

$\rho ABC\left(S{h}_s\left(K_{n,n}\right)\right)=\rho ABC\left(K_{n,n}\right)\left(\sqrt{\frac{\mathrm{sn}-1}{n-1}}\right).$

Proof. By similar arguments as formula (4.3) in Theorem 11,

$specA=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \sqrt{\frac{\mathrm{sn}-1}{n-1}}\hfill \\ \hfill s-1\hfill & \hfill 1\hfill \end{array}\right).$

Since ABC(Sh_s(K_n,n)) = ABC(K_n,n)⊗A, it follows that if η₁, η₂, η₃, … η_n are eigenvalues of ABC(K_n,n) then by Lemma 1.1, we have

$\begin{array}{ll}\hfill \rho ABC\left(S{h}_s\left(K_{n,n}\right)\right)& =ma{x}_{i=1}^n\left|\left(specA\right)\left.\right){\eta }_i\right|\hfill \\ \hfill & =ma{x}_{i=1}^n|{\eta }_i|\left[\sqrt{\frac{\mathrm{sn}-1}{n-1}}\right]\hfill \\ \hfill & =\rho ABC\left(K_{n,n}\right)\left(\sqrt{\frac{\mathrm{sn}-1}{n-1}}\right).\hfill \end{array}$

5 Conclusion and possible applications

The graph energy and Spectral radius are two most emerging concepts in spectral graph theory. These concepts provides a bridge between mathematics and chemistry. You can find the Spectral radius and energy of many graphs in the literature. To examine the Spectral radius and energy of the larger graphs produced by a number of graph operations on a certain regular graph, however, is a challenge we must accept. We reached some quite general findings by concentrating on two graph operations, s-splitting and s-shadow graphs. Additionally, it was established that the new graph’s Spectral radius and energy are multiples of Spectral radius and energy of original regular graph referred as base graph. Our results on graph energies have applications in network analysis particularly dealing with problems of air travel, kirchhoff index, resistance distance, satellite communication, and biology. Our results on Spectral radii are also applicable to the stability theory of time-varying linear systems and linear inclusions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, MM. Investigation, computation and original draft, AB.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Estrada E, Torres L, Rodrguez L, Gutman I. An atom-bond connectivity index modelling the enthalpy of formation of alkanes. Indian J Chem (1998) 37A:849–55.

Google Scholar

2. Estrada E. Atom-bond connectivity and the energetic of branched alkanes. Chem Phys Lett (2008) 463:422–5. doi:10.1016/j.cplett.2008.08.074

CrossRef Full Text | Google Scholar

3. Gutman I, Tosovic J, Radenkovic S, Markovic S. On atom-bond connectivity index and its chemical applicability. Indian J Chem Sect A, Inorg Phys Theor Anal (2012) 51:690–4.

Google Scholar

4. Chen J, Guo X. Extreme atom-bond connectivity index of graphs. MATCH Commun Math.Comput Chem (2011) 65:713–22.

Google Scholar

5. Chen J, Liu J, Guo X. Some upper bounds for the atom-bond connectivity index of graphs. Appl Math Lett (2012) 25:1077–81. doi:10.1016/j.aml.2012.03.021

CrossRef Full Text | Google Scholar

6. Xing R, Zhou B, Du Z. Further results on atom-bond connectivity index of trees. Discrete Appl Math (2010) 158:1536–45. doi:10.1016/j.dam.2010.05.015

CrossRef Full Text | Google Scholar

7. Xing R, Zhou B, Dong F. On atom-bond connectivity index of connected graphs. Discrete Appl Math (2011) 159:1617–30. doi:10.1016/j.dam.2011.06.004

CrossRef Full Text | Google Scholar

8. Zhou B, Xing R. On atom-bond connectivity index. Z Naturforsch A (2011) 66a:61–6. doi:10.5560/zna.2011.66a0061

CrossRef Full Text | Google Scholar

9. Estrada E. The ABC matrix. J Math Chem (2017) 55:1021–33. doi:10.1007/s10910-016-0725-5

CrossRef Full Text | Google Scholar

10. Gutman I. The energy of a graph. Ber Math Statist Sekt Forschungsz Graz (1978) 103:122.

Google Scholar

11. Liu JB, Munir M, Yousaf A, Naseem A, Ayub K. Distance and adjacency energies of multi-level wheel networks. Mathematics (2019) 7:43. doi:10.3390/math7010043

CrossRef Full Text | Google Scholar

12. Zhang X, Bilal A, Munir MM, Rehman HMU. Maximum degree and minimum degree spectral radii of some graph operations. Math Biosci Eng (2022) 19(10):10108–21. doi:10.3934/mbe.2022473

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chu ZQ, Munir M, Yousaf A, Qureshi MI, Liu JB. Laplacian and signless laplacian spectra and energies of multi-step wheels. Math Biosci Eng (2020) 17(4):3649–59. doi:10.3934/mbe.2020206

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Chen X. On ABC eigenvalues and ABC energy. Linear Algebra Appl (2018) 544:141–57. doi:10.1016/j.laa.2018.01.011

CrossRef Full Text | Google Scholar

15. Gao Y, Shao Y. The minimum ABC energy of trees. Linear Algebra Appl (2019) 577:186–203. doi:10.1016/j.laa.2019.04.032

CrossRef Full Text | Google Scholar

16. Ghorbani M, Li X, Nezhaad MH, Wang J. Bounds on the ABC Spectral radius and ABC energy of graphs. Linear Algebra Its Appl (2020) 598:145–64. doi:10.1016/j.laa.2020.03.043

CrossRef Full Text | Google Scholar

17. Yalçin NF, Buyukkose E. Skew ABC energy of digraphs. Commun Fac Sci Univ Ank Ser A1 Math Stat (2022) 71(22022):434–44. doi:10.31801/cfsuasmas.951302

CrossRef Full Text | Google Scholar

18. Singh R, Patekar SC. On the sombor index and sombor energy of m-splitting graph and m-shadow graph of regular graphs (2022). preprint arXiv:2205.09480.

Google Scholar

19. Vaidya SK, Popat KM. Some new results on energy of graphs. MATCH Commun Math Comput Chem (2017) 77:589–94.

Google Scholar

20. Vaidya SK, Popat KM. Energy of m-Splitting and m-Shadow Graphs. Far East J Math Sci (Fjms) (2017) 102(8):1571–8. doi:10.17654/ms102081571

CrossRef Full Text | Google Scholar

21. Sampathkumar E, Walikar HB. On splitting graph of a graph. J Karnatak Univ Sci (1980) 25(13):13–6.

Google Scholar