
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
MINI REVIEW article
Front. Phys. , 12 October 2022
Sec. Condensed Matter Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1013937
The quantum origin of the cuprate pseudogap and its relationship to symmetry-breaking orders is a central conundrum of unconventional superconductors. The difficulty is deeply rooted in modeling simultaneous organizations in multiple degrees of freedom (including spin, momentum, and real space) generated by strong electron-electron correlations. Beyond early theories focusing on the description in spin and momentum space, recent studies turn to examine the spatial organization and intertwining mechanism of multiple orders. In this review, we summarize some progress in understanding the spatial organization of critical fluctuations and highlight the recent discovery of a universal energy-length scaling. This scaling quantitatively explains the nontrivial magnitude and doping dependence of the pseudogap energy and critical temperature and their relations to charge and superconducting ordering. We close with a prospect of the spatial organization mechanism of intertwined orders and its possible composite energy scaling.
The origin of the pseudogap is one of the most critical problems for understanding the unconventional cuprate superconductivity [1–3]. This gap,
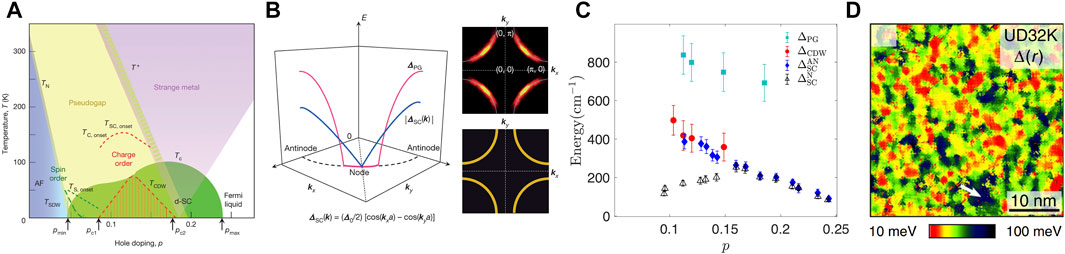
FIGURE 1. Pseudogap phenomena in cuprates. (A) The complex phase diagram for hole-doped cuprates [1], which shows the pseudogap phase and its associations with spin, charge, and superconducting orders. (B) Gap functions, Fermi arcs, and Fermi surface [1]. Once the pseudogap (
Current theories about the pseudogap origin fall into four categories [2, 12], namely, a precursor of an ordered state (e.g., superconductivity [13–15] or spin density wave [16, 17]), a band folding gap induced by a (spin [18, 19] or charge [20, 21]) density wave order (DWO), a hybrid gap induced by intertwined orders [22, 23] (e.g., stripe [24] and pair DWOs [25]), and a spectral feature from strong correlations (e.g., short-ranged magnetic fluctuations [26]) without breaking any symmetry. Although these theories have qualitatively described some pseudogap properties, none of them can precisely describe the whole pseudogap phase and all essential experimental manifestations; thus, there is no consensus on the pseudogap origin [2, 12, 26–28]. For instance, though the precursor to superconductivity could explain the
Therefore, thoroughly elucidating the pseudogap origin requires a unified description of multiple mechanisms to comprehensively describe the whole pseudogap phase and the main experimental manifestations [2, 22, 23]. However, this faces a fundamental difficulty rooted in the dual nature of cuprate electrons [12]. That is, the strong electron-electron correlations together with the chemical disorder generate simultaneous organizations in both momentum and spatial degrees of freedom, which have generally been treated separately as extended (or long-range) and local (or short-range) electronic states, respectively. Most previous theories [26, 30, 32–41] focus on the momentum side, e.g., particle-particle (or particle-hole) pairing with zero (or finite) total momentum, the umklapp scattering, to characterize the electronic dispersion and Fermi arcs. However, the spatial organization also results in nontrivial nanoscale inhomogeneity in the electronic structure, including nanoscale patterns of the gap energy scale (see Figure 1D), Fermi surface, and charge modulation in cuprates [42–50] observed by scanning tunneling microscope (STM). Owing to overlooking these nanoscale inhomogeneities, most momentum-resolved theories can only reach qualitative consistency with globally-averaged experimental observations but can not clarify the subtle local differences, which may be important to examine different mechanisms.
Studying the nontrivial organization mechanism in real space is crucial to breaking through this dilemma. Recently, accompanied by the observations of the nontrivial spatial pattern of charge ordering [46–52] and nematicity [53–56], theories focusing on spatial organization have been proposed for the vestigial nematicity [57], intertwined charge and superconductivity orders [58], and intertwined loop current and DWO [59]. These theories are mainly focused on specific intertwined mechanisms for distinct orders, which lack universality in describing the universal doping dependence of pseudogap energies (
In a real space perspective, the doping dependences of energy scales for the pseudogap [11, 61] correspond to varying spatial organizing structures of collective electron motions during the increase of hole spacing [62–64]. Therefore, the energy-length relation lies at the heart of the pseudogap origin and its relationship with symmetry-breaking orders [65]. It is well known that the strong electron-electron correlations stimulate multiple symmetry-breaking orders in cuprates, whose competitions result in unprecedented prominence of collective fluctuations [1]. These fluctuations are intimately related to and affect the pseudogap phase. For instance, the emergence of magnetic fluctuations [66, 67] and nematicity order coincide with the pseudogap opening temperature
In the following, taking pairing orders as an example, we derive this relation from the spatial organization of critical fluctuations. DWO and superconductivity are particle-hole and particle-particle pairings, respectively, with order parameters expressed by two-point correlation functions. In conventional metals, these orders are usually long-range coherent, so nontrivial pairing mainly occurs in the momentum space [76, 77]. On the contrary, strong electron-electron correlations and chemical disorder in cuprates constrain pairings to be short-range with coherence or correlation lengths at only several nanometers [20, 21, 78–80], revealing nontrivial spatial organizations [81–85]. Thus, we propose that they should be described by two-point correlation functions in real space. Moreover, for critical fluctuations, the universal criticality constrains the correlation function to be a power law versus length (ansatz No. 2), i.e.,
In a classical theory of critical behavior, length scales are continuous coordinates. However, the Mott physics and strong correlations in cuprates result in a local tendency to phase separation [1], forcing the spatial organization of mesoscopic order and fluctuations occurring on specific nanoscales. Specifically, there are two kinds of length scales in the order parameter, i.e., the spatial period of the DWO and the characteristic length of the (charge, spin, or superfluid) density, presenting in phase and amplitude, respectively. Like Emery and Kivelson [13], we assume the critical fluctuations have the particle-wave duality constrained by the Heisenberg uncertainty principle (ansatz No. 3). Therefore, the energy scale corresponding to the two-point correlation function should satisfy an inverse square relation with its appropriate length as follows [65].
where
The scaling in Eq. 1 is universal for various phase-fluctuating orders. It can be derived from a series of physical mechanisms, including the phase-disordering transition (e.g., Berezinskii-Kosterlitz-Thouless (BKT) [86–88] and Bose-Einstein phase transition [89]), the umklapp scattering [65], and quantum kinetic energy of a density modulation1. For these mechanisms,
It is also intriguing to mention that the power law form of the energy-length scaling is universal for both quantum and classical systems. However, the scaling index may vary for different systems owing to different physical mechanisms. For instance, the gravity and electric potentials of a point source are inversely proportional to the distance to this point (−1 index), while the fluctuation energy called Reynolds stress of a turbulent flow is proportional to the square of the stress length (+2 index) [90]. In contrast, for simple quantum phenomena with only one related length scale, the inverse square scaling (−2 index) must be universal due to the dimensional constraints with Planck constant
For the pseudogap origin, charge orders were identified as an important candidate in moderately doped cuprates. Recently, the pseudogap opening at

FIGURE 2. Universal spatial organization of mesoscopic orders and the energy-length scaling associated with pseudogap phase. (A) Schematic diagram of the locally unidirectional CDW along x- and y-axes [91]. (B) Scaling between the spectral gap and the CDW period. Symbols are data determined from the low-temperature (6 K) phase of Pb-Bi2201 samples [42], and the solid line is a prediction of Eq. 3. (C) Distributions of the spectral gap within the Pb-Bi2201 samples. Symbols are STM data from Ref. [42], and the solid line is a prediction from Eq. 4. (D) Doping dependence of the pseudogap onset temperature
Here,
which is a specific expression of Eq. 1.
Taking
Another advantage of the energy-length scaling is its ability to characterize the global phase fluctuations, which was observed as spatial homogeneity of gap amplitude and period between different local CDW plaques. Assuming this phase fluctuations as a Gaussian type, we derive from Eq. 2 a gap distribution as [65]:
where
Furthermore, the pseudogap opening temperature can be defined with the emergence of the particle-hole pairing of CDW [39], implying
As
Besides charge orders, superconducting phase fluctuations have been accepted as an important participator in part of the pseudogap regime [101]. It is well known that the two-dimensionality (2D) and low carrier density result in significant phase fluctuations in underdoped cuprates [13]. In the Berezinskii-Kosterlitz-Thouless (BKT) phase transition scenario [86, 88], the 2D superconducting phase fluctuations are generated by the real-space unbinding of vortex-antivortex pairs at a critical temperature, (see Figure 2E). The balance between the vortex excitation energy and the entropy (i.e.,
where
Although there are other specific contexts to derive the scaling in Eq. 6 with different prefactors [13, 14], the linear scaling between
It is intriguing that the present energy-length scaling (Eq. 1) also applies to the topological excitations of loop current in the strange metal phase at higher temperatures or beyond the pseudogap critical point [108]. These excitations are fluctuating vortices of unpaired electrons, whose characteristic lengths are the thermal de Broglie wavelength (
Section 2 indicates that the pseudogap energies in the moderate doping regime are determined by the phase fluctuating CDW, and the thermally excited superconducting vortices survive in the low-
Here, we propose two critical open questions for the intertwined-order study from the spatial-organization perspective, i.e., what is the nanoscale pattern of intertwined orders in real space and how its composite energy-length scaling behaves. Recent STM and NMR measurements found that the CDW phase for underdoped cuprates [46–49] is locally unidirectional with significant global fluctuations, and the charge order can be locally enhanced in the superconducting vortex core [51, 52]. Thus, we believe there must be some nontrivial spatial organization pattern for intertwined orders of CDW, superconductivity, and loop-current order. For experiments, we suggest a combination of spatially resolved measurements to probe the spatial intertwining pattern of charge density, Cooper pair, and local magnetic excitation. More importantly, we suggest paying particular attention to examining the spatial distribution of topological excitations and orders (e.g., vortices and loop current), which may lie at the heart of intertwined mechanisms and the relationship between pseudogap and strange metal phases [67, 109]. For instance, we suspect that by increasing magnetic fields at low temperatures, superconducting vortices will likely emerge in the transition region between the x- and y-unidirectional CDWs (see Figure 2A) for energy optimization. Since introducing a vortex requires the emergence of a loop current with a varying velocity around a circle and a significant increase of kinetic energy, the transition region with varying wave vectors (contrast to the unidirectional region) and higher kinetic energy (than uniform region1) has both dynamical and thermodynamic advantages. Similarly, as the temperature rises close to
For theory, a critical question is whether intertwined orders have composite energy-length scalings, including characteristic lengths of different orders, or a simple scaling similar to Eq. 1. For example, there exist two anomalous energy scales: one is the antinodal superconducting gap
The strong correlation and chemical disorder result in widespread nanoscale electronic structure in cuprates, making the spatial organization as crucial as the momentum-space organization. Exploring the spatial-organization mechanism of critical fluctuations, we find a simple scaling between the characteristic energy and length of mesoscopic order, which is universal to the phase fluctuations of CDW, superconductivity, and loop current. These results show that the spatial organization of critical fluctuations opens a new way to explore the relationship between the pseudogap and various order parameters and even the spatial organization of intertwined orders. Going forwards, we speculate that a comprehensive theory integrating the organizational principle in both real and momentum spaces is necessary to understand the pseudogap origins thoroughly in the future.
The manuscript was written by RL and ZS.
We acknowledge support from the National Natural Science Foundation of China with Grants Nos. 91952201 and 11452002.
We want to thank Lu-Hao Zhang, Zhen-Yuan Yin, and Yong Ji for their help preparing this manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1For a small
1. Keimer B, Kivelson SA, Norman MR, Uchida S, Zaanen J. From quantum matter to high-temperature superconductivity in copper oxides. Nature (2015) 518:179–86. doi:10.1038/nature14165
2. Kordyuk AA. Pseudogap from ARPES experiment: Three gaps in cuprates and topological superconductivity (Review Article). Low Temperature Phys (2015) 41:319–41. doi:10.1063/1.4919371
3. Hashimoto M, Vishik IM, He RH, Devereaux TP, Shen ZX. Energy gaps in high-transition-temperature cuprate superconductors. Nat Phys (2014) 10:483–95. doi:10.1038/nphys3009
4. Alloul H, Ohno T, Mendels P. 89Y NMR evidence for a fermi-liquid behavior in YBa2Cu3O6+x. Phys Rev Lett (1989) 63:1700–3. doi:10.1103/PhysRevLett.63.1700
5. Warren WW, Walstedt RE, Brennert GF, Cava RJ, Tycko R, Bell RF. Cu spin dynamics and superconducting precursor effects in planes above Tc in YBa2Cu3O6.7. Phys Rev Lett (1989) 62:1193–6. doi:10.1103/PhysRevLett.62.1193
6. Homes CC, Timusk T, Liang R, Bonn DA, Hardy WN. Optical conductivity of c axis oriented YBa2Cu3O6.70: Evidence for a pseudogap. Phys Rev Lett (1993) 71:1645–8. doi:10.1103/PhysRevLett.71.1645
7. Loram JW, Luo J, Cooper J, Liang W, Tallon J. Evidence on the pseudogap and condensate from the electronic specific heat. J Phys Chem Sol (2001) 62:59–64. doi:10.1016/S0022-3697(00)00101-3
8. Ding H, Yokoya T, Campuzano JC, Takahashi T, Randeria M, Norman MR, Spectroscopic evidence for a pseudogap in the normal state of underdoped high-Tc superconductors. Nature (1996) 382:51–4. doi:10.1038/382051a0
9. Marshall DS, Dessau DS, Loeser AG, Park CH, Matsuura AY, Eckstein JN, Unconventional electronic structure Evolution with hole Doping in Bi2Sr2CaCu2O8+δ: Angle-resolved photoemission results. Phys Rev Lett (1996) 76:4841–4. doi:10.1103/PhysRevLett.76.4841
10. Yoshida T, Malaeb W, Ideta S, Lu DH, Moor RG, Shen ZX, Coexistence of a pseudogap and a superconducting gap for the high-Tc superconductor La2-xSrxCuO4 studied by angle-resolved photoemission spectroscopy. Phys Rev B (2016) 93:014513. doi:10.1103/PhysRevB.93.014513
11. Loret B, Auvray N, Gu GD, Forget A, Colson D, Cazayous M, Universal relationship between the energy scales of the pseudogap phase, the superconducting state, and the charge-density-wave order in copper oxide superconductors. Phys Rev B (2020) 101:214520. doi:10.1103/PhysRevB.101.214520
12. Li T. A short review of the recent progresses in the study of the cuprate superconductivity. Chin Phys B (2021) 30:100508. doi:10.1088/1674-1056/abfa04
13. Emery VJ, Kivelson SA. Importance of phase fluctuations in superconductors with small superfluid density. Nature (1995) 374:434–7. doi:10.1038/374434a0
14. Lee PA, Nagaosa N, Wen XG. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev Mod Phys (2006) 78:17–85. doi:10.1103/RevModPhys.78.17
15. Baskaran G, Zou Z, Anderson PW. The resonating valence bond state and high-Tc superconductivity — a mean field theory. Solid State Commun (1987) 63:973–6. doi:10.1016/0038-1098(87)90642-9
16. Sedrakyan TA, Chubukov AV. Pseudogap in underdoped cuprates and spin-density-wave fluctuations. Phys Rev B (2010) 81:174536. doi:10.1103/PhysRevB.81.174536
17. Schmalian J, Pines D, Stojković B. Microscopic theory of weak pseudogap behavior in the underdoped cuprate superconductors: General theory and quasiparticle properties. Phys Rev B (1999) 60:667–86. doi:10.1103/PhysRevB.60.667
18. Yamada K, Lee CH, Kurahashi K, Wada J, Wakimoto S, Ueki S, Doping dependence of the spatially modulated dynamical spin correlations and the superconducting-transition temperature in La2-xSrxCuO4. Phys Rev B (1998) 57:6165–72. doi:10.1103/PhysRevB.57.6165
19. Fujita M, Hiraka H, Matsuda M, Matsuura M, M. Tranquada J, Wakimoto S, Progress in neutron scattering Studies of spin Excitations in high-Tc cuprates. J Phys Soc Jpn (2012) 81:011007. doi:10.1143/jpsj.81.011007
20. Comin R, Damascelli A. Resonant X-ray scattering studies of charge order in cuprates. Annu Rev Condens Matter Phys (2016) 7:369–405. doi:10.1146/annurev-conmatphys-031115-011401
21. Frano A, Blanco-Canosa S, Keimer B, Birgeneau RJ. Charge ordering in superconducting copper oxides. J Phys : Condens Matter (2020) 32:374005. doi:10.1088/1361-648x/ab6140
22. Fradkin E, Kivelson SA, Tranquada JM. Colloquium: Theory of intertwined orders in high temperature superconductors. Rev Mod Phys (2015) 87:457–82. doi:10.1103/RevModPhys.87.457
23. Fernandes RM, Orth PP, Schmalian J. Intertwined vestigial order in quantum materials: Nematicity and beyond. Annu Rev Condens Matter Phys (2019) 10:133–54. doi:10.1146/annurev-conmatphys-031218-013200
24. Tranquada JM, Sternlieb BJ, Axe JD, Nakamura Y, Uchida S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature (1995) 375:561–3. doi:10.1038/375561a0
25. Agterberg DF, Davis JS, Edkins SD, Fradkin E, Van Harlingen DJ, Kivelson SA, The physics of pair-density waves: Cuprate superconductors and beyond. Annu Rev Condens Matter Phys (2020) 11:231–70. doi:10.1146/annurev-conmatphys-031119-050711
26. Qin M, Schafer T, Andergassen S, Corboz P, Gull E. The Hubbard model: A computational perspective. Annu Rev Condens Matter Phys (2022) 13:275–302. doi:10.1146/annurev-conmatphys-090921-033948
27. Arovas DP, Berg E, Kivelson SA, Raghu S. The Hubbard model. Annu Rev Condens Matter Phys (2022) 13:239–74. doi:10.1146/annurev-conmatphys-031620-102024
28. Singh N. Leading theories of the cuprate superconductivity: A critique. Physica C: Superconductivity its Appl (2021) 580:1353782. doi:10.1016/j.physc.2020.1353782
29. He RH, Hashimoto M, Karapetyan H, Koralek JD, Hinton JP, Testaud JP, From a single-band metal to a high-temperature superconductor via two thermal phase transitions. Science (2011) 331:1579–83. doi:10.1126/science.1198415
30. Lee PA. Amperean pairing and the pseudogap phase of cuprate superconductors. Phys Rev X (2014) X4:031017. doi:10.1103/PhysRevX.4.031017
31. Pépin C, Chakraborty D, Grandadam M, Sarkar S. Fluctuations and the Higgs mechanism in underdoped cuprates. Annu Rev Condens Matter Phys (2020) 11:301–23. doi:10.1146/annurev-conmatphys-031218-013125
32. Chakravarty S, Laughlin RB, Morr DK, Nayak C. Hidden order in the cuprates. Phys Rev B (2001) 63:094503. doi:10.1103/PhysRevB.63.094503
33. Li JX, Wu CQ, Lee DH. Checkerboard charge density wave and pseudogap of high-Tc cuprate. Phys Rev B (2006) 74:184515. doi:10.1103/PhysRevB.74.184515
34. Tremblay AMS, Kyung B, Sénéchal D. Pseudogap and high-temperature superconductivity from weak to strong coupling. Towards a quantitative theory (Review Article). Low Temperature Phys (2006) 32:424–51. doi:10.1063/1.2199446
35. Yang K-Y, Rice TM, Zhang F-C. Phenomenological theory of the pseudogap state. Phys Rev B (2006) 73:174501. doi:10.1103/PhysRevB.73.174501
36. Millis AJ, Norman MR. Antiphase stripe order as the origin of electron pockets observed in 1/8-hole-doped cuprates. Phys Rev B (2007) 76:220503. doi:10.1103/PhysRevB.76.220503
37. Norman MR, Kanigel A, Randeria M, Chatterjee U, Campuzano JC. Modeling the Fermi arc in underdoped cuprates. Phys Rev B (2007) 76:174501. doi:10.1103/PhysRevB.76.174501
38. Das T, Markiewicz RS, Bansil A. Competing order scenario of two-gap behavior in hole-doped cuprates. Phys Rev B (2008) 77:134516. doi:10.1103/PhysRevB.77.134516
39. Wang Y, Chubukov A. Charge-density-wave order with momentum (2Q, 0) and (0, 2Q) within the spin-fermion model: Continuous and discrete symmetry breaking, preemptive composite order, and relation to pseudogap in hole-doped cuprates. Phys Rev B (2014) 90:035149. doi:10.1103/PhysRevB.90.035149
40. Robinson NJ, Johnson PD, Rice TM, Tsvelik AM. Anomalies in the pseudogap phase of the cuprates: Competing ground states and the role of umklapp scattering. Rep Prog Phys (2019) 82:126501. doi:10.1088/1361-6633/ab31ed
41. Chakraborty D, Grandadam M, Hamidian MH, Davis JCS, Sidis Y, Pepin C. Fractionalized pair density wave in the pseudogap phase of cuprate superconductors. Phys Rev B (2019) 100:224511. doi:10.1103/PhysRevB.100.224511
42. Webb TA, Boyer MC, Yin Y, Chowdhury D, He Y, Kondo T, Density wave probes cuprate quantum phase transition. Phys Rev X (2019) X9:021021. doi:10.1103/PhysRevX.9.021021
43. Cai P, Ruan W, Peng Y, Ye C, Li X, Hao Z, Visualizing the evolution from the Mott insulator to a charge-ordered insulator in lightly doped cuprates. Nat Phys (2016) 12:1047–51. doi:10.1038/nphys3840
44. Wise WD, Chatterjee K, Boyer MC, Kondo T, Takeuchi T, Ikuta H, Imaging nanoscale Fermi-surface variations in an inhomogeneous superconductor. Nat Phys (2009) 5:213–6. doi:10.1038/nphys1197
45. Zeljkovic I, Xu Z, Wen J, Gu G, Markiewicz RS, Hoffman JE. Imaging the impact of single oxygen atoms on superconducting Bi2+ySr2-yCaCu2O8+x. Science (2012) 337:320–3. doi:10.1126/science.1218648
46. Mesaros A, Fujita K, Edkins SD, Hamidian MH, Eisaki H, Uchida S, Commensurate 4a0-period charge density modulations throughout the Bi2Sr2CaCu2O8+x pseudogap regime. Proc Natl Acad Sci U S A (2016) 113:12661–6. doi:10.1073/pnas.1614247113
47. Zhang Y, Mesaros A, Fujita K, Edkins SD, Hamidian MH, Ch’ng K, Machine learning in electronic-quantum-matter imaging experiments. Nature (2019) 570:484–90. doi:10.1038/s41586-019-1319-8
48. Zhao H, Ren Z, Rachmilowitz B, Schneeloch J, Zhong R, Gu G, Charge-stripe crystal phase in an insulating cuprate. Nat Mater (2019) 18:103–7. doi:10.1038/s41563-018-0243-x
49. Vinograd I, Zhou R, Hirata M, Wu T, Mayaffre H, Kramer S, Locally commensurate charge-density wave with three-unit-cell periodicity in YBa2Cu3Oy. Nat Commun (2021) 12:3274. doi:10.1038/s41467-021-23140-w
50. Wang X, Yuan Y, Xue QK, Li W. Charge ordering in high-temperature superconductors visualized by scanning tunneling microscopy. J Phys : Condens Matter (2019) 32:013002. doi:10.1088/1361-648x/ab41c5
51. Edkins SD, Kostin A, Fujita K, Mackenzie AP, Eisaki H, Uchida S, Magnetic field induced pair density wave state in the cuprate vortex halo. Science (2019) 364:976–80. doi:10.1126/science.aat1773
52. Machida T, Kohsaka Y, Matsuoka K, Iwaya K, Hanaguri T, Tamegai T. Bipartite electronic superstructures in the vortex core of Bi2Sr2CaCu2O8+δ. Nat Commun (2016) 7:11747. doi:10.1038/ncomms11747
53. Ishida K, Hosoi S, Teramoto Y, Usui T, Mizukami Y, Itaka K, Divergent nematic susceptibility near the pseudogap critical point in a cuprate superconductor. J Phys Soc Jpn (2020) 89:064707. doi:10.7566/JPSJ.89.064707
54. Sato Y, Kasahara S, Murayama H, Kasahara Y, Moon EG, Nishizaki T, Thermodynamic evidence for a nematic phase transition at the onset of the pseudogap in YBa2Cu3Oy. Nat Phys (2017) 13:1074–8. doi:10.1038/nphys4205
55. Murayama H, Sato Y, Kurihara R, Kasahara S, Mizukami Y, Kasahara Y, Diagonal nematicity in the pseudogap phase of HgBa2CuO4+δ. Nat Commun (2019) 10:3282. doi:10.1038/s41467-019-11200-1
56. Wu J, Bollinger AT, He X, Bozovic I. Spontaneous breaking of rotational symmetry in copper oxide superconductors. Nature (2017) 547:432–5. doi:10.1038/nature23290
57. Nie L, Tarjus G, Kivelson SA. Quenched disorder and vestigial nematicity in the pseudogap regime of the cuprates. Proc Natl Acad Sci U S A (2014) 111:7980–5. doi:10.1073/pnas.1406019111
58. Hayward LE, Achkar AJ, Hawthorn DG, Melko RG, Sachdev S. Diamagnetism and density-wave order in the pseudogap regime of YBa2Cu3O6+x. Phys Rev B (2014) 90:094515. doi:10.1103/PhysRevB.90.094515
59. Varma CM. Pseudogap and Fermi arcs in underdoped cuprates. Phys Rev B (2019) 99:224516. doi:10.1103/PhysRevB.99.224516
61. Loret B, Auvray N, Gallais Y, Cazayous M, Forget A, Colson D, Intimate link between charge density wave, pseudogap and superconducting energy scales in cuprates. Nat Phys (2019) 15:771–5. doi:10.1038/s41567-019-0509-5
62. Komiya S, Chen HD, Zhang SC, Ando Y. Magic doping fractions for high-temperature superconductors. Phys Rev Lett (2005) 94:207004. doi:10.1103/PhysRevLett.94.207004
63. Proust C, Taillefer L. The remarkable underlying ground states of cuprate superconductors. Annu Rev Condens Matter Phys (2019) 10:409–29. doi:10.1146/annurev-conmatphys-031218-013210
64. Zhang H, Sato H. Universal relationship between Tc and the hole content in p-type cuprate superconductors. Phys Rev Lett (1993) 70:1697–9. doi:10.1103/PhysRevLett.70.1697
65. Li R, She Z-S. Unified energy law for fluctuating density wave orders in cuprate pseudogap phase. Commun Phys (2022) 5:13. doi:10.1038/s42005-021-00789-9
66. Zhang J, Ding Z, Tan C, Huang K, Bernal OO, Ho PC, Discovery of slow magnetic fluctuations and critical slowing down in the pseudogap phase of YBa2 Cu3Oy. Sci Adv (2018) 4:eaao5235. doi:10.1126/sciadv.aao5235
67. Varma CM. Colloquium: Linear in temperature resistivity and associated mysteries including high temperature superconductivity. Rev Mod Phys (2020) 92:031001. doi:10.1103/RevModPhys.92.031001
68. Božović I, He X, Wu J, Bollinger AT. Dependence of the critical temperature in overdoped copper oxides on superfluid density. Nature (2016) 536:309–11. doi:10.1038/nature19061
69. Božović I, He X, Wu J, Bollinger AT. The vanishing superfluid density in cuprates—And why it matters. J Supercond Nov Magn (2018) 31:2683–90. doi:10.1007/s10948-018-4792-7
70. Uemura YJ, Luke GM, Sternlieb BJ, Brewer JH, Carolan JF, Hardy WN, Universal Correlations between Tc and ns/m* (carrier Density over effective mass) in high-Tc cuprate superconductors. Phys Rev Lett (1989) 62:2317–20. doi:10.1103/PhysRevLett.62.2317
71. Hussey NE, Buhot J, Licciardello S. A tale of two metals: Contrasting criticalities in the pnictides and hole-doped cuprates. Rep Prog Phys (2018) 81:052501. doi:10.1088/1361-6633/aaa97c
72. Badoux S, Tabis W, Laliberte F, Grissonnanche G, Vignolle B, Vignolles D, Change of carrier density at the pseudogap critical point of a cuprate superconductor. Nature (2016) 531:210–4. doi:10.1038/nature16983
73. Fujita K, Kim CK, Lee I, Lee J, Hamidian MH, Firmo IA, Simultaneous transitions in cuprate momentum-space topology and electronic symmetry breaking. Science (2014) 344:612–6. doi:10.1126/science.1248783
74. Michon B, Girod C, Badoux S, Kacmarcik J, Ma Q, Dragomir M, Thermodynamic signatures of quantum criticality in cuprate superconductors. Nature (2019) 567:218–22. doi:10.1038/s41586-019-0932-x
75. Efetov KB, Meier H, Pépin C. Pseudogap state near a quantum critical point. Nat Phys (2013) 9:442–6. doi:10.1038/nphys2641
76. Bardeen J, Cooper LN, Schrieffer JR. Theory of superconductivity. Phys Rev (1957) 108:1175–204. doi:10.1103/physrev.108.1175
77. Monceau P. Electronic crystals: An experimental overview. Adv Phys (2012) 61:325–581. doi:10.1080/00018732.2012.719674
78. Wang Y, Ono S, Onose Y, Gu G, Ando Y, Tokura Y, Dependence of upper critical field and pairing strength on doping in cuprates. Science (2003) 299:86–9. doi:10.1126/science.1078422
79. Mourachkine A. Determination of the coherence length and the cooper-pair size in unconventional superconductors by tunneling spectroscopy. J Supercond (2004) 17:711–24. doi:10.1007/s10948-004-0831-7
80. Mukubwa A, Asselmeyer-Maluga T. Electron number density and coherence length of boson-fermion pair in HTSC. Adv High Energ Phys (2022) 2022:1–7. doi:10.1155/2022/8198401
81. Anderson PW, Lee PA, Randeria M, Rice TM, Trivedi N, Zhang FC. The physics behind high-temperature superconducting cuprates: The plain vanilla version of RVB. J Phys : Condens Matter (2004) 16:R755–69. doi:10.1088/0953-8984/16/24/r02
82. Zhang FC, Rice TM. Effective Hamiltonian for the superconducting Cu oxides. Phys Rev B (1988) 37:3759–61. doi:10.1103/physrevb.37.3759
83. Scalapino DJ. Superconductivity and spin fluctuations. J Low Temp Phys (1999) 117:179–88. doi:10.1023/A:1022559920049
84. Chen HD, Vafek O, Yazdani A, Zhang SC. Pair density wave in the pseudogap state of high temperature superconductors. Phys Rev Lett (2004) 93:187002. doi:10.1103/PhysRevLett.93.187002
85. Zhao JY, Two-hole ground state: Dichotomy in pairing symmetry. arXiv. AvaliableAt: https://arxiv.org/abs/2106.14898, (2021).
86. Berezinskii VL. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group II. quantum systems. Sov Phys JETP (1972) 34 610.
87. Kosterlitz JM, Thouless DJ. Long range order and metastability in two dimensional solids and superfluids. (Application of dislocation theory). J Phys C: Solid State Phys (1972) 5:L124–6. doi:10.1088/0022-3719/5/11/002
88. Kosterlitz JM, Thouless DJ. Ordering, metastability and phase transitions in two-dimensional systems. J Phys C: Solid State Phys (1973) 6:1181–203. doi:10.1088/0022-3719/6/7/010
89. Pethick CJ, Smith H. Bose–einstein condensation in dilute gases. 2 ed. Cambridge, UK: Cambridge University Press (2008).
90. She Z-S, Chen X, Hussain F. Quantifying wall turbulence via a symmetry approach: A lie group theory. J Fluid Mech (2017) 827:322–56. doi:10.1017/jfm.2017.464
91. Comin R, Sutarto R, da Silva Neto EH, Chauviere L, Liang R, Hardy WN. Broken translational and rotational symmetry via charge stripe order in underdoped YBa2Cu3O6+y. Science (2015) 347:1335–9. doi:10.1126/science.1258399
92. Wang Y, Li L, Ong NP. Nernst effect in high-Tcsuperconductors. Phys Rev B (2006) 73:024510. doi:10.1103/PhysRevB.73.024510
94. Pelc D, Popcevic P, Pozek M, Greven M, Barisic N. Unusual behavior of cuprates explained by heterogeneous charge localization. Sci Adv (2019) 5:eaau4538. doi:10.1126/sciadv.aau4538
95. Lee PA, Rice TM. Electric field depinning of charge density waves. Phys Rev B (1979) 19:3970–80. doi:10.1103/PhysRevB.19.3970
96. Comin R, Frano A, Yee MM, Yoshida Y, Eisaki H, Schierle E. Charge order Driven by fermi-arc Instability in Bi2Sr2-xLaxCuO6+δ. Science (2014) 343:390–2. doi:10.1126/science.1242996
97. Padilla WJ, Lee YS, Dumm M, Blumberg G, Ono S, Segawa K, Constant effective mass across the phase diagram of high-Tc cuprates. Phys Rev B (2005) 72:060511. doi:10.1103/PhysRevB.72.060511
98. Dai YM, Xu B, Cheng P, Luo HQ, Wen HH, Qiu XG, Doping evolution of the optical scattering rate and effective mass of Bi2Sr2-xLaxCuO6. Phys Rev B (2012) 85:092504. doi:10.1103/PhysRevB.85.092504
99. Peng YY, Fumagalli R, Ding Y, Minola M, Caprara S, Betto D, Re-entrant charge order in overdoped (Bi, Pb)2.12Sr1.88CuO6+δ outside the pseudogap regime. Nat Mater (2018) 17:697–702. doi:10.1038/s41563-018-0108-3
100. He Y, Yin Y, Zech M, Soumyanarayanan A, Yee MM, Williams T, Fermi surface and pseudogap evolution in a cuprate superconductor. Science (2014) 344:608–11. doi:10.1126/science.1248221
101. Keimer B, Moore JE. The physics of quantum materials. Nat Phys (2017) 13:1045–55. doi:10.1038/nphys4302
102. Dordevic SV, Homes CC. Superfluid density in overdoped cuprates: Thin films versus bulk samples. Phys Rev B (2022) 105:214514. doi:10.1103/PhysRevB.105.214514
103. Li L, Wang Y, Komiya S, Ono S, Ando Y, Gu GD, Diamagnetism and Cooper pairing above Tc in cuprates. Phys Rev B (2010) 81:054510. doi:10.1103/PhysRevB.81.054510
104. Jiang X, Li D, Rosenstein B. Strong thermal fluctuations in cuprate superconductors in magnetic fields above Tc. Phys Rev B (2014) 89:064507. doi:10.1103/PhysRevB.89.064507
105. Mukerjee S, Huse DA. Nernst effect in the vortex-liquid regime of a type-II superconductor. Phys Rev B (2004) 70:014506. doi:10.1103/PhysRevB.70.014506
106. Li R, She ZS. A quantitative vortex-fluid description of Nernst effect in Bi-based cuprate high-temperature superconductors. New J Phys (2017) 19:113028. doi:10.1088/1367-2630/aa8cee
107. Loktev VM, Quick RM, Sharapov SG. Phase fluctuations and pseudogap phenomena. Phys Rep (2001) 349:1–123. doi:10.1016/S0370-1573(00)00114-9
108. Li R, She ZS. Emergent mesoscopic quantum vortex and Planckian dissipation in the strange metal phase. New J Phys (2021) 23:043050. doi:10.1088/1367-2630/abeeba
Keywords: pseudogap, spatial organization, critical fluctuations, energy-length scaling, doping dependence
Citation: Li R and She Z-S (2022) Energy-length scaling of critical phase fluctuations in the cuprate pseudogap phase. Front. Phys. 10:1013937. doi: 10.3389/fphy.2022.1013937
Received: 08 August 2022; Accepted: 31 August 2022;
Published: 12 October 2022.
Edited by:
Marcin Matusiak, Institute of Physics, Polish Academy of Sciences, PolandReviewed by:
Adrian Esteban Feiguin, Northeastern University, United StatesCopyright © 2022 Li and She. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhen-Su She, c2hlQHBrdS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.