Phase Field Modeling of Anisotropic Tension Failure of Rock-Like Materials

The tensile fracture is a widespread feature in rock excavation engineering, such as spalling around an opened tunnel. The phase field method (PFD) is a non-local theory to effectively simulate the quasi-brittle fracture of materials, especially for the propagation of a tensile crack. This work is dedicated to study the tensile failure characteristics of rock-like materials by the PFD simulation of the Brazilian test of the intact and fissure disk samples. The numerical results indicate that the tensile strength of the disk sample is anisotropic due to the influence of pre-existing cracks. The peak load decreases at first and then increases with the increase of the inclination angle, following the U-shaped trend. The simulation results also indicate that the wing crack growth is the main failure characteristic. Moreover, the crack propagation path initiates at the tip of the pre-existing crack when the inclination angle is less than 60°. Crack propagation initiates near the tip of the pre-existing crack when the angle is 75°, and it initiates at the middle of the pre-existing crack when the angle is 90°. Finally, all cracks extend to the loading position and approximately parallel to the loading direction. This process is in agreement with the Brazilian test of pre-existing cracks in the laboratory, which can validate the effectiveness of the PFD in simulating the tensile fracture of rock-like materials. This study can provide a reference for the fracture mechanism of the surrounding rock in the underground excavation.

Introduction

Due to the geological tectonic movement or artificial disturbance, the fracture of engineering rock mass exhibits a rich variety of crack patterns under loading or unloading conditions [1–3]. Tensile and compression-shear fractures often occur in practical rock engineering. Because rock-like materials have the unilateral effect (the tensile strength is much lower than the compression strength), the tensile fracture is more likely to occur in practical rock engineering. Moreover, the tensile crack is also found in rock mass under compressive condition due to the effect of its heterogeneity or pre-existing cracks [4, 5]. For example, rock block spalling appears near a cave wall after rock excavation [6]. To avoid the occurrence of engineering disasters, corresponding solution should be developed by numerical simulation in advance. It is therefore very important to develop a numerical method to accurately capture the crack propagation of the surrounding rock.

Rock fracture failure behaviors can be understood by means of on-site monitoring, laboratory test, theoretical analysis, and numerical simulation. Up to now, the mechanics of rock materials can be summarized as strain hardening/softening [7], brittle-ductile transition [8], time-dependent [9], unilateral effect [10], anisotropic behaviors [11], etc. The fracture mechanism of rock has been understood qualitatively and quantitatively by experimental and theoretical methods. The analysis results are limited to a simple configuration or simple stress paths. However, the failure pattern and crack propagation are also affected by the geometry of the engineering problem. The failure characteristics will become more complex. For example, the localization damage and discontinuous deformation failure are often found in rock engineering [12]. The description of these non-linear behaviors needs to improve the existing models, which result in the difficulty in the theoretical analysis and the complexity of model formulation. Moreover, there is a difference between the analytical results and test data due to a simple assumption of uniform stress around cracks [13]. Therefore, it is difficult to satisfy the practical demand only from the aspects of experimental or theoretical analysis. As with the development of numerical methods, the fracture problem of rock-like materials may be described by combining a non-local numerical method (such as, phase field (PF)) and a simple constitutive model.

The phase field method (PFD) is a non-local theory and can capture the crack initiation, propagation, and coalescence of quasi-brittle materials [14, 15], especially for the tension brittle fracture. The discontinuous deformation near cracks can be represented by a phase field variable. Propagation and branching of cracks can be reflected directly in the phase field modeling. The hybrid PFD is further proposed by decomposing the contributions of the driving energy of phase field evolution into tensile and compressive parts [16–18]. So far, PFD has been successfully applied in the simulation of quasi-brittle fracture of materials [15, 19, and 20] and multi-field coupling problems [21, 22]. Compared with the direct approaches for modeling crack propagation, the PFD has the following advantages: without an enrichment function, crack tracking algorithm, and ad hoc criterion for crack initiation.

The purpose of this work was to further promote the application of the PFD in rock mechanics. First, a brief literature overview of mechanical characteristics of rock-like materials and the background of phase field development is given in the introduction. Second, the theoretical framework about the PFD and its anisotropic formulation are introduced to describe the brittle fracture. Then, the finite element discretization of the PFD is derived in Section 3. The Brazilian disk test samples with intact or pre-existing cracks are numerically simulated by the PFD, which is further validated by comparing it with the laboratory Brazilian splitting test results. Finally, some conclusions and further research on the PFD are given at the end of this work.

Phase Field Method (PFD)

Theoretical Foundation Description

The rock-like material failure is the result of crack initiation and propagation. How to accurately predict the crack growth path of engineering materials has always been the focus of scholars. The PFD is an attractive theory to represent discontinuous characteristics near the crack tip by a phase field variable. An elastic body $\Omega \subset {\mathrm{ℝ}}^{n_{dim}} \left(n_{dim}\in \left\{\mathrm{1,2,3}\right\}\right)$ is shown in Figure 1. The body boundaries contain an external boundary $\partial \Omega$ and an internal discontinuous boundary $\Gamma$ within the material. The displacement (Dirichlet) boundary $\partial {\Omega }^u$ and the traction (Neumann) boundary $\partial {\Omega }^t$ constitute the external boundary, that is, $\partial {\Omega }^u\cap \partial {\Omega }^t=\partial \Omega$. $\mathit{n}$ is the outward unit vector normal to boundary $\partial \Omega$. The crack width is abstractly represented by the regularization parameter ${\ell }_0$, which is used as a width scale of the crack in the numerical simulation. The body force b is applied throughout the body, and the traction force $\mathit{t}$ acts on $\partial {\Omega }^t$. The sharp discontinuous field is represented by a phase field variable $\varphi$, which changes from 0 to 1. The material element is fully fractured when $\varphi$ equals to 1, whereas the material element is undamaged when $\varphi$ equals to 0.

FIGURE 1

FIGURE 1. Schematic diagram of diffusion characterization by the phase field.

According to the first law of thermodynamics, the brittle fracture of the material is the result of the system from a non-equilibrium state to equilibrium state, with the energy conversion from the elastic storage energy to the dissipation energy [23]. Moreover, the energy release always drives the total energy to minimize based on the theorem of minimum potential energy. The crack begins to initiate and propagates when the storage energy exceeds the material resistance. The fracture process can be described by adding an auxiliary field according to the variational approach [24]. The total potential energy $\mathit{\Psi }\left(\varphi ,\mathbf{u}\right)$ of the system consists of two parts: internal potential energy ${\mathit{\Psi }}^{\mathit{int}}\left(\varphi ,\mathbf{u}\right)$ and external energy ${\mathit{\Psi }}^{ext}\left(\mathbf{u}\right)$, namely,

$\begin{array}{c}\mathit{\Psi }\left(\varphi ,\mathit{u}\right)={\mathit{\Psi }}^{int}\left(\varphi ,\mathit{u}\right)+{\mathit{\Psi }}^{ext}\left(\mathit{u}\right)\end{array},(1)$

where ${\mathit{\Psi }}^{int}$ can be expressed as the sum of the free energy and fracture energy in Eq.2.a, and ${\mathit{\Psi }}^{ext}$ is formulated by the body force $\mathit{b}$ and the boundary force $\mathit{t}$, presented in Eq.2.b.

$\begin{array}{c}{\mathit{\Psi }}^{int}\left(\varphi ,\mathit{u}\right)={\displaystyle \underset{\mathit{\Omega }}{\mathit{\int }}\psi \left(\mathit{\epsilon }\right)d\mathit{\Omega }+}{\displaystyle \underset{\mathit{\Omega }}{\int }{G}_c\gamma \left(\varphi ,\nabla \varphi \right)d\mathit{\Omega }}\end{array},$(2.a)

$\begin{array}{c}{\mathit{\Psi }}^{ext}\left(\mathit{u}\right)={\displaystyle \underset{\mathit{\Omega }}{\int }\mathit{b}\cdot \mathit{u}d\mathit{\Omega }+}{\displaystyle \underset{\partial \mathit{\Omega }}{\int }\mathit{t}\cdot \mathit{u}d\partial \mathit{\Omega }}\end{array},$(2.b)

where $\psi \left(\mathit{\epsilon }\right)$ is the strain energy density, $\gamma \left(\varphi ,\nabla \varphi \right)$ represents the crack surface density per unit volume, and $G_c$ is the critical fracture energy density. $\psi \left(\mathit{\epsilon }\right)$ needs to further consider the degradation of phase field in fracture modeling. And it can be defined by $\psi \left(\mathit{\epsilon }\right)=g\left(d\right){\psi }_0\left(\mathit{\epsilon }\right)$. Similar to the previous published literature [25], the most used form of $g\left(d\right)$ is taken as the following formulation.

$\begin{array}{c}g\left(d\right)=\left[{\left(1-\varphi \right)}^2+\kappa \right]\end{array},(3)$

where parameter $\kappa$ is selected as a small value to ensure the numerical stability.

The elastic strain energy ${\psi }_0\left(\mathit{\epsilon }\right)$ of an undamaged material is given by the volumetric–deviatoric decomposition.

$\begin{array}{c}{\psi }_0\left(\mathit{\epsilon }\right)=\frac{1}{2}\lambda {\left[tr\left(\mathit{\epsilon }\right)\right]}^2+\mu {\mathit{\epsilon }}^2\end{array},(4)$

where $\lambda$ and $\mu$ are Lamé coefficients, expressed as $\lambda =\frac{E\nu }{\left(1+\nu \right)\left(1-2\upsilon \right)}$ and $\mu =\frac{E}{2\left(1+\upsilon \right)}$.

And the stress tensor of the bulk matrix can be deduced by

$\begin{array}{c}\mathit{\sigma }=\frac{\partial {\psi }_0\left(\mathit{\epsilon }\right)}{\partial \mathit{\epsilon }}=\lambda \left(tr\mathit{\epsilon }\right)+2\mu \epsilon \end{array}.(5)$

As same as the published literatures [19, 26], the crack surface density per unit volume $\gamma \left(\varphi ,\nabla \varphi \right)$ is defined as

$\begin{array}{c}\gamma \left(\varphi ,\nabla \varphi \right)=\frac{1}{2{\ell }_0}{\varphi }^2+\frac{{\ell }_0}{2}{\left(\nabla \varphi \right)}^2\end{array}.(6)$

The crack propagation is a process to minimize the total energy functional. The extreme condition can be determined by the variational principle. The differential form of the total energy with respect to displacement $\mathit{u}$, phase field $\varphi ,$ and its gradient $\nabla \varphi$ can be expressed as

$\begin{array}{c}\delta \mathit{\Psi }\left(\varphi ,\mathit{u}\right)=\frac{\partial \mathit{\Psi }\left(\varphi ,\mathit{u}\right)}{\partial \varphi }\delta \varphi +\frac{\partial \mathit{\Psi }\left(\varphi ,\mathit{u}\right)}{\partial \mathit{u}}\delta u+\frac{\partial \mathit{\Psi }\left(\varphi ,\mathit{u}\right)}{\partial \nabla \varphi }\delta \nabla \varphi =0\end{array}.(7)$

Eq. (7) is satisfied for any increments such as $\delta \varphi$, $\delta \mathit{u}$, and $\delta \nabla \varphi$. The governing equations and boundary conditions are derived by substituting Eq. (1), (2), and (4) into Eq. (7).

The governing equations are as follows:

$\begin{array}{c}\{\begin{array}{cc}-2\left(1-\varphi \right)\psi \left(\mathit{\epsilon }\right)-G_c{\ell }_0\text{Δ}\varphi +\frac{G_c}{{\ell }_0}\varphi =0& \text{in} \mathit{\Omega }\\ div\mathit{\sigma }+\mathit{b}=0& \text{in} \mathit{\Omega }\end{array}\end{array},(8)$

And the boundary conditions are as follows

$\begin{array}{c}\{\begin{array}{cc}\mathit{u}=\overline{\mathit{u}}& \text{on} \partial {\mathit{\Omega }}^u\\ \mathbf{n}\cdot \mathit{\sigma }-\mathit{t}=0& \text{on} \partial {\mathit{\Omega }}^t\\ \nabla \varphi \cdot \mathit{n}=0& \text{on} \partial \mathit{\Omega }\end{array}\end{array}(9)$

where the first equation in Eq. (9) is also called the Dirichlet (displacement) boundary condition and the last two equations are called the Neumann boundary condition.

Given the irreversibility of cracks growth, a history-field $\mathrm{\mathscr{H}}\left(x,t\right)$ is adopted for driving the crack propagation and ensuring the monotonical accumulation of the phase field variable.

$\begin{array}{c}H\left(x,t\right)=\underset{t\in \left[0,t\right]}{\max }\phi \left(\mathit{\epsilon }\right)\end{array}.(10)$

Anisotropic Formulation of PFM

Due to the unilateral effect of rock-like materials, the mechanical properties of material deterioration are only restricted in the tensile condition in this work. The formulation of the strain energy function $\psi \left(\mathit{\epsilon }\right)$ requires to be written as the tension and compression parts, namely.

$\begin{array}{c}\psi \left(\mathit{\epsilon }\right)=g\left(d\right){\phi }^{+}\left(\mathit{\epsilon }\right)+{\phi }^{-}\left(\mathit{\epsilon }\right)\end{array},(11)$

where the tensile part and the compression part of $\psi \left(\mathit{\epsilon }\right)$ are further expressed as

$\begin{array}{c}{\phi }^{+}\left(\mathit{\epsilon }\right)=\frac{1}{2}\lambda \langle tr{\left(\mathit{\epsilon }\right)}_{+}^2+\mu tr\left({\mathit{\epsilon }}_{+}^2\right)\end{array},$(12.a)

$\begin{array}{c}{\phi }^{-}\left(\mathit{\epsilon }\right)=\frac{1}{2}\lambda \langle tr{\left(\mathit{\epsilon }\right)}_{-}^2+\mu tr\left({\mathit{\epsilon }}_{-}^2\right)\end{array},$(12.b)

where the bracket $\left({\cdot }_{+}\right)$ represents the positive value and $\left({\cdot }_{-}\right)$ represents the negative value.

Therefore, the stress tensor can be divided into two parts as seen in.

$\begin{array}{c}\mathit{\sigma }=g\left(d\right){\mathit{\sigma }}_{+}\left(\mathit{\epsilon }\right)+{\mathit{\sigma }}_{-}\left(\mathit{\epsilon }\right)\end{array},(13)$

where the constitutive relation of the bulk matrix is further expressed by the volumetric–deviatoric decomposition in the tensile and compression states.

$\begin{array}{c}{\mathit{\sigma }}_{+}=\frac{\partial \psi \left(\mathit{\epsilon }\right)}{\partial {\mathit{\epsilon }}_{+}}=\lambda \langle tr{\mathit{\epsilon }}_{+}\mathit{I}+2\mu {\left(\mathit{\epsilon }\right)}^{+}\end{array},$(14.a)

$\begin{array}{c}{\mathit{\sigma }}_{-}=\frac{\partial \psi \left(\mathit{\epsilon }\right)}{\partial {\mathit{\epsilon }}_{-}}=\lambda \langle tr{\mathit{\epsilon }}_{-}\mathit{I}+2\mu {\left(\mathit{\epsilon }\right)}^{-}\end{array}.$(14.b)

Eq. (10) can prevent crack propagation healing. However, the same formulation of the strain energy density is not obviously suitable for various crack modes. In order to capture the tension and shear crack modes, a modified phase field model is proposed by distinguishing the critical release rates for these two crack modes [17]. The phase field governing equation can be rearranged as

$\begin{array}{c}-2\left(1-\varphi \right)\left(\frac{{\mathrm{\mathscr{H}}}_t}{G_c^I}+\frac{{\mathrm{\mathscr{H}}}_s}{G_c^{II}}\right)-{\ell }_0\Delta \varphi +\frac{1}{{\ell }_0}\varphi =0\end{array},(15)$

where $G_c^I$ is the critical energy release rate for mode I fracture and $G_c^{II}$ is the critical energy rate for mode II fracture. ${\mathrm{\mathscr{H}}}_t$ and ${\mathrm{\mathscr{H}}}_s$ are the history-field variable contributing to tension mode I and shear mode II, respectively. $\mathrm{\mathscr{H}}$ consists of ${\mathrm{\mathscr{H}}}_t$ and ${\mathrm{\mathscr{H}}}_s$, taking the following definitions.

$\begin{array}{c}{\mathrm{\mathscr{H}}}_t=\underset{t\in \left[0,t\right]}{\max }\left\{\frac{1}{2}\lambda \langle tr{\left(\mathit{\epsilon }\right)}_{+}^2\right\}\end{array},$(16.a)

$\begin{array}{c}{\mathrm{\mathscr{H}}}_s=\underset{t\in \left[0,t\right]}{\max }\left\{\mu {\left({\mathit{\epsilon }}^{+}\right)}^2\right\}\end{array}$(16.b)

Notably, the anisotropic phase field can be returned back to the isotropic phase field in Eq. (8) when the condition $G_c^I=G_c^{II}$ is satisfied.

FE Implementation of the Phase Field Model

The PFD has been successfully solved by the finite element method (FEM) [15], material point method (MPM) [27], and numerical manifold method (NMM) [28]. Because the FEM is widely adopted to simulate in geotechnical engineering, the numerical implementation of the PFM is briefly introduced in the standard FEM in this work. The small deformation assumption is assumed. The strain tensor $\mathit{\epsilon }$ can be defined in terms of the gradient of displacement $\mathit{u}$.

$\begin{array}{c}\epsilon =\frac{1}{2}\left(\nabla \mathit{u}+\nabla {\mathit{u}}^T\right)\end{array},(17)$

The displacement field and the phase field are approximately discretized by the test function and nodal variables, as follows:

$\begin{array}{c}\mathit{u}={\mathit{N}}_I^u\widehat{\mathit{u}}, \varphi ={\mathit{N}}_I^{\varphi }\widehat{\mathit{\varphi }}\end{array},(18)$

where ${\mathit{N}}_I^u$ and ${\mathit{N}}_I^{\varphi }$ are, respectively, the shape functions for displacement field and phase field, and $\widehat{\mathit{u}}$ and $\widehat{\varphi }$ are the displacement vector and the phase field vector of element nodes, respectively. The strain tensor and the phase field gradient $\nabla \varphi$ can be expressed as

$\begin{array}{c}\epsilon ={\mathit{B}}_I^u\widehat{\mathit{u}}, \nabla \varphi ={\mathit{B}}_I^{\varphi }\widehat{\varphi }\end{array},(20)$

The matrix forms of ${\mathit{N}}_I^u$, ${\mathit{N}}_I^{\varphi }$, ${\mathit{B}}_I^u$, and ${\mathit{B}}_I^{\varphi }$ in the two-dimensional space can be expanded as

$\begin{array}{c}{\mathit{N}}_I^u=\left[\begin{array}{cc}\begin{array}{ccc}{N}_1& 0& \dots \end{array}& \begin{array}{cc}{N}_n& 0\end{array}\\ \begin{array}{ccc}0& N_1& \dots \end{array}& \begin{array}{cc}0& N_n\end{array}\end{array}\right], {\mathit{N}}_I^{\varphi }=\left[\begin{array}{ccc}{N}_1& N_2& \begin{array}{cc}\dots & N_n\end{array}\end{array}\right]\end{array},$(21.a)

$\begin{array}{c}{\mathit{B}}_I^u=\left[\begin{array}{ccc}{N}_{1,x}& 0& \begin{array}{ccc}\dots & N_{n,x}& 0\end{array}\\ 0& N_{1,y}& \begin{array}{ccc}\dots & 0& N_{n,y}\end{array}\\ N_{1,y}& N_{1,x}& \begin{array}{ccc}\dots & N_{n,y}& N_{n,x}\end{array}\end{array}\right], {\mathit{B}}_I^{\varphi }=\left[\begin{array}{cc}\begin{array}{cc}{N}_{1,x}& N_{2,x}\end{array}& \begin{array}{cc}\dots & N_{n,x}\end{array}\\ \begin{array}{cc}{N}_{1,y}& N_{2,y}\end{array}& \begin{array}{cc}\dots & N_{n,y}\end{array}\end{array}\right]\end{array},$(21.b)

where $x$ and y are coordinate variables, and$n$ is the number of element nodes.

The brittle fracture modeling of the PFD is transformed to a multi-field problem (displacement field and phase field). By the extremum condition in Eq. (7), the residual vectors corresponding to $\mathit{u}$ and $\varphi$ can be derived in Eq. (22) and (23), respectively.

$\begin{array}{c}{R}_I^u=\frac{\delta \mathit{\Psi }}{\delta \mathit{u}}={\displaystyle \underset{\text{Ω}}{\int }\left[{\left(1-\varphi \right)}^2+\kappa \right]{\left({\mathit{B}}_I^u\right)}^T\mathit{\sigma }d\Omega -}{\displaystyle \underset{\text{Ω}}{\int }{\left({\mathit{N}}_I^u\right)}^T\mathit{b}d\partial \Omega -}{\displaystyle \underset{\partial \text{Ω}}{\int }{\left({\mathit{N}}_I^u\right)}^T\mathit{h}d\partial \Omega }\end{array},(22)$

$\begin{array}{c}{R}_I^{\varphi }=\frac{\delta \mathit{\Psi }}{\delta \varphi }={\displaystyle \underset{\text{Ω}}{\int }{\ell }_0{\left({\mathit{B}}_I^{\varphi }\right)}^T\nabla \varphi +}{\displaystyle \underset{\text{Ω}}{\int }\left[\frac{1}{{\ell }_0}+2\left(\frac{{\mathrm{\mathscr{H}}}_t}{G_c^I}+\frac{{\mathrm{\mathscr{H}}}_s}{G_c^{II}}\right)\right]}{\mathit{N}}_I^{\varphi }\varphi d\Omega -2{\displaystyle \underset{\text{Ω}}{\int }{\mathit{N}}_I^{\varphi }\left(\frac{{\mathrm{\mathscr{H}}}_t}{G_c^I}+\frac{{\mathrm{\mathscr{H}}}_s}{G_c^{II}}\right)d\Omega }\end{array},(23)$

The above equations can also be given by the weak form of the governing equations. Then the staggered algorithm is widely applied for an alternate updating the displacement increment $\delta \mathit{u}$ and of phase field increment $\delta \varphi$ during the phase field modeling. That is, the following equation system is iteratively solved by the Newton–Raphson method.

$\begin{array}{c}\left[\begin{array}{cc}{K}_{ij}^{uu}& 0\\ 0& K_{ij}^{\varphi \varphi }\end{array}\right]\left\{\begin{array}{c}\delta \mathit{u}\\ \delta \varphi \end{array}\right\}=-\left\{\begin{array}{c}{R}_I^u\\ R_I^{\varphi }\end{array}\right\}\end{array},(24)$

where

$\begin{array}{c}{K}_{ij}^{uu}=\frac{\partial R_I^u}{\partial u_j}={\displaystyle \underset{V}{\int }\left[{\left(1-\varphi \right)}^2+\kappa \right]{\left(B_{I,i}^u\right)}^{T}C{B}_{I,j}^{u}dV}\end{array},$(25.a)

$\begin{array}{c}{K}_{ij}^{\varphi \varphi }=\frac{\partial R_I^{\varphi }}{\partial {\varphi }_j}={\displaystyle \underset{V}{\int }{\ell }_0{\left(B_{I,i}^{\varphi }\right)}^T{B}_{I,j}^{\varphi }}+\left[\frac{1}{{\ell }_0}+2\left(\frac{{\mathrm{\mathscr{H}}}_t}{G_c^I}+\frac{{\mathrm{\mathscr{H}}}_s}{G_c^{II}}\right)\right]N_{I,i}^{\varphi }{N}_{I,j}^{\varphi }dV\end{array}.$(25.b)

Numerical Simulation and Analysis

In order to avoid the disturbance damage caused by sample preparation, the tensile fracture is usually studied by an indirect test (such as Brazilian splitting test) in the laboratory. The tensile fracture of rock-like materials is first simulated by the PFD modeling of the Brazilian test of the intact sample. And then, the numerical modeling is further applied in simulating the Brazilian test of the disk sample with a single inclination crack. The anisotropic tensile fracture of rock-like materials is analyzed and compared with the test results. This section will study the tensile fracture of rock-like materials by PHD modeling. The plane strain condition is taken for all numerical tests.

PFD Simulation of Intact Disk Sample

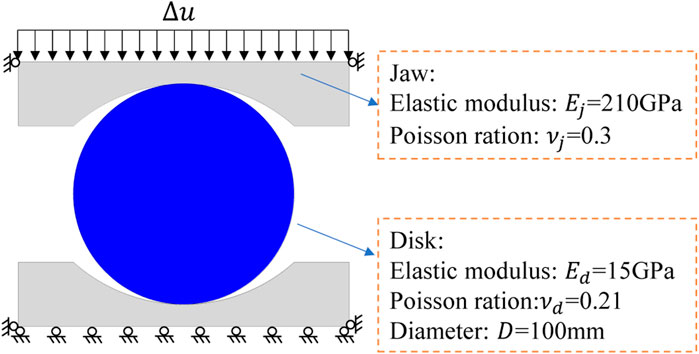
In order to study tensile behaviors of rock-like materials, disk samples were prepared from Portland pozzolana cement (PPC), fine sands, and water [29]. The test results indicate that the tension strength of the intact rock-like material sample is 3.81 MPa, Young’s modulus is 15 GPa, and the Poisson’s ratio is 0.21. The above mechanical indices will be regarded as the basis of determination of model parameters in the following PFD simulation. The test structure consists of two rigid jaws and a disk sample with a radius of 50 mm. In the process of numerical simulation, the sample thickness is taken as 1 mm. The critical fracture energy can be approximately estimated as 1.1 J/m² to match the tensile strength of the material in the test. Because the shear energy is much more than the tensile energy, the relationship between the two is set as $G_c^{II}=10G_c^I$, as the same with the previous literature [17]. Therefore, $G_c^I$ is 0.1 J/m² and $G_c^{II}$ is 1 J/m².

The displacement-controlled mode is applied with the edge of the top jaw in Figure 2. And the loading rate is $1.0\times {10}^{-3}$ mm/step. To facilitate the numerical convergence of this problem, the top and bottom nodes of the disk sample are constrained in the horizontal direction. The structure is discretized into 81,960 mixed triangle and quadrilateral elements. The minimum mesh size is 0.25 mm at axisymmetric lines of the sample. The length scale parameter ${\ell }_0$ affects the structure bearing capacity and crack width. In order to ensure that the simulation strength and test tensile strength are consistent, ${\ell }_0$ is taken as 0.5 mm about twice the minimum size by repeated calculation in this work. In particular, ${\ell }_0$ does not represent the actual crack width because of the smooth processing of the crack domain. The parameter $\kappa =1.0\times {10}^{-7}$ is taken to avoid numerical singularity.

FIGURE 2

FIGURE 2. 2D Brazilian test sample and boundary constraint.

The PFD simulation results of the Brazilian test of intact disk samples are presented in Figure 3. The obvious force drop is found in the force–displacement curves of fissure rocks with various inclined cracks. The peak load is 0.598 KN, and the tensile strength can be calculated as 3.807 MPa, which is consistent with the tensile results in the laboratory. The crack path is middle in the sample and is parallel to the loading direction. This phenomenon is also the same with the failure mode in the test. Therefore, the effectiveness of the PFD simulation of Brazilian splitting is verified.

FIGURE 3

FIGURE 3. PFD simulation of Brazilian splitting mechanical responses of the intact sample.

PFD Simulation of Fissure Disk Sample

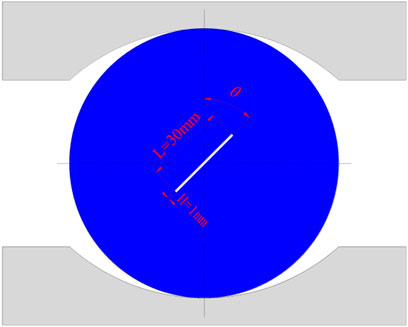
The anisotropic tensile strength is further studied by the PFD modeling of Brazilian disk samples with various inclination cracks. The fissure samples are performed by inserting one crack in the intact disk. The inclination angle $\theta$ is between the length direction of the crack and the vertical direction of the sample, ranging for 0 to 90 with an increment of 15, as shown in Figure 4. The length and width of cracks are, respectively, $L$ = 30 mm and $H$ = 1 mm. The PFD simulation of the Brazilian test of the fissure sample is performed by taking the same model parameters in Section 3.

FIGURE 4

FIGURE 4. 2D Brazilian test of the pre-cracked sample.

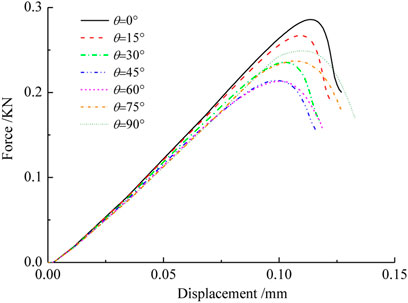
The force–displacement curves are plotted in Figure 5. The results show that the peak load decreases at first and then increases with the increasing inclination angle. The maximum peak load appears at 0°, and the minimum value is at 45°. Therefore, the pre-existing crack causes the anisotropy of tensile strength. In order to represent the anisotropic degree of the tensile strength, a strength ratio is defined by the ratio of peak load between the Brazilian test of the fissure sample and intact sample. The strength ratio changing with the inclination angle is plotted in Figure 6. The changing trend follows the U-shaped distribution, which is also found in the compression test of jointed or bedded rock mass [11, 30].

FIGURE 5

FIGURE 5. Force–displacement curves of the disk sample with different pre-existing cracks.

FIGURE 6

FIGURE 6. Ratio of loads of disk samples with different inclination angles to intact samples.

Based on the Brazilian tests of the disk sample with various inclination angles for a single crack [29], the failure modes between the PFD simulation and test are compared in Figure 7. The result indicates that the final crack path in the numerical simulation process is consistent with the test results. The wing crack is only found in the Brazilian test and the phase field simulation of the pre-existing crack sample. Crack propagation initiates at the crack tip when the inclination angle changes from 0° to 60°. Crack propagation initiates near the crack tip when the angle is 75°, and it initiates at the middle of the crack when the angle is 90°. And then all cracks grow to the loading position and coalesce to form a penetrating crack. Its growth path is curvilinear when the crack angle is at 15°, 30°, 45°, 60°, and 75°, while the path is a straight line, parallel to the loading direction at 0° and 90°. It should be noted that the final crack path is parallel to the loading direction regardless of the crack angle. This is also the main feature of the wing crack development.

FIGURE 7

FIGURE 7. Comparison between the PFD simulation and Brazilian test of disk samples with different inclination angles (test sample failure can be referred to [29]).

Conclusion

The tensile failure behaviors of rock-like materials are studied by the PFD simulation of the Brazilian disk test in this work. The anisotropy tensile fracture is considered by a single crack with various inclination angles in the anisotropic PFD simulation. The simulation results indicate that the peak load is weakened due to the influence of pre-existing cracks. And the changing of peak load with the inclination angle follows a U-shaped trend. The wing crack in the Brazilian test can be reproduced by the PFD simulation. The crack propagation path is affected by the pre-existing crack. Crack propagation initiates at the crack tip when the inclination angle changes from 0 to 60. Crack propagation initiates near the crack tip when the angle is 75, and crack propagation initiates at the middle of the crack when the angle is 90°. Finally, all cracks grow to the loading position and coalesce to form a penetrating crack. The PFD can better simulate the tensile failure of rock-like materials. More attention will be performed on the PFD simulation on compression-shear failure of rock-like materials in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

SW: conceptualization, methodology software, writing original draft, and validation; JZ: writing-review and editing; LZ: methodology and review; WZ: writing review and editing validation. All authors have read and agreed to the published version of the manuscript.

Funding

This study is financially supported by the National Natural Science Foundation of China (Grant No. 52109143) and the Fundamental Research Funds for the Central Universities (Grant No. 2021QN1023).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wang S, Xu W, Yan L, Feng X-T, Xie W-C, Chen H. Experimental Investigation and Failure Mechanism Analysis for Dacite under True Triaxial Unloading Conditions. Eng Geology (2020) 264:105407. doi:10.1016/j.enggeo.2019.105407

CrossRef Full Text | Google Scholar

2. Jiang Q, Su G, Feng X-t., Chen G, Zhang M-z., Liu C. Excavation Optimization and Stability Analysis for Large Underground Caverns under High Geostress: a Case Study of the Chinese Laxiwa Project. Rock Mech Rock Eng (2019) 52:895–915. doi:10.1007/s00603-018-1605-z

CrossRef Full Text | Google Scholar

3. Jiang Q, Yan F, Wu J, Fan Q, Li S, Xu D. Grading Opening and Shearing Deformation of Deep Outward-Dip Shear Belts inside High Slope: A Case Study. Eng Geology (2019) 250:113–29. doi:10.1016/j.enggeo.2019.01.018

CrossRef Full Text | Google Scholar

4. Wang S, Wang H, Xu W, Qian W. Investigation on Mechanical Behaviour of Dacite under Loading and Unloading Conditions. Géotechnique Lett (2019) 9:130–5. doi:10.1680/jgele.18.00193

CrossRef Full Text | Google Scholar

5. Yang SQ, Yang DS, Jing HW, Li YH, Wang SY. An Experimental Study of the Fracture Coalescence Behaviour of Brittle sandstone Specimens Containing Three Fissures. Rock Mech Rock Eng (2012) 45:563–82. doi:10.1007/s00603-011-0206-x

CrossRef Full Text | Google Scholar

6. Cai M, Kaiser PK, Morioka H, Minami M, Maejima T, Tasaka Y, et al. FLAC/PFC Coupled Numerical Simulation of AE in Large-Scale Underground Excavations. Int J Rock Mech Mining Sci (2007) 44:550–64. doi:10.1016/j.ijrmms.2006.09.013

CrossRef Full Text | Google Scholar

7. Wang S, Xu W, Wang W, Jia C. Experimental and Numerical Investigations on the Mechanical Behavior of Fine-Grained Sandstone. Int J Geomech (2018) 18:04017150. doi:10.1061/(ASCE)GM.1943-5622.0001062

CrossRef Full Text | Google Scholar

8. Walton G, Hedayat A, Kim E, Labrie D. Post-yield Strength and Dilatancy Evolution across the Brittle-Ductile Transition in Indiana Limestone. Rock Mech Rock Eng (2017) 50:1691–710. doi:10.1007/s00603-017-1195-1

CrossRef Full Text | Google Scholar

9. Yang S-Q, Hu B, Ranjith P, Xu P. Multi-step Loading Creep Behavior of Red sandstone after thermal Treatments and a Creep Damage Model. Energies (2018) 11:212. doi:10.3390/en11010212

CrossRef Full Text | Google Scholar

10. Welemane H, Goidescu C, Kondo D, Pantalé O, Karama M. Brittle Damage in Initially Anisotropic Materials: A Model Accounting for the Induced Anisotropy and Unilateral Effects. Amm (2015) 784:173–8. doi:10.4028/www.scientific.net/amm.784.173

CrossRef Full Text | Google Scholar

11. Ji H, Zhang JC, Xu WY, Wang RB, Wang HL, Yan L, et al. Experimental Investigation of the Anisotropic Mechanical Properties of a Columnar Jointed Rock Mass: Observations from Laboratory-Based Physical Modelling. Rock Mech Rock Eng (2017) 50:1919–31. doi:10.1007/s00603-017-1192-4

CrossRef Full Text | Google Scholar

12. Shen WQ, Shao JF, Cao YJ, Wang SS, Xu WY. A Micromechanics-Based Enhanced Plastic Damage Model Including Localization Analysis for Heterogeneous Geomaterials. Comput Geotechnics (2020) 122:103512. doi:10.1016/j.compgeo.2020.103512

CrossRef Full Text | Google Scholar

13. Cai M. Fracture Initiation and Propagation in a Brazilian Disc with a Plane Interface: a Numerical Study. Rock Mech Rock Eng (2013) 46:289–302. doi:10.1007/s00603-012-0331-1

CrossRef Full Text | Google Scholar

14. Francfort GA, Marigo J-J. Revisiting Brittle Fracture as an Energy Minimization Problem. J Mech Phys Sol (1998) 46:1319–42. doi:10.1016/S0022-5096(98)00034-9

CrossRef Full Text | Google Scholar

15. Miehe C, Hofacker M, Welschinger F. A Phase Field Model for Rate-independent Crack Propagation: Robust Algorithmic Implementation Based on Operator Splits. Comp Methods Appl Mech Eng (2010) 199:2765–78. doi:10.1016/j.cma.2010.04.011

CrossRef Full Text | Google Scholar

16. Tian F, Tang X, Xu T, Yang J, Li L. A Hybrid Adaptive Finite Element Phase‐field Method for Quasi‐static and Dynamic Brittle Fracture. Int J Numer Methods Eng (2019) 120:1108–25. doi:10.1002/nme.6172

CrossRef Full Text | Google Scholar

17. Zhang X, Sloan SW, Vignes C, Sheng D. A Modification of the Phase-Field Model for Mixed Mode Crack Propagation in Rock-like Materials. Comp Methods Appl Mech Eng (2017) 322:123–36. doi:10.1016/j.cma.2017.04.028

CrossRef Full Text | Google Scholar

18. Wang T, Ye X, Liu Z, Chu D, Zhuang Z. Modeling the Dynamic and Quasi-Static Compression-Shear Failure of Brittle Materials by Explicit Phase Field Method. Comput Mech (2019) 64:1537–56. doi:10.1007/s00466-019-01733-z

CrossRef Full Text | Google Scholar

19. Zhou S-W, Xia C-C. Propagation and Coalescence of Quasi-Static Cracks in Brazilian Disks: An Insight from a Phase Field Model. Acta Geotech. (2019) 14:1195–214. doi:10.1007/s11440-018-0701-2

CrossRef Full Text | Google Scholar

20. Wu J-Y. A Unified Phase-Field Theory for the Mechanics of Damage and Quasi-Brittle Failure. J Mech Phys Sol (2017) 103:72–99. doi:10.1016/j.jmps.2017.03.015

CrossRef Full Text | Google Scholar

21. Yu Z, Shao J, Duveau G, Vu M-N, Armand G. Numerical Modeling of Deformation and Damage Around Underground Excavation by Phase-Field Method with Hydromechanical Coupling. Comput Geotechnics (2021) 138:104369. doi:10.1016/j.cma.2012.01.008doi:10.1016/j.compgeo.2021.104369

CrossRef Full Text | Google Scholar

22. Yu Z, Shao J-F, Vu M-N, Armand G. Numerical Study of Thermo-Hydro-Mechanical Responses of In Situ Heating Test with Phase-Field Model. Int J Rock Mech Mining Sci (2021) 138:104542. doi:10.1016/j.ijrmms.2020.104542

CrossRef Full Text | Google Scholar

23. Anderson TL. Fracture Mechanics: Fundamentals and Applications. New York, NY: CRC Press (2017).

Google Scholar

24. Bourdin B, Francfort GA, Marigo J-J. The Variational Approach to Fracture. J Elasticity (2008) 91:5–148. doi:10.1007/s10659-007-9107-3

CrossRef Full Text | Google Scholar

25. Miehe C, Welschinger F, Hofacker M. Thermodynamically Consistent Phase-Field Models of Fracture: Variational Principles and Multi-Field FE Implementations. Int J Numer Meth Engng (2010) 83:1273–311. doi:10.1002/nme.2861

CrossRef Full Text | Google Scholar

26. Yun K, Kim MH, Chu PH. A Modified Phase Field Model for Predicting the Fracture Behavior of Quasi‐brittle Materials. Int J Numer Methods Eng (2021) 122:5656–75. doi:10.1002/nme.6767

CrossRef Full Text | Google Scholar

27. Kakouris EG, Triantafyllou SP. Material point Method for Crack Propagation in Anisotropic media: a Phase Field Approach. Arch Appl Mech (2018) 88:287–316. doi:10.1007/s00419-017-1272-7

CrossRef Full Text | Google Scholar

28. Yang L, Yang Y, Zheng H. A Phase Field Numerical Manifold Method for Crack Propagation in Quasi-Brittle Materials. Eng Fracture Mech (2021) 241:107427. doi:10.1016/j.engfracmech.2020.107427

CrossRef Full Text | Google Scholar

29. Haeri H, Shahriar K, Marji MF, Moarefvand P. Experimental and Numerical Study of Crack Propagation and Coalescence in Pre-cracked Rock-like Disks. Int J Rock Mech Mining Sci (2014) 67:20–8. doi:10.1016/j.ijrmms.2014.01.008

CrossRef Full Text | Google Scholar

30. Zhang C-L, Armand G, Conil N, Laurich B. Investigation on Anisotropy of Mechanical Properties of Callovo-Oxfordian Claystone. Eng Geology (2019) 251:128–45. doi:10.1016/j.enggeo.2019.02.008

CrossRef Full Text | Google Scholar