Secure Communication Scheme for Brain-Computer Interface Systems Based on High-Dimensional Hyperbolic Sine Chaotic System

Brain-Computer Interface (BCI) is a direct communication pathway between the brain and the external environment without using peripheral nerves and muscles. This emerging topic is suffering from serious issues such as malicious tampering and privacy leakage. To address this issue, we propose a novel communication scheme for BCI Systems. In particular, this scheme first utilizes high-dimensional chaotic systems with hyperbolic sine nonlinearity as the random number generator, then decorrelation operation is used to remove the physical characteristics of the output sequences. Finally, each of the sequences is applied in differential chaos shift keying (DCSK). Since each output sequence corresponds to a unique electrode, the communication data of different electrodes will not interfere with each other. Compared with popular multi-user DSCK schemes using Walsh code sequences, this scheme does not require the channel data of all electrodes while decoding. Therefore, this scheme has higher efficiency. Experimental results on communication data indicate that the proposed scheme can provide a high level of security.

Introduction

Brain-computer interface (BCI) is a real-time communication system in which messages or commands sent by the user do not pass through the brain’s natural output pathways [1]. This technology provides a new way of brain monitoring, human-computer interaction, and it has broad applications in medical rehabilitation and other fields [2]. The representative works of BCI systems mainly involve two paths [3]. The first path is the realization of information exchange and control with the external environment by directly decoding the brain’s instructions [4]. Such applications like BCI-based cursor system [5], robotic arm [6], wheelchair [7], text input method [8] help disabled patients to control external devices without using peripheral nerves and muscles. The second path is rehabilitation, enhancement, and improvement of the central nervous system [9]. By using BCI systems, new rehabilitation paradigms are proposed to help patients to recover from nervous system disease. Such BCI auxiliary training strategy can benefit stroke rehabilitation training [10] and spinal injury rehabilitation training [11].

Most of the above BCI systems use plain-text to transmit EEG data, which have serious issues such as malicious tampering and privacy leakage [12, 13]. For example, an attacker can easily decode the commands from the brain and control the device through tampering [14]. For BCI-based rehabilitation methods, malicious tampering can aggravate the patient’s condition [15]. Therefore, the communication data need to be encrypted to prevent the BCI systems from threats.

The basic communication system consists of an information source and an information sink connected by a channel. Unlike image data or video data, EEG is a high-dimensional and continuous data flow [16]. In BCI systems, the EEG data are collected by the electrode and then converted to digital signals by the AD converter. Next, the digital EEG data flow are transmitted to the servers. The servers extract the features from the EEG signals and decode them to human commands. Considering those characteristics of EEG data and BCI systems, we designed a secure communication scheme to protect the transmissive EEG data flow. In particular, we applied a high-dimensional chaotic system of hyperbolic sine nonlinearity in the differential chaos shift keying (DCSK) scheme to prevent BCI systems from malicious tampering and privacy leakage [17].

DCSK is a chaos-based method for secure communication. Chaotic signals have many special characteristics, such as nonperiodicity, long-term unpredictability, wide spectrum, self- and cross-correlation characteristics [18, 19]. It is worth noting that the chaotic system will not only produce chaotic attractors, but also several independent attractors under certain parameters, that is, multiple coexisting attractors [20–22]. These characteristics meet the requirements of cryptosystem and secure communication system [23, 24]. A large number of literatures have proved that chaos-based image encryption schemes can provide high security and robustness, which can be used as a reliable image cryptosystem [25, 26].

Encryption is an effective way to protect data for information sources and an information sink, while secure communication scheme can protect the transmitted data in channel. DCSK is a secure communication scheme that employ non-periodic and wideband chaotic signals as carriers to achieve the effect of spectrum spreading in the process of digital modulation [27]. The reason why we use this route map is as follows: 1) The transmissive EEG data flow is a digital signal. There is no loss of EEG signal using the DCSK scheme for communication [28]. 2) The transmissive data in the DCSK scheme are the non-periodic chaotic signal or the modulated chaotic signal which can protect the EEG data from malicious tampering and privacy leakage [29]. 3) DCSK scheme is a simple method to achieve secure communication purposes without using chaos synchronization [30].

Since the BCI system is a multi-channel system, the multi-user DCSK schemes are required to protect the EEG data flow. Kolumban et al. first combined the multi-user technology with the DCSK system [31]. In 2005, Frequency Modulated Efficient DCSK, FM-E-DCSK is proposed, which uses a reference signal to modulate multiple information signals to increase the transmission rate [32]. In 2016, Zhang et al. proposed Multi User Segment Shift Differential Chaos Shift Keying, MU-SSDCSK. According to the number of users, this scheme divides the reference signals into signal segments, and then shifts these signal segments and matches them with different Walsh codes to form mutually orthogonal carrying signals [33]. In recent years, the DCSK scheme using Walsh code has gradually become the mainstream multi-user DCSK scheme [34]. However, all the above multi-user DCSK schemes are not suitable for BCI system. This is because BCI system requires high calculation accuracy to extract features from EEG signals [35]. Multiplexing the transmission signal will reduce the accuracy of feature extraction [36]. Although using Walsh codes can solve this problem, it needs all the channels to decode the transmission signal, while BCI systems only use a few of the EEG signals to extract the features corresponding to the command. For example, Zhang et al. selected part of 64-channel for improving BCI illiteracy [37]. Atkinson et al. proposed an improving BCI-based emotion recognition by using 14 channels of 32-electrode channels [38].

High Dimensional Multi User DCSK Scheme

To design an accurate and efficient secure communication scheme, we utilize high dimensional chaotic systems as the pseudo-random number generator, each variable corresponds to one channel which is used in the DCSK scheme. The flowchart is shown in Figure 1.

FIGURE 1

FIGURE 1. Overall flowchart of High dimensional multi user DCSK scheme (HD-MU-DCSK).

In this scheme, the controller selects the communication channel according to the corresponding BCI task. When a specific communication channel is selected, the channel first transmits a decorrelated chaotic sequence of length $\beta$ as a reference signal, then transmits a multiplied modulated signal which has the same length as the decorrelated chaotic sequence. The modulation rule is described as follows:

$S_i=\{\begin{array}{c}{x}_{i}2k\beta <i\le \left(2k+1\right)\beta \\ b_k{x}_{i-\beta } \left(2k+1\right)\beta <i\le 2\left(k+1\right)\beta \end{array}(1)$

Where $x_i$ is the decorrelated chaotic sequence generated by a high dimensional chaotic system, $b_k$ is the transmitted EEG data in BCI system, $\beta$ is the time slot (length of the reference signal and modulated signal), $k$ represents the iteration time.

For the demodulation process, the receiver calculates the correlation between the received signal $r_i$ and the signal $r_{i-\beta }$, which is $r_i$ delayed by $\beta$. The output of the correlator is:

$Z_k={\displaystyle \sum _{\left(2k+1\right)\beta +1}^{2\left(k+1\right)\beta }}{r}_i{r}_{i-\beta }(2)$

Therefore, the information bit $b_k$ can be restored by the sign of the decision variable:

$\widehat{b_k}=sgn\left[Z_k\right](3)$

The difficulty of this scheme is to design a high-dimensional chaotic system to generate the pseudo-random sequences. Reference [39] introduced a new and unified approach for designing desirable dissipative hyperchaotic systems. Reference [40] proposed a design method for generating hyperchaotic cat maps with any desired number of positive Lyapunov exponents. Our previous work proposed a simple method for generating nth order chaotic systems with hyperbolic sine nonlinearity [41]. The proposed scheme utilizes two back-to-back diodes representing hyperbolic sine nonlinearity without any multiplier or subcircuits. Therefore, the proposed high dimensional chaotic systems can achieve both physical simplicity and analytic complexity at the same time.

Secure Communication Scheme for Brain-Computer Interface Based Speller and Microsleep Detector

Here we applied the proposed scheme in BCI-based speller and microsleep detector. Electroencephalography (EEG) -based P300 speller is a type of brain-computer interface (BCI) that uses EEG to allow a user to select characters without physical movement [42]. The EEG-based microsleep detector uses BCI technology to detect drowsiness, which can benefit the drivers to avoid car accidents [43]. If the communication data of these BCI systems have been maliciously tampered, the attackers may cause some serious accidents.

The above BCI systems use 16-electrode to collect EEG signals. Therefore, it is needed to design a chaotic system that has sixteen dimensions. In this paper, EEG data were acquired from 16 scalp sites (extended 10–20 system) using a cap with active Ag/AgCl electrodes. Wet electrodes were used in the cap, and the electrode impedance was modulated to be less than 5 KΩ. The reference electrode was on the bilateral mastoid. A Neuroscan Synamps2 amplifier amplified the EEG signal. The sampling rate of the EEG signal was 1 kHz. We collected EEG data of subjects performing ballistic index finger abduction movements [28], and the data length is about 15 min.

16th-Order Hyperbolic Sine Chaotic System

Based on the design method proposed in Ref. [41], we proposed the 16th-order hyperbolic sine chaotic system, which is described as follows:

$\{\begin{array}{c}\dot{x_1}=x_2-x_1\\ \dot{x_2}=x_3-x_2\\ \dot{x_3}=x_4-x_3\\ \dot{x_4}=x_5-x_4\\ \dot{x_5}=x_6-x_5\\ \dot{x_6}=x_7-x_6\\ \dot{x_7}=x_8-x_7\\ \dot{x_8}=x_9-x_8\\ \dot{x_9}=x_{10}-x_9\\ \dot{x_{10}}=x_{11}-x_{10}\\ \dot{x_{11}}=x_{12}-x_{11}\\ \dot{x_{12}}=x_{13}-x_{12}\\ \dot{x_{13}}=x_{14}-x_{13}\\ \dot{x_{14}}=x_{15}\\ \dot{x_{15}}=x_{16}\\ \dot{x_{16}}=c{x}_{16}-\rho \sinh \left(\phi x_{15}\right)-16x_{14}-16x_{13}-16x_{12}-16x_{11}-16x_{10}-16x_9-16x_8\\ -16x_7-16x_6-16x_5-16x_4-16x_3-16x_2-\frac{1}{32}{x}_1\end{array}(4)$

When $c=1$, the system exhibits chaotic behavior, the waveform is shown as Figure 2, the phase space plot is shown in Figure 3.

FIGURE 2

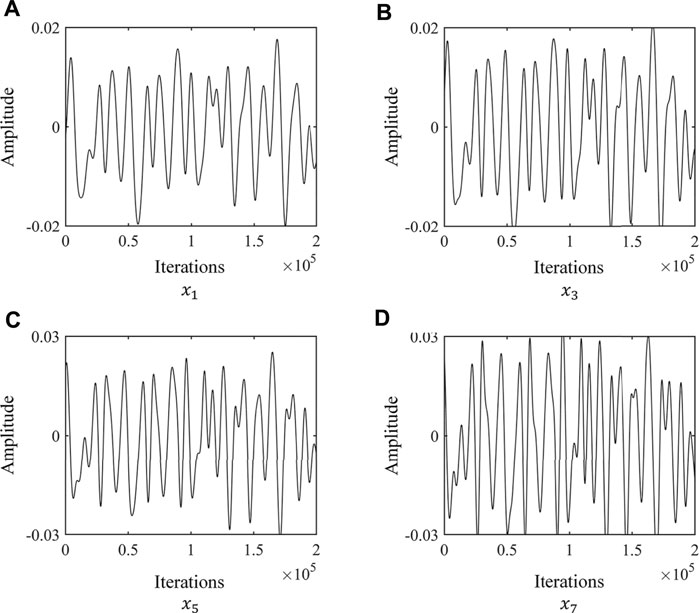
FIGURE 2. Waveform of output sequence: (A), the waveform of $x_1$. (B), the waveform of $x_3$. (C), the waveform of $x_5$. (D), the waveform of $x_7$.

FIGURE 3

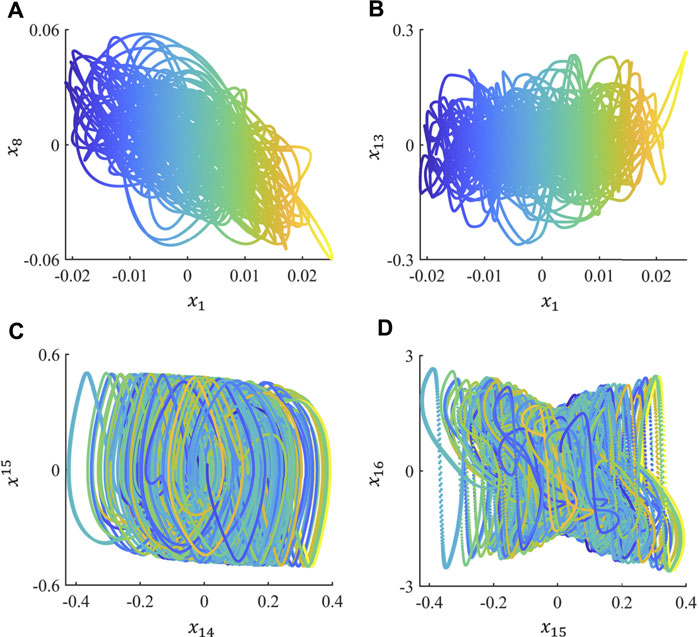
FIGURE 3. phase space plots: (A), the phase space plot of $x_1$ - $x_8$ plane. (B), the phase space plot of $x_1$ - $x_{13}$ plane. (C), the phase space plot of $x_{14}$ - $x_{15}$ plane. (D), the phase space plot of $x_{15}$ - $x_{16}$ plane.

To study the overall dynamic behavior of the proposed system, we plot the Largest Lyapunov exponent spectrum. Lyapunov exponent is a measure of a system’s predictability and sensitivity to changes in its initial conditions. If the largest Lyapunov exponent (LLE) is greater than zero, the system exhibits chaotic behavior. If LLE = 0, the system exhibits periodic behavior. If LLE <0, the system converges to a stable point. When $c= [0, 3]$, The largest Lyapunov exponent spectrum is shown as Figure 4.

FIGURE 4

FIGURE 4. Lyapunov exponent spectrum.

From Figure 4, the chaos exists in $c\in [0.07-2.49]$ except some period windows are embedded.

Physical Characteristics of the Output Sequence

Although the proposed system can generate pseudo-random sequences, it has physical characteristics [45], Figure 5 is the probability density distributions of the output sequence $x_1$, $x_3$, $x_5$, $x_7$.

FIGURE 5

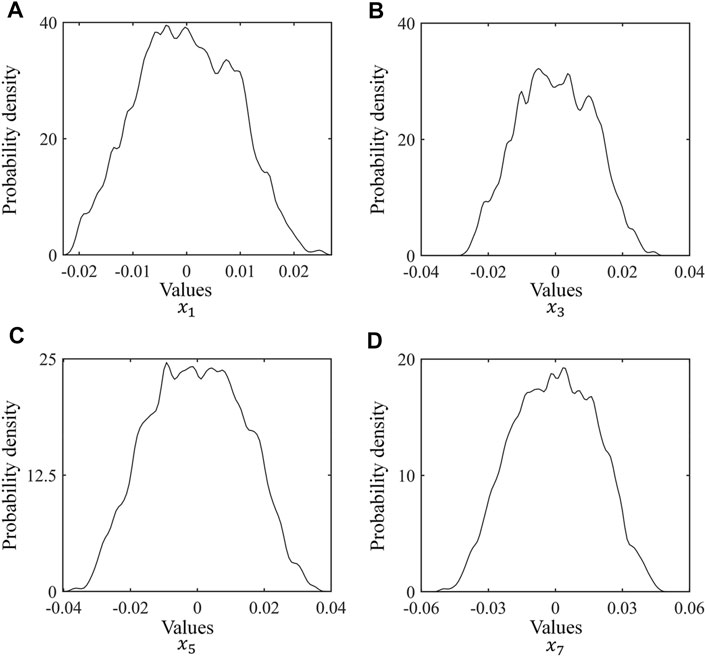
FIGURE 5. Probability density distributions of output sequences. (A), the probability density distributions of the output sequence $x_1$. (B), the probability density distributions of the output sequence $x_3$. (C), the probability density distributions of the output sequence $x_5$. (D), the probability density distributions of the output sequence $x_7$.

From the results of Figure 5, the output sequences have physical characteristics. Therefore, it may be cracked by the side-channel attack. To remove the physical characteristics, we utilize the decorrelation operation:

${\mathit{S}}_{\mathit{out}}={\mathit{S}}_{\mathit{in}}\ast {10}^5-\mathit{floor}\left({\mathit{S}}_{\mathit{in}}\ast {10}^5\right)(5)$

The probability density distributions of the above sequences after decorrelation operation are plotted in Figure 6.

FIGURE 6

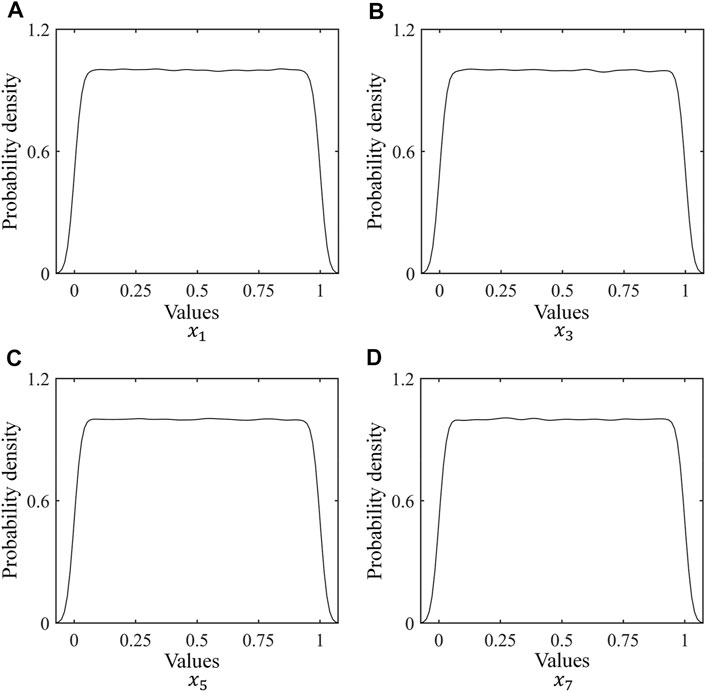
FIGURE 6. Probability density distributions of output sequences after decorrelation operation. (A), the probability density distributions of the above sequence $x_1$. (B), the probability density distributions of the above sequence $x_3$. (C), the probability density distributions of the above sequence $x_5$. (D), the probability density distributions of the above sequence $x_7$.

Experiments

This section is the performance analysis of the proposed scheme, which includes mutual interference suppression, security, bit error rate, and time efficiency.

Mutual Interference Between Channels

The decorrelation operation not only can remove the physical characteristics, but also can suppress mutual interference between channels. We test the Pearson product-moment correlation coefficient (PPMCC) of ${10}^5$ data of two output sequences. The comparative results are shown in Tables 1, 2.

TABLE 1

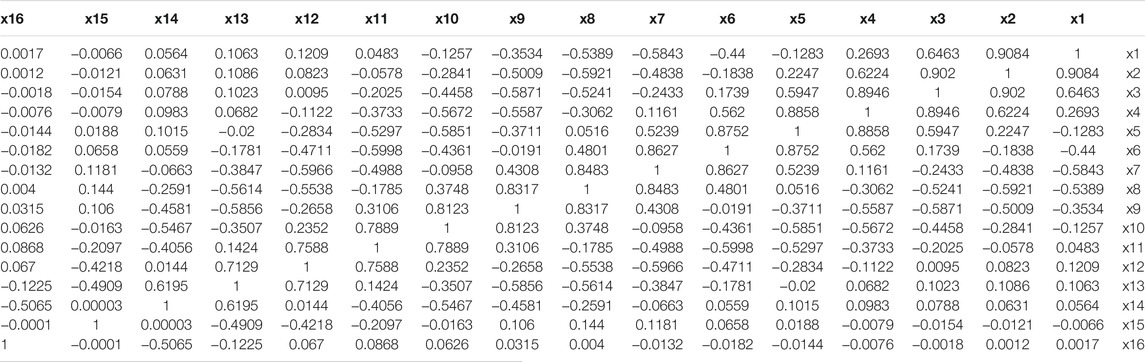
TABLE 1. Pearson product-moment correlation coefficient of the two output sequences before decorrelation operation.

TABLE 2

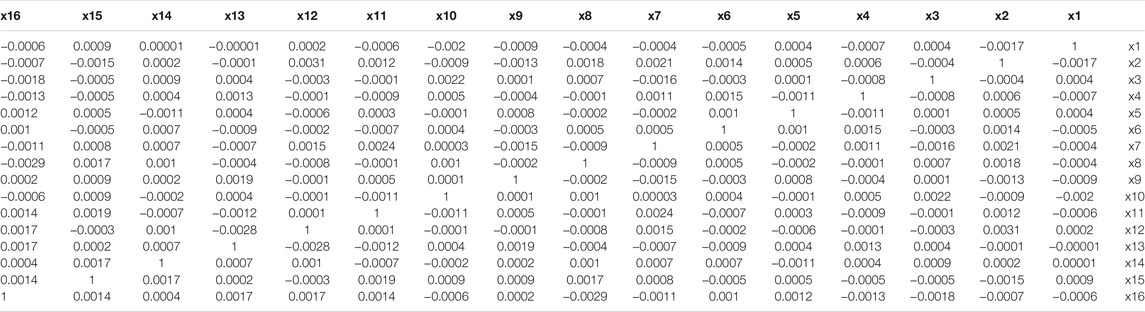
TABLE 2. Pearson product-moment correlation coefficient of the two output sequences after decorrelation operation.

From the results in Table 1. Most PPMCCs are greater than 0.4, some PPMCC like $x_1$ ∼ $x_2$, $x_2$ ∼ $x_3$ are over 0.9, which means the original sequences have strong correlation. From the results in Table 2, PPMCC after decorrelation are less than 0.01, which means the sequences after decorrelation operation have strong interference suppression ability, the communication data flow of different channels will not interfere with each other, which ensures that the BCI systems can accurately extract EEG features.

Key Space Analysis

If the attackers have all the details of the HD-MU-DCSK scheme, this communication protocol will no longer be secure. In this circumstance, the defender can improve the security by frequently changing the secure key. For Eq. 4, all initial conditions and control parameters can set to be the secure keys. As shown in Figure 4, chaos exists in $c\in [0.05, 2.49]$. Suppose all initial conditions and control parameters are equal, the key space will be larger than ${(5.68\times {10}^9)}^{59}\gg {10}^{531}$ (for 32-bit system), if the defender changes secure key every second, the keys can be used for over $3.17\times {10}^{58}$ years. Therefore, the proposed scheme can provide high security level.

Security Analysis

Security is the most important performance considered in this work. To evaluate the data security of the proposed scheme, we use the standard statistical test suite (SP 800–22) for random number generators provided by the National Institute of Standard Technology (NIST). The test results of the output sequence $x_1$ after decorrelation operation is shown in Table 3.

TABLE 3

TABLE 3. Results of SP 800–22 test using $x_1$ after decorrelation operation.

From Tables 3–6, the output sequence $x_1$, $x_3$, $x_5$, and $x_7$ after decorrelation operation can pass all of the NIST tests. Therefore, it can provide a high level of security when these sequences as the carrier signal.

TABLE 4

TABLE 4. Results of SP 800–22 test using $x_3$ after decorrelation operation.

TABLE 5

TABLE 5. Results of SP 800–22 test using $x_5$ after decorrelation operation.

TABLE 6

TABLE 6. Results of SP 800–22 test using $x_7$ after decorrelation operation.

Bit Error Rate

The proposed scheme can carry out secure communication under noisy channels. The performance of the bit error rate is shown in Figure 7.

FIGURE 7

FIGURE 7. BER performance under additive white Gaussian noise (AWGN) channels.

Time Efficiency

We have tested 10⁶ bit data to evaluate the time efficiency performance of the proposed scheme. The computer configuration used in this test is i5-8,265 processor (8-core, 1.60 GHz) with 8 GB memory. The average detailed results are shown in Table 7.

TABLE 7

TABLE 7. Results of time and speed of the scheme.

From the testing results of time efficiency performance, the main factor restricting the speed of this scheme is the generation of chaotic sequences. This is because we utilize Fourth-order Runge-Kutta algorithm to generate the output sequence, each iteration time requires 80 iterations. If a circuit or FPGA is used to generate high-speed pseudo-random numbers, this problem can be solved.

Conclusion and Future Work

In this work, we proposed a secure communication scheme for BCI systems based on high-dimensional hyperbolic sine chaotic systems. The testing results indicate that the proposed scheme can provide a high level of security. The communication data between the electrodes will not cause mutual interference. For the time efficiency of the proposed scheme, the generation of the pseudo-random sequences is the bottleneck restricting the execution speed of the scheme. Designing the corresponding circuit or FPGA system can solve this bottleneck.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XZ raises the issue of security risks of BCI systems. JL designed the secure communication scheme. XZ, XD, DT, and PC performed the experiments. JL wrote the paper. All authors have proposed amendments to the manuscript.

Funding

This study is supported by the Natural Science Foundation of Gansu Province (No. 21JR7RA510), and Distinguished Young Scholars of Gansu Province of China (No. 21JR7RA345).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Jing Lian for the helpful suggestions.

References

1. Wolpaw JR, Birbaumer N, Heetderks WJ, McFarland DJ, Peckham PH, Schalk G, et al. Brain-computer Interface Technology: a Review of the First International Meeting. IEEE Trans Rehab Eng (2000) 8(2):164–73. doi:10.1109/tre.2000.847807

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Ortiz M, Iáñez E, Gaxiola-Tirado JA, Gutiérrez D, Azorín JM. Study of the Functional Brain Connectivity and Lower-Limb Motor Imagery Performance after Transcranial Direct Current Stimulation. Int J Neur Syst (2020) 30(08):2050038. doi:10.1142/s0129065720500380

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Mühl C, Allison B, Nijholt A, Chanel G. A Survey of Affective Brain Computer Interfaces: Principles, State-Of-The-Art, and Challenges[J]. Brain-Computer Inter (2014) 1(2):66–84.

Google Scholar

4. Wolpaw JR, McFarland DJ, Vaughan TM, Schalk G. The Wadsworth Center Brain-Computer Interface (BCI) Research and Development Program. IEEE Trans Neural Syst Rehabil Eng (2003) 11(2):1–4. doi:10.1109/tnsre.2003.814442

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Rohani DA, Sorensen HBD, Puthusserypady S. In: Brain-computer interface using P300 and virtual reality: A gaming approach for treating ADHD[C]//2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE (2014). p. 3606–9.

6. Hsu W-Y. Continuous Eeg Signal Analysis for Asynchronous Bci Application. Int J Neur Syst (2011) 21(04):335–50. doi:10.1142/s0129065711002870

CrossRef Full Text | Google Scholar

7. Wolpaw JR, Birbaumer N, McFarland DJ, Pfurtscheller G, Vaughan TM. Brain-computer Interfaces for Communication and Control. Clin Neurophysiol (2002) 113(6):767–91. doi:10.1016/s1388-2457(02)00057-3

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Dobkin BH. Brain-computer Interface Technology as a Tool to Augment Plasticity and Outcomes for Neurological Rehabilitation. J Physiol (2007) 579(3):637–42. doi:10.1113/jphysiol.2006.123067

CrossRef Full Text | Google Scholar

9. Daly JJ, Huggins JE. Brain-Computer Interface: Current and Emerging Rehabilitation Applications. Arch Phys Med Rehabil (2015) 96(3):S1–S7. doi:10.1016/j.apmr.2015.01.007

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Yang S, Li R, Li H, Xu K, Shi Y, Wang Q, et al. Exploring the Use of Brain-Computer Interfaces in Stroke Neurorehabilitation. Biomed Res Int (2021) 2021:9967348. doi:10.1155/2021/9967348

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Broetz D, Braun C, Weber C, Soekadar SR, Caria A, Birbaumer N. Combination of Brain-Computer Interface Training and Goal-Directed Physical Therapy in Chronic Stroke: A Case Report. Neurorehabil Neural Repair (2010) 24(7):674–9. doi:10.1177/1545968310368683

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Landau O, Cohen A, Gordon S, Nissim N. Mind Your Privacy: Privacy Leakage through BCI Applications Using Machine Learning Methods. Knowledge-Based Syst (2020) 198:105932. doi:10.1016/j.knosys.2020.105932

CrossRef Full Text | Google Scholar

13. Zhu H, Guo Y, Zhang L. An Improved Convolution Merkle Tree-Based Blockchain Electronic Medical Record Secure Storage Scheme. J Inf Security Appl (2021) 61:102952. doi:10.1016/j.jisa.2021.102952

CrossRef Full Text | Google Scholar

14. Takabi H, Bhalotiya A, Alohaly M. In: Brain computer interface (BCI) applications: Privacy threats and countermeasures[C]//2016 IEEE 2nd International Conference on Collaboration and Internet Computing (CIC). IEEE (2016). p. 102–11.

15. Li QQ, Ding D, Conti M. In: Brain-computer interface applications: Security and privacy challenges[C]//2015 IEEE Conference on Communications and Network Security (CNS). IEEE (2015). p. 663–6.

16. Yang F, Zhao X, Jiang W, Gao P, Liu G. Multi-method Fusion of Cross-Subject Emotion Recognition Based on High-Dimensional EEG Features. Front Comput Neurosci (2019) 13:53. doi:10.3389/fncom.2019.00053

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Liu J, Clinton Sprott J, Wang S, Ma Y. Simplest Chaotic System with a Hyperbolic Sine and its Applications in DCSK Scheme. IET Commun (2018) 12(7):809–15. doi:10.1049/iet-com.2017.0455

CrossRef Full Text | Google Scholar

18. Xiong L, Zhang X, Teng S, Qi L, Zhang P. Detecting Weak Signals by Using Memristor-Involved Chua's Circuit and Verification in Experimental Platform. Int J Bifurcation Chaos (2020) 30(13):2050193. doi:10.1142/s021812742050193x

CrossRef Full Text | Google Scholar

19. Ma C, Mou J, Xiong L, Banerjee S, Liu T, Han X. Dynamical Analysis of a New Chaotic System: Asymmetric Multistability, Offset Boosting Control and Circuit Realization. Nonlinear Dyn (2021) 103(3):2867–80. doi:10.1007/s11071-021-06276-8

CrossRef Full Text | Google Scholar

20. Lai Q. A Unified Chaotic System with Various Coexisting Attractors. Int J Bifurcation Chaos (2021) 31(01):2150013. doi:10.1142/s0218127421500139

CrossRef Full Text | Google Scholar

21. Lai Q, Wan Z, Kengne LK, Kamdem Kuate PD, Chen C. Two-memristor-based Chaotic System with Infinite Coexisting Attractors[J]. IEEE Trans Circuits Syst Express Briefs (2020) 68(6):2197–201. doi:10.1109/tcsii.2020.3044096

CrossRef Full Text | Google Scholar

22. Lai Q, Wan Z, Kamdem Kuate PD. Modelling and Circuit Realisation of a New No-Equilibrium Chaotic System with Hidden Attractor and Coexisting Attractors. Electron Lett (2020) 56(20):1044–6. doi:10.1049/el.2020.1630

CrossRef Full Text | Google Scholar

23. Zhu H, Dai L, Liu Y, Wu L. A Three-Dimensional Bit-Level Image Encryption Algorithm with Rubik's Cube Method. Mathematics Comput Simulation (2021) 185:754–70. doi:10.1016/j.matcom.2021.02.009

CrossRef Full Text | Google Scholar

24. Li X, Mou J, Xiong L, Wang Z, Xu J. Fractional-order Double-Ring Erbium-Doped Fiber Laser Chaotic System and its Application on Image Encryption. Opt Laser Tech (2021) 140:107074. doi:10.1016/j.optlastec.2021.107074

CrossRef Full Text | Google Scholar

25. Zhu H, Zhao Y, Song Y. 2D Logistic-Modulated-Sine-Coupling-Logistic Chaotic Map for Image Encryption. IEEE Access (2019) 7:14081–98. doi:10.1109/access.2019.2893538

CrossRef Full Text | Google Scholar

26. Zhu H, Zhang X, Yu H, Zhao C, Zhu Z. An Image Encryption Algorithm Based on Compound Homogeneous Hyper-Chaotic System. Nonlinear Dyn (2017) 89(1):61–79. doi:10.1007/s11071-017-3436-y

CrossRef Full Text | Google Scholar

27. Luo R, Yang H, Meng C, Zhang X. A Novel SR-DCSK-Based Ambient Backscatter Communication System[J]. IEEE Trans Circuits Syst Express Briefs (2021) 1. doi:10.1109/tcsii.2021.3109020

CrossRef Full Text | Google Scholar

28. Zhang X, Li H, Xie T, Liu Y, Chen J, Long J. Movement Speed Effects on Beta-Band Oscillations in Sensorimotor Cortex during Voluntary Activity. J Neurophysiol (2020) 124(2):352–9. doi:10.1152/jn.00238.2020

CrossRef Full Text | Google Scholar

29. Cai X, Xu W, Hong S, Wang L. Discrete W Transform Based Index-Keying M-Ary DCSK for Non-coherent Chaotic Communications. IEEE Commun Lett (2021) 25(9):3104–8. doi:10.1109/lcomm.2021.3095075

CrossRef Full Text | Google Scholar

30. Capligins F, Litvinenko A, Aboltins A, Austrum E, Rusins A Chaotic Jerk Circuit Usage in Communication Systems[C]//2020 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW). IEEE (2020) 1:227–30.

Google Scholar

31. Kolumban G, Kennedy MP, Jako Z, Kis G. Chaotic Communications with Correlator Receivers: Theory and Performance Limits. Proc IEEE (2002) 90(5):711–32. doi:10.1109/jproc.2002.1015003

CrossRef Full Text | Google Scholar

32. Qiu HB, Wang M. Analysis of the System Character of FM-EDCSK[J]. Journal-China Inst Commun (2005) 26(5):113. doi:10.3321/j.issn:1000-436X.2005.05.018

CrossRef Full Text | Google Scholar

33. Zhang G, Zhao C, Zhang T. Performance Analysis of MISO-MU-OHE-DCSK System over Rayleigh Fading Channels. AEU - Int J Elect Commun (2020) 115:153048. doi:10.1016/j.aeue.2019.153048

CrossRef Full Text | Google Scholar

34. Chen P, Wang L, Chen G. DDCSK-walsh Coding: A Reliable Chaotic Modulation-Based Transmission Technique. IEEE Trans Circuits Syst (2012) 59(2):128–32. doi:10.1109/tcsii.2011.2180109

CrossRef Full Text | Google Scholar

35. Zhang X, Guo Y, Gao B, Long J. In: Enhancing Mu-based BCI performance with rhythmic electrical stimulation at alpha frequency[C]//2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE (2019). p. 5540–3. doi:10.1109/EMBC.2019.8857321

CrossRef Full Text

36. Li S, Zhao Y, He L, Wu Z, Li Y. In: Design and performance analysis of a GFDM-DCSK communication system[C]//2016 13th IEEE Annual Consumer Communications & Networking Conference (CCNC). IEEE (2016). p. 802–3.

37. Zhang X, Guo Y, Gao B, Long J. Alpha Frequency Intervention by Electrical Stimulation to Improve Performance in Mu-Based BCI. IEEE Trans Neural Syst Rehabil Eng (2020) 28(6):1262–70. doi:10.1109/tnsre.2020.2987529

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Atkinson J, Campos D. Improving BCI-Based Emotion Recognition by Combining EEG Feature Selection and Kernel Classifiers. Expert Syst Appl (2016) 47:35–41. doi:10.1016/j.eswa.2015.10.049

CrossRef Full Text | Google Scholar

39. Shen C, Yu S, Lu J, Chen G. Designing Hyperchaotic Systems with Any Desired Number of Positive Lyapunov Exponents via A Simple Model. IEEE Trans Circuits Syst (2014) 61(8):2380–9. doi:10.1109/tcsi.2014.2304655

CrossRef Full Text | Google Scholar

40. Wu Y, Hua Z, Zhou Y. $n$ -Dimensional Discrete Cat Map Generation Using Laplace Expansions. IEEE Trans Cybern (2015) 46(11):2622–33. doi:10.1109/TCYB.2015.2483621

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Liu J, Ma J, Lian J, Chang P, Ma Y. An Approach for the Generation of an Nth-Order Chaotic System with Hyperbolic Sine. Entropy (2018) 20(4):230. doi:10.3390/e20040230

PubMed Abstract | CrossRef Full Text | Google Scholar

42. McCann MT, Thompson DE, Syed ZH, Huggins JE. Electrode Subset Selection Methods for an EEG-Based P300 Brain-Computer Interface. Disabil Rehabil Assistive Tech (2015) 10(3):216–20. doi:10.3109/17483107.2014.884174

CrossRef Full Text | Google Scholar

43. Putra AE, Atmaji C, Utami TG. In: EEG-based microsleep detector using microcontroller[C]//2016 8th International Conference on Information Technology and Electrical Engineering (ICITEE). IEEE (2016). p. 1–4.

44. Liu J, Zhang X, Zhao Q, Lian J, Huang F, Ma Y. A Torus-Chaotic System and its Pseudorandom Properties[J]. Complexity (2020) 2020:1–12. doi:10.1155/2020/8315658

CrossRef Full Text | Google Scholar