Studying Heisenberg-like Uncertainty Relation with Weak Values in One-dimensional Harmonic Oscillator

As one of the fundamental traits governing the operation of quantum world, the uncertainty relation, from the perspective of Heisenberg, rules the minimum deviation of two incompatible observations for arbitrary quantum states. Notwithstanding, the original measurements appeared in Heisenberg’s principle are strong such that they may disturb the quantum system itself. Hence an intriguing question is raised: What will happen if the mean values are replaced by weak values in Heisenberg’s uncertainty relation? In this work, we investigate the question in the case of measuring position and momentum in a simple harmonic oscillator via designating one of the eigenkets thereof to the pre-selected state. Astonishingly, the original Heisenberg limit is broken for some post-selected states, designed as a superposition of the pre-selected state and another eigenkets of harmonic oscillator. Moreover, if two distinct coherent states reside in the pre- and post-selected states respectively, the variance reaches the lower bound in common uncertainty principle all the while, which is in accord with the circumstance in Heisenberg’s primitive framework.

1 Introduction

The non-commutativity in quantum mechanics leads to the essential contradistinction between itself and classical mechanics. Among diverse quantum phenomena, the uncertainty relation is representative, which was first uncovered by Heisenberg [1], then generalized via Robertson [2] to any two observables A and B for arbitrary kets of the following form,

$⟨{\left(\mathrm{\Delta }A\right)}^2⟩⟨{\left(\mathrm{\Delta }B\right)}^2⟩\ge \frac{1}{4}{\left|⟨\left[A,B\right]⟩\right|}^2,(1)$

where $⟨{(\mathrm{\Delta }A)}^2⟩≔⟨A^2⟩-{\left(⟨A⟩\right)}^2$, represents the variance of measuring a quantum system via A, so does $⟨{(\mathrm{\Delta }B)}^2⟩$.

However, there exist some shortcomings for standard Heisenberg uncertainty principle (Eq. 1). On the one hand, for instance, the derivation of the z components of angular momentum increases in the case of a three-level problem [3], though the information we have gathered therein increases, which is discordant with classical information theory. Thus the concept of entropy was imported into the field of uncertainty relation [4, 5].

On the other hand, initial uncertainty relation only involves strong measurement, and it may destroy the measured system inevitably in most cases, which leads to another way of exploring Heisenberg uncertainty principle relying on the heritage of weak measurement. In 1988, Y. Aharonov et al. [6] proposed the concept of “weak value” to overcome the blemish of measurement collapse in quantum mechanics. The weak value of an observable O is denoted as

${⟨O⟩}_{\mathrm{w}}≔\frac{\left.⟨{\psi }_{\text{f}}\right|O\left|{\psi }_{\text{i}}\right.⟩}{⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩},(2)$

with $\left|{\psi }_{\text{i}}\right.⟩$ and $\left|{\psi }_{\text{f}}\right.⟩$ representing the states of pre- and post-selections respectively.

In recent illuminating works, Song and Qiao [7] constructed a new type of uncertainty relation in weak measurement with the help of a non-Hermitian operator defined in [8]. Additionally, Hall et al. [9] generalized the representation theorem given by Shikano and Hosoya [10] and studied the uncertainty relation via weak values. Afterwards, Šindelka, and Moiseyev [11] considered a Heisenberg-like situation that measuring a quantum system “weakly” via an observable A without imposing postselection, following a strong measurement by another observable B subsequently. But there is hardly any work involving researching Heisenberg-like uncertainty principle via replacing mean value by weak value merely, which is the simplest case in this field.

In this work, we study the Heisenberg-like uncertainty relation in the case of measuring position and momentum in a one-dimensional (1D) simple harmonic oscillator with the pre-selected state appointed as one of its eigenstates. We found that if post-selected states are specified as a superposition of the pre-selected state and another eigenstates of harmonic oscillator, primitive Heisenberg relation fails. Furthermore, providing the pre- and post-selected states are designed as two distinct coherent states, the variance in the sense of weak values will arrive at the lower bound in usual Heisenberg principle all through, which is in agreement with Heisenberg’s original argument.

This paper is organized as follows: In Section 2 we show our main results about Heisenberg-like uncertainty principle through replacing expectation values by weak values in rudimental Heisenberg’s idea. Four major parts are included in this section. In Section 2.1, we retrospect some basic knowledge about 1D simple harmonic oscillator in occupation number representation. And then in Section 2.2, we study two non-orthonormal cases of selected states by considering $\left|{\psi }_{\text{i}}\right.⟩=\left|0\right.⟩$ and $\left|{\psi }_{\text{i}}\right.⟩=\left|n\right.⟩$ ($n\in {\mathbb{N}}^{\ast }$, i.e., n is a positive integer), respectively. Next in Section 2.3, we explore the orthogonal selected states as the limitation of non-orthogonal circumstances. And in Section 2.4, the pre- and post-selected states are designed as two coherent states. Finally in Section 3, we make a summary and bring up some open questions.

2 Replacing Mean Values by Weak Values

2.1 Simple Harmonic Oscillator in Occupation Number Representation

Set $n\in \mathbb{N}$ the quantum number referring to energy levels of given 1D simple harmonic oscillator with Hamiltonian H. Let $\left|n\right.⟩(n\in \mathbb{N})$ the eigenkets thereof, then via Schrödinger equation $H\left|n\right.⟩=E_n\left|n\right.⟩$, we obtain $E_n=\left(n+1/2\right)\hslash \omega$ as the formula of energy, with ℏ the Plank constant up to a factor 1/(2π), and ω the vibration frequency of corresponding oscillator. Especially when n = 0, E₀ = (1/2)ℏω implies the ground state energy.

Define the annihilation operator a and the creation operator a^†, which satisfy

$\begin{array}{ccc}\hfill & \hfill & a\left|n\right.⟩=\sqrt{n}\left|n-1\right.⟩,\hfill \\ \hfill & \hfill & a^{†}\left|n\right.⟩=\sqrt{n+1}\left|n+1\right.⟩,\hfill \end{array}(3)$

where $a\left|0\right.⟩=0$.

Postulate that $\alpha \equiv \sqrt{m\omega /\hslash }$, X ≡ αx, and $P\equiv \left[\alpha /(m\omega )\right]p$, with m expressing the mass of aforementioned harmonic oscillator. Note that X and P are Hermitian. After that, from the canonical commutative relation (x, p) = iℏ, we have (X, P) = i, together with

$\begin{array}{ccc}\hfill & \hfill & X=\frac{1}{\sqrt{2}}\left(a+a^{†}\right),\hfill \\ \hfill & \hfill & P=\frac{1}{\mathrm{i}\sqrt{2}}\left(a-a^{†}\right).\hfill \end{array}(4)$

Next we will compute the Heisenberg-like uncertainty principle with weak values by combining Eqs 1, 2 and some properties of 1D harmonic oscillator.

2.2 Non-orthonormal Selected States

This subsection includes the situations of non-orthonormal pre- and post-selections. When the pre-selected state is initialized as $\left|n\right.⟩$, its post-selected partner is set as $\cos \theta \left|n\right.⟩+\sin \theta e^{\text{i}\phi }\left|m\right.⟩$, where θ ∈ (0, π/2) ∪ (π/2, π), $\phi \in \left[\left.0,2\pi \right)\right.$ and n ≠ m.

Case 1.—$n=0,\left|{\psi }_{\text{i}}\right.⟩=\left|0\right.⟩$.

In this case, we set $\left|{\psi }_{\text{f}}\right.⟩=\cos \theta \left|0\right.⟩+\sin \theta e^{\text{i}\phi }\left|m\right.⟩$, where θ ∈ (0, π/2) ∪ (π/2, π), $\phi \in \left[\left.0,2\pi \right)\right.$ and $m\in {\mathbb{N}}^{\ast }$. Thereby, $⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩=\cos \theta$, and

$\begin{array}{cc}\hfill {⟨X⟩}_{\mathrm{w}}& =\frac{\left.⟨{\psi }_{\text{f}}\right|X\left|{\psi }_{\text{i}}\right.⟩}{⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩}\hfill \\ \hfill & =\frac{\left[\cos \theta \left.⟨0\right|+\sin \theta e^{-\mathrm{i}\phi }\left.⟨m\right|\right]\left(a+a^{†}\right)\left|0\right.⟩}{\sqrt{2}\cos \theta }\hfill \\ \hfill & =\frac{\tan \theta e^{-\mathrm{i}\phi }⟨m|1⟩}{\sqrt{2}}\hfill \\ \hfill & =\frac{\tan \theta e^{-\mathrm{i}\phi }{\delta }_{m,1}}{\sqrt{2}},\hfill \end{array}$

where δ_{m, n} implies the Kronecker delta symbol.

Thereafter, we arrive at

${\left({⟨X⟩}_{\mathrm{w}}\right)}^2=\frac{{\tan }^2\theta e^{-\mathrm{i}2\phi }{\delta }_{m,1}^2}{2},(5)$

and

$\begin{array}{cc}\hfill {⟨X^2⟩}_{\mathrm{w}}& =\frac{\left.⟨{\psi }_{\text{f}}\right|\left[a^2+a{a}^{†}+a^{†}a+{\left(a^{†}\right)}^2\right]\left|{\psi }_{\text{i}}\right.⟩}{2⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩}\hfill \\ \hfill & =\frac{1+\sqrt{2}\tan \theta e^{-\mathrm{i}\phi }{\delta }_{m,2}}{2}.\hfill \end{array}(6)$

Combine Eq. 6 with Eq. 5 together, then we attain the variance of X in the form of weak value as follows

$\begin{array}{cc}\hfill & {⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2\equiv {⟨X^2⟩}_{\mathrm{w}}-{\left({⟨X⟩}_{\mathrm{w}}\right)}^2\hfill \\ \hfill & =\frac{1+\sqrt{2}\tan \theta e^{-\mathrm{i}\phi }{\delta }_{m,2}-{\tan }^2\theta e^{-\mathrm{i}2\phi }{\delta }_{m,1}^2}{2}.\hfill \end{array}(7)$

On the other hand,

$\begin{array}{cc}\hfill {⟨P⟩}_{\mathrm{w}}& =\frac{\left.⟨{\psi }_{\text{f}}\right|P\left|{\psi }_{\text{i}}\right.⟩}{⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩}\hfill \\ \hfill & =\frac{\left[\cos \theta \left.⟨0\right|+\sin \theta e^{-\mathrm{i}\phi }\left.⟨m\right|\right]\left(a-a^{†}\right)\left|0\right.⟩}{\mathrm{i}\sqrt{2}\cos \theta }\hfill \\ \hfill & =\frac{\mathrm{i}\tan \theta e^{-\mathrm{i}\phi }{\delta }_{m,1}}{\sqrt{2}},\hfill \end{array}$

which indicates that

${\left({⟨P⟩}_{\mathrm{w}}\right)}^2=-\frac{{\tan }^2\theta e^{-\mathrm{i}2\phi }{\delta }_{m,1}^2}{2},(8)$

and

$\begin{array}{cc}\hfill {⟨P^2⟩}_{\mathrm{w}}& =\frac{\left.⟨{\psi }_{\text{f}}\right|\left[a{a}^{†}+a^{†}a-a^2-{\left(a^{†}\right)}^2\right]\left|{\psi }_{\text{i}}\right.⟩}{2⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩}\hfill \\ \hfill & =\frac{1-\sqrt{2}\tan \theta e^{-\mathrm{i}\phi }{\delta }_{m,2}}{2}.\hfill \end{array}(9)$

Therefore,

$\begin{array}{cc}\hfill & {⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\equiv {⟨P^2⟩}_{\mathrm{w}}-{\left({⟨P⟩}_{\mathrm{w}}\right)}^2\hfill \\ \hfill & =\frac{1-\sqrt{2}\tan \theta e^{-\mathrm{i}\phi }{\delta }_{m,2}+{\tan }^2\theta e^{-\mathrm{i}2\phi }{\delta }_{m,1}^2}{2},\hfill \end{array}(10)$

then we can calculate the uncertainty relation in terms of weak values, namely.

$\begin{array}{cc}\hfill {⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2& =\frac{1-{\tan }^2\theta {\left[\sqrt{2}{e}^{-\mathrm{i}\phi }{\delta }_{m,2}-\tan \theta e^{-\mathrm{i}2\phi }{\delta }_{m,1}^2\right]}^2}{4}\hfill \\ \hfill & =\frac{1-{\tan }^2\theta \left[2e^{-\mathrm{i}2\phi }{\delta }_{m,2}^2+{\tan }^2\theta e^{-\mathrm{i}4\phi }{\delta }_{m,1}^4\right]}{4},\hfill \end{array}(11)$

which means that

$\begin{array}{cc}\hfill & \left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|=\left|\frac{1-{\tan }^2\theta \left[2e^{-\mathrm{i}2\phi }{\delta }_{m,2}^2+{\tan }^2\theta e^{-\mathrm{i}4\phi }{\delta }_{m,1}^4\right]}{4}\right|\hfill \\ \hfill & =\frac{1}{4}\left|\left\{1-{\tan }^2\theta \left[2{\delta }_{m,2}^2\cos \left(2\phi \right)+{\tan }^2\theta {\delta }_{m,1}^4\cos \left(4\phi \right)\right]\right\}+\mathrm{i}{\tan }^2\theta \left[2{\delta }_{m,2}^2\sin \left(2\phi \right)+{\tan }^2\theta {\delta }_{m,1}^4\sin \left(4\phi \right)\right]\right|\hfill \\ \hfill & =\frac{1}{4}\sqrt{{\left\{1-{\tan }^2\theta \left[2{\delta }_{m,2}^2\cos \left(2\phi \right)+{\tan }^2\theta {\delta }_{m,1}^4\cos \left(4\phi \right)\right]\right\}}^2+{\tan }^4\theta {\left[2{\delta }_{m,2}^2\sin \left(2\phi \right)+{\tan }^2\theta {\delta }_{m,1}^4\sin \left(4\phi \right)\right]}^2}\hfill \\ \hfill & =\frac{1}{4}\sqrt{1+{\tan }^4\theta \left(4{\delta }_{m,2}^4+{\tan }^4\theta {\delta }_{m,1}^8\right)-2{\tan }^2\theta \left[2{\delta }_{m,2}^2\cos \left(2\phi \right)+{\tan }^2\theta {\delta }_{m,1}^4\cos \left(4\phi \right)\right]}\hfill \\ \hfill & \ge \frac{1}{4}\sqrt{1+{\tan }^4\theta \left(4{\delta }_{m,2}^4+{\tan }^4\theta {\delta }_{m,1}^8\right)-2{\tan }^2\theta \left(2{\delta }_{m,2}^2+{\tan }^2\theta {\delta }_{m,1}^4\right)}\hfill \\ \hfill & =\frac{1}{4}\left|1-{\tan }^2\theta \left(2{\delta }_{m,2}^2+{\tan }^2\theta {\delta }_{m,1}^4\right)\right|.\hfill \end{array}(12)$

Analysis—For A = X, B = P, the Heisenberg uncertainty relation is given by

${⟨\mathrm{\Delta }X⟩}^2{⟨\mathrm{\Delta }P⟩}^2=\left|{⟨\mathrm{\Delta }X⟩}^2{⟨\mathrm{\Delta }P⟩}^2\right|\ge \frac{1}{4}.(13)$

In this work, the Heisenberg-like uncertainty relation with weak values is modified as

$\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\ge \frac{1}{4}.(14)$

We now compare Eq. 12 with Heisenberg-like uncertainty relation (Eq. 14) in virtue of different m.

1) If m ≠ 1 and m ≠ 2, $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|=1/4$, the relation (Eq. 14) holds, and it is in coincidence with the usual Heisenberg uncertainty relation (Eq. 13).

2) If m = 1,

$\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|=\frac{1}{4}\sqrt{1+{\tan }^8\theta -2\cos \left(4\phi \right){\tan }^4\theta }.$

Then we have $(1/4)\left|1-{\tan }^4\theta \right|\le \left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\le (1/4)\left(1+{\tan }^4\theta \right)$, and the left equality sign holds once φ = 0, π/2 or π; While φ = π/4 or 3π/4, the right equality sign is obtained. In the interval of $\theta \in \left(0,\arctan \left(\sqrt[4]{2}\right)\right)\cup \left(\pi -\arctan \left(\sqrt[4]{2}\right),\pi \right)$, it is possible for $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|$ to arrive at some values less than 1/4. While for other legal θ, the uncertainty relation (Eq. 14) holds. See Figure 1 for more details. It is worth mentioning that once $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|$ reaches the lower bound, and θ = π/4 or 3π/4, the variance $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|$ vanishes, and further study shows that ${⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2={⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2=0$, which implies the product of weak values corresponding to two incompatible observables X and P can be measured precisely. The result is reasonable, since strong measurement is substituted by weak measurement, then the disturbance for quantum system weaken, and two incompatible observations may be assured simultaneously.

3) If m = 2,

$\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|=\frac{1}{4}\sqrt{1+4{\tan }^4\theta -4\cos \left(2\phi \right){\tan }^2\theta }.$

FIGURE 1

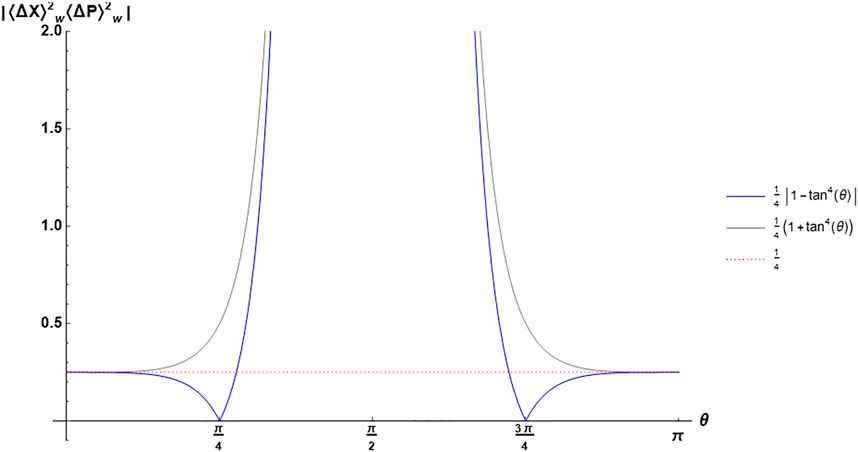
FIGURE 1. The variation diagram of $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|$ with respect to the superposition parameter θ ∈ (0, π/2) ∪ (π/2, π) in the case of $\left|{\psi }_{\text{i}}\right.⟩=\left|0\right.⟩$ and m = 1. The blue line represents the lower bound of $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|$, so does the grey line connecting the upper bound of $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|$, which is greater than 1/4 all the time.

After that, $(1/4)\left|1-2{\tan }^2\theta \right|\le \left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\le (1/4)\left(1+2{\tan }^2\theta \right)$, and the left equality sign holds once φ = 0 or π; While φ = π/2, the right equality sign is obtained. In the case of θ ∈ (0, π/4) ∪ (3π/4, π), it is possible for $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|$ to arrive at some values less than 1/4. And in other cases, the uncertainty relation (Eq. 14) holds. In like manner, there exist two ideal $\theta =\arctan (1/\sqrt{2})$ or $\pi -\arctan (1/\sqrt{2})$ when φ = 0 or π/2, such that the product of the weak values of X and P is affirmatory.

In one word, the Heisenberg uncertainty principle can be broken in the sense of weak values when we fix the pre-selected state as $\left|{\psi }_{\text{i}}\right.⟩=\left|0\right.⟩$, then set the post-selections to the superposition of $\left|0\right.⟩$ and $\left|1\right.⟩$ or $\left|2\right.⟩$. More general cases will be discussed similarly.

Case 2.—$\left|{\psi }_{\text{i}}\right.⟩=\left|n\right.⟩,n\in {\mathbb{N}}^{\ast }$.

Let $\left|{\psi }_{\text{i}}\right.⟩=\left|n\right.⟩$, and $\left|{\psi }_{\text{f}}\right.⟩=\cos \theta \left|n\right.⟩+\sin \theta e^{\text{i}\phi }\left|m\right.⟩$, where θ ∈ (0, π/2) ∪ (π/2, π), $\phi \in \left[\left.0,2\pi \right)\right.$, $n,m\in {\mathbb{N}}^{\ast }$, and n ≠ m. Likewise, $⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩=\cos \theta$, then

$\begin{array}{cc}\hfill {⟨X⟩}_{\mathrm{w}}& =\frac{\left.⟨{\psi }_{\text{f}}\right|X\left|{\psi }_{\text{i}}\right.⟩}{⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩}\hfill \\ \hfill & =\frac{\left[\cos \theta \left.⟨n\right|+\sin \theta e^{-\mathrm{i}\phi }\left.⟨m\right|\right]\left(a+a^{†}\right)\left|n\right.⟩}{\sqrt{2}\cos \theta }\hfill \\ \hfill & =\frac{\tan \theta e^{-\mathrm{i}\phi }\left(\sqrt{n}⟨m|n-1⟩+\sqrt{n+1}⟨m|n+1⟩\right)}{\sqrt{2}}\hfill \\ \hfill & =\frac{\tan \theta e^{-\mathrm{i}\phi }\left(\sqrt{n}{\delta }_{m,n-1}+\sqrt{n+1}{\delta }_{m,n+1}\right)}{\sqrt{2}}.\hfill \end{array}$

In this case,

$\begin{array}{cc}\hfill {\left({⟨X⟩}_{\mathrm{w}}\right)}^2& =\frac{{\tan }^2\theta e^{-\mathrm{i}2\phi }{\left(\sqrt{n}{\delta }_{m,n-1}+\sqrt{n+1}{\delta }_{m,n+1}\right)}^2}{2}\hfill \\ \hfill & =\frac{{\tan }^2\theta e^{-\mathrm{i}2\phi }\left[n{\delta }_{m,n-1}^2+\left(n+1\right){\delta }_{m,n+1}^2\right]}{2}.\hfill \end{array}(15)$

Similarly, we can compute that

$\begin{array}{cc}\hfill {⟨X^2⟩}_{\mathrm{w}}& =\frac{\left.⟨{\psi }_{\text{f}}\right|\left[a^2+a{a}^{†}+a^{†}a+{\left(a^{†}\right)}^2\right]\left|{\psi }_{\text{i}}\right.⟩}{2⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩}\hfill \\ \hfill & =\frac{\left[\cos \theta \left.⟨n\right|+\sin \theta e^{-\mathrm{i}\phi }\left.⟨m\right|\right]\left[a^2+a{a}^{†}+a^{†}a+{\left(a^{†}\right)}^2\right]\left|n\right.⟩}{2\cos \theta }\hfill \\ \hfill & =\frac{\left[\cos \theta \left.⟨n\right|+\sin \theta e^{-\mathrm{i}\phi }\left.⟨m\right|\right]\left[\sqrt{n\left(n-1\right)}\left|n-2\right.⟩+\left(2n+1\right)\left|n\right.⟩+\sqrt{\left(n+1\right)\left(n+2\right)}\left|n+2\right.⟩\right]}{2\cos \theta }\hfill \\ \hfill & =n+\frac{1}{2}+\frac{\tan \theta e^{-\mathrm{i}\phi }\left[\sqrt{n\left(n-1\right)}{\delta }_{m,n-2}+\sqrt{\left(n+1\right)\left(n+2\right)}{\delta }_{m,n+2}\right]}{2}.\hfill \end{array}(16)$

Then

$\begin{array}{cc}\hfill & {⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2\equiv {⟨X^2⟩}_{\mathrm{w}}-{\left({⟨X⟩}_{\mathrm{w}}\right)}^2\hfill \\ \hfill & =n+\frac{1}{2}+\frac{\tan \theta e^{-\mathrm{i}\phi }\left[\sqrt{n\left(n-1\right)}{\delta }_{m,n-2}+\sqrt{\left(n+1\right)\left(n+2\right)}{\delta }_{m,n+2}\right]-{\tan }^2\theta e^{-\mathrm{i}2\phi }\left[n{\delta }_{m,n-1}^2+\left(n+1\right){\delta }_{m,n+1}^2\right]}{2}.\hfill \end{array}(17)$

Similarly, we have

$\begin{array}{cc}\hfill {⟨P⟩}_{\mathrm{w}}& =\frac{\left.⟨{\psi }_{\text{f}}\right|P\left|{\psi }_{\text{i}}\right.⟩}{⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩}\hfill \\ \hfill & =\frac{\left[\cos \theta \left.⟨n\right|+\sin \theta e^{-\mathrm{i}\phi }\left.⟨m\right|\right]\left(a-a^{†}\right)\left|n\right.⟩}{\mathrm{i}\sqrt{2}\cos \theta }\hfill \\ \hfill & =\frac{\mathrm{i}\tan \theta e^{-\mathrm{i}\phi }\left(\sqrt{n+1}{\delta }_{m,n+1}-\sqrt{n}{\delta }_{m,n-1}\right)}{\sqrt{2}},\hfill \end{array}$

which indicates that

${\left({⟨P⟩}_{\mathrm{w}}\right)}^2=-\frac{{\tan }^2\theta e^{-\mathrm{i}2\phi }\left[\left(n+1\right){\delta }_{m,n+1}^2+n{\delta }_{m,n-1}^2\right]}{2},(18)$

and

$\begin{array}{cc}\hfill {⟨P^2⟩}_{\mathrm{w}}& =\frac{\left.⟨{\psi }_{\text{f}}\right|\left[a{a}^{†}+a^{†}a-a^2-{\left(a^{†}\right)}^2\right]\left|{\psi }_{\text{i}}\right.⟩}{2⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩}\hfill \\ \hfill & =\frac{\left[\cos \theta \left.⟨n\right|+\sin \theta e^{-\mathrm{i}\phi }\left.⟨m\right|\right]\left[a{a}^{†}+a^{†}a-a^2-{\left(a^{†}\right)}^2\right]\left|n\right.⟩}{2\cos \theta }\hfill \\ \hfill & =\frac{\left[\cos \theta \left.⟨n\right|+\sin \theta e^{-\mathrm{i}\phi }\left.⟨m\right|\right]\left[\left(2n+1\right)\left|n\right.⟩-\sqrt{n\left(n-1\right)}\left|n-2\right.⟩-\sqrt{\left(n+1\right)\left(n+2\right)}\left|n+2\right.⟩\right]}{2\cos \theta }\hfill \\ \hfill & =n+\frac{1}{2}-\frac{\tan \theta e^{-\mathrm{i}\phi }\left[\sqrt{n\left(n-1\right)}{\delta }_{m,n-2}+\sqrt{\left(n+1\right)\left(n+2\right)}{\delta }_{m,n+2}\right]}{2}.\hfill \end{array}(19)$

Hence,

$\begin{array}{cc}\hfill & {⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\equiv {⟨P^2⟩}_{\mathrm{w}}-{\left({⟨P⟩}_{\mathrm{w}}\right)}^2\hfill \\ \hfill & =n+\frac{1}{2}-\frac{\tan \theta e^{-\mathrm{i}\phi }\left[\sqrt{n\left(n-1\right)}{\delta }_{m,n-2}+\sqrt{\left(n+1\right)\left(n+2\right)}{\delta }_{m,n+2}\right]-{\tan }^2\theta e^{-\mathrm{i}2\phi }\left[\left(n+1\right){\delta }_{m,n+1}^2+n{\delta }_{m,n-1}^2\right]}{2}.\hfill \end{array}(20)$

which means that

$\begin{array}{cc}\hfill & {⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\hfill \\ \hfill & ={\left(n+\frac{1}{2}\right)}^2-\frac{{\left\{\tan \theta e^{-\mathrm{i}\phi }\left[\sqrt{n\left(n-1\right)}{\delta }_{m,n-2}+\sqrt{\left(n+1\right)\left(n+2\right)}{\delta }_{m,n+2}\right]-{\tan }^2\theta e^{-\mathrm{i}2\phi }\left[\left(n+1\right){\delta }_{m,n+1}^2+n{\delta }_{m,n-1}^2\right]\right\}}^2}{4}\hfill \\ \hfill & ={\left(n+\frac{1}{2}\right)}^2-\frac{{\tan }^2\theta e^{-\mathrm{i}2\phi }}{4}\left[n\left(n-1\right){\delta }_{m,n-2}^2+\left(n+1\right)\left(n+2\right){\delta }_{m,n+2}^2\right]-\frac{{\tan }^4\theta e^{-\mathrm{i}4\phi }}{4}\left[{\left(n+1\right)}^2{\delta }_{m,n+1}^4+n^2{\delta }_{m,n-1}^4\right]\hfill \\ \hfill & =\frac{1}{4}\left\{{\left(2n+1\right)}^2-{\tan }^2\theta e^{-\mathrm{i}2\phi }\left[n\left(n-1\right){\delta }_{m,n-2}^2+\left(n+1\right)\left(n+2\right){\delta }_{m,n+2}^2\right]-{\tan }^4\theta e^{-\mathrm{i}4\phi }\left[{\left(n+1\right)}^2{\delta }_{m,n+1}^4+n^2{\delta }_{m,n-1}^4\right]\right\}.\hfill \end{array}(21)$

After that, we can calculate the absolute value of Eq. 21, namely

$\begin{array}{cc}\hfill & \left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\hfill \\ \hfill & =\frac{1}{4}\left|{\left(2n+1\right)}^2-{\tan }^2\theta e^{-\mathrm{i}2\phi }\left[n\left(n-1\right){\delta }_{m,n-2}^2+\left(n+1\right)\left(n+2\right){\delta }_{m,n+2}^2\right]-{\tan }^4\theta e^{-\mathrm{i}4\phi }\left[{\left(n+1\right)}^2{\delta }_{m,n+1}^4+n^2{\delta }_{m,n-1}^4\right]\right|\hfill \\ \hfill & \ge \frac{1}{4}\left|{\left(2n+1\right)}^2-{\tan }^2\theta \left[n\left(n-1\right){\delta }_{m,n-2}^2+\left(n+1\right)\left(n+2\right){\delta }_{m,n+2}^2\right]-{\tan }^4\theta \left[{\left(n+1\right)}^2{\delta }_{m,n+1}^4+n^2{\delta }_{m,n-1}^4\right]\right|.\hfill \end{array}(22)$

Analysis—Analogously, we will analyze the value of m in the following way:

1) If m ≠ n − 2, m ≠ n − 1, m ≠ n + 1 and m ≠ n + 2, $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|=(1/4){(2n+1)}^2>1/4$, because n > 0, thus it coincides with the Heisenberg uncertainty relation.

2) If m = n−2,

$\frac{1}{4}\left|{\left(2n+1\right)}^2-n\left(n-1\right){\tan }^2\theta \right|\le \left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\le \left|{\left(2n+1\right)}^2+n\left(n-1\right){\tan }^2\theta \right|.$

Once n = 1, then $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|=9/4>1/4$, nevertheless, m = n−2 = −1 is illegal. Hence we focus on the situation of n > 1. By $\left|{(2n+1)}^2-n(n-1){\tan }^2\theta \right|\ge 1$, we have ${\tan }^2\theta \ge \left[{(2n+1)}^2+1\right]/\left[n(n-1)\right]$, or ${\tan }^2\theta \le \left[{(2n+1)}^2-1\right]/\left[n(n-1)\right]$, and the uncertainty relation always holds. Otherwise, there exist unviolated situations if $\left[{(2n+1)}^2-1\right]/\left[n(n-1)\right]\le {\tan }^2\theta \le \left[{(2n+1)}^2+1\right]/\left[n(n-1)\right]$.

3) If m = n−1,

$\frac{1}{4}\left|{\left(2n+1\right)}^2-n^2{\tan }^4\theta \right|\le \left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\le \left|{\left(2n+1\right)}^2+n^2{\tan }^4\theta \right|,$

which implies that when ${\tan }^4\theta \ge \left[{(2n+1)}^2+1\right]/n^2$ or ${\tan }^4\theta \le \left[{(2n+1)}^2-1\right]/n^2$, $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\ge 1/4$ forever, while for $\left[{(2n+1)}^2-1\right]/n^2\le {\tan }^4\theta \le \left[{(2n+1)}^2+1\right]/n^2$, the limitation 1/4 may be broken.

4) If m = n + 1,

$\frac{1}{4}\left|{\left(2n+1\right)}^2-{\left(n+1\right)}^2{\tan }^4\theta \right|\le \left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\le \left|{\left(2n+1\right)}^2+{\left(n+1\right)}^2{\tan }^4\theta \right|.$

Therefore when ${\tan }^4\theta \ge \left[{(2n+1)}^2+1\right]/{(n+1)}^2$ or ${\tan }^4\theta \le \left[{(2n+1)}^2-1\right]/{(n+1)}^2$, $\left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\ge 1/4$ all the while, but for $\left[{(2n+1)}^2-1\right]/{(n+1)}^2\le {\tan }^4\theta \le \left[{(2n+1)}^2+1\right]/{(n+1)}^2$, counterexamples could be found.

5) If m = n + 2,

$\frac{1}{4}\left|{\left(2n+1\right)}^2-\left(n+1\right)\left(n+2\right){\tan }^2\theta \right|\le \left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\le \left|{\left(2n+1\right)}^2+\left(n+1\right)\left(n+2\right){\tan }^2\theta \right|.$

After that, via $\left|{(2n+1)}^2-(n+1)(n+2){\tan }^2\theta \right|\ge 1$, we attain ${\tan }^2\theta \ge \left[{(2n+1)}^2+1\right]/\left[(n+1)(n+2)\right]$, or ${\tan }^2\theta \le \left[{(2n+1)}^2-1\right]/\left[(n+1)(n+2)\right]$, and the uncertainty relation is not violated all through. However, in the case of $\left[{(2n+1)}^2-1\right]/\left[(n+1)(n+2)\right]\le {\tan }^2\theta \le \left[{(2n+1)}^2+1\right]/\left[(n+1)(n+2)\right]$, violations might appear.

2.3 Orthonormal Pre- and Post- Selected States

Following the above deduction, when θ → π/2, $⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩\to 0$, or the pre- and post-selected states tend to be mutual orthogonal phase differently. For instance, assume that n = 0 and m = 1, in so doing,

$\frac{1}{4}\left|1-{\tan }^4\theta \right|\le \left|{⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\right|\le \frac{1}{4}\left|1+{\tan }^4\theta \right|,(23)$

and we can see from Figure 1 that once $⟨{\psi }_{\text{f}}|{\psi }_{\text{i}}⟩\to 0$, the product of two deviations in the form of weak values is tending towards infinity, which agrees with Heisenberg’s statement.

2.4 Coherent States of the Simple Harmonic Oscillator

The coherent state of the simple harmonic oscillator is devised to simulate the classical oscillator [12], which can be represented as

$\left|z\right.⟩={\mathrm{e}}^{z{a}^{†}-z^{\ast }a}\left|0\right.⟩={\mathrm{e}}^{-{\left|z\right|}^2}\sum _{n=0}\frac{z^n}{\sqrt{n!}}\left|n\right.⟩,z\in \mathbb{C},(24)$

with the following traits:

$a\left|z\right.⟩=z\left|z\right.⟩,{\left(a\left|z\right.⟩\right)}^{†}=\left.⟨z\right|a^{†}=z^{\ast }\left.⟨z\right|.(25)$

After that, label the pre- and post-selected states as $\left|z_{\text{i}}\right.⟩$ and $\left|z_{\text{f}}\right.⟩$ respectively, then the weak value of X reads

${⟨X⟩}_{\mathrm{w}}=\frac{\left.⟨z_{\text{f}}\right|X\left|z_{\text{i}}\right.⟩}{⟨z_{\text{f}}|z_{\text{i}}⟩}=\frac{\left.⟨z_{\text{f}}\right|\left(a+a^{†}\right)\left|z_{\text{i}}\right.⟩}{\sqrt{2}⟨z_{\text{f}}|z_{\text{i}}⟩}=\frac{z_{\text{f}}^{\ast }+z_{\text{i}}}{\sqrt{2}},(26)$

which implies that

${⟨X⟩}_{\mathrm{w}}^2={\left[\frac{z_{\text{f}}^{\ast }+z_{\text{i}}}{\sqrt{2}}\right]}^2=\frac{{\left(z_{\text{f}}^{\ast }\right)}^2+z_{\text{i}}^2+2z_{\text{f}}^{\ast }{z}_{\text{i}}}{2}.(27)$

For that matter,

$\begin{array}{cc}\hfill {⟨X^2⟩}_{\mathrm{w}}& =\frac{\left.⟨z_{\text{f}}\right|X^2\left|z_{\text{i}}\right.⟩}{⟨z_{\text{f}}|z_{\text{i}}⟩}=\frac{\left.⟨z_{\text{f}}\right|\left[a^2+a{a}^{†}+a^{†}a+{\left(a^{†}\right)}^2\right]\left|z_{\text{i}}\right.⟩}{2⟨z_{\text{f}}|z_{\text{i}}⟩}\hfill \\ \hfill & =\frac{\left.⟨z_{\text{f}}\right|\left[a^2+2a^{†}a+1+{\left(a^{†}\right)}^2\right]\left|z_{\text{i}}\right.⟩}{2⟨z_{\text{f}}|z_{\text{i}}⟩}\hfill \\ \hfill & =\frac{z_{\text{i}}^2+2z_{\text{f}}^{\ast }{z}_{\text{i}}+{\left(z_{\text{f}}^{\ast }\right)}^2+1}{2}.\hfill \end{array}(28)$

Thus,

${⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2\equiv {⟨X^2⟩}_{\mathrm{w}}-{\left({⟨X⟩}_{\mathrm{w}}\right)}^2=\frac{1}{2}.(29)$

With the same argument, the weak value of P can be expressed as

${⟨P⟩}_{\mathrm{w}}=\frac{\left.⟨z_{\text{f}}\right|P\left|z_{\text{i}}\right.⟩}{⟨z_{\text{f}}|z_{\text{i}}⟩}=\frac{\mathrm{i}\left.⟨z_{\text{f}}\right|\left(a^{†}-a\right)\left|z_{\text{i}}\right.⟩}{\sqrt{2}⟨z_{\text{f}}|z_{\text{i}}⟩}=\frac{\mathrm{i}\left(z_{\text{f}}^{\ast }-z_{\text{i}}\right)}{\sqrt{2}},(30)$

then

${⟨P⟩}_{\mathrm{w}}^2={\left[\frac{\mathrm{i}\left(z_{\text{f}}^{\ast }-z_{\text{i}}\right)}{\sqrt{2}}\right]}^2=\frac{2z_{\text{f}}^{\ast }{z}_{\text{i}}-{\left(z_{\text{f}}^{\ast }\right)}^2-z_{\text{i}}^2}{2}.(31)$

Thus,

$\begin{array}{cc}\hfill {⟨P^2⟩}_{\mathrm{w}}& =\frac{\left.⟨z_{\text{f}}\right|P^2\left|z_{\text{i}}\right.⟩}{⟨z_{\text{f}}|z_{\text{i}}⟩}=\frac{\left.⟨z_{\text{f}}\right|\left[a{a}^{†}+a^{†}a-a^2-{\left(a^{†}\right)}^2\right]\left|z_{\text{i}}\right.⟩}{2⟨z_{\text{f}}|z_{\text{i}}⟩}\hfill \\ \hfill & =\frac{\left.⟨z_{\text{f}}\right|\left[2a^{†}a+1-a^2-{\left(a^{†}\right)}^2\right]\left|z_{\text{i}}\right.⟩}{2⟨z_{\text{f}}|z_{\text{i}}⟩}\hfill \\ \hfill & =\frac{2z_{\text{f}}^{\ast }{z}_{\text{i}}-z_{\text{i}}^2-{\left(z_{\text{f}}^{\ast }\right)}^2+1}{2}.\hfill \end{array}(32)$

which means that,

${⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2\equiv {⟨P^2⟩}_{\mathrm{w}}-{\left({⟨P⟩}_{\mathrm{w}}\right)}^2=\frac{1}{2},(33)$

namely

${⟨\mathrm{\Delta }X⟩}_{\mathrm{w}}^2{⟨\mathrm{\Delta }P⟩}_{\mathrm{w}}^2=\frac{1}{4}.(34)$

Obviously, the uncertainty relation for the coherent state of the simple harmonic oscillator in the sense of weak value reaches the lower bound of Heisenberg uncertainty relation (Eq. 13) all the while, which is in accord with the traditional case using expectation value.

3 Summary

We delve into the case of measuring position and momentum in a simple harmonic oscillator with pre-selected states as eigenstates and the post-selections as the superposition states. Remarkably, we find out that Heisenberg’s claim for two incompatible observables fails in the situation of weak values for typical selections listed previously. But the weak value canonical uncertainty relation holds for the simple harmonic oscillator in coherent states.

Our work may offer a beneficial supplement in the field of uncertainty relation with weak measurement, and beat the standard Heisenberg limit. Of course, we do not consider complete process of weak measurement, as none interaction Hamiltonian of quantum system with environment appear, hence the present work is not appropriate for experimental test, which we are struggling for.

In fact, although Heisenberg’s principle is sufficiently elegant and classical in current textbooks, it cannot undergo the test relating to weak measurement [13]. Nevertheless, two generalizations, the one is presented via M. Ozawa [14] and the other is dedicated by C. Branciard [15], about Heisenberg’s work, were successfully verified in the same experiment [13]. Then can we discover a more general and concise uncertainty formula to unify all current results? And why is the nature of quantum world uncertainty (see¹ as one of the 125 open questions in Science)? We may understand these questions more thoroughly by dint of geometry. Some papers have appeared, e.g., [16, 17]. We anticipate more progress on the relation between the uncertainty relations and the weak measurements in the near future.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

X-YF and J-LC contributed to conception and design of the study. X-YF organized the database. X-YF and J-LC performed the statistical analysis. X-YF wrote the first draft of the manuscript. W-MS, JZ, H-XM, and J-LC wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

J-LC was supported by the National Natural Science Foundations of China (Grant Nos 11875167 and 12075001). X-YF, W-MS, and JZ were supported by the Nankai Zhide Foundation. H-XM was supported by the National Natural Science Foundations of China (Grant No. 11901317).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://www.science.org/content/resource/125-questions-exploration-and-discovery

References

1. Heisenberg W Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z Phys (1927) 43:172–98.

CrossRef Full Text | Google Scholar

2. Robertson HP The Uncertainty Principle. Phys Rev (1929) 34:163–4. doi:10.1103/physrev.34.163

CrossRef Full Text | Google Scholar

3. Coles PJ, Berta M, Tomamichel M, Wehner S Entropic Uncertainty Relations and Their Applications. Rev Mod Phys (2017) 89:015002. doi:10.1103/revmodphys.89.015002

CrossRef Full Text | Google Scholar

4. Everett H “Relative State” Formulation of Quantum Mechanics. Rev Mod Phys (1957) 29:454–62. doi:10.1103/revmodphys.29.454

CrossRef Full Text | Google Scholar

5. Hirschman II A Note on Entropy. Am J Math (1957) 79:152–6. doi:10.2307/2372390

CrossRef Full Text | Google Scholar

6. Aharonov Y, Albert DZ, Vaidman L How the Result of a Measurement of a Component of the Spin of a Spin-1/2particle Can Turn Out to Be 100. Phys Rev Lett (1988) 60:1351–4. doi:10.1103/physrevlett.60.1351

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Song Q, Qiao C Uncertainty Equalities and Uncertainty Relation in Weak Measurement. J Univ Chin Acad Sci (2016) 33(1):37. doi:10.7523/j.issn.2095-6134.2016.01.006

CrossRef Full Text | Google Scholar

8. Pati AK, Wu J Uncertainty and Complementarity Relations in Weak Measurement. New York: Cornell University at Ithaca (2014). arXiv:quant-ph/1411.7218v1.

Google Scholar

9. Hall MJW, Pati AK, Wu J Products of Weak Values: Uncertainty Relations, Complementarity, and Incompatibility. Phys Rev A (2016) 93:052118. doi:10.1103/physreva.93.052118

CrossRef Full Text | Google Scholar

10. Shikano Y, Hosoya A Weak Values with Decoherence. J Phys A: Math Theor (2009) 43:025304. doi:10.1088/1751-8113/43/2/025304

CrossRef Full Text | Google Scholar

11. Šindelka1 M, Moiseyev N Quantum Uncertainties and Heisenberg-like Uncertainty Relations for a Weak Measurement Scheme Involving Two Arbitrary Noncommuting Observables. Phys Rev A (2018) 97:012122. doi:10.1103/physreva.97.012122

CrossRef Full Text | Google Scholar

12. Sakurai JJ, Napolitano J Modern Quantum Mechanics. 2nd ed. Cambridge, UK: Cambridge University Press (2017).

Google Scholar

13. Kaneda F, Baek SY, Ozawa M, Edamatsu K Experimental Test of Error-Disturbance Uncertainty Relations by Weak Measurement. Phys Rev Lett (2014) 112:020402. doi:10.1103/physrevlett.112.020402

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ozawa M Universally Valid Reformulation of the Heisenberg Uncertainty Principle on Noise and Disturbance in Measurement. Phys Rev A (2003) 67:042105. doi:10.1103/physreva.67.042105

CrossRef Full Text | Google Scholar

15. Branciard C Error-tradeoff and Error-Disturbance Relations for Incompatible Quantum Measurements. Proc Natl Acad Sci (2013) 110:6742–7. doi:10.1073/pnas.1219331110

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Lobo AC, Ribeiro Cd. A The Geometry of Von-Neumann’s Pre-measurement and Weak Values New York: Cornell University at Ithaca (2011). arXiv:quant-ph/1111.4205v2.

Google Scholar

17. Kechrimparis S, Weigert S Geometry of Uncertainty Relations for Linear Combinations of Position and Momentum. J Phys A: Math Theor (2018) 51:025303. doi:10.1088/1751-8121/aa9cfc

CrossRef Full Text | Google Scholar