
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 20 January 2022
Sec. Statistical and Computational Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.795693
We propose a method of constructing analytical, closed-form expressions for electrostatic/Newtonian potentials of non-uniform polyhedral bodies, in which the density distributions are polynomials of coordinates. Possible applications of the proposed method are spread from astronomy to nanotechnology. The method is based on the use of the generating function for the potential. Explicit expressions for the potential are derived in the case of quadratic or cubic coordinate dependence of the density within a polyhedral body.
Many problems in various physical applications are reduced to expressions of the form
One of them is the determination of the Coulomb (electrostatic) potential from a given distribution of charge. In this respect, ρ(r) is the charge density, and the integration is carried out over the volume V of the charged body. This expression provides also the Newtonian (gravitational) potential of a massive body with a given density distribution ρ(r). Applications of its analytical solutions range from astronomy [1–3] and geophysics [4–7] to the physics of micro- and nanostructures [8–10], as illustrated in Figure 1. Gravitational potentials of asteroids or gravity anomalies have straightforwardly the form of Eq. 1. The magnetic field B(R) of a distributed magnetic moment M(r) (such as a magnetic anomaly or a micromagnet) is proportional to
Where α and β are tensor indexes. Similarly, the electric field E(R) of a distributed electric dipole moment P(r) (for example, in a metallic nanoparticle under illumination) is proportional to
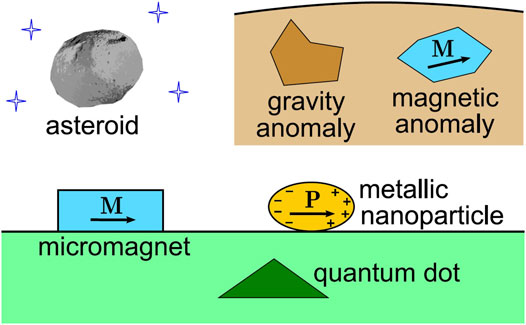
FIGURE 1. Possible applications of analytical solutions of Eq. 1: from astronomy (gravitational fields of asteroids) and Earth sciences (gravity and magnetic anomalies) to the physics of micro-and nanostructures (magnetic fields of nanomagnets, plasmonic resonance of metallic nanoparticles, elastic fields of inclusions such as epitaxial quantum dots).
The elastic displacement vector u(R) due to an inclusion that possesses an eigenstrain ɛ*(r), such as a lattice misfit in an epitaxial quantum dot, also has a similar form,
in the case of an elastically-isotropic medium. Therefore, all the fields considered above can be expressed via potentials having the form of Eq. 1.
There are two generic shapes of the three-dimensional body that enable analytical solutions for potentials φ(R) in closed forms: an ellipsoid [11, 12] and a polyhedron [1, 12]. Analytical solutions are possible not only for a homogeneously charged ellipsoid or a polyhedron, but also for the case of a polynomial dependence of the charge density ρ(x, y, z) on coordinates [2, 8]. We focus here on potentials of polyhedra.
With regard to the charged polyhedra, until recently the analytical solutions in closed forms were found for constant [1, 13], linearly [3, 5, 14–16], quadratically [17–20], or cubically [21, 22] coordinate-dependent charge density. Similar solutions for the elastic strain were obtained in works [8, 23–26]. In a special case of a prismatic body, analytic formulas in closed forms are available for polynomials up to fourth degree [27]. For an arbitrary polynomial charge distribution within a polyhedron, a method of analytical determination of the potential was outlined in Ref. [25] and represented in an algorithmic (recursive) form in Refs. [8, 28]. Similar results in two dimensions can be found in Ref. [29].
In this work, we present an ultimate expression that unifies all known analytical solutions for Newtonian (or Coulomb) potentials of polyhedron-shaped bodies. For this reason, we introduce a generating function
that depends on the geometry of the polyhedron, and on the additional parameter k. One can represent potential φ(R) via the generating function as follows:
where differential operator ∂/∂R acts only “to the right,” on function ρ(R). The derivation of Eq. 6 is given in Supplementary Section S1.
We provide a series expansion of generating function G(R, k) in powers of k. Each term of this expansion is a closed-form expression containing only elementary functions. Writing the series expansion as
where G(0)(R), etc. are expansion coefficients, one obtains from Eq. 6 that
If ρ(R) is a polynomial, the r.h.s. of Eq. 6 contains only a finite number of terms. Therefore, this equation gives an analytical, closed-form expression for the Newtonian potential φ(R) for any polynomial density distribution ρ(R) within a polyhedral body, provided that coefficients G(0)(R), etc. are expressed in a closed form.
Eq. 8, along with the results of Section 2, provides a method of constructing analytical, closed-form expressions for Newtonian (or electrostatic) potentials of non-uniform polyhedral bodies, in which the density distributions are polynomials of coordinates. The method is universal in the sense that any density distribution can be approximated by a polynomial, as well as any shape of a body can be approximated by a polyhedron. It is worth noting that primitive shapes in the finite-difference method are polyhedra, therefore the results of the present paper can be used in connection with finite-difference schemes.
The results of the present paper provide an insight into analytic properties of solutions of linear inhomogeneous partial differential equations (PDEs) possessing a geometry of a polyhedron. Potential φ(R) obeys Poisson’s equation
where χ(R) is a characteristic function of the polyhedron: χ(R) = 1 for R within the polyhedron, otherwise χ(R) = 0. Since function χ(R) is not analytic, the solution φ(R) also must be a non-analytic function of coordinates. However, as we will see later in Eq. 30, the solution can be represented as a sum of analytic functions
The paper is organized as follows. In Section 2, a formula for the generating function in the form of power series is presented. This is the central result of this paper. Then, in Section 3, this formula is tested numerically and applied to calculating the potential. We show how to construct an exact expression in a closed form for potential φ(R) in the case of a polynomial dependence of the charge density on coordinates. Concluding remarks are gathered in Section 4.
As shown in Supplementary Section S2, generating function G(R, k) can be represented as a sum of contributions of all faces, edges and vertices of the polyhedron. In this Section, we report on such a representation, and then, in Section 3, we demonstrate how to obtain exact solutions in closed forms on the basis of the expression for the generating function.
First, we introduce some notations for geometrical entities associated with the polyhedron. Let us use symbols f, e and v for enumerating of polyhedron faces, edges and vertices, correspondingly. For each face f, we introduce a unit normal vector nf to the face directed outwards from the polyhedron, see Figure 2. For each pair (f, e) of a face and an edge adjacent to it, we introduce a unit vector bfe that is parallel to face f, perpendicular to edge e, and directed outwards from face f, as shown in Figure 2. For each pair (e, v) of a face and a vertex lying on it, we define unit vector lev directed from the opposite vertex of edge e towards vertex v (Figure 2). rf and re are radius-vectors of arbitrarily chosen points on face f and on edge e, correspondingly. rv is the radius-vector of vertex v. For a given face f, we introduce function
where dS is the surface element of face f, and r is the radius-vector of this element. One can easily recognize that Ωf(R) is the signed solid angle subtended by face f at point R: its sign is positive (negative) if the outer (inner) side of the face is seen from point R. Similarly, for a given edge e, we define function
where dl is a line element, and r is its radius-vector. One can interpret Le(R) as a potential at point R of edge e considered as a uniform massive rod with the unit linear mass density. In these notations, generating function G(R, k) acquires the following form derived in Supplementary Section S2:
where summations are over polyhedron faces f; over pairs (f, e) of adjacent face f and edge e; and over triples (f, e, v) of adjacent face f, edge e and vertex v.
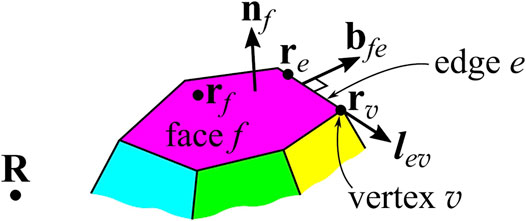
FIGURE 2. Unit vectors and radius-vectors associated with faces, edges, and vertices of the polyhedron. Vector nf is the outward normal vector to face f. Vector bfe lies in the plane of face f and is directed out of this face perpendicular to edge e. Vector lev is directed along edge e toward vertex v from the opposite vertex. rf and re are radius-vectors of arbitrarily chosen points on face f and on edge e, correspondingly. rv is the radius-vector of vertex v, and R is the radius-vector of the observation point.
Expressions for functions
where z = r ⋅n, kz = k ⋅n,
where y = r ⋅b, z = r ⋅n,
where x = r ⋅l, y = r ⋅b, z = r ⋅n,
These formulas provide power series expansions of
In contrast, generating function G(R, k) itself is non-analytical at the surface of the polyhedron. This behavior is related to discontinuity of the Laplacian of potential φ(R) defined by Eq. 1: Δφ(R) = − 4πρ(R) within the polyhedron, and Δφ(R) = 0 outside. It is evident from Eq. 12 that such a non-analytic behavior of the generating function is due to presence of functions Ωf(R), Le(R) and |rv − R| in the r.h.s. Indeed, Ωf has a discontinuity on face f, Le diverges logarithmically on edge e, and |rv − R| has a cusp-like behavior at vertex v. Hence, representation (12) of generating function G(R, k) allows us to detach its calculational complexity from its non-analytic behavior. All non-analiticity of G(R, k) is “grasped” by functions Ωf, Le and |rv − R| that have simple mathematical expressions in closed forms, see Eqs 16, 17. And all calculational complexity of G(R, k) is contained in fully analytical functions
Functions Ωf(R) and Le(R) can be expressed in closed forms via elementary functions. A convenient representation for Le(R) is [8, 13]
where re1 and re2 are radius-vectors of two ends of edge e. For a triangular face, solid angle Ωf(R) can be represented as follows [30, 31]:
where a = rf1 − R, b = rf2 − R, c = rf3 − R, and rf1, rf2, rf3 are radius-vectors of vertices of face f, counted clockwise as seeing from the outer side of the face. Solid angle Ωf(R) must fall into the range ( − 2π, 2π) and have the same sign as [a ×b] ⋅c. The appropriate solution of this equation is
where P and Q are the numerator and the denominator of the r.h.s. of Eq. 17, and atan2 is a function from the math library of C language [31]. If the face is not triangular, one can either break it into triangles, or use other formulas [13, 31] for solid angle Ωf(R).
The representation of generating function G(R, k) in the form of Eqs 12–15 constitutes the main result of the present paper. In Section 3, we will demonstrate that the infinite-series representations for functions
The expression for generating function G(R, k) presented in Section 2 looks rather complicated. It is necessary therefore to verify it. As a natural numerical test, we have used the generating function to derive potential φ(R) for a certain polyhedron and a certain density distribution ρ(R), and have checked that this potential obeys Poisson’s equation.
For the testing purpose, the simplest choice of the density distribution function is
Substituting it into Eq. 1 and comparing with Eq. 5, one can find that
As an example of a polyhedral body, we choose a pyramid with a square base (Figure 3A), having height h = 1 and lateral size (length of a base edge) l = 2. Values of components of vector k are chosen as kx = 0.5, ky = 0.4 and kz = 0.3. When calculating G(R, k), we have kept terms up to
with δ = 10–4. One can see in Figure 3C that Δφ vanishes outside the pyramid, and depend on coordinate exponentially within it. We have checked that the deviation of the numerical value of Δφ from its exact value
does not exceed 10–4 for 1000 randomly chosen points within the cube −2 < x < 2, −2 < y < 2, −2 < z < 2. This deviation is due to errors of the round-off and the difference scheme. The accuracy is sufficient to confirm the correctness of formulas presented in Section 2. The exponential density distribution, Eq. 19, appears in modeling of gravity anomalies [32–34], for example.
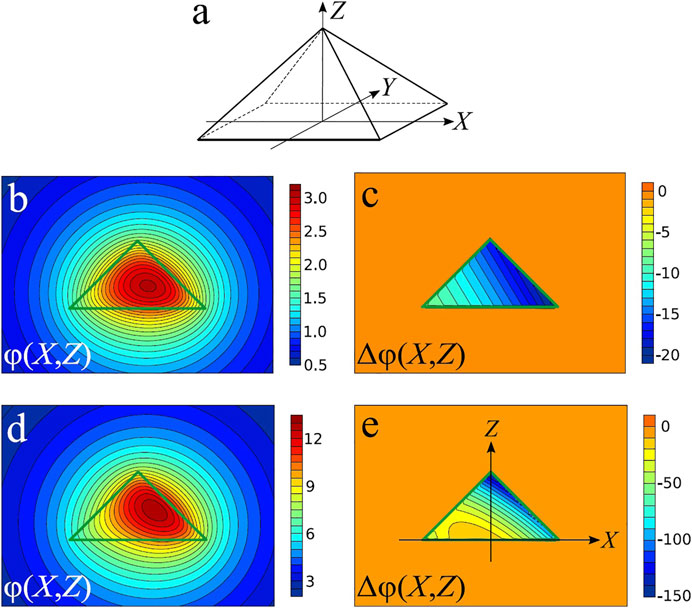
FIGURE 3. Examples of potentials of an inhomogeneously charged polyhedron. (A) An example of a polyhedron: a pyramid with height h = 1 and lateral size (length of a base edge) l = 2. (B,C) Potential φ(X, Z) and its Laplacian Δφ(X, Z) in the case of an exponential density distribution ρ(R) = exp(k ⋅R) with kx = 0.5, ky = 0.4 and kz = 0.3. (D,E) Potential φ(X, Z) and its Laplacian Δφ(X, Z) in the case of a quadratic density distribution ρ(X, Y, Z) = 1 + 2X + 3Y + 4Z + 5X2 + 6Y2 + 7Z2 + 8XY + 9XZ + 10YZ. Plots b, c, d, e are presented in the section by the XZ-plane that passes through the pyramid apex (Y = 0). Green triangles depict the pyramid boundary in the same section.
Expression (20) holds also for complex values of k. Hence, the potential of a polyhedral body with density distribution
is equal to
Similarly, a polyhedral body with density distribution
produces the potential
Now we consider the case of a polynomial density distribution ρ(R) in the body. For definiteness, let ρ(R) be a quadratic function. In order to obtain an expression for potential φ in a closed form, we keep only the terms proportional to k0, k1 and k2 in Eqs 12–15 for functions
We do not need here the higher terms (
In order to get the potential, as explained in Section 1, each entry of vector k in generating function G(R, k) is replaced with differential operator ∂/∂R which acts on density distribution ρ(R). The components kx, ky and kz are thus replaced with lα∂/∂Rα, bα∂/∂Rα and nα∂/∂Rα, correspondingly. In Eq. 27, factor
As a result, we obtain an expression for potential φ(R) in the form of a sum over polyhedron faces, edges and vertices:
where xev = lev ⋅ (rv − R), yfe = bfe ⋅ (re − R), zf = nf ⋅ (rf − R), and functions
Equations 30–33 provide an exact expression for potential φ(R) in a closed form. This expression is valid both within the polyhedral body and outside it, if the density distribution ρ(R) in the body is a quadratic function of coordinates. In the simplified cases of constant or linear function ρ(R), this result is reduced to previously published formulas [1, 8].
Just as for the exponential density distribution, we have performed a numerical test of potential φ(R) obtained by Eqs 30–33. The polyhedron geometry is chosen according to Figure 3A with h = 1 and l = 2. We choose a quadratic polynomial ρ, all coefficients of which are non-zero: ρ(X, Y, Z) = 1 + 2X + 3Y + 4Z + 5X2 + 6Y2 + 7Z2 + 8XY + 9XZ + 10YZ. Potential φ is shown in Figure 3D, and its Laplacian Δφ calculated by difference scheme (21) with δ = 10−4—in Figure 3E. We have checked that, with accuracy ±10–4, Δφ = 0 outside the pyramid, and Δφ = − 4πρ within it.
The same recipe can be applied to any polynomial density distribution. For example, if density distribution ρ(X, Y, Z) contains cubic terms (X3, X2Y and so on), then it is necessary to take into account also terms proportional to k3 in series expansions (12)–(15) for functions
Equations 30–33 with additions 34–36 to functions
This method, based on the results of Section 2 and on Eq. 6, allows us to construct explicit expressions for potentials of arbitrary polyhedra, in which the density distribution functions are polynomials of any degree. One can see that complexity of these expressions grows rapidly (though not exponentially) with the degree of polynomial ρ(R). Our method overcomes this difficulty by “packing” all the complexity into expressions (13)–(15) for functions
We propose a method of constructing analytical, closed-form expressions for Newtonian potentials of massive polyhedral bodies, in which the density distributions ρ(X, Y, Z) are polynomials of coordinates X, Y and Z. The method is based on the power-series representation for generating function G(R, k) presented in Section 2. Explicit expressions for the potential in the case of quadratic or cubic polynomial ρ(X, Y, Z) are derived in Section 3. For a quadratic coordinate dependence of density ρ, the potential can be found by Eqs 30–33. For a cubic coordinate dependence of the density, the same equations with additions Eqs 34–36 to the right-hand sides of Eqs 31–33 are valid. It is possible to extend this scheme to polynomials of any degree, and use it for any polyhedral shape of the body. Potential applications of the proposed method are spread from astronomy to nanotechnology.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
AN: conceptualization, analytical results, numerical calculations and writing the manuscript.
This work is funded by the Ministry of Science and Higher Education of the Russian Federation, grant 075-15-2020-797 (13.1902.21.0024).
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.795693/full#supplementary-material
1. Werner RA. The Gravitational Potential of a Homogeneous Polyhedron or Don't Cut Corners. Celestial Mech Dyn Astr (1994) 59:253–78. doi:10.1007/BF00692875
2. Chandrasekhar S. Ellipsoidal Figures of Equilibrium. New York: Dover Books on Mathematics (1987).
3. Conway JT. Analytical Solution from Vector Potentials for the Gravitational Field of a General Polyhedron. Celest Mech Dyn Astr (2015) 121:17–38. doi:10.1007/s10569-014-9588-x
4. Nagy D. The Gravitational Attraction of a Right Rectangular Prism. Geophysics (1966) 31:362–71. doi:10.1190/1.1439779
5. Holstein H. Gravimagnetic Anomaly Formulas for Polyhedra of Spatially Linear Media. Geophysics (2003) 68:157–67. doi:10.1190/1.1543203
6. Abtahi SM, Pedersen LB, Kamm J, Kalscheuer T. A New Reference Model for 3D Inversion of Airborne Magnetic Data in Hilly Terrain - A Case Study from Northern Sweden. Geophysics (2018) 83:B1–B12. doi:10.1190/geo2016-0331.1
7. Nibisha VA, Ramamma B, Sastry SR, Chakravarthi V. Forward Modelling: Magnetic Anomalies of Arbitrarily Magnetized 2D Fault Sources with Analytically Defined Fault Planes. J Earth Syst Sci (2021) 130:130. doi:10.1007/s12040-021-01634-x
8. Nenashev AV, Dvurechenskii AV. Elastic Strain Field Due to an Inclusion of a Polyhedral Shape with a Non-uniform Lattice Misfit. J Appl Phys (2017) 121:125102. doi:10.1063/1.4978750
9. Eshelby JD. The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proc R Soc Lond A (1957) 241:376–96. doi:10.1098/rspa.1957.0133
10. Mura T. Micromechanics of Defects in Solids. Mechanics of Elastic and Inelastic Solids. Dordrecht, Netherlands: Springer (1987).
11. Landau LD, Lifshitz EM. The Classical Theory of Fields. Course of Theoretical Physics. Amsterdam: Elsevier Science (2013).
12. MacMillan W. The Theory of the Potential. New York: Dover books on physics and mathematical physics Dover Publications (1958).
13. Werner R, Scheeres D. Exterior Gravitation of a Polyhedron Derived and Compared with Harmonic and Mascon Gravitation Representations of Asteroid 4769 Castalia. Celestial Mech Dyn Astr (1997) 65:313–44. doi:10.1007/BF00053511
14. Pohánka V. Optimum Expression for Computation of the Gravity Field of a Polyhedral Body with Linearly Increasing Density. Geophys Prospecting (1998) 46:391–404. doi:10.1046/j.1365-2478.1998.960335.x
15. Hamayun , Prutkin I, Tenzer R. The Optimum Expression for the Gravitational Potential of Polyhedral Bodies Having a Linearly Varying Density Distribution. J Geod (2009) 83:1163–70. doi:10.1007/s00190-009-0334-1 Available at: https://link.springer.com/article/10.1007%2Fs00190-009-0334-1
16. D’Urso MG. Gravity Effects of Polyhedral Bodies with Linearly Varying Density. Celest Mech Dyn Astr (2014) 120:349–72. doi:10.1007/s10569-014-9578-z
17. Rao DB, Prakash MJ, Babu NR. 3D and 21/2 D Modelling of Gravity Anomalies with Variable Density Contrast. Geophys Prospect (1990) 38:411–22. doi:10.1111/j.1365-2478.1990.tb01854.x
18. Gallardo‐Delgado LA, Pérez‐Flores MA, Gómez‐Treviño E. A Versatile Algorithm for Joint 3D Inversion of Gravity and Magnetic Data. Geophysics (2003) 68:949–59. doi:10.1190/1.1581067
19. Gokula AP, Sastry RG. Gravitational Attraction of a Vertical Pyramid Model of Flat Top-And-Bottom with Depth-wise Parabolic Density Variation. J Earth Syst Sci (2015) 124:1735–44. doi:10.1007/s12040-015-0633-2
20. Ren Z, Chen C, Pan K, Kalscheuer T, Maurer H, Tang J. Gravity Anomalies of Arbitrary 3D Polyhedral Bodies with Horizontal and Vertical Mass Contrasts. Surv Geophys (2017) 38:479–502. doi:10.1007/s10712-016-9395-x
21. D’Urso MG, Trotta S. Gravity Anomaly of Polyhedral Bodies Having a Polynomial Density Contrast. Surv Geophys (2017) 38:781–832. doi:10.1007/s10712-017-9411-9
22. Ren Z, Zhong Y, Chen C, Tang J, Kalscheuer T, Maurer H, et al. Gravity Gradient Tensor of Arbitrary 3D Polyhedral Bodies with up to Third-Order Polynomial Horizontal and Vertical Mass Contrasts. Surv Geophys (2018) 39:901–35. doi:10.1007/s10712-018-9467-1
23. Pearson GS, Faux DA. Analytical Solutions for Strain in Pyramidal Quantum Dots. J Appl Phys (2000) 88:730–6. doi:10.1063/1.373729
24. Glas F. Elastic Relaxation of Truncated Pyramidal Quantum Dots and Quantum Wires in a Half Space: An Analytical Calculation. J Appl Phys (2001) 90:3232–41. doi:10.1063/1.1394158
25. Kuvshinov BN. Elastic and Piezoelectric fields Due to Polyhedral Inclusions. Int J Sol Structures (2008) 45:1352–84. doi:10.1016/j.ijsolstr.2007.09.024
26. Nenashev AV, Dvurechenskii AV. Strain Distribution in Quantum Dot of Arbitrary Polyhedral Shape: Analytical Solution. J Appl Phys (2010) 107:064322. doi:10.1063/1.3357302
27. Chen C, Ren Z, Pan K, Tang J, Kalscheuer T, Maurer H, et al. Exact Solutions of the Vertical Gravitational Anomaly for a Polyhedral Prism with Vertical Polynomial Density Contrast of Arbitrary Orders. Geophys J Int (2018) 214:2115–32. doi:10.1093/gji/ggy250
28. Ren Z, Chen C, Zhong Y, Chen H, Kalscheuer T, Maurer H, et al. Recursive Analytical Formulae of Gravitational fields and Gradient Tensors for Polyhedral Bodies with Polynomial Density Contrasts of Arbitrary Non-negative Integer Orders. Surv Geophys (2020) 41:695–722. doi:10.1007/s10712-020-09587-4
29. D’Urso MG. The Gravity Anomaly of a 2d Polygonal Body Having Density Contrast Given by Polynomial Functions. Surv Geophys (2015) 36:391–425. doi:10.1007/s10712-015-9317-3
30. Van Oosterom A, Strackee J. The Solid Angle of a Plane triangle. IEEE Trans Biomed Eng (1983) BME-30:125–6. doi:10.1109/TBME.1983.325207
31. Nenashev AV, Dvurechenskii AV. Strain Distribution in Quantum Dot of Arbitrary Polyhedral Shape: Analytical Solution in Closed Form (2007). Available at: https://arxiv.org/pdf/0707.2183.pdf
32. Cordell L. Gravity Analysis Using an Exponential Density‐depth Function-san Jacinto Graben, California. Geophysics (1973) 38:684–90. doi:10.1190/1.1440367
33. Chakravarthi V, Pramod Kumar M, Ramamma B, Rajeswara Sastry S. Automatic Gravity Modeling of Sedimentary Basins by Means of Polygonal Source Geometry and Exponential Density Contrast Variation: Two Space Domain Based Algorithms. J Appl Geophys (2016) 124:54–61. doi:10.1016/j.jappgeo.2015.11.007
Keywords: potential theory, generating function, Poisson equation, polyhedron, exact solution, gravity anomaly, eigenstrain
Citation: Nenashev AV (2022) Generating Function Method for Calculating the Potentials of Inhomogeneous Polyhedra. Front. Phys. 9:795693. doi: 10.3389/fphy.2021.795693
Received: 15 October 2021; Accepted: 24 December 2021;
Published: 20 January 2022.
Edited by:
Oleg N. Kirillov, Northumbria University, United KingdomReviewed by:
Alexander V. Zolotaryuk, Bogolyubov Institute for Theoretical Physics (NAN Ukraine), UkraineCopyright © 2022 Nenashev. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alexey Vladimirovich Nenashev, bmVuYXNoZXZAaXNwLm5zYy5ydQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.