Can Lightning Network’s Autopilot Function Use BA Model as the Underlying Network?

By extending micropayment channel technology and building a transaction network, the Lightning Network solves inefficient bitcoin transactions. Currently, more than 1,000 Bitcoins have been deposited in the Lightning Network. In designing the Lightning Network routing protocol, simulating its transactions, and evaluating the network robustness, researchers have almost always used the Barabasi Albert Model as a substrate network. In particular, as the network grows in size, it becomes particularly important to automatically establish links for the network of joined nodes—the autopilot function—and it becomes a crucial question whether the Barabasi Albert Model as the underlying network for the autopilot function conforms to the real topology of the Lightning Network. In this paper, we construct the temporal network of Lightning Network and compare the topological properties of Lightning Network with those of Barabasi Albert Model of the same scale in detail. Lightning Network has a large gap with Barabasi Albert Model in terms of assortativity and network diameter. We found that nodes tend to connect to nodes with greater Closeness Centrality in terms of node preference connectivity. Our findings suggest that using the Barabasi Albert Model as the underlying network for the autopilot function is not a reasonable choice.

1 Introduction

Bitcoin [1], one of the representatives of blockchain technology, has been developing rapidly since its inception, but since its release Bitcoin has been suffering from problems such as latency, throughput, capacity [2–6]. Using payment channels [7] to enable off-chain payments has become a promising solution to the bitcoin scalability problem. For the bitcoin network, if there are multiple transactions between two accounts, there is no need for both parties to synchronize their respective fund states to the bitcoin network at the end of each transaction, The two parties can build their own transaction channel and deposit a certain amount of money, and then synchronize the status of both parties’ funds to the bitcoin network when the final transaction is completed. This ensures the final state of the funds, reduces the waiting time for both parties on the inefficient bitcoin network and increases the frequency of transactions, and also solves the storage and even privacy problems.

The Lightning Network [8] is developed from micropayment channel technology, extending the one-way payment channel into a two-way payment channel. It solves the historical contract voiding problem in the dual-channel through RSMC.¹ The problem of cross-node transactions is solved by HTLC,² which finally forms a trusted distributed payment network under the chain. As shown in Figure 1, node A and node B need to make a transaction, and nBTC can be jointly funded between A and B in a 2-2 signature address, where A contributes n1 BTC and B contributes n2 BTC, n1+n2 = n. When the transaction ends, A and B use their own keys to retrieve the funds belonging to them. Similarly, B and C can jointly fund the channel between B and C. When A and C need to transact, since there is no directly connected channel between A and C, A and C can transact through B, and B can earn a certain fee. Since its launch in January 2018, the Lightning Network has grown by leaps and bounds so far to a network of over 10,000 nodes, nearly 40,000 edges, and over 1,000 bitcoins stored in channels.

FIGURE 1

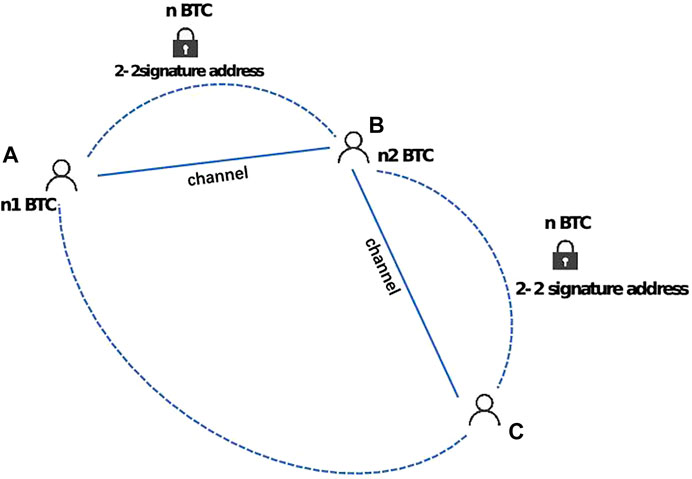
FIGURE 1. Illustration of payment channel network. A and B can jointly contribute n bitcoins to establish a channel, and when they need to trade, they can do so through the channel. And when there is no channel between A and C, the transaction can be done through B.

The rapid development of the Lightning Network has generated a great deal of interest in their topological properties. Although the transaction data in the Lightning Network is not publicly available, the channels between nodes in the network are viewable and recordable in real-time.³ Therefore, collecting data from the date of release of the Lightning Network and building the network allows us to analyze how the Lightning Network has evolved.

The efficiency of routing [9], the simulation of transactions [10–18], and the robustness of the Lightning Network [19–21] are utterly dependent on the underlying topology of the network. After the release of the Lightning Network white paper, most of the studies simulated the Lightning Network using the Barabasi Albert Model [22] as the underlying network, although there were studies that used star topology as the underlying structure for simulation [10–14]. Since the launch of the Lightning Network, selecting appropriate connections for the newly added nodes sparked a heated discussion in the community due to the increase of its network size.⁴ The community discussion focused on the appropriateness of using the Barabasi Albert Model as a guiding model when setting the nodes to autopilot mode.

In general, whether the topological properties of the Lightning Network are similar to those of the Barabasi Albert Model is an urgent question to be answered, which concerns the design of routing protocols, the simulation of transactions, the robustness of the network, and various other aspects. In Martinazzi et al’s study [11,15,18,19], the degree distribution of the Lightning Network conforms to the Barabasi Albert Model, and the distribution of the edge nodes of the Barabasi Albert Model is also a good approximation of the edge nodes in the Lightning Network. However, our analysis shows that the edge nodes of the Lightning Network are not similar to those of the Barabasi Albert Model, although the distribution of degrees of the Lightning Network fits the Barabasi Albert Model of the same size with decreasing errors. There is a massive gap between it and the Barabasi Albert Model in terms of diameter, assortativity, and connectivity mechanism of the network. We explored the possible reasons for this gap. Also, the preferential connection mechanism[22] of the Barabasi Albert Model does not apply to the connection mechanism of the whole Lightning Network. By extracting the newly created connections in the Lightning Network, we argue that the newly joined nodes prefer to connect nodes with greater Betweenness Centrality than the degree-first connection mechanism. We argue that using the Barabasi Albert Model to simulate the topology of the Lightning Network is not a perfect choice.

Our main contributions can be summarized as follows:

• We constructed the network topology of the Lightning Network for almost 1,200 days and analyzed the topological evolution of the network.

• We point out by comparing the Barabasi Albert Model of the same size that although the error in fitting the distribution of the Lightning Network degree is getting smaller, its diameter is much enlarged due to the crosstalk between the nodes compared to the Barabasi Albert Model of the same size.

• We point out that the Lightning Network is the exact opposite of the assortativity by comparing the Barabasi Albert Model of the same size, which may come from the connection mechanism of the merchant nodes in the Lightning Network.

• We find that the newly joined nodes in the Lightning Network preferentially connect the nodes with greater Closeness Centrality than the degree-first connections.

2 Related Work

Current research on the Lightning Network focuses on three aspects: topological properties [15,19,20,23–28], security [9,14,29–35], and routing methods [11,12,17,36–39]. Although all the above studies are very important aspects of Lightning Network, they are strictly dependent on the underlying topological network. In the process of simulating Lightning Network using the underlying topology, different teams have proposed different topologies [10,11,13–17], but in the end, there is a preference to use the Barabasi Albert Model as the underlying network for relevant simulations, especially in the future development of the network, whether to use the Barabasi Albert Model as the underlying network for autopilot function in particular, the question of whether to use the Barabasi Albert Model as the underlying network for the automatic driving function has also become the focus of community discussions (isb, 2020). Therefore, it is a very important issue to figure out whether the topology of the Lightning network is similar to that of the Barabasi Albert Model.

In terms of the connection of nodes, Bertucci et al. [26] investigated that the competition between nodes followed the Bertrand model⁵ and pointed out that the centralized network structure must not be the optimal network structure. Rincon et al. [33] classified the connections between nodes in the network into three types and evaluated the contribution of different kinds of connections to the network structure. Avarikioti et al. [6] analyzed the impact of different charging mechanisms of nodes on the robustness and connectivity of the network. Avarikioti et al.[24] then analyzed the structure and the equilibrium of the Lightning Network from the perspective of the network creation game [40]. They considered a node as a decision-making individual. They analyzed the effect of the node’s policy on the optimal structure of the network from the perspective of the network creation game. Lange et al. [28] analyzed how the network would evolve under different connection strategies of nodes. This is the first article to predict the future development of the network from a network topology perspective. However, the article only directly selects Betweenness Centrality, Closeness Centrality, and degree as the connection metrics of nodes to predict the future development of the network. It is not clear whether the selection of metrics is consistent with the development of the Lightning Network.

3 Data and Basic Definitions

In this section, we will describe in detail how we acquire and process the data and how we build the data of the network into graphs.

3.1 Datasets

We collected data from the website³ for all channels of the Lightning Network from the date of birth - January 12, 2018, to April 20, 2021, for a total of 147,256 channels. From the birth of the Lightning Network to April 20, 2021, the Lightning Network has 147,256 channels, which includes channels that have been closed and channels that are still open. The information of each channel contains the following fields:

• short_channel_id: a set of numbers of length 16 which represents channel identity

• satoshis: channel capacity between two nodes, 1BTC = 1,00,000,000 satoshis

• nodes: unique identification of nodes at both ends of the channel

• open/close: contains a lot of information about the opening and closing of the channel, where the channel opening and closing time is the key information.

By keeping the short_channel_id, satoshis, nodes fields in the original data above, the channel open and close times in the open and close fields are processed as the standard time day_open_time and day_close_time. we separate the two nodes in nodes filed, since node id is unique in the network, and to speed up the process, we replace the two nodes in the nodes field with unique numbers, and denote them as node0_id and node1_id, and day_open_time and day_close_time are the time when the edges in the network are connected and disconnect time. Our processed set of fields is as follows:

short_channel_id, satoshis, day_open_time day_close_time, node0_id, node1_id.

Building the information of the channel into a network requires using the fields

node0_id, node1_id, day_open_time, day_close_time.

At this point, we can process the raw data and obtain the data that can analyze the Lightning Network channels and construct the Lightning Network’s evolution.

3.2 Construction of Graphs

Our goal is to construct a temporal graph of the Lightning Network, analyze the topological property changes since the Lightning Network has been online, and compare it with the same size Barabasi Albert Model. Therefore, we have processed the channel data of the Lightning Network so that we can reconstruct the growth of the Lightning Network and analyze it.

The Lightning Network can be represented using a timestamped undirected graph G = (V, E, W, To, Tc), where V represents the set of nodes in the Lightning Network, E represents the edges between nodes, i.e., the channel in the original data, and W represents the capacity in the channel, i.e., the satoshis of the original data. To and Tc represent the time when the channel is opened and closed. For example.

((7093, 12 913), 505149x622x0, 300 000, 2018/1/20/9 : 43, 2019/8/31/18 : 34).

This indicates that a channel 505149x622x0 with a capacity of 300 000 satoshis exists between nodes 7,093 and 12 913, which was opened on 2018/1/20/9 : 43 and closed on 2019/8/31/18 : 34.

We read the data in days, and we add the node and the edge to the network when the time of edge creation is read, and we delete the edge when the time of its closure is read. When the degree of the node is 0, we consider this node dead. It should be noted that the channels in the Lightning Network are available in both directions, i.e., as long as a channel exists between the nodes, then whoever initiates the transaction can do so, so we use an undirected graph for the representation. At the same time, there is more than one connected component in the Lightning Network, but the largest connected component occupies more than 95% of the nodes, so the rest of the analysis in this paper is based on the largest connected component, except for the channel analysis, because the analysis of the channel is not required to build a graph.

4 Methods and Results

In this section, we will first start from the topological point of view; after analyzing the three stages of development of the Lightning Network, we fit the distribution of the degrees of the Lightning Network with 100 days interval, analyze the variation of the assortativity, diameter, etc. of the network and compare it with the network of the same Barabasi Albert Model. In the section of preferential connection of nodes, we analyzed the problem of preferential connection of new nodes of the Lightning Network by obtaining the data of newly created edges.

4.1 Topology Analysis

4.1.1 The Three Stages of Development of the Lightning Network

The idea of the Lightning Network was proposed by [8] in 2016 and officially launched on January 12, 2018, and by April 20, 2021, the Lightning Network already has 10,930 nodes and 39,962 edges. The visualization of the Lightning Network is shown in Figure 2.

FIGURE 2

FIGURE 2. Lightning Network Visualization - April 20, 2021. The presence of a large number of star structures at the edge of the network.

The development of network nodes and edges is shown in Figure 3. Where the x-axis represents the time and the y-axis represents the number. The blue line represents the development of nodes, and the yellow line is the development of edges. We can divide the development of the Lightning Network into three stages. The first stage, from January 2018 to January 2019, we call the “start-up period.” This phase is characterized by the slow growth of both nodes and edges, and the network is still in a relatively preliminary stage. The second phase is from January 2019 to June 2019, which we call the “outbreak period.” This phase is characterized by the fact that in addition to the accelerated growth of nodes, edges start to grow wildly. Edges overgrew during this phase from less than 10,000 to a peak of over 40,000. In addition to the increasing number of bitcoin transactions, a campaign called “Lightning Torch” was launched in January 2019 and played a huge role. The drive covered dozens of countries around the world and was attended by many vital influencers, resulting in an almost exaggerated growth of the network. However, after rapid growth, the Lightning Network experienced a decline in size. We call the period from June 2019 to now a “cooling-off period.” The edges in the network continue to drop and eventually stabilize around 35,000, and node growth begins to slow down. Such a trend has been maintained until now. We believe this is due to the irrational growth experienced in the last round. Due to the propagation effect, Lightning Network enthusiasts started to join the network and build more edges, but as a transaction network, after the irrational growth, the “supply” market of the Lightning Network became larger than the “demand” market. The edges between nodes are “over-resourced,” and the number of edges is decreasing. The reason why the number of edges has remained stable around 35,000 after June 2019 is also that the network is in a state of “supply and demand balance.” As you can see, after January 2021, there is a new increase in the number of nodes and edges in the network. This is because the price of Bitcoin has increased dramatically, from under $30,000 to over $50,000 as of April 20, 2021. What we can speculate about the development of the Lightning Network after April 20 is that it will see a new round of growth if the price of bitcoin continues to rise.

FIGURE 3

FIGURE 3. Lightning network nodes and edges growing with time.

4.1.2 Degree Distribution

The degree distribution refers to the proportion of nodes corresponding to the degree in the network. By constructing the Lightning Network as a simple undirected graph, we can calculate the degree distribution of nodes as time changes. First, we tested whether the degree distribution of the Lightning Network conforms to the scale-free property. In a scale-free network, the probability that a node with node degree k is selected to generate a new connection satisfies the following equation [22,41,42]:

$P\left(k\right)=k^{-\alpha }(1)$

The P(k) represents the probability of being selected nodes, where k is the degree of the node and α is the parameter, usually between 2 and 3. To verify whether the Lightning Network meets the scale-free property, we fit it using the python package powerlaw, which is more advanced than previous fitting tools and is also easier to use [43]. We give the fitted parameters α and error sigma by powerlaw.

Figure 4 gives the complementary cumulative distribution of degrees of the Lightning Network every hundred days, where the x-axis is the degree of the node, and the y-axis tabulates the probability that the node is greater than the degree corresponding to the x-axis. Invariably, the Lightning Network shows a decline in the distribution at the tail, which indicates the presence of hub nodes with vast degrees connected to other nodes in the network. The red line is the result of the fit using powerlaw, and Table 1 gives the fitted parameters α and the corresponding error sigma. It can be seen that except for the slightly larger error at the beginning of the development of the Lightning Network, the error of the Lightning Network fit after 400 days is less than 5%, which indicates that the Lightning Network is a scale-free network. The error at the beginning may be that the size of the network is still relatively small.

FIGURE 4

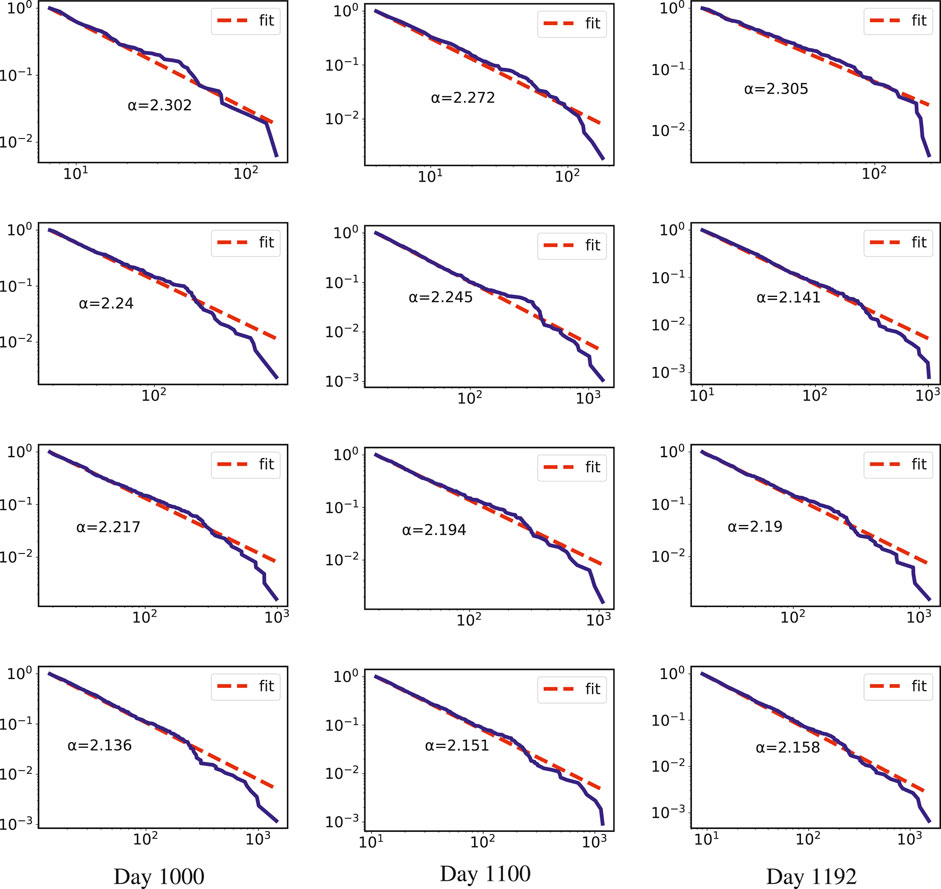
FIGURE 4. Complementary cumulative distribution of degrees per 100 days of the network and parameters fitted using powerlaw.

TABLE 1

TABLE 1. Parameters and errors of the fit.

4.1.3 Disassortativity

In a network, nodes between different degrees may be random or inclined. Degree assortativity is mainly used to examine whether nodes of similar degrees tend to connect. A network is said to be assortative or positively correlated if nodes with large (small) degrees tend to connect nodes with large (small) degrees overall. If nodes with a large (small) degree tend to connect nodes with a small (large) degree, then the network is said to be disassortative or negatively correlated [44]. The equation for assortatvity is as follows:

$r=\frac{⟨k_i{k}_j⟩-⟨k_i⟩⟨k_j⟩}{\sqrt{\left(⟨k_i^2⟩-{⟨k_i⟩}^2\right)\times \left(⟨k_j^2⟩-{⟨k_j⟩}^2\right)}}(2)$

Where k_i and k_j are degrees of the nodes at either end of a link and $<>$ represents the average overall links. It varies between -1 and 1: For r > 0 the network is assortative, for r < 0 the network is disassortative, and for r = 0 the network is neutral. If a network’s assortativity is positive, hub nodes tend to be connected with other hubs and vice versa.

We calculated the assortativity coefficient for the network. The x-axis is the time, and the y-axis is the assortativity coefficient. Since the number of nodes in the first 2 days of the network is small, we cannot calculate the assortativity coefficient for the network. The assortativity coefficient from the third day is shown in Figure 5, except for the third day and the fourth day, the value is greater than 0. From the fifth day until the last day, the assortativity of the network is less than 0. This indicates that the network is disassortative, i.e., Smaller nodes tend to be connected to larger nodes and vice versa.

FIGURE 5

FIGURE 5. Network assortativity changes.

Since there are some thresholds in the configuration of the Lightning Network, nodes with payment needs that want to access the network, these service providers offer excellent options to easily access the Lightning Network using their products by paying only the appropriate amount of money. As an example, the fifth-largest node in the network, OpenNode⁶, is dedicated to providing access to commercial payments. OpenNode currently has a total of 793 channels, accounting for 1.787% of the total number of channels in the network. Other nodes such as CoinGate⁷, with 1,214 channels or 2.736% of the total number of channels in the network, provide similar services. There are not a few such nodes in the network. Instead, as shown in Figure 2, many similar nodes exist at the edges of the network, forming a local star structure, which could be the reason for the disassortativity of the Lightning Network.

We also calculate the assortativity of the Barabasi Albert Model of the same size, and we can observe that the assortativity of the Barabasi Albert Model is almost the exact opposite of that of the Lightning Network. However, it also shows some disassortativity. It gradually stabilizes around -0.03 as the network size increases, while the lightning network finally stabilizes around −0.2, a difference of two orders of magnitude.

Current research [45] has shown that the assortativity affects the efficiency of information dissemination in the network, and the existence of larger nodes in the lightning network as hub nodes can accelerate the process of information dissemination to a certain extent. At the early stage of lightning network construction, the community was committed to developing the lightning network into a peer-to-peer structure, and as a result, relevant routing algorithms were designed, and the topology of the network was constructed. However, as the size of the network increased, hub nodes still appeared. Perhaps as the network grows in size and changes in property, the network’s routing protocols may need to be updated to accommodate the new topology.

4.1.4 Diameter

The diameter of a network is the maximum value of the shortest path between any two nodes in the network. Thus, it is a fundamental criterion used to measure the level of connectivity of a network. In general, individuals in a smaller diameter group are connected through fewer intermediates, and transfers between individuals may be faster than in a larger diameter group [44].

The diameter of the Lightning Network evolves, as shown in Figure 6. Its diameter rises rapidly, reaches 12 within the first 200 days, and maintains 12 for the vast majority of the subsequent time, reaching a maximum diameter of 14, but then drops back to 12. Meanwhile, we compare the diameter of the Lightning Network with that of a BA network [46] of the same size, where the same size means that both networks have the same number of nodes and the similar number of edges. The results are shown in Table 2. Surprisingly, although the size is the same, the diameters of the two networks are vastly different. The trends are also entirely different. The diameter of the Lightning Network is at least twice as large as that of the BA network most of the time. The diameter of the Lightning Network rises slightly and then stabilizes at 12, while the diameter of the BA network is decreasing.

FIGURE 6

FIGURE 6. Diameter change of the network.

TABLE 2

TABLE 2. Changes in network diameter before and after removing tandem nodes and comparison with BA model.

Why the diameter of the Lightning Network is such a trend, we explored the reason for its creation by finding the maximum shortest path between nodes. Figure 7 shows the visualization of the Lightning Network on day 100, and it is easy to see that there are many tandem connections between nodes at the edge of the network. Figure 8 shows the visualization of the Lightning Network on day 200, and we can see that this crosstalk becomes more serious. Between day 100 and day 200, the diameter of the Lightning Network increased from 9 to 12 and has been maintained up to now. We extracted the longest and shortest paths at each stage and found that these longest diameters were associated with one of the crosstalk structures [15 307, 6,504, 2,947, 13 555, 9,610, 13 606, … … ]. We removed this tandem structure, recalculated the diameter change of the network every 100 days, and found that the network’s diameter decreased, as shown in Table 2. This indicates that the presence of this crosstalk structure has been influencing the diameter of the network. Although the longest crosstalk structure in the network was removed, the network’s diameter still reached 11 because other crosstalk structures in the network affected the network’s diameter. The crosstalk phenomenon between nodes caused the rapid increase in node diameter at the beginning of the development of the Lightning Network. This crosstalk has been influencing the network’s diameter. From the [23], it is known that there are three reasons for nodes to establish connections in the Lightning Network: 1. Business/Financial Interests, 2. Gratification from social connections and promoting participation in the network, and 3. privacy, transparency, and autonomy of the community. As the tandem connection between nodes does not lead to increased benefits and may cause a decrease in transaction efficiency or even an increase in transaction costs. This tandem also does not lead to a sense of participation in the autonomous community because it is only one connected node and does not generate influence. So one possible reason is that it is a social behavior. The act of social crosstalk between nodes expands the diameter of the network, and this phenomenon is prevalent in the Lightning Network.

FIGURE 7

FIGURE 7. Day 100 Visualization of networks and their tandem nodes. A large number of tandem structures can be seen at the edges; The solid red line shows the network’s diameter.

FIGURE 8

FIGURE 8. Day 200 Visualization of networks and their tandem nodes. As the network grew in size, the same sequence of day 100 strung together more nodes and formed a ring in the network (top left part of the figure), which has been having a massive impact on the network’s diameter.

4.2 Channel and Node Preference Connection Analysis

In this section, we will analyze the Lightning Network channels from a channel point of view and the tendency of the connections between the nodes.

4.2.1 Channel Analysis

Channels are the foundation of the Lightning Network transactions, and a specific capacity exists for the nodes at both ends of the channel to make transactions (as shown in Figure 1). The nodes top up the capacity at both ends of the channel after it has been established. Thanks to the robust privacy design of the Lightning Network, only the starting node, and the destination node can know the specific information between the nodes of the transaction [11]. Therefore, the Lightning Network channel analysis helps us understand more deeply the composition of the funds of each node in the Lightning Network and clarify the status of the channel.

Whether a channel in a Lightning Network is disconnected after it is established depends on the nodes at both ends. There are three modes of channel disconnection in the Lightning Network: Cooperative close, Force close, and Fraudulent Force close. In a cooperative close, both channel participants agree to close the channel and settle the final state of the channel onto the blockchain. If only one participant is online or if the participants disagree on the state of the channel, one participant can perform a force close of the channel without the cooperation of the other participant. If a node in the channel tries to broadcast a transaction that is not recognized by both parties, this channel closure is called Fraudulent Force Close. A penalty transaction punishes a malicious node for attempting a fraudulent force close. The penalty transaction transfers the malicious node’s portion of the funds in the channel to the node that they were attempting to defraud⁸.

The status of channel openings and closures in the Lightning Network is shown in Table 3, from January 12, 2018 to April 20, 2021, the Lightning Network has generated a total of 147,256 channels, of which 44,200 channels are still open and 103,056 channels have been closed. Among the 103,056 channels that have been closed, the largest number of channels were closed in the cooperative mode as shown in Table 4, reaching 69,088. The number of channels closed in the force close mode is 32,439. It is reassuring to note that only 32 channels were closed as fraudulent froce closures over this long period of time. The remaining 1,497 channel closures are not recorded in our data.

TABLE 3

TABLE 3. The number of channels opened and closed.

TABLE 4

TABLE 4. The number of channels with different closing methods.

We calculated the lifetime of the closed channels based on when the channels were opened and closed. As shown in Figure 9, where the x-axis is time, and the y-axis is the duration of channel survival, we took the logarithm of the corresponding values. What can be derived from the figure is that there are few channels with survival times greater than 800 days, the number of edges with survival times between 50 and 800 days is approximately linearly distributed, and the number of edges with less than 50 days is again more. The largest number of edges with a survival time of 1 day is 3,699, and there are also nearly 3,000 edges with a survival time of fewer than 24 h. This may indicate that single small transactions are more present in the network.

FIGURE 9

FIGURE 9. Channel life time distribution.

In terms of the capacity of the channels, the difference between different channels is vast, as shown in Table 3, the largest capacity of the channels is up to 5,00,000,000 satoshis (5BTC), and the smallest capacity is 1,050 satoshis (0.00 000 105BTC). The average is 3,1,32 ,041 satoshis, and the median is 5,97 ,920 stoshis. We can speculate that the vast majority of channel capacities in the network are small. The specific distribution of the capacity of the channels is shown in Table 4. Channels with a capacity of fewer than 100,000,000 satoshis (1BTC) are in an absolute position, accounting for more than 99.7% of the total. This is because it is more cost-effective to use the Bitcoin network for larger transactions, and the Lightning Network itself is designed for small amounts of transactions. Therefore, channels with capacities greater than 1BTC are in the minority, and these channels with huge capacities almost always come from the merchant nodes in the network. For example, for nodes larger than 4BTC, the relationship between these nodes is derived by comparing them with the data on 1 ml.com⁹. Unsurprisingly, these channels with huge capacity are connections between merchant nodes in the Lightning Network. For example, the channel with short_channel_id 649417x2162x1 connects the fourth largest node in the Lightning Network, Bitrefill¹⁰, and the second-largest node, bfx_lnd1¹¹. Among them, bfx_lnd1 has a total capacity of 106 BTC, accounting for 8.431% of the entire network capacity, and 339 connections exist, accounting for about 0.7% of the number of channels in the entire network. And the three channels 660987x443x0, 656429x1122x0, 678588x1581x0 are all associated with the largest node in the Lightning Network, ACINQ¹², which has a total capacity of 148 BTC, accounting for 11.728% of the entire network capacity.

4.2.2 Preferential Connection Mechanism for Nodes

Looking for an answer to this question, we can think in several ways.

First, inspired by the scale-free property of the Lightning Network, we check whether the directionality of the newly connected tilts of nodes conforms to the degree-preferential attachment model. In the degree-preferential attachment model proposed by Barabasi and Albert [22], new nodes tend to be connected to existing nodes with higher degree rather than existing nodes with a lower degree. Mathematically, the probability of connecting a new node is shown in Eq. 1.

Then, starting from Closeness Centrality [47] and Betweenness Centrality [48]. Closeness Centrality describes the distance from a network node to other nodes. The Betweenness Centrality represents the number of shortest paths through a node.

Closeness Centrality of a node v is given by the expression

$CC\left(u\right)=\frac{N}{{\sum }_{u\ne v}d\left(u,v\right)}(3)$

where N is the number of nodes in the graph and d (u, v) is the distance between node u and v. Closeness Centrality measures how close a node is to all other nodes.

Betweenness Centrality of a node v is given by the expression

$BC\left(v\right)=\sum _{s\ne v\ne t}\frac{{\sigma }_{st}\left(v\right)}{{\sigma }_{st}}(4)$

where σ_st, where σ_st is total number of shortest paths between node s and t, while σ_st(v) is the number of those paths, that pass through v.

Under the assumption that the Lightning Network uses the shortest path for transactions, Betweenness Centrality and Closeness Centrality have practical implications. When the nodes in the network have high Betweenness Centrality, the nodes can earn more fees. On the other hand, when the nodes in the network have high Closeness Centrality, the nodes theoretically spend less when making their transactions [24].

To determine whether nodes in the Lightning Network establish new connections, we first need to obtain the newly established connections in the Lightning Network and know who initiated the connections. Still, our data do not provide the relevant information. We first extracted the dates when all nodes in the Lightning Network first appeared to solve this problem. The purpose of this is based on a straightforward fact: a node that wants to enter the network must have established a connection with another node by itself, because if no connection exists by itself, then this node cannot be discovered by other nodes so that it cannot be selected by other nodes to create any new connection. So when this node appears for the first time, it means that this node has actively established connections with other nodes in the network. This way, we get the data for the new connection.

To be able to explore the tendency of the nodes to be connected, we calculated the degree of the nodes in the network, Closeness Centrality, Betweenness Centrality. and to make the data uniform, we filtered the data between day 500 and day 1,000 because the network is almost in a stable state during this time, the edges almost remained constant and the nodes grew very little.

If the nodes in the network use the degree-preferential attachment model [22], then nodes with larger degrees are more likely to acquire more connections. However, as shown in Figure 10A, where the x-axis is the degree and the y-axis is the number of new connections in the response interval. It can be concluded that there is no degree-preferential attachment for new connections in the network, but rather a situation where the number of connections gets smaller as the degree increases. Most of the nodes in the network are connected to nodes with degree less than 200, which indicates that nodes do not have a strong tendency to connect to nodes with greater degree.

FIGURE 10

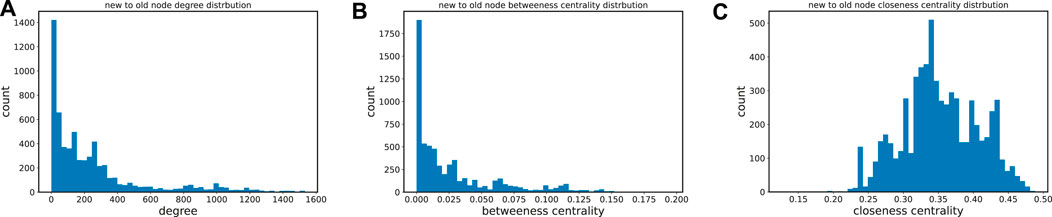
FIGURE 10. (A). Distribution of the degrees of the nodes connected by the newly added nodes (B). Distribution of the closeness centrality of the nodes connected by the newly added nodes. (C). Distribution of Betweenness Centrality of the nodes connected by the newly added nodes.

The same result appears for Betweenness Centrality. Figure 10B shows where the x-axis is the Betweenness Centrality of the nodes, and the y-axis is the number of connections that respond. The larger the value of the Betweenness Centrality of the nodes in the network, the fewer connections they attract. Most of the nodes are connected to nodes with smaller Betweenness Centrality. This indicates that the tendency to connect nodes with more significant Betweenness Centrality is also not strong.

Figure 10C shows the relationship between newly created edges and Closeness Centrality, where the x-axis is the Closeness Centrality of the node and the y-axis is the number of responsive connections. This is quite different from the distribution of degree and closeness, where the attraction to the node rises as the Closeness Centrality of the node increases, reaching a maximum around 0.35, followed by a decline. This indicates that nodes in the network with greater Closeness Centrality are more likely to be connected to newly entering nodes if they have greater Closeness Centrality than degree and Betweenness Centrality. Nodes tend to connect to nodes with greater Closeness Centrality.

It has been shown that among the attacks against degree and centrality, the attacks against degree can cause more damage with a significant decrease in the average degree and average connectivity while being split into multiple connected components [20]. If the Barabasi Albert Model is used as the underlying network, its degree prioritization will connect with more severe security risks as the network size increases. They are using Betweenness Centrality as the connectivity goal is more in line with the development of the network and the security of the network.

5 Conclusion

In this paper, we investigate the differences between Lightning Network and Barabasi Albert Model in terms of assortativity, diameter, and node-preferred connectivity, starting from whether the Lightning Network is similar to the Barabasi Albert Model, and discuss the reasons behind the special properties generated by the Lightning Network.

Our analysis shows that as the size of the Lightning Network continues to expand, its assortativity shows an entirely different trend from that of the Barabasi Albert Model, although the error in its fitting coefficients becomes smaller. We think this may be related to the death of the merchant nodes and edges in the Lightning Network. Currently, there is still a threshold for ordinary people to use Lightning Network, and when the merchant nodes provide simple access, there will be many endpoints that establish connections with the merchant nodes, while the death of edges may cause the creation of assortativity. The Lightning Network diameter is larger than the Barabasi Albert Model of the same size, and we found that it is related to the crosstalk between nodes in the network by extracting the diameter connections in it.

In terms of the tendency of nodes to connect, we first analyzed the channel closure, the distribution of the capacity. We found that only a few channels in the network are closed in a penalty way, indicating that the Lightning Network’s security mechanism is excellent. Also, we found that the high-capacity channels in the network are established between massive nodes in the network, while most of the channels have shallow capacity. This is ideally in line with the original design of the Lightning Network. In terms of the connection propensity of nodes, we extracted the edge-building information of newly joined nodes in the network and performed the propensity analysis of node connections. We found that nodes in the network are more inclined to connect with nodes closer to greater Closeness Centrality than degree and Betweenness Centrality.

Our findings suggest that although the Lightning Network is similar to the Barabasi Albert Model in the degree distribution, there is a significant gap in assortativity and diameter again. The assortativity and diameter are vital parameters for the network to face cascade failures and improve network efficiency. therefore, Our findings can provide insights into the simulation and autopilot function of lightning networks.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The characteristics examined by ZW were selected, RZ and YS completed the analysis of the various indicators of the network, and all authors participated in the preparation of the article as well as its improvement.

Funding

This research was supported by the Zhejiang Provincial Natural Science Foundation of China under Grant No. LY20F030012; in part by the National Natural Science Foundation of China under Grant No. 62176080.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Mr. fiatjaf for providing the data of the Lightning Network.

Footnotes

¹[Dataset] (2021). Rsmc. [Online]. Available: https://github.com/lightningnetwork/lightning-rfc/

²[Dataset] (2021). Htlc. [Online]. Available: https://github.com/lightningnetwork/lightning-rfc/blob/master/02-peer-protocol.md/

³[Dataset] (2021). lnchannels. [Online]. Available: https://ln.bigsun.xyz/

⁴[Dataset] (2020). is the barabasi albert model a reasonable choice for the autopilot? [Online]. Available: https://github.com/lightningnetwork/lnd/issues/677

⁵[Dataset] (2021). Bertrandcompetition. [Online]. Available: https://en.wikipedia.org/wiki/Bertrand_competition

⁶[Dataset] (2021). opennode. [Online]. Available: https://www.opennode.com/

⁷[Dataset] (2021). coingate. [Online]. Available: https://www.coingate.com/

⁸[Dataset] (2021). Types. [Online]. Available: https://github.com/lightningnetwork/lightning-rfc

⁹[Dataset] (2021). 1ml.com. [Online]. Available: https://www.1ml.com/

¹⁰[Dataset] (2021). bitrefill. [Online]. Available: https://www.bitrefill.com/

¹¹[Dataset] (2021). bfxlnd1. [Online]. Available: https://www.bitfinex.com/

¹²[Dataset] (2021). Acinq. [Online]. Available: https://acinq.co/

References

1. Nakamoto S. Bitcoin: A Peer-To-Peer Electronic Cash System. Decentralized Business Rev (2008) 21260.

Google Scholar

2. Croman K, Decker C, Eyal I, Gencer AE, Juels A, Kosba A, et al. On Scaling Decentralized Blockchains. In: International conference on financial cryptography and data security. Berlin, Heidelberg: Springer (2016). p. 106–25. doi:10.1007/978-3-662-53357-4_8

CrossRef Full Text | Google Scholar

3. Georgiadis E. How many Transactions Per Second Can Bitcoin Really Handle? Theoretically. IACR Cryptol Eprint Arch (2019) 416.

Google Scholar

4. Gervais A, Karame GO, Wüst K, Glykantzis V, Ritzdorf H, Capkun S. On the Security and Performance of Proof of Work Blockchains. In: Proceedings of the 2016 ACM SIGSAC conference on computer and communications security; 2016 Oct; Vienna, Austria (2016). p. 3–16. doi:10.1145/2976749.2978341

CrossRef Full Text | Google Scholar

5. Sompolinsky Y, Zohar A (2013). Accelerating Bitcoin’s Transaction Processing. Fast Money Grows on Trees, Not Chains.

Google Scholar

6. Avarikioti G, Janssen G, Wang Y, Wattenhofer R. Payment Network Design with Fees. In: Data Privacy Management, Cryptocurrencies and Blockchain Technology. Springer (2018). p. 76–84. doi:10.1007/978-3-030-00305-0_6

CrossRef Full Text | Google Scholar

7. Decker C, Wattenhofer R. A Fast and Scalable Payment Network with Bitcoin Duplex Micropayment Channels. In: Symposium on Self-Stabilizing Systems. Cham: Springer (2015). p. 3–18. doi:10.1007/978-3-319-21741-3_1

CrossRef Full Text | Google Scholar

8. Poon J, Dryja T (2016). The Bitcoin Lightning Network: Scalable Off-Chain Instant Payments.

Google Scholar

9. Tang W, Wang W, Fanti G, Oh S. Privacy-utility Tradeoffs in Routing Cryptocurrency over Payment Channel Networks. Proc ACM Meas Anal Comput Syst (2020) 4:1–39. doi:10.1145/3392147

CrossRef Full Text | Google Scholar

10. Prihodko P, Zhigulin S, Sahno M, Ostrovskiy A, Osuntokun O. Flare: An Approach to Routing in Lightning Network. Moscow: White Paper (2016). p. 144.

Google Scholar

11. Béres F, Seres IA, Benczúr AA (2019). A Cryptoeconomic Traffic Analysis of Bitcoin’s Lightning Network. arXiv preprint arXiv:1911.09432.

Google Scholar

12. Engelmann F, Kopp H, Kargl F, Glaser F, Weinhardt C. Towards an Economic Analysis of Routing in Payment Channel Networks. In: Proceedings of the 1st Workshop on Scalable and Resilient Infrastructures for Distributed Ledgers; 2017 Dec 11–15; Las Vegas, NV (2017). p. 1–6. doi:10.1145/3152824.3152826

CrossRef Full Text | Google Scholar

13. Brânzei S, Segal-Halevi E, Zohar A (2017). How to Charge Lightning. arXiv preprint arXiv:1712.10222.

Google Scholar

14. Rohrer E, Malliaris J, Tschorsch F. Discharged Payment Channels: Quantifying the Lightning Network’s Resilience to Topology-Based Attacks. In: 2019 IEEE European Symposium on Security and Privacy Workshops (EuroS&PW). IEEE (2019). p. 347–56.

Google Scholar

15. Guo Y, Tong J, Feng C. A Measurement Study of Bitcoin Lightning Network. In: 2019 IEEE International Conference on Blockchain (Blockchain). Atlanta, GA. IEEE (2019). p. 202–11. doi:10.1109/blockchain.2019.00034

CrossRef Full Text | Google Scholar

16. Ersoy O, Roos S, Erkin Z. How to Profit from Payments Channels. In: International Conference on Financial Cryptography and Data Security. Cham: Springer (2020). p. 284–303. doi:10.1007/978-3-030-51280-4_16

CrossRef Full Text | Google Scholar

17. Conoscenti M, Vetrò A, De Martin J, Spini F. The Cloth Simulator for Htlc Payment Networks with Introductory Lightning Network Performance Results. Information (2018) 9:223. doi:10.3390/info9090223

CrossRef Full Text | Google Scholar

18. Martinazzi S (2019). The Evolution of Lightning Network’s Topology during its First Year and the Influence over its Core Values. arXiv preprint arXiv:1902.07307.

Google Scholar

19. Martinazzi S, Flori A. The Evolving Topology of the Lightning Network: Centralization, Efficiency, Robustness, Synchronization, and Anonymity. PloS one (2020) 15:e0225966. doi:10.1371/journal.pone.0225966

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Lee S, Kim H. On the Robustness of Lightning Network in Bitcoin. Pervasive Mobile Comput (2020) 61:101108. doi:10.1016/j.pmcj.2019.101108

CrossRef Full Text | Google Scholar

21. Seres IA, Gulyás L, Nagy DA, Burcsi P. Topological Analysis of Bitcoin's Lightning Network. In: Mathematical Research for Blockchain Economy. Springer (2020). p. 1–12. doi:10.1007/978-3-030-37110-4_1

CrossRef Full Text | Google Scholar

22. Barabási A-L, Albert R. Emergence of Scaling in Random Networks. science (1999) 286:509–12. doi:10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Rincon D, Wu EY, Dewar S, Zhu D. Identifying Beneficial Connection Types in Payment Channel Networks: The Case of Lightning. University of California Berkeley (2020).

Google Scholar

24. Avarikioti Z, Heimbach L, Wang Y, Wattenhofer R. Ride the Lightning: The Game Theory of Payment Channels. In: International Conference on Financial Cryptography and Data Security. Cham: Springer (2020). p. 264–83. doi:10.1007/978-3-030-51280-4_15

CrossRef Full Text | Google Scholar

25. Khan N. Lightning Network: A Comparative Review of Transaction Fees and Data Analysis. In: International Congress on Blockchain and Applications. Cham: Springer (2019). p. 11–8. doi:10.1007/978-3-030-23813-1_2

CrossRef Full Text | Google Scholar

26. Bertucci L (2020). Incentives on the Lightning Network: A Blockchain-Based Payment Network. . In: Proceedings of Paris December 2020 Finance Meeting EUROFIDAI-ESSEC.

Google Scholar

27. Bartolucci S, Caccioli F, Vivo P. A Percolation Model for the Emergence of the Bitcoin Lightning Network. Sci Rep (2020) 10:4488–14. doi:10.1038/s41598-020-61137-5

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Lange K, Rohrer E, Tschorsch F (2021). On the Impact of Attachment Strategies for Payment Channel Networks. arXiv preprint arXiv:2102.09256.

CrossRef Full Text | Google Scholar

29. Malavolta G, Moreno-Sanchez P, Kate A, Maffei M, Ravi S. Concurrency and Privacy with Payment-Channel Networks. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security; 2017 Oct 30–Nov 3; Dallas, TX (2017). p. 455–71. doi:10.1145/3133956.3134096

CrossRef Full Text | Google Scholar

30. Tikhomirov S, Moreno-Sanchez P, Maffei M. A Quantitative Analysis of Security, Anonymity and Scalability for the Lightning Network. In: 2020 IEEE European Symposium on Security and Privacy Workshops (EuroS&PW); 2020 Sept 7–11; Genoa, Italy. IEEE (2020). p. 387–96. doi:10.1109/eurospw51379.2020.00059

CrossRef Full Text | Google Scholar

31. Mazumdar S, Banerjee P, Ruj S (2020). Griefing-penalty: Countermeasure for Griefing Attack in Lightning Network. arXiv preprint arXiv:2005.09327.

Google Scholar

32. Tsabary I, Yechieli M, Manuskin A, Eyal I. Mad-htlc: Because Htlc Is Crazy-Cheap to Attack. In: 2021 IEEE Symposium on Security and Privacy (SP); 2021 May 24–27; San Francisco, CA (2021). IEEE. p. 1230–48. doi:10.1109/SP40001.2021.00080

CrossRef Full Text | Google Scholar

33. Rohrer E, Tschorsch F. Counting Down Thunder: Timing Attacks on Privacy in Payment Channel Networks. In: Proceedings of the 2nd ACM Conference on Advances in Financial Technologies; 2020 Oct 21–23; New York, NY (2020). p. 214–27. doi:10.1145/3419614.3423262

CrossRef Full Text | Google Scholar

34. Lu Z, Han R, Yu J. Bank Run Payment Channel Networks. IACR Cryptol Eprint Arch (2020) 2020:456.

Google Scholar

35. Harris J, Zohar A. Flood & Loot: a Systemic Attack on the Lightning Network. In: Proceedings of the 2nd ACM Conference on Advances in Financial Technologies; 2020 Oct 21–23; New York, NY (2020). p. 202–13. doi:10.1145/3419614.3423248

CrossRef Full Text | Google Scholar

36. Zhang Y, Yang D, Xue G. Cheapay: An Optimal Algorithm for Fee Minimization in Blockchain-Based Payment Channel Networks. In: ICC 2019-2019 IEEE International Conference on Communications (ICC); 2019 May 20–24; Shanghai, China. IEEE (2019). p. 1–6. doi:10.1109/icc.2019.8761804

CrossRef Full Text | Google Scholar

37. Sivaraman V, Venkatakrishnan SB, Ruan K, Negi P, Yang L, Mittal R, et al. High Throughput Cryptocurrency Routing in Payment Channel Networks. In: 17th {USENIX} Symposium on Networked Systems Design and Implementation ({NSDI} 20); 2020 Feb 25–27; Santa Clara, CA (2020). p. 777–96.

Google Scholar

38. Pickhardt R, Nowostawski M. Imbalance Measure and Proactive Channel Rebalancing Algorithm for the Lightning Network. In: 2020 IEEE International Conference on Blockchain and Cryptocurrency (ICBC); 2020 May 2–6; Toronto, ON, Canada. IEEE (2020). p. 1–5. doi:10.1109/icbc48266.2020.9169456

CrossRef Full Text | Google Scholar

39. Di Stasi G, Avallone S, Canonico R, Ventre G. Routing Payments on the Lightning Network. In: 2018 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData); 2018 Jul 30–Aug 3; Halifax, NS, Canada. IEEE (2018). p. 1161–70. doi:10.1109/cybermatics_2018.2018.00209

CrossRef Full Text | Google Scholar

40. Fabrikant A, Luthra A, Maneva E, Papadimitriou CH, Shenker S. On a Network Creation Game. In: Proceedings of the twenty-second annual symposium on Principles of distributed computing; 2003 Jul 13–16; Boston, MA (2003). p. 347–51. doi:10.1145/872035.872088

CrossRef Full Text | Google Scholar

41. Adamic LA, Huberman BA, Barabási A, Albert R, Jeong H, Bianconi G. Power-law Distribution of the World Wide Web. science (2000) 287:2115. doi:10.1126/science.287.5461.2115a

CrossRef Full Text | Google Scholar

42. Huang K, Wu S, Li F, Yang C, Gui W. Fault Diagnosis of Hydraulic Systems Based on Deep Learning Model with Multirate Data Samples. In: IEEE Transactions on Neural Networks and Learning Systems. IEEE (2021). doi:10.1109/tnnls.2021.3083401

CrossRef Full Text | Google Scholar

43. Alstott J, Bullmore E, Plenz D. Powerlaw: a python Package for Analysis of Heavy-Tailed Distributions. PloS one (2014) 9:e85777. doi:10.1371/journal.pone.0085777

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Xu M, Pan Q, Muscoloni A, Xia H, Cannistraci CV. Modular Gateway-Ness Connectivity and Structural Core Organization in Maritime Network Science. Nat Commun (2020) 11:2849–15. doi:10.1038/s41467-020-16619-5

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Murakami M, Ishikura S, Kominami D, Shimokawa T, Murata M. Robustness and Efficiency in Interconnected Networks with Changes in Network Assortativity. Appl Netw Sci (2017) 2:6. doi:10.1007/s41109-017-0025-4

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Albert R, Barabási A-L. Statistical Mechanics of Complex Networks. Rev Mod Phys (2002) 74:47–97. doi:10.1103/revmodphys.74.47

CrossRef Full Text | Google Scholar

47. Bavelas A. Communication Patterns in Task‐Oriented Groups. The J Acoust Soc America (1950) 22:725–30. doi:10.1121/1.1906679

CrossRef Full Text | Google Scholar

48. Brandes U. On Variants of Shortest-Path Betweenness Centrality and Their Generic Computation. Social Networks (2008) 30:136–45. doi:10.1016/j.socnet.2007.11.001

CrossRef Full Text | Google Scholar