Study on Power Grid Partition and Attack Strategies Based on Complex Networks

Based on the community discovery method in complex network theory, a power grid partition method considering generator nodes and network weightings is proposed. Firstly, the weighted network model of a power system is established, an improved Fast-Newman hierarchical algorithm and a weighted modular Q function index are introduced, and the partitioning algorithm process is practically improved combined with the characteristics of the actual power grid. Then, the partition results of several IEEE test systems with the improved algorithm and with the Fast-Newman algorithm are compared to demonstrate its effectiveness and correctness. Subsequently, on the basis of subnet partition, two kinds of network attack strategies are proposed. One is attacking the maximum degree node of each subnet, and the other is attacking the maximum betweenness node of each subnet. Meanwhile, considering the two traditional intentional attack strategies, that is, attacking the maximum degree nodes or attacking the maximum betweenness nodes of the whole network, the cascading fault survivability of different types of networks under four attack strategies is simulated and analyzed. It was found that the proposed two attack strategies based on subnet partition are better than the two traditional intentional attack strategies.

1 Introduction

With the construction of ultra-high voltage grids, smart grids, and clean energy-based energy Internet, the gradual interconnection of large grids has taken shape and continues to develop and improve on this basis. At the same time, as the scale of a power system expands, the reliability analysis and calculation of the power system becomes more and more complex and difficult [1, 2]. In recent years, researchers have tried to use the complex network theory to model and analyze the power grid and made good progress [3, 4]. One of the most important properties of complex networks is community structure, which refers to the close connection of nodes within a community and the sparse connection among the communities [4]. The application of this property can provide reference for power grid planning [5, 6].

In order to ensure the safe and stable operation and management of regional power grids, it is very important to carry out network planning in a reasonable and feasible way. In order to realize the online monitoring of grid operation status and fast dispatch of decision-making, power workers generally divide a grid into several sub-regions and manage each sub-region separately, which effectively improves the processing speed and reduces the calculation amount [7]. Analysis of power grid status and formulation of reasonable dispatching strategies are crucial to the management of a power grid. Usually, a network is divided based on the working experience of the power workers or the administrative area where the nodes are located [8], which obviously does not accurately reflect the state correlation between the components of the grid and cannot adapt to the changing operational state of the grid. The literature [9] proposed the concept of modularity, then modularity became the evaluation standard of community division, and the optimization of modular Q-function became the mainstream of research [10–14]. In [11], modularity Q was used as an index to evaluate the partition results, but it could not reflect the electrical and physical characteristics of a power grid, so it could not evaluate the partition results of power grids well. The literature [12] put forward the concept of power supply modularity combined with power supply correlation strength and improved the Fast-Newman algorithm to automatically identify the community structure of a power grid. In [13], two different types of genetic algorithms were improved and analyzed to solve the problem of community detection in a power system. The results show that genetic algorithm is a fast and effective method to deal with community detection in a large-scale power grid. The literature [15] proposed a new community division method based on resistance distance and similarity, where the distance function between nodes was defined by similarity, and the distance between communities was calculated by the distance between nodes. A power grid was divided into several communities according to whether the nearest neighbor nodes were in the same community.

At present, most of the community detection methods focus on the unweighted networks whose edge denotes whether there is a connection between nodes, regardless of the strength of the connection. However, in the real world, a real network is always complex, and the interaction strength between nodes is different. The unweighted network is not enough to reflect the relationship of objects in real life [16], so the study on weighted networks has a practical significance. The literature [17] overcame the resolution limitation of the traditional community detection method based on modularization by adding a weight term in the modularization formula for the purpose of detecting community which is small enough compared with the whole network. In [18], four weighted network models were established by using power flow and line impedance as the weights of edges, respectively. Then, the examples were simulated with four different models to verify the role of community structure in power grids. However, it was not verified and analyzed in combination with the actual application scenario of the power grid partition. The literature [19] proposed the index of node similarity, which was used to assign nodes with the greatest similarity to the same community. However, the community detection method of the model is mainly based on the pure topological structure of an undirected and unweighted network, without considering the function of a community. Therefore, it cannot fully reflect the electrical characteristics of a power grid.

According to the management of a power grid, each community should at least contain one generator node to ensure the supply of power. Otherwise, it will not work normally after isolation. In order to ensure the normal work of each subnet after power grid partition, this paper proposes an improved Fast-Newman algorithm based on the Fast-Newman algorithm. This improved algorithm considers generators and the weight of a network, overcoming the shortcomings of traditional partition methods which only focus on topology or only focus on electrical characteristics. Furthermore, it was noticed that previous studies on network attack strategies mainly applied random attack or deliberate attack to attack the node with the largest degree value or the node with the largest betweenness in a network. These attack strategies may not make full use of the network structure information, look too simple, and lack effective data mining in the early stage [20–22].Therefore, on the basis of subnet partition, this paper proposes a new network attack strategy. The cascading failure invulnerability of different types of networks under several attack strategies is simulated and compared with each other. It was found that the attack effect of our attack strategy is better than that of traditional attack strategies.

2 Basic Concepts

2.1 Community Structure

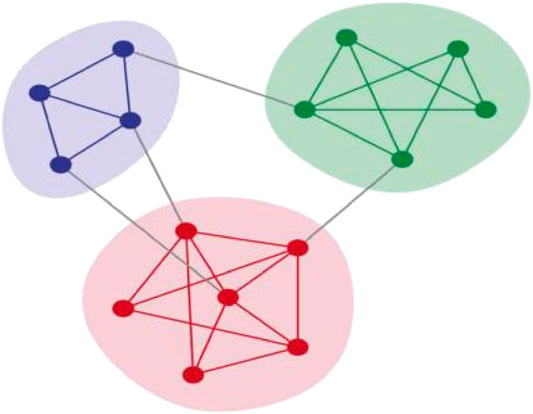
In nature and society, things with similar characteristics are often more closely related to each other—for example, people in a tribe have more frequent connections than those who are not members of the tribe. A closely connected community means that information or rumors spread faster among them than that in a sparsely connected community, people with the same hobbies are more likely to become friends, and so on. If things and their relationships are represented as a network, then the regions (node sets) whose nodes are closely connected in the network are called communities. If there is a community in a network, it is said to have a community structure. Community partition is equivalent to grouping nodes in a network. Community structure is very common in real networks. It is important to find the basic community structure in a network, for a single community behaves like a node of the network, which is beneficial to network study. On the one hand, identifying these substructures in a network can provide insights into how network functions and topologies affect each other. On the other hand, communities usually have attributes that are completely different from the average attributes of the network. By only focusing on the average properties, one will usually miss many important and interesting functions within the network. Generally speaking, the nodes in a community are densely connected, while connections among communities are relatively sparse. Detecting communities in a network can help us find the objects with the same function in the system, study the relationship among different communities, infer the missing attributes in the nodes, and make a reasonable prediction of the undiscovered relationship between nodes so as to better understand the underlying structure of the network and the information contained in it. Community discovery has been successfully applied in many areas of real life, such as anti-terrorism detection, behavior prediction, recommendation system, and so on [23, 24]. Community detection in a network is one of the hotspots in modern network science. Figure 1 is a graph of community structure, where different communities are distinguished by different colors. It can be seen that there are three communities in the network, and the density of connections in each community is relatively higher than that among communities. In other words, community structure is a dense subgraph with distinct boundaries in the network.

FIGURE 1

FIGURE 1. Diagram of community structure.

2.2 Weighted Power Grid Model

When modeling a power grid, the generators and load buses are usually regarded as nodes, the lines between nodes are regarded as edges, and double circuit or multi-circuit lines are usually combined into one edge. The complex network theory uses node set V, edge set E, and edge weight set $W$ to describe a complex network. For different types of networks and different research purposes, the definition of weight is also diversified, and the weighting method can usually be divided into two categories: similarity weights and dissimilarity weights. The similarity weight indicates the degree of correlation between two nodes; the closer the relationship between nodes, the larger the weight, and vice versa. The dissimilarity weights have an opposite meaning; the smaller the correlation between nodes, the greater the weight. According to the needs of study, when analyzing a power system, we use the above-mentioned two weighting methods to model a power grid. This paper considers three types of models of a power grid and carry out a comparative analysis of detection community. The first one is an unweighted network model, where the weight of each line is uniformly set to 1. The second one is a weighted network model, where the line reactance value $X_{ij}$ is taken as the weight of the edge, which belongs to the dissimilarity weights. The third one is a weighted network model where the line conductance value $Y_{ij}=1/X_{ij}$ is taken as the weight of the edge, which belongs to similarity weight. The weight setting in the models is shown in Eq. 1, where the data comes from Matpower 6.0 [25].

$\{\begin{array}{c}{W}_{ij}=1\\ W_{ij}=X_{ij}\\ W_{ij}=Y_{ij}\end{array}(1)$

2.3 Q-Function Model Based on Weighted Network

The literature [26] proposed the concept of modularity to measure the rationality of subnet division of unweighted networks. The literature [18] extended the definition of modularity to weighted networks. The modularity Q function under weighted networks is defined as follows:

$Q^w={\displaystyle \sum _s\left(e_w^{ss}-{\left(a_{ss}^w\right)}^2\right)}(2)$

where $e_w^{ss}=1/2T{\displaystyle \sum _{ij}{w}_{ij}\delta \left(c_i,s\right)\delta \left(c_j,s\right)}$ is the proportion of the sum of the weights of the edges connecting the internal nodes of the community s to the total weights, $c_i$ denotes the subnet where node i locates, $a_{ss}^w=1/2T{\displaystyle \sum _i{T}_i\delta \left(c_i,s\right)}$ is the proportion of the sum of the weights of all the nodes in the community s to the total weights, $T_i$ is the weight of node i which equals to the sum of the weights of the edges directly connected to node i, and T is the total weights of all the edges of the network. $Q^w\in \left[\mathrm{0,1}\right]$, for random network with equal weights; $Q^w=0$, values other than 0 indicate deviations from randomness. The larger the proportion of the sum of the weights of the edges connecting the internal nodes of the communities to the total weights, the larger is $Q^w$.

3 An Improved Algorithm of Power Grid Partition Based on Community Discovery

Combined with the physical and topological characteristics of a power grid, the Fast-Newman aggregation algorithm [26] is improved to ensure that each subnet includes at least one generator node after division and to improve the accuracy of subnet division. The steps of the improved algorithm proposed in this paper are as follows:

1) According to the real network architecture, the weighted network model of a power system is established, and various data of nodes and edges in the power grid are obtained from Matpower 6.0. The edge weights of the network are defined according to Eq. 1.

2) Introduce the modularity $Q$ function index, improve it according to the edge weight, and define the modularity function $Q^w$ of the power grid with the weighted model according to Eq. 2.

3) Initialization—each generator node in the network is divided as a subnet to form an initial subnet structure, without considering the load nodes. The modularity $Q_0^w$ of the network is calculated according to Eq. 2.

4) Each node i in the network is incorporated into one of the adjacent subnets and calculates the increment $\Delta Q^w$ of the whole network modularity brought by each combination. Node i is eventually incorporated into the adjacent subnet that makes the value of $\Delta Q^w$ maximum. $\Delta Q^w=Q^{w^{\prime }}-Q^w$, where $Q^{w^{\prime }}$ is calculated after the node i is joined into an adjacent subnet, and $Q^w$ is calculated before the node i is joined.

5) The network obtained in step 4 is compressed, and each subnet is condensed into a node. The sum of the weights of the nodes in the original subnet is assigned to the agglomerated new node, and all the connected edges between the two subnets are agglomerated into one edge. The weight of the agglomerated edges between the subnets is the sum of the weights of all the connected edges in the original subnets, so a new compressed network is obtained.

6) Repeat step 4 until the change of a belonging subnet of any node cannot increase the $\Delta Q^w$ value, $Q^w$ value will not change, and nodes will not be moved. Find out the partition result corresponding to the maximum modularity value $Q^w$ in the process of merging, which is the optimal subnet partition result.

The above-mentioned algorithm can be summarized into two stages. Steps 1–4 are to find the optimal solution of Q value based on the existing network, and steps 5–6 are the subnet combination of the division results obtained in the above-mentioned steps to obtain the updated network. After all the steps are completed, it is a round. Then, the algorithm will automatically enter the next round until the Q value no longer changes. Finally, the subnet division corresponding to the Q value is the final subnet division result. The overall time complexity of the algorithm is $O\left(m\left(m+N\right)\right)$ , where m is the number of edges and N is the number of nodes. Compared with the original division method, the improved algorithm not only ensures that each subnet after division has a generator to supply power to the loads but also comprehensively considers the topology and electrical characteristics of a power system, making the division more realistic.

4 Experimental Analysis

Based on the Fast-Newman agglomeration algorithm, this paper proposes an improved power grid subnet division method which considers generator nodes and weighted network models. According to the three network weighting methods defined in Eq. 1, IEEE14, IEEE30, IEEE39, IEEE118, and IEEE2383 standard test networks are divided using our improved algorithm. The modularity Q values with using the three weighting methods are calculated and compared with the Fast-Newman algorithm. Table 1 shows the data table of the modularity Q value of each system under the four different cases, and Figure 2 shows the comparison histogram of the Q value of each network.

TABLE 1

TABLE 1. Modularity Q value of each system under four different methods.

FIGURE 2

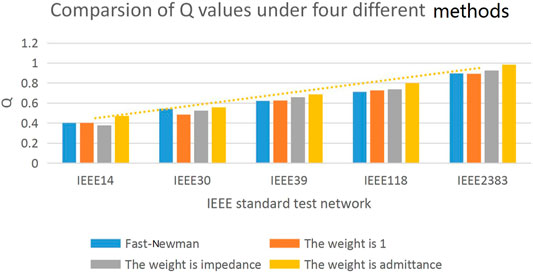
FIGURE 2. Comparison histogram of the Q value of each network in the four different division methods.

In the simulation, the weight refers to the weight of a connected edge, and we define the four division methods as follows: (1) Fast-Newman algorithm, (2) unweighted network (with the weight being 1), (3) impedance weight, and (4) admittance weight. The yellow dashed line in Figure 2 is the trend line of the modularity Q value under the fourth division method. It can be seen that, with the increase of network size, Q values are improved in different degrees under the four division methods, which indicates that this kind of algorithm is suitable for the division of large and complex networks. The larger the Q value is, the better the effect of subnet division is. Figure 2 shows that the modularity function Q of different networks is maximum under the fourth weighting method. Next, we mainly conduct a comparative analysis and discussion on the division results of the first and fourth types. The subnet division results are shown in Figure 3, Figure 4, and Figure 5.

FIGURE 3

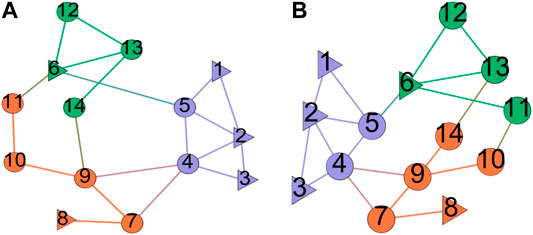
FIGURE 3. The community structure of IEEE14 network in two division modes. (A) Fast-Newman. (B) Improved algorithm with admittance weight.

FIGURE 4

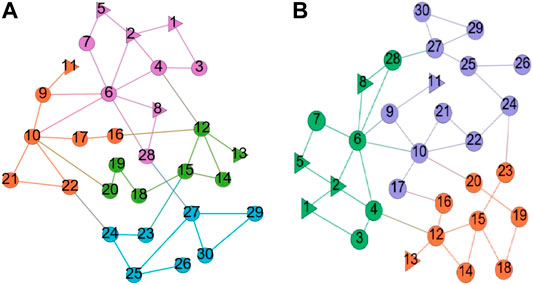
FIGURE 4. The community structure of IEEE30 network in two division modes. (A) Fast-Newman. (B) Improved algorithm with admittance weight.

FIGURE 5

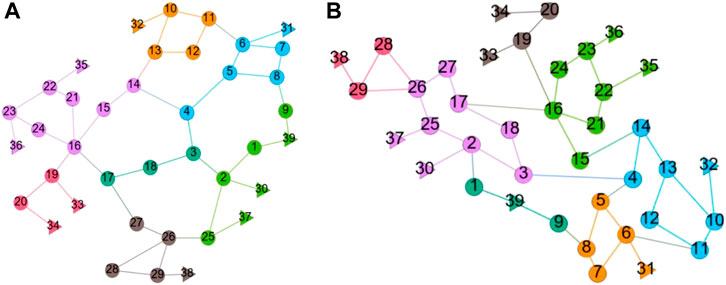
FIGURE 5. The community structure of IEEE39 network in two division modes. (A) Fast-Newman. (B) Improved algorithm with admittance weight.

Figure 3, Figure 4, and Figure 5 show the community structures of IEEE14, IEEE30, and IEEE39 standard networks in the two division modes. We use different colors to distinguish the divided subnets. The triangle symbol denotes the generator node, and the circular symbol denotes the load node. The IEEE14 standard network is divided into three communities in the two methods, the IEEE30 standard network is divided into four and three communities in the two methods, and the IEEE39 standard network is divided into seven communities in the two methods. It was found that, in the IEEE14 standard network, at least one generator is reserved in each subnet under the two division results, while in the IEEE30 and IEEE39 networks, only the fourth division method ensures that each divided subnet has at least one generator. In the Fast-Newman division method, it appears that there is no generator in one subnet of the IEEE30 and IEEE39 networks (see the blue marker subnet in IEEE 30 and the dark green marker subnet in IEEE 39), which is often defective in an actual power system operation.

When a transmission line in a power grid is damaged or removed, if the usual emergency control measures could not prevent the propagation of the fault, we can take active splitting measures to split the power grid into multiple “islands” according to the result of the pre-division so as to prevent the large-scale spread of the fault. After the splitting of a power grid, the key to the normal operation of each sub-network is the generator. The Fast-Newman aggregation algorithm cannot guarantee that every subnet has at least one generator after dividing the power grid. However, the improved Fast-Newman algorithm can do this work. It takes generators into account in the initialization step of the algorithm and to combine the electrical and topological characteristics of the network so that it can find a more realistic community division of the power grid. Since each subnet has one or more generators, we can take a series of stability measures for the subnets after grid splitting, such as boost or load shedding, to control the propagation of cascading faults to the greatest extent. In addition, considering both the division results and Q-values, we can see that the division result of the admittance model is the most reasonable and the community structure is the most obvious in the four models, which indicates that the community structure of the grids is prevalent and the weight of admittance has a facilitating effect on the community division in the proposed IEEE standard networks.

5 Cascading Failure Attack Strategy Based on Subnet Division

Network invulnerability refers to the ability of a system to maintain its normal operation when some nodes or links in it are damaged by random failure or deliberate destruction. The stronger the network invulnerability, the better its robustness. The study in the previous two sections shows that most of the actual power grids have a community structure. Using this nature of the power grids to do network partition can facilitate the control and management of the power grids. Furthermore, we can apply the community-based attack strategy to the network invulnerability research, which is rare in the network attack strategy research. How to use network topology and functional information to obtain the best attack effect at least cost remains to be further studied.

In the study of cascading failures in a network, the most used model is “capacity–load” model, and the most commonly used attack strategies are random attack strategy, which attack random chosen nodes, and deliberate attack strategy, which attack the nodes with the largest degree value or the largest betweenness in a network. However, the model and these attack strategies may not make full use of the network structure and functional information. This paper proposes a new attack strategy with consideration of the community structure of a power grid. The cascading fault of a power grid is simulated with applying the DC power flow model [27], which can better reflect the electrical characteristics of the power grid. With the DC power flow model, the current loading of a transmission line is defined as the current through it, and its capacity is $1+\alpha$ times of its initial value $I_{ij}\left(0\right)$. Power loading of a node is defined as $v_i\ast I_{oi}$, where $I_{oi}$ is the sum of currents flowing out of node $i$, and its capacity is $1+\beta$ times of its initial value. The capacity of each node is set to be large enough to avoid tripping during a cascading failure process. We vary the tolerance ratio of the transmission lines $\alpha$ while assessing the robustness of a power grid.

Based on the previous subnet division, this section will study degree-based and betweenness-based attack strategies, respectively. Each attack strategy includes global attack and community attack—for example, in the fourth division method of Section 4, IEEE39 standard network is divided into seven communities. Then, we will attack the nodes with the largest degree or betweenness in each community at the same time. Similarly, sorting the nodes in descending order of degree or betweenness, attack the first seven nodes with the largest degree or the largest betweenness value in the whole network, and observe the network invulnerability effect under the four attack strategies. The methods of attacking maximum degree nodes in the whole network and attacking maximum betweenness nodes in the whole network is called the MDA method and the MBA method, respectively. The method of attacking the maximum degree node of each subnet is called SMDA method, and the method of attacking the maximum betweenness node of each subnet is called SMBA method. In particular, the external connection of the subnet is removed when calculating the maximum degree node and the maximum betweenness node of the subnet. The simulation experiments on IEEE 39, IEEE 118, and IEEE 2383 standard test networks are carried out, respectively. The number of attacked nodes in each network is equal to the number of communities of that network. The average remaining power percentage (APM) defined in [28] is used to quantify the robustness of the power grid, where $\mathrm{APM}=1/M{\displaystyle \sum P_m/P}$, P_m is the maintained generation power of the generators after cascade failure, and P is the generation power of the generators before cascading failure. M is the number of times the experiment was repeated. After the cascade failure stops, the larger the APM, the better the robustness of the network. The simulation results are shown in Figure 6 and Figure 7.

FIGURE 6

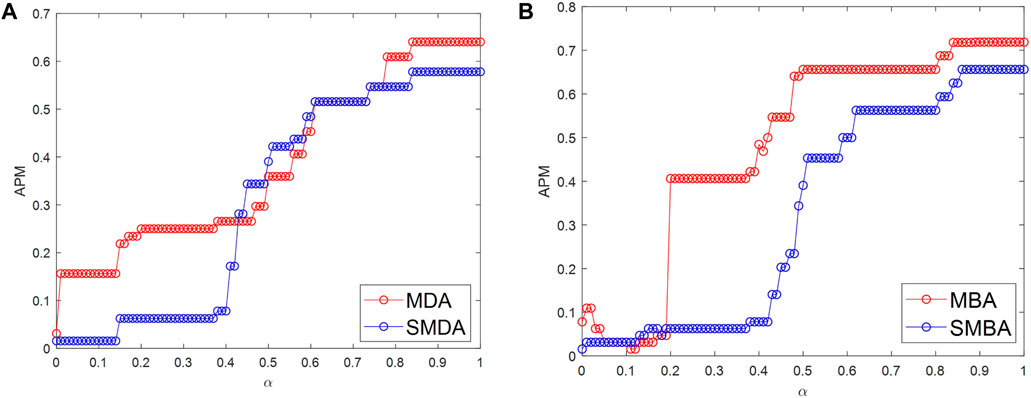
FIGURE 6. Robustness comparison of IEEE118 network under different attack strategies. (A) Attack strategy based on degree. (B) Attack strategy based on betweenness.

Using the improved algorithm, IEEE 39, IEEE 118, and IEEE2383 are divided into 7 subnets, 11 subnets, and 86 subnets, respectively, which equal to the attacked nodes in each network. Figure 6 and Figure 7 show the network robustness comparison of IEEE39, IEEE118, and IEEE2383 standard networks under different attack strategies.

FIGURE 7

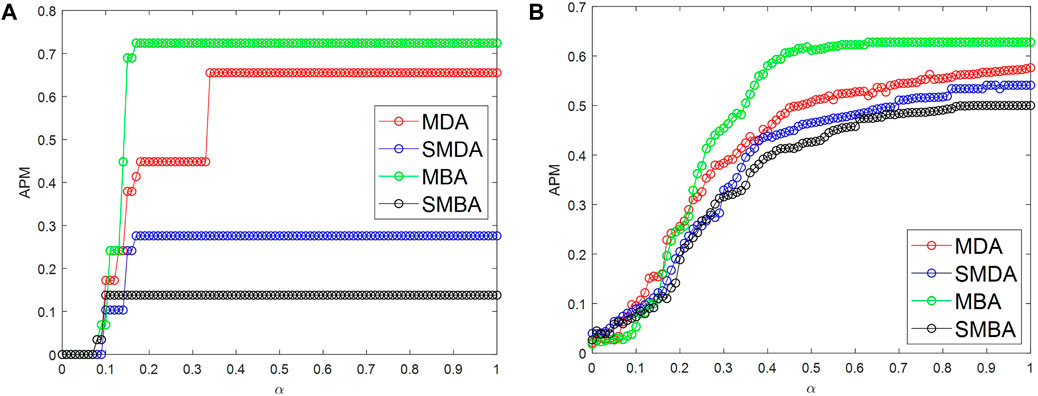
FIGURE 7. Robustness comparison diagram of the network under four attack strategies. (A) IEEE 39. (B) IEEE2383.

It can be seen that, between the degree-based attack or the betweenness-based attack, the attack effect of the attack strategy based on the subnet partition method proposed in this paper generally is better than that based on the global degree or betweenness.

Figure 7A is the robustness comparison of the IEEE39 standard network under four attack strategies, and Figure 7B is the robustness comparison of the IEEE2383 standard network under the four attack strategies. In the four attack strategies, the network shows a different invulnerability. The scale of cascading failures is the smallest when the nodes with the largest betweenness of the whole network were attacked, and the scale of network cascade failures is the largest when the nodes with the largest betweenness of the communities were attacked. The other two attack effects from strong to weak are attacking the largest degree nodes in the communities and attacking the largest degree nodes in the networks. To analyze the differences of attacked nodes under four attack strategies, the n maximum degree nodes in the network (n is the number of communities) are denoted as set $N_a$, and the n maximum degree nodes in each communities are denoted as set $N_b$, then $f_a=\mathrm{card}\left(N_a\cap N_b\right)/\mathrm{card}\left(N_a\right)$ is the ratio of the number of nodes that belong to $N_a\cap N_b$ to the number of nodes $N_a$. In a similar way, the n largest betweenness nodes in the network are denoted as set $N_c$, and the n largest betweenness nodes in each communities are denoted as set $N_d$, $f_b=\mathrm{card}\left(N_c\cap N_d\right)/\mathrm{card}\left(N_c\right)$ is the ratio of the number of nodes that belong to $N_c\cap N_d$ to the number of nodes $N_c$. The calculated results of the three networks are shown in Table 2.

TABLE 2

TABLE 2. The differences of attacked nodes under four attack strategies.

It can be seen from Table 2 that the value of $f_a$ is far greater than that of $f_b$ in the three networks, which means that most of the nodes with the largest degree in the community are the nodes with the largest degree of the whole network. However, the nodes with the largest betweenness in the communities usually are not those nodes with the largest betweenness of the whole network. Therefore, the attack effects of MBA and SMBA are the most different.

6 Conclusion

Based on community discovery in complex network theory, this paper proposes a power grid partitioning method considering generator nodes and connection weight. Firstly, the weighted network model of a power system is established. Then, the improved Fast-Newman hierarchy algorithm and a weighted modular Q function index are introduced, and the improvement of the partition process is carried out according to the characteristics of the actual power grid. Finally, the improved algorithm is compared with Fast-Newman algorithm to demonstrate its effectiveness and correctness. The sub-network partition method proposed in this paper comprehensively considers the electrical characteristics and topological characteristics of a power system. It ensures that each sub-network has at least one generator node after network partition, which can provide power supply for the loads of the sub-network after the breakdown of the power grid. It has a certain guiding significance for power grid partition.

In addition, several cascading fault attack strategies are studied based on the results of the subnet partition. The cascading fault scales are compared in several IEEE standard test networks for attacking those nodes with the largest degree or the largest betweenness of each subnet and for attacking the same number nodes with the largest degree or the largest betweenness of the whole network. The study shows that the attack strategy with attacking the largest betweenness node of each subnet is the best one. It means that subnet partition has a significant value on the identification of the key nodes of a power grid. Attacking the maximum betweenness node of each subnet has very serious attack consequences.

This paper only considers that each subnet contains generator nodes when partitioning a power grid and does not consider the power balance of power generation and power consumption in each subnet. In further research, the power of generators and loads can be taken into account when partitioning a power grid so that the difference between power generation and power consumption in each subnet is as small as possible. In this way, when a subnet needs to be disconnected from the main power grid for a serious fault, generator tripping and load shedding can be minimized.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/MATPOWER/matpower.

Author Contributions

YZ and HL performed the analysis. HL validated the analysis and drafted the manuscript. YZ reviewed the manuscript. YZ designed the research. All authors have read and approved the content of the manuscript.

Funding

We acknowledge support from the National Natural Science Foundation of China (grants 12162005 and 11562003) and the Guangxi Innovation Driven Development Project Guike AA21077015.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2021.790218/full#supplementary-material

References

1. Jia Y, Xu Z. A Direct Solution to Biobjective Partitioning Problem in Electric Power Networks. IEEE Trans Power Syst (2017) 32(3):2481–3. doi:10.1109/TPWRS.2016.2607638

CrossRef Full Text | Google Scholar

2. Karimipour H, Dinavahi V. Parallel Domain Decomposition Based Distributed State Estimation for Large-Scale Power Systems. IEEE Trans Ind Applicat (2015) 52(2):1. doi:10.1109/TIA.2015.2483703

CrossRef Full Text | Google Scholar

3. Chu C-C, Iu HH-C. Complex Networks Theory for Modern Smart Grid Applications: A Survey. IEEE J Emerg Sel Top Circuits Syst. (2017) 7(2):177–91. doi:10.1109/JETCAS.2017.2692243

CrossRef Full Text | Google Scholar

4. Dao VL, Bothorel C, Lenca P. Community Structure: A Comparative Evaluation of Community Detection Methods. Net Sci (2020) 8(1):1–41. doi:10.1017/nws.2019.59

CrossRef Full Text | Google Scholar

5. Mehrjerdi H, Lefebvre S, Saad M, Asber D. A Decentralized Control of Partitioned Power Networks for Voltage Regulation and Prevention against Disturbance Propagation. IEEE Trans Power Syst (2013) 28(2):1461–9. doi:10.1109/TPWRS.2012.2225154

CrossRef Full Text | Google Scholar

6. Li Z, Lou Y, Liu J, Liu S, Yang F, Fu Y. Optimal Partition of Power Distribution Network Service Areas Based on Improved K-Means Algorithm. In: International Conference on Power System Technology; 2014 Oct 20-22; Chengdu, China. IEEE (2014).

Google Scholar

7. Pahwa S, Youssef M, Schumm P, Scoglio C, Schulz N. Optimal Intentional Islanding to Enhance the Robustness of Power Grid Networks. Physica A: Stat Mech its Appl (2013) 392(17):3741–54. doi:10.1016/j.physa.2013.03.029

CrossRef Full Text | Google Scholar

8. Wang T, Li Y, Gu X, Jinghua J. Identification of the Key Transmission Sections Considering Optimization of Geographical Partition Boundary for Power Grids. Trans China Electrotechnical Soc (2014) 29(4):220–8. doi:10.19595/j.cnki.1000-6753.tces.2014.04.029

CrossRef Full Text | Google Scholar

9. Newman MEJ, Girvan M. Finding and Evaluating Community Structure in Networks. Phys Rev E (2004) 69(2):026113. doi:10.1103/PhysRevE.69.026113

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Agarwal G, Kempe D. Modularity-maximizing Graph Communities via Mathematical Programming. Eur Phys J B (2008) 66(3):409–18. doi:10.1140/epjb/e2008-00425-1

CrossRef Full Text | Google Scholar

11. Li Z, Zhang S, Wang R-S, Zhang X-S, Chen L. Quantitative Function for Community Detection. Phys Rev E (2008) 77(3):036109. doi:10.1103/PhysRevE.77.036109

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wei G. Power Grid Oriented Community and its Detection Method. Comp Appl Softw (2021) 38(04):88–94. doi:10.3969/j.Issn.1000-386x.2021.04.015

CrossRef Full Text | Google Scholar

13. Guerrero M, Montoya FG, Baños R, Alcayde A, Gil C. Community Detection in National-Scale High Voltage Transmission Networks Using Genetic Algorithms. Adv Eng Inform (2018) 38:232–41. doi:10.1016/j.aei.2018.07.001

CrossRef Full Text | Google Scholar

14. Newman MEJ. Finding Community Structure in Networks Using the Eigenvectors of Matrices. Phys Rev E (2006) 74:036104. doi:10.1103/PhysRevE.74.036104

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Lu P, Yu Z, Guo Y. A Novel Algorithm for Community Detection Based on Resistance Distance and Similarity. Mod Phys Lett B (2021) 35(09):2150164. doi:10.1142/s0217984921501645

CrossRef Full Text | Google Scholar

16. Li S, Jiang L, Wu X, Han W, Zhao D, Wang Z. A Weighted Network Community Detection Algorithm Based on Deep Learning. Appl Maths Comput (2021) 401(7):126012. doi:10.1016/j.amc.2021.126012

CrossRef Full Text | Google Scholar

17. Haq NF, Moradi M, Wang ZJ. Community Structure Detection from Networks with Weighted Modularity. Pattern Recognition Lett (2019) 122:14–22. doi:10.1016/j.patrec.2019.02.005

CrossRef Full Text | Google Scholar

18. Pan G, Wang X, Peng X, Wu X-M. Study of Power Grid Partition Identification Method Based on Community Structure Detection. Power Syst Prot Control (2013) 41(13):122–7.

Google Scholar

19. Chen Z, Xie Z, Zhang Q. Community Detection Based on Local Topological Information and its Application in Power Grid. Neurocomputing (2015) 170:384–92. doi:10.1016/j.neucom.2015.04.093

CrossRef Full Text | Google Scholar

20. Xia Y, Fan J, Hill D. Cascading Failure in Watts-Strogatz Small-World Networks. Physica A: Stat Mech its Appl (2010) 389(6):1281–5. doi:10.1016/j.physa.2009.11.037

CrossRef Full Text | Google Scholar

21. Yang G, Qi X, Liu L. Research on Network Robustness Based on Different Deliberate Attack Methods. Physica A: Stat Mech its Appl (2020) 545:123588. doi:10.1016/j.physa.2019.123588

CrossRef Full Text | Google Scholar

22. Li H, Du J, Peng X, Ding C Research on Cascading Invulnerability of Community Structure Networks under Intentional-Attack. J Comp Appl (2014) 34(4):935–8. doi:10.11772/j.issn.1001-9081.2014.04.0935

CrossRef Full Text | Google Scholar

23. Pizzuti C. Evolutionary Computation for Community Detection in Networks: A Review. IEEE Trans Evol Computat (2018) 22(3):464–83. doi:10.1109/TEVC.2017.2737600

CrossRef Full Text | Google Scholar

24. Shang Y. Generalized K-Core Percolation in Networks with Community Structure. SIAM J Appl Math (2020) 80(3):1272–89. doi:10.1137/19M1290607

CrossRef Full Text | Google Scholar

25. Zimmerman RD, Murillo-Sanchez CE, Thomas RJ, MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans Power Syst (2011) 26(1):12–9. doi:10.1109/TPWRS.2010.2051168

CrossRef Full Text | Google Scholar

26. Newman MEJ. Fast Algorithm for Detecting Community Structure in Networks. Phys Rev E (2004) 69(6):066133. doi:10.1103/PhysRevE.69.066133

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhang X, Tse CK. Assessment of Robustness of Power Systems from a Network Perspective. IEEE J Emerging Selected Top Circuits Syst (2015) 5(3):456–64. doi:10.1109/JETCAS.2015.2462152

CrossRef Full Text | Google Scholar

28. Wu J, Zhang X, Ma S, Rong Z, Tse CK. Bifurcation in Transmission Networks under Variation of Link Capacity. Int J Bifurcation Chaos (2018) 28(07):1850093. doi:10.1142/S0218127418500931

CrossRef Full Text | Google Scholar