Localization of Hidden Attractors in Chua’s System With Absolute Nonlinearity and Its FPGA Implementation

Investigation of the classical self-excited and hidden attractors in the modified Chua’s circuit is a hot and interesting topic. In this article, a novel Chua’s circuit system with an absolute item is investigated. According to the mathematical model, dynamic characteristics are analyzed, including symmetry, equilibrium stability analysis, Hopf bifurcation analysis, Lyapunov exponents, bifurcation diagram, and the basin of attraction. The hidden attractors are located theoretically. Then, the coexistence of the hidden limit cycle and self-excited chaotic attractors are observed numerically and experimentally. The numerical simulation results are consistent with the FPGA implementation results. It shows that the hidden attractor can be localized in the digital circuit.

1 Introduction

According to Jenkins [1] and Kuznetsov et al. [2], there are two kinds of attractors, namely, the self-excited attractors and the hidden attractors. It can be distinguished by considering whether the basin of attraction of an attractor intersects any arbitrarily small open neighborhood of an equilibrium. If it does, the attractor is a self-excited attractor; otherwise, it is hidden. Generally, the “self-excited” attractors are generated in a system from a small vicinity of an unstable equilibrium. However, for instance, the hidden attractor can be generated by a system without equilibria [3–5] or with one stable zero equilibrium [6–8]. Meanwhile, there is a concept in the nonlinear systems, which is the “extreme multistability” [9–12]. Those attractors are obtained in a multistability system with given parameters but using different initial conditions. Although the definitions of the hidden attractors and coexisting attractors are not the same, they can be observed using different initial conditions. Currently, investigation of the multiple coexisting hidden attractors in the nonlinear systems is a research hotspot [13–16]. It means that multiple coexisting attractors and hidden attractors are both found in the system with different initial conditions [17].

Currently, the multiple coexisting attractors can be analyzed by using the basin attraction plots [18, 19] in the initial condition plane in which different initial conditions are used, and characteristics of the attractors such as size, center of gravity, and bounds are considered. Usually, different colors represent different kinds of attractors in the initial condition plane. Also, there could be some rules for choosing the initial conditions for systems, such as the symmetric coexisting chaotic systems [20–22] and the self-reproducing chaotic systems [23, 24]. However, as the basin of attraction of the hidden attractors is not connected with equilibria, it should be noted that the location of hidden attractors could be a challenging task. At present, hidden attractors have been widely investigated by researchers such as Leonov et al. [8, 25, 26], Sajad et al. [27], Dudkowski et al. [28], Zhang et al. [29], and Stankevich et al. [30]. Especially, the method by Leonov et al. [8, 25, 26] can locate the exact positions of the hidden attractors for the given systems. In real applications, dynamics of the systems with hidden attractors is determined not only by the parameters but also by the initial conditions.

In 1984, a system was derived based on Chua’s circuit [31] with two capacitors, one inductor, one resistor, and one nonlinear element, and it shows that its attractor is different from that of the Lorenz system and Chen system. In 1986, the existence of chaotic attractors in Chua’s circuit was proven mathematically [32]. Because of its rich dynamic characteristic behaviors and plasticity of the nonlinear item, Chua’s circuit has aroused much interest of scholars. Zhong et al. [33] implemented Chua’s circuit with a cubic nonlinearity. Moreover, the bifurcation, chaos, hidden attractors, and synchronization of different Chua’s circuits were investigated in Refs. [34–36]. Meanwhile, designing multiscroll chaotic systems based on Chua’s system by expanding the index two saddle coke equilibrium points has aroused, increasing research interests [37, 38]. Furthermore, hidden attractors and coexisting attractors in Chua’s circuit have been widely investigated [39, 40]. By replacing the nonlinear element in Chua’s circuit with memristor, memristor-based Chua’s circuits are designed, and then dynamic analysis and applications of those circuits are carried out [41–43]. In conclusion, Chua’s circuit provides a basis for designing nonlinear circuits with complex dynamic behaviors.

In the real applications, to find hidden chaotic attractors, we need to use the particular initial conditions. Thus, analog circuit implementation for hidden attractors becomes a key issue. Although analog circuit implementation of chaotic systems can generate real chaos, the initial conditions cannot be set, artificially and accurately. Compared with analog circuit implementation, digital circuit implementation of chaotic systems has the advantages such as reproducibility, good stability, and good controllability. Meanwhile, the initial conditions can be set accordingly. As a result, digital circuit implementation including DSP implementation [44], FPGA implementation [45], and microcontroller implementation [46] of chaotic systems has aroused much research interest. However, there are few reports regarding digital circuit implementation of hidden chaotic systems with observation of hidden attractors in the oscilloscope.

Motivated by the above discussions, in this article, a Chua’s system with an absolute item is investigated. Then, the dissipativity, equilibria, stability, and Hopf bifurcation diagram are studied, and the coexistence hidden attractors are investigated theoretically and demonstrated by numerical simulation and FPGA circuit realization. Specifically, we will use the method proposed by Leonov et al. [8, 25, 26] to find the initial conditions for the hidden attractors. Phase diagram and basin attraction plots are used to verify the effectiveness of the analyses.

The rest of this article is organized as follows. In Section 2, the modified Chua’s system is presented, and its equilibrium analysis, Hopf bifurcation analysis, bifurcation diagram, Lyapunov exponents, coexisting attractors, and basin attractions are analyzed. In Section 3, location of the hidden attractors in Chua’s circuit system is investigated theoretically and numerically. In Section 4, FPGA implementation of Chua’s system is carried out, and hidden attractors are observed. Finally, the results are summarized in Section 5.

2 The Modified Chua’s System and Its Dynamics

The absolute circuit x|x| can increase the nonlinearity of the circuit. For instance, Tang et al. [47, 48] introduced the absolute function x|x| to Chua’s system and Chen system and show the role of the function as a chaos generator in nonautonomous systems. Here, a Chua’s system with absolute item is investigated, and the system is defined by [47, 48]

$\left\{\begin{array}{c}\dot{x}=\alpha (y+mx-x|x|)\hfill \\ \dot{y}=x-cy+z\hfill \\ \dot{z}=-\beta y\hfill \end{array}\right.,(1)$

where α, β, c, and m are the system parameters, and x, y, and z are the state variables.

2.1 Basic Properties and Equilibria

2.1.1 Dissipativity

According to system (1), we have

$\nabla V=\frac{\partial \dot{x}}{\partial x}+\frac{\partial \dot{y}}{\partial y}+\frac{\partial \dot{z}}{\partial z}=\alpha \left(m-|x|-xsgn(x)-\frac{1}{\alpha }\right).(2)$

Obviously, when $m<\frac{1}{\alpha }$, we get ∇V < 0. It means that the system is dissipative. At this point, the solution of system (1) is bounded and could be chaotic.

2.1.2 Symmetry

As system (1) satisfies (x, y, z) ↔ ( −x, −y, −z), it is symmetric to the origin in the state variable space.

2.1.3 Equilibria and Stability

The equilibrium points of the system are (0, 0, 0) and (±m, 0, ∓m).

Theorem 1 If α > 0, β > 0, and m > 0 hold, the equilibria point O(0, 0, 0) is unstable.

Proof The Jacobian matrix of system (1) at the equilibria point O(0, 0, 0) is given by

$J_0=\left|\begin{array}{ccc}\hfill \alpha m\hfill & \hfill \alpha \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill -c\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill -\beta \hfill & \hfill 0\hfill \end{array}\right|,(3)$

Then, its characteristic equation is denoted as

$P_0(\lambda )={\lambda }^3+{\lambda }^2(c-\alpha m)+\lambda (\beta -\alpha -\alpha m)-\alpha \beta m=0.(4)$

If α > 0, β > 0, and m > 0, we have −αβm < 0. According to the Routh–Hurwitz criterion, Eq.(4) has at least one positive real solution. It means that the system is unstable at the point O(0, 0, 0) if α, β, and m are positive real numbers. End proof.For the equilibria point P_± = (±m, 0, ∓m), the Jacobian matrix is

$J_{\pm }=\left|\begin{array}{ccc}\hfill -\alpha m\hfill & \hfill \alpha \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill -c\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill -\beta \hfill & \hfill 0\hfill \end{array}\right|,(5)$

and its characteristic equation is

${\lambda }^3+{\lambda }^2(c+\alpha m)+\lambda (\beta -\alpha +\alpha cm)+\alpha \beta m=0.(6)$

Let p = c + αm, q = β − α + αcm, and r = αβm, we have

${\lambda }^3+p{\lambda }^2+q\lambda +r=0.(7)$

As α > 0, β > 0, c > 0, and m > 0, thus r > 0, thus Eq. 7 has at least one negative root. Let f(λ) = λ³ + pλ² + qλ + r, thus $\frac{df(\lambda )}{d\lambda }=3{\lambda }^2+2p\lambda +q$. When Δ = p² − 3q is defined, the following theorem is obtained.

Theorem 2 If Δ < 0, then the system has no positive roots and it is asymptotically stable. If Δ ≥ 0, ${\lambda }_0=\frac{1}{3}(-p+\sqrt{\mathrm{\Delta }})>0$ and f(λ₀) ≤ 0, the system has two positive roots, then P_± are unstable saddle points.

2.1.4 Hopf Bifurcation Analysis

According to the above section, the equilibria point O(0, 0, 0) is unstable. Thus, we focus on the bifurcation near the equilibria point P_±(±m, 0 ∓ m). Suppose that there is a pair of pure imaginary roots $i\omega \left(\omega >0\right)$; according to Eq. 7, we have

$\left\{\begin{array}{c}-{\omega }^3+\omega (\beta -\alpha +\alpha cm)=0\hfill \\ -{\omega }^2(c+\alpha m)+\alpha \beta m=0\hfill \end{array}\right..(8)$

Set the system parameter α as the bifurcation parameter, based on Eq. 8, we obtain

${\alpha }^2(c{m}^2-m)+\alpha (-c+c^{2}m)+c\beta =0.(9)$

When α > 0, we have the following conclusions: (1) if cm ≥ 1, then Eq. 7 has no positive roots; (2) if cm < 1, then Eq. 6 has one positive root.

As α > 0 is the bifurcation parameter, the critical point α_H satisfies the following equation:

$\left\{\begin{array}{c}{\alpha }_H=\frac{-c(cm-1)-\sqrt{\mathrm{\Delta }}}{2m(cm-1)}\hfill \\ \omega =\sqrt{\frac{\alpha \beta m}{c+\alpha m}}\hfill \end{array}\right..(10)$

where $\mathrm{\Delta }={(-c+c^{2}m)}^2-4(-m+c{m}^2)c\beta$.

Differentiating Eq. 6 versus α, we have

$\frac{d\lambda }{d\alpha }=-\frac{{\lambda }^{2}m+\lambda (cm-1)+\beta m}{3{\lambda }^2+2\lambda (c+\alpha m)+\lambda (\beta -\alpha +\alpha cm)}.(11)$

Substituting α_H to Eq. 11 and λ(α_H) = iω, the calculation result is

${\left.\frac{d\mathrm{Re}(\lambda )}{d\alpha }\right|}_{\alpha ={\alpha }_H}=-\frac{{\omega }^2(cm-1)(c+{\alpha }_{H}m)}{2{\omega }^4+2{\omega }^2{(c+{\alpha }_{H}m)}^2}.(12)$

According to Eq. 12, when cm < 1, ${\left.\frac{d\mathrm{Re}(\lambda )}{d\alpha }\right|}_{\alpha ={\alpha }_H}>0$. Thus, we have the result as presented in Theorem 3.

Theorem 3When the parameter α passes through the critical value α_H, system (1) undergoes a Hopf bifurcation at equilibria P_±(±m, 0 ∓ m).

2.2 Dynamic Analysis

Set β = 100, m = 0.2, and c = 1.6, bifurcation diagram and Lyapunov exponents of the system with α are illustrated in Figure 1. For the bifurcation diagrams, the initial conditions for the red are [x₀, y₀, z₀] = [0.01, 0, 0.01]; the initial conditions for the blue is [x₀, y₀, z₀] = [−0.01, 0, −0.01]. It shows that when α < 70, the system has coexisting attractors and enters to chaos through period doubling bifurcation. After this, the system has periodic windows with the increase of α. It indicates that the system has rich dynamics.

FIGURE 1

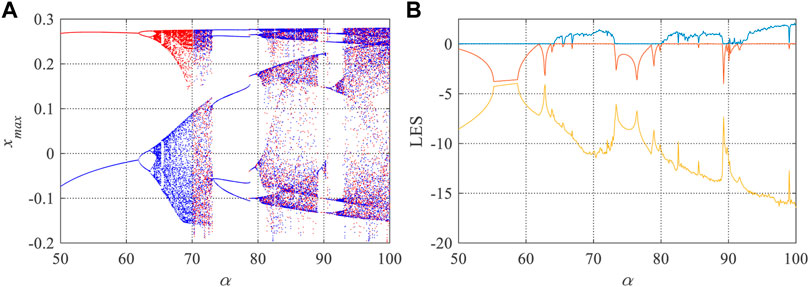
FIGURE 1. Dynamics of the modified Chua’s system with the variation of the parameter α. (A) Bifurcation diagram; (B) Lyapunov exponents (LEs).

2.3 Multistability With Symmetry

First, fix α = 50, β = 100, m = 0.2, and c = 1.6. x₀ varies from −2 to 2 with step size of 0.0268, y₀ varies from −0.2 to 0.2 with step size of 0.0027, and y₀ varies from −4 to 4 with step size of 0.0537. Set z₀ = −1 and α = 50, basin of attraction in the x₀ − y₀ plane is presented (Figure 2A). Let y₀ = −0.1 and x₀ = 0.3, basins of attraction in the x₀ − z₀ plane and y₀ − z₀ are illustrated in Figures 2B,C, respectively. Moreover, when α = 69, let z₀ = −1, y₀ = 0.1 and x₀ = 0.3, basins of attraction in the x₀ − y₀ plane, x₀ − z₀ plane, and y₀ − z₀ are shown in Figures 2D,E,F, respectively. It shows that the system has three coexisting states with different initial conditions.

FIGURE 2

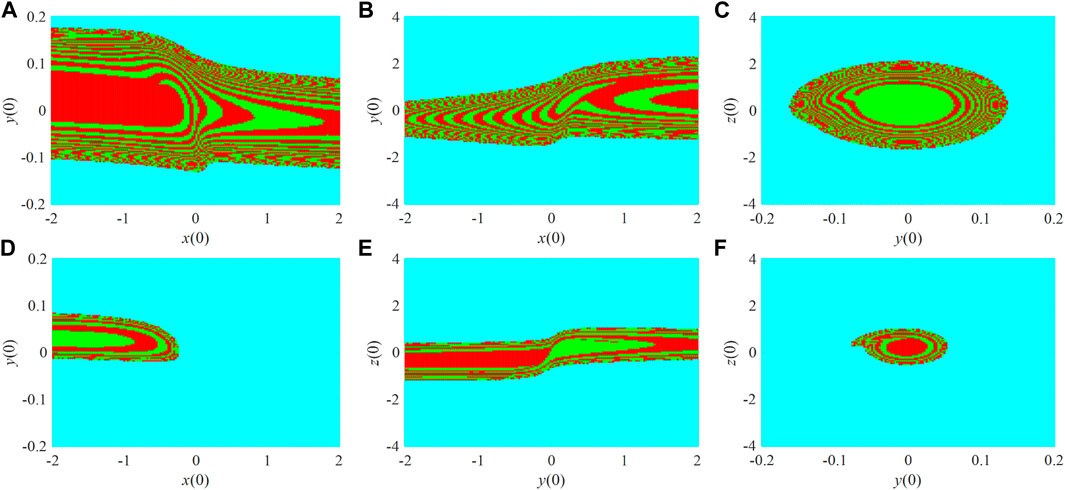
FIGURE 2. Basin of attractions of the system with different α and in different planes. (A) α = 50, z₀ = −1, and x₀ − y₀ plane; (B) α = 50, y₀ = −0.1, and x₀ − z₀ plane; (C) α = 50, x₀ = 0.3, and y₀ − z₀ plane; (D) α = 69, z₀ = −1, and x₀ − y₀ plane; (E) α = 69, y₀ = 0.1, and x₀ − z₀ plane; (F) α = 69, x₀ = 0.3, and y₀ − z₀ plane.

Moreover, phase diagrams of Chua’s system with different parameters and initial conditions are presented. The initial conditions for the red attractors are [x₀, y₀, z₀] = [0.01, 0, 0.01], and the initial conditions for the blue attractors are [x₀, y₀, z₀] = [−0.01, 0, −0.01]. Phase diagrams with α = 60, α = 63, α = 63.8, α = 69, α = 72, and α = 75 are shown in Figure 3. Coexisting symmetric periodic-1, periodic-2, and periodic-4 attractors are found in Figures 3A–C; coexisting chaotic attractors are observed in Figure 3D. Figures 3E,F do not show coexisting attractors, but different chaotic attractor and periodic circle are found. However, it shows only two coexisting symmetric attractors. Meanwhile, it shows that there are third regions in the basin attractions; thus, there should be one more attractor that is hidden. In the next section, hidden attractors in Chua’s system are investigated.

FIGURE 3

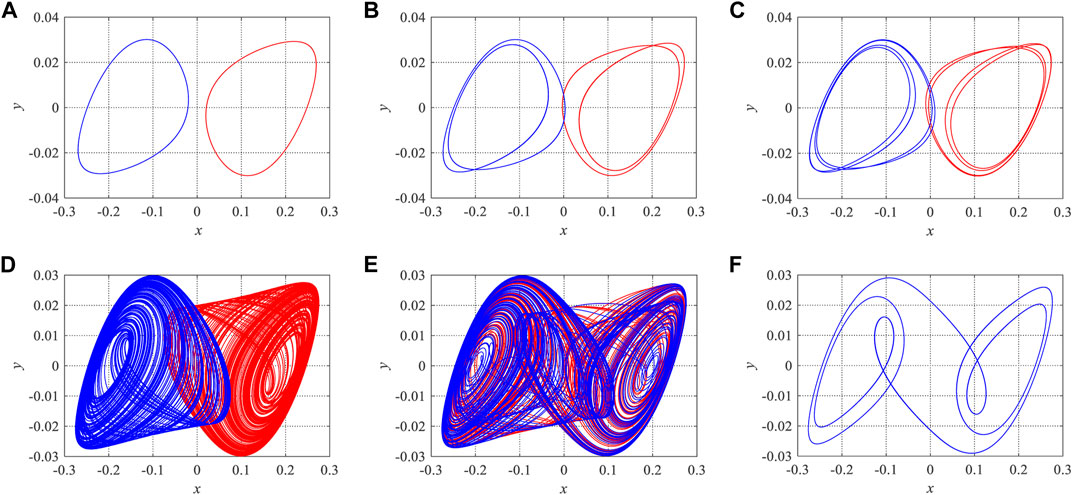
FIGURE 3. Phase diagram of the modified Chua’s system with different values of the parameter α, the red attractor with initial condition $[x_0,y_0,z_0]=\left[\right.0.01,\mathrm{0,0.01}$ and blue attractor with initial condition [x₀, y₀, z₀] = [ −0.01, 0, −0.01]. (A) α = 60, (B) α = 63, (C) α = 63.8, (D) α = 69, (E) α = 72, (F) α = 75.

3 Hidden Attractors

3.1 Localization of Hidden Attractors

Leonov et al. [8, 25, 26] proposed a scheme that is used to find the location of the hidden attractors in the chaotic systems. We here use this method to find the initial conditions for the hidden attractors in the system (1). According to the scheme, the system is rewritten as a lure’s system, which is given by

$\frac{dx}{dt}=Px+q\psi (r^{\ast }x),x\in R^3,(13)$

where $P=\left(\begin{array}{ccc}\hfill \alpha m\hfill & \hfill \alpha \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill -c\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill -\beta \hfill & \hfill 0\hfill \end{array}\right)$, $q=\left(\begin{array}{c}\hfill -\alpha \hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)$, $r=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)$, $\psi (\sigma )=\sigma \left|\sigma \right|$. Let k be the coefficient of harmonic linearization, and ɛ be an infinitesimal number, the system (13) can be rewritten as

$\frac{dx}{dt}=P_{0}x+q\epsilon \delta (r^{\ast }x).(14)$

where $P_0=\left(\begin{array}{ccc}\hfill \alpha \left(m+k\right)\hfill & \hfill \alpha \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill -c\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill -\beta \hfill & \hfill 0\hfill \end{array}\right)$, ${\lambda }_{\mathrm{1,2}}^{P_0}=\pm i\omega 0$, ${\lambda }_3^{P_0}=-d<0$ and δ(σ) = ψ(σ) − kσ.

Using nonsingular linear transformation x = Sy, the system (14) can be transformed as

$\frac{dy}{dt}=Hx+b\epsilon \varphi (u^{\ast }y)(15)$

where $\mathbf{H}=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -{\omega }_0\hfill & \hfill 0\hfill \\ \hfill {\omega }_0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -d\hfill \end{array}\right)$, $b=\left(\begin{array}{c}\hfill b_1\hfill \\ \hfill b_2\hfill \\ \hfill 1\hfill \end{array}\right)$ and $u=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill -h\hfill \end{array}\right)$.

The transfer function of the system (15) can be expressed as

$W_H(p)=\frac{-b_{1}p+b_2{\omega }_0}{p^2+{\omega }_0^2}+\frac{h}{p+d}(16)$

The transfer functions of system (14) can be expressed as

$W_{P_0}(p)=r^{\ast }{(P_0-pI)}^{-1}q(17)$

where p is complex variables; ω₀ is the initial frequency, which can be calculated by ImW_H(ω₀) = 0; k is the harmonic linearization coefficient, which can be calculated by $k=-{(R_e{W}_H(i{\omega }_0))}^{-1}$. From the equivalence of the transfer functions of system (14) and system (15), then it can be concluded:

$\left\{\begin{array}{c}k=(\beta -\alpha (1+cm)-{\omega }_0^2)/\alpha c\hfill \\ d=({\omega }_0^2-\beta +\alpha +c^2)/c\hfill \\ h=(\alpha \beta -\alpha cd+\alpha d^2)/({\omega }_0^2+d^2)\hfill \\ b_1=(\alpha \beta -\alpha cd-\alpha {\omega }_0^2)/({\omega }_0^2+d^2)\hfill \\ b_2=(\alpha c{\omega }_0^2+\alpha \beta d-\alpha d{\omega }_0^2)/({\omega }_0({\omega }_0^2+d^2))\hfill \end{array}\right.(18)$

The system (14) is transformed by nonsingular linear transformation; it can be concluded that:

$\left\{\begin{array}{c}H=S^{-1}{P}_{0}S\hfill \\ b=S^{-1}q\hfill \\ u^{\ast }=r^{\ast }S\hfill \end{array}\right.\cdot (19)$

Let $S=\left(\begin{array}{ccc}\hfill s_{11}\hfill & \hfill s_{12}\hfill & \hfill s_{13}\hfill \\ \hfill s_{21}\hfill & \hfill s_{22}\hfill & \hfill s_{23}\hfill \\ \hfill s_{31}\hfill & \hfill s_{32}\hfill & \hfill s_{33}\hfill \end{array}\right)$, we can obtain

$\left\{\begin{array}{c}{s}_{11}=1,s_{12}=0,s_{13}=-h\hfill \\ s_{21}=-(m+k)\hfill \\ s_{22}=-\frac{{\omega }_0}{\alpha }\hfill \\ s_{23}=-\frac{h(\alpha (m+k)+d)}{\alpha }\hfill \\ s_{31}=-\frac{\beta }{\alpha },s_{32}=-\frac{\beta (m+k)}{{\omega }_0}\hfill \\ s_{33}=\frac{h\beta (\alpha (m+k)+d)}{\alpha d}\hfill \end{array}\right.\cdot (20)$

For the infinitesimal number ɛ, the initial value of system (15) is

$y(0)=\left(\begin{array}{c}\hfill y_1(0)\hfill \\ \hfill y_2(0)\hfill \\ \hfill y_3(0)\hfill \end{array}\right)=\left(\begin{array}{c}\hfill a_0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right).(21)$

$$

$x\left(0\right)=Sy(0)=S\left(\begin{array}{c}\hfill x_1(0)\hfill \\ \hfill x_2(0)\hfill \\ \hfill x_3(0)\hfill \end{array}\right)=\left(\begin{array}{c}\hfill a_0{s}_{11}\hfill \\ \hfill a_0{s}_{21}\hfill \\ \hfill a_0{s}_{31}\hfill \end{array}\right).(22)$

In this way, the initial value of the system (1) is as follows:

$\left\{\begin{array}{c}x\left(0\right)=a_0\hfill \\ y\left(0\right)=-a_0\left(m+k\right)\hfill \\ z\left(0\right)=-a_0\frac{\beta }{\alpha }\hfill \end{array}\right.(23)$

here, the description function of a₀ can be calculated as follows:

$\mathrm{\Phi }(a)={\int }_0^{2\pi /{\omega }_0}\left({\phi }_1\left(t\right)+{\phi }_2\left(t\right)\right)dt(24)$

where ${\phi }_1\left(t\right)={\delta }_1\left((\cos {\omega }_{0}t)a,(\sin {\omega }_{0}t)a,0\right)\cos {\omega }_{0}t$ and ${\phi }_2\left(t\right)={\delta }_2\left((\cos {\omega }_{0}t)a,(\sin {\omega }_{0}t)a,0\right)\sin {\omega }_{0}t$. The description function satisfies Φ(a₀) = 0 and $</b><b>b_1\frac{d\mathrm{\Phi }(a)}{da}{|}_{a=a_0}\ne 0</b><b>$.

3.2 Numerical Verification

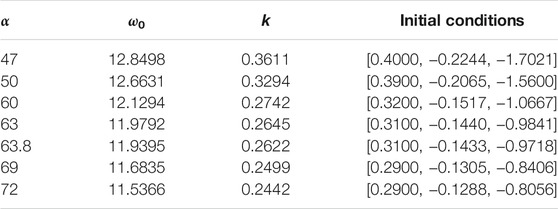
Set β = 100, m = 0.2, and c = 1.6, the initial conditions of hidden attractors for different α are presented in Table 1. Meanwhile, values of ω₀ and k are listed, correspondingly. Based on the initial condition obtained, the coexisting hidden attractors, limited circles, and chaotic attractors are presented in Figure 4. It shows that the hidden attractors are not chaotic, but they are periodic circles.

TABLE 1

TABLE 1. Initial conditions of hidden attractors for different α.

FIGURE 4

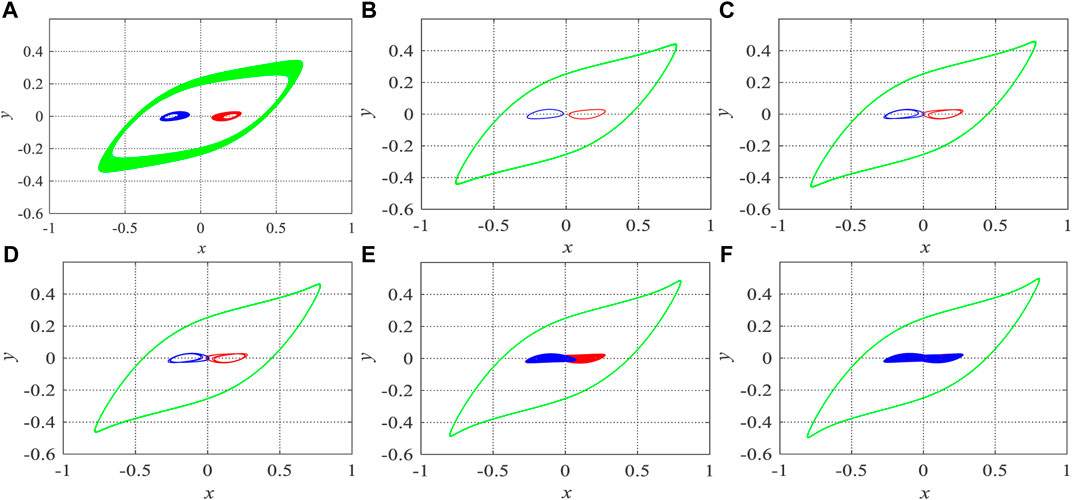
FIGURE 4. Coexisting hidden attractors of Chua’s system, where the red attractors and blue attractors are those from Figure 3, and the green attractors are the hidden attractors. (A) α = 50, [x₀, y₀, z₀] = [0.3900, −0.2065, 1.5600]; (B) α = 60, [x₀, y₀, z₀] = [0.3200, −0.1517, 1.0667]; (C) α = 63, [x₀, y₀, z₀] = [0.3100, −0.1440, 0.9841]; (D) α = 63.8, [x₀, y₀, z₀] = [0.3100, −0.1433, 0.9718]; (E) α = 69, [x₀, y₀, z₀] = [0.2900, −0.1305, 0.8406]; (F) α = 72, [x₀, y₀, z₀] = [0.2900, −0.1288, 0.8056].

4 FPGA Implementation

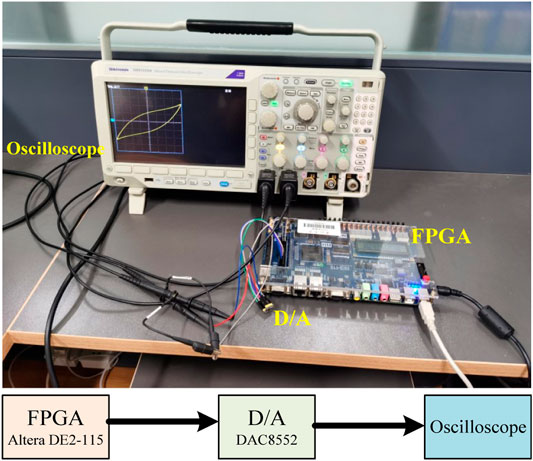
In this section, FPGA implementation of Chua’s system is carried out. We implement Chua’s system in Altera DE2-115 with EP4CE115F29C7. Figure 5 shows the physical implementation platform of Chua’s system with absolution item, where the system is solved by the fourth-order Runge–Kutta algorithm. Then, the output of the Altera DE2-115 contains two 16-bit current and voltage signals, which are converted by the DAC8552 chip. The obtained attractors are displayed in the oscilloscope and captured for further analysis.

FIGURE 5

FIGURE 5. FPGA implementation platform.

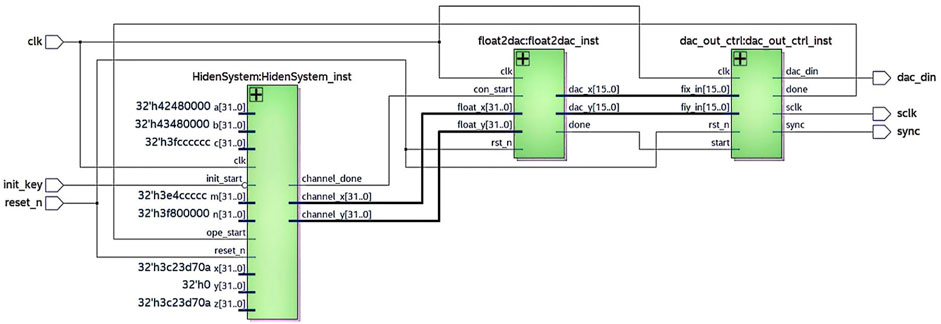
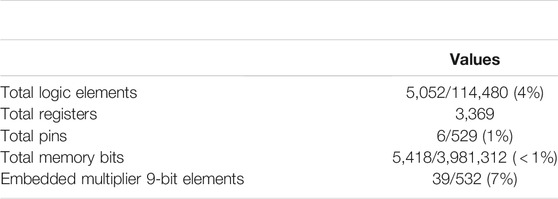
System chart based on the FPGA implementation is shown in Figure 6. There are three modules including system module, float number to DAC input number module, and DAC output control module. As a result, the generated signals are sent to DAC8552. The total resources occupied by the system are presented in Table 2. The total logic elements, total memory bits, and embedded multiplier 9-bit elements costs are 4%, 0.14%, and 7%, respectively. In addition, the designed system requires very little logic, register, and memory resources.

FIGURE 6

FIGURE 6. System chart based on the FPGA implementation.

TABLE 2

TABLE 2. Compilation resource report

The obtained phase diagrams are presented in Figure 7. And the parameter and initial conditions for Figure 7A are α = 60 and [x₀, y₀, z₀] = [0.3200, −0.1517, 1.0667]; those for Figure 7B are α = 63, [x₀, y₀, z₀] = [0.3100, −0.1440, 0.9841]; those for Figure 7C are α = 69, [x₀, y₀, z₀] = [0.2900, −0.1305, 0.8406]; and those for Figure 7D are α = 72, [x₀, y₀, z₀] = [0.2900, −0.1288, 0.8056]. Meanwhile, for the given parameters, the coexisting periodic circles or chaotic attractors are presented with initial conditions [x₀, y₀, z₀] = [0.01, 0, 0.01] and [x₀, y₀, z₀] = [−0.01, 0, −0.01]. For a given α, the captured phase diagrams are put together in the same figure, and coexisting hidden attractors are observed in the FPGA digital circuit.

FIGURE 7

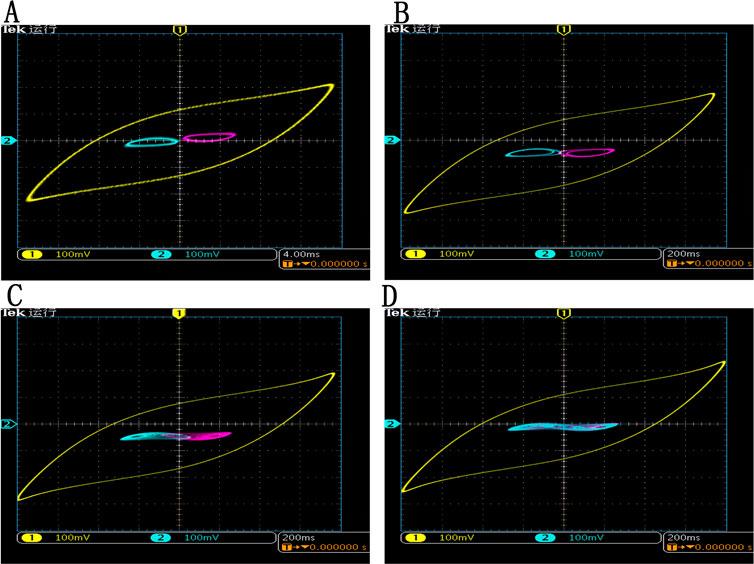
FIGURE 7. Coexisting hidden attractors based on the FPGA. (A) α = 60, [x₀, y₀, z₀] = [0.3200, −0.1517, 1.0667], (B) α = 63, [x₀, y₀, z₀] = [0.3100, −0.1440, 0.9841], (C) α = 69, [x₀, y₀, z₀] = [0.2900, − 0.1305, 0.8406], (D) α = 72, [x₀, y₀, z₀] = [0.2900, −0.1288, 0.8056].

The main difficulty for analog circuit implementation of hidden attractor chaotic system is to locate the initial conditions. Thus, it is almost impossible to find the target hidden attractors in the analog circuits. However, when the hidden chaotic system is realized in the FPGA circuit, the initial condition can be set; thus, hidden attractors can be observed.

5 Conclusion

In this article, dynamics and hidden attractors and modified Chua’s circuit with an absolute item are investigated. The dynamics of the system is analyzed by means of stability analysis, Hopf bifurcation, Lyapunov exponents, bifurcation diagrams, phase diagrams, and basin of attraction plots. It shows that the system has rich dynamics with the variation of the system parameter α, and the system enters to chaos through period-doubling bifurcation. The locations of the hidden periodic circles are found by using the describing function method. The coexisting hidden periodic circles, chaotic attractors, and periodic circles are observed. Finally, the FPGA digital circuit of the system is realized. It shows that the FPGA results are consistent with the numerical simulation results.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XW, system analysis, draft written; HW FPGA implementation, manuscript revisement; SH, numerical analysis, checking the whole analysis.

Funding

This work was supported by the Natural Science Foundation of China (Nos. 62061008, 61901530, 62071496, 11747150), the Natural Science Foundation of Hunan Province (No. 2020JJ5767), the Guizhou Provincial Science and Technology Foundation (No. 20181115), the Guizhou Province Science and Technology Plan Project (No. 2018 5769) and the Doctoral Scientific Research Foundation of Guizhou Normal University (2017).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Jenkins A. Self-oscillation. Phys Rep (2013) 525(2):167–222. doi:10.1016/j.physrep.2012.10.007

CrossRef Full Text | Google Scholar

2. Kuznetsov NV, Kuznetsova OA, Leonov GA, Mokaev TN, Stankevich NV. Hidden Attractors Localization in Chua Circuit via the Describing Function Method. IFAC-PapersOnLine (2017) 50(1):2651–6. doi:10.1016/j.ifacol.2017.08.470

CrossRef Full Text | Google Scholar

3. Thanh Pham V, Volos C, Jafari S, Kapitaniak T. Coexistence of Hidden Chaotic Attractors in a Novel No-Equilibrium System. Nonlinear Dyn (2017) 87(3):2001–10.

CrossRef Full Text | Google Scholar

4. Leonov GA, Kuznetsov NV, Mokaev TN. Hidden Attractor and Homoclinic Orbit in Lorenz-like System Describing Convective Fluid Motion in Rotating Cavity. Commun Nonlinear Sci Numer Simulation (2015) 28(1-3):166–74. doi:10.1016/j.cnsns.2015.04.007

CrossRef Full Text | Google Scholar

5. Tutueva AV, Karimov TI, Nepomuceno EG, Butusov DN. Detection of Hidden Oscillations in Systems without Equilibrium. Int J Bifurcation Chaos (2021) 31(03):2150043. doi:10.1142/s0218127421500437

CrossRef Full Text | Google Scholar

6. Bao BC, Jiang P, Xu Q, Chen M. Hidden Attractors in a Practical Chua's Circuit Based on a Modified Chua's Diode. Electron Lett (2016) 52(1):23–5. doi:10.1049/el.2015.2493

CrossRef Full Text | Google Scholar

7. Li Q, Zeng H, Yang X. On Hidden Twin Attractors and Bifurcation in the Chua’s Circuit. Nonlinear Dyn (2014) 77(2):255–66. doi:10.1007/s11071-014-1290-8

CrossRef Full Text | Google Scholar

8. Leonov GA, Kuznetsov NV, Vagaitsev VI. Localization of Hidden Chuaʼs Attractors. Phys Lett A (2011) 375(23):2230–3. doi:10.1016/j.physleta.2011.04.037

CrossRef Full Text | Google Scholar

9. Pisarchik A, Jaimes-Reátegui R, Rodríguez-Flores C, García-López J, Huerta-Cuellar G, Martín-Pasquín F. Secure Chaotic Communication Based on Extreme Multistability. J Franklin Inst (2021) 358(4):2561–75. doi:10.1016/j.jfranklin.2021.01.013

CrossRef Full Text | Google Scholar

10. Yuan F, Wang G, Wang X. Extreme Multistability in a Memristor-Based Multi-Scroll Hyper-Chaotic System. Chaos (2016) 26(7):073107. doi:10.1063/1.4958296

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Jafari S, Ahmadi A, Khalaf AJM, Abdolmohammadi HR, Pham V-T, Alsaadi FE. A New Hidden Chaotic Attractor with Extreme Multi-Stability. AEU - Int J Electro Commun (2018) 89:131–5. doi:10.1016/j.aeue.2018.03.037

CrossRef Full Text | Google Scholar

12. Chen M, Sun M, Bao B, Wu H, Xu Q, Wang J. Controlling Extreme Multistability of Memristor Emulator-Based Dynamical Circuit in Flux-Charge Domain. Nonlinear Dyn (2018) 91(2):1395–412. doi:10.1007/s11071-017-3952-9

CrossRef Full Text | Google Scholar

13. Bayani A, Rajagopal K, Khalaf AJM, Jafari S, Leutcho GD, Kengne J. Dynamical Analysis of a New Multistable Chaotic System with Hidden Attractor: Antimonotonicity, Coexisting Multiple Attractors, and Offset Boosting. Phys Lett A (2019) 383(13):1450–6. doi:10.1016/j.physleta.2019.02.005

CrossRef Full Text | Google Scholar

14. Liu L, Du C, Zhang X, Li J, Shi S. Dynamics and Entropy Analysis for a New 4-d Hyperchaotic System with Coexisting Hidden Attractors. Entropy (2019) 21(3):287. doi:10.3390/e21030287

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Liu T, Yan H, Banerjee S, Mou J. A Fractional-Order Chaotic System with Hidden Attractor and Self-Excited Attractor and its Dsp Implementation. Chaos, Solitons & Fractals (2021) 145:110791. doi:10.1016/j.chaos.2021.110791

CrossRef Full Text | Google Scholar

16. Bao H, Hu A, Liu W, Bao B. Hidden Bursting Firings and Bifurcation Mechanisms in Memristive Neuron Model with Threshold Electromagnetic Induction. IEEE Trans Neural Netw Learn Syst (2019) 31(2):502–11. doi:10.1109/TNNLS.2019.2905137

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Xu Q, Cheng S, Ju Z, Chen M, Wu H. Asymmetric Coexisting Bifurcations and Multi-Stability in an Asymmetric Memristive Diode-Bridge-Based Jerk Circuit. Chin J Phys (2021) 70:69–81. doi:10.1016/j.cjph.2020.11.007

CrossRef Full Text | Google Scholar

18. Li C, Sprott JC. Chaotic Flows with a Single Nonquadratic Term. Phys Lett A (2014) 378(3):178–83. doi:10.1016/j.physleta.2013.11.004

CrossRef Full Text | Google Scholar

19. Li C, Sprott JC. Multistability in a Butterfly Flow. Int J Bifurcation Chaos (2013) 23(12):1350199. doi:10.1142/s021812741350199x

CrossRef Full Text | Google Scholar

20. Lai Q. A Unified Chaotic System with Various Coexisting Attractors. Int J Bifurcation Chaos (2021) 31(01):2150013. doi:10.1142/s0218127421500139

CrossRef Full Text | Google Scholar

21. Lai Q, Nestor T, Kengne J, Zhao X-W. Coexisting Attractors and Circuit Implementation of a New 4d Chaotic System with Two Equilibria. Chaos, Solitons & Fractals (2018) 107:92–102. doi:10.1016/j.chaos.2017.12.023

CrossRef Full Text | Google Scholar

22. Wang Y, Sun K, He S, Wang H. Dynamics of Fractional-Order Sinusoidally Forced Simplified Lorenz System and its Synchronization. Eur Phys J Spec Top (2014) 223(8):1591–600. doi:10.1140/epjst/e2014-02181-3

CrossRef Full Text | Google Scholar

23. Li C, Sprott JC, Hu W, Xu Y. Infinite Multistability in a Self-Reproducing Chaotic System. Int J Bifurcation Chaos (2017) 27(10):1750160. doi:10.1142/s0218127417501607

CrossRef Full Text | Google Scholar

24. He S, Li C, Sun K, Jafari S. Multivariate Multiscale Complexity Analysis of Self-Reproducing Chaotic Systems. Entropy (2018) 20(8):556. doi:10.3390/e20080556

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Leonov GA, Kuznetsov NV, Vagaitsev VI. Hidden Attractor in Smooth Chua Systems. Physica D: Nonlinear Phenomena (2012) 241(18):1482–6. doi:10.1016/j.physd.2012.05.016

CrossRef Full Text | Google Scholar

26. Leonov GA, Kuznetsov NV. Hidden Attractors in Dynamical Systems. From Hidden Oscillations in Hilbert-kolmogorov, Aizerman, and Kalman Problems to Hidden Chaotic Attractor in Chua Circuits. Int J Bifurcation Chaos (2013) 23(01):1330002. doi:10.1142/s0218127413300024

CrossRef Full Text | Google Scholar

27. Jafari S, Sprott JC, Nazarimehr F. Recent New Examples of Hidden Attractors. Eur Phys J Spec Top (2015) 224(8):1469–76. doi:10.1140/epjst/e2015-02472-1

CrossRef Full Text | Google Scholar

28. Dudkowski D, Jafari S, Kapitaniak T, Kuznetsov NV, Leonov GA, Prasad A. Hidden Attractors in Dynamical Systems. Phys Rep (2016) 637:1–50. doi:10.1016/j.physrep.2016.05.002

CrossRef Full Text | Google Scholar

29. Zhang S, Zeng Y, Li Z, Wang M, Xiong L. Generating One to Four-wing Hidden Attractors in a Novel 4d No-Equilibrium Chaotic System with Extreme Multistability. Chaos (2018) 28(1):013113. doi:10.1063/1.5006214

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Stankevich NV, Kuznetsov NV, Leonov GA, Chua LO. Scenario of the Birth of Hidden Attractors in the Chua Circuit. Int J Bifurcation Chaos (2017) 27(12):1730038. doi:10.1142/s0218127417300385

CrossRef Full Text | Google Scholar

31. Matsumoto T. A Chaotic Attractor from Chua's Circuit. IEEE Trans Circuits Syst (1984) 31(12):1055–8. doi:10.1109/tcs.1984.1085459

CrossRef Full Text | Google Scholar

32. Chua L, Komuro M, Matsumoto T. The Double Scroll Family. IEEE Trans Circuits Syst (1986) 33(11):1072–118. doi:10.1109/tcs.1986.1085869

CrossRef Full Text | Google Scholar

33. Guo-Qun Zhong G. Implementation of Chua's Circuit with a Cubic Nonlinearity. IEEE Trans Circuits Syst (1994) 41(12):934–41. doi:10.1109/81.340866

CrossRef Full Text | Google Scholar

34. Zhao H, Lin Y, Dai Y. Hidden Attractors and Dynamics of a General Autonomous van der Pol-Duffing Oscillator. Int J Bifurcation Chaos (2014) 24(06):1450080. doi:10.1142/s0218127414500801

CrossRef Full Text | Google Scholar

35. Yang J, Zhao L. Bifurcation Analysis and Chaos Control of the Modified Chua's Circuit System. Chaos, Solitons & Fractals (2015) 77:332–9. doi:10.1016/j.chaos.2015.05.028

CrossRef Full Text | Google Scholar

36. Kiseleva MA, Kudryashova EV, Kuznetsov NV, Kuznetsov OA, Leonov GA, Yuldashev MV. Hidden and Self-Excited Attractors in Chua Circuit: Synchronization and Spice Simulation. Int J Parallel, Emergent Distributed Syst (2018) 33(5):513–23. doi:10.1080/17445760.2018.1439490

CrossRef Full Text | Google Scholar

37. Gámez-Guzmán L, Cruz-Hernández C, López-Gutiérrez RM, García-Guerrero EESynchronization of Chua’s Circuits with Multi-Scroll Attractors: Application to Communication. Commun Nonlinear Sci Numer Simulation (2009) 14(6):2765–75.

Google Scholar

38. Senouci A, Boukabou A. Fuzzy Modeling, Stabilization and Synchronization of Multi-Scroll Chaotic Systems. Optik (2016) 127(13):5351–8. doi:10.1016/j.ijleo.2016.03.019

CrossRef Full Text | Google Scholar

39. Menacer T, Lozi R, Chua LO. Hidden Bifurcations in the Multispiral Chua Attractor. Int J Bifurcation Chaos (2016) 26(14):1630039. doi:10.1142/s0218127416300391

CrossRef Full Text | Google Scholar

40. Chen M, Li M, Yu Q, Bao B, Xu Q, Wang J. Dynamics of Self-Excited Attractors and Hidden Attractors in Generalized Memristor-Based Chua’s Circuit. Nonlinear Dyn (2015) 81(1-2):215–26. doi:10.1007/s11071-015-1983-7

CrossRef Full Text | Google Scholar

41. Xu Q, Lin Y, Bao B, Chen M. Multiple Attractors in a Non-ideal Active Voltage-Controlled Memristor Based Chua's Circuit. Chaos, Solitons & Fractals (2016) 83:186–200. doi:10.1016/j.chaos.2015.12.007

CrossRef Full Text | Google Scholar

42. Peng G, Min F. Multistability Analysis, Circuit Implementations and Application in Image Encryption of a Novel Memristive Chaotic Circuit. Nonlinear Dyn (2017) 90(3):1607–25. doi:10.1007/s11071-017-3752-2

CrossRef Full Text | Google Scholar

43. Abdirash M, Dolzhikova I, Pappachen James A. Brief Tutorial on Hp Memristor-Based Chua’s Chaotic Oscillator. In: 2018 International Conference on Computing and Network Communications (CoCoNet). IEEE (2018). p. 122–9.

Google Scholar

44. Liu T, Banerjee S, Yan H, Mou J. Dynamical Analysis of the Improper Fractional-Order 2d-Sclmm and its Dsp Implementation. The Eur Phys J Plus (2021) 136(5):1–17. doi:10.1140/epjp/s13360-021-01503-y

CrossRef Full Text | Google Scholar

45. Xu Q, Tan X, Zhu D, Bao H, Hu Y, Bao B. Bifurcations to Bursting and Spiking in the Chay Neuron and Their Validation in a Digital Circuit. Chaos, Solitons & Fractals (2020) 141:110353. doi:10.1016/j.chaos.2020.110353

CrossRef Full Text | Google Scholar

46. Köse E, Mühürcü A. Realization of a Digital Chaotic Oscillator by Using a Low Cost Microcontroller. Eng Rev (2017) 37(3):341–8.

Google Scholar

47. Tang K-S, Man KF, Zhong G, Chen G. Modified Chua’s Circuit with x|x|. Control Theor Appl (2003) 20(2):223–7. doi:10.3969/j.issn.1000-8152.2003.02.011

CrossRef Full Text | Google Scholar

48. Tang K-S, Man KF, Zhong G-Q, Chen G. Generating Chaos via x|x|. IEEE Trans Circuits Syst (2001) 48(5):636–41. doi:10.1109/81.922468

CrossRef Full Text | Google Scholar