- 1School of Science, Xi'an University of Architecture and Technology, Xi'an, China
- 2School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an, China
- 3School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo, China
- 4National Engineering Laboratory for Modern Silk, College of Textile and Clothing Engineering, Soochow University, Suzhou, China
Pull-in instability was an important phenomenon in microelectromechanical systems (MEMS). In the past, MEMS were usually assumed to work in an ideal environment. But in the real circumstances, MEMS often work in dust-filled air, which is equivalent to working in porous media, that's mean fractal space. In this paper, we studied MEMS in fractal space and established the corresponding model. At the same time, we can control the occurrence time and stable time of pull-in by adjusting the value of the fractal index, and obtain a stable pull-in phenomenon.
Introduction
In recent years, Microelectromechanical systems (MEMS) has received extensive attention from scientific researchers. In the operation of MEMS, a pull-in effect will occur. The pull-in voltage analysis of the electrostatic drive device is of great significance to the efficient operation and reliability of the device. Many literatures have conducted a lot of analysis on the dynamic pull-in of MEMS models of linear materials [1–5]. There are many materials used to prepare electrostatic MEMS devices, and among many materials, graphene is considered an excellent material for these devices [6].
Under normal circumstances, the MEMS we consider are in a smooth medium, which can also be called a continuous space. However, with the pollution of the environment, these electronic devices have to work in a porous medium full of particles. Under such conditions, it will inevitably affect the work of electronic devices, and thus also affect the pull-in. So, in this case, we need to analyze MEMS in fractal space. Fractal theory is an excellent tool for dealing with various mathematical problems and some physical phenomena in porous media [7–9]. Because of the diversity application of fractal, it is widely used in various fields [10–22].
In this paper, we analyzed MEMS in the fractal space and established the corresponding fractal model. After that, we explored its impact on pull-in by selecting different fractional derivatives, and realized the effective control of timing for pull-in occurrence, and obtain a stable pull-in condition.
Fractal MEMS Model
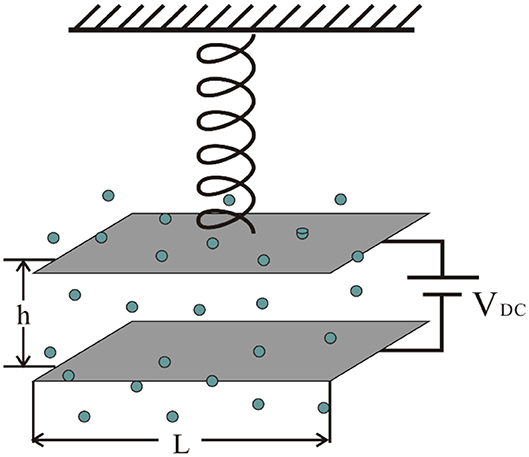
Consider a dual parallel plate model driven by electrostatic forces. The graphene ribbon with a cross-sectional area of A′ is connected to the movable and fixed base components, and the initial distance is h. The movable part is a plate with area A and mass m, as shown in Figure 1. Graphene materials follow the Equation (1) [23, 24],
where σ, ε, E represent the axial stress, axial strain, Young's modulus, and elastic stiffness constant, respectively. The moving part is affected by the restoring force Frproduced by the axial displacement of the graphene belt and the electrostatic force Fe produced by the applied voltage V. According to Equation (1), Fr and Fe can be write as [1, 6],
Where ε0 is electric emissivity. Using Newton's second law of motion, the equation of motion of the moving part can be expressed as,
Equation (4) can be transformed as Equation (5),
Where , , , .
In the fractal space, the fractal derivative is defined as [25–29],
If the Micro-electromechanical system work in the porous medium as shown in Figure 1, we should consider it in fractal place. So, based on Equation (5), the fractal MEMS can be written as,
We assume the initial conditions are u(0) = 0, u′(0) = 0.
Results and Discussion
In Equation (7), when a and k take different values, it will correspond to different equations. It is worth noting that only in the presence of electrostatic force, that is a = 0, under steady-state conditions, our model is simplified to the well-known Nathan model or parallel plate capacitor model [6].
The initial conditions are u(0) = 0, u′(0) = 0.
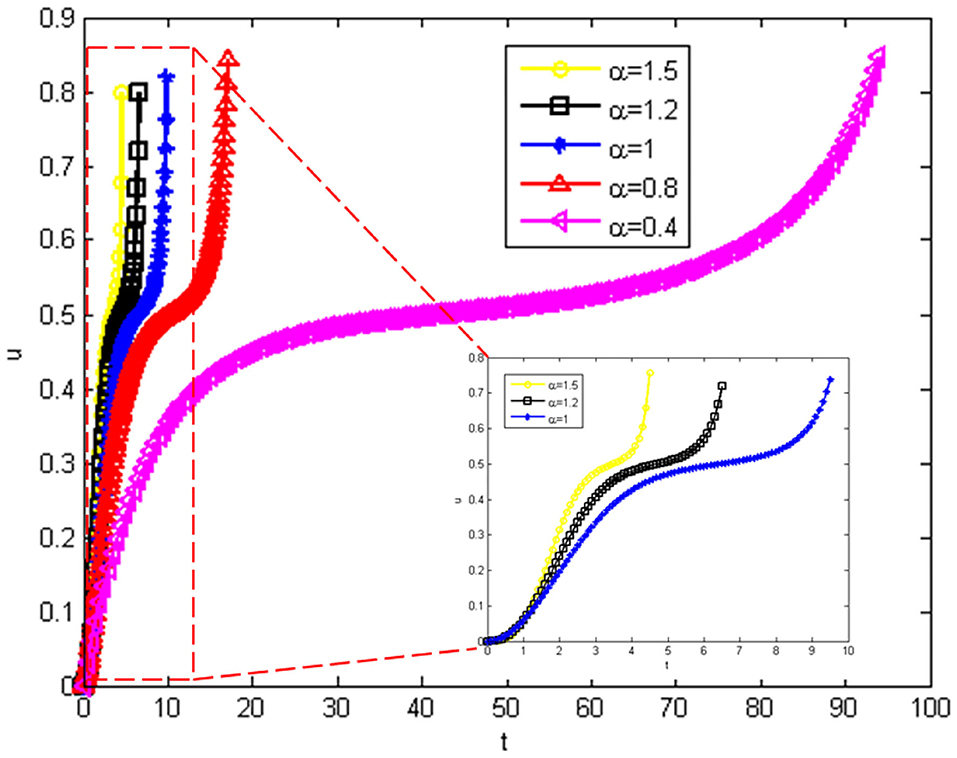
As shown in Figure 2, the numerical solution corresponding to different α in Equation (7) is given. We can see that when k exceeds the critical value, a pull-in phenomenon occurs [1]. Figure 2 shows the Pull-in curve calculated under the three cases of α > 1, α = 1, and α < 1. It can be seen that whenα > 1, Pull-in will happen very soon. From the enlarged picture, it can also be seen that there is a short platform. When α < 1, the occurrence of pull-in will become slower and slower as a decreases. When α = 0.4, a very long platform appears. At this time, relatively speaking, the occurrence of pull-in at α = 1.5 is almost instantaneously. It can be seen that the fractal model of MEMS we have established can control the occurrence time of pull-in and the stable time by adjusting the value of the fractional index.
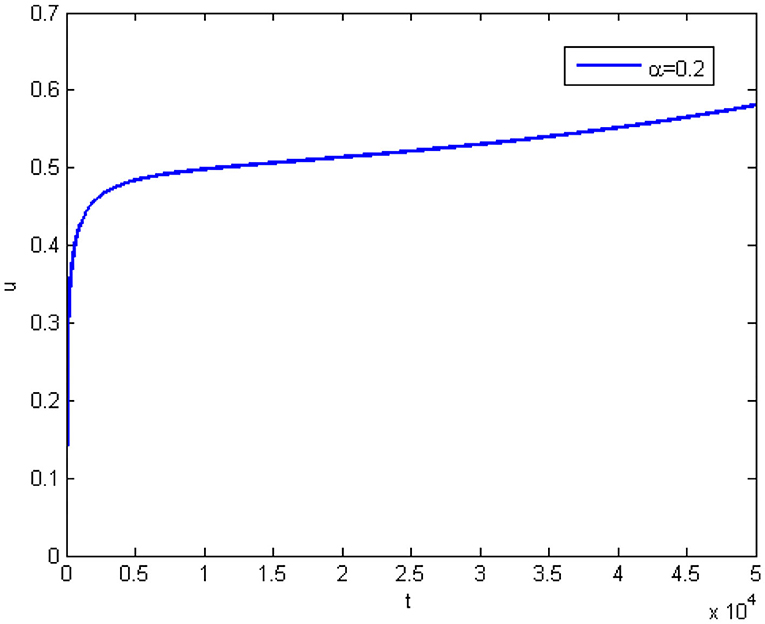
Figure 3 shows the pull-in curve when α = 0.2. It can be seen that the platform at this time has become quite long, which also means that the pull-in is infinitely delayed, which means that we have obtained a stable pull-in. And when it is smaller, the pull-in will be more stable.
Conclusion
In this paper, we studied MEMS which prepared via graphene in fractal space and established a corresponding fractal model. In the fractal space, by discussing different fractional index α, we found that we can control the occurrence and stable time of pull-in by adjusting the fractional index. The fractal model of MEMS we established can broaden the application range of it, which can be used in any discontinuous media. Pull in stability can guide MEMS to work more efficiently.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
DT and C-HH designed the experiments. DT performed data analysis and wrote the paper. J-HH revised the paper. All authors read and contributed to the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Skrzypacz P, Kadyrov S, Nurakhmetov D, We D. Analysis of dynamic pull-in voltage of a graphene MEMS model. Nonlinear Anal Real World Appl. (2019) 45:581–9. doi: 10.1016/j.nonrwa.2018.07.025
2. Anjum N, He JH. Homotopy perturbation method for N/MEMS oscillators. Math Methods Appl Sci. (2020). doi: 10.1002/mma.6583
3. Anjum N, He JH. Analysis of nonlinear vibration of nano/microelectromechanical system switch induced by electromagnetic force under zero initial conditions. Alexandria Eng J. (2020) 59:4343–52. doi: 10.1016/j.aej.2020.07.039
4. He JH, Nurakhmetov D, Skrzypacz P, Wei D. Dynamic pull-in for micro-electromechanical device with a current-carrying conductor. J Low Freq Noise Vibrat Active Control. (2019) 1461348419847298. doi: 10.1177/1461348419847298
5. Shishesaz M, Shirbani MM, Sedighi HM, Hajnayeb A. Design and analytical modeling of magneto-electromechanical characteristics of a novel magneto-electro-elastic vibration-based energy harvesting system. J Sound Vibrat. (2018) 425:149–69. doi: 10.1016/j.jsv.2018.03.030
6. Anjum N, He JH. Nonlinear dynamic analysis of vibratory behavior of a graphene nano/microelectromechanical system. Math Methods Appl Sci. (2020). doi: 10.1002/mma.6699
7. He JH. Variational principle for the generalized KdV-burgers equation with fractal derivatives for shallow water waves. J Appl Comput Mech. (2020) 6:735–40. doi: 10.22055/JACM.2019.14813
8. Tian D, Ain QT, Anjum N, He C-H, Cheng B. Fractal N/MEMs: from pull-in instability to pull-in stability. Fractals. (2020). doi: 10.1142/S0218348X21500304
9. He JH, Ji FY. Taylor series solution for Lane–Emden equation. J Math Chem. (2019) 57:1932–4. doi: 10.1007/s10910-019-01048-7
10. Tian D, He CH. A fractal micro-electromechanical system and its pull-in stability. J Low Freq Noise Vibrat Active Control. (2020). doi: 10.1177/1461348420984041
11. Fan J, Yang X, Liu Y. Fractal calculus for analysis of wool fiber: mathematical insight of its biomechanism. J Eng Fibers Fabrics. (2019) 14:1558925019872200. doi: 10.1177/1558925019872200
12. Wang Y, Deng Q. Fractal derivative model for tsunami traveling. Fractals. (2019) 27:1950017. doi: 10.1142/S0218348X19500178
13. He CH, Shen Y, Ji FY, He J-H. Taylor series solution for fractal Bratu-type equation arising in electrospinning process. Fractals. (2020) 28:2050011. doi: 10.1142/S0218348X20500115
14. He JH. A fractal variational theory for one-dimensional compressible flow in a microgravity space. Fractals. (2020) 28:2050024. doi: 10.1142/S0218348X20500243
15. Lin L, Yao SW, Li H. Silver ion release from Ag/PET hollow fibers: mathematical model and its application to food packing. J Eng Fibers Fabrics. (2020) 15:1558925020935448. doi: 10.1177/1558925020935448
16. Wang Y, Yao SW, Yang HW. A fractal derivative model for snow's thermal insulation property. Thermal Sci. (2019) 23:2351–4. doi: 10.2298/TSCI1904351W
17. Lin L, Yao SW. Fractal diffusion of silver ions in hollow cylinders with unsmooth inner surface. J Eng Fibers Fabrics. (2019) 14:1558925019895643. doi: 10.1177/1558925019895643
18. Liu H, Yao SW, Yang H, Liu J. A fractal rate model for adsorption kinetics at solid/solution interface. Thermal Sci. (2019) 23:2477–80. doi: 10.2298/TSCI1904477L
19. Lin L, Yao SW. Release oscillation in a hollow fiber-Part 1: mathematical model and fast estimation of its frequency. J Low Freq Noise Vibrat Active Control. (2019) 38:1703–7. doi: 10.1177/1461348419836347
20. Ain QT, He JH. On two-scale dimension and its applications. Thermal Sci. (2019) 23:1707–12. doi: 10.2298/TSCI190408138A
21. He JH, Ain QT. New promises and future challenges of fractal calculus: from two-scale thermodynamics to fractal variational principle. Thermal Sci. (2020) 24:659–81. doi: 10.2298/TSCI200127065H
22. He JH, Ji FY. Two-scale mathematics and fractional calculus for thermodynamics. Thermal Sci. (2019) 23:2131–3. doi: 10.2298/TSCI1904131H
23. Lee C. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science. (2008) 321:385–8. doi: 10.1126/science.1157996
24. Lu C, Huang R. Nonlinear mechanics of single-atomic-layer graphene sheets. Int J Appl Mech. (2019) 1:443–67. doi: 10.1142/S1758825109000228
25. Parvate A, Gangal AD. Calculus on fractal subsets of real-line I: formulation. Fractals. (2009) 17:53–148. doi: 10.1142/S0218348X09004181
26. Parvate A, Gangal AD. Calculus on fractal subsets of real line II: conjugacy with ordinary calculus. Fractals. (2011) 19:271–90. doi: 10.1142/S0218348X11005440
27. Parvate A, Satin S, Gangal AD. Calculus on fractal curves in R{n}. Fractals. (2011) 19:15–27. doi: 10.1142/S0218348X1100518X
Keywords: micro-electromechanical systems, pull-in, fractal space, porous medium, fractal derivative
Citation: Tian D, He C-H and He J-H (2021) Fractal Pull-in Stability Theory for Microelectromechanical Systems. Front. Phys. 9:606011. doi: 10.3389/fphy.2021.606011
Received: 14 September 2020; Accepted: 08 March 2021;
Published: 31 March 2021.
Edited by:
Hamid M. Sedighi, Shahid Chamran University of Ahvaz, IranReviewed by:
Jamal Zare, Shahrekord University, IranHijaz Ahmad, University of Engineering and Technology, Peshawar, Pakistan
Copyright © 2021 Tian, He and He. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dan Tian, dGlhbmRhbkB4YXVhdC5lZHUuY24=; Ji-Huan He, aGVqaWh1YW5Ac3VkYS5lZHUuY24=
 Dan Tian
Dan Tian Chun-Hui He2
Chun-Hui He2 Ji-Huan He
Ji-Huan He