Ghost Interaction of Breathers

Mutual interaction of localized nonlinear waves, e.g., solitons and modulation instability patterns, is a fascinating and intensively-studied topic of nonlinear science. Here we report the observation of a novel type of breather interaction in telecommunication optical fibers, in which two identical breathers propagate with opposite group velocities. Under controlled conditions, neither amplification nor annihilation occurs at the collision point and most interestingly, the respective envelope amplitude, resulting from the interaction, almost equals another envelope maximum of either oscillating and counterpropagating breather. This ghost-like breather interaction dynamics is fully described by an N-breather solution of the nonlinear Schrödinger equation.

Introduction

The study of both, formation and interaction of localized waves has been a central task in nonlinear physics during the last decades, including plasma physics, fluid dynamics, Bose-Einstein condensates and photonics. Among different types of nonlinear localized waves, solitons are the most representative and ideal testbed to investigate nonlinear wave interactions due to their intrinsic particle-like properties during propagation [1–4]. A generic and relevant case of study for various fields of research is the elastic and nonlinear interaction of envelope solitons, which can be described by the focusing one-dimensional nonlinear Schrödinger equation (NLSE). In this conservative and integrable system, the possible collision of solitons with different velocities does not affect their shape or velocity after interaction, and their main physical properties keep unchanged. In general, the interaction-induced displacement in position and phase shift are independent on the relative phases of the envelope solitons. However, collision dynamics in the interaction region strongly depends on the relative phases. Consequently, in the simplest case of two-soliton collision with opposite velocities, as shown in Figures 1A1–D1 the two solitons appear to attract with each other and cross (forming a transient peak) in the in-phase configuration, while they seem to repel each other and as such stay apart in the out-of-phase case. The wave magnitude at the central point of collision then evolves from the sum of the two solitons’ amplitudes (i.e., amplification) to their difference (i.e., annihilation), respectively. A large range of theoretical descriptions, numerical simulations and experimental observations of such soliton interactions and their possible synchronization have been reported earlier [5–12].

FIGURE 1

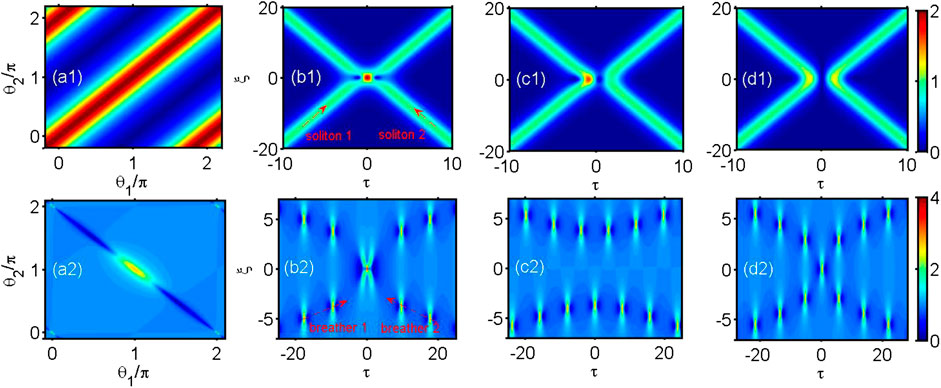
FIGURE 1. Typical temporal evolution of soliton-pair interaction (first line) and breather-pair interaction (second line). (A1) Dependence of amplitude at the soliton collision point $\left|{\psi }_{2S}\left(\mathrm{0,0}\right)\right|$ on the soliton phases ${\theta }_1$ and ${\theta }_2$. (B1–D1) Amplitude evolution of soliton collision with soliton phases: ${\theta }_1=0$, ${\theta }_2=0$ (b1); ${\theta }_1=\pi /2$, ${\theta }_2=0$ (c1); ${\theta }_1=\pi$, ${\theta }_2=0$ (d1). (b1-d1) are plotted based on the two-soliton solution of NLSE with the soliton parameters: angular frequencies ${\text{Ω}}_1=-{\text{Ω}}_2=0.5;$ soliton amplitudes $A_1=A_2=1$. (A2) Dependence of amplitude at the breather collision point $\left|{\psi }_{2B}\left(\mathrm{0,0}\right)\right|$ on temporal phases ${\theta }_1$ and ${\theta }_2$. Prototypes of interactions include Amplification (B2), Annihilation (C2), and “Ghost interaction” (D2). (A1–D2) are plotted based on the one-pair breather solution of NLSE. In all these cases, key parameters of breathers are listed as follows $R_1=R_2=1.05$, ${\alpha }_1=-{\alpha }_2=0.4,$${\mu }_1={\mu }_2=0$. while ${\theta }_1={\theta }_2=0$ for (B2); ${\theta }_1={\theta }_2=\pi /2$ for (C2) and ${\theta }_1={\theta }_2=\pi$ for (D2). Red arrows in (B1) and (B2) indicate the moving motions of solitons and breathers respectively.

Besides solitons, breather solutions of the NLSE are also exciting examples to investigate nonlinear wave interactions because of the salient complexities of breather synchronization in relation to their self-oscillating properties. From this point of view, phase-sensitive breather interactions are now widely studied [13–22]. More particularly, for co-propagative breathers, breather molecules can be formed when group velocity and temporal phase of breathers are perfectly synchronized, while for counter-propagating breathers, the phase-sensitive collision process exhibits various dynamical behaviors. Two of them have been studied in detail in the context of rogue wave formation, namely amplification and annihilation cases that resemble soliton collisions. The above interactions are fully described by N-breather solutions of the NLSE [16, 18]. However, the two-breather collision has been recently found to provide a peculiar third configuration for particular phases, neither of the above-mentioned cases, the later leads to a peak amplitude at the central point of collision equivalent to the single breather amplitude before or after the collision. Phenomenologically, it seems that one breather mysteriously disappears in the nonlinear interaction region, but it then appears after that. That is why this intriguing breather interaction was vividly termed by “ghost interaction” [19]. Its generalization to the N-breather interaction is still under investigation. However, both, detailed analysis and experimental confirmation of this remarkable dynamics for the simplest two-breather collision are still to emerge into light.

To address this scientific gap, we present the observation of ghost interaction of two breathers in a single-pass telecommunication optical fiber experiment. By means of the Fourier-transform pulse shaping technique applied to an optical frequency comb, we generate the initial condition for two counter-propagating breathers with desired temporal phases. The experimental results are in excellent agreement with the exact two-breather solution of the NLSE. We confirm that this peculiar phase-sensitive breather interaction is strictly different to the well-known soliton interactions. Our study paves the way for novel directions of investigation in the rich landscape of complex nonlinear wave dynamics [23–26].

Method

Theoretical Model and Breather Solutions

Our theoretical framework and starting point is based on the dimensionless form of the self-focusing 1D-NLSE:

$\mathit{i}{\mathit{\psi }}_{\mathit{\xi }}+\frac{1}{2}{\mathit{\psi }}_{\mathit{\tau \tau }}+{\left|\mathit{\psi }\right|}^2\mathit{\psi }=0,(1)$

where subscripts stand for partial differentiations. Here, $\psi$ is a wave envelope, which is a function of $\xi$ (a scaled propagation distance or longitudinal variable) and $\tau$ (a co-moving time, or transverse variable, moving with the wave group-velocity). This conventional form of the NLSE is widely used to describe the nonlinear dynamics of one-dimensional optical and water waves [25]. This integrable equation can be solved using various techniques and admits a wide class of unstable pulsating solutions known as breathers [13]. The simplest cases (i.e., first-order breathers) are well-known localized structures emerging from the modulation instability process [26]. The general one-breather solution is a localized wave envelope which coat the plane wave in space-time and propagate with a particular group velocity and oscillating period in relation to carrier. This also includes limiting cases such as time-periodic Akhmediev breathers [13], space-periodic Kuznetsov-Ma breathers [27, 28] and the doubly-localized Peregrine breather [29], which have been observed in various experimental configurations [30–37]. Higher-order breathers can be simply generated by considering the interaction of the above elementary breathers, thus, associated to the nonlinear superposition of multiple breathers [13, 38, 39]. More generally, the NLSE has an exact N-breather solution, which can be constructed by appropriate integration technique by studying the auxiliary linear Zakharov-Shabat system. More technical details to solve the NLSE, e.g., applications of the dressing method are reported in Refs. [16, 18]. In the following, we restrict our work to the general two-breather solution. It has four main parameters $R_{\mathrm{1,2}}$, ${\alpha }_{\mathrm{1,2}}$ (subscripts 1 and 2 correspond to the first and second breather) which control the main breather properties (localization, group velocity, and oscillation) and four additional parameters ${\mu }_{\mathrm{1,2}}\in \left[-\infty ,\infty \right]$ and ${\theta }_{\mathrm{1,2}}$ varying between 0 et 2 $\pi$ that define the location and phase of each breather. More details can be found in Ref. [40]. In particular, we study the simplest one-pair breather solution ${\psi }_{2\text{B}}$ with breathers moving in opposite directions in the $\left(\xi ,\tau \right)$ -plane that can be obtained by setting $R_1=R_2=1+\epsilon =R$, ${\alpha }_1=-{\alpha }_2=\alpha$. The resulting solution can be written as follows:

${\mathit{\psi }}_{2B}\left(\xi ,\tau \right)=\left[1+\left({\mathit{R}}^2-\frac{1}{{\mathit{R}}^2}\right)\frac{\mathit{N}}{\Delta }sin2\mathit{\alpha }\right]{\mathit{e}}^{\mathit{i\xi }},(2)$

where

$N=\left(R-\frac{1}{R}\right)\text{sin}\alpha \left({\left|q_1\right|}^2{q}_{21}^{\ast }{q}_{22}+{\left|q_2\right|}^2{q}_{11}^{\ast }{q}_{12}\right)-i\left(R+\frac{1}{R}\right)\text{cos}\alpha \left[\left(q_1^{\ast }{q}_2\right)q_{21}^{\ast }{q}_{12}-\left(q_1{q}_2^{\ast }\right)q_{11}^{\ast }{q}_{22}\right]$

and

$\Delta ={\left(R+\frac{1}{R}\right)}^2{\text{cos}}^2\alpha {\left|q_{11}{q}_{22}-q_{12}{q}_{21}\right|}^2+{\left(R+\frac{1}{R}\right)}^2{\left|q_1\right|}^2{\left|q_2\right|}^2{\text{sin}}^2\alpha$

In these expressions, $q_i=\left(q_{i1},q_{i2}\right)$ with $i=\mathrm{1,2}$ as a two-component vector function, which contains the following components:

$q_{11}=e^{-{\phi }_1}-\frac{e^{-{\phi }_1-i\alpha }}{R},q_{12}=e^{{\phi }_1}-\frac{e^{-{\phi }_1-i\alpha }}{R},q_{21}=e^{-{\phi }_2}-\frac{e^{{\phi }_1+i\alpha }}{R},q_{22}=e^{{\phi }_2}-\frac{e^{-{\phi }_2+i\alpha }}{R}$

with ${\phi }_1=\eta \tau +\gamma \xi +\frac{{\mu }_1}{2}+i\left(k\tau +\omega \xi +\frac{{\theta }_1}{2}\right)$ and ${\phi }_2=\eta \tau -\gamma \xi +\frac{{\mu }_2}{2}-i\left(k\tau -\omega \xi +\frac{{\theta }_2}{2}\right)$.

The parameters $\eta , k, \gamma$ and $\omega$ are defined as:

$\eta =-\frac{1}{2}\left(R-\frac{1}{R}\right)\text{cos}\alpha ,k=-\frac{1}{2}\left(R+\frac{1}{R}\right)\text{sin}\alpha ,\gamma =-\frac{1}{2}\left(R^2+\frac{1}{R^2}\right)\text{sin}2\alpha \omega =\frac{1}{2}\left(R^2-\frac{1}{R^2}\right)\text{cos}2\alpha$

Figures 1A2–D2 presents the interaction of a pair of counter-propagating breathers when $R_1=R_2=1.05$, ${\alpha }_1=-{\alpha }_2=0.4,$ thus corresponding to two identical and symmetric breathers propagating with the same oscillating frequency but opposite group velocities. Here, we fixed the temporal position ${\mu }_{\mathrm{1,2}}=0$, so the central point of collision locates at the origin $\left(\xi =0,\tau =0\right)$. According to the two-breather solution of the NLSE, we continuously vary the breather phase ${\theta }_{\mathrm{1,2}}$ over the full range $\left[0, 2\pi \right]$ to analyze its impact on the resulting waveform and amplitude at the origin. As shown in Figure 1A2, the amplitude of the collision-induced wave $\left|{\psi }_{2B}\left(\mathrm{0,0}\right)\right|$ strongly depends on ${\theta }_{\mathrm{1,2}}$ values, the maximum is obtained for ${\theta }_{\mathrm{1,2}}=0$ or ${\theta }_{\mathrm{1,2}}=2\pi$, when synchronization of the maximal amplitude of pulsating breathers is perfectly reached. When ${\theta }_{\mathrm{1,2}}\sim \pi /2$, the amplitude at the central point of collision decreases to a minimum value close to the constant background amplitude $\left|{\psi }_0\right|\sim 1$. Interestingly, there is another local peak of $\left|{\psi }_{2B}\left(\mathrm{0,0}\right)\right|$ at ${\theta }_{\mathrm{1,2}}=\pi$, whose amplitude is very close to that of a single breather before or after the collision $\left|{\psi }_1\right|\sim 2.7$. In order to improve the unveiling of the space-time dynamics of such breather interactions, we depict the full wave evolution in Figure 1B2–D2 for the following cases: 1) ${\theta }_1={\theta }_2=0$, the synchronized collision of breathers that generates a rogue peak with extremely high amplitude (already reported experimentally in Ref. [15]); 2) ${\theta }_1={\theta }_2=\pi /2$, the quasi-annihilation of breathers that gives rise to very small perturbations located on the plane wave (already reported experimentally in Ref. [19]). However, note that in this case, we observe a jump of wave field symmetry before and after the collision of these two breathers because of the noticeable $\pi$ -phase shift (see Figure 1C2). This specific configuration of breather collision also known as superregular breathers can be regarded as a prototype of small localized perturbations of the plane wave for describing modulation instability [16]; 3) ${\theta }_1={\theta }_2=\pi$, the two breathers are almost transformed into a single one in the main local interaction and interaction region, at the origin $\left|{\psi }_{2\text{B}}\left(\mathrm{0,0}\right)\right|\text{∼}\left|{\psi }_1\right|$, which raises the impression that one breather has vanished (see Figure 1D2).

We emphasize that such ghost interaction of breathers as illustrated in Figure 1D2 cannot occur for the soliton counterpart (see Figures 1A1–D1). To clarify this point, we compare systematically the phase-dependent soliton collision and the phase-dependent breather collision. Similarly, we consider a pair of counter-propagating solitons with the amplitudes $A_1=A_2=A$ and the frequencies ${\text{Ω}}_1=-{\text{Ω}}_2=\text{Ω}$. In this configuration, the two-soliton solution (on zero-background) can be written in the following form [18]:

${\mathit{\psi }}_{2\mathbf{S}}\left(\mathit{\xi },\mathit{\tau }\right)=2\mathit{A}\frac{{\Omega }^2\left({\left|{\mathit{q}}_1\right|}^2{\mathit{q}}_{21}^{\mathit{\ast }}{\mathit{q}}_{22}+{\left|{\mathit{q}}_2\right|}^2{\mathit{q}}_{11}^{\mathit{\ast }}{\mathit{q}}_{12}\right)-\mathit{i}\mathbf{A}\Omega \left[\left({\mathit{q}}_1^{\mathit{*}}{\mathit{q}}_2\right){\mathit{q}}_{21}^{\mathit{\ast }}{\mathit{q}}_{12}-\left({\mathit{q}}_2^{\mathit{\ast }}{\mathit{q}}_1\right){\mathit{q}}_{11}^{\mathit{\ast }}{\mathit{q}}_{22}\right]}{A^2{\left|{\mathit{q}}_{11}{\mathit{q}}_{22}-{\mathit{q}}_{12}{\mathit{q}}_{21}\right|}^2+{\Omega }^2{\left|{\mathit{q}}_1\right|}^2{\left|{\mathit{q}}_2\right|}^2}{\mathit{e}}^{\mathit{i\xi }},(3)$

In this expression, $q_i=\left(q_{i1},q_{i2}\right)$ with $i=\mathrm{1,2}$ is a two-component vector function having the following components: $q_{11}=e^{-{\phi }_1}$, $q_{12}=e^{{\phi }_1}$, $q_{21}=e^{-{\phi }_2}$, $q_{22}=e^{{\phi }_2}$, with

$\begin{array}{l}{\phi }_1=\frac{A}{2}\tau +\frac{A\text{Ω}}{2}\xi +\frac{{\mu }_1}{2}+i\left(\frac{\text{Ω}}{2}\tau +\frac{{\text{Ω}}^2-{\text{A}}^2}{4}\xi +\frac{{\theta }_1}{2}\right)\mathrm{and}\\ {\phi }_2=\frac{A}{2}\tau -\frac{A\text{Ω}}{2}\xi +\frac{{\mu }_2}{2}+i\left(-\frac{\text{Ω}}{2}\tau +\frac{{\text{Ω}}^2-{\text{A}}^2}{4}\xi +\frac{{\theta }_2}{2}\right).\end{array}$

Again, the $\mu$ and $\theta$ are key parameter to control the soliton position and phase. We set ${\mu }_1={\mu }_2=0$ and Figure 1A1 demonstrates the dependence of the amplitude at the collision point $\left|{\psi }_{2\text{S}}\left(\mathrm{0,0}\right)\right|$ on ${\theta }_1$ and ${\theta }_2$. Compared to the breather collisions, here the key parameter for soliton collision is the relative soliton phase ${\theta }_1-{\theta }_2$. In general, amplification interaction occurs for ${\theta }_1-{\theta }_2=0$, and annihilation interaction happens for ${\theta }_1-{\theta }_2= \pi .$ While for other values of relative soliton phase, $\left|{\psi }_{2\text{S}}\left(\mathrm{0,0}\right)\right|$ keeps being low $\left(\sim 0\right)$, and a partial energy exchange occurs from one soliton to another in the collision area which leads to a remarkable significant time-parity symmetry transformation (examples shown in Figures 1B1–D1).

Experimental Setup

In order to validate these theoretical predictions with respect to ghost interaction of breathers, we have performed experiments with light waves propagating in high-speed telecommunication-grade components, as depicted in Figure 2. The main challenge here is the arbitrary wave shaping to establish the specific initial excitation of counter-propagating breathers with desired phases in the $\left(\xi ,\tau \right)$ -plane (more details can be found in Ref. [41]).

FIGURE 2

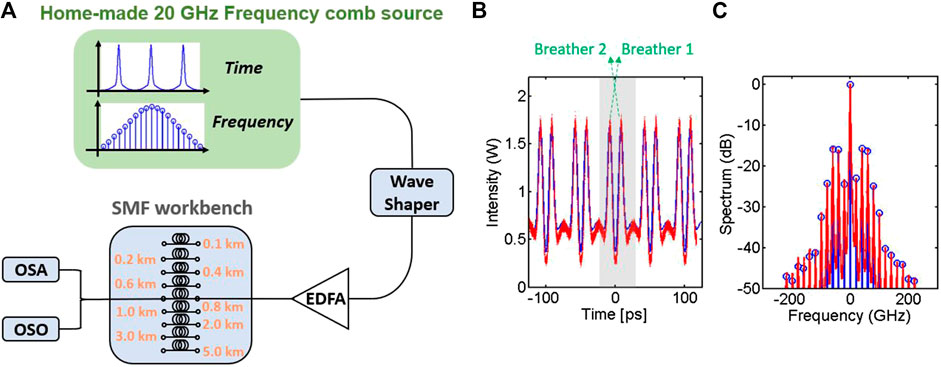
FIGURE 2. Experimental setup and generation of initial conditions. (A) Schematic diagram of the experimental setup. EDFA: erbium-doped fiber amplification; SMF: single mode fiber; OSA: optical spectral analyzer; OSO: optical sampling oscilloscope. Shaded-green box represents the home-made frequency comb source with a repetition rate of 20 GHz. (B–C) Designed initial conditions at 20 GHz repetition rate for a pair of contra-propagative breathers in both temporal and spectral domains. Solid blue lines are theoretical curves; Solid red lines are experimental measurements. Here breather parameters are: $R_{\mathrm{1,2}}=1.5$, ${\alpha }_1=-{\alpha }_2=0.5$, ${\mu }_{\mathrm{1,2}}=0$, ${\theta }_{\mathrm{1,2}}=\pi$.

To this end, a 20 GHz optical frequency comb passes through a programmable optical filter (wave-shaper) to precisely control both amplitude and phase characteristics of each comb line. As a result, we can synthesize any arbitrary perturbation of a continuous wave background in a time-periodic pattern whose frequency is equal to the comb spacing. This temporal pattern is then amplified by erbium-doped fiber amplifier (EDFA) to achieve the exact excitation of the two-breather solution in terms of average power for nonlinear propagation into our single-mode optical fiber (SMF). The corresponding temporal and spectral power profiles of the light-wave are presented in Figures 2B–C. Note that the initial condition for the breather pair is time-periodic with a period of $50$ ps. Hereafter, we select the center time slot $\left(-25 \text{ps}<t<25 \text{ps}\right)$ to investigate the collision dynamics of the breather pair as shown in gray shaded area in Figure 2B. The nonlinear propagation is studied with different lengths of the same fiber and characterized by means of an optical sampling oscilloscope (OSO) with sub-picosecond resolution in the time domain and a high dynamics-range optical spectrum analyzer (OSA) in the Fourier domain. The maximum propagation distance fixed was chosen to limit the impact of linear propagation losses in our optical fiber as well as possible interaction occurring between neighboring elements of the periodic pattern. Our fiber properties are the following: group velocity dispersion ${\beta }_2=-21.1 {\text{ps}}^2{\text{km}}^{-1}$, linear losses $\alpha =0.2 {\text{dB km}}^{-1}$, and nonlinear coefficient $\gamma =1.2 {\text{W}}^{-1}{\text{km}}^{-1}$.

Results

We present our experimental results on the nonlinear space-time evolution of the breather pair studied in the above theoretical section, for the specific temporal phases ${\theta }_1={\theta }_2=\pi$. To this purpose, we fixed the average power to $P_0=0.74 W$. Then, we gradually increase the propagation distance (i.e., the fiber length) by a step of 100 m. The correspondence between normalized and physical units can be retrieved by making use of the following relations between dimensional distance $z \left(m\right)$ and time $t \left(s\right)$ with the previously mentioned normalized units: $z=\xi L_{NL}$ and $t=\tau t_0$. In these expressions, the characteristic (nonlinear) length and time scales are $L_{NL}={\left(\gamma P_0\right)}^{-1}\sim 1216 \text{m}$ and $t_0=\sqrt{\left|{\beta }_2\right|L_{NL}}\sim 4.74\text{ps}$, respectively. The dimensional optical field $A\left(z,t\right)\left({\text{W}}^{1/2}\right)$ is $A=\sqrt{P_0} \psi$.

Figures 3A1–A2 presents the concatenation of temporal (amplitude) profiles and power spectra which were recorded at the output of the distinct fiber segments with increasing length. The careful control of phases allows to observe the ghost interaction between the counter-propagating breathers. The full space-time dynamics is indeed in excellent agreement with theory shown in Figures 3B1–B2. We can notice the five mains peaks appearing during the whole evolution studied in Figure 3A1: two peaks at ${\xi }_1\sim -2.2$ for the two breathers before collision; one peak at ${\xi }_2\sim 0$ at the collision point; and two peaks at ${\xi }_3\sim 2.2$ for the two breathers after the collision. Correspondingly, we observe the maxima of spectral broadening for respectively $\xi ={\xi }_1$, $\xi ={\xi }_2$ and $\xi ={\xi }_3$ (shown in Figure 3A2), thus, confirming the different nonlinear temporal focusing patterns. Figure 3C1 presents the comparison of the recorded temporal waveforms for $\left|\psi \left(\xi ={\xi }_1,\tau \right)\right|$, $\left|\psi \left(\xi ={\xi }_2,\tau \right)\right|$ and $\left|\psi \left(\xi ={\xi }_3,\tau \right)\right|$. Strikingly, all these five peaks are found to nearly exhibit similar waveforms and maximum amplitudes, this is also corroborated by the spectral analysis reported in Figure 3C2. Only very minor discrepancies can be noticed mainly ascribed to the linear propagation losses in our optical fiber and some artifacts of the initial wave shaping.

FIGURE 3

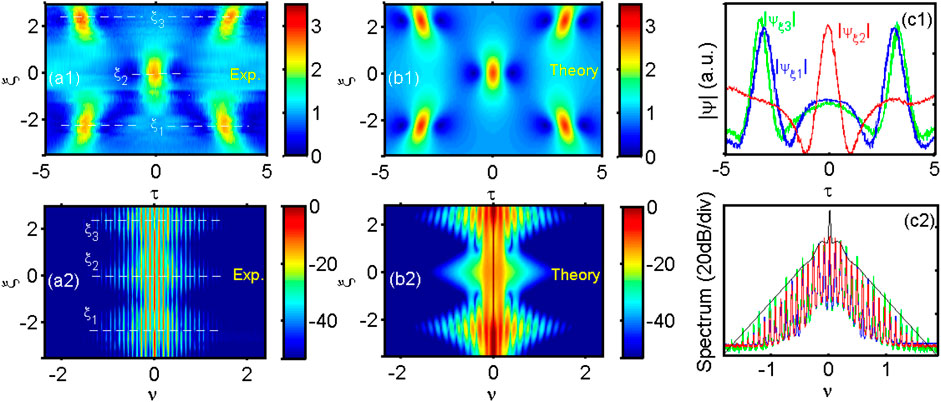
FIGURE 3. Experimental observation of ghost interaction of two breathers. Color maps showing the evolution of temporal amplitude (A1) and power spectrum (A2) for the two breathers observed in experiment. Dashed white lines indicate the position of local maximum amplitudes, which are also the position of largest spectral broadenings, before collision (${\xi }_1\sim -2.2$), during collision (${\xi }_2\sim 0$) and after collision (${\xi }_3\sim 2.2$). (B1–B2) Corresponding theoretical predictions based on the two-breather solution of NLSE. (C1) Comparison of the amplitude profiles measured at $\xi ={\xi }_1$ (blue curve), $\xi ={\xi }_2$ (red curve) and $\xi ={\xi }_3$ (green curve). (C2) Comparison of power spectra recorded at $\xi ={\xi }_1$ (blue curve), $\xi ={\xi }_2$ (red curve) and $\xi ={\xi }_3$ (green curve). Thin dark curve is the theoretical spectrum at $\xi =0$. Key parameters of the breather pair: $R_{\mathrm{1,2}}=1.5$, ${\alpha }_1=-{\alpha }_2=0.5$, ${\mu }_{\mathrm{1,2}}=0$, ${\theta }_{\mathrm{1,2}}=\pi$.

Discussion

As shown above, during the ghost interaction of two breathers, only a single breather peak remains occurrent at the collision point. The reason for this intriguing phenomenon is related to the fact that there is a continuous and varying power exchange between the background and each localized perturbation all along the propagation, which is an intrinsic property of breathers. Therefore, when these two breathers nonlinearly interact near the collision point, for a given particular phase-collision-interaction, one of the breather peaks appears to be almost hidden in the background and then emerges again after the collision by following the energy conservation. Moreover, the breather pair keeps the spatial and temporal symmetry during the whole evolution. It is also worth to mention that such peculiar ghost interaction does not occur in conventional soliton-soliton collision scenarios because of the lack of pulse-background energy exchange [see Figures 1A1–D1].

In summary, we performed a systematic theoretical comparison between the phase-sensitive soliton-soliton collisions and breather-breather collisions. All different configurations are fully described by the exact N-breather solution of the NLSE. More importantly, we provided the first experimental observation of the very fascinating type of ghost interaction of breathers, which confirms our theoretical predictions. We also point out that our study is here restricted to the interaction of two identic counter-propagating breathers, while much more complicated many-body interactions of breathers with asymmetric conditions, including different amplitudes and/or oscillating frequencies, still require further investigations. Our current results concede a novel step toward the understanding of interactions between localized waves in nonlinear physics. These may naturally lead to encourage further relevant experimental studies and theoretical investigations in various fields of nonlinear wave physics.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made significant contributions to the theoretical and experimental developments, data acquisition, results interpretation and manuscript writing.

Funding

French National Research Agency (PIA2/ISITE-BFC, Grant No. ANR-15-IDEX-03, “Breathing Light” project). Theoretical part of the work was supported by Russian Science Foundation (Grant No. 19-72-30028).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Dauxois T, Peyrard M. Physics of solitons. Cambridge: Cambridge University Press (2006).

PubMed Abstract | Google Scholar

2. Kivshar Y, Agrawal G. Optical solitons: from fibers to photonic crystals. London: Academic Press (2003).

PubMed Abstract | Google Scholar

3. Zabusky N, Kruskal M. Interaction of “solitons” in a collisionless plasmas and the recurrence of initial states. Phys Rev Lett (1965) 15:240. doi:10.1103/PhysRevLett.15.240

CrossRef Full Text | Google Scholar

4. Stegeman G, Segev M. Optical spatial solitons and their interactions: universality and diversity. Science (1999) 286:1518. doi:10.1126/science.286.5444.1518

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zakharov V, Shabat A. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of wave in nonlinear media. Sov Phys JETP (1972) 34:62. Available from: http://www.jetp.ac.ru/cgi-bin/dn/e_034_01_0062.pdf (Accessed January 1972).

Google Scholar

6. Yuen H, Lake B. Nonlinear dynamics of deep-water gravity waves. Adv Appl Mech (1982) 22:67. doi:10.1016/S0065-2156(08)70066-8

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gordon J. Interaction forces among solitons in optical fibers. Opt Lett (1983) 8:596. doi:10.1364/OL.8.000596

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Mitschke F, Mollenaurer L. Experimental observation of interaction forces between solitons in optical fibers. Opt Lett (1987) 12:355. doi:10.1364/OL.12.000355

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Islam M, Soccolich C, Gordon J. Ultrafast digital soliton logic gates. Opt Quant Electron (1992) 24:S1215. doi:10.1007/BF00624671

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Antikainen A, Erkintalo M, Dudley J, Genty G. On the phase-dependent manifestation of optical rogue waves. Nonlinearity (2012) 25:R73. doi:10.1088/0951-7715/25/7/R73

CrossRef Full Text | Google Scholar

11. Nguyen JHV, Dyke P, Luo D, Malomed BA, Hulet RG. Collisions of matter-wave solitons. Nat Phys (2014) 10:918. doi:10.1038/nphys3135

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Sun Y-H. Soliton synchronization in the forcing nonlinear Schrodinger equation. Phys Rev E (2016) 93:052222. doi:10.1103/PhysRevE.93.052222

CrossRef Full Text | Google Scholar

13. Akhmediev N, Ankiewicz A. Nonlinear pulses and beams. London: Chapman & Hall (1997).

PubMed Abstract | Google Scholar

14. Akhmediev N, Soto-Crespo J, Ankiewicz A. Extreme waves that appear from nowhere: on the nature of rogue waves. Phys Lett (2009) 373:2137. doi:10.1016/j.physleta.2009.04.023

CrossRef Full Text | Google Scholar

15. Frisquet B, Kibler B, Millot G. Collision of Akhmediev breathers in nonlinear fiber optics. Phys Rev X (2013) 3:041032. doi:10.1103/PhysRevX.3.041032

CrossRef Full Text | Google Scholar

16. Zakharov V, Gelash A. Nonlinear stage of modulation instability. Phys Rev Lett (2013) 111:054101. doi:10.1103/PhysRevLett.111.054101

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Chabchoub A, Akhmediev N. Observation of rogue wave triplets in water waves. Phys Lett (2013) 377:2590. doi:10.1016/j.physleta.2013.07.027

CrossRef Full Text | Google Scholar

18. Gelash A, Zakharov V. Superregular solitonic solutions: a novel scenario for the nonlinear stage of modulation instability. Nonlinearity (2014) 27:R1. doi:10.1088/0951-7715/27/4/R1

CrossRef Full Text | Google Scholar

19. Kibler B, Chabchoub A, Gelash A, Akhmediev N, Zakharov V. Superregular breathers in optics and hydrodynamics: omnipresent modulation instability beyond simple periodicity. Phys Rev X (2015) 5:041026. doi:10.1103/PhysRevX.5.041026

CrossRef Full Text | Google Scholar

20. Xu G, Gelash A, Chabchoub A, Zakharov V, Kibler B. Breather wave molecules. Phys Rev Lett (2019) 122:084101. doi:10.1103/PhysRevLett.122.084101

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wu Y, Liu C, Yang Z, Yang W. Breather interaction properties induced by self-steepening and space-time correction. Chin Phys Lett (2020) 37:040501. doi:10.1088/0256-307X/37/4/040501

CrossRef Full Text | Google Scholar

22. Gelash A. Formation of rogue waves from a locally perturbed condensate. Phys Rev E (2018) 97:022208. doi:10.1103/PhysRevE.97.022208

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Xu G, Chabchoub A, Pelinovsky DE, Kibler B. Observation of modulation instability and rogue breathers on stationary periodic waves. Phys. Rev. Res. (2020) 2:033528. doi:10.1103/PhysRevResearch.2.033528

CrossRef Full Text | Google Scholar

24. Copie F, Randoux S, Suret P. The Physics of the one-dimensional nonlinear Schrödinger equation in fiber optics: rogue waves, modulation instability and self-focusing phenomena. Rev. Phys. (2020) 5:100037. doi:10.1016/j.revip.2019.100037

CrossRef Full Text | Google Scholar

25. Dudley JM, Genty G, Mussot A, Chabchoub A, Dias F. Rogue waves and analogies in optics and oceanography. Nat. Phys. Rev. (2019) 1:675. doi:10.1038/s42254-019-0100-0

CrossRef Full Text | Google Scholar

26. Dudley JM, Dias F, Erkintalo M, Genty G. Instability, breathers and rogue waves in optics. Nat Photon (2014) 8:755. doi:10.1038/nphoton.2014.220

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kuznetsov E. On solitons in parametrically unstable plasma. Dokl Akad Nauk SSSR (1977) 236:575. Available from: http://mi.mathnet.ru/eng/dan41246 (Accessed May 2 1977).

PubMed Abstract | Google Scholar

28. Ma Y. The perturbed plan-wave solutions of the cubic Schrodinger equation. Stud Appl Math (1979) 60:43. doi:10.1002/sapm197960143

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Peregrine D. Water waves, nonlinear Schrodinger equation and their solutions. J. Aust. Soc. Series B, Appl. Math. (1983) 25:16. doi:10.1017/S0334270000003891

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine soliton in nonlinear fiber optics. Nat Phys (2010) 6:790. doi:10.1038/nphys1740

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Kibler B, Fatome J, Finot C, Millot G, Genty G, Wetzel B, et al. Observation of Kuznetsov-Ma soliton dynamics in optical fiber. Sci Rep (2012) 2:463. doi:10.1038/srep00463

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Chabchoub A, Hoffmann N, Akhmediev N. Phys Rev Lett (2011) 106:204502. doi:10.1103/PhysRevLett.106.204502

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Bailung H, Sharma SK, Nakamura Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/PhysRevLett.107.255005

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Chabchoub A, Kibler B, Dudley JM, Akhmediev A. Hydrodynamics of periodic breathers. Phil. Trans. R. Soc. A (2014) 372:20140005. doi:10.1098/rsta.2014.0005

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Närhi M, Wetzel B, Billet C, Toenger S, Sylvestre T, Merolla J-M, et al. Nat. Commun., Real-time measurements of spontaneous breathers and rogue wave events in optical fiber modulation instability. Nat Commun (2016) 7:13675. doi:10.1038/ncomms13675

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Suret P, El Koussaifi R, Tikan A, Evain C, Randoux S, Szwaj C, et al. Bielawski S. Single-shot observation of optical rogue waves in integrable turbulence using time microscopy. Nat Commun (2016) 7:13136. doi:10.1038/ncomms13136

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Xu G, Hammani K, Chabchoub A, Dudley JM, Kibler B, Finot C. Phase evolution of Peregrine-like breathers in optics and hydrodynamics. Phys Rev E (2019) 99:012207. doi:10.1103/PhysRevE.99.012207

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Erkintalo M, Hammani K, Kibler B, Finot C, Akhmediev N, Dudley JM, et al. Genty G. Higher-order modulation instability in nonlinear fiber optics. Phys Rev Lett (2011) 107:253901. doi:10.1103/PhysRevLett.107.253901

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Kedziora D, Ankiewicz A, Akhmediev N. Classifying the hierarchy of nonlinear-Schrodinger-equation rogue-wave solutions. Phys Rev E (2013) 88:013207. doi:10.1103/PhysRevE.88.013207

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Kibler B, Chabchoub A, Gelash A, Akhmediev N, Zakharov V. Ubiquitous nature of modulation instability: from periodic to localized perturbations. In: Wabnitz S, editor. Nonlinear guided wave optics. Bristol: IOP Publishing (2017).

Google Scholar

41. Frisquet B, Chabchoub A, Fatome J, Finot C, Kibler B, Millot G. Two-stage linear-nonlinear shaping of an optical frequency comb as rogue nonlinear-Schrödinger-equation-solution generator. Phys. Rev. A (2014) 89:023821. doi:10.1103/PhysRevA.89.023821

CrossRef Full Text | Google Scholar