
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 06 November 2019
Sec. Statistical and Computational Physics
Volume 7 - 2019 | https://doi.org/10.3389/fphy.2019.00164
This article is part of the Research Topic Recent Trends in Computational Fluid Dynamics View all 20 articles
In this article, the migration of nanomaterials through a permeable domain was modeled numerically. Aluminum oxide was dispersed into testing fluid which was selected water in the current paper. Utilizing Darcy LAW for a porous medium helps us to find simpler form of equations. Influences of shape factor and radiation on the thermal conduct of nanoparticles within a porous region were scrutinized. Nanomaterial within such region is applied under the Lorentz force. CVFEM approach for simulation goals has been applied. This approach provides the advantages of two common CFD methods. Impacts of radiation, magnetic, buoyancy parameters on the treatment of nanomaterials were demonstrated. Outcomes showed that greater amounts of shape factor cause stronger convection. Reverse relationships exist between the Hartmann number and temperature gradient.
Nanotechnology is one of the most interesting fields nowadays. It is interesting due to its vast applications in solar cells, food, fuel cells, batteries, and fuel, etc. In simple, nanotechnology has made its way to each and every branch. Investigators started interest in this field and developed a new sub-branch of nanotechnology, nanofluids. Nanofluids were utilized by Choi [1] for the first time. In real-world fluids exist in abundance, among all, nanopowders can be offered as the most applicable fluids both from its use and its unique nature. Nanofluids are two-phase nanometer-size fluids in which base fluid ranging up to 100 nm. Nanofluids are used in metal oxides, oxides ceramics, and allotropes of carbon and in other chemical stable elements. Nanoparticles nowadays play a key role in thermal analysis. Pak and Cho [2] used titanium dioxide and, and found an improvement in the heat flux. Nanofluids in which the nanoparticles size range less than are considered more ideal [3]. Radiation impact on nanomaterial flow was performed by Zeeshan et al. [4] and they added the impact of MHD on titanium dioxide transportation. Impose of nanomaterial into usual carrier fluid leads to greater conductivity [5–10]. Copper oxide migration within an absorptive medium with the use of Lorentz force in the actuality of magnetic force has been demonstrated by Sheikholeslami [11]. A numerical survey is performed by Sheikholeslami [12] for CuO-H2O nanofluid in a penetrable medium with the help of a microscopic technique. Shah et al. [13] have worked on the 3-D nanofluid flow of third-grade fluid with physical properties inside a rotating frame. An analytical investigation is performed by Dawar et al. [14] for Casson fluid with MHD carbon nanotubes (CNT's) inside a rotating channel. A numerical survey is presented by Sheikholeslami and Shehzad [15] by analyzing Fe3O4–H2O nanofluid flow with inside a permeable channel. To depict the changes in flow style in the appearance of Kelvin forces, Sheikholeslami and Vajravelu [16] examined the FHD impact on nanomaterial flow. CNT migration in a time-dependent problem has been analyzed by Ahmed et al. [17] and they supposed the plate is porous and Lorentz force was added in momentum equations. The transfer of heat due to convection of ferrofluid is described by Yimin et al. [18]. In recent years, Thermal irreversibility in nanofluid through a pipe with a turbulator by means of FVM was analyzed by Sheikholeslami et al. [19]. For a detailed survey, interested readers are referred to Sheikholeslami et al. [20], Dat et al. [21], Bhatti et al. [22], Sheikholeslami [23], Cattaneo [24], Sheikholeslami and Shehzad [25] for more detail and related study of nanofluids flow. Cattaneo [24] made a modification in the thermal relaxation time to improve the heat transfer effects. Cattaneo attempt made for a specific material and obtained some interesting results in the heat transmission investigation by presenting an innovative flux approach. A Maxwell fluid was realized to this model by Mustafa [26] for the study of upper convection. A numerical investigation is performed by Ai and Sandeep [27] by considering this model for MHD Casson-ferrofluid for heat transfer analysis. Previous articles on Nanomaterials for dissimilar phenomena and their usages can be found [28–33]. Sheikholeslami et al. [34] recently presented the application of electric and magnetic field of nanofluid and ferrofluid and with transfer in an enclosure walls. Jawad et al. [35, 36] studied nanofluid thin film and their applications. Nasir et al. [37, 38] have studied 3-D nanomaterial flow CNTs and thermal analysis along a stretching surface. Entropy generation in nanofluid flow can be studied in Alharbi et al. [39]. The studied of nanofluids are further extended to liquid film due to its abundant uses in various sciences [40–48]. Nanomaterial transportation over a wedge was scrutinized by Hassan et al. [49]. An experimental approach was performed by Sheikholeslami et al. [50] to study the boiling of refrigerant with the use of nanoparticles.
Though there is intense research in the literature about nanofluid modeling and the MHD effect in different categories, there is still limited information about the complex geometries and Darcy model. Additionally, the radiative effect is an important source. The determination of this article is to study the migration of nanopowder within a porous space. The effects of shape factor and radiation on the thermal conduct of nanomaterials within a porous space were scrutinized.
In this modeling and simulation, water-based nanofluid exists through permeable geometry has considered. Impact of Lorentz force and thermal behavior are taken on nanofluid. Sketch of the porous tank is depicted in Figure 1. Nanofluid is thermally conducting and impact of Lorentz force was involved. Control Volume finite element technique with a triangular element has been used (see Figure 1). Needed boundary constraints were established in Figure 1. The Darcy LAW [15] is involved for porous terms.
Nanopowder migration through a permeable domain with the help of Darcy model was considered in the current article and involving single-phase model results in below equations:
The fundamental characteristics of nanofluid are estimated as:
To apply the effects of shape factor and kBrownian, the following correlations were examined:
Equation (11) presents a dimensionless form:
So, the last format of equations is:
The mentioned variables in Equation (13) are:
Besides, summarizations of boundaries are:
Nuloc and Nuave are:
Sheikholeslami [29] has been discovered a new approach namely CVFEM for analyzing thermal problems. This technique utilizes a triangular element and the Gauss-Seidel approach uses for the final step of calculating scalars. Tables 1–3 illustrate the properties of carrier fluid. Grid size must be independent of outcomes and we present special cases in Table 4. Validation for presents study for nanofluid [5] are presented in Figure 2 and provide nice accuracy.
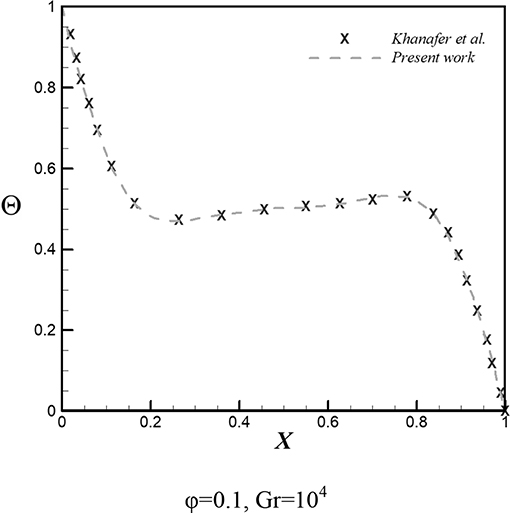
Figure 2. Justification for nanofluid [5].
In this article transportation of electrically and thermally conducting nanomaterial with different shapes were modeled numerically. Aluminum oxide was dispersed into testing fluid which was selected water in current paper. Utilizing Darcy low for porous medium helps us to find simpler form of equations. Impacts of shape factor and the radiation on thermal conduct of nanoparticles inside a permeable space were investigated. Impacts of Radiation parameter, shape factor, magnetic force, and fraction of alumina have been demonstrated. The Darcy Law is involved for a permeable term in geometry.
Impacts of imposing nanopowders into H2O by selecting other parameters are shown in Figure 3. Actually this is the nanofluid scattering rule. It is observed that nanofluid motion augmented with the imposing of nanoparticles. The impacts of Hartmann for different cases were plotted in Figures 4, 5. Impose of the Lorentz effect declines the motion of nanoparticles. Actually, with the augmentation of the magnetic parameter, the top two eddies were amalgamate together and the thermal spiral disappear. It is observed that adding magnetic impact, stronger conduction occurs. Reverse relationships exist between the Hartmann number and temperature gradient. Impacts of scrutinized variables on Nusselt number were displayed in Figure 6. Variations for different cases are presented here.
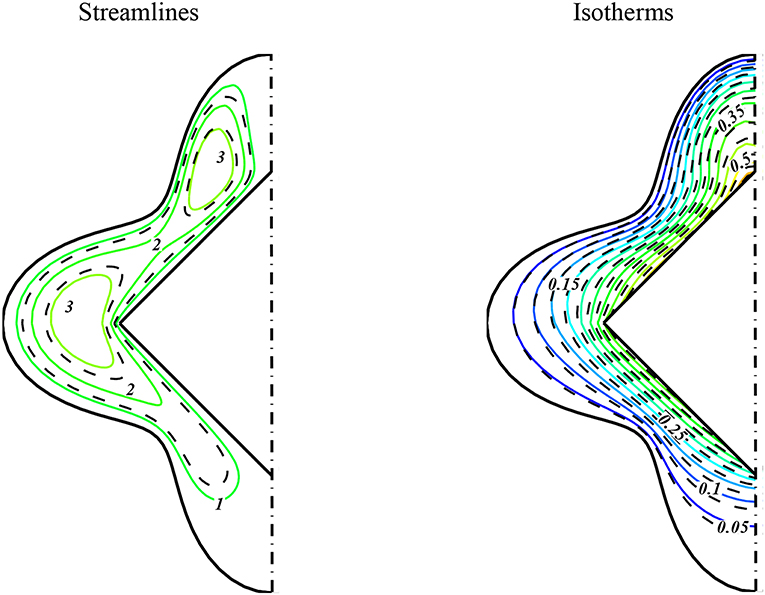
Figure 3. Changing in behavior of nanofluid with rise of ϕ on nanofluid behavior. (ϕ = 0.04 (–) and ϕ = 0 (– – –)) when m = 5.7, Rd = 0.8, Ra = 600, Ha = 0.
Distortion of isotherms augments in consequence of augment in buoyancy and makes stronger vortex which indicates the growth of free convection. With the domination of convective mode, isotherms become more complex with generating plume. Therefore, increasing permeability and buoyancy term makes the Nusselt number to augment. Resistance against the nanomaterial migration reduces with augment of Lorentz forces and in turn, Nusselt number can reduce. Temperature distribution becomes less complex with involving magnetic field and higher Lorentz force can eliminate the plumes. Shear stress among nanoparticles declines with augment of permeability of the region. So, the power of the flow augments with rise of permeability which indicates greater convective flow. The influence of permeability on the style of nanofluid flow reduces with decreasing buoyancy forces. Greater nanofluid mixing occurs within the domain with the rise of buoyancy forces and this influence reduces with imposing magnetic field. Resistance against the nanomaterial migration declines with augment of Darcy number but opposite phenomena appear with augment of the Hartmann number. Magnetic forces work against buoyancy forces, which can reduce the strength of streamline and imposing greater magnetic force, leads to conduction domination. The temperature gradient becomes independent on the Lorentz forces again, owing to the weakening of the buoyancy.
Changes of Nusselt number respect to variables are presented in Figure 6. The mathematical relationship has presented in Equation (18).
It is concluded that the augment in distortion of temperature with buoyancy terms and permeability enhances the gradient of temperature. Moreover, transmission mode improves with a boost of the Lorentz force. Thus, convection diminishes with the escalation of the magnetic field. It is found from Figure 6 that Nusselt number is augmenting function for radiation parameter.
In current CVFEM simulation, nanomaterial was offered as a feasible way to more augmentation of convection in permeable tank and various shapes of powder ware involved. To manage the migration of particles, magnetic forces was employed, and the influence of radiation has been imposed in the energy equation. Outcomes prove that augmenting Lorentz force declines the convection and make isotherms to lower dense near the wall. An indirect relationship was reported for temperature gradient and Lorentz forces. Furthered distortion was observed in isotherms with the rise of buoyancy force.
The datasets generated for this study are available on request to the corresponding author.
ZS developed the numerical method and led the manuscript preparation. HB and PK contributed to the code development and to the article preparation. AS and PT contributed to the analysis and discussion of the results.
This research was funded by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This project was supported by the Theoretical and Computational Science (TaCS) Center under Computational and Applied Science for Smart Innovation Research Cluster (CLASSIC), Faculty of Science, KMUTT.
1. Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles. ASME Int Mech Eng Congr Expos. (1995) 231:99–105.
2. Pak BC, Cho YI. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp Heat Transfer. (1998) 11:151–70. doi: 10.1080/08916159808946559
3. Sheikholeslami M, Rokni HB. Magnetic nanofluid flow and convective heat transfer in a porous cavity considering Brownian motion effects. Phys Fluids. (2018) 30:1. doi: 10.1063/1.5012517
4. Zeeshan A, Shehzad N, Abbas T, Ellahi R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy. (2019) 21:236. doi: 10.3390/e21030236
5. Khanafer K, Vafai K, Lightstone M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int J Heat Mass Transf . (2003) 46:3639–53. doi: 10.1016/S0017-9310(03)00156-X
6. Sheikholeslami M, Shehzad SA. CVFEM for influence of external magnetic source on Fe3O4-H2O nanofluid behavior in a permeable cavity considering shape effect. Int J Heat Mass Transf . (2017) 115:180–91. doi: 10.1016/j.ijheatmasstransfer.2017.07.045
7. Sheikholeslami M, Jafaryar M, Hedayat M, Shafee A, Li Z, Nguyen TK, et al. Heat transfer and turbulent simulation of nanomaterial due to compound turbulator including irreversibility analysis. Int J Heat Mass Transf . (2019) 137:1290–300. doi: 10.1016/j.ijheatmasstransfer.2019.04.030
8. Farshad SA, Sheikholeslami M. Nanofluid flow inside a solar collector utilizing twisted tape considering exergy and entropy analysis. Renew Energy. (2019) 141:246–58. doi: 10.1016/j.renene.2019.04.007
9. Sheikholeslami M, Zareei A, Jafaryar M, Li Z, Smida A, Tlili I. Heat transfer simulation during charging of nanoparticle enhanced PCM within a channel. Phys A. (2019) 525:557–65. doi: 10.1016/j.physa.2019.03.082
10. Sheikholeslami M, Jafaryar M, Shafee A, Li Z, Haq UH. Heat transfer of nanoparticles employing innovative turbulator considering entropy generation. Int J Heat Mass Transf. (2019) 136:1233–40. doi: 10.1016/j.ijheatmasstransfer.2019.03.091
11. Sheikholeslami M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. J Mol Liquids. (2018) 249:921–9. doi: 10.1016/j.molliq.2017.11.118
12. Sheikholeslami M. Numerical investigation for CuO-H2O nanofluid flow in a porous channel with magnetic field using mesoscopic method. J Mol Liquids. (2018) 249:739–46. doi: 10.1016/j.molliq.2017.11.069
13. Shah Z, Islam S, Gul T, Bonyah E, Khan MA. Three dimensional third grade nanofluid flow in a rotating system between parallel plates with Brownian motion and thermophoresis effects. Results Phys. (2018) 10:36–45. doi: 10.1016/j.rinp.2018.05.020
14. Dawar A, Shah Z, Khan W, Idrees M, Islam S. Unsteady squeezing flow of MHD CNTS nanofluid in rotating channels with entropy generation and viscous dissipation. Adv Mech Eng. (2019) 10:1–18. doi: 10.1177/1687814018823100
15. Sheikholeslami M, Shehzad SA. Numerical analysis of Fe3O4-H2O nanofluid flow in permeable media under the effect of external magnetic source. Int J Heat Mass Transf. (2018) 118:182–92. doi: 10.1016/j.ijheatmasstransfer.2017.10.113
16. Sheikholeslami M, Vajravelu K. Nanofluid flow and heat transfer in a cavity with variable magnetic field. Appl Math Comput. (2017) 298:272–82. doi: 10.1016/j.amc.2016.11.025
17. Ahmed Z, Nadeem S, Saleem S, Ellahi R. Numerical study of unsteady flow and heat transfer CNT-based MHD nanofluid with variable viscosity over a permeable shrinking surface. Int J Num Methods Heat Fluid Flow. (2019). doi: 10.1108/HFF-04-2019-0346. [Epub ahead of print].
18. Yimin X, Li Q, Ye M. Investigations of convective heat transfer in ferrofluid microflows using lattice-Boltzmann approach. Int J Thermal Sci. (2007) 46:105–11. doi: 10.1016/j.ijthermalsci.2006.04.002
19. Sheikholeslami M, Jafaryar M, Ali JA, Hamad SM, Divsalar A, Shafee A, et al. Simulation of turbulent flow of nanofluid due to existence of new effective turbulator involving entropy generation. J Mol Liquids. (2019) 291:111283. doi: 10.1016/j.molliq.2019.111283
20. Sheikholeslami M, Haq RU, Shafee A, Li Z, Elaraki YG, Tlili I. Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchanger. Int J Heat Mass Transf. (2019) 135:470–8. doi: 10.1016/j.ijheatmasstransfer.2019.02.003
21. Dat DV, Shah Z, Sheikholeslami M, Shafee A, Nguyen TK. Numerical investigation of MHD nanomaterial convective migration and heat transfer within a sinusoidal porous cavity. Phys Scr. (2019) 94:115225. doi: 10.1088/1402-4896/ab2ced
22. Bhatti MM, Abbas T, Rashidi MM. A new numerical simulation of MHD stagnation-point flow over a permeable stretching/ shrinking sheet in porous media with heat transfer. Iran J Sci Technol Trans A Sci. (2017) 41:779–85. doi: 10.1007/s40995-016-0027-6
23. Sheikholeslami M. Magnetic field influence on CuO-H2O nanofluid convective flow in a permeable cavity considering various shapes for nanoparticles. Int J Hydrogen Energy. (2017) 42:19611–21. doi: 10.1016/j.ijhydene.2017.06.121
24. Cattaneo C. Sulla conduzionedelcalore. AttiSemin Mat Fis Univ Modena Reggio Emilia. (1948) 3:83–101.
25. Sheikholeslami M, Shehzad SA. CVFEM simulation for nanofluid migration in a porous medium using Darcy model. Int J Heat Mass Transf. (2018) 122:1264–71. doi: 10.1016/j.ijheatmasstransfer.2018.02.080
26. Mustafa M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell flud. AIP Adv. (2015) 5:047109. doi: 10.1063/1.4917306
27. Ali ME, Sandeep N. Cattaneo-Christov model for radiative heat transfer of magnetohydrodynamic Casson-ferrofluid: a numerical study. Results Phys. (2017) 7:21–30. doi: 10.1016/j.rinp.2016.11.055
28. Sheikholeslami M, Rokni HB. Influence of EFD viscosity on nanofluid forced convection in a cavity with sinusoidal wall. J Mol Liquids. (2017) 232:390–5. doi: 10.1016/j.molliq.2017.02.042
29. Sheikholeslami M. Application of Control Volume Based Finite Element Method (CVFEM) for Nanofluid Flow and Heat Transfer. Elsevier (2019).
30. Sheikholeslami M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput Methods Appl Mech Eng. (2019) 344:319–33. doi: 10.1016/j.cma.2018.09.044
31. Sheikholeslami M. Numerical approach for MHD Al2O3-water nanofluid transportation inside a permeable medium using innovative computer method. Comput Methods Appl Mech Eng. (2019) 344:306–18. doi: 10.1016/j.cma.2018.09.042
32. Sheikholeslami M, Zeeshan A. Analysis of flow and heat transfer in water based nanofluid due to magnetic field in a porous enclosure with constant heat flux using CVFEM. Comput Methods Appl Mech Eng. (2017) 320:68–81. doi: 10.1016/j.cma.2017.03.024
33. Sheikholeslami M, Shah Z, Tassaddiq A, Shafee A, Khan I. Application of electric field transfer in an enclosure including double for augmentation of ferrofluid heat moving walls. IEEE Access. (2019) 7:21048–56. doi: 10.1109/ACCESS.2019.2896206
34. Sheikholeslami M, Shah Z, Shafi A, Khan I, Itili I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci Rep. (2019) 9:1196. doi: 10.1038/s41598-018-37964-y
35. Jawad M, Shah Z, Islam S, Bonyah E, Khan ZA. Darcy-Forchheimer flow of MHD nanofluid thin film flow with Joule dissipation and Navier's partial slip. J Phys Commun. (2018) 11:115014. doi: 10.1088/2399-6528/aaeddf
36. Jawad M, Shah Z, Islam S, Majdoubi J, Tlili I, Khan W, et al. Impact of nonlinear thermal radiation and the viscous dissipation effect on the unsteady three-dimensional rotating flow of single-wall carbon nanotubes with aqueous suspensions. Symmetry. (2019) 11:207. doi: 10.3390/sym11020207
37. Nasir S, Shah Z, Islam S, Khan W, Bonyah E, Ayaz M, et al. Three dimensional Darcy-Forchheimer radiated flow of single and multiwall carbon nanotubes over a rotating stretchable disk with convective heat generation and absorption. AIP Adv. (2019) 9:035031. doi: 10.1063/1.5087468
38. Nasir S, Shah Z, Islam S, Khan W, Khan SN. Radiative flow of magneto hydrodynamics single-walled carbon nanotube over a convectively heated stretchable rotating disk with velocity slip effect. Adv Mech Eng. (2019) 11:1–11. doi: 10.1177/1687814019827713
39. Alharbi SO, Dawar A, Shah Z, Khan W, Idrees M, Islam S, et al. Entropy generation in MHD eyring–powell fluid flow over an unsteady oscillatory porous stretching surface under the impact of thermal radiation and heat source/sink. Appl Sci. (2018) 8:2588. doi: 10.3390/app8122588
40. Sheikholeslami M, Mahian O. Enhancement of PCM solidification using inorganic nanoparticles and an external magnetic field with application in energy storage systems. J Clean Prod. (2019) 215:963–77. doi: 10.1016/j.jclepro.2019.01.122
41. Khan NS, Gul T, Kumam P, Shah Z, Islam S, Khan W, et al. Influence of inclined magnetic field on Carreau nanoliquid thin film flow and heat transfer with graphene nanoparticles. Energies. (2019) 12:1459. doi: 10.3390/en12081459
42. Saeed A, Islam S, Dawar A, Shah Z, Kumam P, Khan W. Influence of Cattaneo–Christov heat flux on MHD Jeffrey, Maxwell, and Oldroyd-B nanofluids with homogeneous-heterogeneous reaction. Symmetry. (2019) 11:439. doi: 10.3390/sym11030439
43. Sheikholeslami M, Ghasemi A. Solidification heat transfer of nanofluid in existence of thermal radiation by means of FEM. Int J Heat Mass Transf. (2018) 123:418–31. doi: 10.1016/j.ijheatmasstransfer.2018.02.095
44. Gao W, Wang WF. The eccentric connectivity polynomial of two classes of nanotubes. Chaos Solit Fract. (2016) 89:290–4. doi: 10.1016/j.chaos.2015.11.035
45. Qin Y, He Y, Hiller JE, Mei G. A new water-retaining paver block for reducing runoff and cooling pavement. J Clean Prod. (2018) 199:948–56. doi: 10.1016/j.jclepro.2018.07.250
46. Sheikholeslami M. Finite element method for PCM solidification in existence of CuO nanoparticles. J Mol Liquids. (2018) 265:347–55. doi: 10.1016/j.molliq.2018.05.132
47. Jalali E, Akbari OA, Sarafraz MM, Abbas T, Safaei MR. Heat transfer of Oil/MWCNT nanofluid jet injection inside a rectangular microchannel. Symmetry. (2019) 11:757. doi: 10.3390/sym11060757
48. Qin Y, He H, Ou X, Bao T. Experimental study on darkening water-rich mud tailings for accelerating desiccation. J Clean Prod. (2019) 240:118235. doi: 10.1016/j.jclepro.2019.118235
49. Hassan M, Ellahi R, Bhatti MM, Zeeshan A. A comparative study on magnetic and non-magnetic particles in nanofluid propagating over a wedge. Can J Phys. (2018) 97:277–85. doi: 10.1139/cjp-2018-0159
50. Sheikholeslami M, Rezaeianjouybari B, Darzi M, Shafee A, Li Z, Nguyen TK. Application of nano-refrigerant for boiling heat transfer enhancement employing an experimental study. Int J Heat Mass Transf. (2019) 141:974–80. doi: 10.1016/j.ijheatmasstransfer.2019.07.043
Keywords: nanoparticle's shape, porous space, magnetic force, darcy LAW, radiation, nanofluid, CVFEM
Citation: Shah Z, Babazadeh H, Kumam P, Shafee A and Thounthong P (2019) Numerical Simulation of Magnetohydrodynamic Nanofluids Under the Influence of Shape Factor and Thermal Transport in a Porous Media Using CVFEM. Front. Phys. 7:164. doi: 10.3389/fphy.2019.00164
Received: 19 August 2019; Accepted: 11 October 2019;
Published: 06 November 2019.
Edited by:
Muhammad Mubashir Bhatti, Shanghai University, ChinaReviewed by:
Tehseen Abbas, University of Education Lahore, PakistanCopyright © 2019 Shah, Babazadeh, Kumam, Shafee and Thounthong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zahir Shah, emFoaXIuc2hhQGttdXR0LmFjLnRo; Poom Kumam, cG9vbS5rdW1Aa211dHQuYWMudGg=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.