Optical and electrical properties of thiarubrine A simulated via the Hückel method and the nonequilibrium Green’s function

Introduction: Thiarubrine A, a fascinating class of linear carbon chains, can be extracted from certain plants and are known for their photolabile pigment properties.

Methods: In this study, a modified Hückel method to investigate the optical properties of thiarubrine A has been employed, determining its absorption spectrum and wavelength-dependent complex refractive index. Additionally, using the nonequilibrium Green’s function formalism, the conductance of a single thiarubrine A molecule has been derived.

Results and discussion: Light absorption, complex refractive index dispersion, and conductance of thiarubrine A have been simulated. Exploiting its photolability, a light-induced switch in single-molecule conductance has been demonstrated through ultraviolet-visible irradiation, which produces a photoproduct containing a thiophene group. These findings enhance our understanding of the optical properties of naturally occurring polyynes and highlight their potential applications in single-molecule junctions for nanoelectronics.

Introduction

Linear chains of carbon atoms can exist in two idealized isomeric forms: cumulenes, characterized by consecutive double bonds (C=C=C) (Fujiwara et al., 1991), and polyynes, which feature alternating single and triple bonds (C-C≡C) (Matsutani et al., 2009; Chalifoux and Tykwinski, 2010; Chalifoux et al., 2009). Polyynes are particularly intriguing due to their unique optical and electrical properties (Milani et al., 2009; Fazzi et al., 2013; Milani et al., 2017; Gao and Tykwinski, 2022; Marabotti et al., 2021). Many organisms can synthesize polyynes (Minto and Blacklock, 2008). Among these, thiarubrines stand out as a significant class, garnering attention for their distinctive reactivity, unique biological activity, and potential medicinal applications (Block et al., 1996; Wang et al., 1998). Thiarubrines are red, phototoxic polyynes found in the Asteraceae family (Balza and Towers, 1993), notable for their high instability in light (Page and Towers, 2002). The optical properties of these polyynes can be theoretically studied using various methods, such as the Hückel method. In Hückel theory, molecular orbitals are expressed as linear combinations of atomic orbitals (LCAOs). The key approximations in this theory include the following: i) the Born–Oppenheimer approximation, which assumes fixed nuclei positions; and ii) the representation of molecular orbitals as linear combinations of p_z orbitals, neglecting electron–electron interactions (Guy and Troy, 2022). With the Hamiltonian built within the framework of the Hückel theory, it is possible to find the conductance of the single molecule via the use of nonequilibrium Green’s function formalism.

In this study, a modified Hückel method, as detailed by Solomon et al. (2011), has been utilized to investigate the optical properties of thiarubrine A. Its absorption spectrum and wavelength-dependent complex refractive index have been determined. Additionally, using nonequilibrium Green’s function formalism, the conductance of a single thiarubrine A molecule has been derived. Finally, by leveraging the photolability of thiarubrine A, which produces a thiophene-containing photoproduct upon ultraviolet-visible irradiation, a light-induced switch in the single molecule’s conductance has been demonstrated.

Methods

Herein, a modified Hückel method, following has been Solomon et al. (2011), followed. Within this framework, the time-independent Schrödinger equation is given by the following Equation 1:

$H\left|\psi \right.〉=E\left|\psi \right.〉.(1)$

Here, H represents the Hamiltonian, ψ represents the eigenfunction, and E represents the eigenvalue. Subsequently, eigenvalues and eigenfunctions have been determined. In order to find the transition probabilities, the Fermi golden rule has been used (Equation 2):

${\mathrm{\Gamma }}_{i\to j}=\frac{2\pi }{\hslash }{\left|〈{\psi }^j\left|H\right|{\psi }^i〉\right|}^2.(2)$

The transition probabilities have been estimated between the highest occupied molecular orbital (HOMO) and the lowest unoccupied orbitals. Gaussian peaks have been used for the simulation of the absorption spectra. Studying the transitions from the ground state i to the different jth excited states, the absorption coefficient can be written as in Equation 3:

$\alpha \left(E\right)={\sum }_j{\mathrm{\Gamma }}_{i\to j}\mathit{exp}\left(\frac{{\left(E-\left(E_j-E_i\right)\right)}^2}{{2c}^2}\right),(3)$

with a linewidth c of the peaks of 0.2 eV. In order to extract from the absorption spectrum the imaginary part of the complex refractive index, the following expression (Equation 4) has been used, modifying the one reported in Kohandani and Saini (2022):

$k\left(E\right)=\frac{A\alpha \left(E\right)}{4\pi },(4)$

with the parameter A set to $1\times {10}^{15}$. The real part of the complex refractive index can be obtained via the Kramers–Kronig relations (Pankove, 1975) (Equation 5):

$n\left(\overline{\nu }\right)-1=\frac{2}{\pi }\mathcal{P}{\int }_0^{\infty }\frac{\omega k\left(\omega \right)}{{\omega }^2-{\overline{\nu }}^2}d\omega .(5)$

It is noteworthy that the Kramers–Kronig relations are Hilbert transforms (Ogilvie and Fee, 2013). In the case of the real part of the refractive index, a constant offset of 1.5 has been applied, as in Scotognella (2020); Wiebeler et al. (2014).

The complex refractive index can be thus written as in Equation 6:

$n\left(E\right)=n_{real}\left(E\right)+k\left(E\right).(6)$

For the calculation of the elastic transmission, nonequilibrium Green’s function formalism has been employed, following Solomon et al. (2011). Assuming that only a single site of the molecule couples to each electrode, for thiarubrine A, the vector for the left electrode is (Equation 7):

$V_L=\left[\begin{array}{ccccccccccccccc}\gamma & 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right].(7)$

However, the vector for the right electrode is (Equation 8):

$V_R=\left[\begin{array}{ccccccccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& \gamma & 0& 0\end{array}\right].(8)$

The value of $\gamma$ is −1 eV, following Solomon et al. (2011). The broadening function is (Equation 9)

${\mathrm{\Gamma }}^{L\left(R\right)}=2\pi \rho V_{L\left(R\right)}{V}_{L\left(R\right)}^{†},(9)$

where $\rho$ is the density of state of the electrode, set to 1/2π (eV)⁻¹ [following Solomon et al. (2011)]. With the broadening function, it is possible to determine the tunneling self-energy, which is purely imaginary (Equation 10):

${\mathrm{\Sigma }}_T^{L\left(R\right)}=-\frac{i}{2}{\mathrm{\Gamma }}^{L\left(R\right)}.(10)$

The energy-dependent retarded Green’s function can thus be determined as in Equation 11:

$G^r\left(E\right)={\left(E-H_{mol}-{\mathrm{\Sigma }}_T^L-{\mathrm{\Sigma }}_T^R\right)}^{-1}.(11)$

The advanced Green’s function $G^a\left(E\right)$ is the conjugated transpose of the retarded Green’s function. With the broadening functions and Green’s functions, it is possible to determine the energy-dependent elastic transmission (Equation 12):

$T\left(E\right)=Tr\left[{\mathrm{\Gamma }}^L{G}^r\left(E\right){\mathrm{\Gamma }}^R{G}^a\left(E\right)\right].(12)$

The transmission is related to the conductance through the (Chang et al., 2014) (Equation 13):

$G=G_{0}T\left(E_F\right).(13)$

$G_0$ is the quantum of conductance (with value $7.748\times {10}^{-5}S$).

For density functional theory (DFT) calculations, the geometries of molecules have been optimized with the Avogadro package (Hanwell et al., 2012). The electronic transitions have been calculated by means of the density functional theory, with the ORCA package, developed by Frank Neese and coworkers (Neese, 2012). In these calculations, the B3LYP functional has been employed (Lee et al., 1988). Moreover, the Ahlrichs split valence basis set (Schäfer et al., 1992), together with the all-electron nonrelativistic basis set SVPalls1 (Eichkorn et al., 1997; Schäfer et al., 1994), the Libint library (E.∼F.∼Valeev, 2014), and the Libxc library (Lehtola et al., 2018; Marques et al., 2012), has been employed. For the modified neglect of diatomic overlap method (MNDO) calculations (Dewar and Thiel, 1977), the ORCA package has been employed.

Results and discussion

In Figure 1, the chemical formula of thiarubrine A has been drawn. In order to construct the Hamiltonian in the framework of the Hückel method, numbering of the molecule atomic site has been adopted, as depicted in Figure 1.

Figure 1

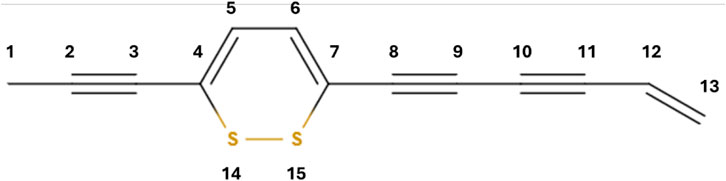
Figure 1. Chemical structure of thiarubrine A. The numbering of the atomic site corresponds to the index in the Hamiltonian.

Thus, the Hamiltonian for thiarubrine A has been built in the following way (Equation 14):

$H=\left[\begin{array}{ccccccccccccccc}a& b& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ b& a& bT& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& bT& a& b& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& b& a& bD& 0& 0& 0& 0& 0& 0& 0& 0& bS& 0\\ 0& 0& 0& bD& a& b& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& b& a& bD& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& bD& a& b& 0& 0& 0& 0& 0& 0& bS\\ 0& 0& 0& 0& 0& 0& b& a& bT& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& bT& a& b& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& b& a& bT& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& bT& a& b& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& b& a& bD& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& bD& a& 0& 0\\ 0& 0& 0& bS& 0& 0& 0& 0& 0& 0& 0& 0& 0& aS& bB\\ 0& 0& 0& 0& 0& 0& bS& 0& 0& 0& 0& 0& 0& bB& aS\end{array}\right].(14)$

In the Hamiltonian, a is the on-site energy for carbon atoms, b is the carbon–carbon single-bond coupling element, bD is the carbon–carbon double-bond coupling element, bT is the carbon–carbon single-bond coupling element, aS is the on-site energy for sulfur atoms, bB is the sulfur–sulfur single-bond coupling element, and bS is the carbon–sulfur single-bond coupling element. Taking into account the experimental absorption spectrum of thiarubrine A (Page and Towers, 2002; Reyes et al., 2001), with characteristic peaks at 345 nm and 490 nm, a fair agreement is found with the parameters reported in Table 1.

Table 1

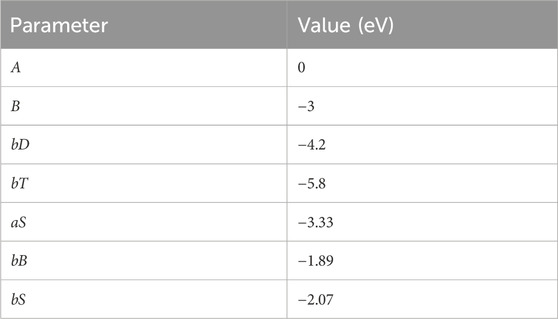
Table 1. Parameters used in the Hamiltonian used in the time-independent Schrödinger equation (Equation 1) for thiarubrine A.

The simulated absorption spectrum is depicted in Figure 2. The peaks correspond to oscillator strengths of the different electronic transitions, as described in Equation 3. In Supplementry Appendix Figure A1 in the Appendix, the absorption spectrum of thiarubrine A, calculated with the modified Hückel method, with DFT, and the MNDO method, is reported. A fair agreement between the modified Hückel method and DFT is found, with the lowest transition at 484 nm using the modified Hückel method and at 517 nm using the DFT, respectively. The lowest transition using the MNDO method is at longer wavelengths, i.e., 627 nm, but shows a small oscillator strength, while the second lowest transition, with a higher oscillator strength, is at 433 nm. The first 12 transitions used for the absorption spectrum are reported in Supplementary Appendix Table SA1, while the employed optimized geometry of thiarubrine A is reported in Supplementary Appendix Table SA3.

Figure 2

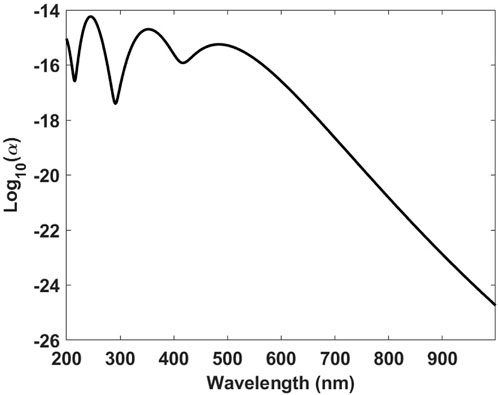
Figure 2. Absorption spectrum with peaks corresponding to oscillator strengths of the different electronic transitions for thiarubrine A (a peak linewidth of 0.2 eV).

By using Equations 4, 5, it is possible to determine the wavelength-dependent complex refractive index of thiarubrine A, starting from the calculated absorption spectrum. The real part (black curve) and the imaginary part (red curve) of the refractive index are depicted in Figure 3.

Figure 3

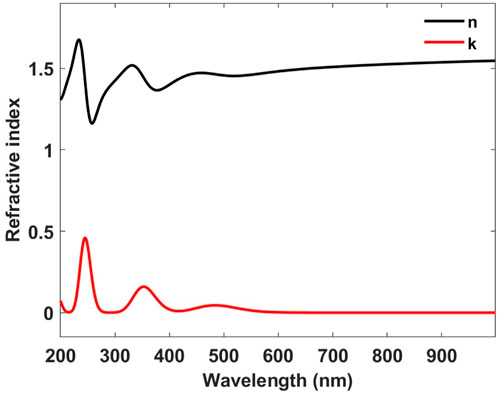
Figure 3. Real part (black curve) and the imaginary part (red curve) of the refractive index of thiarubrine A.

By employing the nonequilibrium Green’s function formalism, it is possible to determine the elastic transmission of thiarubrine A (Equation 12), depicted in Figure 4.

Figure 4

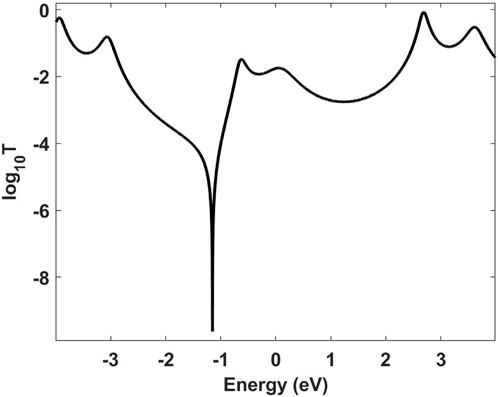
Figure 4. Transmission spectrum of thiarubrine A determined via nonequilibrium Green’s function formalism.

Setting the Fermi energy at 0 eV, the conductance of the molecule is 1.35 µS (Equation 13). Upon light irradiation, thiarubrine A is converted to a photoproduct thiophene A, depicted in Figure 5 (Page and Towers, 2002).

Figure 5

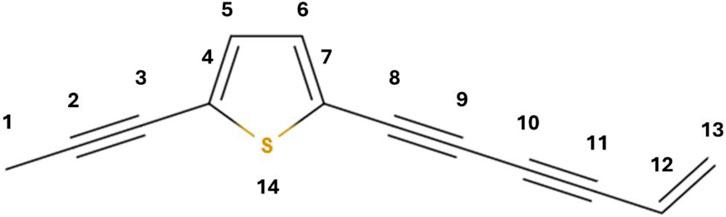
Figure 5. Chemical structure of thiophene A. The numbering of the atomic site corresponds to the index in the Hamiltonian.

The Hamiltonian H′ related to the photoproduct thiophene A can be written in the following way (Equation 15):

$H^{\prime }=\left[\begin{array}{cccccccccccccc}a& b& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ b& a& bT& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& bT& a& b& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& b& a& bD& 0& 0& 0& 0& 0& 0& 0& 0& bS\\ 0& 0& 0& bD& a& b& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& b& a& bD& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& bD& a& b& 0& 0& 0& 0& 0& bS\\ 0& 0& 0& 0& 0& 0& b& a& bT& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& bT& a& b& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& b& a& bT& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& bT& a& b& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& b& a& bD& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& bD& a& 0\\ 0& 0& 0& bS& 0& 0& bS& 0& 0& 0& 0& 0& 0& aS\end{array}\right].(15)$

The values of the parameters used in the Hamiltonian H′ for thiophene A are the same ones of the Hamiltonian H for thiarubrine A. In Supplementry Appendix Figure A2 in the Appendix, the calculated absorption spectrum, calculated with the modified Hückel method, DFT, and the MNDO method, of thiophene A, is reported. The DFT lowest transition is at 319 nm, significantly higher with respect to that calculated with the MNDO method (i.e., 394 nm) and modified Hückel method (i.e., 437 nm). There are reports of incorrect results with DFT for thiophene (Prlj et al., 2015). For this, a comparison of absorption spectra calculated by different methods has proved necessary. The first 12 transitions used for the absorption spectrum are reported in Supplementary Appendix Table SA2, while the employed optimized geometry of thiophene A is reported in Supplementary Appendix Table SA4.

For thiophene A, the conductance, calculated using Equation 13, is 0.56 µS. Thus, a light-induced variation in the electrical behavior can be achieved in the presented molecular system. The advantage of using the thiarubrine A molecule is twofold: (i) on one hand, polyynes are considered good candidates for molecular wires as electronic transport along the sp-carbon chain should be independent of rotation about the single bonds (Gao et al., 2025); (ii) thiarubrine A under the effect of light can be precisely converted to thiophene A with the resulting change in conductance. It is noteworthy that the conductance of thiarubrine A is more than double with respect to that of the thiophene-based molecule T1 reported in Chang et al. (2014). The conductance can also be studied by carefully analyzing orbitals for the different molecules. There are relevant reports of the prediction of charge transport parameters in organic semiconductors (Fazzi et al., 2011). In this work, the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of thiarubrine A and thiophene A are reported. However, a careful study on the relationship between the orbitals of the two molecules and the properties related to charge transport in them is beyond the scope of this paper and could be the subject of future studies.

Conclusion

In this work, the optical and electric properties of the molecule thiarubrine A have been simulated by using a modified Hückel method [exhaustively described in Solomon et al. (2011)] and the nonequilibrium Green’s function formalism. The strength of this simple model lies in the fact that by constructing a Hamiltonian, it is possible to simulate the optical and electronic properties of the investigated molecules. The simulated absorption spectrum has been determined, and by choosing the proper parameters in the Hamiltonian, good matching with the experimental data can be found. From the simulated absorption spectrum, it is possible to derive the wavelength-dependent complex refractive index. Moreover, with the employment of nonequilibrium Green’s function formalism, the conductance of the single molecule has been found. Taking into account the photolability of thiarubrine A, via light irradiation, a change in conductance can be achieved. Such findings can be interesting for the understanding of the optical properties of polyynes occurring in nature and for their exploitation in nanoelectronics.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

FS: conceptualization, methodology, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme [grant agreement No. (816313)].

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphot.2025.1535015/full#supplementary-material

References

Balza, F., and Towers, G. H. N. (1993). “Naturally occurring C13 dithiacyclohexadienes and thiophenes from the Asteraceae,” in Methods in plant biochemistry (New York: Alkaloids and Sulphur Compounds), 8, 551–572. Academic Press.

Google Scholar

Block, E., Page, J., Toscano, J. P., Wang, C.-X., Zhang, X., DeOrazio, R., et al. (1996). Photochemistry of thiarubrine A and other 1,2-dithiins: formation of 2,6-Dithiabicyclo[3.1.0]hex-3-enes. J. Am. Chem. Soc. 118 (19), 4719–4720. doi:10.1021/ja960589v

CrossRef Full Text | Google Scholar

Chalifoux, W. A., McDonald, R., Ferguson, M. J., and Tykwinski, R. R. (2009). tert-Butyl-End-Capped polyynes: crystallographic evidence of reduced bond-length alternation. Angew. Chem. Int. Ed. 48 (42), 7915–7919. doi:10.1002/anie.200902760

PubMed Abstract | CrossRef Full Text | Google Scholar

Chalifoux, W. A., and Tykwinski, R. R. (2010). Synthesis of polyynes to model the sp-carbon allotrope carbyne. Nat. Chem. 2 (11), 967–971. doi:10.1038/nchem.828

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, W. B., Mai, C.-K., Kotiuga, M., Neaton, J. B., Bazan, G. C., and Segalman, R. A. (2014). Controlling the thermoelectric properties of thiophene-derived single-molecule junctions. Chem. Mater. 26 (24), 7229–7235. doi:10.1021/cm504254n

CrossRef Full Text | Google Scholar

Dewar, M. J. S., and Thiel, W. (1977). Ground states of molecules. 38. The MNDO method. Approximations and parameters. J. Am. Chem. Soc. 99 (15), 4899–4907. doi:10.1021/ja00457a004

CrossRef Full Text | Google Scholar

Eichkorn, K., Weigend, F., Treutler, O., and Ahlrichs, R. (1997). Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chem. Accounts Theory, Comput. Model. Theor. Chimica Acta 97 (1–4), 119–124. doi:10.1007/s002140050244

CrossRef Full Text | Google Scholar

Fazzi, D., Caironi, M., and Castiglioni, C. (2011). Quantum-chemical insights into the prediction of charge transport parameters for a naphthalenetetracarboxydiimide-based copolymer with enhanced electron mobility. J. Am. Chem. Soc. 133 (47), 19056–19059. doi:10.1021/ja208824d

PubMed Abstract | CrossRef Full Text | Google Scholar

Fazzi, D., Scotognella, F., Milani, A., Brida, D., Manzoni, C., Cinquanta, E., et al. (2013). Ultrafast spectroscopy of linear carbon chains: the case of dinaphthylpolyynes. Phys. Chem. Chem. Phys. 15 (23), 9384–9391. doi:10.1039/C3CP50508A

PubMed Abstract | CrossRef Full Text | Google Scholar

Fujiwara, K., Sakai, H., and Hirama, M. (1991). Enyne[3]cumulene. Synthesis and mode of aromatization. J. Org. Chem. 56 (5), 1688–1689. doi:10.1021/jo00005a006

CrossRef Full Text | Google Scholar

Gao, Y., Leary, E., Palomino-Ruiz, L., Malagón, J. M., González, M. T., Krempe, M., et al. (2025). Length-dependent conduction of polyynes: searching for the limit of the tunneling regime. J. Am. Chem. Soc. 147 (5), 4052–4059. doi:10.1021/jacs.4c12895

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Y., and Tykwinski, R. R. (2022). Advances in polyynes to model carbyne. Accounts Chem. Res. 55 (24), 3616–3630. doi:10.1021/acs.accounts.2c00662

PubMed Abstract | CrossRef Full Text | Google Scholar

Guy, G. R., and Troy, V. V. (2022). Physical chemistry. MIT OpenCourseWare. Available online at: https://ocw.mit.edu/courses/chemistry/5-61-physical-chemistry-fall-2007/(Accessed February 5, 2022).

Google Scholar

Hanwell, M. D., Curtis, D. E., Lonie, D. C., Vandermeersch, T., Zurek, E., and Hutchison, G. R. (2012). Avogadro: an advanced semantic chemical editor, visualization, and analysis platform. J. Cheminformatics 4 (1), 17. doi:10.1186/1758-2946-4-17

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohandani, R., and Saini, S. S. (2022). Extracting optical absorption characteristics from semiconductor nanowire arrays. Nanotechnology 33 (39), 395204. doi:10.1088/1361-6528/ac74cc

CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37 (2), 785–789. doi:10.1103/PhysRevB.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehtola, S., Steigemann, C., Oliveira, M. J. T., and Marques, M. A. L. (2018). Recent developments in libxc—a comprehensive library of functionals for density functional theory. SoftwareX 7, 1–5. doi:10.1016/j.softx.2017.11.002

CrossRef Full Text | Google Scholar

Marabotti, P., Milani, A., Lucotti, A., Brambilla, L., Tommasini, M., Castiglioni, C., et al. (2021). Vibrational and nonlinear optical properties of amine-capped push-pull polyynes by infrared and Raman spectroscopy. Carbon Trends 5, 100115. doi:10.1016/j.cartre.2021.100115

CrossRef Full Text | Google Scholar

Marques, M. A. L., Oliveira, M. J. T., and Burnus, T. (2012). Libxc: a library of exchange and correlation functionals for density functional theory. Comput. Phys. Commun. 183 (10), 2272–2281. doi:10.1016/j.cpc.2012.05.007

CrossRef Full Text | Google Scholar

Matsutani, R., Ozaki, F., Yamamoto, R., Sanada, T., Okada, Y., and Kojima, K. (2009). Preparation of polyynes up to C22H2 by liquid-phase laser ablation and their immobilization into SiO2 gel. Carbon 47 (7), 1659–1663. doi:10.1016/j.carbon.2009.02.026

CrossRef Full Text | Google Scholar

Milani, A., Tommasini, M., Barbieri, V., Lucotti, A., Russo, V., Cataldo, F., et al. (2017). Semiconductor-to-Metal transition in carbon-atom wires driven by sp2 conjugated end groups. J. Phys. Chem. C 121 (19), 10562–10570. doi:10.1021/acs.jpcc.7b02246

CrossRef Full Text | Google Scholar

Milani, A., Tommasini, M., and Zerbi, G. (2009). Connection among Raman wavenumbers, bond length alternation and energy gap in polyynes. J. Raman Spectrosc. 40 (12), 1931–1934. doi:10.1002/jrs.2342

CrossRef Full Text | Google Scholar

Minto, R. E., and Blacklock, B. J. (2008). Biosynthesis and function of polyacetylenes and allied natural products. Prog. Lipid Res. 47 (4), 233–306. doi:10.1016/j.plipres.2008.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Neese, F. (2012). The ORCA program system. WIREs Comput. Mol. Sci. 2 (1), 73–78. doi:10.1002/wcms.81

CrossRef Full Text | Google Scholar

Ogilvie, J. F., and Fee, G. J. (2013). Equivalence of kramers-kronig and fourier transforms to convert between optical dispersion and optical spectra. MATCH – Commun. Math. Comput. Chem. 69, 249–262.

Google Scholar

Page, J., and Towers, N. (2002). Anthocyanins protect light-sensitive thiarubrine phototoxins. Planta 215 (3), 478–484. doi:10.1007/s00425-002-0769-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Pankove, J. I. (1975). Optical processes in semiconductors (Unabridged republication, with slight corrections). Dover Publications, Inc.

Google Scholar

Prlj, A., Curchod, B. F. E., Fabrizio, A., Floryan, L., and Corminboeuf, C. (2015). Qualitatively incorrect features in the TDDFT spectrum of thiophene-based compounds. J. Phys. Chem. Lett. 6 (1), 13–21. doi:10.1021/jz5022087

PubMed Abstract | CrossRef Full Text | Google Scholar

Reyes, J., Morton, M., Hoffman, G. G., O’Shea, K. E., and Downum, K. (2001). Isolation and spectral analysis of naturally occurring thiarubrine A. J. Chem. Educ. 78 (6), 781. doi:10.1021/ed078p781

CrossRef Full Text | Google Scholar

Schäfer, A., Horn, H., and Ahlrichs, R. (1992). Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 97 (4), 2571–2577. doi:10.1063/1.463096

CrossRef Full Text | Google Scholar

Schäfer, A., Huber, C., and Ahlrichs, R. (1994). Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 100 (8), 5829–5835. doi:10.1063/1.467146

CrossRef Full Text | Google Scholar

Scotognella, F. (2020). Multilayer plasmonic photonic structures embedding photochromic molecules or optical gain molecules. Phys. E Low-Dimensional Syst. Nanostructures 120, 114081. doi:10.1016/j.physe.2020.114081

CrossRef Full Text | Google Scholar

Solomon, G. C., Bergfield, J. P., Stafford, C. A., and Ratner, M. A. (2011). When “small” terms matter: coupled interference features in the transport properties of cross-conjugated molecules. Beilstein J. Nanotechnol. 2 (1), 862–871. doi:10.3762/bjnano.2.95

PubMed Abstract | CrossRef Full Text | Google Scholar

Valeev, E. F. (2014). A library for the evaluation of molecular integrals of many-body operators over Gaussian functions. Available online at: http://libint.valeyev.net/.

Google Scholar

Wang, Y., Koreeda, M., Chatterji, T., and Gates, K. S. (1998). Total synthesis and DNA-cleaving properties of thiarubrine C. J. Org. Chem. 63 (24), 8644–8645. doi:10.1021/jo981849p

CrossRef Full Text | Google Scholar

Wiebeler, C., Bader, C. A., Meier, C., and Schumacher, S. (2014). Optical spectrum, perceived color, refractive index, and non-adiabatic dynamics of the photochromic diarylethene CMTE. Phys. Chem. Chem. Phys. 16 (28), 14531–14538. doi:10.1039/C3CP55490B

PubMed Abstract | CrossRef Full Text | Google Scholar