- HYLAB—Hybrid Photonics Laboratory, Institute for Electro and Microengineering, EPFL, Lausanne, Switzerland
Frequency up-conversion has become amongst the most prevalent techniques for detection of terahertz waves in metrology systems. State-of-the-art up-conversion techniques rely on the coherent transferring of the information encoded in all degrees of freedom of a terahertz wave to either the near-infrared or visible domain, where detectors are readily accessible. This allows for an indirect reconstruction of the terahertz wave. However, unlike most up-conversion methods employed in photonics which are concentrating on narrowband tones (at both terahertz and near-infrared frequencies), a broadband, hence temporally constrained, terahertz transient is sampled on time-scales shorter than its oscillation period. Here, femtosecond laser pules serve as temporal gates. In this perspective, we highlight several hallmarks of terahertz metrology that originate from these sub-cycle measurement capabilities and elaborate why this enables studies in fundamental and applied science, with a particular focus on novel measurement concepts in classical and quantum. We focus on so-far demonstrated detection performance in bulk non-linear crystals. Finally, we discuss current challenges and the most pressing questions ahead.
1 Introduction
Electric field metrology aims to achieve ultimate precision in the characterisation of the spatio-temporal evolution of the electromagnetic field of a wave. This is a very meaningful endeavour since the precise spatio-temporal waveform has direct implications in most of the physical processes that involve light, for example the way and strength light interacts with matter or with other light fields. Light’s properties change as it propagates through a medium in a way that depends on the properties of both the medium and the wave itself. Therefore, ultra-fast phenomena inside materials can be probed by analyzing the properties of custom-tailored light on sub-cycle scales after it has interacted with the medium Raimond et al., 2001.
Characterising the spatio-temporal pattern of a wave is however quite a technical feat: it requires measuring the entire set of degrees of freedom, i.e., amplitude, frequency, phase, polarisation and spatial mode of a wave at once. This is generally possible when dealing with classical states of light. In the quantum limit however, measuring all degrees of freedom of a quantum state of light with arbitrary spatio-temporal precision is prohibited by Heisenberg’s uncertainty principle Loudon, 2000. Here, the measurement of a certain variable with high precision will concomitantly introduce an imprecision in its conjugate variable. This is then manifested through quantum noise that limits the precision of the measurement. Also in this context, sub-cycle spatio-temporal scales are the relevant ones and being able to measure them provides important knowledge about squeezing or anti-squeezing present in the system. This can be in turn leveraged to perform metrology beyond the shot noise limit. Finally, having access to all degrees of freedom on sub-cycle timescales opens up the possibility for single- and few-cycle temporal states to be considered as a viable basis for quantum information processing Brecht et al., 2015.
The examples above provide only a glimpse of the importance of developing sub-cycle metrology tools that can determine all degrees of freedom at once. This has proven extremely challenging across all frequency regimes, and the terahertz makes no exception. More than 20 years of research Dhillon et al., 2017 have resulted in electro-optic sampling being the leading metrology technique. This is a rather unique methodology that can provide, in principle, quantitative reconstruction of the amplitude, phase, polarisation, frequency and spatial mode of a THz waveform on sub-cycle spatio-temporal scales. As a result, sub-cycle quantum metrology has recently emerged as a young and exciting field. It aims to measure sub-cycle signatures down to signal levels that are commensurate with quantum states of light. Since this can be achieved in both the temporal and the spatial domain, this opened up studies about the very nature of these peculiar states. Theoretical proposals were made to probe fundamental hypotheses in special relativity in a table-top experiment using electro-optic sampling Moskalenko et al., 2015; Guedes et al., 2019: realising an Unruh-Dewitt detector Onoe et al., 2022, probing local and non-local correlations of vacuum fields Lindel et al., 2020 or probing the dynamic Casimir force. Experimental studies corroborated these proposals, with direct measurement of the vacuum ground state Riek et al. (2015) and its correlations in space-time Benea-Chelmus et al., 2019, photon statistics of lasers around their threshold Benea-Chelmus et al., 2016, demonstration of Hilbert transforms Sulzer et al., 2020, existence of entanglement outside the lightcone Settembrini et al., 2022 or squeezed temporal states Riek et al., 2017. On the counter side, a very recent theoretical work shows that sub-cycle metrology of terahertz fields may provide information about spatio-temporal properties of dispersive coupled light-matter systems De Liberato., 2019, about the Purcell effect Lindel et al., 2022, or quantum susceptibilities Kizmann et al., 2022.
Despite this initial progress, measuring all degrees of freedom of quantum states of light in the terahertz remains a laborious and challenging task. In this perspective, we discuss—by virtue of contrast—the advantages of electro-optic sampling as opposed to narrowband up-conversion techniques from a fundamental point of view. In the second part 2, we elaborate on the conceptual difference between narrowband up-conversion, which is the most prevalent in photonics, and broadband up-conversion, which gives access to a sub-cycle portion of the terahertz waveform. We corner its unique advantages by proposing five hallmarks of terahertz field metrology, in 3. In the fourth part 4, we discuss challenges and opportunities ahead when connecting the two realms: sub-cycle metrology with the advantages quantum-level sensitivity. A particular focus will lie on existing important challenges of bulk systems and an outlook of important milestones to be addressed ahead.
2 Metrology on sub-THz-cycle scales
Electro-optic sampling relies on the optical up-conversion of a spatio-temporal terahertz wave
χ(2) is in general a three-dimensional tensor that describes all possible combinations of mixing between the components of the near-infrared and terahertz fields. As a result, the information about the amplitude, phase, polarisation and frequency of the sampled terahertz radiation is generally preserved in the up-conversion process. One can show that the resulting non-linear field takes the shape of
Depending on the relative vectorial orientation of the polarisation of the probe field, described by
Two distinct approaches can be followed, depending on the spectral characteristics of the two mixing beams: narrowband or broadband up-conversion. We discuss them graphically in Figure 1 both from a time-domain and from a frequency-domain perspective. In Figure 1A, a narrowband probe is mixed with a narrowband THz tone. Consequently, the up-conversion is temporally extended over many cycles of the THz tone and the resulting probe signal is characterised by a beating period equal to the THz frequency. In the frequency domain, the narrowband THz tone is up-shifted to the near-infrared range and is well resolved from the original probe tone. Hence, in this case we operate in the resolved sideband regime. To retrieve the amplitude and phase information about the up-converted terahertz waveform, the beating between the up-shifted tone and the original probe tone can be used. It needs to be detected at an intensity detector with an electronic bandwidth larger than the terahertz frequency. Consequently, the lack of photodetectors with terahertz bandwidth strongly limits the maximal terahertz frequency that can be detected in this fashion.
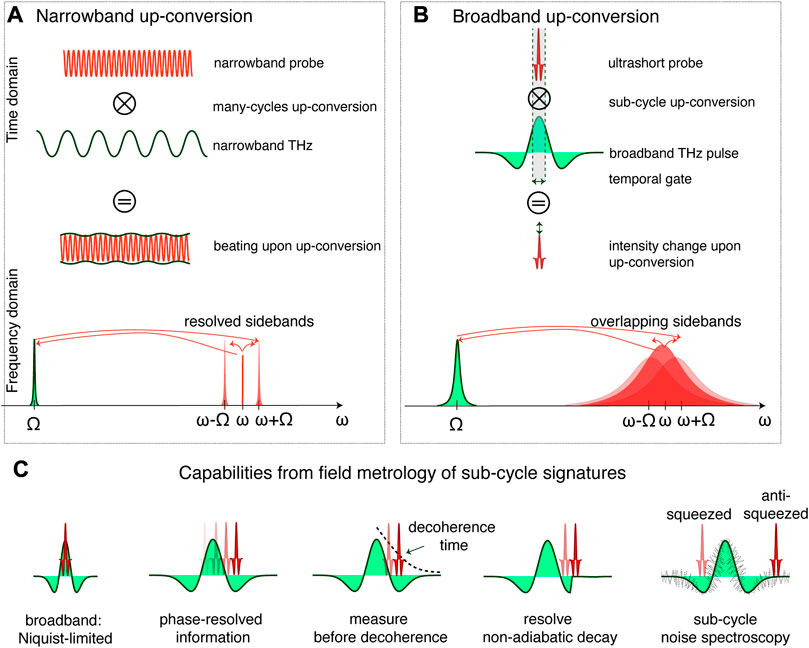
FIGURE 1. Today’s capabilities of terahertz field metrology stem from utilizing broadband up-conversion by mixing a terahertz wave with a femtosecond probe pulse, which has a duration that is typically much shorter than a terahertz cycle. This approach is distinct from narrow-band up-conversion shown in (A), where a narrowband probe beam is mixed with a narrowband THz wave (featured by a linewidth much narrower that its central frequency), thus resulting into a beating modulation of the probe at the THz frequency. In the frequency domain, the up-conversion process leads to the formation of well resolved sidebands. In contrast, broadband up-conversion shown in (B) employs ultrashort pulses to effectively gate the up-conversion process to occur on timescales that are shorter than one cycle of THz oscillation. In the frequency domain, this leads to the formation of sidebands that overlap significantly with the original probe spectrum, leading to a modulation of its either intensity or phase. This metrology technique, called electro-optic sampling, effectively probes only a sub-cycle portion of the terahertz waveform, much like an oscilloscope does to a radio-frequency signal. (C) The access to sub-cycle signatures of a THz waveform leads to several capabilities that have become the hallmarks of terahertz metrology: broadband detection, phase-resolved information, measurement before decoherence, resolution of non-adiabatic decay and sub-cycle noise spectroscopy.
Broadband up-conversion, shown in Figure 1B, stands in contrast to the previously mentioned approach. In this case, the probe beam is an ultrashort pulse, the width of which satisfies
Here ETHz(x, y, z, t) is the sub-cycle portion of the real THz field with which the probe pulse is overlapped in time and space. Consequently, by simply displacing the probe pulse in time or space, one can access other space-time points of the terahertz waveform in a quantitative manner.
An essential feature of electro-optic sampling is that the availability of shot-noise limited intensity detectors in the near-infrared can be paired with ultra-stable femtosecond laser systems, so as to bypass the necessity of shot-noise limited detectors in the terahertz range that would otherwise become compelling. State-of-the-art laser technologies routinely provide ultrashort (i.e., from sub-picosecond down to a few tens of femtoseconds) pulsed beams in the near-infrared, and they are tunable in a relatively large range of wavelengths.
3 Hallmarks of terahertz metrology
Multiple unique capabilities arise from the spatio-temporal resolution to sub-THz-cycle scales provided by the femtosecond pulses in electro-optic sampling, graphically summarized in Figure 1C.
We succinctly summarize these capabilities by proposing five hallmarks that set terahertz field metrology via broadband up-conversion apart from other terahertz detection techniques, typically featuring detection schemes aimed at retrieving the average intensity of the terahertz wave.
1. Broadband detection: sub-THz-cycle metrology is capable of detecting broadband THz radiation, down to single-cycle waveforms. The upper frequency limit is imposed by the Nyquist criterion where
2. Phase-resolved information: Electro-optic sampling allows for the recording of the entire THz time-varying waveform, in terms of both amplitude and phase simultaneously Jepsen (2019). This is achieved by scanning the relative delay between the THz and probe pulses, within their temporal window of interaction. In particular, phase information recovery enables for broadband measurements of the complex refractive index van Exter et al., 1989 e.g. of THz-transparent materials, but also of materials that have strong dispersion due to the proximity to phonon resonances.
3. Measurement before decoherence: full characterization of the THz waveform can be performed before loss of phase coherence. This property allows to resolve a decay of e.g., a given material excitation after it has been driven coherently by a waveform in the terahertz Zhang et al., 2014. In addition, this allows for the characterization of incoherent sources e.g., through a measurement of their first order coherence function Benea-Chelmus et al., 2016.
4. Snapshot of non-adiabatic processes: as the temporal resolution provided by the femtosecond pulse is typically in the order of 100 femtoseconds, signatures that happen on much shorter time-scales than one terahertz oscillation cycle can be resolved. This capability has been explored to characterise the response of supercoductors in the non-adiabatic excitation regime Matsunaga et al., 2013 or to characterize abrupt switch-off of light-matter systems Halbhuber et al., 2020; Mornhinweg et al., 2021.
5. Sub-cycle noise spectroscopy: by studying the noise properties of the sampled terahertz transients as a function of space-time, quantum properties of the THz waveforms can be revealed. This property has been instrumental for characterisation of the ground state of light—vacuum field fluctuations Riek et al., 2015, Benea-Chelmus et al., 2019, Settembrini et al., 2022.
4 State of the art detection in bulk crystals, challenges and opportunities ahead
Today, the vast majority of terahertz-compatible metrology techniques rely on bulk non-linear crystals. The THz waveform is co-propagating with an ultrashort probe pulse. Their transverse profile inside the bulk medium is well-approximated by Gaussian beams, yet featuring spot diameters with significantly different sizes, dictated by a wavelength ratio higher than a factor of 100. This implies that the magnitude of the sampled THz waveform is strongly determined by the use of focusing optics. The latter imposes a minimal confinement volume due to the diffraction limit. At the detection crystal, a sub-THz-cycle spatial overlap between probe and THz spots can be realised. This scheme comes with several advantages and shortcomings. On the one hand, the probe pulse power should be chosen sufficiently high so as to maximize the signal-to-noise ratio of the measurements, i.e. by reaching the shot-noise-limited regime, much like in any homodyne detection technique. On the other hand, the sampled THz electric field strength ETHz(x, y, z, t) is mainly enhanced by focusing effect, while the effective interaction length l (between probe and THz beams) is limited by both the focusing condition of the two beams and their phase-matching, the latter being linked to the refractive indices at near-infrared and terahertz frequencies. For this reason, a careful compromise should be achieved in order to optimize the overall detection efficiency in a certain terahertz band, by simultaneously optimizing phase matching and THz focusing at the detection crystal, both being conditions mutually dependent upon each other.
Zinc telluride (ZnTe) is historically the most utilized material at THz frequencies Nahata et al., 1996 as it is naturally phase-matched (in a collinear propagation geometry) with the 800 nm line emitted by Ti:Sapphire lasers. Since the band-gap of ZnTe (2.26 eV) is larger than the energy associated to 800 nm-photons (1.55 eV), it can be optically pumped without introducing a significant free-carrier absorption, while featuring moderate dispersion in a broad optical range. Because of this, ZnTe allows for a remarkably simple implementation of the electro-optic sampling technique, which can be also extended to broadband regimes (ultrashort THz transients), since the large spectral linewidth of the laser pulse (
In conclusion, from the standpoint of temporal resolution, electro-optic sampling can nowadays be pushed to the extreme of using few-femtosecond pulses, in order to measure ultrashort transients featuring bandwidth extending up to the mid-infrared and even near-infrared. Looking ahead, several important milestones will need to be addressed in order to make sub-cycle metrology at the quantum level broadly accessible, and hence make full use of the hallmarks we propose. The most pressing ones, currently partially a field of intense research, relate to an increase in sensitivity, up to regimes superior to the conventional shot-noise limited detection in zinc telluride. This is mainly pursued by leveraging on advantages brought by miniaturisation: 1. to engineer the near-field and far-field spatio-temporal distribution of terahertz wave e.g. by using on-chip terahertz cavities or antennas integrated photonic circuits Salamin et al., 2019; Benea-Chelmus et al., 2020 or metasurfaces and 2. to engineer the probe pulse itself by custom-tailored non-linearities inside tailored on-chip waveguides and its further interaction with the local terahertz field. However, we foresee that limitations of the on-chip probe pulse energies need careful consideration, because both signal-to-noise ratio of the field measurement and the efficiency of undesired spurious non-linear processes increases with high probe powers. Furthermore, many of such on-chip detection schemes have not yet been characterised in the terahertz at cryogenic temperatures, which are necessary for operation at zero thermal occupation. On the other side, miniaturisation may provide a way to integrate novel material systems that allow innovative measurement protocols such as e.g. of the magnetic field via the magneto-optical Kerr effect as was recently done in bulk Weiss et al., 2023, exploitation of higher order non-linear processes such as χ(3) towards on-chip terahertz field induces second harmonic generation (TFISH) Cook et al., 1999, full polarisation state reconstruction, single-shot terahertz acquisition, use of pre-conditioned probes Virally et al., 2021, development of multi-pulse sensing techniques beyond two individual probe pulses towards correlations beyond the first and second order coherence of the electric field that is possible today.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
IB and AT contributed equally to the manuscript.
Funding
IB acknowledges funding from the Swiss National Science Foundation under the PRIMA grant number 201547.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Benea-Chelmus, I.-C., Bonzon, C., Maissen, C., Scalari, G., Beck, M., and Faist, J. (2016). Subcycle measurement of intensity correlations in the terahertz frequency range. Phys. Rev. A 93, 043812. doi:10.1103/PhysRevA.93.043812
Benea-Chelmus, I.-C., Salamin, Y., Settembrini, F. F., Fedoryshyn, Y., Heni, W., Elder, D. L., et al. (2020). Electro-optic interface for ultrasensitive intracavity electric field measurements at microwave and terahertz frequencies. Optica 7, 498–505. doi:10.1364/OPTICA.384160
Benea-Chelmus, I.-C., Settembrini, F., Scalari, G., and Faist, J. (2019). Electric field correlation measurements on the electromagnetic vacuum state. Nature 568, 202–206. doi:10.1038/s41586-019-1083-9
Brecht, B., Reddy, D. V., Silberhorn, C., and Raymer, M. G. (2015). Photon temporal modes: A complete framework for quantum information science. Phys. Rev. X 5, 041017. doi:10.1103/PhysRevX.5.041017
Cook, D. J., Chen, J. X., Morlino, E. A., and Hochstrasser, R. M. (1999). Terahertz-field-induced second-harmonic generation measurements of liquid dynamics. Chem. Phys. Lett. 309, 221–228. doi:10.1016/S0009-2614(99)00668-5
Cui, W., Schiff-Kearn, A. W., Zhang, E., Couture, N., Tani, F., Novoa, D., et al. (2018). Broadband and tunable time-resolved thz system using argon-filled hollow-core photonic crystal fiber. Apl. Photonics 3, 111301. doi:10.1063/1.5043270
De Liberato, S. (2019). Electro-optical sampling of quantum vacuum fluctuations in dispersive dielectrics.
Dhillon, S. S., Vitiello, M. S., Linfield, E. H., Davies, A. G., Hoffmann, M. C., Booske, J., et al. (2017). The 2017 terahertz science and technology roadmap. J. Phys. D. Appl. Phys. 50, 043001. doi:10.1088/1361-6463/50/4/043001
Guedes, T. L., Kizmann, M., Seletskiy, D. V., Leitenstorfer, A., Burkard, G., and Moskalenko, A. S. (2019). Spectra of ultrabroadband squeezed pulses and the finite-time unruh-davies effect. Phys. Rev. Lett. 122, 053604. doi:10.1103/PhysRevLett.122.053604
Halbhuber, M., Mornhinweg, J., Zeller, V., Ciuti, C., Bougeard, D., Huber, R., et al. (2020). Non-adiabatic stripping of a cavity field from electrons in the deep-strong coupling regime. Nat. Photonics 14, 675–679. doi:10.1038/s41566-020-0673-2
Huber, R., Brodschelm, A., Tauser, F., and Leitenstorfer, A. (2000). Generation and field-resolved detection of femtosecond electromagnetic pulses tunable up to 41 THz. Appl. Phys. Lett. 76, 3191–3193. doi:10.1063/1.126625
Jepsen, P. U. (2019). Phase retrieval in terahertz time-domain measurements: A “how to” tutorial. J. Infrared, Millim. Terahertz Waves 40, 395–411. doi:10.1007/s10762-019-00578-0
Kizmann, M., Moskalenko, A. S., Leitenstorfer, A., Burkard, G., and Mukamel, S. (2022). Quantum susceptibilities in time-domain sampling of electric field fluctuations. Laser & Photonics Rev. 16, 2100423. doi:10.1002/lpor.202100423
Lindel, F., Bennett, R., and Buhmann, S. Y. (2020). Theory of polaritonic quantum-vacuum detection. Phys. Rev. A 102, 041701. doi:10.1103/PhysRevA.102.041701
Lindel, F., Settembrini, F. F., Bennett, R., and Buhmann, S. Y. (2022). Probing the Purcell effect without radiative decay: Lessons in the frequency and time domains. New J. Phys. 24, 013006. doi:10.1088/1367-2630/ac434e
Matsunaga, R., Hamada, Y. I., Makise, K., Uzawa, Y., Terai, H., Wang, Z., et al. (2013). Higgs amplitude mode in the bcs superconductors nb1-xtixN induced by terahertz pulse excitation. Phys. Rev. Lett. 111, 057002. doi:10.1103/PhysRevLett.111.057002
Mornhinweg, J., Halbhuber, M., Ciuti, C., Bougeard, D., Huber, R., and Lange, C. (2021). Tailored subcycle nonlinearities of ultrastrong light-matter coupling. Phys. Rev. Lett. 126, 177404. doi:10.1103/PhysRevLett.126.177404
Moskalenko, A. S., Riek, C., Seletskiy, D. V., Burkard, G., and Leitenstorfer, A. (2015). Paraxial theory of direct electro-optic sampling of the quantum vacuum. Phys. Rev. Lett. 115, 263601. doi:10.1103/PhysRevLett.115.263601
Nahata, A., Weling, A. S., and Heinz, T. F. (1996). A wideband coherent terahertz spectroscopy system using optical rectification and electro-optic sampling. Appl. Phys. Lett. 69, 2321–2323. doi:10.1063/1.117511
Neu, J., and Schmuttenmaer, C. A. (2018). Tutorial: An introduction to terahertz time domain spectroscopy (thz-tds). J. Appl. Phys. 124, 231101. doi:10.1063/1.5047659
Onoe, S., Guedes, T. L. M., Moskalenko, A. S., Leitenstorfer, A., Burkard, G., and Ralph, T. C. (2022). Realizing a rapidly switched Unruh-DeWitt detector through electro-optic sampling of the electromagnetic vacuum. Phys. Rev. D. 105, 056023. doi:10.1103/PhysRevD.105.056023
Piccoli, R., Rovere, A., Jeong, Y.-G., Jia, Y., Zanotto, L., Légaré, F., et al. (2019). Extremely broadband terahertz generation via pulse compression of an Ytterbium laser amplifier. Opt. Express 27, 32659–32665. doi:10.1364/OE.27.032659
Raimond, J. M., Brune, M., and Haroche, S. (2001). Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565–582. doi:10.1103/RevModPhys.73.565
Riek, C., Seletskiy, D. V., Moskalenko, A. S., Schmidt, J. F., Krauspe, P., Eckart, S., et al. (2015). Direct sampling of electric-field vacuum fluctuations. Science 350, 420–423. doi:10.1126/science.aac9788
Riek, C., Sulzer, P., Seeger, M., Moskalenko, A. S., Burkard, G., Seletskiy, D. V., et al. (2017). Subcycle quantum electrodynamics. Nature 541, 376–379. doi:10.1038/nature21024
Salamin, Y., Benea-Chelmus, I.-C., Fedoryshyn, Y., Heni, W., Elder, D. L., Dalton, L. R., et al. (2019). Compact and ultra-efficient broadband plasmonic terahertz field detector. Nat. Commun. 10, 5550. doi:10.1038/s41467-019-13490-x
Settembrini, F. F., Lindel, F., Herter, A. M., Buhmann, S. Y., and Faist, J. (2022). Detection of quantum-vacuum field correlations outside the light cone. Nat. Commun. 13, 3383. doi:10.1038/s41467-022-31081-1
Sulzer, P., Oguchi, K., Huster, J., Kizmann, M., Guedes, T. L. M., Liehl, A., et al. (2020). Determination of the electric field and its Hilbert transform in femtosecond electro-optic sampling. Phys. Rev. A 101, 033821. doi:10.1103/PhysRevA.101.033821
Takayanagi, J., Jinno, H., Ichino, S., Suizu, K., Yamashita, M., Ouchi, T., et al. (2009). High-resolution time-of-flight terahertz tomography using a femtosecond fiber laser. Opt. Express 17, 7533–7539. doi:10.1364/OE.17.007533
van Exter, M., Fattinger, C., and Grischkowsky, D. (1989). Terahertz time-domain spectroscopy of water vapor. Opt. Lett. 14, 1128–1130. doi:10.1364/OL.14.001128
Virally, S., Cusson, P., and Seletskiy, D. V. (2021). Enhanced electro-optic sampling with quantum probes. Phys. Rev. Lett. 127, 270504. doi:10.1103/PhysRevLett.127.270504
Weiss, M. A., Herbst, A., Schlegel, J., Dannegger, T., Evers, M., Donges, A., et al. (2023). Ultrafast spontaneous spin switching in an antiferromagnet. doi:10.48550/ARXIV.2301.02006
Woerner, M., Kuehn, W., Bowlan, P., Reimann, K., and Elsaesser, T. (2013). Ultrafast two-dimensional terahertz spectroscopy of elementary excitations in solids. New J. Phys. 15, 025039. doi:10.1088/1367-2630/15/2/025039
Wu, Q., and Zhang, X. (1995). Free-space electro-optic sampling of terahertz beams. Appl. Phys. Lett. 67, 3523–3525. doi:10.1063/1.114909
Keywords: quantum metrology, terahertz, sub-cycle, upconversion, frequency conversion, non-linear optics
Citation: Benea-Chelmus I-C and Tomasino A (2023) Resolving sub-cycle signatures: A perspective on hallmarks of terahertz metrology. Front. Photonics 4:1119172. doi: 10.3389/fphot.2023.1119172
Received: 08 December 2022; Accepted: 27 March 2023;
Published: 13 April 2023.
Edited by:
Yahya Moubarak Meziani, University of Salamanca, SpainReviewed by:
Mira Naftaly, National Physical Laboratory, United KingdomCopyright © 2023 Benea-Chelmus and Tomasino. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ileana-Cristina Benea-Chelmus, Y3Jpc3RpbmEuYmVuZWFAZXBmbC5jaA==
 Ileana-Cristina Benea-Chelmus
Ileana-Cristina Benea-Chelmus Alessandro Tomasino
Alessandro Tomasino