- 1Department of Chemical and Biomolecular Engineering, University of California, Los Angeles, Los Angeles, CA, United States
- 2Materials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA, United States
- 3Department of Chemistry, University of California, Berkeley, Berkeley, CA, United States
- 4Kavli Energy NanoScience Institute, Berkeley, CA, United States
- 5Molecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, CA, United States
- 6Department of Materials Science and Engineering, University of California, Berkeley, Berkeley, CA, United States
Despite the extraordinary advances in solar cell efficiency in laboratory settings, the deployment of solar cells continues to be limited to low efficiency (<25%) silicon cells because of cost. In this work, we take advantage of the extraordinary optical properties afforded by nanophotonic structures to create a photonic luminescent solar concentrator for an InGaP-Si multijunction concentrator cell. Finite difference time domain (FDTD) simulations demonstrated a concentrator that could effectively capture, downconvert, and guide concentrated light to an InGaP subcell while still transmitting longer wavelengths to a Si subcell. We fabricated the photonic luminescent solar concentrator, which was comprised of CdSe/CdS quantum dots embedded within alternating layers of Si3N4 and SiO2, and experimentally verified the optical performance, showing a 40% increase in light guiding and a significant reduction in reabsorption losses in the plane of the luminescent concentrator as compared to traditional designs. Finally, we utilized modified detailed balance calculations that accounted for cell and optical losses and showed >30% efficiencies are possible with this design, demonstrating the potential to meet the demands for high efficiency, inexpensive solar modules.
1 Introduction
Cost has been, and continues to be, a major challenge for photovoltaics deployment. Though there have been significant advancements in solar cell efficiency, the deployment of high efficiency photovoltaic designs (>30%) has been decreasing over the last decade (Wiesenfarth et al., 2017). This is because these high efficiency designs rely on costly and complex concentrating multijunction designs, wherein concentrating optics are used with multiple solar absorbers that absorb different parts of the solar spectrum to both convert more of the spectrum and minimize thermalization losses (Imenes and Mills, 2004; King et al., 2012; Polman and Atwater, 2012; Eisler et al., 2019). The cells in these multijunction designs, III-V materials, are costly to fabricate—a 28% efficiency single junction GaAs cell is modeled as $69/W (Horowitz et al., 2018). Silicon flat plate cells, while significantly less efficient (18%–25%), have been the long-established industry standard and currently only $.25/W for 22% efficiency (Smith et al., 2020). While we are generating significant electricity from renewable sources (20.1% from renewables in 2021), the United States is still generating a very small percentage of our electricity from solar power (2.8%) (U.S. Energy Information Administration Office of Energy Analysis, 2021). If we want to generate a significant amount of electricity from solar energy, like we are from wind (9.2%) or hydropower (6.3%), we need a new solar module paradigm where optical management and architectures can maximize solar energy conversion while maintaining low production costs.
Luminescent solar concentrators (LSCs) have been proposed as a viable pathway to high efficiency, low cost photovoltaics because they should be able to achieve the high concentration and spectral selectivity for concentrating multijunction designs while being very inexpensive to manufacture (Goetzberger, 1978; Batchelder et al., 1979; Slooff et al., 2008; van Sark et al., 2008; Debije and Verbunt, 2012; Zhao and Lunt, 2013; Sol et al., 2018; Wu et al., 2018). Unlike traditional lens and trough concentrators, which rely on geometrically refracting or reflecting light to concentrate, LSCs operate by using a luminophore-doped slab that absorbs high energy photons and then waveguides the downshifted luminophore emission to the edges of the sheet where it can be absorbed and converted by a solar cell. The costs can be significantly reduced for this design because of its solution-processed materials and thin, flat form-factor; Wu et al. (2018) estimated the cost of their quantum dot-based LSC as $5.01/m2. Further, LSCs can do things that are impossible for traditional lenses and troughs. Because LSCs do not rely on using the angle (or etendue) of light to create the concentration, they can theoretically achieve concentrations orders of magnitude higher than the maximum for traditional designs (Yablonovitch, 1980; Smestad et al., 1990).
While LSC designs possess great potential, an LSC with a significant concentration of (>100x) has not been fabricated in the four decades since its invention (Bronstein et al., 2015; Rafiee et al., 2019). This has been primarily due to the lack of high quantum yield luminophores and poor waveguiding efficiency of luminesced photons. With the recent developments of near unity quantum yields with large Stokes shifts in quantum dots (Hanifi et al., 2019), the focus has shifted to photon management to effectively guide photoluminescence to the edges (Peters et al., 2009; Verbunt et al., 2013). Initial LSC designs relied solely on total internal reflection for photoluminescence waveguiding which can theoretically achieve trapping efficiencies over 90% (Mulder et al., 2010). However, this has been nearly impossible to fabricate as it requires a non-absorbing and high refractive index slab (n ≥ 2.3), precluding most solution-processed polymers (Liu and Ueda, 2009). For example, typical matrices, such as poly (lauryl) methacrylate (PLMA), have low refractive indices (n = 1.44) which limit the LSC trapping maximum to 74%. To reduce these losses, recent designs have employed wavelength-selective filters to reflect photoluminescence back into the polymer slab (Bronstein et al., 2015; Connell and Ferry, 2016; Connell et al., 2018; Wang et al., 2020), using anisotropically emitting luminophores to minimize emission into these escape angles (Mulder et al., 2010; Shen et al., 2014), and embedding the luminophores within a photonic crystal to only allow photoluminescence into oblique, trapped, angles, also known as a photonic luminescent solar concentrator (PLSC) (Debije et al., 2010; Gutmann et al., 2012; Verbunt et al., 2012; Leem et al., 2014; Bauser et al., 2020; van der Burgt et al., 2021). These designs show great promise to strongly increase the light trapping, but they only focus on the luminescent concentrator as a standalone structure instead of a component in a multijunction device.
We seek to further optimize and understand the 1D photonic crystal design for integration into a multijunction design, enabling a high efficiency and low cost module for greater solar deployment. Here, we explored a photonic LSC (PLSC) for a InGaP-Si tandem PV cell. We used multiple simulations to design an LSC that maximizes both high photoluminescence trapping for the light designated for the InGaP subcell and transparency for light designated for the Si subcell. We then fabricated a test structure of the design to study its photoluminescence trapping capabilities and demonstrated how light shaping designs such as these can potentially minimize other common LSC losses, such as reabsorption. Finally, we show the pathways to >30% efficiency photovoltaics using this design.
2 Materials and Methods
2.1 Modeling and Design
In this work, we optimized a photonic LSC (PLSC) for an InGaP-Si tandem PV design (Figure 1A) because >30% efficiency is possible with this bandgap combination but is cost prohibitive because of the expensive III-V semiconductor growth process (Essig et al., 2016; Phelan et al., 2021). III-V cells are approximately three orders of magnitude costlier than silicon cells on a per area basis ($19,320/m2 versus $44.2/m2) so we propose to reduce the area coverage of the costly III-V’s by including inexpensive luminescent concentrators (∼$5/m2) (Horowitz et al., 2018; Wu et al., 2018; Smith et al., 2020). The cost impact of replacing the III-V cell area with would be immense: assuming an LSC concentrator of 100x and a 34% module, we could have high efficiency photovoltaics at less than $1/W. We first optimized a nanophotonic design that maximizes luminophore emission into total internal reflection modes. We designed a structure consisting of alternating high and low dielectric layers as this can maximize emission into high angles for a given design wavelength. Gutmann et al. (2012) showed through simulations that trapping efficiencies of 99.7% are possible with a 1D photonic crystal of alternating quarter wavelength layers of n = 1.5 and n = 2.0. In our design, we investigate two combinations of refractive indices (n = 1.5/n = 2.1 and n = 1.5/n = 2.4) and use CdSe/CdS quantum dots as our emitters, which have demonstrated near unity quantum yields and excellent stability properties (Hanifi et al., 2019). Our choice for luminophore wavelength (624 nm) and top subcell (InGaP) was driven by the near unity quantum yield of CdSe/CdS quantum dots at that wavelength and the fact that InGaP (Eg = 1.84 eV) is a near ideal tandem partner for silicon (Yu et al., 2016). Figure 1B shows a schematic of our modeled structure, which consists of a set of five high-low refractive index pairs above and below a central layer consisting of the CdSe/CdS quantum dots. Instead of using a Bragg Reflector composed of quarter wavelength layers as was demonstrated previously (Goldschmidt et al., 2010), we chose to vary the thicknesses of the layers not only to maximize the photoluminescence trapping, but also to maximize transparency for all wavelengths greater than the CdSe/CdS emission, allowing this to be used in a high efficiency, multijunction structure.
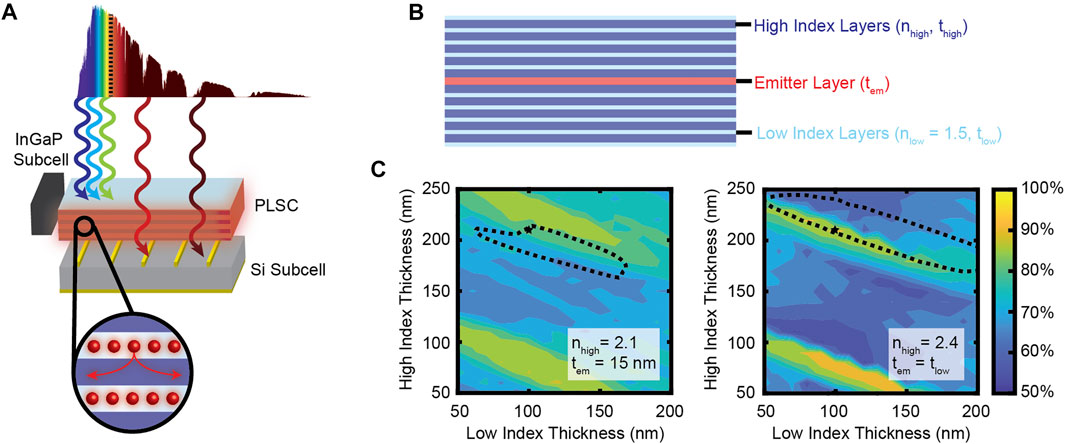
FIGURE 1. (A) Schematic of the Photonic Luminescent Solar Concentrator (PSLC) multijunction design. High energy light is absorbed and concentrated by a PLSC for conversion by an InGaP subcell while low energy light (λ > 700 nm) is transmitted to a Si subcell. (B) Schematic of the simulated PLSC. A central layer of thickness tem containing the dipole emitters is surrounded by 5 pairs of high (thigh, nhigh) and low (tlow, nlow) refractive index layers on each side. The layer thicknesses and the high refractive index (nhigh) are varied. (C) Results of the FDTD optimization. The collection efficiency of the PLSC (contour color) is plotted against the thickness of the high refractive index layer and the thickness of the low refractive index layer. The left plot shows the optimization when the refractive index of the high index layer is 2.1 and the emitter thickness is 15 nm. The right plot shows the optimization when the refractive index of the high index layer is 2.4 and the emitter thickness is the same thickness of the low index layers (perfectly periodic). The area within the overlayed black contour shows where the transmission to the bottom junction is >90%.
This design was adapted into a finite-difference time-domain (Lumerical FDTD) simulation as shown in Supplementary Figure S1. Three dipole sources were placed at the center of the luminophore layer to represent a random quantum dot emission and perfectly matched layer (PML) boundaries were used at the top and side interfaces to monitor the escaped and trapped light, respectively. The simulation width was set at 20 μm to accurately capture the escaped and collected light fractions. The fraction of collected photoluminescence was determined by dividing the light collected by monitors within the stack by the total light in the system (light trapped in the stack and light escaped from the stack). The thicknesses of the high (thigh) and low refractive index layers (tlow) were each varied to determine the best luminescence trapping for a given refractive index combination (1.5/2.1 versus 1.5/2.4) and for a given emitter layer thickness (tem).
The total modeled efficiency of the multijunction cell with a 100x PLSC was determined by a modified detailed balance calculation and is described in the Supplementary Material (Warmann et al., 2017; Eisler et al., 2019). First, the light transmission, reflection, and absorption of the PLSC was calculated using the open-source optical simulation software OpenFilters (Larouche and Martinu, 2008), which uses the transfer matrix method to determine the Fresnel coefficients of a planar multilayer stack. We input the refractive indices and layer thicknesses of a given design and determined the transmission, reflection, and absorption for varying CdSe/CdS optical density and number of repeating layers. We modeled the periodic structures (tem = tlow) and assumed every low index layer had quantum dot luminophores as in Figure 1A. The imaginary refractive index, k, of the low index layers was calculated using absorption data (Figure 2A) of the synthesized CdSe/CdS quantum dots and was modified for different optical densities. The resulting spectra were used to modify the AM1.5G solar flux and determine the photon flux to each subcell. The Si subcell photon flux is simply the transmission-modified AM1.5G solar flux. Because the PLSC downshifts the absorbed light, the InGaP subcell flux was calculated by summing the absorption-modified photon flux and creating a normal distribution with that number of photons centered at the emission wavelength of the CdSe/CdS quantum dots. This flux was multiplied by the quantum yield and the photoluminescence collection efficiency raised to the power of the number of reabsorption events, as defined in (Olson et al., 1981). This combined calculation accounts for the quantum dot losses, escape losses, and reabsorption losses. The modeled power generated by each subcell is determined by a modified detailed balance calculation that uses the external radiative efficiency (ERE) and fraction of ideal short circuit current to more realistically estimate the photovoltaic conversion losses (Warmann et al., 2017; Eisler et al., 2019). Here, we assumed EREs of 5% and 1% and fraction ideal current of 90% and 96% for the InGaP and Si subcells, respectively, as based on the current records (Warmann et al., 2017; Green et al., 2022). The given power of each subcell was scaled by the respective concentration factor (100x for InGaP, 1x for Si), summed, and then divided by the incident power of the Sun to yield the modeled multijunction cell efficiency for this design.
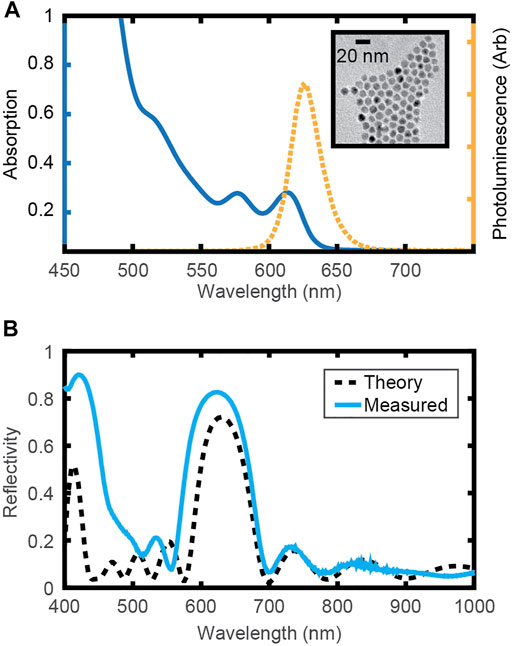
FIGURE 2. (A) Absorption and photoluminescence of the CdSe/CdS quantum dot emitters in hexanes. The inset shows a TEM image of the quantum dots. (B) Reflectivity of the fabricated half PLSC structure on a glass coverslip compared to the theoretical reflectivity of the half structure.
2.2 Fabrication of Test Design
Fabrication of the photonic luminescent solar concentrator was achieved in three steps: 1) synthesis of the luminophores, 2) fabrication of the alternating high-low refractive index stack, and 3) integration of the luminophores into the stack. We synthesized high quantum yield CdSe/CdS quantum dots to use as the luminophores in our structure. We followed the process outlined in (Hanifi et al., 2019): CdSe core quantum dots were synthesized via a hot injection synthesis and then subsequently shelled with seven monolayers of CdS. The thickness of the shell was chosen to maximize the quantum yield (Hanifi et al., 2019) and to create an optimal photoluminescence energy (1.99 eV) for our design which uses an InGaP top junction. The absorption and photoluminescence of the CdSe/CdS quantum dots is shown in Figure 2A. The CdSe/CdS quantum dots have a maximum photoluminescence at 624 nm and have a measured quantum yield of 98% (Supplementary Figure S4).
For this study, we investigated test structures comprised of the luminophore quantum dots on one half of the substrate design, hereby called the PLSC half structure. Although this is not the complete luminescent concentrator, this PLSC half structure makes the angular emission characterization—the most important parameter for the proof-of-concept—significantly easier. To create this half stack, we used plasma enhanced chemical vapor depositions (PECVD) to grow alternating layers of Si3N4 and SiO2, which have measured refractive indices of 2.1 and 1.5, respectively (Supplementary Tables S1–2). The resulting transmission of the half structure is shown in Figure 2B. The fabricated half structure shows a slight blueshift in the reflection peak and reduction of transmission below 450 nm, likely due to mixing of Si3N4 and SiO2 on the PECVD chamber walls that occurs during longer depositions. Finally, the CdSe/CdS quantum dots were self-assembled following a previous study (Gu et al., 2017): CdSe/CdS dots in hexanes were dropcast onto ethylene glycol-filled Teflon troughs and subsequently covered, forming a large area (∼1 cm × 1 cm) monolayer film as the hexanes slowly evaporated. The CdSe/CdS quantum dot monolayer film was then integrated into the PLSC by stamping the substrate onto the monolayer and using a vacuum chamber to evaporate any residual ethylene glycol.
2.3 Characterization of Structure
We compared the performance of quantum dots on the PLSC half structure with quantum dots on a bare glass coverslip to investigate how the photonic structure affects the photoluminescence losses. We first characterized the angular emission of this design by using back focal plane imaging (Lieb et al., 2004; Curto et al., 2010; Hartmann et al., 2013; Iyer et al., 2020). Because light is automatically sorted by angle in a microscope objective, there is a plane inside the objective where the angular emission pattern of a sample is in focus, known as the back focal plane (Supplementary Figure S5). This pattern can be imaged by adjusting the image focal plane from the sample to this back focal plane, creating a 2D projection of the angular emission pattern on the camera. For a luminescent concentrator design, we need to minimize the light emitted towards the center, which represents light emitted at angles that can escape the structure, and maximize light emitted at the outer perimeter of the circle, which represents light emitted at very oblique angles and thus will be collected.
We also investigated how the photonic structure affects photoluminescence reabsorption, another significant loss mechanism in LSC’s (Albers et al., 2013; Li S. et al., 2020; de Clercq et al., 2021). Increased reabsorption will redshift the photoluminescence peak of the sample because of the inner filter effect (IFE): only photons with sufficient energy (greater or equal to the bandgap of an absorber) can be absorbed so the higher energy photons are more likely to be absorbed and then downshifted to a longer wavelength (Kubista et al., 1994). We measured the IFE using a setup as described in (Koc et al., 2017) where a sample was excited by a 405 nm laser spot and the spatially resolved emission spectra were recorded using a spectrometer coupled to an imaging CCD. The spatially dependent wavelength redshift and intensity were then modeled by a stochastic simulation where a set of quantum dot emitters would undergo random encounters as it advanced forward in distance. We started with a Gaussian distribution of quantum dot emitters that matched the experimental data of the center excitation spot and varied probabilities of effective reabsorption within the LSC plane, quantum yield, and removal (scattered, guided away, etc.) to determine the best fit to the experimental data. Further details are included in the Supplementary Material.
3 Results
3.1 Luminescent Concentrator Design Space
The first goal of this work was to demonstrate a photonic luminescent solar concentrator (PLSC) design that would minimize photoluminescence escape losses while still being suitable for incorporation into a multijunction design. Figure 1C shows the fraction of collected light as a function of the thicknesses of the low and high refractive index layers resulting from our FDTD simulations; the left figure shows the optimization for nhigh = 2.1 and a thin emitting layer (tem = 15 nm) while the right figure shows the optimization for nhigh = 2.4 and a periodic structure (tem = tlow). Additional optimizations are included in the supplementary material (Supplementary Figure S3). The highest collection efficiencies (maximum = 95%) are seen in for nhigh = 2.4. High collection efficiency (>80%) is also seen for nhigh = 2.1, mostly for very thin emitter thicknesses (tem). Both of these trends are expected given that evanescent photoluminescent emission couples most effectively into another layer when there is a high refractive index contrast and the emitter is at the interface (Lukosz and Kunz 1977). For both optimizations, the optimal collection efficiencies lie on a diagonal pattern because of the constructive and destructive interference wavelengths. The diagonals that show a maximum light trapping represent where the reflection for the photoluminescence emission (∼620 nm) is the highest (Supplementary Figure S2). This trend is consistent with other photonic LSC work as the nearfield photoluminescence trapping is maximum for a structure whose reflectivity maximum is designed for the emission wavelength (Gutmann et al., 2012).
There are multiple designs with high photoluminescence trapping (>90%) for both nhigh = 2.1 and nhigh = 2.4. However, the final design must also be transparent for longer wavelengths for effective use in a multijunction architecture. Figure 1C also includes black contour lines showing where the AM1.5G-weighted transmission of longer wavelengths (700–1,100 nm) for the Si subcell is 90%; all designs within each contour have transmissions ≥ 90%. This adds a significant constraint on the design space. While previous designs have used a Bragg stack comprised of quarter wavelength layers (Gutmann et al., 2012), the quarter wavelength thicknesses for our design (tlow = 104 nm, thigh = 65–74 nm) do not meet the requirements for high transmission of longer wavelengths. Instead, the optimum for both high collection and high long wavelength transparency occurs for thicker high index layers and thinner low index layers. Because we grew the structure using Si3N4 (n = 2.1) and SiO2 (n = 1.5) and would use a thin emitting layer in our characterization, we chose our stack to have tlow = 100 nm and thigh = 210 nm thicknesses. This corresponded to a photoluminescence trapping of 85% and a long wavelength transmission of 90%, minimizing the optical losses to each subcell.
3.2 Characterization of Luminescent Concentrator Test Structure
After fabricating the structure as outlined in Section 2.2, we determined the angular emission (Figure 3) and reabsorption (Figure 4) for quantum dots on a control substrate (plain class coverslip) and our PLSC half structure. The first characterization focuses on how the PLSC structure affects the photoluminescence escape losses. Figure 3A shows photographs of the CdSe/CdS quantum dots on a plain glass coverslip (control) and on the PLSC half structure under black light illumination. Qualitatively, the PLSC half structure is guiding significantly more of the quantum dot photoluminescence into oblique angles: while the photoluminescence (red light) is seen at both the top and sides of the control structure, indicating emission at shallow and oblique angles, photoluminescence is only seen at the sides of the PLSC half structure, indicating that the light is mostly emitted into modes that are directly guided to the edge of the substrate. Figure 3B also shows the full BFP images which show the projected photoluminescence intensity versus the polar angle (read from the center outward as normal to oblique angles) and the azimuthal angle (read around the circle). We include a dotted line representing the total internal reflection angle of an air-glass interface (42°); signal within the dotted line represents light emitted within the escape cone while signal outside the dotted line represents light that is guided. There is a significant difference in the control and PLSC half structure emission patterns. The PLSC half structure exhibits almost no emission at low angles while the control structure has significant emission at angles where light would escape. Figure 3B also shows the extracted intensity as a function of polar angle for each structure, which illustrates the significant change in emission from shallow to very oblique angles. To quantitatively determine the percent increase in trapping, we integrate the intensity with respect to polar angle
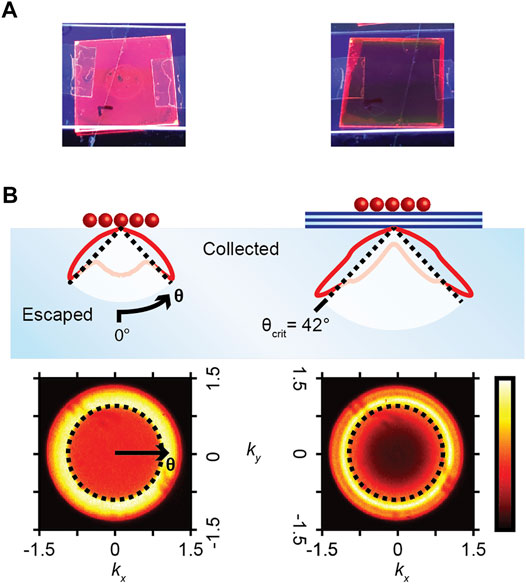
FIGURE 3. Angular emission characterization of the PLSC half structure (A) Photographs of UV-illuminated CdSe/CdS quantum dots on a bare glass coverslip (left) and on the PLSC half structure (right). (B) PL intensity as a function of angle for the quantum dots on a bare coverslip (left) and on the PLSC half structure (right). The total internal reflection angle is denoted by the dotted line: all light emitted at angles higher than the critical angle is collected and all light emitted at smaller angles escapes. These intensities are extracted from back focal plane (BFP) images (below), which are 2D projections of the 3D emission pattern.
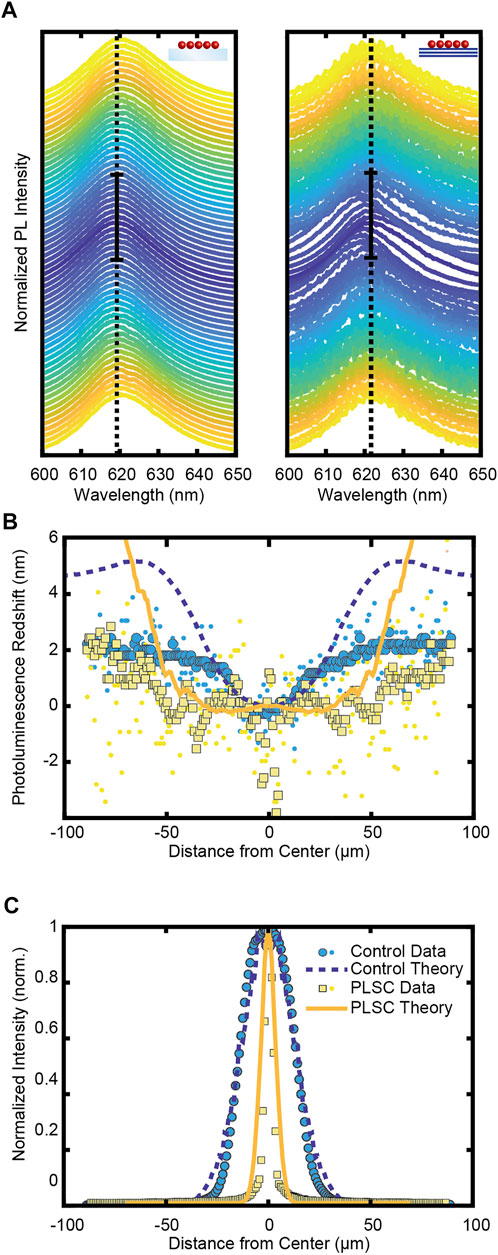
FIGURE 4. Reabsorption characterization of the PLSC half structure (A) Normalized photoluminescence of CdSe/CdS emission on the bare coverslip (left) and on the PLSC half structure (right) as a function of distance. Distance is measured from the center of laser excitation (indigo) outward (yellow). The solid black line shows the laser beam diameter and the dotted black line shows the center wavelength of the laser excitation point. (B,C) Measured and modeled redshift (B) and intensity (C) of the emission as a function of distance from the excitation center for the bare coverslip (teal circles) and the PLSC half structure (yellow squares). For the redshift (B), the redshift is represented by both the center wavelengths from Gaussian fits of each photoluminescence curve (larger markers) and the wavelength at the maximum intensity value (small dots). The theoretical redshift and normalized intensities (Supplementary Figure S6) are overlayed as solid lines for the bare coverslip (blue) and PLSC half structure (yellow).
The spatial photoluminescence was also measured to determine how a photonic structure affected another major LSC loss mechanism: photoluminescence parasitic reabsorption. Figure 4A shows the normalized photoluminescence of each sample from the laser excitation (indigo) as a function of distance. As distance increases, the photoluminescence spectra will redshift due to the inner filter effect; therefore a sample with a higher redshift corresponds to more parasitic reabsorption (Supplementary Figure S6). The photoluminescence intensity will decrease with increasing distance because of imperfect quantum yield and will decrease more rapidly if light is guided away from the luminophore layer as it can no longer be reabsorbed and therefore detected on the camera. The dotted black line shows the center wavelength of emission at the point of laser excitation for each sample, and there is a noticeably larger redshift in the control sample as compared to the PLSC half structure. We plot the redshift (Figure 4B) and intensity (Figure 4C) as a function of distance for both samples. The redshift increases more rapidly for the control sample but the intensity decreases more rapidly for the PLSC half structure. Both trends occur because the PLSC half structure is more effective at guiding light into high angle modes (Figure 3B). The more light that is guided into high angle modes, the more rapidly the spatial photoluminescence intensity will decrease because less light is escaping and being detected by the camera (Figure 4C), hence why the intensity decreases more rapidly for the PLSC half structure. Additionally, guiding photoluminescence into higher angle modes should reduce the effective path length to collection which in turn will reduce the probability of interaction with the quantum dot layer, reducing the likelihood of reabsorption. This is observed in Figure 4B, as the photoluminescence redshift is smaller for the PLSC half structure. Using a stochastic model to predict how the effective reabsorption within the plane of the LSC would correlate to photoluminescence redshift, we show that the fitted effective absorption length in the emitter layer (solid line in Figures 4B,C) corresponds to 10 cm−1 for the control sample and 0.01 cm−1 for the PLSC half structure, a decrease in several orders of magnitude. Not only does the PLSC design prevent more photoluminescence from escaping, but it is also significantly more tolerant to reabsorption of the emitters.
3.3 Modeled Efficiency of the PLSC Multijunction Cell
Finally, we modelled the efficiency of a multijunction cell with a 100x PLSC with a periodic structure (tem = tlow = 100 nm, thigh = 210 nm) for nhigh = 2.1 (photoluminescence collection = 74%, Figure 5A) and nhigh = 2.4 (photoluminescence collection = 89%, Figure 5B). We varied the number of layers (total thickness of the device) and the optical density of the quantum dots (measured at 450 nm) to determine the optimum device parameters since there is a tradeoff due to the spectrum-splitting nature of the device. More layers and a higher optical density will increase the photon flux to the InGaP subcell, which ensures the higher energy photons are converted at the higher voltage, but this also increases the likelihood of reflection or parasitic absorption of lower energy photons that were meant for the Si subcell. This leads to the maximum efficiencies occurring for low thicknesses (low total number of layers) and optical densities between 3 and 3.5. Despite the significant difference in photoluminescence trapping, both designs are capable of 30% cell efficiency because of the high concentration and higher voltage conversion of the InGaP subcell. Further, the higher contrast design (nhigh = 2.4) has a maximum efficiency of 33.4%, a considerable improvement over single junction Si cells (Green et al., 2022).
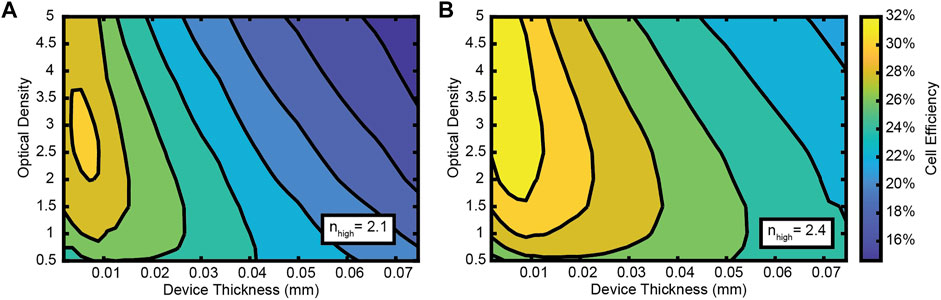
FIGURE 5. Modeled efficiency of a full PLSC. Multijunction cell efficiency (contours) is plotted as a function of CdSe/CdS optical density at 450 nm (quantum dot concentration) and PLSC thickness (number of layers). The efficiency is plotted for periodic structures (tlow = 100 nm, thigh = 210 nm) for nhigh = 2.1 (A) and nhigh = 2.4 (B). Both designs are capable of >30% efficiency.
4 Discussion
Here we have demonstrated that a photonic luminescent solar concentrator can be optimized simultaneously for high concentration and for use in a spectrum-splitting, multijunction InGaP-Si cell. By moving beyond the Bragg stack design, we showed that high photoluminescence trapping (>80%) and high transparency to lower wavelengths (>90%) is possible, with the best designs for layers with high refractive index contrast (i.e., nlow = 1.5, nhigh = 2.4). We experimentally verified a significant reduction in two of the major LSC loss mechanisms, namely photoluminescence escape and the reabsorption within the LSC plane, in our PLSC half structure. Because the nanophotonic design changes the angular emission light pattern of the luminophores, the ratio of photoluminescence in guided modes (θ ≥ critical angle) to total photoluminescence increased by 40% and the effective absorption coefficient in the LSC plane is reduced by four orders of magnitude with the inclusion of the photonic element. Finally, we showed that >30% efficiency cells are possible even with the less optimal refractive index contrast (nlow = 1.5, nhigh = 2.1). Despite having a lower photoluminescence trapping of 74%, this design shows a significant increase in efficiency over a single junction Si cell, demonstrating the potential in multijunction cell designs.
The development of near unity quantum yield luminophores and sophisticated nanophotonic structures could finally usher in the next generation of high efficiency and inexpensive spectrum-splitting photovoltaics. While embedding luminophores within a photonic crystal inherently makes PLSC designs more complex than the traditional LSC design, there have been significant advancements in nanofabrication, such as nanoimprint lithography (Shneidman et al., 2018; Wang et al., 2018) and polymer coextrusion (Kazmierczak et al., 2007; Li Z et al., 2020), that could enable these designs to be inexpensive and scalable. Our work, along with the growing literature of photonic luminescent solar concentrator designs, demonstrates the need to develop nanophotonic design elements to realize a luminescent solar concentrator with a significant (>100x) concentration. Further, the design principles discussed in this work can be extended to any number of junctions or any multijunction design, such as a series of luminescent solar concentrators (Imenes and Mills 2004), creating a pathway for >50% efficiency solar modules that can support sustainable energy generation.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
CE conceived the idea, fabricated the PLSC half structures, performed all optical characterization, contributed to the reabsorption stochastic model, and led the writing of the manuscript. LP performed all multijunction cell efficiency models and contributed to the writing of the manuscript. ZN synthesized the CdSe/CdS quantum dots and performed the absorption, photoluminescence, and quantum yield measurements. CL created the initial reabsorption stochastic model. AS fabricated the multilayer stacks, contributed to the writing of the manuscript, and advised the project. AA contributed to the writing of the manuscript and advised the project.
Funding
CE was supported by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy (EERE), specifically the EERE Postdoctoral Fellowship during her postdoc at Lawrence Berkeley National Laboratory. Work at the Molecular Foundry by CE and AS was supported by the DOE, Office of Science, Office of Basic Energy Sciences, under contract DE-AC02-05CH11231.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank Dr. Christopher T. Chen for performing ellipsometry measurements of the PECVD-grown materials and Dr. Matthew Koc for guidance on the reabsorption measurement and many helpful discussions. CE would like to thank CT. Chen, J. Eisler-Chen, and L. Eisler-Chen for their feedback and support. Part of the work was carried out as a user project at Molecular Foundry. Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract Nos. DE-AC02-05CH11231. The views expressed herein do not necessarily represent the views of the U.S. Department of Energy or the United States Government.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphot.2022.932913/full#supplementary-material
References
Albers, P. T. M., Bastiaansen, C. W. M., and Debije, M. G. (2013). Dual Waveguide Patterned Luminescent Solar Concentrators. Sol. Energy 95, 216–223. doi:10.1016/j.solener.2013.06.014
Batchelder, J. S., Zewai, A. H., and Cole, T. (1979). Luminescent Solar Concentrators 1: Theory of Operation and Techniques for Performance Evaluation. Appl. Opt. 18 (18), 3090. doi:10.1364/AO.18.003090
Bauser, H. C., Bukowsky, C. R., Phelan, M., Weigand, W., Needell, D. R., Holman, Z. C., et al. (2020). Photonic Crystal Waveguides for >90% Light Trapping Efficiency in Luminescent Solar Concentrators. ACS Photonics 7 (8), 2122–2131. doi:10.1021/acsphotonics.0c00593
Bronstein, N. D., Yao, Y., Xu, L., O’Brien, E., Powers, A. S., Ferry, V. E., et al. (2015). Quantum Dot Luminescent Concentrator Cavity Exhibiting 30-Fold Concentration. ACS Photonics 2 (11), 1576–1583. doi:10.1021/acsphotonics.5b00334
Connell, R., and Ferry, V. E. (2016). Integrating Photonics with Luminescent Solar Concentrators: Optical Transport in the Presence of Photonic Mirrors. J. Phys. Chem. C 120 (37), 20991–20997. doi:10.1021/acs.jpcc.6b03304
Connell, R., Pinnell, C., and Ferry, V. E. (2018). Designing Spectrally-Selective Mirrors for Use in Luminescent Solar Concentrators. J. Opt. 20 (2), 024009. doi:10.1088/2040-8986/aaa074
Curto, A. G., Volpe, G., Taminiau, T. H., Kreuzer, M. P., Quidant, R., and van Hulst, N. F. (2010). Unidirectional Emission of a Quantum Dot Coupled to a Nanoantenna. Science 329 (5994), 930–933. doi:10.1126/science.1191922
de Clercq, D. M., Chan, S. V., Hardy, J., Price, M. B., and Davis, N. J. L. K. (2021). Reducing Reabsorption in Luminescent Solar Concentrators with a Self-Assembling Polymer Matrix. J. Luminescence 236, 118095. doi:10.1016/j.jlumin.2021.118095
Debije, M. G., Van, M.-P., Verbunt, P. P. C., Kastelijn, M. J., van der Blom, R. H. L., Verbunt, P. P. C., et al. (2010). Effect on the Output of a Luminescent Solar Concentrator on Application of Organic Wavelength-Selective Mirrors. Appl. Opt. 49 (4), 745. doi:10.1364/AO.49.000745
Debije, M. G., and Verbunt, P. P. C. (2012). Thirty Years of Luminescent Solar Concentrator Research: Solar Energy for the Built Environment. Adv. Energy Mat. 2, 12–35. doi:10.1002/aenm.201100554
Eisler, C. N., Flowers, C. A., Warmann, E. C., Lloyd, J. V., Espinet-Gonzalez, P., Darbe, S., et al. (2019). The Polyhedral Specular Reflector: A Spectrum-Splitting Multijunction Design to Achieve Ultrahigh (50%) Solar Module Efficiencies. IEEE J. Photovoltaics 9 (1), 174–182. doi:10.1109/JPHOTOV.2018.2872109
Essig, S., Steiner, M. A., Allebé, C., Geisz, J. F., Paviet-Salomon, B., Scott, W., et al. (2016). Realization of GaInP/Si Dual-Junction Solar Cells with 29.8% 1-Sun Efficiency. IEEE J. Photovoltaics 6 (4), 1012–1019. doi:10.1109/JPHOTOV.2016.2549746
Goetzberger, A. (1978). Fluorescent Solar Energy Collectors: Operating Conditions with Diffuse Light. Appl. Phys. 16 (4), 399–404. doi:10.1007/BF00885865
Goldschmidt, J. C., Peters, M., Gutmann, J., Steidl, L., Zentel, R., Bläsi, B., et al. (2010). Increasing Fluorescent Concentrator Light Collection Efficiency by Restricting the Angular Emission Characteristic of the Incorporated Luminescent Material: the 'Nano-Fluko' Concept. Proc. SPIE 7725, 77250S. doi:10.1117/12.854278
Green, M. A., Dunlop, E. D., Hohl‐Ebinger, J., Yoshita, M., Kopidakis, N., and Hao, X. (2022). Solar Cell Efficiency Tables (Version 59). Prog. Photovoltaics 30 (1), 3–12. doi:10.1002/pip.3506
Gu, X. W., Ye, X., Koshy, D. M., Vachhani, S., Hosemann, P., and Alivisatos, A. P. (2017). Tolerance to Structural Disorder and Tunable Mechanical Behavior in Self-Assembled Superlattices of Polymer-Grafted Nanocrystals. Proc. Natl. Acad. Sci. U.S.A. 114 (11), 2836–2841. doi:10.1073/pnas.1618508114
Gutmann, J., Peters, M., Bläsi, B., Hermle, M., Gombert, A., Zappe, H., et al. (2012). Electromagnetic Simulations of a Photonic Luminescent Solar Concentrator. Opt. Express 20 (S2), A157. doi:10.1364/OE.20.00A157
Hanifi, D. A., Bronstein, N. D., Koscher, B. A., Nett, Z., Swabeck, J. K., Takano, K., et al. (2019). Redefining Near-Unity Luminescence in Quantum Dots with Photothermal Threshold Quantum Yield. Science 363 (6432), 1199–1202. doi:10.1126/science.aat3803
Hartmann, N., Piatkowski, D., Ciesielski, R., Mackowski, S., and Hartschuh, A. (2013). Radiation Channels Close to a Plasmonic Nanowire Visualized by Back Focal Plane Imaging. ACS Nano 7 (11), 10257–10262. doi:10.1021/nn404611q
Horowitz, K. A. W., Remo, T., Smith, B., and Ptak, A. (2018). A Techno-Economic Analysis and Cost Reduction Roadmap for III-V Solar Cells. NREL/TP-6A20-72103 Golden, CO. Available at: https://www.nrel.gov/docs/fy19osti/72103.pdf (Accessed Nov 27, 2018).
Imenes, A. G., and Mills, D. R. (2004). Spectral Beam Splitting Technology for Increased Conversion Efficiency in Solar Concentrating Systems: A Review. Sol. Energy Mater. Sol. Cells 84 (1–4), 19–69. doi:10.1016/j.solmat.2004.01.038
Iyer, P. P., DeCrescent, R. A., Mohtashami, Y., Lheureux, G., Butakov, N. A., Alhassan, A., et al. (2020). Unidirectional Luminescence from InGaN/GaN Quantum-Well Metasurfaces. Nat. Photon. 14 (9), 543–548. doi:10.1038/s41566-020-0641-x
Kazmierczak, T., Song, H., Hiltner, A., and Baer, E. (2007). Polymeric One-Dimensional Photonic Crystals by Continuous Coextrusion. Macromol. Rapid Commun. 28 (23), 2210–2216. doi:10.1002/marc.200700367
King, R. R., Bhusari, D., Larrabee, D., Liu, X., Rehder, E., Edmondson, K., et al. (2012). Solar Cell Generations over 40 % Efficiency. Prog. Photovoltaics Res. Appl. 20, 801–815. doi:10.1002/pip1255
Koc, M. A., Raja, S. N., Hanson, L. A., Nguyen, S. C., Borys, N. J., Nguyen, S. C., et al. (2017). Characterizing Photon Reabsorption in Quantum Dot-Polymer Composites for Use as Displacement Sensors. ACS Nano 11 (2), 2075–2084. doi:10.1021/acsnano.6b08277
Kubista, M., Sjöback, R., Eriksson, S., and Albinsson, B. (1994). Experimental Correction for the Inner-Filter Effect in Fluorescence Spectra. Analyst 119 (3), 417–419. doi:10.1039/AN9941900417
Larouche, S., and Martinu, L. (2008). OpenFilters: Open-Source Software for the Design, Optimization, and Synthesis of Optical Filters. Appl. Opt. 47 (13), C219–C230. doi:10.1364/AO.47.00C219
Leem, J. W., Guan, X.-Y., and Yu, J. S. (2014). Tunable Distributed Bragg Reflectors with Wide-Angle and Broadband High-Reflectivity Using Nanoporous/Dense Titanium Dioxide Film Stacks for Visible Wavelength Applications. Opt. Express 22 (15), 18519. doi:10.1364/oe.22.018519
Li, S., Liu, H., Chen, W., Zhou, Z., Wu, D., Lu, R., et al. (2020). Low Reabsorption and Stability Enhanced Luminescent Solar Concentrators Based on Silica Encapsulated Quantum Rods. Sol. Energy Mater. Sol. Cells 206, 110321. doi:10.1016/j.solmat.2019.110321
Li, Z., Olah, A., and Baer, E. (2020). Micro- and Nano-Layered Processing of New Polymeric Systems. Prog. Polym. Sci. 102, 101210. doi:10.1016/j.progpolymsci.2020.101210
Lieb, M. A., Zavislan, J. M., and Novotny, L. (2004). Single-Molecule Orientations Determined by Direct Emission Pattern Imaging. J. Opt. Soc. Am. B 21 (6), 1210. doi:10.1364/JOSAB.21.001210
Liu, J.-g., and Ueda, M. (2009). High Refractive Index Polymers: Fundamental Research and Practical Applications. J. Mat. Chem. 19 (47), 8907–8919. doi:10.1039/b909690f
Lukosz, W., and Kunz, R. E. (1977). Light Emission by Magnetic and Electric Dipoles Close to a Plane Interface I Total Radiated Power. J. Opt. Soc. Am. 67 (12), 1607. doi:10.1364/JOSA.67.001607
Mulder, C. L., Reusswig, P. D., Velázquez, A. M., Kim, H., Rotschild, C., and Baldo, M. A. (2010). Dye Alignment in Luminescent Solar Concentrators: I Vertical Alignment for Improved Waveguide Coupling. Opt. Express 18 (S1), A79. doi:10.1364/OE.18.000A79
Olson, R. W., Loring, R. F., and Fayer, M. D. (1981). Luminescent Solar Concentrators and the Reabsorption Problem. Appl. Opt. 20 (17), 2934. doi:10.1364/AO.20.002934
Peters, M., Goldschmidt, J. C., Löper, P., Bläsi, B., and Gombert, A. (2009). The Effect of Photonic Structures on the Light Guiding Efficiency of Fluorescent Concentrators. J. Appl. Phys. 105 (1), 014909. doi:10.1063/1.2996081
Phelan, M., Needell, D. R., Bauser, H., Su, H., Deceglie, M., Theingi, S., et al. (2021). Outdoor Performance of a Tandem InGaP/Si Photovoltaic Luminescent Solar Concentrator. Sol. Energy Mater. Sol. Cells 223, 110945. doi:10.1016/j.solmat.2020.110945
Polman, A., and Atwater, H. A. (2012). Photonic Design Principles for Ultrahigh-Efficiency Photovoltaics. Nat. Mater 11 (3), 174–177. doi:10.1038/nmat3263
Rafiee, M., Chandra, S., Ahmed, H., and McCormack, S. J. (2019). An Overview of Various Configurations of Luminescent Solar Concentrators for Photovoltaic Applications. Opt. Mater. 91, 212–227. doi:10.1016/j.optmat.2019.01.007
Shen, Y., Jia, Y., Sheng, X., Shen, L., Rogers, J. A., and Giebink, N. C. (2014). Nonimaging Optical Gain in Luminescent Concentration through Photonic Control of Emission Étendue. ACS Photonics 1 (8), 746–753. doi:10.1021/ph500196r
Shneidman, A. V., Becker, K. P., Lukas, M. A., Torgerson, N., Wang, C., Reshef, O., et al. (2018). All-Polymer Integrated Optical Resonators by Roll-To-Roll Nanoimprint Lithography. ACS Photonics 5 (5), 1839–1845. doi:10.1021/acsphotonics.8b00022
Slooff, L. H., Bende, E. E., Burgers, A. R., Budel, T., Pravettoni, M., Kenny, R. P., et al. (2008). A Luminescent Solar Concentrator with 7.1% Power Conversion Efficiency. Phys. Status Solidi - Rapid Res. Lett. 2 (6), 257–259. doi:10.1002/pssr.200802186
Smestad, G., Ries, H., Winston, R., and Yablonovitch, E. (1990). The Thermodynamic Limits of Light Concentrators. Sol. Energy Mater. 21 (2–3), 99–111. doi:10.1016/0165-1633(90)90047-5
Smith, B. L., Woodhouse, M., Horowitz, K. A. W., Silverman, T. J., Zuboy, J., and Margolis, R. M. (2020). Photovoltaic \(PV\) Module Technologies: 2020 Benchmark Costs and Technology Evolution Framework Results. NREL/TP-7A40-78173 Golden, CO. Available at: www.nrel.gov/publications (Accessed Nov 02, 2021).
Sol, J. A. H. P., Timmermans, G. H., Breugel, A. J., Schenning, A. P. H. J., and Debije, M. G. (2018). Multistate Luminescent Solar Concentrator "Smart" Windows. Adv. Energy Mat. 8 (12), 1702922. doi:10.1002/aenm.201702922
U.S. Energy Information Administration Office of Energy Analysis (2021). “Annual Energy Outlook 2021.” Idependant Statistics And Analysis. Available at: www.Eia.Gov (Accessed June 23, 2022).
van Sark, W. G. J. H. M., Barnham, K. W. J., Slooff, L. H., Chatten, A. J., Büchtemann, A., Meyer, A., et al. (2008). Luminescent Solar Concentrators - A Review of Recent resultsLuminescent Solar Concentrators-Aa Review of Recent Results. Opt. Express 16 (26), 21773–21792. doi:10.1364/OE.16.021773
van der Burgt, J. S., Needell, D. R., Veeken, T., Polman, A., Garnett, E. C., and Atwater, H. A. (2021). Unlocking Higher Power Efficiencies in Luminescent Solar Concentrators through Anisotropic Luminophore Emission. ACS Appl. Mat. Interfaces 13, 40742–40753. doi:10.1021/acsami.1c12547
Verbunt, P. P. C., Sánchez-Somolinos, C., Broer, D. J., and Debije, M. G. (2013). Anisotropic Light Emissions in Luminescent Solar Concentrators-Isotropic Systems. Opt. Express 21 (S3), A485. doi:10.1364/oe.21.00a485
Verbunt, P. P. C., Tsoi, S., Debije, M. G., Boer, D. J., Bastiaansen, C. W. M., Lin, C.-W., et al. (2012). Increased Efficiency of Luminescent Solar Concentrators after Application of Organic Wavelength Selective Mirrors. Opt. Express 20 (S5), A655. doi:10.1364/OE.20.00A655
Wang, J., Yuan, Y., Zhu, H., Cai, T., Fang, Y., and Chen, O. (2020). Three-Dimensional Macroporous Photonic Crystal Enhanced Photon Collection for Quantum Dot-Based Luminescent Solar Concentrator. Nano Energy 67, 104217. doi:10.1016/j.nanoen.2019.104217
Wang, S., Dou, X., Chen, L., Fang, Y., Wang, A., Shen, H., et al. (2018). Enhanced Light Out-Coupling Efficiency of Quantum Dot Light Emitting Diodes by Nanoimprint Lithography. Nanoscale 10 (24), 11651–11656. doi:10.1039/c8nr02082e
Warmann, E. C., Flowers, C., Lloyd, J., Eisler, C. N., Escarra, M. D., and Atwater, H. A. (2017). Design of Photovoltaics for Modules with 50% Efficiency. Energy Sci. Eng. 5 (2), 69–80. doi:10.1002/ese3.155
Wiesenfarth, M, Philipps, S P., Bett, A W., Horowitz, K, and Kurtz, S (2017). Current Status of Concentrator Photovoltaic (CPV) Technology. NREL/TP-5J00-65130.
Wu, K., Li, H., and Klimov, V. I. (2018). Tandem Luminescent Solar Concentrators Based on Engineered Quantum Dots. Nat. Phot. 12 (2), 105–110. doi:10.1038/s41566-017-0070-7
Yablonovitch, E. (1980). Thermodynamics of the Fluorescent Planar Concentrator. J. Opt. Soc. Am. 70 (11), 1362. doi:10.1364/JOSA.70.001362
Yu, Z., Leilaeioun, M., and Holman, Z. (2016). Selecting Tandem Partners for Silicon Solar Cells. Nat. Energy 1 (11), 16137. doi:10.1038/nenergy.2016.137
Keywords: luminescent solar concentrator (LSC), photovoltaic (PV), back focal plane imaging, solar cell (PV), photonic, concentrator (CPV), spectrum-splitting, luminescent materials
Citation: Eisler CN, Parsons LE, Nett Z, Love C, Schwartzberg AM and Alivisatos AP (2022) Photonic Luminescent Solar Concentrator Design for High Efficiency, Low Cost Multijunction Photovoltaics. Front. Photonics 3:932913. doi: 10.3389/fphot.2022.932913
Received: 30 April 2022; Accepted: 08 June 2022;
Published: 06 July 2022.
Edited by:
Martina Schmid, University of Duisburg-Essen, GermanyCopyright © 2022 Eisler, Parsons, Nett, Love, Schwartzberg and Alivisatos. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Carissa N. Eisler, Y2Vpc2xlckB1Y2xhLmVkdQ==
†These authors have contributed equally to this work
 Carissa N. Eisler
Carissa N. Eisler Lindsey E. Parsons
Lindsey E. Parsons Zachary Nett2,3,4†
Zachary Nett2,3,4†