Mid-Infrared Frequency Generation via Intermodal Difference Frequency Generation in AlGaAs-On-Insulator Waveguides

We investigate theoretically mid-infrared (MIR) generation via difference frequency generation in multimode AlGaAs-on insulator (AlGaAs-OI) waveguides. The large refractive index difference between the AlGaAs core and the silica cladding shrinks the modes size down to the sub-μm² scale, and, together with AlGaAs strong second-order nonlinear polarization, empowers strong nonlinear effects. As a result, efficient MIR generation is obtained in few-cm long waveguides with sub-μm² transverse section, where higher order modes are exploited to achieve the phase-matching condition. These observations suggest that multimode AlGaAs-OI waveguides could represent a novel promising platform for on-chip, compact MIR sources.

1 Introduction

Mid-infrared (MIR) optical sources are key tools in a diverse range of fields spanning medicine, defence, and environmental gas sensing (Pitruzzello and Krauss, 2018; Tognazzi et al., 2021). Today, quantum cascade lasers (QCLs) represent a compact and versatile technology for MIR generation with performance peaking in the range from 4 to 10 μm (Yao et al., 2012). Shorter wavelengths can be achieved in rare Earth-doped silica, fluoride, and chalcogenide fiber lasers (Richardson et al., 2010; Sanghera et al., 2009; Fortin et al., 2015). Compared to QCL, these lasers allow high-output CW power but this comes at the expenses of increased bulkiness.

Highly nonlinear crystals bring a good compromise between wide MIR tunability and compactness. The light-matter interaction in these crystals leads to the conversion of an input pump frequency into a different frequency via second - or third - order nonlinear processes. Today, commercial lithium-niobate (LiNbO₃) few-cm long waveguides are widely employed for MIR generation through difference frequency generation (DFG) (Kuma et al., 2013; Büchter et al., 2009; Kishimoto et al., 2016).

DFG is a second-order nonlinear process where a pump and a seed beam respectively at frequencies ω_p and ω_s interact to give rise to a new beam, the idler, at the frequency ω_i = ω_p − ω_s. In the DFG process, one pump photon is converted into a seed photon and an idler photon (Saleh and Teich (1991)), leading to seed amplification and idler generation as represented in Figure 1.

FIGURE 1

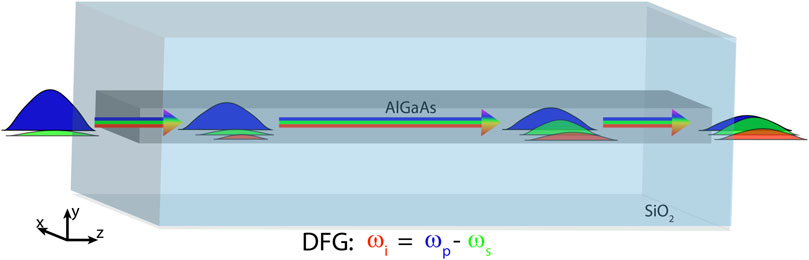
FIGURE 1. Sketch of the DFG process in a rectangular AlGaAs waveguide fully embedded in a SiO₂ cladding. An intense pump (blue) and a weak seed (green) at the waveguide input interact inside the waveguide, leading to seed amplification and idler generation (red).

In order for the process to be efficient, it must be phase-matched. Several phase-matching schemes have been developed and have been incorporated into crystals and small devices alike; these range from the heating of the crystal (Lee et al., 2005; Luo et al., 2018) to quasi phase-matching schemes such as periodic poling (Franken and Ward, 1963; Yamada et al., 1993).

Compared to LiNbO₃, Aluminum gallium arsenide exhibits some key features (Celebrano et al., 2021). Indeed, AlGaAs has a larger quadratic susceptibility d₁₄ ≈ 50 pm/V for AlGaAs at 1,550 nm (Carletti et al., 2015; Yang et al., 2007), whereas d₃₃ ≈ 25 pm/V for LiNBO₃ at 1,550 nm (Schiek and Pertsch, 2012). This reduces the length over which efficient nonlinear conversion is achieved, and then ultimately the crystal size, implying to a more compact final device. Furthermore, AlGaAs refractive index is substantially larger than the one of LiNbO₃, being $>$3 for AlGaAs at telecommunication wavelengths (Adachi (1985)), whereas ∼ 2.2 for LiNbO₃ (Smith et al. (1976)). This leads to extremely efficient mode confinement in AlGaAs on insulator (AlGaAs-OI) waveguides with silica cladding, reducing the modal area down to fractions of μm². These features, along with a relatively low two-photon absorption (TPA) (Villeneuve et al. (1993)), make the recently developed AlGaAs-OI platform an appealing prospect for efficient nonlinear conversion (Xie et al., 2020; May et al., 2019, 2021).

In this article, we explore this platform for efficient MIR generation through DFG theoretically and numerically. One of the major issues of the phase-matching condition is resolved by exploiting higher order guided modes in multimode waveguides. Indeed, while keeping the cross-section size smaller than 1 μm², we can still find several guided modes thanks to the high-index contrast between the AlGaAs core and the SiO₂ cladding. By playing on the Al_xGa_1−xAs composition (percentage of Aluminum x) and the geometry of the waveguide, it is possible to find a structure with different modes at the seed, idler, and pump frequencies whose propagation constants satisfy the phase-matching relation.

The multimode approach has successfully been applied to second harmonic generation (SHG) in waveguides where typically nonrectangular geometries (e.g. M-shaped) assist the phase-matching (Chowdhury and McCaughan (2000); Oster and Fouckhardt (2001); Moutzouris et al. (2003); Abolghasem et al. (2009); Dong et al. (2006); Ducci et al. (2004); Han et al. (2010); Ishikawa and Kondo (2009); Hong et al. (2018); Luo et al. (2018)). On the other hand, DFG for MIR generation has been relatively unexplored so far. Early works by Fiore et al. (1998) used selectively oxidized AlGa-AlAs waveguides to produce birefringent phase-matching. Advancements in the field were later shown by Logan et al. (2013) who proposed a multilayer AlGaAs waveguide to achieve efficient DFG and Stievater et al. (2014) who successfully employed subwavelength GaAs waveguide suspended in air. These seminal works involve a rather complicated geometry, which may be difficult to fabricate or handle. On the contrary, in this article, we focus on the basic rectangular geometry, which relaxes the fabrication complexity and simplifies the light coupling into the waveguide. Specifically, we investigate the nonlinear conversion efficiency achieved via DFG by taking into account the major related impairments, which are represented by linear losses, concurrent third-order nonlinear processes, modal differential group velocity, and finally the damage threshold that put a limit on the amount of pump power that can be coupled into the waveguide.

2 Theoretical Analysis

AlGaAs has a zincblende structure. One of the most common cut directions is along the waveguide axis. In this case the second-order nonlinear tensor exhibits 3 main contributions d₁₄ = d₂₅ = d₃₆ = d_eff (Kuo and Fejer (2018)). Consequently at the idler and pump frequencies the following relations hold true for the second-order nonlinear polarization P⁽²⁾ as a function of the electric field E:

$\begin{array}{ll}\hfill P_a^{(2)}({\omega }_i)=& 2{ϵ}_0{d}_{e\mathit{ff}}(E_b^{\ast }({\omega }_s)E_c({\omega }_p)+E_c^{\ast }({\omega }_s)E_b({\omega }_p))\hfill \end{array}(\mathrm{1a})$

$\begin{array}{ll}\hfill P_a^{(2)}({\omega }_p)=& 2{ϵ}_0{d}_{e\mathit{ff}}(E_b({\omega }_s)E_c({\omega }_i)+E_c({\omega }_s)E_b({\omega }_i))\hfill \end{array}(\mathrm{1b})$

where a ≠ b ≠ c = {x, y, z} and ϵ₀ is the vacuum permittivity. An equation similar to Eq. (1)(a) holds true for the seed by exchanging ω_s and ω_i. It is evident that the nonlinear polarization is boosted by the presence of a large longitudinal (z) component of the modes in play, as outlined by Poulvellarie et al. (2020). This is only achieved when at least one of the waveguide transverse dimensions is of the order of λ_p/n_core or smaller, λ_p being the pump wavelength and n_core the AlGaAs refractive index. We simulate the propagation of light into the waveguide via two separate approaches, namely finite element method (FEM), and coupled amplitude equations (CAEs).

In the first case, we solve Maxwell’s equations using the finite-element-method solver of the commercial software COMSOL Multiphysics (Gandolfi et al. (2020a,b, 2021); Ronchi et al. (2021); Rocco et al. (2021)):

$\nabla \times \left(\frac{1}{{\mu }_r}\nabla \times \mathbf{E}\left({\omega }_n\right)\right)-k_0^2\left({\omega }_n\right){\epsilon }_r\mathbf{E}\left({\omega }_n\right)={\mu }_0{\omega }_n^2{\mathbf{P}}^{(2)}\left({\omega }_n\right),(2)$

where ω_n = ω_p,s,i is one of the three frequencies into play and k₀ the free space wave number. The three equations for the pump, the seed, and the idler are coupled through the nonlinear polarization terms appearing on the right-hand side, defined in Eq. (1). Details of the numerical model are reported in the Appendix.

In the case of CAEs, we assume the total electromagnetic field E(ω_n), H(ω_n) oscillating with frequency ω_n is coupled to one guided mode of the waveguide and is factorized as follows:

$\mathbf{E}(x,y,z,{\omega }_n)=A_n{(z)\mathcal{E}}_n(x,y)e^{-i{\omega }_{n}t+i{\beta }_{n}z},\mathbf{H}(x,y,z,{\omega }_n)=A_n{(z)\mathcal{H}}_n(x,y)e^{-i{\omega }_{n}t+i{\beta }_{n}z}.(3)$

Here ${\mathcal{E}}_n(x,y)$ and ${\mathcal{H}}_n(x,y)$ represent respectively the transverse electric and magnetic field vectors of the mode, whereas A_n(z) and β_n are respectively the corresponding slowly varying amplitude and the propagation constant. The mode is normalized so that the integral of the Poynting vector along the propagation direction z is unitary, namely $N_n=(1/2){\int }_{xy}({\mathcal{E}}_n\times {\mathcal{H}}_n^{\ast })\cdot \widehat{\mathbf{z}}dxdy=1$. According to this normalization, |A_n|²(z) indicates the total power at position z and at frequency ω_n.

By following the steps outlined in Kolesik and Moloney (2004), we obtain the following system of coupled equations for the amplitudes:

$\begin{array}{ll}\hfill \frac{d{A}_i}{dz}& =-\frac{{\alpha }_i}{2}-i\sqrt{2}{\omega }_i{ϵ}_0{d}_{e\mathit{ff}}\widehat{S}{A}_p{A}_s^{\ast }{e}^{i\mathrm{\Delta }\beta z}+i{\gamma }_i{A}_i|A_i{|}^2\hfill \end{array}(\mathrm{4a})$

$\begin{array}{ll}\hfill \frac{d{A}_p}{dz}& =-\frac{{\alpha }_p}{2}-i\sqrt{2}{\omega }_p{ϵ}_0{d}_{e\mathit{ff}}\widehat{S}{A}_i{A}_s{e}^{-i\mathrm{\Delta }\beta z}+i{\gamma }_p{A}_p|A_p{|}^2.\hfill \end{array}(\mathrm{4b})$

An equation similar to Eq. (4a) holds true for the seed by exchanging indices s and i. Here, Δβ = β_p − β_s − β_i is the phase mismatch term, whereas α_n (n = {p, s, i}) represents the linear losses, which are typically induced by absorption and scattering due to inhomogeneities and imperfections (e.g. surface roughness). The overlap coefficient $\widehat{S}$ is calculated as follows:

$\widehat{S}=\frac{{\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }\mathrm{\Phi }\cdot u(x,y)dxdy}{N_i{N}_p{N}_s},(5)$

where

$\mathrm{\Phi }={\mathcal{E}}_{px}^{\ast }({\mathcal{E}}_{iy}{\mathcal{E}}_{sz}+{\mathcal{E}}_{sy}{\mathcal{E}}_{iz})+{\mathcal{E}}_{py}^{\ast }({\mathcal{E}}_{ix}{\mathcal{E}}_{sz}+{\mathcal{E}}_{sx}{\mathcal{E}}_{iz})+{\mathcal{E}}_{pz}^{\ast }({\mathcal{E}}_{ix}{\mathcal{E}}_{sy}+{\mathcal{E}}_{sx}{\mathcal{E}}_{iy})(6)$

and the function u(x, y) is 1 inside the core and 0 otherwise.

Differently from Kolesik and Moloney (2004), in Eq. (4a) we also include the self-phase modulation (SPM) terms that are related to the third-order nonlinearity. Indeed, in addition to a large second-order nonlinear response, AlGaAs also possesses a strong third-order nonlinear response that modifies the phase of the waves and may substantially broaden their spectra. The SPM coefficient reads γ_n = (n₂(ω_n)ω_n)/(cA_eff (ω_n)), where n₂ (ω_n) and A_eff are respectively the nonlinear refractive index and the modal effective area at frequency ω_n (Agrawal (2013)), with n₂ ∼ 3 × 10^–17 W/m² at 1,550 nm for AlGaAs (Boyd (2008)).

3 Results

Dimensions tuning to achieve the phase-matching condition. To maximize the DFG efficiency we should identify the waveguide dimensions and modes that allow us to achieve the phase-matching condition Δβ = 0. However, the choice of the geometry and of the involved modes depend on the wavelengths into play. Here we restrict the pump wavelength to the C + L telecommunication spectral region (1,535–1,600 nm), where a vast selection of optical sources is available. We fix the aluminum content to x = 25%, which is in line with recent literature (May et al. (2019, 2021)) as it keeps TPA low in the C + L band where the wavelength of the intense pump lies (see Adachi (1985) for the corresponding refractive index). Note, however, that similar results to those discussed in this article may be obtained for different choices of aluminum content, with 20% < x < 30%.

Moreover, we aim to generate an idler in the MIR region between 3,000 nm and 4,000 nm. As previously mentioned, at least one waveguide dimension should be of the order of λ_p/n_core or lower to boost the second-order nonlinear polarization. We then set the waveguide thickness in the range 240–300 nm. For such a small thickness the higher order modes at the targeted MIR wavelengths (3,000–4,000 nm) are weakly confined, leading to a low overlap coefficient $\widehat{S}$ and then poor DFG efficiency. To avoid this issue, we choose the fundamental TE00 mode for both the seed and the idler. Under all these conditions, it turns out that phase-matching is possible only for a pump coupled to the TM01 mode. Note however that this mode is well confined for the pump wavelengths under analysis (1,535–1,600 nm).

Figure 2A shows the pump and idler wavelengths that satisfy the phase-matching condition Δβ = β_p − β_s − β_i = 0 for a rectangular waveguide with a fixed thickness of L_y = 265 nm, and width L_x varying from 1,000 to 1,600 nm (colored lines). The propagation constants β_p,s,i are calculated through a mode solver. It should be noted that the seed wavelength is fixed via the relation ω_s = ω_p − ω_i.

FIGURE 2

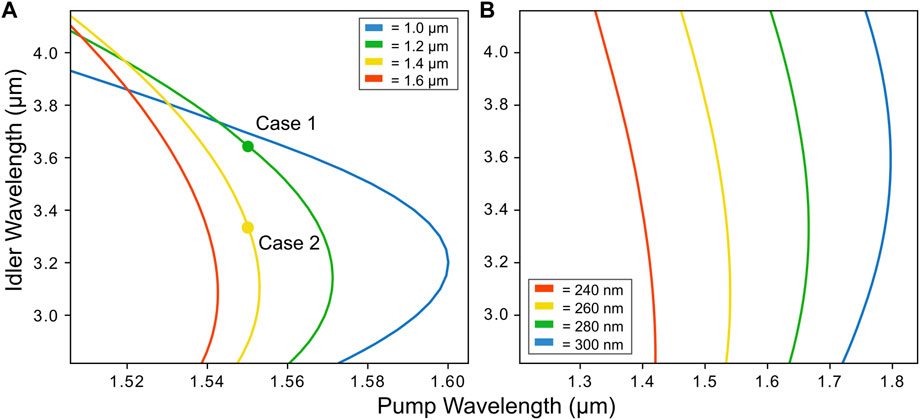
FIGURE 2. Phase-matching diagrams. The colored lines denote the pump and idler wavelengths where the phase-matching condition Δβ = β_p − β_s − β_i =0 occurs. (A) L_y =265 nm kept fixed, L_x varying from 1 to 1.6 μm. The green and yellow circles indicate the case L_x = 1.2 μm (case 1) and 1.6 μm (case 2), respectively, for a pump of 1,550 nm (B) L_x =1.2 μm kept fixed, L_y varying from 240 to 300 nm.

From Figure 2A we observe that phase-matching for an idler in the MIR band 3,000–4,000 nm can be achieved either by varying the pump wavelength or the waveguide width. In particular, for a fixed idler wavelength, a variation of tens of nanometers in the waveguide width can be easily compensated by shifting the pump wavelength a few nanometers. This makes the system robust against inaccuracies at fabrication stage. On the other hand, Figure 2B displays the phase-matching trend for a fixed width of 1,200 nm and a varying thickness. In this case, variations as small as 20 nm in the thickness result in a shift of the pump wavelength as large as 100 nm. Therefore, unless having at disposition a pump source tunable over a bandwidth ≫ 100 nm, an error of ±10 nm in the thickness may compromise the phase-matching and then drastically reduce the conversion efficiency. Based on the results in Figure 2, we now fix the pump wavelength at 1,550 nm and select two widths from Figure 2A for further study: 1,200 nm and 1,400 nm will be referred to as case 1 and case 2. The corresponding wavelengths that yield phase-matching are summarized in Table 1.

TABLE 1

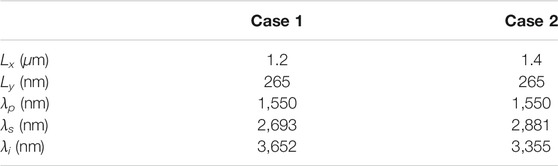
TABLE 1. Summary of the waveguide dimensions and the pump, seed and idler wavelengths for the two selected cases.

FEM simulations of Eq. (2) are compared to the CAEs (Eq. (4a)) for the parameters outlined in case 1. The CAEs are then simulated for both case 1 and 2 whilst varying the loss between 0 dB/cm to 5 dB/cm. For the sake of simplicity, here we consider that all the waves have the same loss coefficient (α_P = α_S = α_I). Note that prior to the numerical solution of Eq. (4a), we evaluate the overlap coefficient $\widehat{S}$ by computing the relevant modes at the wavelengths of interest via a mode solver, namely for case 1: TM01 (pump) at 1550nm, TE00 (seed) at 2,693 nm, and TE00 (idler) at 3,652 nm; for case 2: TM01 (pump) at 1550nm, TE00 (seed) at 2,881 nm, and TE00 (idler) at 3,355 nm.

Comparison between FEM and CAEs. For our analysis, we use an input pump power P_p = |A_p (0)|² = 1 W, whereas P_s = |A_s (0)|² = 1 mW for the seed. Figure 3A shows a comparison between FEM and CAEs simulations for case 1 and in the absence of losses (α_p = α_s = α_i = 0). The two approaches exhibit very similar results, thus validating the CAEs model that is less computationally demanding and order of magnitudes faster than FEM simulations. In particular, only few seconds are required for solving the CAEs model, whereas several hours are requested to solve the FEM model. Figure 3B shows the profiles of the modes at the seed, idler, and pump wavelength. Figure 3C reports the maps of the electric field norm for the seed, idler, and pump. We define the optimal length L_opt as the propagation length for which the pump conversion (and, hence, the idler generation) is maximized (for the case displayed in Figure 3A, L_opt = 1.7 cm). The larger the pump power, the faster the conversion from the pump to the idler therefore reducing the optimal length. Increasing values of losses reduce the average pump power, which in turn increases the optimal length, as reported in Figure 4A.

FIGURE 3

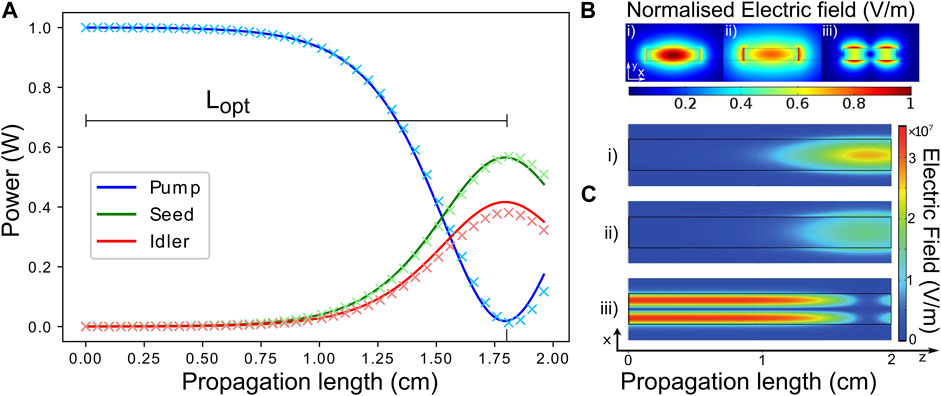
FIGURE 3. (A) Comparison FEM (crosses) versus CAEs (solid lines) simulations for case 1 (L_x =1,200 nm, L_y =265 nm, λ_p =1,550 nm, λ_s =2,693 nm, and λ_i =3,652 nm) in the absence of losses. The two methods provide very similar results. L_opt =1.75 cm indicates the propagation length where maximum pump conversion is achieved. (B) Intensity of the modal electric fields in the xy plane for the TE00 seed (i), TE00 idler (ii), and TM01 pump (iii). (C) Electric field calculated from FEM simulations at the seed (i), idler (ii), and pump (iii) frequencies over the xz plane.

FIGURE 4

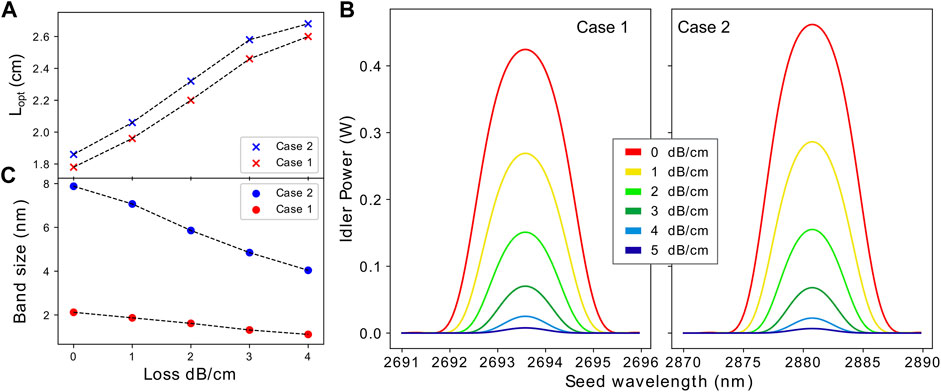
FIGURE 4. (A) Optimal waveguide length vs loss coefficients where the phase-matching condition Δβ = 0 is satisfied. (B) Idler power generated in cases 1 and 2, for a 1 W, 1,550 nm wavelength pump over a range of seed wavelengths and loss values of the waveguide, where propagation length is set to the optimal length displayed in (A). The idler wavelength is obtained by the relation ω_i = ω_p − ω_s. (C) Full-width-half-maximum versus loss coefficient for the bands illustrated in panel (B).

Figure 4B displays the pump-to-idler conversion efficiency at the end of the waveguide versus the seed wavelength and the loss coefficient, when the waveguide length L_wvg = L_opt. As expected, a peak of conversion is observed in correspondence of the phase-matching condition (seed wavelength ∼ 2,693 nm and ∼ 2,881 nm in cases 1 and 2, respectively). Moreover, we note that in both cases a loss coefficient of 5 dB/cm annihilates the DFG. For losses in the range 2–3 dB/cm (May et al., 2021), pump-to-idler efficiency of 7-16% can be achieved instead, with a bandwidth of ∼ 5 nm in case 2, as depicted in Figure 4C. Large conversion up to ∼ 30% is achieved if the waveguide losses are further decreased down to ∼ 1 dB (Pu et al. (2016); Ottaviano et al. (2016)).

Experimental scenario. At conclusion of this section, it is worth discussing a possible experimental scenario based on the parameters proposed above. First, it should be noted that a 1 W pump power roughly corresponds to a power density of P_p/A = 0.31 GW/cm² and 0.27 GW/cm² for cases 1 and 2, respectively, where A is the cross-section surface of the waveguide. While a CW beam with such a power density is likely to damage the waveguide, pulses a few-hundred picoseconds wide are not (Nikogosyan, 2005; Garg et al., 2003). Nevertheless, if we employ a pulsed pump, the generated idler itself will occur as short pulses of about the same duration even in the presence of a continuous-wave seed. The differential inverse group velocity (ΔIGV) among the TM01 mode at the pump wavelength and the TE00 mode at the idler wavelength will cause a relative time delay ΔT = L_wvgΔIGV that may compromise the temporal overlap of the two pulses, and then the efficiency of the DFG, whenever ΔT is comparable with the pulse duration of the pump and the idler. We have however verified that in our simulations the ΔIGV is of the order of 4 × 10^–9 s/m, which correspond to a time delay of tens of picoseconds. This does not impair the DFG dynamics as long as the pump pulse width is hundreds of picoseconds or more.

It is worth noting that for such a pulse width, SPM has little to no effect. More precisely, SPM induces a nonlinear phase accumulation that can shift the phase-matching condition, and that occurs in both CW and pulsed regime. We have verified that this effect is negligible for pump powers up to 1W. In addition, SPM leads to spectral broadening and pulse reshaping in the pulsed regime, which can be simulated by adding dispersion terms (e.g. group velocity dispersion + third-order dispersion) to Eq. (4a). However, our simulations show that for pump peak powers of 1W and pulse widths $>100$ ps there is no significant spectral broadening nor pulse reshaping.

4 Conclusion

In this article we have explored theoretically the possibility of developing tiny on-chip MIR optical sources based on DFG in AlGaAs-OI waveguides. By focusing on a basic rectangular geometry, phase-matching is not achievable when pump, seed, and idler are all coupled to the fundamental mode. However, it can be achieved when resorting to higher order modes. The large core-to-cladding refractive index difference along with the strong nonlinear polarization response leads to effective DFG in waveguides as short as a few cm and with sub-μm² cross-section. For example, we have shown that in a 1.7 cm long waveguide with 265 × 1,200 nm² cross-section pumped by a TM01-beam at wavelength 1,550 nm and seeded by a TE00-beam at wavelengths around 2,693 nm, it is possible to generate a MIR-idler around 3,652 nm with a pump-to-idler conversion efficiency up to 15% when linear losses are 2 dB/cm. The relatively low-damage threshold of AlGaAs as well as the concurrent and substantial third-order nonlinearity put a constraint on the pump power. We have seen however that few-hundreds picosecond pump sources with Watt-level peak power represent a viable solution that is not impaired by the pump-idler differential group velocity. All our results have been confirmed by FEM simulations that validate the fast simulation model based on CAEs.

It is worth noting that our analysis is not exhaustive. The maximum output MIR (idler) power ($\sim 0.4$ W in Figure 3) in our analysis is limited by the relatively low pump power and is lower than in QCLs where several watts can be achieved. However, we believe an optimal search over the waveguide dimensions as well as the pump and seed power and wavelengths would increase the maximum conversion. More complex schemes, like arrays of coupled waveguides, may further raise the output power.

To conclude with, we believe the results discussed in this work shed a light on the bright potential of the AlGaAs-OI platform for the development of a new generation of extremely compact, on-chip MIR sources.

Appendix: Comsol Multiphysics Model

In this section we describe the FEM model developed with COMSOL Multiphysics. The waveguide was modeled with a block of width L_x, thickness L_y, and length L_z—representing the core, surrounded by a much bigger block, of width L_clad, thickness L_clad, and length L_z— mimicking the cladding.

The refractive index of Al_0.25Ga_0.75As (Adachi (1985)) and SiO₂ (Agrawal (2013)) were assigned to the core and cladding, respectively.

The solution of the model relies on two steps.

(i) We computed the waveguide modes at the pump, the seed, and idler wavelengths. This is done by solving a 2D problem on a cross-sectional plane of the waveguide. In this way, we evaluated the electric field profile of the modes TE00 (for the seed and the idler) and TM01 (for the pump) and their propagation constants β_n (n = p, s, i).

(ii) We introduced three Electromagnetic Waves, Beam Envelopes physics to address the equations ruling the pump, the seed, and the idler (Eq. (2)). In a nutshell, since the modes propagation constants are known from the previous step of the computation, it is possible to factorize the electric field as: ${\mathbf{E}}_n={\mathbf{E}}_n^{\prime }\exp (i{\beta }_{n}z)$, where ${\mathbf{E}}_n^{\prime }$ is a slowly varying function (Mizuyama (2018)). COMSOL Multiphysics solves ${\mathbf{E}}_n^{\prime }$ (n = p, s, i), and the discretization of the spatial domain may be short enough to follow the variations of the envelope function, but not so short to follow the spatial oscillations of electric field. This fact considerably reduced the computational burden, because the spatial discretization to follow the envelope may be much coarser than the light wavelength.

The external polarizations, defined in Eq. 1 and appearing on the right-hand side of Eq. (2), were assigned only in the core domain, because χ⁽²⁾ is negligible in the material composing the cladding (i.e. SiO₂).

The electric field of the computed modes is mainly confined along the waveguide. L_clad was chosen large enough to have the external boundary truncating the cladding where the electric field is negligible. Hence, the external boundary of the computation domain does not alter the results. For the sake of solving the model, scattering boundary conditions were applied on the external faces of the cladding.

The waveguide modes were excited by means of ports, placed at the beginning of the waveguide. At the other side of the waveguide, a matched boundary condition was applied to truncate the domain without spurious reflections (i.e. this boundary condition allows the outflow of the light from the simulation domain as if the waveguide continued indefinitely after the end of the considered domain).

To perform the two aforementioned steps for the solution of the model, we introduced two studies in COMSOL Multiphysics. (i) To excite the desired modes for the pump, the seed, and the idler, we added a study with three boundary modes analysis steps (one for every wavelength that has to be considered). In each study step, the effective refractive index of the mode to be launched in the waveguide is provided. For this computation, the frequency imposed in the Electromagnetic Waves, Beam Envelopes nodes is dictated by the solver. By running this study, we compute the electric field profile (in the planes of the ports) of the desired modes and their propagation constants.

(ii) To compute the electric field in all the waveguide, another study is necessary. This study has to compute only the envelope function of the electric field, since the propagation constant of the modes, the electric field profiles, and phases are known from the previous study. The second study has a frequency domain study step. The frequencies to be provided in the Electromagnetic Waves, Beam Envelopes nodes have to be set as user defined: in each Electromagnetic Waves, Beam Envelope node the user has to write the correct frequency (of pump, seed, or idler).

We used this approach to study the waveguide of dimensions L_x = 1,200 nm and L_y = 265 nm (case 1 in Figure 2). To compute the desired modes with a good precision, we chose L_clad = 6L_x. This is a good compromise to obtain the modes with the effective refractive index close to the target value and to limit the computational burden. Also the mesh size in the plane of the ports was optimized. In particular, the mesh size in the core domain was smaller than λ_p/20, whereas in the cladding the mesh was kept finer in the region close to the core, where the electric fields are not negligible. The mesh developed on the ports plane was swept along the waveguide length, setting 5 mesh nodes every 1 mm along the waveguide length. These settings for the mesh were necessary to achieve the model convergence and to obtain a reasonable result.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JH performed the theoretical and numerical analysis. MGa, YF, and MGu also contributed to numerical analysis throughout. All authors participated in analysis of the results and manuscript writing.

Funding

JH, YF, and MGu, acknowledge funding from the European Research Council under the H2020 Programme (ERC Starting Grant No. 802682, MODES project). The work of MGa and CDA is partially funded by the European Union Horizon 2020 Research and Innovation programme under Grant Agreement No. 899673; by the National Research Council Joint Laboratories program, Project No. SAC.AD002.026 (OMEN); and by the Italian Ministry of University and Research (MIUR) through the PRIN project NOMEN Grant No. 2017MP7F8F.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abolghasem, P., Han, J., Bijlani, B. J., Arjmand, A., and Helmy, A. S. (2009). Continuous-wave Second Harmonic Generation in Bragg Reflection Waveguides. Opt. Express 17, 9460–9467. doi:10.1364/OE.17.009460

PubMed Abstract | CrossRef Full Text | Google Scholar

Adachi, S. (1985). GaAs, AlAs, and AlxGa1–xAs: Material Parameters for Use in Research and Device Applications. J. Appl. Phys. 58, R1–R29. doi:10.1063/1.336070

CrossRef Full Text | Google Scholar

Agrawal, G. (2013). Nonlinear Fiber Optics. 5th ed. Optics and Photonics Academic Press.

Google Scholar

Boyd, R. W. (2008). Nonlinear Optics. 3rd Edition. Tensor Nature of the Third-Order Susceptibility Elsevier.

Google Scholar

Büchter, K.-D. F., Herrmann, H., Langrock, C., Fejer, M. M., and Sohler, W. (2009). All-optical Ti:PPLN Wavelength Conversion Modules for Free-Space Optical Transmission Links in the Mid-infrared. Opt. Lett. 34, 470–472. doi:10.1364/OL.34.000470

PubMed Abstract | CrossRef Full Text | Google Scholar

Carletti, L., Locatelli, A., Stepanenko, O., Leo, G., and De Angelis, C. (2015). Enhanced Second-Harmonic Generation from Magnetic Resonance in AlGaAs Nanoantennas. Opt. Express 23, 26544–26550. doi:10.1364/OE.23.026544

PubMed Abstract | CrossRef Full Text | Google Scholar

Celebrano, M., Rocco, D., Gandolfi, M., Zilli, A., Rusconi, F., Tognazzi, A., et al. (2021). Optical Tuning of Dielectric Nanoantennas for Thermo-Optically Reconfigurable Nonlinear Metasurfaces. Opt. Lett. 46, 2453–2456. doi:10.1364/ol.420790

PubMed Abstract | CrossRef Full Text | Google Scholar

Chowdhury, A., and McCaughan, L. (2000). Continuously Phase-Matched M-Waveguides for Second-Order Nonlinear Upconversion. IEEE Photon. Technol. Lett. 12, 486–488. doi:10.1109/68.841261

CrossRef Full Text | Google Scholar

Dong, P., Upham, J., Jugessur, A., and Kirk, A. G. (2006). Observation of Continuous-Wave Second-Harmonic Generation in Semiconductor Waveguide Directional Couplers. Opt. Express 14, 2256–2262. doi:10.1364/OE.14.002256

PubMed Abstract | CrossRef Full Text | Google Scholar

Ducci, S., Lanco, L., Berger, V., De Rossi, A., Ortiz, V., and Calligaro, M. (2004). Continuous-wave Second-Harmonic Generation in Modal Phase Matched Semiconductor Waveguides. Appl. Phys. Lett. 84, 2974–2976. doi:10.1063/1.1703847

CrossRef Full Text | Google Scholar

Fiore, A., Berger, V., Rosencher, E., Bravetti, P., and Nagle, J. (1998). Phase Matching Using an Isotropic Nonlinear Optical Material. Nature 391, 463–466. doi:10.1038/35091

CrossRef Full Text | Google Scholar

Fortin, V., Bernier, M., Bah, S. T., and Vallée, R. (2015). 30 W Fluoride Glass All-Fiber Laser at 294 μm. Opt. Lett. 40, 2882–2885. doi:10.1364/OL.40.002882

PubMed Abstract | CrossRef Full Text | Google Scholar

Franken, P. A., and Ward, J. F. (1963). Optical Harmonics and Nonlinear Phenomena. Rev. Mod. Phys. 35, 23–39. doi:10.1103/RevModPhys.35.23

CrossRef Full Text | Google Scholar

Gandolfi, M., Banfi, F., and Glorieux, C. (2020a). Optical Wavelength Dependence of Photoacoustic Signal of Gold Nanofluid. Photoacoustics 20, 100199. doi:10.1016/j.pacs.2020.100199

PubMed Abstract | CrossRef Full Text | Google Scholar

Gandolfi, M., Giannetti, C., and Banfi, F. (2020b). Temperonic crystal: A Superlattice for Temperature Waves in Graphene. Phys. Rev. Lett. 125, 265901. doi:10.1103/physrevlett.125.265901

PubMed Abstract | CrossRef Full Text | Google Scholar

Gandolfi, M., Tognazzi, A., Rocco, D., De Angelis, C., and Carletti, L. (2021). Near-unity Third-Harmonic Circular Dichroism Driven by a Quasibound State in the Continuum in Asymmetric Silicon Metasurfaces. Phys. Rev. A. 104, 023524. doi:10.1103/PhysRevA.104.023524

CrossRef Full Text | Google Scholar

Garg, A., Kapoor, A., and Tripathi, K. N. (2003). Laser-induced Damage Studies in GaAs. Opt. Laser Tech. 35, 21–24. doi:10.1016/S0030-3992(02)00118-4

CrossRef Full Text | Google Scholar

Han, J.-B., Abolghasem, P., Kang, D., Bijlani, B. J., and Helmy, A. S. (2010). Difference-frequency Generation in AlGaAs Bragg Reflection Waveguides. Opt. Lett. 35, 2334–2336. doi:10.1364/OL.35.002334

PubMed Abstract | CrossRef Full Text | Google Scholar

Hong, L.-H., Chen, B.-Q., Hu, C.-Y., and Li, Z.-Y. (2018). Analytical Solution of Second-Harmonic Generation in a Lithium-Niobate-Birefringence Thin-Film Waveguide via Modal Phase Matching. Phys. Rev. A. 98, 023820. doi:10.1103/PhysRevA.98.023820

CrossRef Full Text | Google Scholar

Ishikawa, H., and Kondo, T. (2009). Birefringent Phase Matching in Thin Rectangular High-Index-Contrast Waveguides. Appl. Phys. Express 2, 042202. doi:10.1143/apex.2.042202

CrossRef Full Text | Google Scholar

Kishimoto, T., Inafune, K., Ogawa, Y., Sasaki, H., and Murai, H. (2016). Highly Efficient Phase-Sensitive Parametric Gain in Periodically Poled LiNbO_3 ridge Waveguide. Opt. Lett. 41, 1905–1908. doi:10.1364/OL.41.001905

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolesik, M., and Moloney, J. V. (2004). Nonlinear Optical Pulse Propagation Simulation: From Maxwell's to Unidirectional Equations. Phys. Rev. E 70, 036604. doi:10.1103/PhysRevE.70.036604

CrossRef Full Text | Google Scholar

Kuma, S., Miyamoto, Y., Tsutsumi, K., Sasao, N., and Uetake, S. (2013). 48 μm Difference-Frequency Generation Using a Waveguide-PPLN crystal and its Application to Mid-infrared Lamb-Dip Spectroscopy. Opt. Lett. 38, 2825–2828. doi:10.1364/OL.38.002825

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuo, P. S., and Fejer, M. M. (2018). Mixing of Polarization States in Zincblende Nonlinear Optical Crystals. Opt. Express 26, 26971–26984. doi:10.1364/OE.26.026971

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, Y.-L., Yu, B.-A., Jung, C., Noh, Y.-C., Lee, J., and Ko, D.-K. (2005). All-optical Wavelength Conversion and Tuning by the Cascaded Sum- and Difference Frequency Generation (cSFG/DFG) in a Temperature Gradient Controlled Ti:PPLN Channel Waveguide. Opt. Express 13, 2988–2993. doi:10.1364/OPEX.13.002988

PubMed Abstract | CrossRef Full Text | Google Scholar

Logan, D. F., Giguere, M., Villeneuve, A., and Helmy, A. S. (2013). Widely Tunable Mid-infrared Generation via Frequency Conversion in Semiconductor Waveguides. Opt. Lett. 38, 4457–4460. doi:10.1364/OL.38.004457

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, R., He, Y., Liang, H., Li, M., and Lin, Q. (2018). Highly Tunable Efficient Second-Harmonic Generation in a Lithium Niobate Nanophotonic Waveguide. Optica 5, 1006–1011. doi:10.1364/OPTICA.5.001006

CrossRef Full Text | Google Scholar

May, S., Clerici, M., and Sorel, M. (2021). Supercontinuum Generation in Dispersion Engineered AlGaAs-On-Insulator Waveguides. Sci. Rep. 11, 2052. doi:10.1038/s41598-021-81555-3

PubMed Abstract | CrossRef Full Text | Google Scholar

May, S., Kues, M., Clerici, M., and Sorel, M. (2019). Second-harmonic Generation in AlGaAs-On-Insulator Waveguides. Opt. Lett. 44, 1339–1342. doi:10.1364/OL.44.001339

PubMed Abstract | CrossRef Full Text | Google Scholar

Mizuyama, Y. (2018). How to Use the Beam Envelopes Method for Wave Optics Simulations. Available at: https://www.comsol.com/blogs/how-to-use-the-beam-envelopes-method-for-wave-optics-simulations/.

Google Scholar

Moutzouris, K., Venugopal Rao, S., Ebrahimzadeh, M., De Rossi, A., Calligaro, M., Ortiz, V., et al. (2003). Second-harmonic Generation through Optimized Modal Phase Matching in Semiconductor Waveguides. Appl. Phys. Lett. 83, 620–622. doi:10.1063/1.1596726

CrossRef Full Text | Google Scholar

Nikogosyan, D. (20052005). Nonlinear Optical Crystals: A Complete Survey. Springer Science+Business Media, Inc., 428. ISBN 978-0-387-22022-2. doi:10.1007/b138685

CrossRef Full Text | Google Scholar

Oster, B., and Fouckhardt, H. (2001). M-waveguide Structures for Direct Phase Matching in AlGaAs. Appl. Phys. B 73, 535–540. doi:10.1007/s003400100704

CrossRef Full Text | Google Scholar

Ottaviano, L., Pu, M., Semenova, E., and Yvind, K. (2016). Low-loss High-Confinement Waveguides and Microring Resonators in AlGaAs-On-Insulator. Opt. Lett. 41, 3996–3999. doi:10.1364/OL.41.003996

PubMed Abstract | CrossRef Full Text | Google Scholar

Pitruzzello, G., and Krauss, T. F. (2018). Photonic crystal Resonances for Sensing and Imaging. J. Opt. 20, 073004. doi:10.1088/2040-8986/aac75b

CrossRef Full Text | Google Scholar

Poulvellarie, N., Dave, U., Alexander, K., Ciret, C., Billet, M., Mas Arabi, C., et al. (2020). Second-harmonic Generation Enabled by Longitudinal Electric-Field Components in Photonic Wire Waveguides. Phys. Rev. A. 102, 023521. doi:10.1103/PhysRevA.102.023521

CrossRef Full Text | Google Scholar

Pu, M., Ottaviano, L., Semenova, E., and Yvind, K. (2016). Efficient Frequency Comb Generation in AlGaAs-On-Insulator. Optica 3, 823–826. doi:10.1364/OPTICA.3.000823

CrossRef Full Text | Google Scholar

Richardson, D. J., Nilsson, J., and Clarkson, W. A. (2010). High Power Fiber Lasers: Current Status and Future Perspectives [Invited]. J. Opt. Soc. Am. B 27, B63–B92. doi:10.1364/JOSAB.27.000B63

CrossRef Full Text | Google Scholar

Rocco, D., Gandolfi, M., Tognazzi, A., Pashina, O., Zograf, G., Frizyuk, K., et al. (2021). Opto-thermally Controlled Beam Steering in Nonlinear All-Dielectric Metastructures. Opt. Express 29, 37128–37139. doi:10.1364/oe.440564

PubMed Abstract | CrossRef Full Text | Google Scholar

Ronchi, A., Sterzi, A., Gandolfi, M., Belarouci, A., Giannetti, C., Fatti, N. D., et al. (2021). Discrimination of Nano-Objects via Cluster Analysis Techniques Applied to Time-Resolved Thermo-Acoustic Microscopy. Ultrasonics 114, 106403. doi:10.1016/j.ultras.2021.106403

PubMed Abstract | CrossRef Full Text | Google Scholar

Saleh, B. E. A., and Teich, M. C. (1991). Fundamentals of Photonics. John Wiley & Sons. doi:10.1002/0471213748

CrossRef Full Text | Google Scholar

Sanghera, J. S., Brandon Shaw, L., and Aggarwal, I. D. (2009). Chalcogenide Glass-Fiber-Based Mid-IR Sources and Applications. IEEE J. Select. Top. Quan. Electron. 15, 114–119. doi:10.1109/JSTQE.2008.2010245

CrossRef Full Text | Google Scholar

Schiek, R., and Pertsch, T. (2012). Absolute Measurement of the Quadratic Nonlinear Susceptibility of Lithium Niobate in Waveguides. Opt. Mater. Express 2, 126–139. doi:10.1364/OME.2.000126

CrossRef Full Text | Google Scholar

Smith, D. S., Riccius, H. D., and Edwin, R. P. (1976). Refractive Indices of Lithium Niobate. Opt. Commun. 17, 332–335. doi:10.1016/0030-4018(76)90273-X

CrossRef Full Text | Google Scholar

Stievater, T. H., Mahon, R., Park, D., Rabinovich, W. S., Pruessner, M. W., Khurgin, J. B., et al. (2014). Mid-infrared Difference-Frequency Generation in Suspended GaAs Waveguides. Opt. Lett. 39, 945–948. doi:10.1364/OL.39.000945

PubMed Abstract | CrossRef Full Text | Google Scholar

Tognazzi, A., Rocco, D., Gandolfi, M., Locatelli, A., Carletti, L., and De Angelis, C. (2021). High Quality Factor Silicon Membrane Metasurface for Intensity-Based Refractive index Sensing. Optics 2, 193–199. doi:10.3390/opt2030018

CrossRef Full Text | Google Scholar

Villeneuve, A., Yang, C. C., Stegeman, G. I., Lin, C. H., and Lin, H. H. (1993). Nonlinear Refractive‐index and Two Photon‐absorption Near Half the Band gap in AlGaAs. Appl. Phys. Lett. 62, 2465–2467. doi:10.1063/1.109320

CrossRef Full Text | Google Scholar

Xie, W., Chang, L., Shu, H., Norman, J. C., Peters, J. D., Wang, X., et al. (2020). Ultrahigh-Q AlGaAs-On-Insulator Microresonators for Integrated Nonlinear Photonics. Opt. Express 28, 32894–32906. doi:10.1364/OE.405343

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamada, M., Nada, N., Saitoh, M., and Watanabe, K. (1993). First‐order Quasi‐phase Matched LiNbO3waveguide Periodically Poled by Applying an External Field for Efficient Blue Second‐harmonic Generation. Appl. Phys. Lett. 62, 435–436. doi:10.1063/1.108925

CrossRef Full Text | Google Scholar

Yang, Z., Chak, P., Bristow, A. D., van Driel, H. M., Iyer, R., Aitchison, J. S., et al. (2007). Enhanced Second-Harmonic Generation in AlGaAs Microring Resonators. Opt. Lett. 32, 826–828. doi:10.1364/OL.32.000826

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, Y., Hoffman, A. J., and Gmachl, C. F. (2012). Mid-infrared Quantum cascade Lasers. Nat. Photon 6, 432–439. doi:10.1038/nphoton.2012.143

CrossRef Full Text | Google Scholar