- 1School of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu, China
- 2School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu, China
- 3The 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang, China
This paper presents a unique approach for wavelet-based MRI brain image de-noising. Adaptive soft and hard threshold functions are first proposed to improve the results of standard soft and hard threshold functions for image de-noising in the wavelet domain. Then, we applied the newly emerged improved adaptive generalized Gaussian distributed oriented threshold function (improved AGGD) on the MRI images to improve the results of the adaptive soft and hard threshold functions and also to display, this non-linear and data-driven function can work promisingly even in de-noising the medical images. The most important characteristic of this function is that it is dependent on the image since it is combined with an adaptive generalized Gaussian distribution function.Traditional thresholding neural network (TNN) and optimized based noise reduction have good results but fail to keep the visual quality and may blur some parts of an image. In TNN and optimized based image de-noising, it was required to use Least-mean-square (LMS) learning and optimization algorithms, respectively to find the optimum threshold value and parameters of the threshold functions which was time consuming. To address these issues, the improved AGGD based image de-noising approach is introduced to enhance the qualitative and quantitative performance of the above mentioned image de-noising techniques. De-noising using improved AGGD threshold function provides better results in terms of Peak Signal to Noise Ratio (PSNR) and also faster processing time since there is no need to use any Least-mean-square (LMS) learning and optimization algorithms for obtaining the optimum value and parameters of the thresholding functions. The experimental results indicate that image de-noising using improved AGGD threshold performs pretty well comparing with the adaptive threshold, standard threshold, improved wavelet threshold, and the optimized based noise reduction methods.
1. Introduction
Image de-noising is among the most important tasks in image and signal processing. Wide range of unwanted noises may affect the visual quality of images. The noise can affect an image during the processes of acquisition and transmission which can cause deflection from an original image. It is obvious that the image quality and resolution may be contaminated by these artifacts so that it is required to do image de-noising as the first step before any further analysis, such as super-resolution, classification and any qualitative and quantitative measurement.
One of the most crucial issues in image de-noising is keeping the most influential characteristics of the images and removing the non-important characteristics. Noise removal has become one of the critical pre-processing steps in many applications like remote sensing, satellite and biomedical image processing (Golilarz et al., 2019b). Some of these noises can affect the appearance and damage the attribute of an image. Others may not be continuous and they occur randomly. In this case, it is very difficult to get rid of these kinds of noises. However, many methods have been proposed for reducing the possible noises from the images and enhancing their quality.
Yuan and Ghanem (2015) introduced a new approach for image restoration in the presence of impulse noise. Weighted couple sparse representation has been introduced by Chen et al. (2015). To remove multimodal noise using semi-supervised learning on big data, Yin et al. (2018) introduced a highly accurate image reconstruction. Garnett et al. (2005) introduced a universal noise reduction algorithm combined with an impulse detector. Median- type noise detectors and detail-preserving regularization based noise removal are proposed by Chan et al. (2005). Moreover, impulse noise reduction with Gaussian curvature of image surface is proposed by Miura et al. (2013). Lin et al. (2010) introduced impulse noise suppression using a new adaptive center weighted median (ACWM) filter. A new impulse detector combined with weighted median filter is proposed by Dong and Xu (2007) to obtain the directional weighted median (DWM) filter. Universal noise reduction using a switching bilateral filter combined with a noise detector is utilized by Lin et al. (2010). The standard deviation to acquire the optimal direction is proposed by Awad (2011) as a new technique to discard the noise from images influenced by random-valued impulse noise. In 2013, Lu et al. proposed sparse coding for noise removing with spike and slab prior (Lu et al., 2013). Noise reduction utilizing a scale mixture of Gaussians was presented by Portilla et al. (2003). In this technique, the components have been explained with a statistical model. Additionally, the estimation of mode in high-dimensional spaces using flat-top kernels has been proposed in a study conducted by De Decker et al. (2011). Recently, wavelet and thresholding based noise reduction has become very common among researchers in the field of image and signal processing. Many techniques have been introduced to discard the noises and keep the most significant characteristics of images in the wavelet domain.
Chang et al. (2000) proposed context modeling for parameter estimation of each component which is adaptive to wavelet thresholding. It is clear, this component is modeled as a random variable for GGD. Based on the obtained results, this method has better performance than orthogonal transform. Speckle noise reduction utilizing a Bayesian multiscale method is introduced by Achim et al. (2001). An empirical Bayes method with Jeffrey's non-informative prior is also a noise removal method based on wavelet transform proposed by Figueiredo and Nowak (2001). Şendur and Selesnick (2002) proposed bivariate shrinkage function for image denoising using wavelet transform. Image de-noising using joint inter- and interscale statistical model, translation invariant wavelet transformations, and Bayesian wavelet shrinkage based on heavy-tailed modeling have been proposed by Pizurica et al. (2002), Achim et al. (2003), and Sveinsson and Benediktsson (2003), respectively.
Starck et al. (2002) proposed the curvelet transform for noise reduction. Additionally, sparse and redundant representations over learned dictionaries for noise removing is proposed by Elad and Aharon (2006). The local adaptive wiener filter approach for noise suppression in wavelet domain is introduced by Li et al. (2011). Image de-noising with an un-decimated wavelet transform (UWT) utilizing soft thresholding function is introduced by Golilarz and Demirel (2018a). Furthermore, image de-noising based on translation invariant wavelet transform combined with smooth sigmoid based shrinkage (SSBS) function is introduced by Golilarz et al. (2017). Adapting to unknown smoothness via wavelet shrinkage is introduced by Donoho and Johnstone (1995).
To improve the quality and performance of the previous method, Coifman and Donoho (1995) proposed translation-invariant de-noising. Numerous literature has emerged for thresholding neural network (TNN) based noise suppression. Thresholding neural network (TNN) for adaptive noise reduction is proposed by Zhang (2001). In this study, new types of soft and hard threshold functions have been presented to be utilized as the activation function in TNN. These threshold functions are differentiable and non-linear. Moreover, thresholding neural network-based noise reduction with a smooth sigmoid based shrinkage and TNN using an improved threshold function have been proposed by Golilarz and Demirel (2017) and Golilarz and Demirel (2018b), respectively. Image denoising in the wavelet domain based on improved TNN and cycle spinning has been conducted in a study proposed by Sahraeian et al. (2007). In this study, the authors utilized a new adaptive improved threshold function combined with cycle spinning to enhance the results of TNN based image de-noising using adaptive thresholding. Besides, Nasri and Nezamabadi-pour (2009) presented a new adaptive thresholding function for wavelet based noise removal. In their research, they introduced a new TNN combined with a new type of adaptive function with three shape tuning parameters to improve the Zhang's approach (Zhang, 2001). Golilarz et al. (2018) introduced a new method for hyperspectral remote sensing image de-noising utilizing 3D un-decimated wavelet transform with a new improved soft thresholding function to improve the results of previous threshold based noise removal. Qian (2018) proposed an algorithm for image de-noising utilizing an enhanced thresholding and median filter. One of the drawbacks and limitations of utilizing TNN based noise reduction is that it is time-consuming. Gradient-based learning is used in TNN to attain the optimum threshold value. Therefore, to address this problem, Bhandari et al. (2016) proposed optimized adaptive thresholding based image de-noising which they used JADE optimization algorithm instead of the steepest descent gradient based LMS method to decrease the computational time for attaining the optimum threshold value and other parameters.
To improve the efficiency of de-noising based on JADE algorithm, Golilarz et al. (2019b) utilized Harris Hawks optimization (HHO) algorithm (Heidari et al., 2019) in the first stage, and then improved adaptive generalized Gaussian distribution (AGGD) threshold function (Golilarz et al., 2019a) is used to enhance the quality of optimized based image de-noising approach, and lessen the computational time as well. The authors indicated that in improved AGGD based noise removal, the optimum value can be acquired without using any LMS learning and optimization algorithm. This advantage can save the processing time. In addition, the performance of wavelet thresholding can be enhanced using the adaptive GGD function because it provides us with more information about the image which the noisy constituents can be controlled well utilizing this adaptive function.
In this research, in the first stage we present adaptive soft and adaptive hard threshold to improve the results of standard hard and standard soft threshold function. In standard hard threshold, the small components are set to zero but adaptive soft and adaptive hard threshold can tune these coefficients using AGGD function in the interval [−σn, σn]. The results proved that adaptive threshold acts better than standard threshold in image de-noising. Additionally, to enhance the performance of image de-noising using optimization algorithms, improved adaptive generalized Gaussian distribution (AGGD) threshold is used for MRI brain image de-nosing. Moreover, we compared the proposed method with improved wavelet threshold proposed by Zhang et al. (2019). Experimental results prove the superiority of the proposed method over standard threshold, adaptive threshold, optimization (Golilarz et al., 2019b), and improved wavelet threshold (Zhang et al., 2019) based image de-noising methods.
2. Wavelet Based Image De-noising
To get the output de-noised image in the wavelet domain, we can do as follows (Golilarz et al., 2019b). Firstly, by applying wavelet transform we will get wavelet coefficients. These components can be sorted in two main groups: those carrying the most significant features of images and those having the non-important characteristics, with the former is the detail coefficient and latter is the non-important coefficients or noisy constituents. Next, these wavelet coefficients which we got from the first step, should be tuned using a suitable threshold value to preserve the crucial features and attribute of the image and discard the non-important components. These tuned components are called as thresholded wavelet coefficients. Then, it is time to apply the inverse wavelet transform (IWT) on these tuned thresholded wavelet coefficients providing us with the noise free image. On this matter, it is an important task to use a suitable threshold function and a threshold value since it plays an important role in getting our desired output de-noised image.
2.1. Definition of Noise, Threshold, and Mean Square Error
Assume that the noisy vector is as: f=[f0,f1,….fN-1]Tf=[f0,f1,….fN−1]T which is contaminated by additive white Gaussian noise (AWGN):
where, ui represents the input noise-free wavelet constituents and ni is the iid (independent and identically distributed) Gaussian noise.
Then, assume the data vector without noise as U=[u0,u1,…,uN-1]T and the thresholded output vector as |Û=[û0,û1,…,ûN-1]T Admittedly, the main goal in image de-noising is to minimize the Mean Square Error risk (Nasri and Nezamabadi-pour, 2009). The Mean Square Error (MSE) risk can be obtained as follows:
where, N is the size of the sub-band, (ui) is the input coefficients and ^ui the thresholded wavelet coefficients (Nasri and Nezamabadi-pour, 2009).
Noise removal in the wavelet domain requires applying a proper threshold function and the threshold value. The universal threshold value (tuni) can be obtained based on VisuShrink technique using the equation below (Donoho and Johnstone, 1994). VisuShrink applies a universal threshold to all of the wavelet detail constituents. This threshold is known to discard additive Gaussian noise with high probability tending to result in overly smooth image appearance due to the fact that the threshold may be big because of its dependancy to the number of samples, n.
where, n is the sample size and σ is the robust median estimator (Donoho and Johnstone, 1994) as follows:
where, G(i, j) is the components in the HH1 sub-band (Donoho and Johnstone, 1994).
2.2. Thresholding Neural Network (TNN)
Thresholding neural network based (space scale adaptive) noise reduction is proposed by Zhang (2001). In this network, there is linear transform which is fixed, and activation function which can be adaptive. The input of TNN is noisy image in which the linear orthogonal transform can be applied on it to get noisy components. Note that η is the non-linear activation function. The noisy coefficients need to be passed through this function to get thresholded wavelet coefficients. Eventually, by applying inverse linear orthogonal transform, we will attain output de-noised image (Golilarz and Demirel, 2018b). Zhang introduced two types of the non-linear threshold, namely: improved soft, and improved hard threshold functions as follows (Zhang, 2001). These functions with different λ and μ values are shown in Figure 1.
where, ηsoft is the improved soft threshold function. Here, x is the wavelet component, t is the threshold value and λ > 0 is a user-defined function parameter (Zhang, 2001).
where, ηhard is the improved hard threshold function, x is the wavelet components, t is the threshold value and μ > 0 is a user-defined function parameter (Zhang, 2001). In this network, the optimum threshold value in the step L is given below (Golilarz and Demirel, 2017):
where, Δt(L) is as:
where θ is learning rate and J(t) is the MSE risk function.
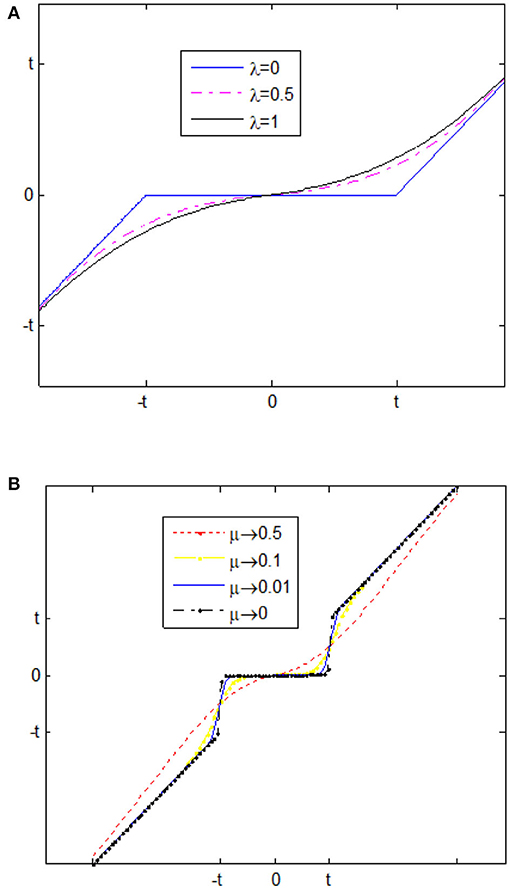
Figure 1. (A) is Zhang's improved soft threshold, and (B) is Zhang's improved hard threshold (Zhang, 2001).
To improve the efficiency and speed of Zhang's proposed TNN, Nasri and Nezamabadi-pour (2009) introduced a new thresholding neural network in the wavelet domain. Despite the Zhang's network which is space scale adaptive, this network is sub-band adaptive noise reduction (Nasri and Nezamabadi-pour, 2009). Similarly, the activation function is also non-linear and data-driven. The whole procedure of acquiring the de-noised image is mentioned above. In adaptive wavelet-based noise removal techniques, the threshold functions are chosen to be non-linear and adaptive. In this case, to improve the capability of the threshold functions, instead of setting the noisy components (below the threshold value) to zero by standard threshold functions, we can adjust and control these small coefficients using polynomial functions (Bhandari et al., 2016).
2.3. Optimized Based Image De-noising
Noise reduction using an optimized adaptive threshold function combined with nature-inspired optimization algorithms is introduced by Bhandari et al. (2016). The authors presented several optimization algorithms for satellite image de-noising. It was proved that image de-noising using TNN with steepest descent learning is time-consuming so that utilizing the optimization instead of LMS learning algorithm not only can improve the quality but also can increase the speed remarkably. Bhandari et al. (2016), utilized several different evolutionary for image de-noising. In their study, they used Differential Evolution (DE) (Storn and Price, 1997), Particle Swarm Optimization (PSO) (Poli et al., 2007), Wind Driven Optimization (WDO) (Bayraktar et al., 2011), Firefly Algorithm (FA) (Yang, 2010), Cuckoo Search (CS) Algorithm (Yang and Deb, 2009), and JADE algorithm (Zhang and Sanderson, 2009) as the optimizers to obtain the optimized thresholded wavelet coefficients in the process of getting the de-noised image. At the end, it was shown that using JADE algorithm performs better than other optimization algorithms in terms of PSNR values and qualitative results. By getting motivation from this paper, Golilarz et al. (2019b) attempted to improve the cited results by proposing a new technique. Then, it is proposed to apply another meta-heuristic optimizer (Harris Hawks Optimizer introduced by Heidari et al., 2019) instead of using JADE algorithm in the optimization process. The results showed the superiority of HHO based image de-noising method.
The main steps of obtaining the desired de-noised image using an optimization algorithm are as follows (Bhandari et al., 2016):
1. Apply a discrete wavelet transform on input noisy image (AWGN with zero mean and standard deviation of) to get noisy coefficients. Then, we can set the parameters of the optimization algorithm (number of iterations, number of solutions, scale parameters, etc.).
2. The noisy coefficients can be passed through an optimization algorithm consisting of the adaptive function so that the solution for the optimization algorithm can be acquired.
3. After computing it through threshold function, the best fitness values for each solution can be obtained (Bhandari et al., 2016).
4. After passing these parameters through adaptive function, we can get optimized thresholded wavelet coefficients.
5. Inverse discrete wavelet transform (IDWT) can be applied to these coefficients to get output de-noised image.
3. Adaptive Threshold for t = σn
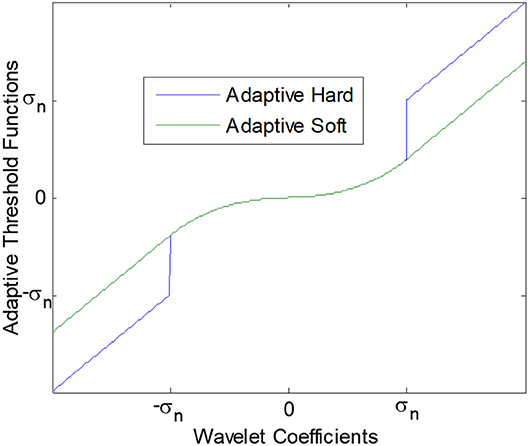
3.1. Adaptive Hard Threshold
This function consists of two main parts: in the interval [−σn, σn], which is an AGGD oriented function, and behind the interval which is the identity function. As can be seen in Figure 2, since it is discontinuous, we call it an adaptive hard threshold function. We call this function as “tune and keep” since it keeps large coefficients behind the interval and unlike the standard hard threshold function, we can tune the small noisy coefficients instead of setting them to zero. This function is formulated below.
where s(x)=σn(ex22σ2n-12), x is the coefficient, and t = σn is the threshold value.
3.2. Adaptive Soft Threshold
The main difference between this function and the adaptive hard threshold is its continuity. As Figure 2 adaptive threshold function which is given below. We call this function as “tune and shrink” since it shrinks large coefficients behind the interval by the threshold value but unlike the standard soft threshold function, it is possible to tune the small noisy coefficients instead of setting them to zero.
where, β(x) is the adaptive soft threshold, s(x)=σn(ex22σ2n-12), x is the coefficient, and t = σn is the threshold value.
4. Improved AGGD Threshold for t > σn
Golilarz et al., in 2019 proposed an adaptive generalized Gaussian distribution (AGGD) oriented threshold for image de-noising (Golilarz et al., 2019a). This function is data-driven, non-linear, and also flexible and fitted to any kind of images so that it can be shaped in various images. These are the most important characteristics of this function. It is proved that in the interval [−t, t], this function tunes the non-important constituents using an adaptive GGD threshold function instead of setting these coefficients to zero. Admittedly, this characteristic enhances the capability and flexibility of this function. The AGGD threshold function is given as (Golilarz et al., 2019a):
where, s(x)=σn(ex22σn2-12), x is the coefficient, σn is the robust median estimator and t is the threshold value. This value is the inter section of x and s(x).
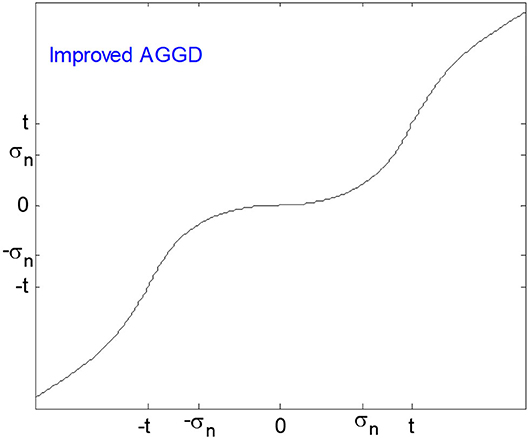
Golilarz et al. (2019b) improved the capability, quality, and speed of their former method (AGGD) by proposing an improved version of AGGD threshold function which results in an enhancement in both qualitative and quantitative results. This function is completely non-linear and differentiable by an adaptive generalized Gaussian distribution function in the interval [−t, t], and another non-linear function behind the interval. Obviously, the whole coefficients can be tuned using non-linear and data-driven functions. Like the AGGD threshold function, the threshold value can be obtained without using any optimization and steepest descent learning algorithms. Figure 3 shows improved AGGD function. This function is formulated as follows:
where, μ(x) is the improved AGGD threshold, s(x)=σn(ex22σ2n-12), x is the coefficient, σn is the robust median estimator and t is the threshold value.
5. Experimental Results
In this part we used four experiments to show the superiority of using improved AGGD method both qualitatively and quantitatively. In this research we used Peak Signal to Noise Ratio(PSNR) and MSE to evaluate the performance analysis of different de-noising techniques. MSE and PSNR (dB) can be obtained as follows:
where d is the original image, ˆd is the de-noised image and M, N are the size of image (Bhandari et al., 2016).
where MSE is the mean square error.
In this part, we analyzed the use of wavelet based noise reduction with adaptive GGD threshold to improve the visual quality of MRI brain images in clinical researches and investigation which may be affected to unwanted noises during receiving and transmitting procedures. Particularly, we applied improved AGGD threshold on brain images in the wavelet domain to evaluate the effectiveness and efficiency of the proposed method in de-noising the medical images in comparison with other techniques.
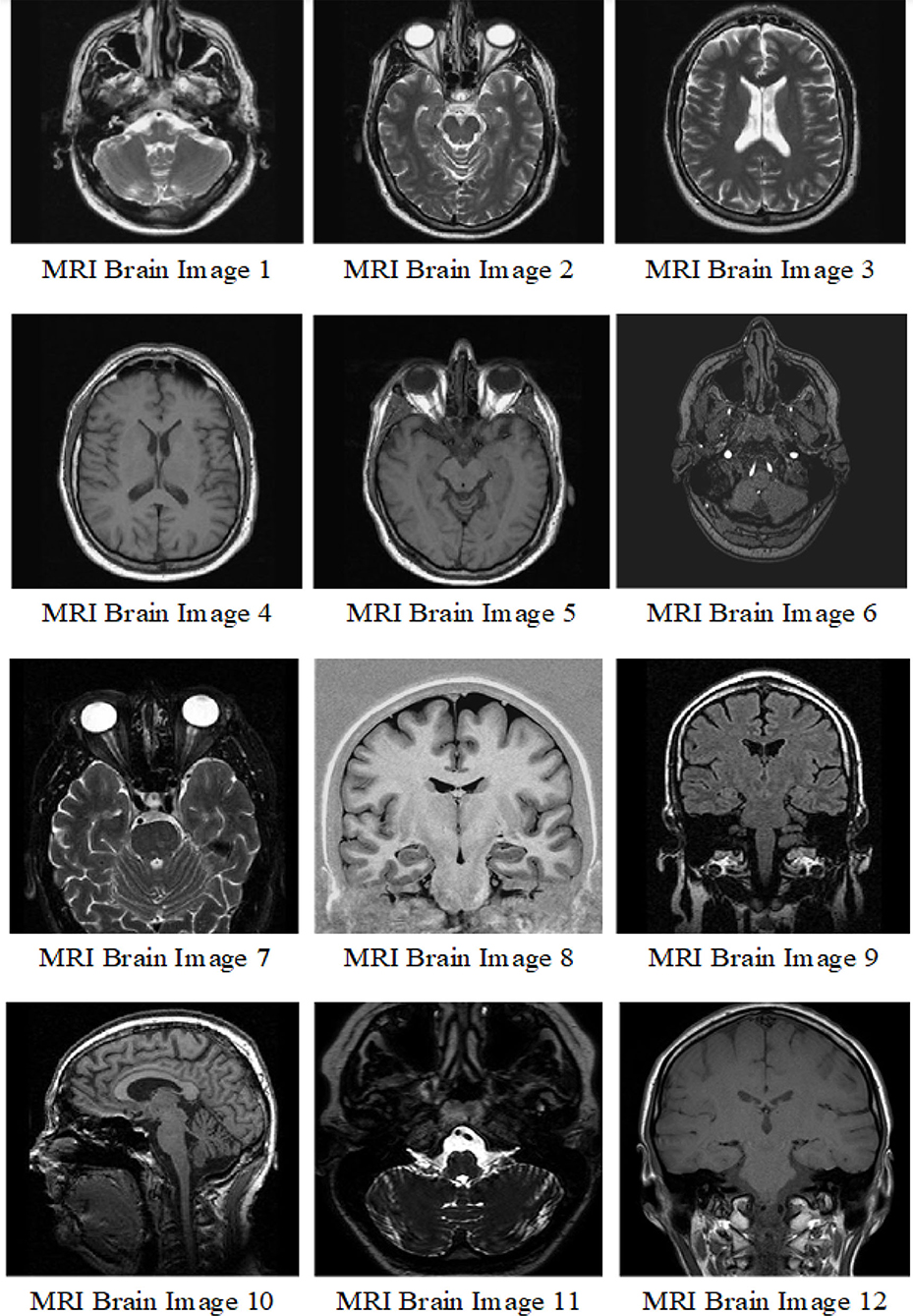
Here we utilized 12 MRI brain images which are shown in Figure 4. The dataset is available in Dataset (2020). The images are affected by additive white Gaussian noise AWGN with zero mean and different variance values. In these experiments we utilized Db4 wavelet with one level of decomposition. For HHO algorithm, the parameters are same with those in the original work of HHO (Heidari et al., 2019).
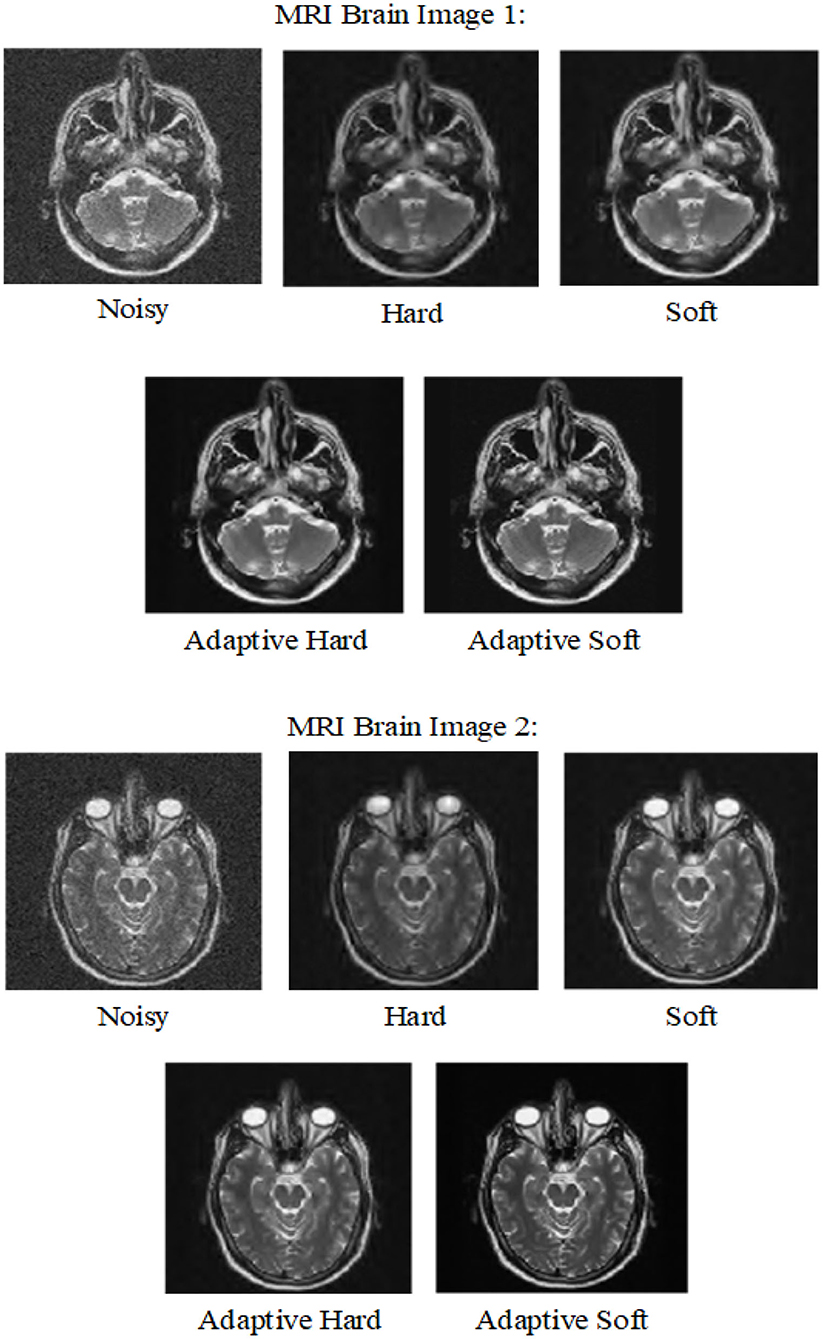
In the first experiment, as can be seen from Tables 1, 2, we compare adaptive soft, adaptive hard with standard soft and standard hard threshold functions in terms of PSNR and MSE. In this experiment we used MRI images 1–2. In addition in Figure 5, we can see the visual comparison of these methods. It is obvious that adaptive soft threshold performs well comparing with adaptive hard, standard soft, and standard hard threshold function for image de-noising.
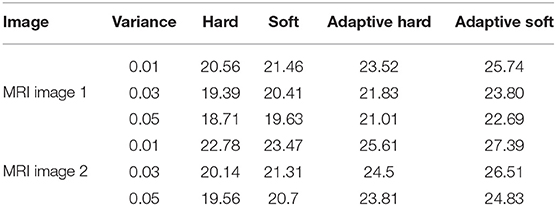
Table 1. Performance analysis of adaptive and standard threshold for MRI image de-noising in terms of PSNR values.
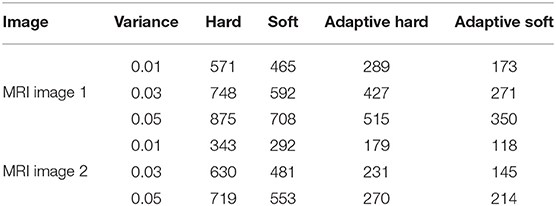
Table 2. Performance analysis of adaptive and standard threshold for MRI image de-noising in terms of MSE.
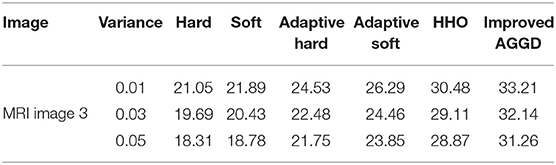
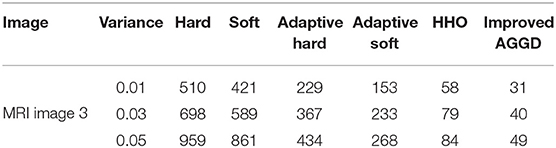
In the second experiment, in Tables 3, 4, we compared improved AGGD with de-noising using Harris Hawks Optimization (HHO) based noise reduction (Golilarz et al., 2019b), adaptive soft, adaptive hard, standard soft, and standard hard thresholds. Note that we used MRI Brain Image 3. Additionally, in Figure 6 we compared these techniques visually. It is obvious that improved AGGD performs better than other de-noising techniques.
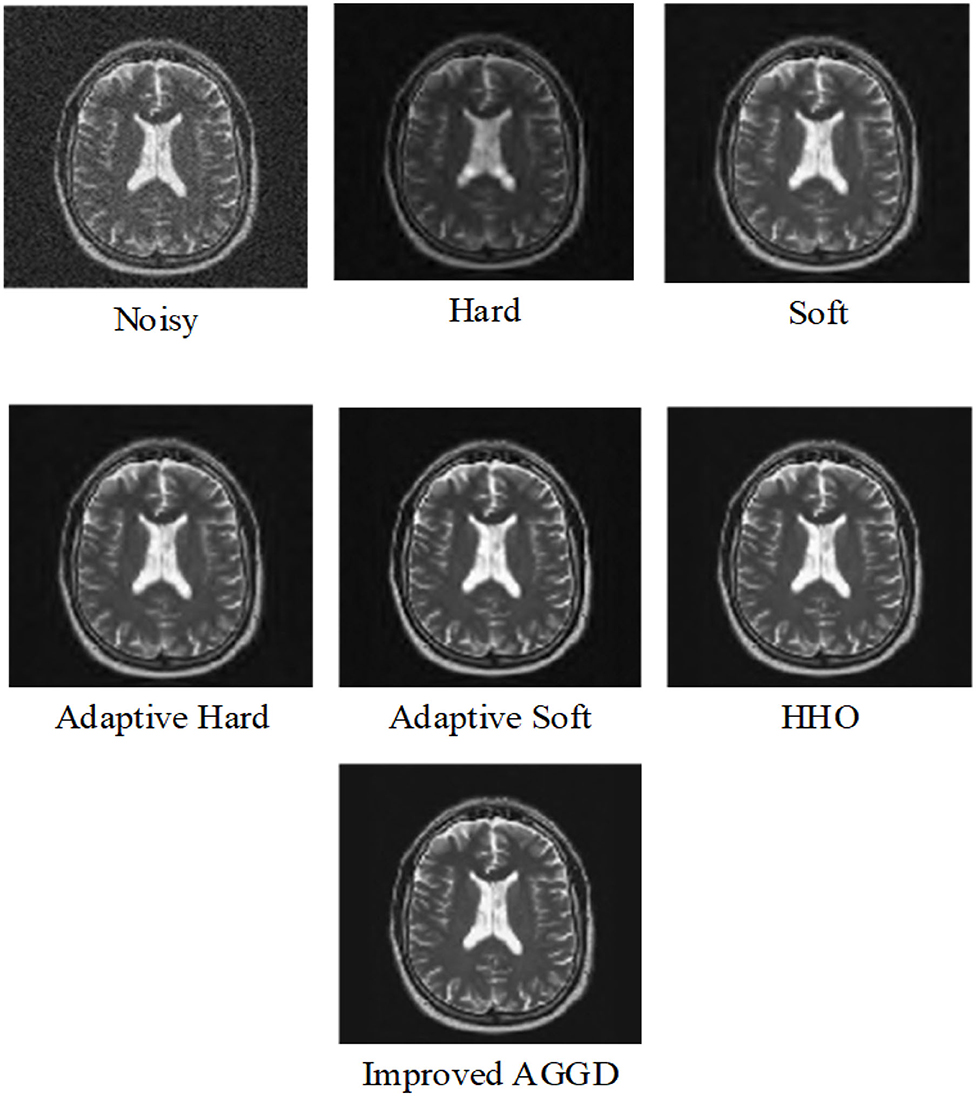
Figure 6. Comparison of visual inspection between different noise reduction methods for MRI Brain Image 3 for variance 0.03.
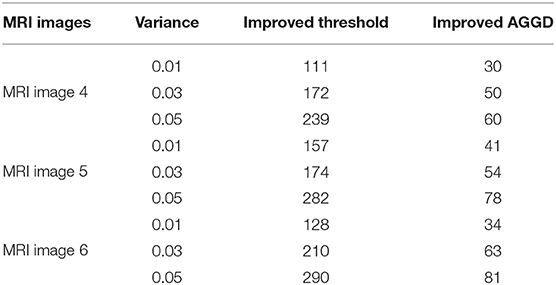
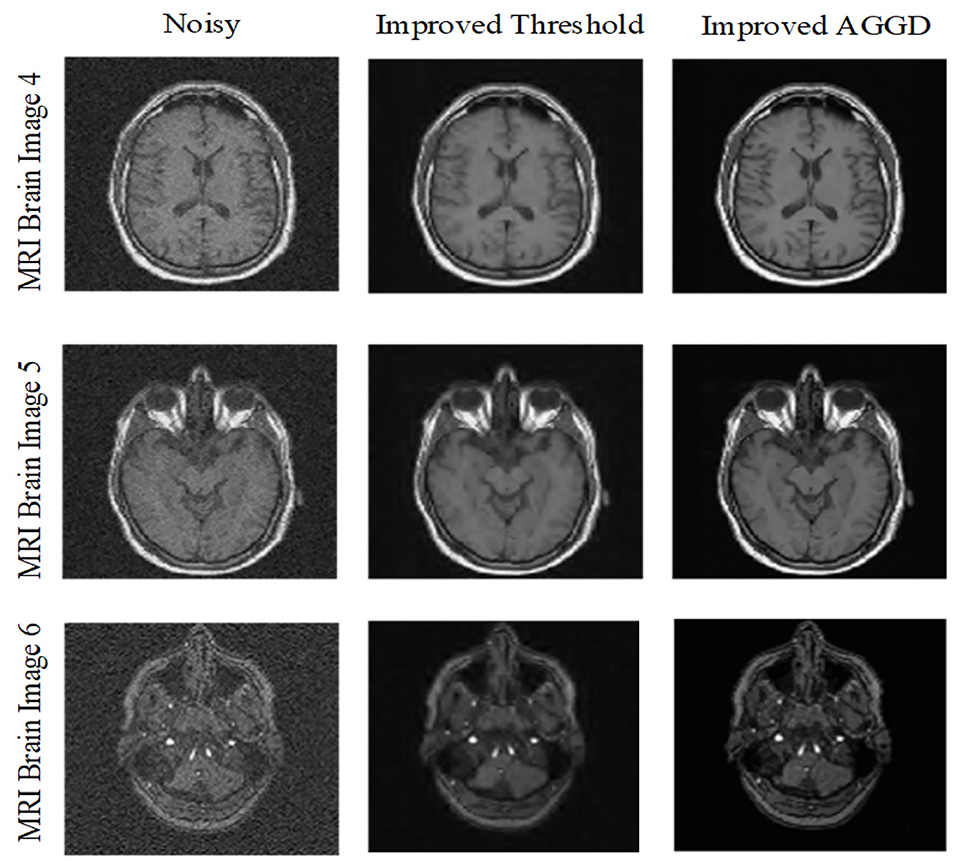
In the third experiment we compared proposed improved AGGD with improved threshold (Zhang et al., 2019). Here we used MRI Brain Images 4–6. As can be seen from Tables 5, 6, improved AGGD performs better than improved threshold function for MRI brain image de-noising. Moreover, Figure 7 shows the superiority of the proposed technique over improved threshold function qualitatively.
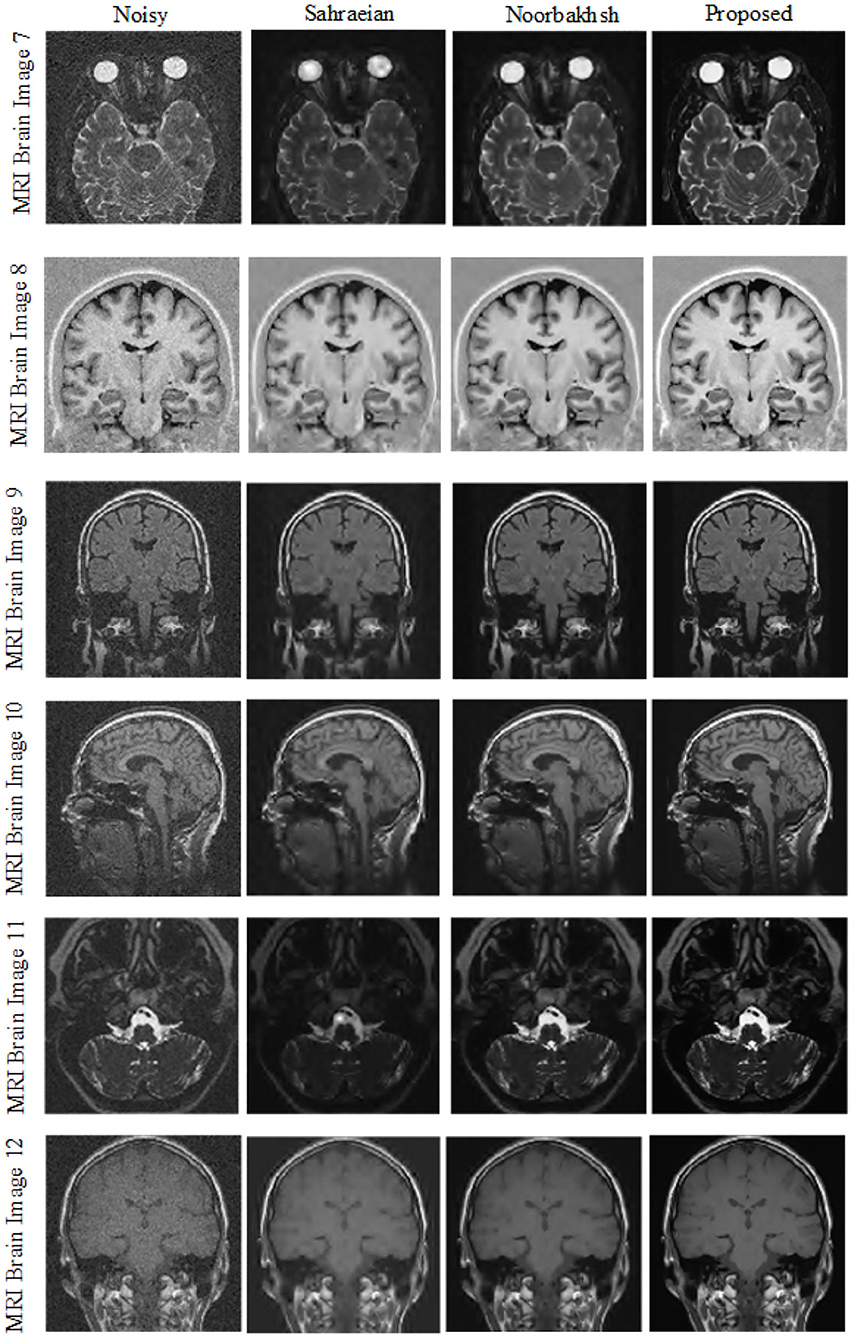
In the fourth experiment we compared the proposed method with Sahraeian et al. (2007) and Noorbakhsh's technique (Golilarz et al., 2018) as well. Here we used MRI Brain Images 7–12. From Table 7 we can conclude that improved AGGD performs better than Sahraeian and Noorbakhsh's proposed method for MRI brain image de-noising. Additionally, we can see this comparison visually in Figure 8.

Table 7. Performance analysis of proposed method compared with Sahraeian and Noorbakhsh's technique for MRI brain image de-noising in terms of PSNR values.
The improved AGGD based image de-noising is presented to enhance both quality and the processing time. In the last experiment, we compared the processing time among various image de-noising methods. The computational cost of improved AGGD function is cheaper than improved threshold, HHO, adaptive soft, adaptive hard, standard soft and standard hard threshold functions. The speed and computational time among different noise suppression techniques has been compared in Table 8 for MRI brain Image 1 for variance 0.01. For HHO, the time is the average of 10 runs. For all the implementations and experimental results, we used Matlab programming language on a computer with Intel core i7 and 16 GB RAM.
6. Conclusion
In this study, a new method for wavelet-based MRI image de-noising is presented. Firstly, adaptive soft and hard threshold functions are introduced to improve the performance of standard threshold functions in the wavelet domain. Secondly, we used the newly emerged improved adaptive generalized Gaussian distributed oriented threshold function (improved AGGD) on the MRI images to show that, this data driven and image dependent threshold function performs well comparing with adaptive soft and hard threshold functions. Recently, image de-noising in the wavelet domain attracts lots of attentions in image and signal processing. Previous TNN and optimized based noise removal methods have good results but still the quality of an image needs to be enhanced and improved. TNN and optimized based noise reduction methods, require to utilize Least-mean-square (LMS) learning and optimization algorithms, respectively for acquiring the value of the optimum threshold and the parameters of the threshold functions which this process was time consuming. The improved AGGD based image de-noising is presented to solve these drawbacks. The computational cost of improved AGGD method is quite cheaper than the above mentioned techniques because we are in no use of LMS learning and optimization algorithms. This approach has good results in terms of PSNR values. The experimental analysis proves the superiority of improved AGGD threshold over adaptive threshold, standard threshold, improved wavelet threshold, and the optimized based noise reduction methods. For the future work, we will extend this work to deal with other forms of noise like impulse noise and non-Gaussian noise as well.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.mr-tip.com/serv1.php?type=db1&dbs=Brain%20MRI.
Author Contributions
NA, HG, RK, LA, YF, and CL conceived and designed the research and wrote the paper. HG, LA, YF, and CL provided the data. HG supervised the study. NA, LA, YF, and CL analyzed the data. HG, RK, LA, YF, and CL revised the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This research was supported by the National Natural Science Foundation of China under Grant No. 61673085.
Conflict of Interest
CL was employed by The 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang, China.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Achim, A., Bezerianos, A., and Tsakalides, P. (2001). Novel Bayesian multiscale method for speckle removal in medical ultrasound images. IEEE Trans. Med. Imaging 20, 772–783. doi: 10.1109/42.938245
Achim, A., Tsakalides, P., and Bezerianos, A. (2003). SAR image denoising via Bayesian wavelet shrinkage based on heavy-tailed modeling. IEEE Trans. Geosci. Rem. Sens. 41, 1773–1784. doi: 10.1109/TGRS.2003.813488
Awad, A. S. (2011). Standard deviation for obtaining the optimal direction in the removal of impulse noise. IEEE Signal Process. Lett. 18, 407–410. doi: 10.1109/LSP.2011.2154330
Bayraktar, Z., Turpin, J. P., and Werner, D. H. (2011). Nature-inspired optimization of high-impedance metasurfaces with ultrasmall interwoven unit cells. IEEE Antennas Wireless Propagat. Lett. 10, 1563–1566. doi: 10.1109/LAWP.2011.2178224
Bhandari, A. K., Kumar, D., Kumar, A., and Singh, G. K. (2016). Optimal sub-band adaptive thresholding based edge preserved satellite image denoising using adaptive differential evolution algorithm. Neurocomputing 174, 698–721. doi: 10.1016/j.neucom.2015.09.079
Chan, R. H., Ho, C. W., and Nikolova, M. (2005). Salt-and-pepper noise removal by median-type noise detectors and detail-preserving regularization. IEEE Trans. Image Process. 14, 1479–1485. doi: 10.1109/TIP.2005.852196
Chang, S. G., Yu, B., and Vetterli, M. (2000). Spatially adaptive wavelet thresholding with context modeling for image denoising. IEEE Trans. Image Process. 9, 1522–1531. doi: 10.1109/83.862630
Chen, C. L. P., Liu, L., Chen, L., Tang, Y. Y., and Zhou, Y. (2015). Weighted couple sparse representation with classified regularization for impulse noise removal. IEEE Trans. Image Process. 24, 4014–4026. doi: 10.1109/TIP.2015.2456432
Coifman, R. R., and Donoho, D. L. (1995). Translation-Invariant De-Noising, (New York, NY: Springer).
Dataset (2020). Brain MRI. Available online at: https://www.mr-tip.com/serv1.php?type=db1&dbs=brainmri
De Decker, A., François, D., Verleysen, M., and Lee, J. A. (2011). Mode estimation in high-dimensional spaces with flat-top kernels: application to image denoising. Neurocomputing 74, 1402–1410. doi: 10.1016/j.neucom.2010.12.013
Dong, Y., and Xu, S. (2007). A new directional weighted median filter for removal of random-valued impulse noise. IEEE Signal Process. Lett. 14, 193–196. doi: 10.1109/LSP.2006.884014
Donoho, D. L., and Johnstone, I. M. (1995). Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 90, 1200–1224. doi: 10.1080/01621459.1995.10476626
Donoho, D. L., and Johnstone, J. M. (1994). Ideal spatial adaptation by wavelet shrinkage. Biometrika 81, 425–455. doi: 10.1093/biomet/81.3.425
Elad, M., and Aharon, M. (2006). Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 15, 3736–3745. doi: 10.1109/TIP.2006.881969
Figueiredo, M. A., and Nowak, R. D. (2001). Wavelet-based image estimation: an empirical Bayes approach using Jeffreys' noninformative prior. IEEE Trans. Image Process. 10, 1322–1331. doi: 10.1109/83.941856
Garnett, R., Huegerich, T., Chui, C., and He, W. (2005). A universal noise removal algorithm with an impulse detector. IEEE Trans. Image Process. 14, 1747–1754. doi: 10.1109/TIP.2005.857261
Golilarz, N. A., and Demirel, H. (2017). Thresholding neural network (TNN) based noise reduction with a new improved thresholding function. CRPASE 3, 81–84.
Golilarz, N. A., and Demirel, H. (2018a). “Image de-noising using un-decimated wavelet transform (UWT) with soft thresholding technique,” in Proceedings–9th International Conference on Computational Intelligence and Communication Networks, CICN 2017 (Girne). doi: 10.1109/CICN.2017.8319347
Golilarz, N. A., and Demirel, H. (2018b). “Thresholding neural network (TNN) with smooth sigmoid based shrinkage (SSBS) function for image de-noising,” in Proceedings–9th International Conference on Computational Intelligence and Communication Networks, CICN 2017 (Girne). doi: 10.1109/CICN.2017.8319358
Golilarz, N. A., Demirel, H., and Gao, H. (2019a). Adaptive generalized gaussian distribution oriented thresholding function for image de-noising. Int. J. Adv. Comput. Sci. Appl. 10, 10–15. doi: 10.14569/IJACSA.2019.0100202
Golilarz, N. A., Gao, H., Ali, W., and Shahid, M. (2018). “Hyper-spectral remote sensing image de-noising with three dimensional wavelet transform utilizing smooth nonlinear soft thresholding function,” in 2018 15th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP) (Chengdu: IEEE), 142–146. doi: 10.1109/ICCWAMTIP.2018.8632597
Golilarz, N. A., Gao, H., and Demirel, H. (2019b). Satellite image de-noising with Harris Hawks meta heuristic optimization algorithm and improved adaptive generalized gaussian distribution threshold function. IEEE Access 7, 57459–57468. doi: 10.1109/ACCESS.2019.2914101
Golilarz, N. A., Robert, N., Addeh, J., and Salehpour, A. (2017). Translation invariant wavelet based noise reduction using a new smooth non-linear improved thresholding function. CRPASE 3, 104–108.
Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., and Chen, H. (2019). Harris Hawks optimization: algorithm and applications. Fut. Gen. Comput. Syst. 97, 849–872. doi: 10.1016/j.future.2019.02.028
Li, D., Wang, Y., and Fang, T. (2011). “Wavelet image denoising algorithm based on local adaptive wiener filtering,” in Proceedings 2011 International Conference on Mechatronic Science, Electric Engineering and Computer, MEC 2011, (Jilin).
Lin, C. H., Tsai, J. S., and Chiu, C. T. (2010). “Switching bilateral filter with a texture/noise detector for universal noise removal,” in ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing—Proceedings (Dallas, TX). doi: 10.1109/ICASSP.2010.5495475
Lu, X., Yuan, Y., and Yan, P. (2013). Sparse coding for image denoising using spike and slab prior. Neurocomputing 106, 12–20. doi: 10.1016/j.neucom.2012.09.014
Miura, S., Tsuji, H., and Kimura, T. (2013). “Randomly valued impulse noise removal using Gaussian curvature of image surface,” in ISPACS 2013–2013 International Symposium on Intelligent Signal Processing and Communication Systems (Naha). doi: 10.1109/ISPACS.2013.6704563
Nasri, M., and Nezamabadi-pour, H. (2009). Image denoising in the wavelet domain using a new adaptive thresholding function. Neurocomputing 72, 1012–1025. doi: 10.1016/j.neucom.2008.04.016
Pizurica, A., Philips, W., Lemahieu, I., and Acheroy, M. (2002). A joint inter-and intrascale statistical model for bayesian wavelet based image denoising. IEEE Trans. Image Process. 11, 545–557. doi: 10.1109/TIP.2002.1006401
Poli, R., Kennedy, J., and Blackwell, T. (2007). Particle swarm optimization: an overview. Swarm Intell. 1, 33–57. doi: 10.1007/s11721-007-0002-0
Portilla, J., Strela, V., Wainwright, M. J., and Simoncelli, E. P. (2003). Image denoising using scale mixtures of gaussians in the wavelet domain. IEEE Trans. Image Process. 12, 1338–1351. doi: 10.1109/TIP.2003.818640
Qian, Y. (2018). “Image denoising algorithm based on improved wavelet threshold function and median filter,” in 2018 IEEE 18th International Conference on Communication Technology (ICCT) (Chongqing: IEEE), 1197–1202. doi: 10.1109/ICCT.2018.8599921
Sahraeian, S. M., Marvasti, F., and Sadati, N. (2007). “Wavelet image denoising based on improved thresholding neural network and cycle spinning,” in ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing—Proceedings (Honolulu, HI). doi: 10.1109/ICASSP.2007.365975
Şendur, L., and Selesnick, I. W. (2002). Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Trans. Signal Process. 50, 2744–2756. doi: 10.1109/ICASSP.2002.1005979
Starck, J. L., Candès, E. J., and Donoho, D. L. (2002). The curvelet transform for image denoising. IEEE Trans. Image Process. 11, 670–684. doi: 10.1109/TIP.2002.1014998
Storn, R., and Price, K. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11, 341–359. doi: 10.1023/A:1008202821328
Sveinsson, J. R., and Benediktsson, J. A. (2003). Almost translation invariant wavelet transformations for speckle reduction of SAR images. IEEE Trans. Geosci. Rem. Sens. 41, 2404–2408. doi: 10.1109/TGRS.2003.817844
Yang, X.-S. (2010). “Firefly algorithm, levy flights and global optimization,” in Research and Development in Intelligent Systems XXVI, eds M. Bramer, R. Ellis, and M. Petridis (London: Springer), 209–218. doi: 10.1007/978-1-84882-983-1_15
Yang, X.-S., and Deb, S. (2009). “Cuckoo search via lévy flights,” in 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC) (Coimbatore: IEEE), 210–214. doi: 10.1109/NABIC.2009.5393690
Yin, J. L., Chen, B. H., and Li, Y. (2018). Highly accurate image reconstruction for multimodal noise suppression using semisupervised learning on big data. IEEE Trans. Multimed. 20, 3045–3056. doi: 10.1109/TMM.2018.2820910
Yuan, G., and Ghanem, B. (2015). “l0tv: a new method for image restoration in the presence of impulse noise,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Boston, MA) 5369–5377.
Zhang, J., and Sanderson, A. C. (2009). JADE: adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 13, 945–958. doi: 10.1109/TEVC.2009.2014613
Zhang, X. P. (2001). Thresholding neural network for adaptive noise reduction. IEEE Trans. Neural Netw. 12, 567–584. doi: 10.1109/72.925559
Keywords: wavelet, MRI image de-noising, AGGD, adaptive threshold, PSNR
Citation: Amiri Golilarz N, Gao H, Kumar R, Ali L, Fu Y and Li C (2020) Adaptive Wavelet Based MRI Brain Image De-noising. Front. Neurosci. 14:728. doi: 10.3389/fnins.2020.00728
Received: 28 March 2020; Accepted: 18 June 2020;
Published: 22 July 2020.
Edited by:
John Ashburner, University College London, United KingdomReviewed by:
Zhifang Pan, Wenzhou Medical University, ChinaGulsher Ali Baloch, Sukkur IBA University, Pakistan
Muhammad Aksam, COMSATS University Islamabad, Lahore Campus, Pakistan
Copyright © 2020 Amiri Golilarz, Gao, Kumar, Ali, Fu and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Noorbakhsh Amiri Golilarz, noorbakhsh.amiri@std.uestc.edu.cn; Hui Gao, huigao@uestc.edu.cn
 Noorbakhsh Amiri Golilarz
Noorbakhsh Amiri Golilarz