- 1School of Science, Xuchang University, Xuchang, Henan, China
- 2School of Mathematics and Statistics, Northwestern Polytechnical University, Xi’an, Shaanxi, China
- 3School of Mathematics and Statistics, North China University of Water Resources and Electric Power, Zhengzhou, Henan, China
This paper investigates the Hamiltonian energy of a modified Hindmarsh–Rose (HR) model to observe its effect on short-term memory. A Hamiltonian energy function and its variable function are given in the reduced system with a single node according to Helmholtz’s theorem. We consider the role of the coupling strength and the links between neurons in the pattern formation to show that the coupling and cooperative neurons are necessary for generating the fire or a clear short-term memory when all the neurons are in sync. Then, we consider the effect of the degree and external stimulus from other neurons on the emergence and disappearance of short-term memory, which illustrates that generating short-term memory requires much energy, and the coupling strength could further reduce energy consumption. Finally, the dynamical mechanisms of the generation of short-term memory are concluded.
1 Introduction
Short-term memory is a primary cognitive function of the brain. The transitions between the spontaneous and persistent states could lead to the emergence and disappearance of short-term memory in a bistable system (Amit and Brunel, 1997). Continuous neural activity without external inputs was deemed an expression of short-term memory (Wang, 2001). A phenomenological model of spatial working memory was developed to examine the dynamical interactions of multiple feedback mechanisms (Carter and Wang, 2007). A growing body of evidence suggests memories may be kept through the mutual effect of persistent neural activity and activity-silent dynamics (Stokes, 2015; Barbosa et al., 2020). Gaussian noise was treated as an essential factor in neuronal activity and its toggle switch (memory maintenance) (Zheng et al., 2020b). Memory maintenance through persistent neural activity and a synaptic mechanism was compared in mice and two types of artificial neural networks to show their differences (Hu et al., 2021). Then, computational modeling was constructed to prove how the circuits and networks affect working memory, which provides a novel theory for memory maintenance (Ghazizadeh and Ching, 2020). In addition, the encoding style of the input information of the short-term memory was investigated to illustrate the dynamical mechanisms of short-term memory (Ichikawa and Kaneko, 2021; Jones and Ching, 2022; Zhou et al., 2023). Hamilton energy, representing the utilization of energy (actual energy in the generation of short-term memory), should be considered to illustrate the dynamic mechanism of the generation of short-term memory.
Hindmarsh–Rose (HR) model (1) (x is the membrane potential, y is the recovery variable of the fast current of K+ or Na+, and z is the adaptation variable of the slow current of Ca+ or other ions) was proposed to show the membrane potential of neuronal activity (Hindmarsh and Rose, 1982), which has rich dynamical behaviors (Wang et al. 2021a; Wang et al. 2021b; Wang et al. 2022).
The synchronization and bifurcation (Song and Xu, 2013; Liebovitch et al., 2011; Kumar et al., 2016; Zheng et al. 2020a; Zheng et al. 2024; Zheng et al. 2023) of the HR model were often studied to demonstrate the dynamical mechanism of chaotic bursting or spikes (Shi and Wang, 2012; Wu et al., 2016; You, 2023a). The interplay between neurons was analyzed to present the effect of the parameters and coupling strength on the appropriate functioning of the system (Lepek and Fronczak, 2018; Rajagopal et al., 2019; You, 2023b). Energy is necessary for neuron activity (Attwell and Laughlin, 2001). The Hamiltonian energy function is a vital tool to evaluate energy consumption when neurons are active (Torrealdea et al., 2006). The average energy consumption of the HR model was given to display the energy consumption ratio in different situations, which could help optimize energy use (Torrealdea et al., 2009; Song et al., 2015; Usha and Subha, 2019). The Hamilton energy balance of different functional neurons was discussed through the coupling strength, which contributes to designing functional assistive devices (Zhang et al., 2022; Yu et al., 2023). Although the HR model could explain the generation of short-term memory (Zheng et al., 2022), the utilization of energy should be further stated in short-term memory.
Short-term memory results from neuronal activity coming with a change in energy, and a physical neuron circuit plays a vital role in the synergistic effect of neurons and the generation of short-term memory. In this paper, the pattern formation of a modified HR model is investigated to find the dynamical mechanism of how the coupling strength and links (degree) affect the generation of short-term memory. The Hamiltonian energy function is derived in the HR model with a single node, which means the energy consumption varies at different states of neuronal activity. Then, the degree and stimuli from other neurons are studied through bifurcation, which means the energy is necessary to generate short-term memory. Finally, the related dynamical and biological mechanisms are obtained.
2 Model description
As the membrane potential of neurons is often coupled with others, the following network-organized HR model is introduced:
where xi is the membrane potential, I represents the ith neuron and i = 1, … , n, yi is the recovery variable of the fast current of K+ or Na+, and zi is the adaptation variable of the slow current of Ca+ or other ions. D1 is the coupling strength between neurons. Lij(t) = Aij – δijki, where Aij is the adjacent matrix and ki is the degree of the ith node.
In order to obtain the Hamiltonian energy function of system (2), we consider a simplified model with a single node through the mean-field approach (McCullen and Wagenknecht, 2016). The reduced system is
where (x0, y0, z0) (Zheng et al., 2022) is the equilibrium point of system (2) without a network, and x0 makes Iext = f(x) = −c + dx2 + ax3 − bx2 + s (x − xr) + Iext + d1ki (x0 − xi) hold. In addition, x0 is the external stimulus from other neurons.
In this paper, we mainly investigate the dynamical behaviors of system (3) and its Hamiltonian equation. According to Helmholtz’s theorem (Donald and Rose, 1986), an autonomous ordinary differential equation
where G(X) is a skew-symmetric matrix in the Hamiltonian system. If G(X) is not a skew-symmetric matrix in a generalized Hamiltonian system, G(X) can be divided into two parts G(X) = G1(X) + G2(X): a skew-symmetric matrix G1(X) and a symmetric matrix G2(X) (Sarasola et al., 2004). H(X) is an energy function. Then, we have
For the network-organized HR model (3), it can be written as (Torrealdea et al., 2006; Torrealdea et al., 2009; Song et al., 2015; Usha and Subha, 2019)
where
Furthermore, we obtain the Hamiltonian energy function as (Zhang et al., 2022)
Namely,
where a general solution can be expressed as
and
3 Numerical results and discussion
In this section, the finite difference method is applied to find numerical solutions for the network-organized HR model (3) with time step dt = 0.01. These parameters a = 1, b = 3, c = 1, d = 5, r = 0.01, s = 4 are set (Zheng et al., 2022). The small-world network is constructed with W (n, K, p) (the number of node n, nearest neighbor K, and reconnection probability p), which can be found can be found at https://github.com/zhengqianqian35/network-code. We give the concept of the average Hamiltonian energy for time and nodes:
where the integration period is set at T = 5,000 time units. In order to exclude the influence of initial conditions, t0 is the starting time of the cycle after the system tends to a stable state. In addition, we assume H = H (xi, yi, zi)/100. From Figure 1, only one real equilibrium point (x0, y0, z0) exists in system (1) when a = 1, b = 3, c = 1, d = 5, r = 0.01, s = 4, which guarantees the uniqueness of system (3).
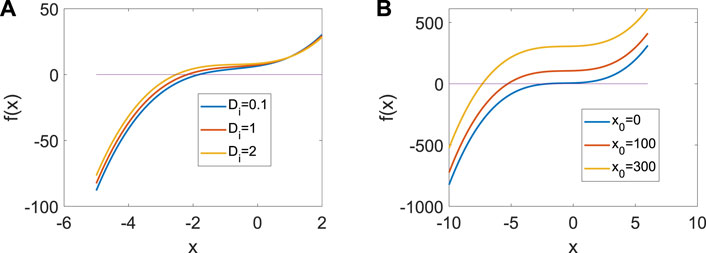
Figure 1. Distribution of the equilibrium point in system (3) when a = | 1, b = | 3, c = | 1, d = | 5, r = | 0.01, s = | 4. (A) Distribution of the equilibrium point when x0 | = | 1. (B) Distribution of the equilibrium point when Di = | 1.
In general, the generation of neural function results from the collaboration of multiple neurons. Therefore, we consider the strength d1 of the coupling between neurons and the number of links K. First, a small-world network with W (100, 8, 0.01) is given. The pattern formation is chaotic (Figure 2A) when the strength d = 0.01 is weak, which means the nervous system does not work. The pattern formation starts to become clear and tends to sync with the increase of d1 (Figure 2b,c). Ultimately, the pattern formation becomes synchronized; namely, all the neurons become completely phase synchronized (Figure 2D). The short-term memory needs to be clarified when d1 is weak. Only when all the neurons work perfectly together is a clear short-term memory formed (Figure 2), which is also the mechanism by which adequate short-term memory is produced.
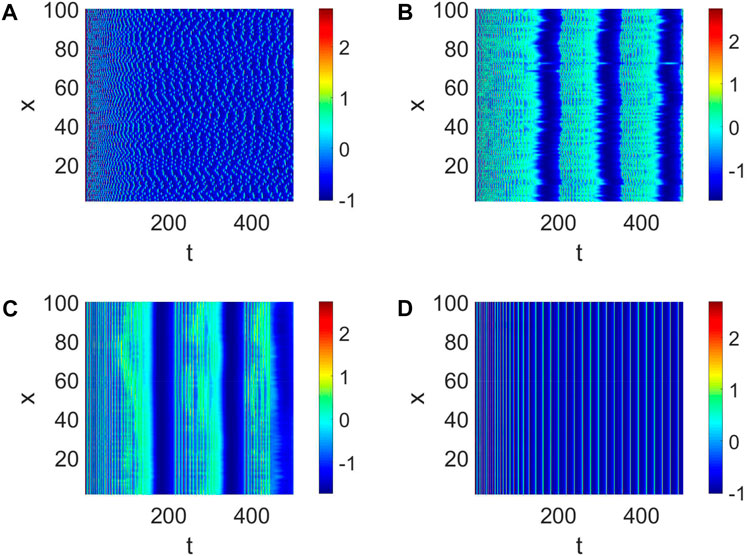
Figure 2. Pattern formation when Iext = | 4 and W (100, | 8, | 0.01). (A) Pattern formation when d1 | = | 0.01. (B) Pattern formation when d1 | = | 0.05. (C) Pattern formation when d1 | = | 0.3. (D) Pattern formation when d1 | = | 1.
Then, the number of cooperative neurons will be considered to generate short-term memory. The links between neurons can be treated as the number of collaborative neurons in our analysis, which could be measured by K. When K is small, the pattern formation is chaotic, and every neuron is relatively independent (Figure 3A). This condition is not suitable for the generation of short-term memory. When K = 2, the pattern formation shows some neurons are in sync (Figure 3B); namely, multiple short-term memories are produced simultaneously. In this case, short-term memory is often fuzzy. The short-term memory gradually becomes clear when K becomes large (Figure 3C). Eventually, multiple neurons work together to form a clear short-term memory when all the neurons are in sync (Figure 3D).
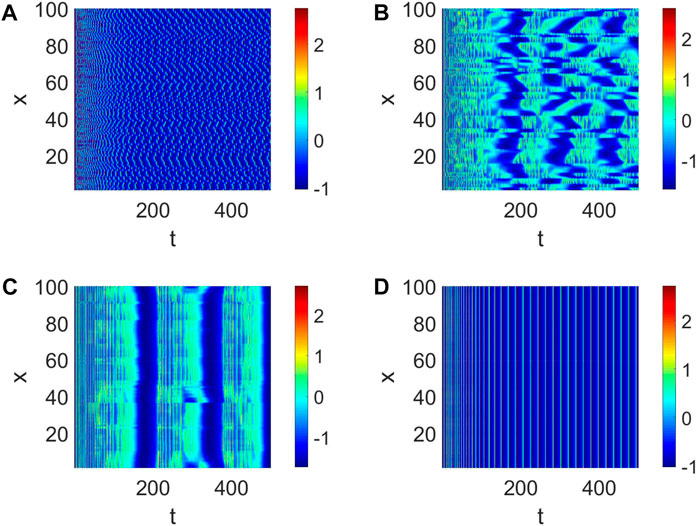
Figure 3. Pattern formation when Iext = | 4, d1 | = | 1 and W (100, K, | 0.01). (A) Pattern formation when K = | 0. (B) Pattern formation when K = | 2. (C) Pattern formation when K = | 4. (D) Pattern formation when K = | 6.
Finally, it is found that the link probability does not work because p cannot change the number of cooperative neurons and the coupling strength.
3.1 Hamiltonian energy with external stimulus
System (3) can be written as
where Di = d1ki (d1 = 0.01), and the effect of x0 is similar to Iext when Di is a constant. Iext and the coupling strength play a vital role in the electrical activity, which is the basis of the generation of fire. Therefore, we consider the role of Iext and Di in the Hamiltonian energy, change in Hamiltonian energy, and membrane potential when x0 = 1.
It is well known that the coupling between neurons is necessary for generating fire or short-term memory (Figure 2). Because only the ith neuron evolutes with system (4), and other neurons are fixed at (x0, y0, z0), Di can also be regarded as the size of the network degree. When the coupling strength is small, or the number of links is few, no spike or memory is generated; namely, the neurons are resting (Figure 4A). The membrane potential began to change periodically with the increase in Di, which means the emergence and disappearance of short-term memory (Figure 4B). Meanwhile, the Hamiltonian energy and change in Hamiltonian energy change with the membrane potential, which means the generation of the short-term memory takes more energy. However, short-term memory is the result of multiple neurons working together. If one neuron is very tightly connected to other neurons, all the neurons will tend to be in one state because other neurons are fixed at (x0, y0, z0). Namely, system (4) of a neuron will tend to a stable state when Di is larger (Figure 4C).
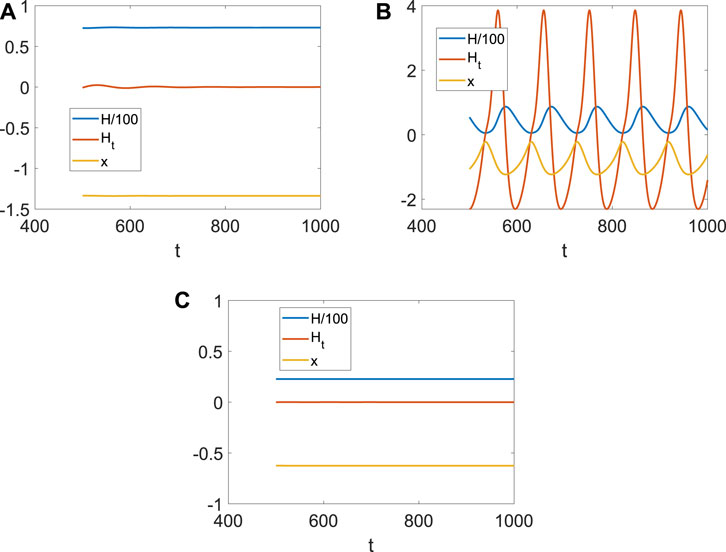
Figure 4. Hamiltonian energy, change in Hamiltonian energy, and membrane potential when Iext = | 1, x0 | = | 1. (A) Evolution when Di = | 0.1. (B) Evolution when Di = | 1. (C) Evolution when Di = | 1.5.
Next, we show the continuous changes in x, H1, H2 with Di (Figure 5). From Figure 5A, the bifurcation occurs with the increase in Di. The average Hamiltonian energy decreases gradually at the beginning because the utilization of energy is relatively low when the neuron is in a resting state (Figure 5B). When the membrane potential is periodic, the average Hamiltonian energy will be a sudden increase (Figure 5B). Meanwhile, the rise of coupling strength also reduces the consumption of Hamiltonian energy, which is why the average Hamiltonian energy decreases with Di (Figure 5B). It is found that the max–min value of Hamiltonian energy (Figure 5C) and its variation (Figure 5D) is significantly associated with the bifurcation, which is essential to show the relationship between the consumption of energy and the membrane potential (the generation of short-term memory). In a word, generating short-term memory will take a lot of energy, and the coupling strength could further reduce energy consumption.
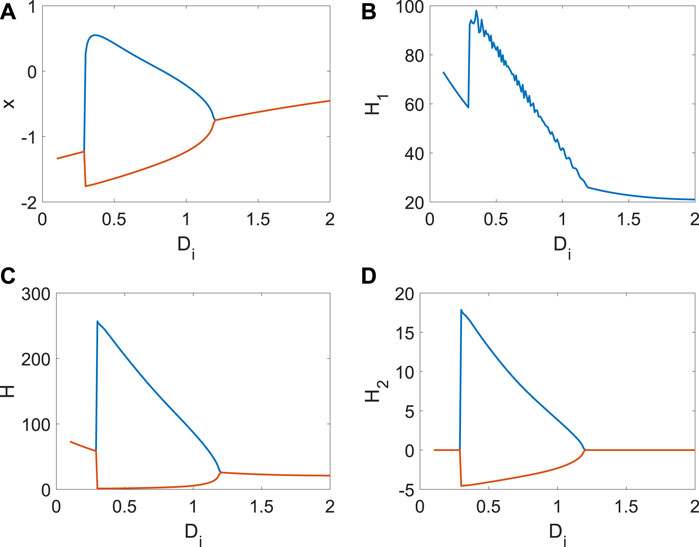
Figure 5. Average Hamiltonian energy, average change in Hamiltonian energy, and membrane potential when Iext = | 1. (A) Bifurcation of membrane potential. (B) Average Hamiltonian energy. (C) Max–min value of Hamiltonian energy. (D) Max–min value of Hamiltonian energy variation.
The role of x0 from other neurons’ external stimulus (Li et al., 2024b; Li et al., 2024a; Du et al., 2024) is the same as Iext when other parameters are fixed. When the external stimulation of other neurons contributing to the ith neuron is weak, system (4) (the Hamiltonian energy, change in Hamiltonian energy, and membrane potential) is stable (Figure 4A). The periodical spike occurs (Figure 6A) in the membrane potential when x0 increases, which corresponds to the emergence and disappearance of short-term memory. It is found that energy consumption is relatively large in preparation for the spike, and the energy varies significantly in the spike (Figure 6A), which can be treated as an indicator of the generation of the spike (short-term memory). The frequency of spikes will increase (Figure 6B) when external stimuli are enhanced. However, it is insufficient to support two identical spikes of membrane potential x (Figure 6B) due to the lack of external stimulus or the Hamiltonian energy H (Figure 6B). Therefore, the formation of short-term memory requires a process of accumulating energy, and the energy breaks out when a spike occurs. The more energy accumulates, the greater the energy change (Ht). If x0 continues to increase, there will be more spikes, but their intensity is different (Figure 6C). A constant spike is created when x0 is very large (Figure 6D), which is also the ordinary emergence and disappearance of short-term memory. However, the external stimulus from other neurons will inhibit the generation of the spike and put the ith neuron in a resting state (Figure 7A). From Figure 7, the spike is impossible without extensive external energy input, and it has excellent fluctuations at the beginning (Figure 7A). We find the average Hamiltonian energy increases with x0 (Figure 7B). The max–min value of Hamiltonian energy (Figure 7C) and the max–min value of Hamiltonian energy variation (Figure 7D) are consistent with the bifurcation of x.
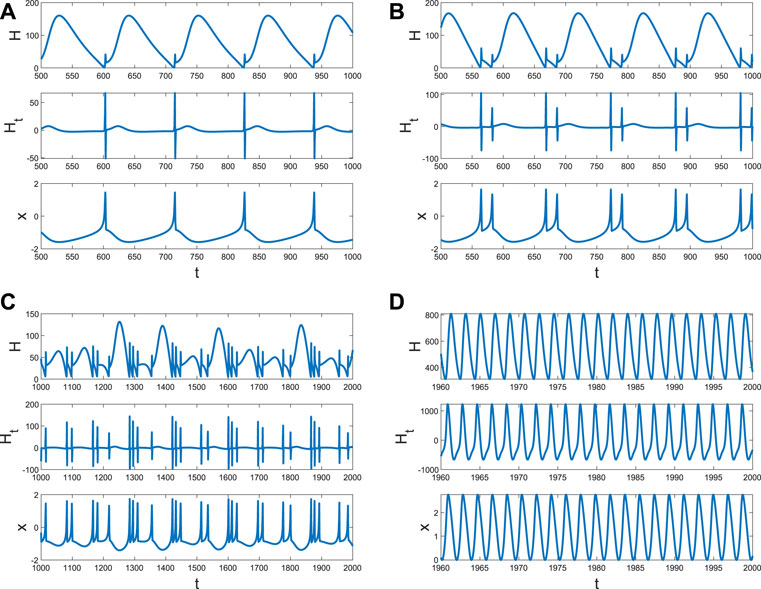
Figure 6. Hamiltonian energy, change in Hamiltonian energy, and membrane potential when Di = | 0.1, Iext = | 1. (A) Evolution when x0 | = | 5. (B) Evolution when x0 | = | 10. (C) Evolution when x0 | = | 20. (D) Evolution when x0 | = | 200.
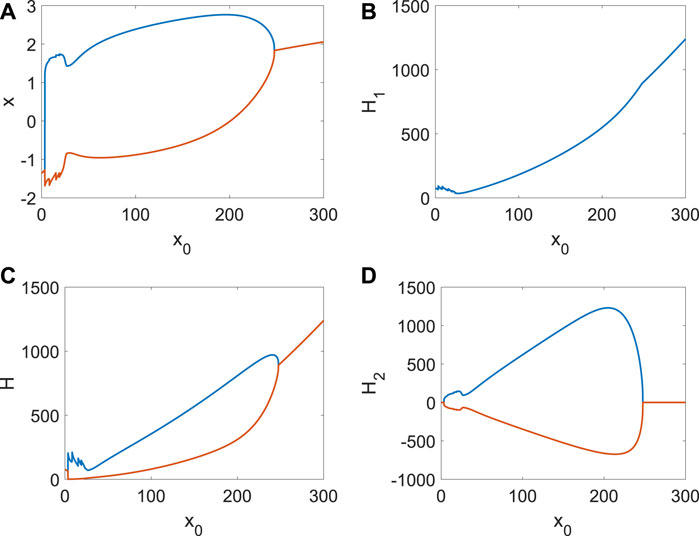
Figure 7. Average Hamiltonian energy, change in Hamiltonian energy, and membrane potential when Di = | 1, Iext = | 1. (A) Bifurcation of membrane potential. (B) Average Hamiltonian energy. (C) Max–min value of Hamiltonian energy. (D) Max–min value of Hamiltonian energy variation.
Finally, we conclude the dynamical mechanism of the generation of short-term memory: the energy from other neurons is necessary for short-term memory, proving that short-term memory results from multiple neuronal activities. Energy requires a process of accumulation to maintain a complete spike. The excessive influence of other neurons can make the ith neurons lose their dominance and align with the dynamic behaviors of other neurons.
4 Conclusion
Energy plays a vital role in neuronal activity, which is the basis of the generation of short-term memory. In this paper, the pattern formation could represent the collecting dynamics of short-term memory through the Hamiltonian energy, showing the neuronal activity in generating short-term memory. Therefore, the interplay between neurons is considered through a simple network to show the effect of the external stimulus and coupling strength (degree) on the dynamical behaviors. It is found that the Hamiltonian energy, change in the Hamiltonian energy, and membrane potential are consistent. The excessive influence of other neurons can make the ith neurons lose their dominance and align with the dynamic behaviors of other neurons, which could show the synergistic effect of neurons through a physical neuron circuit. In addition, the energy from other neurons is necessary for short-term memory, proving that short-term memory results from multiple neuronal activities. Generating short-term memory requires much energy, and energy requires a process of accumulation to maintain a complete spike. Meanwhile, the coupling strength could further reduce energy consumption, which provides a novel way to reduce the energy consumption in information storage and processing. However, more short-term memory descriptions should be completed next.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
QZ: writing–original draft and writing–review and editing. YX: writing–original draft and writing–review and editing. JS: writing–original draft and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (12002297 and 12272135), Basic Research Project of Universities in Henan Province (21zx009), Program for Science & Technology Innovation Talents in Universities of Henan Province (22HASTIT018), Funding of Henan Province for merit-based overseas students (2023), Outstanding Young Backbone Teacher of Xuchang University (2022), and Training Program for Young Key Teachers in Colleges and Universities of Henan Province (2023GGJS144). Natural Science Foundation of Henan (242300421396).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Amit, D. J., and Brunel, N. (1997). Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb. Cortex 7, 237–252. doi:10.1093/cercor/7.3.237
Attwell, D., and Laughlin, S. B. (2001). An energy budget for signaling in the grey matter of the brain. J. Cerebr. Blood F. Mater. 21, 1133–1145. doi:10.1097/00004647-200110000-00001
Barbosa, J., Stein, H., Martinez, R. L., Galan-Gadea, A., Li, S., Dalmau, J., et al. (2020). Interplay between persistent activity and activity-silent dynamics in the prefrontal cortex underlies serial biases in working memory. Nat. Neurosci. 23, 1016–1024. doi:10.1038/s41593-020-0644-4
Carter, E., and Wang, X. (2007). Cannabinoid-mediated disinhibition and working memory: dynamical interplay of multiple feedback mechanisms in a continuous attractor model of prefrontal cortex. Cereb. Cortex 17, 16–26. doi:10.1093/cercor/bhm103
Donald, H., and Rose, R. (1986). Helmholtz’s theorem revisited. Am. J. Phys. 54, 552–554. doi:10.1119/1.14562
Du, X., Xu, Y., Liu, Q., Liu, C., Yue, X., Liu, X., et al. (2024). Shimmy dynamics in a dual-wheel nose landing gear with freeplay under stochastic wind disturbances. Nonlinear Dynam 112, 2477–2499. doi:10.1007/s11071-023-09182-3
Ghazizadeh, E., and Ching, S. (2020). Slow manifolds within network dynamics encode working memory efficiently and robustly. PLoS Comput. Biol. 17, e1009366. doi:10.1371/journal.pcbi.1009366
Hindmarsh, J., and Rose, R. (1982). A model of the nerve impulse using two first-order differential equations. Nature 296, 162–164. doi:10.1038/296162a0
Hu, B., Garrett, M. E., Groblewski, P. A., Ollerenshaw, D. R., Shang, J., Roll, K., et al. (2021). Adaptation supports short-term memory in a visual change detection task. PLoS Comput. Biol. 17, e1009246. doi:10.1371/journal.pcbi.1009246
Ichikawa, K., and Kaneko, K. (2021). Short-term memory by transient oscillatory dynamics in recurrent neural networks. Phys. Rev. Res. 3, 033193. doi:10.1103/physrevresearch.3.033193
Jones, B., and Ching, S. (2022). Synthesizing network dynamics for short-term memory of impulsive inputs. Proc. IEEE Conf. Decis. Control 2022, 6836–6841. doi:10.1109/cdc51059.2022.9993238
Kumar, R. S., Sugumaran, G., Raja, R., Zhu, Q., and Raja, U. K. (2016). New stability criterion of neural networks with leakage delays and impulses: a piecewise delay method. Cogn. Neurodynamics 10, 85–98. doi:10.1007/s11571-015-9356-y
Lepek, M., and Fronczak, P. (2018). Spatial evolution of hindmarsh-rose neural network with time delays. Nonlinear Dyn. 92, 751–761. doi:10.1007/s11071-018-4088-2
Li, Y., Suleiman, K., and Xu, Y. (2024a). Anomalous diffusion, non-gaussianity, nonergodicity, and confinement in stochastic-scaled brownian motion with diffusing diffusivity dynamics. Phys. Rev. E 109, 014139. doi:10.1103/PhysRevE.109.014139
Li, Y., Zhu, Q., Xu, Y., and Tian, R. (2024b). Enhanced fault diagnosis via stochastic resonance in a piecewise asymmetric bistable system. Chaos 34, 011101. doi:10.1063/5.0188335
Liebovitch, L. S., Norman, M. D., Su, J., and Gottman, J. M. (2011). Mathematical model of the dynamics of psychotherapy. Cogn. Neurodynamics 5, 265–275. doi:10.1007/s11571-011-9157-x
McCullen, N., and Wagenknecht, T. (2016). Pattern formation on networks: from localised activity to turing patterns. Sci. Rep.-UK 6, 27397–27398. doi:10.1038/srep27397
Rajagopal, K., Khalaf, A. J., Parastesh, F., Moroz, I., Karthikeyan, A., and Jafari, S. (2019). Dynamical behavior and network analysis of an extended hindmarsh-rose neuron model. Nonlinear Dyn. 98, 477–487. doi:10.1007/s11071-019-05205-0
Sarasola, C., Torrealdea, F. J., d’Anjou, A., Moujahid, A., and Grana, M. (2004). Energy balance in feedback synchronization of chaotic systems. Phys. Rev. E 69, 011606. doi:10.1103/PhysRevE.69.011606
Shi, X., and Wang, Z. (2012). Adaptive synchronization of time delay hindmarsh-rose neuron system via self-feedback. Nonlinear Dyn. 69, 2147–2153. doi:10.1007/s11071-012-0415-1
Song, X., Jin, W., and Ma, J. (2015). Energy dependence on the electric activities of a neuron. Chin. Phys. B 24, 128710. doi:10.1088/1674-1056/24/12/128710
Song, Z. G., and Xu, J. (2013). Stability switches and double hopf bifurcation in a two-neural network system with multiple delays. Cogn. Neurodynamics 3, 505–521. doi:10.1007/s11571-013-9254-0
Stokes, M. (2015). Activity-silent working memory in prefrontal cortex: a dynamic coding framework. Trends Cogn. Sci. 19, 394–405. doi:10.1016/j.tics.2015.05.004
Torrealdea, F. J., d Anjou, A., Grana, M., and Sarasola, C. (2006). Energy aspects of the synchronization of model neurons. Phys. Rev. E 74, 011905. doi:10.1103/PhysRevE.74.011905
Torrealdea, F. J., Sarasola, C., and d Anjou, A. (2009). Energy consumption and information transmission in model neurons. Chaos Solit. Fract. 40, 60–68. doi:10.1016/j.chaos.2007.07.050
Usha, K., and Subha, P. A. (2019). Energy feedback and synchronous dynamics of hindmarsh-rose neuron model with memristor. Chin. Phys. B 28, 020502. doi:10.1088/1674-1056/28/2/020502
Wang, X. (2001). Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. 24, 455–463. doi:10.1016/s0166-2236(00)01868-3
Wang, Z., Li, Y., Xu, Y., Kapitaniak, T., and Kurths, J. (2022). Coherence-resonance chimeras in coupled hr neurons with alpha-stable levy noise. J. Stat. Mech-Theory E. 2022, 053501–053515. doi:10.1088/1742-5468/ac6254
Wang, Z., Xu, Y., Li, Y., Kapitaniak, T., and Kurths, J. (2021a). Chimera states in coupled hindmarsh-rose neurons with α-stable noise. Chaos Solit. Fract. 148, 110976. doi:10.1016/j.chaos.2021.110976
Wang, Z., Xu, Y., Li, Y., and Kurths, J. (2021b). The probability density function of interspike intervals in an fhn model with α-stable noise. Eur. Phys. J. Plus 136, 299–314. doi:10.1140/epjp/s13360-021-01245-x
Wu, K., Luo, T., Lu, H., and Wang, Y. (2016). Bifurcation study of neuron firing activity of the modified hindmarsh-rose model. Neural comput. applic. 27, 739–747. doi:10.1007/s00521-015-1892-1
You, Y. (2023a). Exponential synchronization of memristive hindmarsh-rose neural networks. Nonlinear Anal-Real 73, 103909. doi:10.1016/j.nonrwa.2023.103909
You, Y. (2023b). Global dynamics of diffusive hindmarsh-rose equations with memristors. Nonlinear Anal-Real 71, 103827. doi:10.1016/j.nonrwa.2022.103827
Yu, X., Bao, H., Chen, M., and Bao, B. (2023). Energy balance via memristor synapse in morris-lecar two-neuron network with fpga implementation. Chaos Solit. Fract. 171, 113442. doi:10.1016/j.chaos.2023.113442
Zhang, L., Xiong, L., An, X., and Shi, Q. (2022). Hamilton energy balance and synchronization behaviors of two functional neurons. Cogn. Neurodynamics 2022, 1683–1702. doi:10.1007/s11571-022-09908-w
Zheng, Q., Shen, J., Pandey, V., Guan, L., and Guo, Y. (2023). Turing instability in a network-organized epidemic model with delay. Chaos Solit. Fract. 168, 113205. doi:10.1016/j.chaos.2023.113205
Zheng, Q., Shen, J., Pandey, V., Yuan, X., and Guan, L. (2024). Pattern selection mechanism from the equilibrium point and limit cycle. Chaos 32, 023124. doi:10.1063/5.0187810
Zheng, Q., Shen, J., and Xu, Y. (2020a). Turing instability in the reaction-diffusion network. Phys. Rev. E 102, 062215. doi:10.1103/PhysRevE.102.062215
Zheng, Q., Shen, J., and Xu, Y. (2020b). Spontaneous activity induced by Gaussian noise in the network organized fitzhugh-nagumo model. Nat. Neurosci. 2020, 1–12. doi:10.1155/2020/6651441
Zheng, Q., Shen, J., Zhang, R., Guan, L., and Xu, Y. (2022). Spatiotemporal patterns in a general networked hindmarsh-rose model. Front. Physiol. 13, 1–9. doi:10.3389/fphys.2022.936982
Keywords: HR, pattern formation, network, matrix, Turing instability, delay
Citation: Zheng Q, Xu Y and Shen J (2024) Hamiltonian energy in a modified Hindmarsh–Rose model. Front. Netw. Physiol. 4:1362778. doi: 10.3389/fnetp.2024.1362778
Received: 29 December 2023; Accepted: 04 March 2024;
Published: 26 March 2024.
Edited by:
Eckehard Schöll, Technical University of Berlin, GermanyReviewed by:
Ling Kang, Fudan University, ChinaAnna Zakharova, Humboldt University of Berlin, Germany
Copyright © 2024 Zheng, Xu and Shen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yong Xu, aHN1eDNAbndwdS5lZHUuY24=; Jianwei Shen, eGNqd3NoZW5AZ21haWwuY29t
 Qianqian Zheng
Qianqian Zheng Yong Xu
Yong Xu Jianwei Shen
Jianwei Shen