
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Netw. Physiol. , 16 January 2024
Sec. Networks in the Brain System
Volume 3 - 2023 | https://doi.org/10.3389/fnetp.2023.1338864
This article is part of the Research Topic The Network Theory of Epilepsy at Twenty View all 14 articles
Epilepsy is now considered a network disease that affects the brain across multiple levels of spatial and temporal scales. The paradigm shift from an epileptic focus—a discrete cortical area from which seizures originate—to a widespread epileptic network—spanning lobes and hemispheres—considerably advanced our understanding of epilepsy and continues to influence both research and clinical treatment of this multi-faceted high-impact neurological disorder. The epileptic network, however, is not static but evolves in time which requires novel approaches for an in-depth characterization. In this review, we discuss conceptual basics of network theory and critically examine state-of-the-art recording techniques and analysis tools used to assess and characterize a time-evolving human epileptic brain network. We give an account on current shortcomings and highlight potential developments towards an improved clinical management of epilepsy.
Epilepsy is the third most common neurological disorder with a worldwide prevalence of about 1% (Beghi et al., 2019; World Health Organization [WHO], 2019). Epilepsy is clinically diagnosed by multiple epileptic seizures or by an epilepsy syndrome or by a single seizure and a probability of at least 60% for further seizures to occur over the next 10 years (Fisher et al., 2005). An epileptic seizure is defined as a transient occurrence of symptoms due to abnormal excessive or synchronous neuronal activity in the brain (Fisher et al., 2005). It can appear due to an acute disease of the brain (e.g., acute symptomatic seizures due to brain abscess), due to systemic disorders (i.e., metabolic disturbances), or as a symptom of a chronic disease, i.e., epilepsy. The disease can be treated sufficiently well in about two-thirds of people with epilepsy (Kwan and Brodie, 2000; Chen et al., 2018), while the other third needs intensive diagnostics and extensive therapy attempts such as non-pharmaceutical interventions (e.g., resective epilepsy surgery, neurostimulation) which in some cases are associated with significant risks or side effects. The people’s willingness to undergo more difficult or risky therapies depends on the burden of the disease being treated. The burden of epilepsy is composed of several factors: comorbidities (Mesraoua et al., 2020), psychosocial impairment, social stigma (Kwon et al., 2022), medico-legal restriction, direct and indirect costs (Strzelczyk et al., 2008; Allers et al., 2015) and—as to be expected—seizures, their treatment and potential complications (Noe, 2019; Mesraoua et al., 2020). The apparent unpredictability of most seizures not only increases the risk of injuries and discomfort, but also imposes loss of autonomy, fear of seizures as well as psychosocial stress (Lang et al., 2022), thereby impacting massively on the quality of life of those affected and their caregivers (Baker et al., 1997; Chiang et al., 2020; Strzelczyk et al., 2023). Thus understanding emergence, propagation, and cessation of epileptic seizures is generally assumed to be crucial to understand the nature of epilepsy, and to understand and establish diagnostic approaches as well as treatment options.
Classification of seizures, epilepsies, and epilepsy syndromes changed over time (Merlis, 1970; Dreifuss et al., 1985; Commission on Classification and Terminology of the International League Against Epilepsy, 1989; Berg and Scheffer, 2011), and an increasingly sophisticated work-up was demanded in clinical daily practice to better understand, characterize, and treat the disease. Moreover, the dichotomy of focal and generalized epilepsy was questioned (Lüders et al., 2009). In the clinical context, the origin of epileptic seizures has been inferred firstly from structural changes and secondly from semiology, i.e., behavioral changes during a seizure. Electrophysiological changes associated with behavioral changes were used as a bridge for diagnosis and referred to as “ictal patterns”. This led to the model of a focal seizure origin and, for a long time, to assignments of involved brain regions to the different zones in presurgical epilepsy diagnosis (symptomatogenic zone, irritative zone, seizure onset zone, epileptogenic lesion, epileptogenic zone, eloquent cortex) (Rosenow and Lüders, 2001). Follow-up data, however, demonstrated that only a portion of subjects treated with focal therapies such as epilepsy surgery (Téllez-Zenteno et al., 2005) or focal brain stimulation achieves long-term seizure freedom (Simpson et al., 2022), which raises doubts about the usefulness of the concept of a focal seizure origin. Furthermore, a similar cerebral lesion does not cause seizures in every subject, so a “proconvulsive” disposition must be suspected.
The epileptic brain should not be viewed as a temporarily disturbed normal brain since it differs from a normal brain in many structural and functional aspects, and seizures take up only a small fraction of a subject’s lifetime. Function and dysfunction of the adaptive dynamical system epileptic brain are interacting processes that cover various time scales and are influenced by various endogenous and exogenous factors. These range from seizures and biological rhythms to treatments with antiseizure medication, neurostimulation, or epilepsy surgery. Moreover, the brain’s dynamics are influenced by its intricate structural complexity; due to its intrinsic plasticity and adaptiveness, dynamics can modify structure (Sporns, 2022). Together, this calls for sophisticated approaches to improve our understanding of the epileptic brain’s complex structure-(dys)functions relationship.
Research over the last decades has demonstrated the excellent suitability of the network approach to the complex system brain in health and disease (Bullmore and Sporns, 2009; 2012; Avena-Koenigsberger et al., 2018). The explicit time-dependence of the epileptic brain, however, required an additional change in perspective from a static to a time-evolving network. We here review this novel perspective, its concepts, definitions, and accomplishments, and discuss possible translations into clinical practice.
In her seminal work, Susan Spencer considered a network to be a functionally and anatomically connected, bilaterally represented, set of cortical and subcortical brain structures and regions in which activity in any one part affects activity in all the others. The essential operational component of this definition is the observation that vulnerability to seizure activity in any one part of the network is influenced by activity everywhere else in the network, and that the network as a whole is responsible for the clinical and electrographic phenomena that we associate with human seizures. Implicit in this idea is that the seizures may entrain this large neural network from any given part, such that it becomes irrelevant to discuss the “onset” of seizures in any specific part of the network. In other words, the electrical hyperexcitability associated with seizure activity reverberates within the neural structures of the network, which operate together and inextricably to culminate in the eventual expression of seizures (Spencer, 2002).
BOX 1 The number of papers on epileptic brain network published during the past three decades (sourced via Google Scholar using the keywords “epileptic network” and “epileptogenic network”).
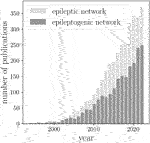
Since then, epileptic brain network studies (sometimes also referred to as an epileptogenic network) increased by almost a factor of 30 (Box 1). In 2010, the term network was included in the revised terminology and concepts for organization of seizures and epilepsies of the International League against Epilepsy (Berg et al., 2010). This highlighted the transition from the old concepts of an epileptic focus and various cortical zones involved in epilepsy (Rosenow and Lüders, 2001) to an epileptic network spanning lobes and hemispheres. Today, epilepsy is considered a network disease. The progress made in this highly interdisciplinary research field has been repeatedly summarized in a number of reviews [see, e.g. (Richardson, 2010; Kramer and Cash, 2012; Laufs, 2012; Engel et al., 2013; van Diessen et al., 2013; Chiang and Haneef, 2014; Stam, 2014; van Mierlo et al., 2014; Bernhardt et al., 2015; Bartolomei et al., 2017; Zijlmans et al., 2019; Gil et al., 2020; Royer et al., 2022a)]. A large number of studies provided increasing evidence for an epileptic brain network to differ from healthy ones, both structurally (Whelan et al., 2018; Hatton et al., 2020; Larivière et al., 2020; Sisodiya et al., 2022) and functionally (Chavez et al., 2010; Horstmann et al., 2010; Zhang et al., 2011; Richardson, 2012; Caciagli et al., 2014; Chiang et al., 2015; Foit et al., 2020; Pegg et al., 2020; Slinger et al., 2022). Moreover, studies demonstrated that the network approach allows for an improved understanding of the dynamics of seizures [both generalized and focal (Schindler et al., 2007b; Ponten et al., 2007; Kramer et al., 2008; Schindler et al., 2008; Ponten et al., 2009; Zaveri et al., 2009; Kramer et al., 2010; Kuhnert et al., 2010; Wilke et al., 2011; Bialonski and Lehnertz, 2013; Varotto et al., 2012; Burns et al., 2014; Geier et al., 2015a; Geier et al., 2015b; Zubler et al., 2015; Lopes et al., 2018; Rungratsameetaweemana et al., 2022)] and of the complex interplay between the epileptic process and physiologic activities (Kuhnert et al., 2013; Yaffe et al., 2015; Garcia-Ramos et al., 2016; Vecchio et al., 2016; Steiger et al., 2017; Tailby et al., 2018; Yang et al., 2018; Zaveri et al., 2020; Mutti et al., 2022; Roliz and Kothare, 2022), possibly mediated by the same neural substrate.
Some studies [see, e.g., Zijlmans et al. (2019) for an overview] attempted to integrate the concepts of an epileptic focus and of the aforementioned cortical zones into the concept of an epileptic network by considering the former ones as hubs or hub-like structures, i.e., strongly connected (functionally and/or structurally) network components that significantly impact on the network. The characteristic of being strongly connected, however, is only one of many other properties (cf. Section 3.2) that emphasize a network component as important for both structure and function of an epileptic brain network. Studies going beyond hubs or hub-like structures attribute a rather subordinate role to the epileptic focus and zones for seizure dynamics and for the many (patho-)physiologic phenomena seen in between seizures (Geier et al., 2015a; Geier et al., 2015b; Geier and Lehnertz, 2017b; Geier and Lehnertz, 2017a; Bröhl and Lehnertz, 2019; Rings et al., 2019b; Fruengel et al., 2020; Bröhl and Lehnertz, 2022).
In 2003, John Milton and Peter Jung considered epilepsy as a dynamic disease and defined an epileptic system as a dynamic, ever-changing and evolving, distributed system of neurons that controls the onset, propagation, and arrest of epileptic seizures and coined the term evolving epileptic network (Milton and Jung, 2003). This concept initially received only little attention. It regained interest, however, with the fusion of time-series-analysis techniques and graph-theoretical concepts necessary to investigate evolving (or time-dependent/temporal/multiplex/multilayer) networks (Holme and Saramäki, 2012; Boccaletti et al., 2014; Kivelä et al., 2014; Lehnertz et al., 2014; Muldoon and Bassett, 2016) and with the development of techniques that allow recording and storage of spatially extended brain dynamics assessed over extended periods of time (days to weeks and beyond).
In a brain network and depending on the chosen spatial scale, a vertex may represent a single cell (e.g., neuron), a group of cells (e.g., cortical columns), or a brain region (e.g., parcellated area) and an edge some connection between vertices. If an edge represents a physical/anatomical connection (single synapses, fiber bundles, or groups of fiber bundles), then the network is referred to as structural network (Park and Friston, 2013). If an edge represents some functional interaction between vertices (characterized by the interaction’s strength, direction, and functional form), then the network is called a functional network (Park and Friston, 2013).
Various imaging and recording techniques can be used to assess structure and dynamics of a time-evolving epileptic brain network on different spatial and temporal scales and with different levels of invasiveness (see Table 1).
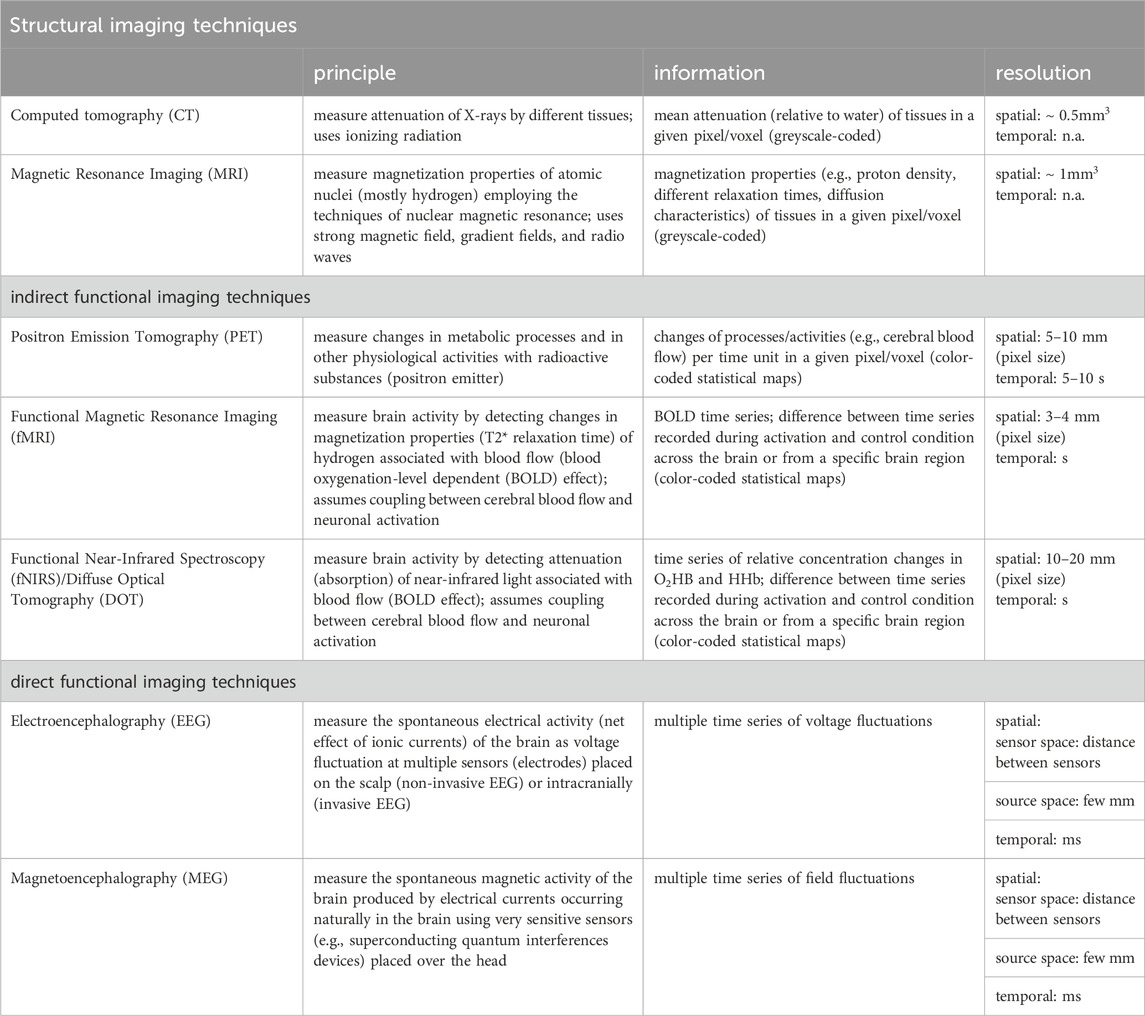
TABLE 1. Structural and (indirect/direct) functional imaging and recording techniques predominantly used to assess structure and dynamics of a time-evolving epileptic brain network (principle: physical mechanisms underlying the measurement; information: information provided by images/time series; n.a. not applicable).
Among the structural neuroimaging techniques, x-ray computed tomography (CT) (Ginat and Gupta, 2014; Pelc, 2014) and magnetic resonance imaging (MRI) (Mori et al., 2005; Atlas, 2009) allow the non-invasive study of the whole brain at different levels of spatial resolution, ranging from millimeter-sized voxels to cortical areas and beyond. During the recording, time-dependent structural changes (Fjell and Walhovd, 2010) are assumed to be negligible. Due to a comparatively better differentiability of gray and white matter, particularly MRI and diffusion MRI (Bammer, 2003) are often used to probe the topological organization of the brain (Duncan, 2009; Engel et al., 2013; Duncan et al., 2016; Whelan et al., 2018; Sotiropoulos and Zalesky, 2019; Yeh et al., 2021; Zhang et al., 2022). In a structural network (also referred to as structural connectivity (Horwitz, 2003) or structural connectome), discrete regions of gray matter represent a network’s vertices and white matter fibers a network’s edges. In order to identify such network constituents, a large number of approaches is employed to parcellate the brain (Eickhoff et al., 2018; Amunts et al., 2020; Bijsterbosch et al., 2020; Royer et al., 2022b) and to identify and characterize white matter fibers (Mori and Van Zijl, 2002; Jeurissen et al., 2019). The variety of techniques requires appropriate approaches to verify and increase the reproducibility of results (Bonilha et al., 2015; Welton et al., 2015; Zalesky et al., 2016; Roine et al., 2019; Lawrence et al., 2021; Alemán-Gómez et al., 2022; Borrelli et al., 2022; Seider et al., 2022; Charvet, 2023; Madole et al., 2023).
Among the functional neuroimaging techniques, positron emission tomography (PET) (Phelps and Mazziotta, 1985; Juhász and Chugani, 2003; Muehllehner and Karp, 2006; Vaquero and Kinahan, 2015; Watabe and Hatazawa, 2019; Seshadri et al., 2021), functional magnetic resonance imaging (fMRI) (Detre, 2004; Buxton, 2013), functional near-infrared spectroscopy (fNIRS) (Jöbsis, 1977; Villringer and Chance, 1997; Ferrari and Quaresima, 2012; Nguyen et al., 2018; Chen et al., 2020), or (high-density) diffuse optical tomography (DOT) (Eggebrecht et al., 2014; Wheelock et al., 2019) can provide non-invasive indirect access to transient neural activity (time scale: some 10 to some 100 milliseconds) by measuring transient changes in cerebral blood flow and/or metabolic processes (time scale: up to some 10 s) assumed to be related to neuronal activation [neurovascular coupling hypothesis; Roy and Sherrington (1890); Huneau et al. (2015); Kaplan et al. (2020); Drew (2022)]. While providing whole-brain coverage, the temporal resolution of these techniques ranges in the order of seconds and is, in general, dictated by the respective imaging device. An exception is MR-encephalography (Hennig et al., 2021), which also allows whole-brain coverage in 100 ms and with a spatial resolution that compares to the other techniques (few millimeters) (Rapisarda et al., 2010; Torricelli et al., 2014; Chaimowet al., 2018). Statistical dependencies (correlation, cross-correlation) between recorded signals from pairs of vertices (from voxels to cortical areas) are often used to define edges of a functional network [also referred to as functional connectivity (Friston, 2011) or functional connectome].
Direct non-invasive access to both transient and ongoing neural activities is achieved with electroencephalography [EEG (Niedermeyer and Lopes da Silva, 2005)] and with magnetoencephalography [MEG (Baillet, 2017)], both of which allow whole-head coverage and have high temporal resolution (few milliseconds). So far, only EEG allows for the continuous recording of brain dynamics over extended periods of time [days to weeks and beyond (Lehnertz et al., 2017; 2021; Milne-Ives et al., 2023)]. This may also be achieved in the future with further improvements of optically-pumped magnetometer MEG systems (Hill et al., 2019; Boto et al., 2021; Pedersen et al., 2022; Hillebrand et al., 2023). An additional access to the brain’s dynamics at the meso- (
EEG/MEG-based techniques allow to capture a wide spectrum of physiological and pathophysiological activities on various time scales and as such, often require other, more sophisticated time-series-analysis techniques (see Section 3.2) to characterize interactions between the sampled brain regions. Properties of interactions are then used to define edges of a functional network whose vertices are usually associated with sensors (EEG-electrodes, MEG-magnetometers) that capture the dynamics of the sampled neuronal substrate. The number of network vertices may range from a few ten to a few hundred, depending on recording technique and research question. Instead of estimating properties of interactions in sensor-space, it has been proposed to do so in source-space to overcome the problems of volume conduction (EEG) and field spread (MEG) [see, e.g., van Mierlo et al. (2019); Koutlis et al. (2021); Sadaghiani et al. (2022); Chiarion et al. (2023) and references therein]. Nevertheless, localizing the sources of EEG/MEG activities in the brain constitutes an inverse problem that lacks a unique solution (von Helmholtz, 1853) and source-space-based network approaches continue to be critically discussed (Colclough et al., 2016; Palva et al., 2018; Koutlis et al., 2021; Adamovich et al., 2022; Pourmotabbed et al., 2022; Schaworonkow and Nikulin, 2022; Hatlestad-Hall et al., 2023).
As with the structural neuroimaging techniques, the variety of approaches and methods used in functional network research requires appropriate approaches to verify and increase the reproducibility of results (Niu et al., 2013; Zuo et al., 2014; Zuo and Xing, 2014; Geng et al., 2017; Adamovich et al., 2022; Bottino et al., 2022; Kato et al., 2022; Rolle et al., 2022; Wang et al., 2022; Helwegen et al., 2023). This applies even more to the fusion of structural and functional imaging techniques (Luat and Chugani, 2008; Aiello et al., 2016; Babaeeghazvini et al., 2021; Wu et al., 2021) as well as to the combined use of different functional imaging techniques (e.g., EEG-fNIRS or EEG-fMRI) that is often pursued to balance the disadvantages of one method with the advantages of another method (Machado et al., 2011; Nguyen et al., 2012; Centeno and Carmichael, 2014; Obrig, 2014; Pittau and Vulliemoz, 2015; Tousseyn et al., 2015; Abreu et al., 2018; Sanz-Garcia et al., 2018; Rizkallah et al., 2020; Anderson et al., 2021; Bernabei et al., 2021; Uchitel et al., 2021; Ikemoto et al., 2022; Li et al., 2022; Mulert and Lemieux, 2023).
Having recorded the dynamics of various brain regions as multivariate time series, a common way to construct a functional brain network consists of associating network vertices with sampled brain regions and network edges with properties of an interaction (strength, direction, functional form) between pairs of brain regions derived from their dynamics (cf. Figure 1).
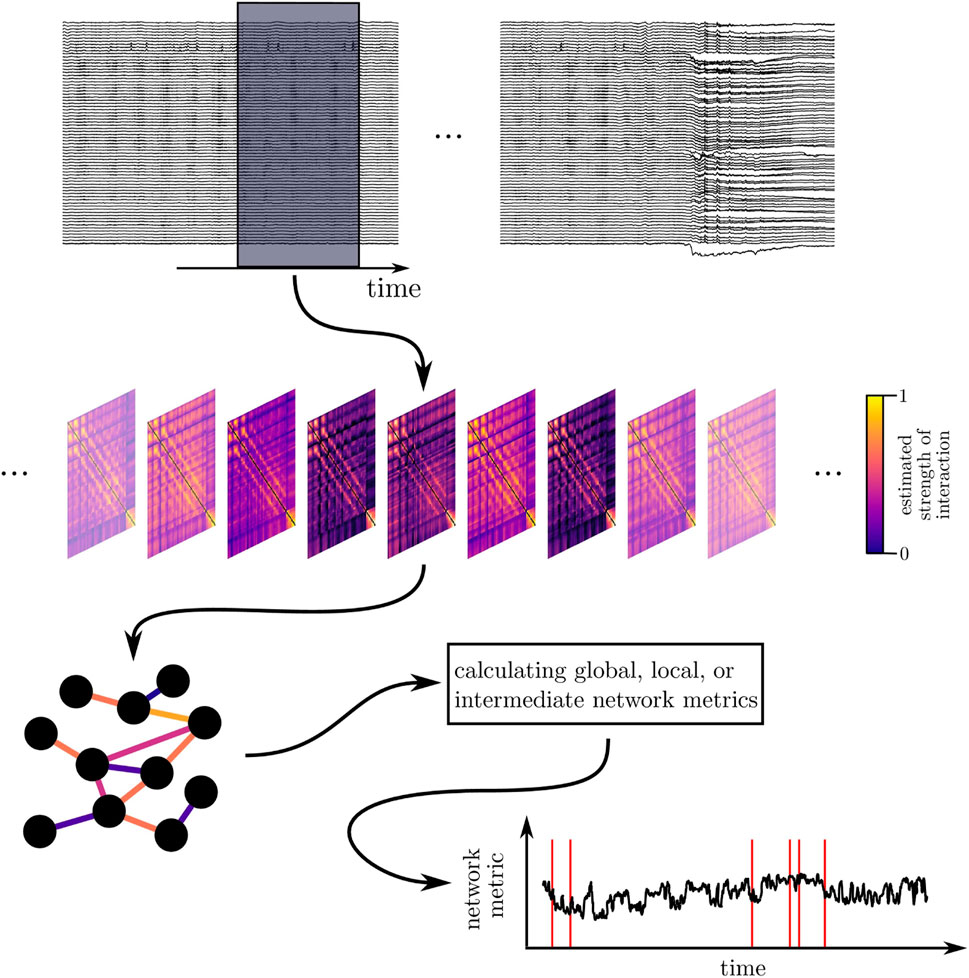
FIGURE 1. Schematic of deriving and characterizing a time-evolving epileptic brain network. Top: sliding-window analysis: long-lasting multichannel EEG recordings are segmented into successive (non-)overlapping windows. Middle: time-dependent sequence of interaction matrices (functional brain networks): each matrix contains estimates of an interaction property (here: strength of interaction) calculated from EEG data within a given window for all pairs of sampled brain regions. Bottom: a network analysis approach renders a time-dependent sequence of a network metric, which is then subject to further analyses. Red lines exemplarily indicate occurrence of epileptic seizures.
The latter ansatz is often pursued in cases where a perturbation-based approach (actio est reactio) is either unfeasible or not constructive. Properties of an interaction can then be estimated with diverse linear and nonlinear, bi- and multivariate time-series-analysis techniques grounded in statistics (Rodgers and Nicewander, 1988; Hamilton, 2020), nonlinear dynamics (Kantz and Schreiber, 2003; Datseris and Parlitz, 2022), synchronization theory (Arnhold et al., 1999; Pikovsky et al., 2001; Stankovski et al., 2012; Rosenblum and Pikovsky, 2023), statistical physics (Tabar, 2019), and information theory (Hlaváčková-Schindler et al., 2007), among others.
Given that interactions can manifest themselves in many (also conceptually) different ways (such as the diverse forms of synchronization, flow of information, or similarity) and since there is no one-fits-all analysis technique for all types of data or interactions (Pereda et al., 2005; Kreuz et al., 2007; Wendling et al., 2009; Höller et al., 2017), the choice of a time-series-analysis technique is often dictated by the specific research question. Examples of some of the available techniques to estimate properties of interactions are listed in Table 2. Also, depending on the employed recording technique (alongside with the sampling interval; see above), time series can cover various time scales of brain dynamics and include signal properties reflecting different physiological and pathophysiological phenomena. Especially for EEG and MEG recordings, the temporal resolution allows for the separation of the signal into various frequency bands of neural oscillations.
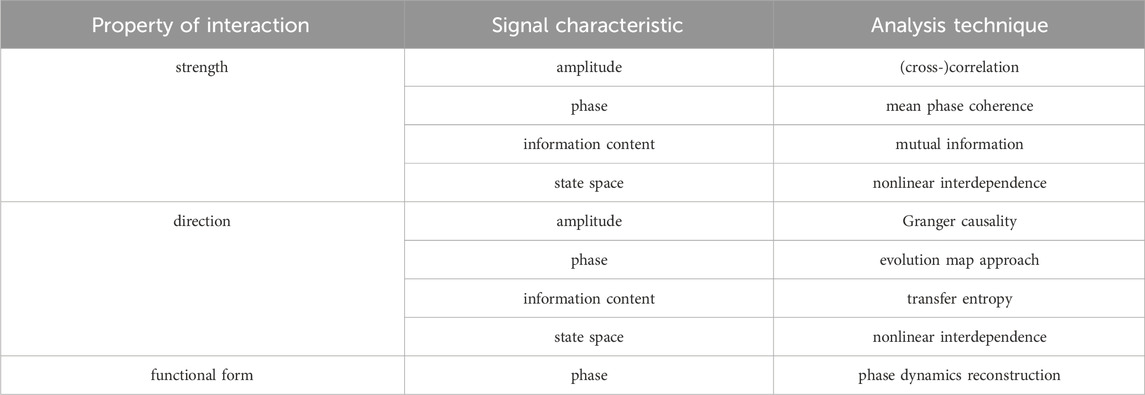
TABLE 2. Examples of time series analysis techniques used to characterize properties of an interaction based on different signal characteristics. The strength of an interaction quantifies the level of interdependence between two brain regions. Estimators for the strength of an interaction are predominantly based on the idea that more (abstractly) similar dynamics reflect a stronger coupling between regions. The direction of an interaction assesses which of the two interacting brain regions is driving the other. Estimators for the direction of an interaction are usually based on assumptions about cause and effect in the larger system respectively on models for the temporal evolution of the regions’ dynamics. The functional form of interaction describes the relationship between two brain regions as a mathematical model. Estimators for the functional form of an interaction have the dual task of setting up an appropriate model for the involved interdependencies and of appraising model parameters, which typically requires strong assumptions and in-depth knowledge of the involved dynamics.
However, spectral limits of brain activity often associated with these frequency bands might vary in time or between brain regions. It also might not be useful to investigate frequency bands without discernible power, while a broader perspective may include otherwise unnoticed phenomena (Osterhage et al., 2007a; Frei et al., 2010; Gerster et al., 2022). In addition, the human brain has to be regarded as an open, dissipative, and adaptive dynamical system and is inherently non-stationary. Most methods to characterize properties of interactions, however, require the system to be (at least approximately) stationary to yield robust and reliable characterizations. Thus, time series of recordings of brain dynamics are typically cut into segments of appropriate duration whose choice is usually a compromise between the required statistical accuracy for the characterization and approximate stationarity within a segment’s duration [see Lehnertz et al. (2017) for details]. Together, experimental conditions and handling of the brain’s non-stationarity result in the investigation of either carefully-selected segments (possibly influencing findings with selection bias) or of sequences of (non-) overlapping segments or windows (moving-window approach).
Estimates of properties of an interaction can be affected by a number of influencing factors that may arise from specifics of the applied recording techniques, specifics and uncertainties of the various time-series-analysis techniques (cf. Box 2) or due to unavoidable noise contamination. To at least minimize these influences and to improve reliability of estimates, the surrogate approach from statistical hypothesis testing can be employed. This bootstrapping approach begins with formulating an appropriate null hypothesis (Efron, 2004), which specifies properties of influencing factors that might lead to the results of an analysis (cf. Box 3).
BOX 2 The majority of estimators for the strength of an interaction increase non-proportional (i.e., non linear) with an increase of the coupling strength (assuming one knows the true mechanisms for an interaction between two systems (brain regions)). On the one hand, this depends very much on the systems under investigation, but also the choice of the time-series-analysis technique plays an important role. Even in the case of strong coupling, amplitude-based (blue) or information-theory-based estimators (purple) may indicate a low or medium strength of interaction. In contrast, a phase-based estimator (red) already reaches its maximum value. In the first case, the two systems would be interpreted as weakly interacting or even independent, while the second case would indicate a stronger interaction or even a complete alignment (synchronization).
BOX 3 A null model is a statistical model that is built on a null hypothesis. It makes an assumption about a fact, which can be evaluated by way of a statistical test. Using a null model one can test whether analysis results are purely coincidental and cannot be traced back to specific influencing factors. If the test confirms the null model, this is not a proof for its correctness. It only leads to a rejection of the hypothesis of the previously assumed dependence on the influencing factors. A null model can not be proven, but only disproved. With suitable methods, so-called surrogates can be created from the original time series (top) or from networks (bottom), whereby the influencing factor to be investigated is hidden and factors to be investigated are masked out. If analysis results for the original data differ from those for a sufficiently large number of surrogates, then the null hypothesis can be rejected with ascertainable certainty. The investigated influencing factor then plays a significant role and must be taken into account when interpreting findings.
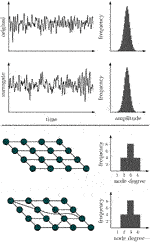
The null hypothesis represents the case for which the obtained findings are consequent to the influencing factors and not to the properties of interest of the investigated system. From this null hypothesis, a pertinent model (the so-called null model) is created, and an ensemble of surrogate data is generated by simulating realizations of the model with Monte Carlo methods (Efron, 1982). In these realizations, all relevant statistical and dynamical aspects of the original data are preserved—except the properties which are tested for. If some discriminating statistics of the original data falls outside the expectation range for the surrogate ensemble, the null hypothesis can be rejected with reasonable confidence (depending on the number of statistically independent constrained realizations). In this case, an alternative hypothesis has to be accepted—i.e., findings are likely due to the properties of the system. However, the surrogate approach does not specify alternative hypotheses nor is it a validation of any specific alternative hypothesis’ accurateness.
For properties of interactions, constrained realizations of the multivariate time series can be generated by randomizing the aspect of a recorded dynamics on which the estimator for the property of an interaction is based (Schreiber, 1998; Schreiber and Schmitz, 2000; Andrzejak et al., 2003a; Paluš, 2007; Rings et al., 2020). However, the associated surrogate techniques are exclusively designed for the strength of an interaction as the formulation of null hypotheses for the direction of an interaction (linkable to properties of time series for an appropriate null model) continues to be an unsolved problem. The same applies to null hypotheses for the functional form of an interaction.
Having estimated the relevant property of interaction for all pairs of brain regions, the values of the estimates then set up an interaction matrix
Subsequently, a binary or weighted and directed or undirected network can be constructed from this matrix.
An undirected binary network describes the brain in terms of connected or disconnected vertices and can be represented by a symmetric adjacency matrix
If it is additionally of interest which brain regions interact how strongly, an undirected weighted network provides this information. Represented by a symmetric weight matrix
A directed binary network describes the brain by depicting which brain region drives which other region. Extending the concept of undirected binary networks, directed networks can be described by an asymmetric adjacency matrix
Of note, direction of interaction does not generally inform of strength of interaction, and combining both information in a directed and weighted network is a not conclusively solved problem. When merging strength and direction of interaction, it is important to remember that both properties are different but not unrelated (Lehnertz and Dickten, 2015). The often-employed interpretation of the modulus of an estimator for the direction of interaction as strength of interaction might not consistently be accurate and can lead to severe misconceptions—particularly for uncoupled or strongly coupled systems (Osterhage et al., 2007b; Paluš and Vejmelka, 2007; Lehnertz and Dickten, 2015; Günther et al., 2022). It is conceptually unclear how weights should be assigned to forward and backward direction of the edges. Strength of interaction is symmetric under exchange of two vertices, while direction of interaction is not. In addition, many concepts employed to estimate properties of interactions can currently not be mapped to each other. The easiest way to avoid resulting problems is to estimate strength and direction of interaction separately but using methods that are based on the same concepts (e.g., phase synchronization or information flow).
There is also no commonly accepted method to utilize functional forms of interaction to derive networks, and doing so would require an abstract, possibly symbolic assignment of edges. Hypothetically, a system’s equations of motion could already be considered a symbolic network were a vertex represents an elementary unit’s self-dynamics function and an edge represents a coupling function. However, how to interpret the multitude of possible functions involved as a network’s component is highly ambiguous.
Having derived a functional brain network from observed data, the next task is to characterize the network’s properties and internal organization. While there are a multitude of different network metrics based on concepts and methods from graph theory [see, e.g., Rubinov and Sporns (2010); Newman (2018); Cimini et al. (2019) for an overview; Box 4], they are predominantly defined for undirected (binary or weighted) networks and each metric reflects specific topological or spectral network properties. Network metrics for directed networks are still subject of current research. Two necessary concepts for a characterization of a network are distance and shortest paths. A path is the collection of edges that need to be traversed to reach a constituent starting at another one, and the respective path length (which is equivalent to the distance) is either the number of edges that are traversed in case of a binary network, or the sum of the inverse weights of these edges in case of a weighted network. There are multiple paths between every constituents, and shortest paths are the ones whose path lengths are minimal. Generally, network metrics can be categorized according to the network scale for which they are defined—i.e., from the global scale encompassing the whole network to the local scale of single vertices and edges.
BOX 4 Properties of a network can be assessed with different local-to-global network metrics. Local network metrics (top) assess how individual vertices or edges are integrated into the larger network. These metrics can also be used to determine the importance (centrality) of vertices and edges for the network on the basis of objective criteria. For example, a vertex with a high degree (or strength in case of a weighted network) has a strong influence on the network; conversely, the influence of the network on this vertex can be estimated. Betweenness centrality can be used, e.g., to rate the importance of a vertex (or an edge) for the flow of information in a network. Since a vertex (edge) with a high betweenness centrality is traversed by a large number of paths, it acts like a bottleneck in the network. Global network metrics (bottom) evaluate a network as a whole. For example, if the mean value over all local clustering coefficients of a network takes on a high value, then vertices are closely connected to their neighboring vertices (clique formation) In a network whose average shortest path length is large, vertices are only weakly connected with their neighboring vertices; the network tends to break up into different regions. A (dis-)assortative network, vertices tend to connect with other vertices that are (dis-)similar in some way.
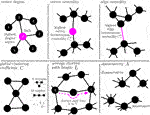
On the global scale, network metrics describe the arrangement of vertices and edges according to topological concepts such as transitivity [vertices that are connected to two other vertices that are connected themselves; evaluated with, e.g. (global) clustering coefficient (Watts and Strogatz, 1998)], efficiency [information or mass transport in a network is facilitated by short paths; e.g., average shortest path length (Newman, 2001)], or assortativity [vertices with the same or similar properties are connected preferentially (Newman, 2002)].
In greater detail, the global clustering coefficient assess the number of closed triplets in relation to the total number of triplets in the network and characterizes a network’s functional segregation; segregation decreases with increasing values of the coefficient, however both excessive large or small values indicate a breakdown of segregation. The average shortest path length characterizes a networks functional integration; the shorter the path, the more integrated is the network (cf. Box 5). Assortativity characterizes the mixing of vertices with the similar properties (typically assessed with local network metrics) through being connected (Newman, 2003; Bialonski and Lehnertz, 2013); if edges preferentially connect vertices with a similar (dissimilar) property, such networks are called assortative (disassortative). Disassortative networks are more vulnerable to perturbations and appear to be easier to synchronize than assortative networks (Motter et al., 2005; di Bernardo et al., 2007).
BOX 5 Following Tononi et al. (1994), integration can be defined as an effective global cooperation between different subsystems (brain regions). Segregation can be defined as the decomposition of a system into sufficiently independent specialized processing subsystems.
Additionally, methods from linear algebra can be employed to investigate spectral properties of a network’s associated adjacency or weight matrix, which then can be related to a network’s emergent global dynamics [for an overview see (Atay et al., 2006; Comellas and Gago, 2007)]. Synchronizability, e.g., characterizes the stability of a global synchronization state, i.e., a network’s propensity to synchronize (Barahona and Pecora, 2002). However, for an interpretation of synchronizability of human brain networks, one should keep in mind that some of this metric’s fundamental assumptions are not fulfilled in this system—for synchronizability, it is assumed that all vertices are associated with dynamics of the same type with largely identical control parameters which strongly disagrees with the spatial heterogeneity of brain dynamics (Papo and Buldú, 2019).
Although it is possible to compensate for this heterogeneity to some degree (while accepting other constraining assumptions) (Sun et al., 2009; Nishikawa and Motter, 2010; Zhang and Motter, 2017), a global synchronization state is fortunately not achieved in the brain (and would indicate complete dysfunction)—an inveterate conceptional issue. Consequently, synchronizability should only ever be treated as an indicator of stability properties of a network’s associated dynamics instead of face value.
Global network metrics can also be used to define indices that are thought to be specific to the network’s topology. For example, global clustering coefficient and average shortest path are often merged to assess whether a given network has a small-world-like topology or not (Bassett and Bullmore, 2006), and this property has been reported for both structural and functional, physiological and pathophysiological brain networks in the past (Reijneveld et al., 2007; Bullmore and Sporns, 2009; Stam, 2014). These findings, however, are strongly contested (Bialonski et al., 2010; Hlinka et al., 2012; Hilgetag and Goulas, 2016; Papo et al., 2016) due to the identification of various factors that can influence the characterization of networks. Confusingly, the literature frequently refers to various metrics and underlying concepts with different, sometimes overlapping names—e.g., the metric “average shortest path length” and the metric “average communication efficiency” are identical and both are indicators of the conceptual “efficiency” of a network.
On the local scale, network constituents (vertices as well as edges), can be characterized with so-called centrality metrics. These metrics evaluate a constituent according to the various roles it can play in a network [for an overview see, e.g., Koschützki et al. (2005); Kuhnert et al. (2012); Bröhl and Lehnertz (2019)]. Typically, centrality metrics are based either on the strength with which a constituent is connected to the rest of the network (strength-based; e.g., strength centrality or eigenvector centrality) or on their involvement in the organization of shortest paths in a network (path-based; e.g., betweenness centrality or closeness centrality). Constituents with high strength-based centrality values are typically considered to affect (and to be affected by) the rest of the network more strongly than constituents with smaller values and are often called hubs. Constituents with high path-based centrality values are thought to be important for information or mass transport phenomena on networks, e.g., by being bridges connecting remote network regions (high betweenness centrality) or by reaching other constituents via especially short shortest paths (high closeness centrality).
Local network metrics are also frequently used to assess importance of network constituents by establishing rankings of vertices or of edges (Ghoshal and Barabási, 2011; Lü et al., 2016; Liao et al., 2017). While many studies concentrate on the most important constituents (i.e., the vertex or edge with the highest centrality value), information from the full spectrum of centrality values can be educational when considering the network’s complete internal organization.
Extensions of network metrics to an intermediate, mesoscopic scale are subject of current research. In principle, sub-networks can be identified via, e.g., community or module detection (Fortunato and Hric, 2016) or shell or web decompositions (Bröhl and Lehnertz, 2019; Kong et al., 2019) on this scale and then characterized with global or local metrics instead of the whole networks. However, most sub-network identification schemes are themselves based on local network metrics, which might lead to an overemphasis on the concept behind the used local metric. Also, the interpretation of such a characterization of sub-networks is hitherto unclear. Alternatively, the relative amounts of so-called graphlets or motifs (smallest sub-networks interpreted as generic building blocks) can be investigated and related to theoretical arguments about the roles of these objects in a network (Newman, 2006; Alon, 2007; Ribeiro et al., 2021).
In principle, estimating network metrics can be affected by the same adverse influences that also affect the estimation of properties of interactions—either by error propagation or by influencing a researcher’s decision about how to derive the network based on preliminary results (e.g., a higher average strength of interaction might bias the decided-on level of a threshold for a binary network). Especially, oversampling (effectively recording the same dynamics multiple times) and common sources (due to, e.g., referential recording) can lead to misinterpretations (Porz et al., 2014) since especially estimators for strength of interaction identify largely identical time series as an indication of very strong interactions, which in turn influence, e.g., strength-based centrality metrics. In addition, statistical uncertainties from the estimation of properties of interactions can be amplified in unexpected ways when they are merged into network metrics. In some of these cases, so-called network surrogates (cf. Box 3) can be employed to improve reliability and reduce adverse influences (Ansmann and Lehnertz, 2011; 2012; Wiedermann et al., 2016; Stahn and Lehnertz, 2017; Váša and Mišić, 2022). These surrogates are constrained realizations of the investigated network by randomizing edges (or their weights) while preserving selected network properties such as network size, density of edges, or distribution of edge weights. Then, to decide to which extent a metric of a given network is determined by these properties, its value can be compared to the values for surrogates of this network. Associated null hypotheses typically state that the internal network organization assessed by the network metric is random under the constraint of the preserved properties.
Finally, to trace time-dependent changes of a network and its internal organization over time, networks are derived for each of the above-mentioned segments of time series of recordings of brain dynamics. This results in a sequence of snapshot networks—the time-evolving functional brain network—and time series of the various network metrics, which can be again investigated with methods from time series analysis (cf. Figure 1).
In the previous subsection, we critically assessed the construction of a (snapshot) functional brain network from windowed data of observed brain dynamics (such as EEG, MEG, or fMRI) using bivariate time-series-analysis techniques and the characterization of this network using graph-theoretical concepts and methods. Performing such analyses for successive windows of observed data results in a temporal sequence of snapshot functional brain networks together with time series of the networks’ metrics, both at a temporal resolution that results from the duration of an analysis window. The sequence and the respective time series form the basis for in-depth studies of a time-evolving brain network which can potentially provide more detailed information about the network’s temporal fluctuations and its complex interplay with ongoing physiologic activities compared to what can be achieved with snippets of recordings of brain dynamics that usually last only a few tens of seconds. Among others, the temporal fluctuations can inform about the significance of averaged quantities such as mean values of some network metrics (Lehnertz et al., 2017; 2021) that are widely used in the network neurosciences.
The identification of spontaneous or induced (patho-)physiologic changes within a sequence of snapshot networks requires estimating some distance or (dis-)similarity between two (not necessarily successive) networks (or adjacency matrices). Finding suitable metrics for such a comparison, however, continues to be a difficult task (Bronstein et al., 2006; Andrade et al., 2008; Muskulus et al., 2009; Dimitriadis et al., 2010; Gao et al., 2010; van Wijk et al., 2010; Mémoli, 2011; De Domenico and Biamonte, 2016; Schieber et al., 2017; Fraiman and Fraiman, 2018; Carpi et al., 2019; Martínez and Chavez, 2019; Hartle et al., 2020; Mheich et al., 2020; Lacasa et al., 2021). Difficulties might even aggravate if network size (number of vertices) and edge density depend on time.
An alternative approach is offered by the investigation of time series of the networks’ metrics employing the powerful spectrum of methods from (linear/nonlinear) uni-, bi-, or multivariate time-series-analysis (Bendat and Piersol, 1980; Haykin, 1983; Pikovsky et al., 2001; Kantz and Schreiber, 2003; Reinsel, 2003; Lütkepohl, 2005; Wen and Cheong, 2021; Caligiuri et al., 2023). Statistical (Efron, 1982; Basseville and Nikiforov et al., 1993; Anderson, 2011) as well as Fourier and related analyses (Press and Rybicki, 1989; Huang et al., 1998; Percival and Walden, 2000; Kantelhardt et al., 2001; Bloomfield, 2004) can help to detect anomalies and change points (Aminikhanghahi and Cook, 2017) as well as to assess correlations and periodicities (for an example, see Figure 2). Bi- and multivariate analyses facilitate identification of relationships and interdependencies between time series of different networks’ metrics assessed on the various network scales—from single constituents via communities to the wider network. Before closing this section, we briefly mention another, but so far insufficiently studied analysis approach to investigate time-evolving functional brain networks. It is based on the concept of a multilayer network (Boccaletti et al., 2014; Kivelä et al., 2014; Presigny and Fallani, 2022), which is a complex network structure that consists of multiple networks (e.g., a sequence of snapshot networks). Despite a continuous development of metrics to characterize such a network of networks (Battiston et al., 2014; De Domenico et al., 2015; Nicosia and Latora, 2015; Iacovacci and Bianconi, 2016; Ghariblou et al., 2017; Mandke et al., 2018; Tudisco et al., 2018; Zaoli et al., 2021), applications in the neurosciences and related fields mostly center around frequency-based decompositions or structural and functional decomposition (De Domenico, 2017; Buldú and Porter, 2018; Vaiana and Muldoon, 2020). Due to a number of fundamental problems that arise with this approach, a meaningful interpretation of multilayer brain networks is still to be explored (Buldú and Papo, 2018; Mandke et al., 2018).
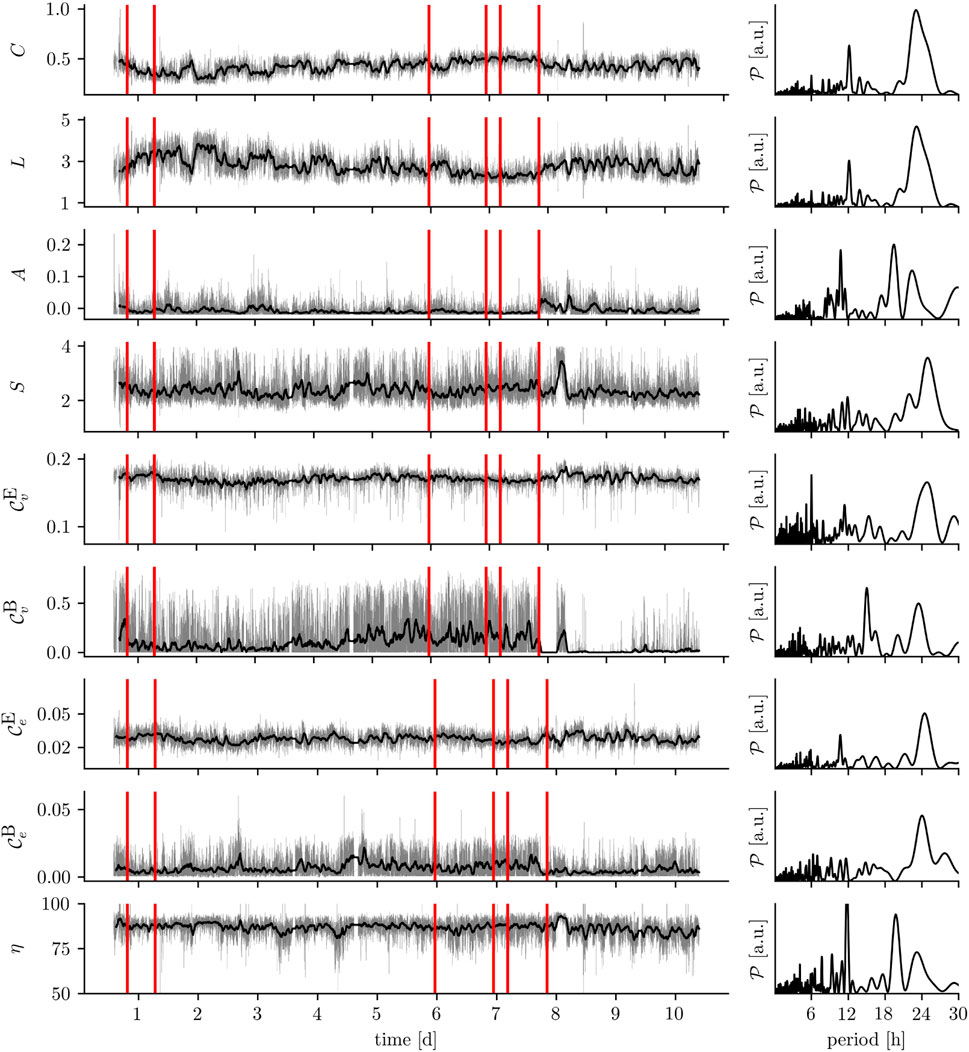
FIGURE 2. Exemplary time series of various network metrics: global clustering coefficient C, average shortest path length L, assortativity A, synchronizability S, eigenvector centrality
Various studies reported increased global clustering coefficients and—although to a lesser extent—average shortest path lengths of time-evolving epileptic brain networks during focal and primary generalized seizures [see, e.g. (Ponten et al., 2007; Kramer et al., 2008; Schindler et al., 2008; Ponten et al., 2009; Kramer et al., 2010)] compared to the seconds before or after a seizure. For 100 focal seizures from 60 people with epilepsy, this observation could be made irrespective of their anatomical onset location (Schindler et al., 2008). If investigated with high temporal resolution (Schindler et al., 2008; Kramer et al., 2010), both network metrics exhibited a concave-like temporal evolution which points to a movement from a more random toward a more regular and more segregated and then back toward a more random functional topology of the epileptic brain network (cf. Box 6). A similar evolution was also observed for time-evolving epileptic brain networks during status epilepticus (Kuhnert et al., 2010).
BOX 6 Schematic change of exemplary global network metric (here: global clustering coefficient and average shortest path length) and changes of the functional topology during seizure.
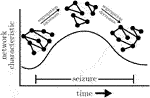
Some authors (Ponten et al., 2007; Kramer et al., 2008; 2010) interpreted the evolution to reflect the small-world topology of short paths and high clustering (Watts and Strogatz, 1998), which is thought to support efficient communication between brain regions at the lowest energetic cost under physiological and pathophysiological conditions (Bassett and Bullmore, 2006; Reijneveld et al., 2007; Bullmore and Sporns, 2012; Stam, 2014). The validity of such an interpretation, however, continues to be matter of considerable debate (Bialonski et al., 2010; Gerhard et al., 2011; Hlinka et al., 2012; Hilgetag and Goulas, 2016; Papo et al., 2016; Hlinka et al., 2017; Zanin et al., 2018) given a large number of factors that have been identified to impact on global clustering coefficient and average shortest path length.
For the same 100 focal seizures from 60 people with epilepsy mentioned above, Bialonski and Lehnertz (2013) reported on a concave-like temporal evolution of assortativity, with a more assortative topology during seizures than during the seconds before or after a seizure. Interestingly, assortativity decreased already prior to seizure end. An increasing assortativity indicates a division of the evolving epileptic brain network into groups of brain regions that are only sparsely interconnected, if at all. Such networks have a comparatively resilient core of mutually interconnected high-degree vertices as has been observed by Zubler et al. (2015) for 198 seizures from 27 people with epilepsy. This core makes epileptic brain networks during seizures quite robust against perturbations, which might explain the mixed success of active brain stimulation to interrupt seizures (Morrell, 2006; Hirsch and Schulze-Bonhage, 2023).
It is important to note that the aforementioned topological network alterations are not accompanied by an increased network synchronization [see, e.g., Schindler et al. (2007b; a); Cash (2013); Majumdar et al. (2014)], which puts into perspective the textbook description of seizures as hypersynchronous events (see also Jiruska et al., 2013). Rather, studies on network synchronization and on the networks’ synchronizability indicate that the changing network topology during seizures is accompanied by an initially decreased network synchronization and decreased stability of the globally synchronized state, both of which increase already prior to seizure end (Schindler et al., 2008; Kramer et al., 2010; Khambhati et al., 2015; Frassineti et al., 2021; Rungratsameetaweemana et al., 2022; Salami et al., 2022). These synchronization phenomena may thus be considered as an emergent (network-topology-mediated) self-regulatory mechanism for seizure termination (Lado and Moshé, 2008; Kramer et al., 2012). It is also important to note that the seizure-related topological network alterations are similar across different types of epilepsies, seizures, medication, age, gender, and other clinical features (see also Haneef and Chiang, 2014). This might point to a common mechanism underlying seizure dynamics in the epileptic brain network (Lehnertz et al., 2014).
In addition to these global aspects of time-evolving epileptic brain networks, several studies investigated the role that network vertices and edges play in seizure evolution (Kramer et al., 2008; Wilke et al., 2011; Varotto et al., 2012; Burns et al., 2014; Geier et al., 2015a; Zubler et al., 2015; Goodfellow et al., 2016; Geier and Lehnertz, 2017b; Bröhl and Lehnertz, 2019; Bröhl and Lehnertz, 2022). Employing various centrality and other metrics to characterize a constituent’s importance for seizure dynamics, most studies reported these metrics to exhibit a high temporal variability as seizures evolve, both inter- and intraindividually. While some studies reported most important vertices (if based on a metric’s temporal mean) to coincide with the clinically defined seizure onset zone (SOZ), other studies could not confirm such a relationship. Rather, network vertices associated with brain regions deemed unaffected by the pathology and more recently also edges (Bröhl and Lehnertz, 2019; Bröhl and Lehnertz, 2022) that functionally connect these vertices were reported as most important during the course of a seizure. If at all, vertices that can be associated with the SOZ gained importance towards the end of a seizure (Burns et al., 2014; Geier et al., 2015a; Zubler et al., 2015).
It remains to be investigated which factors could have led to these inconsistencies, apart from methodological issues (Geier and Lehnertz, 2017b). Nevertheless, the observation of network constituents that are most important during seizures but appear to be unrelated to pathological brain tissue not only underlines the significance of the concept of an epileptic network but also puts into perspective the role of the epileptic focus in seizure dynamics (see also Paz and Huguenard, 2015). One might speculate whether such network constituents represent potential targets for focused therapeutic interventions.
Despite the well-known observation that vulnerability to seizure activity in any one part of the network is influenced by activity everywhere else in the network, and that the network as a whole is responsible for the clinical and electrographic phenomena that we associate with human seizures (Spencer, 2002), we still lack a sufficient quantitative assessment of the time-evolving epileptic brain network’s metrics (from the local to the global network scale) that would help to improve understanding of how the network generates seizures (Kuhlmann et al., 2018; Lehnertz, 2021; Lehnertz et al., 2023) as well as other pathophysiological phenomena (Weiss et al., 2022).
Nevertheless, first indications for certain network reconfigurations to promote the formation of a pre-seizure state could be derived from retrospective studies that investigated macroscopic metrics of time-evolving epileptic brain networks. Kuhnert et al. (2010) analyzed more than 2,100 h of continuous intracranial EEG recordings from 13 subjects with epilepsy during which 75 focal onset seizures and one status epilepticus occurred. From the time series of global clustering coefficients and average shortest path lengths, the authors observed the distributions of these metrics from pre-ictal periods [assumed duration: 4 h; cf. Mormann et al. (2006)] to significantly deviate from the respective distributions of metrics derived from inter-ictal data. Both these global metrics of network structure attained higher values (on average) pre-ictally in the majority of subjects, which the authors interpreted as indications for a loss of functional long-range connections during the pre-ictal period. Geier et al. (2015b) performed similar analysis for assortativity (here: degree-degree correlations) based on more than 1,000 h of continuous intracranial EEG recordings from seven subjects with epilepsy during which 16 focal onset seizures occurred. Pre-ictally, a slightly less assortative mixing of time-evolving epileptic brain networks was observed, which might indicate these networks to be less robust against (endogenous and/or exogenous) perturbations. Both, Kuhnert et al. (2010) and Geier et al. (2015b) stressed, however, the strong influence of daily rhythms seen in the time series of the investigated network metrics (cf. Section 4.3) that would need to be taken into account to avoid misinterpretations (see also Takahashi et al., 2012).
More recently, Rings et al. (2019a) used the network approach to develop a time-series-analysis technique that allows tracing resilience of a networked dynamical system (Fischer et al., 2022), such as the brain. The authors investigated more than 3,200 h of continuous intracranial EEG recordings from 43 subjects with epilepsy during which 112 focal onset seizures occurred. They observed the distribution of the network resilience estimator (dynamical resistance) from 4 h pre-ictal periods to significantly deviate from the respective distribution of the metric derived from inter-ictal data. The achieved high, above-chance-level predictive performance [evaluated with seizure time surrogates (Andrzejak et al., 2003b)] of dynamical resistance would qualify this resilience estimator for seizure-prediction studies. In passing, we note that other estimators of resilience such as those related to the concept of critical slowing down failed to achieve a sufficient predictive performance (Milanowski and Suffczynski, 2016; Wilkat et al., 2019; Hagemann et al., 2021) rating this concept overly simplistic for the human epileptic brain. Interestingly, dynamical resistance increased in the hours prior to the vast majority of seizures. Although one would expect intuitively resilience to decrease in order to facilitate the generation of a seizure, the authors speculated that the reduced effectiveness of antiseizure medication may account for the observed increase. One might also speculate [see the discussions in Frei et al. (2010); Zaveri et al. (2020)] that a pre-ictally increased brain resilience could also reflect the epileptic brain network’s ability to efficiently defy control because of its intrinsic plasticity and adaptiveness. In this context, epilepsy may be viewed as a “learned” disease and seizures as an abnormal learned response to recurrent perturbations—such as seizures (Turrigiano, 1999; Hsu et al., 2008; Lignani et al., 2020; Issa et al., 2023).
In addition to studies on pre-seizure-state-related alterations of functional segregation and integration as well as of robustness of the time-evolving epileptic brain network, further in-depth insights into pre-seizure network reconfigurations could be achieved with investigations of time-dependent changes of properties of the network’s vertices and edges. Tauste Campo et al. (2018) investigated non-continuous intracranial EEG recordings from 10 subjects with epilepsy and used an averaged vertex eigenvector centrality to characterize network state variability. The authors observed network states to become less variable a few hours preceding a global functional connectivity reduction before seizure onset [cf. Mormann et al. (2000; 2003); Kuhlmann et al. (2010); Lehnertz et al. (2016)].
Analyzing retrospectively more than 3,200 h of continuous intracranial EEG recordings from 38 subjects with epilepsy during which 97 focal onset seizures occurred, Rings et al. (2019b) observed distributions of vertex centrality (strength and betweenness centrality) and edge weight from 4 h pre-ictal periods to significantly deviate from the respective distributions of these local network metrics derived from inter-ictal data. The authors reported high, above chance level predictive performance for these deviations and observed that most brain regions (vertices) whose dynamics carried predictive information were connected by most of the edges whose time-dependent weight changes carried predictive information. These vertices, however, never played a central role in the investigated time-evolving epileptic brain networks. More importantly, these vertices were entirely associated with brain regions far off the clinically defined SOZ.
Based on these observations, the authors proposed a scenario for the generation of seizure precursors in a time-evolving epileptic brain network (cf. Box 7): endogenous and/or exogenous factors trigger a rearrangement of the network’s path structure which eventually leads to a formation of bottlenecks in brain regions deemed unaffected by the pathological process which in turn impairs physiologic brain communication [cf. (Avena-Koenigsberger et al., 2018)]. These brain regions, being part of the large-scale epileptic brain network, generate and sustain normal, physiologic brain dynamics during the inter-ictal intervals. Moreover, they also appear to efficiently control the dynamics of vertices related to the SOZ (Lehnertz and Dickten, 2015; Dickten et al., 2016; Johnson et al., 2023).
BOX 7 The path-structure (i.e., layout of the paths in the network) of the functional network is altered prior to seizure, culminating in the forming of bottlenecks. Black networks represent the average functional network in the respective interval. Dotted edges indicate lower interaction strength.

Fruengel et al. (2020) investigated retrospectively continuous intracranial EEG recordings that were part of previous studies (Lehnertz et al., 2016; Rings et al., 2019b) and employed different strength- and path-based vertex centrality metrics (strength, eigenvector, closeness and betweenness centrality) to further improve understanding of local and global reconfigurations of the time-evolving epileptic brain network during the pre-seizure period. The authors observed distributions of vertex centrality from 4 h pre-ictal periods preceding 99 seizures to significantly deviate from the respective distributions of these local network metrics derived from inter-ictal data. As a result of high, above chance level predictive performances for these deviations in various brain regions, they proposed several major scenarios for a pre-seizure reconfiguration of the time-evolving epileptic brain network. With these scenarios, pre-seizure changes in the network are not necessarily confined to specific brain regions. Rather, local and global reconfigurations of the time-evolving epileptic brain network appear to affect virtually all network constituents, i.e., various vertices (brain regions) and the edges (functional connections) between them. Focusing on the pre-seizure changes in degree and betweenness centrality of vertices associated with the SOZ, Sumsky and Greenfield Jr (2022) recently reported similar findings in the seconds prior to 143 seizures from 20 subjects with epilepsy and investigating a comparable amount of continuous intracranial EEG recordings (more than 3,300 h).
If a time-evolving epileptic (and non-epileptic) brain network is derived from continuous multiday, intracranial or scalp-recorded EEG, virtually all time series of the network’s metrics—from local to global—exhibit large fluctuations over time which appear to be partly periodic (cf. Figure 2). These periodicities can be correlated with the circadian and various ultradian rhythms (Kuhnert et al., 2010; Takahashi et al., 2012; Lehnertz et al., 2014; Geier et al., 2015b; Geier and Lehnertz, 2017a; Lehnertz et al., 2017; Rings et al., 2019a; Chiosa et al., 2019; Mitsis et al., 2020; Healy et al., 2021; Lehnertz et al., 2021; Bröhl et al., 2023), which are also thought to modulate seizure risk (Bernard, 2021; Karoly et al., 2021) and seizure dynamics (Schroeder et al., 2020). Despite these large periodic fluctuations, additional alterations of network metrics can be observed on shorter time scales (some tens of seconds to few minutes) typically covered in clinical and research studies. These (mostly time-averaged) alterations of metrics seen in epileptic brains clearly differ from those seen in healthy ones (Chavez et al., 2010; Horstmann et al., 2010; Vlooswijk et al., 2011; Zhang et al., 2011; Richardson, 2012; Caciagli et al., 2014; Haneef and Chiang, 2014; Stam, 2014; Chiang et al., 2015; Foit et al., 2020; Pegg et al., 2020; Slinger et al., 2022). Importantly, they also differ between different types of epilepsy (Lee et al., 2006; Barzegaran et al., 2012; Bartolomei et al., 2013; Chowdhury et al., 2014; van Diessen et al., 2016; Rosch et al., 2018; Kinney-Lang et al., 2019; Lopes et al., 2019; Marino et al., 2019; Ahmadi et al., 2020; Pegg et al., 2020; Woldman et al., 2020; Pegg et al., 2021; Slinger et al., 2022; Tufa et al., 2022). Identifying alterations of network metrics is thus thought to contribute to improving differential diagnosis, treatment, surgical planning, and estimation of prognosis.
This perspective is further supported by research findings of alterations of network metrics due to factors that are known to modulate the epileptic process such as cognition (Kuhnert et al., 2013; Shine, 2019), treatment with antiseizure medication (Anderson et al., 2020; Hatlestad-Hall et al., 2021) and with neuromodulation such as deep brain stimulation (Khaledi-Nasab et al., 2022; Vetkas et al., 2022), responsive neurostimulation (Piper et al., 2022), and vagus nerve stimulation (VNS) (Fraschini et al., 2014). As regards the latter, investigations in larger groups of subjects with epilepsy and in healthy controls (Rings et al., 2021; von Wrede et al., 2021; 2022a; b) demonstrated that short-term, non-invasive transcutaneous auricular VNS can induce small but measurable immediate and enduring alterations of global metrics of the time-evolving epileptic brain network while leaving its local metrics essentially unchanged. The differential alterations of local and global network metrics can be understood using the model of stimulation-mediated stretching and compression of the time-evolving epileptic brain network proposed by Rings et al. (2021). This model takes into account the changes of the network’s path structure (average shortest path length) and of its tendency to form tightly knit groups of vertices (global clustering coefficient) as well as the centrality (importance) hierarchies of vertices and edges to characterize stimulation-mediated modifications of the larger network. The authors conjectured that these topology-modifying stretching and compression effects likewise impact on the network’s assortativity and synchronizability, thereby enhancing its robustness and stability.
Recently, Lehnertz et al. (2023a) reported on a similar reconfiguration and modification of networks together with their stability and robustness properties in a group of 20 subjects with and without epilepsy upon a short-term manual visceral-osteopathic stimulation of the vagus nerve at the abdomen. This finding may add to the current discussion on the importance of the gut-brain axis in the treatment of epilepsy (Ding et al., 2021; Sinha et al., 2022) and to further enhance our understanding of how multiple organs in the human body dynamically interact as a network and integrate their functions to generate (patho-)physiological states (Ivanov, 2021).
Summarizing the findings achieved so far, we propose a model for the temporal evolution of the epileptic brain network (cf. Figure 3A). To this end, we consider an abstract “phase-space” that is spanned by the networks’ global clustering coefficients C, average shortest path lengths L, and synchronizabilities S to capture the diurnal variation of segregation, integration, and the networks’ propensity to synchronize (although they are correlated, we use C and L to facilitate readability). The networks’ motion in this space is largely dominated by the circadian rhythm (with a period length of about 24 h; cf. Figure 2), with a comparably lower (higher) segregation (integration) as well as an increased propensity to synchronize during daytimes. This global motion is modulated by ultradian rhythms with period lengths around 12 h and shorter, seen during both night- and daytimes (cf. Figure 2). These modulations likely reflect different sleep/vigilance states and their accompanying modifications of critical network properties [such as segregation and integration (Deco et al., 2015) as well as the propensity (or vulnerability) to be synchronized by an admissible input activation] may account for the well-known fluctuations of epileptic activities and seizure occurrence (Spencer et al., 2016; Khan et al., 2018). Interestingly, the networks’ motion is, in general, only sparsely modulated by comparably short-lasting exogenous (e.g., neurostimulation; cf. Section 4.3 and Figure 3B) and endogenous perturbations (seizures; cf. Section 4.1 and Figure 3C). Nevertheless, the specific manner of these modulations provides novel insights into the effectiveness of neurostimulation/-modulation approaches as well as into network mechanisms of pre-seizure dynamics (cf. Section 4.2), seizure generation, spread, and termination.
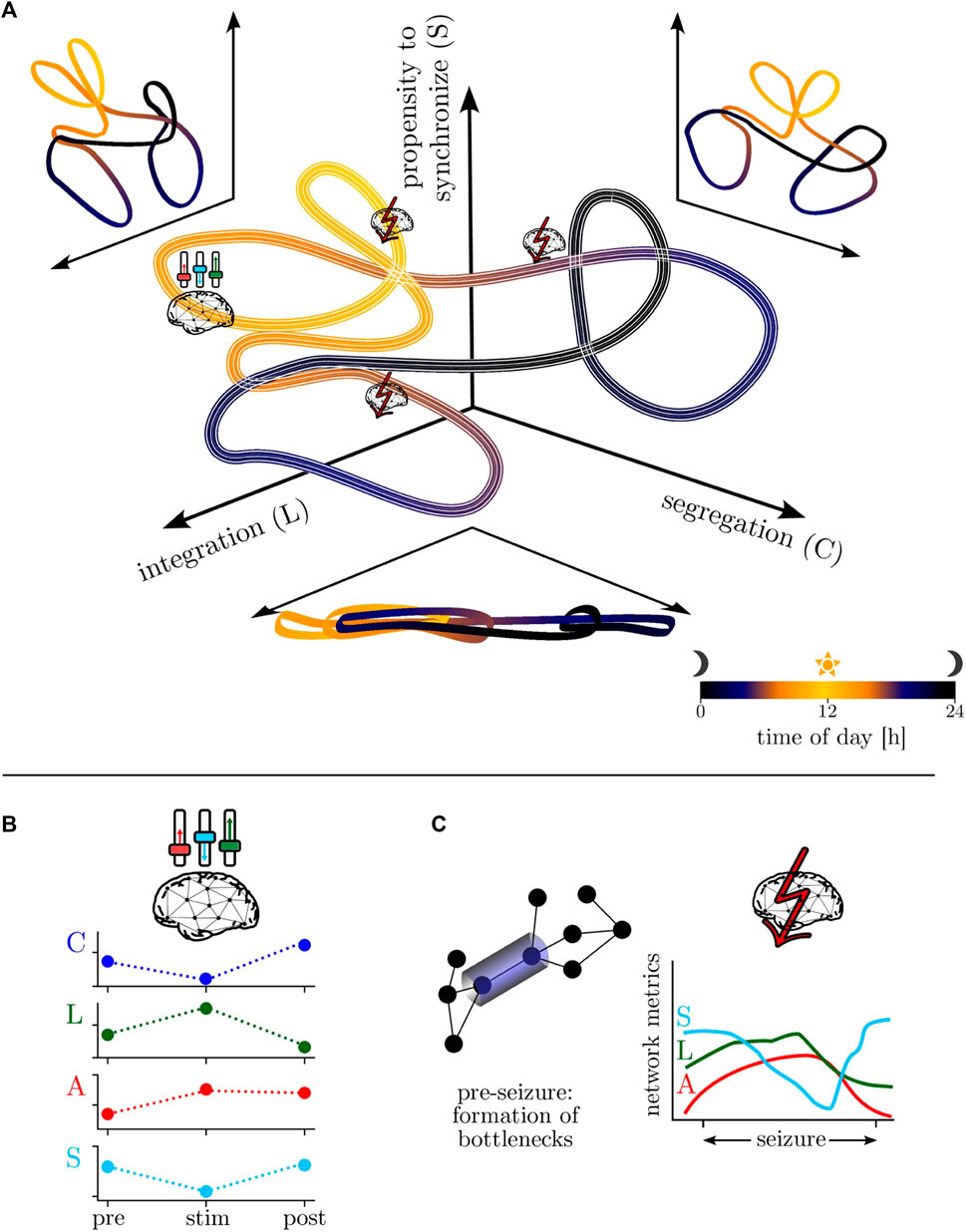
FIGURE 3. (A) Model of the temporal evolution of the epileptic brain network in an abstract “phase-space”—spanned by the networks’ properties of segregation, integration, and propensity to synchronize—over the day-night cycle (color-coded). Line thickness encodes infradian variability. (B) Schematic of neurostimulation-induced modifications of global network properties (global clustering coefficient C, average shortest path length L, assortativity A, synchronizability S; local ones remain essentially unchanged). (C) Schematic of local network modifications (here: formation of bottlenecks) related to pre-seizure dynamics and of global modifications related to seizure dynamics.
Initiated by Susan Spencer’s seminal work on neural networks in human epilepsy, the last two decades have seen quite a number of accomplishments in defining and characterizing the epileptic brain network, including an important change in perspective from a static to a time-evolving network (cf. Li et al., 2017), which better takes into account the fact that epilepsy is a dynamic disease. Nevertheless, much remains to be completed in the coming years, and several issues need to be addressed to advance the field.
Beginning with collecting the brain’s structure and dynamics, there is a strong need for a recording technique that allows one to capture the multiple spatial and temporal scales of the epileptic process. If different recording techniques are used, there is still the problem of an unambiguous fusion of the different scales (Schevon et al., 2019; Driscoll et al., 2021; Presigny and Fallani, 2022). Likewise, suitable strategies to avoid spatial and temporal oversampling of brain dynamics are urgently needed since oversampling can lead to severe misinterpretations of network characteristics (Bialonski et al., 2010; Zalesky et al., 2010; Bialonski et al., 2011; Joudaki et al., 2012; Montes-Restrepo et al., 2014; Porz et al., 2014; Puce and Hämäläinen, 2017; Conrad et al., 2020; Vorderwülbecke et al., 2020; Iivanainen et al., 2021; Allouch et al., 2023). It remains to be shown whether recent developments of edge/vertex removal strategies (Bellingeri et al., 2020; Bröhl and Lehnertz, 2023) [or, in case of undersampling, techniques to predict edges (Zhou, 2021) and to detect hidden vertices (Su et al., 2012)] can help to avoid misinterpreting characteristics of the time-evolving epileptic brain network.
Open questions related to deriving functional brain networks from recordings of brain dynamics were recently summarized by Korhonen et al. (2021). Beyond that, we note that defining network edges from properties of an interaction between pairs of brain regions derived from their dynamics is predominantly based on bivariate time-series-analysis techniques that assume a deterministic mechanism behind interactions and any stochastic aspect is treated as mere measurement noise. Recent developments in characterizing two-dimensional stochastic processes (Rydin Gorjão et al., 2019; Aslim et al., 2021) based on the Kramers–Moyal expansion might provide novel insights into stochastic interactions in the future. Likewise, a further improved characterization of the temporal structure of the brain’s dynamics could be achieved with bivariate ordinal time-series-analysis techniques (Lehnertz, 2023) that allow one to assess both strength and direction of an interaction. Moreover, while there is an increasing interest in so-called higher-order interactions (Battiston et al., 2021; Bianconi, 2021; Boccaletti et al., 2023) (interactions between more than pairs of brain regions), it remains unclear how to estimate the relevant higher-order interactions from time-series data and what advantages such hyper networks will provide aside from theoretical arguments.
In Sections 3.3 and 3.4, we presented network metrics and analysis tools to characterize a time-evolving brain network and briefly discussed their pros and cons. Most concepts and metrics were initially developed to characterize static networks and are not immediately transferable to a time-evolving network. Recently proposed analysis tools for time-dependent networks [see, e.g., De Domenico (2017); Thompson et al. (2017); Salcedo-Sanz et al. (2022)] are either not straightforward to convert to weighted and complete networks (as in case of EEG-derived functional brain networks) or wait for proof of their suitability for characterizing a time-evolving epileptic brain network. In general, concepts and metrics proposed and used to characterize static networks need to be redefined or appropriately extended to time-evolving networks, also to account for the impact of time ordering on causal relationships in weighted and directed networks.
Additional in-depth insights into the complex behavior of a time-evolving epileptic brain network prior to and during seizures could be achieved with novel concepts and tools to characterize signal propagation in complex networks (Hens et al., 2019; Ji et al., 2023) and synchronized dynamics of time-varying networks (Ghosh et al., 2022). Considering the recent promising developments of centrality concepts and metrics to characterize properties of edges as well as the edges’ time-varying role in the larger network (Bröhl and Lehnertz, 2019; Bröhl and Lehnertz, 2022; Contisciani et al., 2022; Altafini et al., 2023), adopting an edge-centric perspective (cf. Faskowitz et al., 2022; Novelli and Razi, 2022) could lead to a further improved understanding of the time-evolving epileptic brain network and its control (Sinha et al., 2022; Lehnertz et al., 2023; Frauscher et al., 2023).
A variety of computational/mathematical models for epilepsy have been proposed [see, e.g., Lytton (2008); Holt and Netoff (2013); Depannemaecker et al. (2021); Pathak et al. (2022)], mostly based on concepts from dynamical systems theory. The majority of these models focuses on seizure dynamics (initiation, spread, termination) only, and the network character of the disease is only rarely taken into account (Kalitzin et al., 2019; Goodfellow et al., 2022). Seizure-like events (states of synchronous rhythmic activity), however, may also emerge spontaneously—i.e., without a change in control parameters—from an oscillator network with some balance between regular and random topology (Rothkegel and Lehnertz, 2014; Ansmann et al., 2016; Gerster et al., 2020; Anesiadis and Provata, 2022; Wu et al., 2022). Other mechanisms behind tipping phenomena include noise-, rate-, and shock-induced tipping [see, e.g., Ashwin et al. (2012); Feudel et al. (2018); Ritchie et al. (2023); Swierczek-Jereczek et al. (2023)]. A better understanding of how seizures emerge from an aberrant, time-evolving epileptic brain network would profit from considering, e.g., critical transition scenarios other than bifurcation-induced tipping which may be too simplistic for the human epileptic brain (Wilkat et al., 2019). Neither of these phenomena require any change of the system’s stability, and various time-series-analysis techniques have been proposed to identify early warning indicators (George et al., 2021; Heßler and Kamps, 2022).
Similarly, a better understanding of the longer time scales of brain dynamics that govern the recurrence of seizures would profit from considering mechanisms that can give rise to various long term, fluctuating behavior. We here mention switching phenomena related to the different types of intermittency (Perez Velazquez et al., 1999; Rizzi et al., 2016; Pisarchik et al., 2018), switching in fast-slow systems (Kuehn, 2011) and in heteroclinic networks (Kirst and Timme, 2008; Aguiar et al., 2011; Bick and Field, 2017; Morrison and Young, 2022; Meyer-Ortmanns, 2023) multistability (Lopes da Silva et al., 2003; Takeshita et al., 2007; Rothkegel and Lehnertz, 2009; Breakspear, 2017; Pisarchik and Hramov, 2022), and metastability (Kelso, 2012; Tognoli and Kelso, 2014; Rossi et al., 2023). The validity of such models could be tested if continuous long-term recordings of brain dynamics—covering weeks to months [see, e.g., Weisdorf et al. (2019); Duun-Henriksen et al. (2020)]—would be publically available.
In order to consolidate the network approach into clinical practice, the following issues would need to be tackled.
Diagnosing epilepsy: The understanding and treatment of epilepsy requires a clear-cut diagnosis of the possibly underlying disease, allocation of syndromes, and distinction from other neurological and non-neurological diseases, in comparison to a healthy brain. Nevertheless, the techniques currently used routinely only allow a clear-cut diagnosis in, on average, 50% of the subjects (Oto, 2017; Elger and Hoppe, 2018; Amin and Benbadis, 2019), which can probably be related to a number of confounding factors. It can be conjectured that the incorporation of the concept of a time-evolving epileptic brain network into aforementioned differentiation steps can lead to an improved diagnosing and classification of epilepsy, even on a personalized level (Nabbout and Kuchenbuch, 2020).
Choosing treatment: Currently, clinical decisions regarding treatment options are primarily guided by the epilepsy syndrome and its burden. Despite several options [e.g., pharmacological treatment (Kwan and Brodie, 2000; Wandschneider and Koepp, 2016; Höller et al., 2018; Höller and Nardone, 2021), surgical treatment (Téllez-Zenteno et al., 2007), nutritional treatment (Pizzo et al., 2022), neurostimulation (Schulze-Bonhage, 2019; Piper et al., 2022); see Lehnertz et al. (2023) for an overview of network-based treatment concepts], the treatment is successful in only about half of the cases. Moreover, from a clinical point of view, the goal of epilepsy treatment is seizure freedom and if this is not possible reduction of seizure frequency and burden of the disease. However, the epileptic brain is not a temporarily disturbed normal brain, and a seizure is not a clinical sign of a transient dysfunction of a normal brain. Therefore, on a conceptual level, the treatment of epilepsy should be addressed more as the treatment of an evolving epileptic brain rather than treating seizures. Further investigation into the network-modulating effects of different interventions—adopted to the time-evolving epileptic brain network—is vital to provide physicians with information about the best and most promising treatment options in individual treatment situations.
Optimizing and monitoring therapy: Treating subjects with epilepsy means to achieve a situation in which the subject not only has no seizures, despite the disease epilepsy, but also is able to live an unimpaired life. Impairments result not only from seizures, but also possibly from an underlying structural correlate, and the epilepsy treatment. A thorough clinical action includes therapy monitoring, adapting therapies to the current situation, and preferably acting with foresight in order to avoid anticipatory therapy consequences. However, available data is limited by the subjective perception and possible inadequate sampling of other influencing dynamics and their interactions [e.g., pharmacokinetics, biological rhythms, fluctuations of the endocrinal system (Lehnertz et al., 2020; Healy et al., 2021)], and hence is not yet sufficient to reliably inform such clinical action. Individual tracking the epileptic brain’s network changes over the time—not only during seizures, but also in response to chronic treatment, during everyday activities and therapeutic ad hoc interventions—are needed, to unveil the potential for tailored epilepsy treatment. This treatment should be targeted at the time-evolving epileptic brain network and keep it in states in which the subject can live everyday life without impairment. For a treatment to be successful in the long term, it is essential to keep in mind the brain’s adaptivity and learning capabilities, and to modulate them in an appropriate way to achieve a healthier brain network which “unlearned” epilepsy.
Recognizing epilepsy as a network disease has sparked extensive and expanding research, which led to much progress towards the understanding of the human epileptic brain as well as prediction and control of its dynamics. This has reshaped the comprehension and perception of epilepsy, entailing a paradigm shift from a clinically defined epileptic focus via a spatially and functionally extended epileptic network to a large-scale, time-evolving epileptic brain network, whose changes comprise various temporal and spatial scales. Although such an approach poses a difficult task, the last two decades have been coined by novel insights and progression, ranging from recording the brain’s structure and dynamics at various spatial and temporal scales to constructing functional brain networks and investigating their properties with various innovative and adapted customized tools of analysis. Insights achieved so far regarding the temporal evolution of the epileptic brain network show great potential for clinical translation, progressing and maturing the state-of-art of diagnosis and treatment of epilepsy. Further studies on the temporal-evolution of epileptic and other diseased brain networks in comparison to non-affected brains will help to achieve these goals.
TB: Writing–original draft, Writing–review and editing. TR: Writing–original draft, Writing–review and editing. JP: Writing–original draft, Writing–review and editing. RvW: Writing–original draft, Writing–review and editing. KL: Writing–original draft, Writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Verein zur Foerderung der Epilepsieforschung e.V. (Bonn).
We thank Manuel Adams and Max Potratzki for fruitful discussions.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors RvW and KL declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abreu, R., Leal, A., and Figueiredo, P. (2018). EEG-informed fMRI: a review of data analysis methods. Front. Hum. Neurosci. 12, 29. doi:10.3389/fnhum.2018.00029
Adamovich, T., Zakharov, I., Tabueva, A., and Malykh, S. (2022). The thresholding problem and variability in the EEG graph network parameters. Sci. Rep. 12, 18659. doi:10.1038/s41598-022-22079-2
Aguiar, M., Ashwin, P., Dias, A., and Field, M. (2011). Dynamics of coupled cell networks: synchrony, heteroclinic cycles and inflation. J. Nonlin. Sci. 21, 271–323. doi:10.1007/s00332-010-9083-9
Ahmadi, N., Pei, Y., Carrette, E., Aldenkamp, A. P., and Pechenizkiy, M. (2020). Eeg-based classification of epilepsy and PNES: EEG microstate and functional brain network features. Brain Inf. 7, 6–22. doi:10.1186/s40708-020-00107-z
Aiello, M., Cavaliere, C., and Salvatore, M. (2016). Hybrid PET/MR imaging and brain connectivity. Front. Neurosci. 10, 64. doi:10.3389/fnins.2016.00064
Alemán-Gómez, Y., Griffa, A., Houde, J.-C., Najdenovska, E., Magon, S., Cuadra, M. B., et al. (2022). A multi-scale probabilistic atlas of the human connectome. Sci. Data 9, 516. doi:10.1038/s41597-022-01624-8
Allers, K., Essue, B. M., Hackett, M. L., Muhunthan, J., Anderson, C. S., Pickles, K., et al. (2015). The economic impact of epilepsy: a systematic review. BMC Neurol. 15, 245–316. doi:10.1186/s12883-015-0494-y
Allouch, S., Kabbara, A., Duprez, J., Khalil, M., Modolo, J., and Hassan, M. (2023). Effect of channel density, inverse solutions and connectivity measures on EEG resting-state networks reconstruction: a simulation study. NeuroImage 271, 120006. doi:10.1016/j.neuroimage.2023.120006
Alon, U. (2007). Network motifs: theory and experimental approaches. Nat. Rev. Gen. 8, 450–461. doi:10.1038/nrg2102
Altafini, D., Bini, D. A., Cutini, V., Meini, B., and Poloni, F. (2023). An edge centrality measure based on the Kemeny constant. SIAM J. Matrix Anal. Appl. 44, 648–669. doi:10.1137/22m1486728
Amin, U., and Benbadis, S. R. (2019). The role of EEG in the erroneous diagnosis of epilepsy. J. Clin. Neurophysiol. 36, 294–297. doi:10.1097/WNP.0000000000000572
Aminikhanghahi, S., and Cook, D. J. (2017). A survey of methods for time series change point detection. Knowl. Inf. Syst. 51, 339–367. doi:10.1007/s10115-016-0987-z
Amunts, K., Mohlberg, H., Bludau, S., and Zilles, K. (2020). Julich-Brain: a 3D probabilistic atlas of the human brain’s cytoarchitecture. Science 369, 988–992. doi:10.1126/science.abb4588
Anastasiadou, M. N., Christodoulakis, M., Papathanasiou, E. S., Papacostas, S. S., Hadjipapas, A., and Mitsis, G. D. (2019). Graph theoretical characteristics of EEG-based functional brain networks in patients with epilepsy: the effect of reference choice and volume conduction. Front. Neurosci. 13, 221. doi:10.3389/fnins.2019.00221
Anderson, D. E., Madhavan, D., and Swaminathan, A. (2020). Global brain network dynamics predict therapeutic responsiveness to cannabidiol treatment for refractory epilepsy. Brain Commun. 2, fcaa140. doi:10.1093/braincomms/fcaa140
Anderson, D. N., Charlebois, C. M., Smith, E. H., Arain, A. M., Davis, T. S., and Rolston, J. D. (2021). Probabilistic comparison of gray and white matter coverage between depth and surface intracranial electrodes in epilepsy. Sci. Rep. 11, 24155. doi:10.1038/s41598-021-03414-5
Andrade, R. F., Miranda, J. G., Pinho, S. T., and Lobão, T. P. (2008). Measuring distances between complex networks. Phys. Lett. A 372, 5265–5269. doi:10.1016/j.physleta.2008.06.044
Andrzejak, R. G., Kraskov, A., Stögbauer, H., Mormann, F., and Kreuz, T. (2003a). Bivariate surrogate techniques: necessity, strengths, and caveats. Phys. Rev. E 68, 066202. doi:10.1103/PhysRevE.68.066202
Andrzejak, R. G., Mormann, F., Kreuz, T., Rieke, C., Kraskov, A., Elger, C. E., et al. (2003b). Testing the null hypothesis of the nonexistence of a preseizure state. Phys. Rev. E 67, 010901. (R). doi:10.1103/PhysRevE.67.010901
Anesiadis, K., and Provata, A. (2022). Synchronization in multiplex leaky integrate-and-fire networks with nonlocal interactions. Front. Netw. Physiol. 2, 910862. doi:10.3389/fnetp.2022.910862
Ansmann, G., and Lehnertz, K. (2011). Constrained randomization of weighted networks. Phys. Rev. E 84, 026103. doi:10.1103/PhysRevE.84.026103
Ansmann, G., and Lehnertz, K. (2012). Surrogate-assisted analysis of weighted functional brain networks. J. Neurosci. Methods 208, 165–172. doi:10.1016/j.jneumeth.2012.05.008
Ansmann, G., Lehnertz, K., and Feudel, U. (2016). Self-induced switchings between multiple space-time patterns on complex networks of excitable units. Phys. Rev. X 6, 011030. doi:10.1103/PhysRevX.6.011030
Arnhold, J., Grassberger, P., Lehnertz, K., and Elger, C. E. (1999). A robust method for detecting interdependences: application to intracranially recorded EEG. Phys. D. 134, 419–430. doi:10.1016/s0167-2789(99)00140-2
Ashwin, P., Wieczorek, S., Vitolo, R., and Cox, P. (2012). Tipping points in open systems: bifurcation, noise-induced and rate-dependent examples in the climate system. Phil. Trans. Roy. Soc. A 370, 1166–1184. doi:10.1098/rsta.2011.0306
Aslim, E., Rings, T., Zabawa, L., and Lehnertz, K. (2021). Enhancing the accuracy of a data-driven reconstruction of bivariate jump-diffusion models with corrections for higher orders of the sampling interval. J. Stat. Mechan. Theor. Exp. 2021, 033406. doi:10.1088/1742-5468/abe59a
Atay, F. M., Bıyıkoğlu, T., and Jost, J. (2006). Network synchronization: spectral versus statistical properties. Phys. D. 224, 35–41. doi:10.1016/j.physd.2006.09.018
Atlas, S. W. (2009). Magnetic resonance imaging of the brain and spine, 1. Lippincott Williams & Wilkins.
Avena-Koenigsberger, A., Misic, B., and Sporns, O. (2018). Communication dynamics in complex brain networks. Nat. Rev. Neurosci. 19, 17–33. doi:10.1038/nrn.2017.149
Babaeeghazvini, P., Rueda-Delgado, L. M., Gooijers, J., Swinnen, S. P., and Daffertshofer, A. (2021). Brain structural and functional connectivity: a review of combined works of diffusion magnetic resonance imaging and electro-encephalography. Front. Hum. Neurosci. 15, 721206. doi:10.3389/fnhum.2021.721206
Babiloni, C., Barry, R. J., Başar, E., Blinowska, K. J., Cichocki, A., Drinkenburg, W. H., et al. (2020). International Federation of Clinical Neurophysiology (IFCN)–EEG research workgroup: recommendations on frequency and topographic analysis of resting state EEG rhythms. Part 1: applications in clinical research studies. Clin. Neurophysiol. 131, 285–307. doi:10.1016/j.clinph.2019.06.234
Baillet, S. (2017). Magnetoencephalography for brain electrophysiology and imaging. Nat. Neurosci. 20, 327–339. doi:10.1038/nn.4504
Baker, G. A., Jacoby, A., Buck, D., Stalgis, C., and Monnet, D. (1997). Quality of life of people with epilepsy: a European study. Epilepsia 38, 353–362. doi:10.1111/j.1528-1157.1997.tb01128.x
Bammer, R. (2003). Basic principles of diffusion-weighted imaging. Eur. J. Radiol. 45, 169–184. doi:10.1016/s0720-048x(02)00303-0
Barahona, M., and Pecora, L. M. (2002). Synchronization in small-world systems. Phys. Rev. Lett. 89, 054101. doi:10.1103/PhysRevLett.89.054101
Bartolomei, F., Bettus, G., Stam, C. J., and Guye, M. (2013). Interictal network properties in mesial temporal lobe epilepsy: a graph theoretical study from intracerebral recordings. Clin. Neurophysiol. 124, 2345–2353. doi:10.1016/j.clinph.2013.06.003
Bartolomei, F., Lagarde, S., Wendling, F., McGonigal, A., Jirsa, V., Guye, M., et al. (2017). Defining epileptogenic networks: contribution of SEEG and signal analysis. Epilepsia 58, 1131–1147. doi:10.1111/epi.13791
Barzegaran, E., Joudaki, A., Jalili, M., Rossetti, A. O., Frackowiak, R. S., and Knyazeva, M. G. (2012). Properties of functional brain networks correlate with frequency of psychogenic non-epileptic seizures. Front. Hum. Neurosci. 6, 335. doi:10.3389/fnhum.2012.00335
Bassett, D. S., and Bullmore, E. (2006). Small-world brain networks. Neurosci. 12, 512–523. doi:10.1177/1073858406293182
Basseville, M., and Nikiforov, I. V. (1993). Detection of abrupt changes: theory and application, 104. Englewood Cliffs, N. J.: Prentice Hall.
Battiston, F., Amico, E., Barrat, A., Bianconi, G., Ferraz de Arruda, G., Franceschiello, B., et al. (2021). The physics of higher-order interactions in complex systems. Nat. Phys. 17, 1093–1098. doi:10.1038/s41567-021-01371-4
Battiston, F., Nicosia, V., and Latora, V. (2014). Structural measures for multiplex networks. Phys. Rev. E 89, 032804. doi:10.1103/PhysRevE.89.032804
Beghi, E., Giussani, G., Nichols, E., Abd-Allah, F., Abdela, J., Abdelalim, A., et al. (2019). Global, regional, and national burden of epilepsy, 1990–2016: a systematic analysis for the global burden of disease study 2016. Lancet Neurol. 18, 357–375. doi:10.1016/S1474-4422(18)30454-X
Bellingeri, M., Bevacqua, D., Scotognella, F., Alfieri, R., and Cassi, D. (2020). A comparative analysis of link removal strategies in real complex weighted networks. Sci. Rep. 10, 3911. doi:10.1038/s41598-020-60298-7
Bendat, J. S., and Piersol, A. G. (1980). Engineering applications of correlation and spectral analysis. New York: Wiley-Interscience.
Berg, A. T., Berkovic, S. F., Brodie, M. J., Buchhalter, J., Cross, J. H., van Emde Boas, W., et al. (2010). Revised terminology and concepts for organization of seizures and epilepsies: report of the ILAE commission on classification and terminology, 2005–2009. Epilepsia 51, 676–685. doi:10.1111/j.1528-1167.2010.02522.x
Berg, A. T., and Scheffer, I. E. (2011). New concepts in classification of the epilepsies: entering the 21st century. Epilepsia 52, 1058–1062. doi:10.1111/j.1528-1167.2011.03101.x
Bernabei, J. M., Arnold, T. C., Shah, P., Revell, A., Ong, I. Z., Kini, L. G., et al. (2021). Electrocorticography and stereo EEG provide distinct measures of brain connectivity: implications for network models. Brain Commun. 3, fcab156. doi:10.1093/braincomms/fcab156
Bernard, C. (2021). Circadian/multidien molecular oscillations and rhythmicity of epilepsy (MORE). Epilepsia 62, S49–S68. doi:10.1111/epi.16716
Bernhardt, B. C., Bonilha, L., and Gross, D. W. (2015). Network analysis for a network disorder: the emerging role of graph theory in the study of epilepsy. Epilepsy Behav. 50, 162–170. doi:10.1016/j.yebeh.2015.06.005
Bialonski, S., Horstmann, M., and Lehnertz, K. (2010). From brain to earth and climate systems: small-world interaction networks or not? Chaos 20, 013134. doi:10.1063/1.3360561
Bialonski, S., and Lehnertz, K. (2013). Assortative mixing in functional brain networks during epileptic seizures. Chaos 23, 033139. doi:10.1063/1.4821915
Bialonski, S., Wendler, M., and Lehnertz, K. (2011). Unraveling spurious properties of interaction networks with tailored random networks. PLoS ONE 6, e22826. doi:10.1371/journal.pone.0022826
Bick, C., and Field, M. (2017). Asynchronous networks and event driven dynamics. Nonlinearity 30, 558–594. doi:10.1088/1361-6544/aa4f62
Bijsterbosch, J., Harrison, S. J., Jbabdi, S., Woolrich, M., Beckmann, C., Smith, S., et al. (2020). Challenges and future directions for representations of functional brain organization. Nat. Neurosci. 23, 1484–1495. doi:10.1038/s41593-020-00726-z
Boccaletti, S., Bianconi, G., Criado, R., Del Genio, C. I., Gómez-Gardenes, J., Romance, M., et al. (2014). The structure and dynamics of multilayer networks. Phys. Rep. 544, 1–122. doi:10.1016/j.physrep.2014.07.001
Boccaletti, S., De Lellis, P., del Genio, C., Alfaro-Bittner, K., Criado, R., Jalan, S., et al. (2023). The structure and dynamics of networks with higher order interactions. Phys. Rep. 1018, 1–64. doi:10.1016/j.physrep.2023.04.002
Bonilha, L., Gleichgerrcht, E., Fridriksson, J., Rorden, C., Breedlove, J. L., Nesland, T., et al. (2015). Reproducibility of the structural brain connectome derived from diffusion tensor imaging. PloS one 10, e0135247. doi:10.1371/journal.pone.0135247
Borrelli, P., Cavaliere, C., Salvatore, M., Jovicich, J., and Aiello, M. (2022). Structural brain network reproducibility: influence of different diffusion acquisition and tractography reconstruction schemes on graph metrics. Brain Connect. 12, 754–767. doi:10.1089/brain.2021.0123
Boto, E., Hill, R. M., Rea, M., Holmes, N., Seedat, Z. A., Leggett, J., et al. (2021). Measuring functional connectivity with wearable MEG. NeuroImage 230, 117815. doi:10.1016/j.neuroimage.2021.117815
Bottino, F., Lucignani, M., Pasquini, L., Mastrogiovanni, M., Gazzellini, S., Ritrovato, M., et al. (2022). Spatial stability of functional networks: a measure to assess the robustness of graph-theoretical metrics to spatial errors related to brain parcellation. Front. Neurosci. 15, 736524. doi:10.3389/fnins.2021.736524
Breakspear, M. (2017). Dynamic models of large-scale brain activity. Nat. Neurosci. 20, 340–352. doi:10.1038/nn.4497
Bröhl, T., and Lehnertz, K. (2019). Centrality-based identification of important edges in complex networks. Chaos 29, 033115. doi:10.1063/1.5081098
Bröhl, T., and Lehnertz, K. (2022). A straightforward edge centrality concept derived from generalizing degree and strength. Sci. Rep. 12, 4407. doi:10.1038/s41598-022-08254-5
Bröhl, T., and Lehnertz, K. (2023). A perturbation-based approach to identifying potentially superfluous network constituents. Chaos An Interdiscip. J. Nonlinear Sci. 33, 063119. doi:10.1063/5.0152030
Bröhl, T., von Wrede, R., and Lehnertz, K. (2023). Impact of biological rhythms on the importance hierarchy of constituents in time-dependent functional brain networks. Front. Netw. Physiol. 3, 1237004. doi:10.3389/fnetp.2023.1237004
Bronstein, A. M., Bronstein, M. M., and Kimmel, R. (2006). Efficient computation of isometry-invariant distances between surfaces. SIAM J. Sci. Comput. 28, 1812–1836. doi:10.1137/050639296
Buldú, J. M., and Papo, D. (2018). Can multilayer brain networks be a real step forward? Comment on Network science of biological systems at different scales: a review by M. Gosak et al. Phys. Life Rev. 24, 153–155. doi:10.1016/j.plrev.2017.12.007
Buldú, J. M., and Porter, M. A. (2018). Frequency-based brain networks: from a multiplex framework to a full multilayer description. Netw. Neurosci. 2, 418–441. doi:10.1162/netn_a_00033
Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198. doi:10.1038/nrn2575
Bullmore, E., and Sporns, O. (2012). The economy of brain network organization. Nat. Rev. Neurosci. 13, 336–349. doi:10.1038/nrn3214
Burns, S. P., Santaniello, S., Yaffe, R. B., Jouny, C. C., Crone, N. E., Bergey, G. K., et al. (2014). Network dynamics of the brain and influence of the epileptic seizure onset zone. Proc. Natl. Acad. Sci. U.S.A. 111, E5321–E5330. doi:10.1073/pnas.1401752111
Buxton, R. B. (2013). The physics of functional magnetic resonance imaging (fMRI). Rep. Prog. Phys. 76, 096601. doi:10.1088/0034-4885/76/9/096601
Caciagli, L., Bernhardt, B. C., Hong, S.-J., Bernasconi, A., and Bernasconi, N. (2014). Functional network alterations and their structural substrate in drug-resistant epilepsy. Front. Neurosci. 8, 411. doi:10.3389/fnins.2014.00411
Caligiuri, A., Eguíluz, V. M., Di Gaetano, L., Galla, T., and Lacasa, L. (2023). Lyapunov exponents for temporal networks. Phys. Rev. E 107, 044305. doi:10.1103/PhysRevE.107.044305
Carpi, L. C., Schieber, T. A., Pardalos, P. M., Marfany, G., Masoller, C., Díaz-Guilera, A., et al. (2019). Assessing diversity in multiplex networks. Sci. Rep. 9, 4511. doi:10.1038/s41598-019-38869-0
Cash, S. S. (2013). Status epilepticus as a system disturbance: is status epilepticus due to synchronization or desynchronization? Epilepsia 54, 37–39. doi:10.1111/epi.12273
Centeno, M., and Carmichael, D. W. (2014). Network connectivity in epilepsy: resting state fMRI and EEG–fMRI contributions. Front. Neurol. 5, 93. doi:10.3389/fneur.2014.00093
Chaimow, D., Yacoub, E., Uğurbil, K., and Shmuel, A. (2018). Spatial specificity of the functional MRI blood oxygenation response relative to neuronal activity. Neuroimage 164, 32–47. doi:10.1016/j.neuroimage.2017.08.077
Charvet, C. J. (2023). Mapping human brain pathways: challenges and opportunities in the integration of scales. Brain Behav. Evol. 98, 194–209. doi:10.1159/000530317
Chavez, M., Valencia, M., Navarro, V., Latora, V., and Martinerie, J. (2010). Functional modularity of background activities in normal and epileptic brain networks. Phys. Rev. Lett. 104, 118701. doi:10.1103/PhysRevLett.104.118701
Chen, W.-L., Wagner, J., Heugel, N., Sugar, J., Lee, Y.-W., Conant, L., et al. (2020). Functional near-infrared spectroscopy and its clinical application in the field of neuroscience: advances and future directions. Front. Neurosci. 14, 724. doi:10.3389/fnins.2020.00724
Chen, Z., Brodie, M., Liew, D., and Kwan, P. (2018). Treatment outcomes in patients with newly diagnosed epilepsy treated with established and new antiepileptic drugs: a 30-year longitudinal cohort study. JAMA Neurol. 75, 279–286. doi:10.1001/jamaneurol.2017.3949
Chiang, S., and Haneef, Z. (2014). Graph theory findings in the pathophysiology of temporal lobe epilepsy. Clin. Neurophysiol. 125, 1295–1305. doi:10.1016/j.clinph.2014.04.004
Chiang, S., Moss, R., Patel, A. D., and Rao, V. R. (2020). Seizure detection devices and health-related quality of life: a patient-and caregiver-centered evaluation. Epilepsy Behav. 105, 106963. doi:10.1016/j.yebeh.2020.106963
Chiang, S., Stern, J. M., Engel, J., and Haneef, Z. (2015). Structural-functional coupling changes in temporal lobe epilepsy. Brain Res. 1616, 45–57. doi:10.1016/j.brainres.2015.04.052
Chiarion, G., Sparacino, L., Antonacci, Y., Faes, L., and Mesin, L. (2023). Connectivity analysis in EEG data: a tutorial review of the state of the art and emerging trends. Bioengineering 10, 372. doi:10.3390/bioengineering10030372
Chiosa, V., Ciolac, D., Groppa, S., Koirala, N., Pintea, B., Vataman, A., et al. (2019). Large-scale network architecture and associated structural cortico-subcortical abnormalities in patients with sleep/awake-related seizures. Sleep 42, zsz006. doi:10.1093/sleep/zsz006
Chowdhury, F. A., Woldman, W., FitzGerald, T. H., Elwes, R. D., Nashef, L., Terry, J. R., et al. (2014). Revealing a brain network endophenotype in families with idiopathic generalised epilepsy. PloS one 9, e110136. doi:10.1371/journal.pone.0110136
Cimini, G., Squartini, T., Saracco, F., Garlaschelli, D., Gabrielli, A., and Caldarelli, G. (2019). The statistical physics of real-world networks. Nat. Rev. Phys. 1, 58–71. doi:10.1038/s42254-018-0002-6
Colclough, G. L., Woolrich, M. W., Tewarie, P. K., Brookes, M. J., Quinn, A. J., and Smith, S. M. (2016). How reliable are MEG resting-state connectivity metrics? NeuroImage 138, 284–293. doi:10.1016/j.neuroimage.2016.05.070
Comellas, F., and Gago, S. (2007). Synchronizability of complex networks. J. Phys. A 40, 4483–4492. doi:10.1088/1751-8113/40/17/006
Commission on Classification and Terminology of the International League Against Epilepsy (1989). Proposal for revised classification of epilepsies and epileptic syndromes. Commission on classification and terminology of the international League against epilepsy. Epilepsia 30, 389–399. doi:10.1111/j.1528-1157.1989.tb05316.x
Conrad, E. C., Bernabei, J. M., Kini, L. G., Shah, P., Mikhail, F., Kheder, A., et al. (2020). The sensitivity of network statistics to incomplete electrode sampling on intracranial EEG. Netw. Neurosci. 4, 484–506. doi:10.1162/netn_a_00131
Contisciani, M., Battiston, F., and De Bacco, C. (2022). Inference of hyperedges and overlapping communities in hypergraphs. Nat. Commun. 13, 7229. doi:10.1038/s41467-022-34714-7
Datseris, G., and Parlitz, U. (2022). Nonlinear dynamics: a concise introduction interlaced with code. Springer Nature.
Deco, G., Tononi, G., Boly, M., and Kringelbach, M. L. (2015). Rethinking segregation and integration: contributions of whole-brain modelling. Nat. Rev. Neurosci. 16, 430–439. doi:10.1038/nrn3963
De Domenico, M. (2017). Multilayer modeling and analysis of human brain networks. GIGASCIENCE 6, 1–8. doi:10.1093/gigascience/gix004
De Domenico, M., and Biamonte, J. (2016). Spectral entropies as information-theoretic tools for complex network comparison. Phys. Rev. X 6, 041062. doi:10.1103/physrevx.6.041062
De Domenico, M., Solé-Ribalta, A., Omodei, E., Gómez, S., and Arenas, A. (2015). Ranking in interconnected multilayer networks reveals versatile nodes. Nat. Commun. 6, 6868. doi:10.1038/ncomms7868
Depannemaecker, D., Destexhe, A., Jirsa, V., and Bernard, C. (2021). Modeling seizures: from single neurons to networks. Seizure 90, 4–8. doi:10.1016/j.seizure.2021.06.015
Detre, J. A. (2004). fMRI: applications in epilepsy. Epilepsia 45, 26–31. doi:10.1111/j.0013-9580.2004.04006.x
di Bernardo, M., Garofalo, F., and Sorrentino, F. (2007). Effects of degree correlation on the synchronization of networks of oscillators. Int. J. Bifurc. Chaos Appl. Sci. Eng. 17, 3499–3506. doi:10.1142/s0218127407019263
Dickten, H., Porz, S., Elger, C. E., and Lehnertz, K. (2016). Weighted and directed interactions in evolving large-scale epileptic brain networks. Sci. Rep. 6, 34824. doi:10.1038/srep34824
Dimitriadis, S. I., Laskaris, N. A., Tsirka, V., Vourkas, M., Micheloyannis, S., and Fotopoulos, S. (2010). Tracking brain dynamics via time-dependent network analysis. J. Neurosci. Methods 193, 145–155. doi:10.1016/j.jneumeth.2010.08.027
Ding, M., Lang, Y., Shu, H., Shao, J., and Cui, L. (2021). Microbiota–gut–brain axis and epilepsy: a review on mechanisms and potential therapeutics. Front. Immunol. 12, 742449. doi:10.3389/fimmu.2021.742449
Dreifuss, F., Martinez-Lage, M., and Johns, R. A. (1985). Proposal for classification of epilepsies and epileptic syndromes. Commission on classification and terminology of the international League against epilepsy. Epilepsia 26, 268–278. doi:10.1111/j.1528-1157.1985.tb05417.x
Drew, P. J. (2022). Neurovascular coupling: motive unknown. Trends Neurosci. 45, 809–819. doi:10.1016/j.tins.2022.08.004
Driscoll, N., Rosch, R. E., Murphy, B. B., Ashourvan, A., Vishnubhotla, R., Dickens, O. O., et al. (2021). Multimodal in vivo recording using transparent graphene microelectrodes illuminates spatiotemporal seizure dynamics at the microscale. Commun. Biol. 4, 136. doi:10.1038/s42003-021-01670-9
Duncan, J. (2009). The current status of neuroimaging for epilepsy. Curr. Opin. Neurol. 22, 179–184. doi:10.1097/WCO.0b013e328328f260
Duncan, J. S., Winston, G. P., Koepp, M. J., and Ourselin, S. (2016). Brain imaging in the assessment for epilepsy surgery. Lancet Neurol. 15, 420–433. doi:10.1016/S1474-4422(15)00383-X
Duun-Henriksen, J., Baud, M., Richardson, M. P., Cook, M., Kouvas, G., Heasman, J. M., et al. (2020). A new era in electroencephalographic monitoring? Subscalp devices for ultra–long-term recordings. Epilepsia 61, 1805–1817. doi:10.1111/epi.16630
Efron, B. (1982). The jackknife, the bootstrap and other resampling plans. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics. doi:10.1137/1.9781611970319
Efron, B. (2004). Large-scale simultaneous hypothesis testing: the choice of a null hypothesis. JASA 99, 96–104. doi:10.1198/016214504000000089
Eggebrecht, A. T., Ferradal, S. L., Robichaux-Viehoever, A., Hassanpour, M. S., Dehghani, H., Snyder, A. Z., et al. (2014). Mapping distributed brain function and networks with diffuse optical tomography. Nat. Photonics 8, 448–454. doi:10.1038/nphoton.2014.107
Eickhoff, S. B., Yeo, B. T., and Genon, S. (2018). Imaging-based parcellations of the human brain. Nat. Rev. Neurosci. 19, 672–686. doi:10.1038/s41583-018-0071-7
Elger, C. E., and Hoppe, C. (2018). Diagnostic challenges in epilepsy: seizure under-reporting and seizure detection. Lancet Neurol. 1, 279–288. doi:10.1016/S1474-4422(18)30038-3
Engel, J., Thompson, P. M., Stern, J. M., Staba, R. J., Bragin, A., and Mody, I. (2013). Connectomics and epilepsy. Curr. Opin. Neurol. 26, 186–194. doi:10.1097/WCO.0b013e32835ee5b8
Faskowitz, J., Betzel, R. F., and Sporns, O. (2022). Edges in brain networks: contributions to models of structure and function. Netw. Neurosci. 6, 1–28. doi:10.1162/netn_a_00204
Ferrari, M., and Quaresima, V. (2012). A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application. Neuroimage 63, 921–935. doi:10.1016/j.neuroimage.2012.03.049
Feudel, U., Pisarchik, A. N., and Showalter, K. (2018). Multistability and tipping: from mathematics and physics to climate and brain–Minireview and preface to the focus issue. Chaos 28, 033501. doi:10.1063/1.5027718
Fischer, T., Rings, T., Reza Rahimi Tabar, M., and Lehnertz, K. (2022). Towards a data-driven estimation of resilience in networked dynamical systems: designing a versatile testbed. Front. Netw. Physiol. 2, 838142. doi:10.3389/fnetp.2022.838142
Fisher, R. S., van Emde Boas, W., Blume, W., Elger, C. E., Genton, P., Lee, P., et al. (2005). Epileptic seizures and epilepsy: definitions proposed by the international League against epilepsy (ILAE) and the international bureau for epilepsy (IBE). Epilepsia 46, 470–472. doi:10.1111/j.0013-9580.2005.66104.x
Fjell, A. M., and Walhovd, K. B. (2010). Structural brain changes in aging: courses, causes and cognitive consequences. Rev. Neurosci. 21, 187–221. doi:10.1515/revneuro.2010.21.3.187
Foit, N. A., Bernasconi, A., and Bernasconi, N. (2020). Functional networks in epilepsy presurgical evaluation. Neurosurg. Clin. N. Am. 31, 395–405. doi:10.1016/j.nec.2020.03.004
Fortunato, S., and Hric, D. (2016). Community detection in networks: a user guide. Phys. Rep. 659, 1–44. doi:10.1016/j.physrep.2016.09.002
Fraiman, D., and Fraiman, R. (2018). An ANOVA approach for statistical comparisons of brain networks. Sci. Rep. 8, 4746. doi:10.1038/s41598-018-23152-5
Fraschini, M., Demuru, M., Puligheddu, M., Floridia, S., Polizzi, L., Maleci, A., et al. (2014). The re-organization of functional brain networks in pharmaco-resistant epileptic patients who respond to VNS. Neurosci. Lett. 580, 153–157. doi:10.1016/j.neulet.2014.08.010
Frassineti, L., Parente, A., and Manfredi, C. (2021). Multiparametric EEG analysis of brain network dynamics during neonatal seizures. J. Neurosci. Methods 348, 109003. doi:10.1016/j.jneumeth.2020.109003
Frauscher, B., Bartolomei, F., Baud, M. O., Smith, R. J., Worrell, G., and Lundstrom, B. N. (2023). Stimulation to probe, excite, and inhibit the epileptic brain. Epilepsia. doi:10.1111/epi.17640
Frei, M. G., Zaveri, H. P., Arthurs, S., Bergey, G. K., Jouny, C., Lehnertz, K., et al. (2010). Controversies in epilepsy: debates held during the fourth international workshop on seizure prediction. Epilepsy Behav. 19, 4–16. doi:10.1016/j.yebeh.2010.06.009
Friston, K. J. (2011). Functional and effective connectivity: a review. Brain Connect. 1, 13–36. doi:10.1089/brain.2011.0008
Fruengel, R., Bröhl, T., Rings, T., and Lehnertz, K. (2020). Reconfiguration of human evolving large-scale epileptic brain networks prior to seizures: an evaluation with node centralities. Sci. Rep. 10, 21921. doi:10.1038/s41598-020-78899-7
Gao, X., Xiao, B., Tao, D., and Li, X. (2010). A survey of graph edit distance. Pattern Anal. Appl. 13, 113–129. doi:10.1007/s10044-008-0141-y
Garcia-Ramos, C., Lin, J. J., Kellermann, T. S., Bonilha, L., Prabhakaran, V., and Hermann, B. P. (2016). Graph theory and cognition: a complementary avenue for examining neuropsychological status in epilepsy. Epilepsy Behav. 64, 329–335. doi:10.1016/j.yebeh.2016.02.032
Geier, C., Bialonski, S., Elger, C. E., and Lehnertz, K. (2015a). How important is the seizure onset zone for seizure dynamics? Seizure 25, 160–166. doi:10.1016/j.seizure.2014.10.013
Geier, C., and Lehnertz, K. (2017a). Long-term variability of importance of brain regions in evolving epileptic brain networks. Chaos 27, 043112. doi:10.1063/1.4979796
Geier, C., and Lehnertz, K. (2017b). Which brain regions are important for seizure dynamics in epileptic networks? Influence of link identification and EEG recording montage on node centralities. Int. J. Neural Syst. 27, 1650033. doi:10.1142/S0129065716500337
Geier, C., Lehnertz, K., and Bialonski, S. (2015b). Time-dependent degree-degree correlations in epileptic brain networks: from assortative to dissortative mixing. Front. Hum. Neurosci. 9, 462. doi:10.3389/fnhum.2015.00462
Geng, S., Liu, X., Biswal, B. B., and Niu, H. (2017). Effect of resting-state fNIRS scanning duration on functional brain connectivity and graph theory metrics of brain network. Front. Neurosci. 11, 392. doi:10.3389/fnins.2017.00392
George, S. V., Kachhara, S., and Ambika, G. (2021). Early warning signals for critical transitions in complex systems. Phys. Scr. 98, 072002. doi:10.1088/1402-4896/acde20
Gerhard, F., Pipa, G., Lima, B., Neuenschwander, S., and Gerstner, W. (2011). Extraction of network topology from multi-electrode recordings: is there a small-world effect? Front. Comput. Neurosci. 5, 4. doi:10.3389/fncom.2011.00004
Gerster, M., Berner, R., Sawicki, J., Zakharova, A., Škoch, A., Hlinka, J., et al. (2020). FitzHugh–Nagumo oscillators on complex networks mimic epileptic-seizure-related synchronization phenomena. Chaos An Interdiscip. J. Nonlinear Sci. 30, 123130. doi:10.1063/5.0021420
Gerster, M., Waterstraat, G., Litvak, V., Lehnertz, K., Schnitzler, A., Florin, E., et al. (2022). Separating neural oscillations from aperiodic 1/f activity: challenges and recommendations. Neuroinformatics 20, 991–1012. doi:10.1007/s12021-022-09581-8
Ghariblou, S., Salehi, M., Magnani, M., and Jalili, M. (2017). Shortest paths in multiplex networks. Sci. Rep. 7, 2142. doi:10.1038/s41598-017-01655-x
Ghosh, D., Frasca, M., Rizzo, A., Majhi, S., Rakshit, S., Alfaro-Bittner, K., et al. (2022). The synchronized dynamics of time-varying networks. Phys. Rep. 949, 1–63. doi:10.1016/j.physrep.2021.10.006
Ghoshal, G., and Barabási, A.-L. (2011). Ranking stability and super-stable nodes in complex networks. Nat. Commun. 2, 394. doi:10.1038/ncomms1396
Gil, F., Padilla, N., Soria-Pastor, S., Setoain, X., Boget, T., Rumiá, J., et al. (2020). Beyond the epileptic focus: functional epileptic networks in focal epilepsy. Cereb. Cortex 30, 2338–2357. doi:10.1093/cercor/bhz243
Ginat, D. T., and Gupta, R. (2014). Advances in computed tomography imaging technology. Annu. Rev. Biomed. Eng. 16, 431–453. doi:10.1146/annurev-bioeng-121813-113601
Goodfellow, M., Andrzejak, R., Masoller, C., and Lehnertz, K. (2022). What models and tools can contribute to a better understanding of brain activity? Front. Netw. Physiol. 2, 907995. doi:10.3389/fnetp.2022.907995
Goodfellow, M., Rummel, C., Abela, E., Richardson, M. P., Schindler, K., and Terry, J. R. (2016). Estimation of brain network ictogenicity predicts outcome from epilepsy surgery. Sci. Rep. 6, 29215. doi:10.1038/srep29215
Günther, M., Kantelhardt, J. W., and Bartsch, R. P. (2022). The reconstruction of causal networks in physiology. Front. Netw. Physiol. 2, 893743. doi:10.3389/fnetp.2022.893743
Hagemann, A., Wilting, J., Samimizad, B., Mormann, F., and Priesemann, V. (2021). Assessing criticality in pre-seizure single-neuron activity of human epileptic cortex. PLoS Comput. Biol. 17, e1008773. doi:10.1371/journal.pcbi.1008773
Hagemann, D., Naumann, E., and Thayer, J. F. (2001). The quest for the EEG reference revisited: a glance from brain asymmetry research. Psychophysiol 38, 847–857. doi:10.1111/1469-8986.3850847
Haneef, Z., and Chiang, S. (2014). Clinical correlates of graph theory findings in temporal lobe epilepsy. Seizure 23, 809–818. doi:10.1016/j.seizure.2014.07.004
Hartle, H., Klein, B., McCabe, S., Daniels, A., St-Onge, G., Murphy, C., et al. (2020). Network comparison and the within-ensemble graph distance. Proc. Roy. Soc. A 476, 20190744. doi:10.1098/rspa.2019.0744
Hatlestad-Hall, C., Bruña, R., Erichsen, A., Andersson, V., Syvertsen, M. R., Skogan, A. H., et al. (2021). The organization of functional neurocognitive networks in focal epilepsy correlates with domain-specific cognitive performance. J. Neurosci. Res. 99, 2669–2687. doi:10.1002/jnr.24896
Hatlestad-Hall, C., Bruña, R., Liljeström, M., Renvall, H., Heuser, K., Taubøll, E., et al. (2023). Reliable evaluation of functional connectivity and graph theory measures in source-level EEG: how many electrodes are enough? Clin. Neurophysiol. 150, 1–16. doi:10.1016/j.clinph.2023.03.002
Hatton, S. N., Huynh, K. H., Bonilha, L., Abela, E., Alhusaini, S., Altmann, A., et al. (2020). White matter abnormalities across different epilepsy syndromes in adults: an ENIGMA-Epilepsy study. Brain 143, 2454–2473. doi:10.1093/brain/awaa200
Haykin, S. (1983). Nonlinear methods of spectral analysis. Berlin, Heidelberg: Springer. doi:10.1007/3-540-12386-5
Healy, K. L., Morris, A. R., and Liu, A. C. (2021). Circadian synchrony: sleep, nutrition, and physical activity. Front. Netw. Physiol. 1, 732243. doi:10.3389/fnetp.2021.732243
Helwegen, K., Libedinsky, I., and van den Heuvel, M. P. (2023). Statistical power in network neuroscience. Trends Cogn. Sci. 27, 282–301. doi:10.1016/j.tics.2022.12.011
Hennig, J., Kiviniemi, V., Riemenschneider, B., Barghoorn, A., Akin, B., Wang, F., et al. (2021). 15 years MR-encephalography. Magn. Reson. Mat. Phys. Biol. Med. 34, 85–108. doi:10.1007/s10334-020-00891-z
Hens, C., Harush, U., Haber, S., Cohen, R., and Barzel, B. (2019). Spatiotemporal signal propagation in complex networks. Nat. Phys. 15, 403–412. doi:10.1038/s41567-018-0409-0
Heßler, M., and Kamps, O. (2022). Bayesian on-line anticipation of critical transitions. New J. Phys. 24, 063021. doi:10.1088/1367-2630/ac46d4
Hilgetag, C. C., and Goulas, A. (2016). Is the brain really a small-world network? Brain Struct. Funct. 221, 2361–2366. doi:10.1007/s00429-015-1035-6
Hill, R. M., Boto, E., Holmes, N., Hartley, C., Seedat, Z. A., Leggett, J., et al. (2019). A tool for functional brain imaging with lifespan compliance. Nat. Commun. 10, 4785. doi:10.1038/s41467-019-12486-x
Hillebrand, A., Holmes, N., Sijsma, N., O’Neill, G. C., Tierney, T. M., Liberton, N., et al. (2023). Non-invasive measurements of ictal and interictal epileptiform activity using optically pumped magnetometers. Sci. Rep. 13, 4623. doi:10.1038/s41598-023-31111-y
Hirsch, M., and Schulze-Bonhage, A. (2023). Efficacy of ictal neurostimulation—English version. Clin. Epileptol. 1, 157–162. doi:10.1007/s10309-023-00597-x
Hlaváčková-Schindler, K., Paluš, M., Vejmelka, M., and Bhattacharya, J. (2007). Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 441, 1–46. doi:10.1016/j.physrep.2006.12.004
Hlinka, J., Hartman, D., Jajcay, N., Tomeček, D., Tintěra, J., and Paluš, M. (2017). Small-world bias of correlation networks: from brain to climate. Chaos 27, 035812. doi:10.1063/1.4977951
Hlinka, J., Hartman, D., and Paluš, M. (2012). Small-world topology of functional connectivity in randomly connected dynamical systems. Chaos 22, 033107. doi:10.1063/1.4732541
Höller, Y., Helmstaedter, C., and Lehnertz, K. (2018). Quantitative pharmaco-electroencephalography in antiepileptic drug research. CNS Drugs 32, 839–848. doi:10.1007/s40263-018-0557-x
Höller, Y., and Nardone, R. (2021). Quantitative EEG biomarkers for epilepsy and their relation to chemical biomarkers. Adv. Clin. Chem. 102, 271–336. doi:10.1016/bs.acc.2020.08.004
Höller, Y., Uhl, A., Bathke, A., Thomschewski, A., Butz, K., Nardone, R., et al. (2017). Reliability of EEG measures of interaction: a paradigm shift is needed to fight the reproducibility crisis. Front. Hum. Neurosci. 11, 441. doi:10.3389/fnhum.2017.00441
Holme, P., and Saramäki, J. (2012). Temporal networks. Phys. Rep. 519, 97–125. doi:10.1016/j.physrep.2012.03.001
Holt, A. B., and Netoff, T. I. (2013). Computational modeling of epilepsy for an experimental neurologist. Exp. Neurol. 244, 75–86. doi:10.1016/j.expneurol.2012.05.003
Horstmann, M.-T., Bialonski, S., Noennig, N., Mai, H., Prusseit, J., Wellmer, J., et al. (2010). State dependent properties of epileptic brain networks: comparative graph-theoretical analyses of simultaneously recorded EEG and MEG. Clin. Neurophysiol. 121, 172–185. doi:10.1016/j.clinph.2009.10.013
Horwitz, B. (2003). The elusive concept of brain connectivity. Neuroimage 19, 466–470. doi:10.1016/s1053-8119(03)00112-5
Hsu, D., Chen, W., Hsu, M., and Beggs, J. M. (2008). An open hypothesis: is epilepsy learned, and can it be unlearned? Epilepsy Behav. 13, 511–522. doi:10.1016/j.yebeh.2008.05.007
Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., et al. (1998). The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Roy. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 454, 903–995. doi:10.1098/rspa.1998.0193
Huneau, C., Benali, H., and Chabriat, H. (2015). Investigating human neurovascular coupling using functional neuroimaging: a critical review of dynamic models. Front. Neurosci. 9, 467. doi:10.3389/fnins.2015.00467
Iacovacci, J., and Bianconi, G. (2016). Extracting information from multiplex networks. Chaos An Interdiscip. J. Nonlinear Sci. 26, 065306. doi:10.1063/1.4953161
Iivanainen, J., Mäkinen, A. J., Zetter, R., Stenroos, M., Ilmoniemi, R. J., and Parkkonen, L. (2021). Spatial sampling of MEG and EEG based on generalized spatial-frequency analysis and optimal design. NeuroImage 245, 118747. doi:10.1016/j.neuroimage.2021.118747
Ikemoto, S., von Ellenrieder, N., and Gotman, J. (2022). Electroencephalography–functional magnetic resonance imaging of epileptiform discharges: noninvasive investigation of the whole brain. Epilepsia 63, 2725–2744. doi:10.1111/epi.17364
Issa, N. P., Nunn, K. C., Wu, S., Haider, H. A., and Tao, J. X. (2023). Putative roles for homeostatic plasticity in epileptogenesis. Epilepsia 64, 539–552. doi:10.1111/epi.17500
Ivanov, P. C. (2021). The new field of network physiology: building the human physiolome. Front. Netw. Physiol. 1, 711778. doi:10.3389/fnetp.2021.711778
Jeurissen, B., Descoteaux, M., Mori, S., and Leemans, A. (2019). Diffusion MRI fiber tractography of the brain. NMR Biomed. 32, e3785. doi:10.1002/nbm.3785
Ji, P., Ye, J., Mu, Y., Lin, W., Tian, Y., Hens, C., et al. (2023). Signal propagation in complex networks. Phys. Rep. 1017, 1–96. doi:10.1016/j.physrep.2023.03.005
Jiruska, P., de Curtis, M., Jefferys, J. G. R., Schevon, C. A., Schiff, S. J., and Schindler, K. (2013). Synchronization and desynchronization in epilepsy: controversies and hypotheses. J. Physiol. 591, 787–797. doi:10.1113/jphysiol.2012.239590
Jöbsis, F. F. (1977). Noninvasive, infrared monitoring of cerebral and myocardial oxygen sufficiency and circulatory parameters. Science 198, 1264–1267. doi:10.1126/science.929199
Johnson, G. W., Doss, D. J., Morgan, V. L., Paulo, D. L., Cai, L. Y., Shless, J. S., et al. (2023). The interictal suppression hypothesis in focal epilepsy: network-level supporting evidence. Brain 146, 2828–2845. doi:10.1093/brain/awad016
Joudaki, A., Salehi, N., Jalili, M., and Knyazeva, M. G. (2012). EEG-based functional brain networks: does the network size matter? PLoS ONE 7, e35673. doi:10.1371/journal.pone.0035673
Juhász, C., and Chugani, H. T. (2003). Imaging the epileptic brain with positron emission tomography. Neuroimaging Clin. 13, 705–716. doi:10.1016/s1052-5149(03)00090-x
Kalitzin, S., Petkov, G., Suffczynski, P., Grigorovsky, V., Bardakjian, B. L., da Silva, F. L., et al. (2019). Epilepsy as a manifestation of a multistate network of oscillatory systems. Neurobiol. Dis. 130, 104488. doi:10.1016/j.nbd.2019.104488
Kantelhardt, J. W., Koscielny-Bunde, E., Rego, H. H., Havlin, S., and Bunde, A. (2001). Detecting long-range correlations with detrended fluctuation analysis. Phys. A 295, 441–454. doi:10.1016/s0378-4371(01)00144-3
Kantz, H., and Schreiber, T. (2003). Nonlinear time series analysis. 2nd edn. Cambridge, UK: Cambridge University Press. doi:10.1017/CBO9780511755798
Kaplan, L., Chow, B. W., and Gu, C. (2020). Neuronal regulation of the blood–brain barrier and neurovascular coupling. Nat. Rev. Neurosci. 21, 416–432. doi:10.1038/s41583-020-0322-2
Karoly, P. J., Rao, V. R., Gregg, N. M., Worrell, G. A., Bernard, C., Cook, M. J., et al. (2021). Cycles in epilepsy. Nat. Rev. Neurol. 17, 267–284. doi:10.1038/s41582-021-00464-1
Kato, S., Bagarinao, E., Isoda, H., Koyama, S., Watanabe, H., Maesawa, S., et al. (2022). Reproducibility of functional connectivity metrics estimated from resting-state functional MRI with differences in days, coils, and global signal regression. Radiol. Phys. Technol. 15, 298–310. doi:10.1007/s12194-022-00670-6
Kelso, J. S. (2012). Multistability and metastability: understanding dynamic coordination in the brain. Phil. Trans. Roy. Soc. B 367, 906–918. doi:10.1098/rstb.2011.0351
Khaledi-Nasab, A., Kromer, J. A., and Tass, P. A. (2022). Long-lasting desynchronization of plastic neuronal networks by double-random coordinated reset stimulation. Front. Netw. Physiol. 2, 864859. doi:10.3389/fnetp.2022.864859
Khambhati, A. N., Davis, K. A., Oommen, B. S., Chen, S. H., Lucas, T. H., Litt, B., et al. (2015). Dynamic network drivers of seizure generation, propagation and termination in human neocortical epilepsy. PLoS Comput. Biol. 11, e1004608–19. doi:10.1371/journal.pcbi.1004608
Khan, S., Nobili, L., Khatami, R., Loddenkemper, T., Cajochen, C., Dijk, D.-J., et al. (2018). Circadian rhythm and epilepsy. Lancet Neurol. 17, 1098–1108. doi:10.1016/S1474-4422(18)30335-1
Kinney-Lang, E., Yoong, M., Hunter, M., Tallur, K. K., Shetty, J., McLellan, A., et al. (2019). Analysis of EEG networks and their correlation with cognitive impairment in preschool children with epilepsy. Epilepsy Behav. 90, 45–56. doi:10.1016/j.yebeh.2018.11.011
Kirst, C., and Timme, M. (2008). From networks of unstable attractors to heteroclinic switching. Phys. Rev. E 78, 065201. doi:10.1103/PhysRevE.78.065201
Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., and Porter, M. A. (2014). Multilayer networks. J. Complex Netw. 2, 203–271. doi:10.1093/comnet/cnu016
Kong, Y.-X., Shi, G.-Y., Wu, R.-J., and Zhang, Y.-C. (2019). k-core: theories and applications. Phys. Rep. 832, 1–32. doi:10.1016/j.physrep.2019.10.004
Korhonen, O., Zanin, M., and Papo, D. (2021). Principles and open questions in functional brain network reconstruction. Hum. Brain Mapp. 42, 3680–3711. doi:10.1002/hbm.25462
Koschützki, D., Lehmann, K., Peeters, L., Richter, S., Tenfelde-Podehl, D., and Zlotowski, O. (2005). Centrality indices. 3418 of Lect. Notes Comput. Sci. 16–61. doi:10.1007/978-3-540-31955-9_3
Koutlis, C., Kimiskidis, V. K., and Kugiumtzis, D. (2021). Comparison of causality network estimation in the sensor and source space: simulation and application on EEG. Front. Netw. Physiol. 1, 706487. doi:10.3389/fnetp.2021.706487
Kramer, M. A., and Cash, S. S. (2012). Epilepsy as a disorder of cortical network organization. Neurosci. 18, 360–372. doi:10.1177/1073858411422754
Kramer, M. A., Eden, U. T., Cash, S. S., and Kolaczyk, E. D. (2009). Network inference with confidence from multivariate time series. Phys. Rev. E 79, 061916. doi:10.1103/PhysRevE.79.061916
Kramer, M. A., Eden, U. T., Kolaczyk, E. D., Zepeda, R., Eskandar, E. N., and Cash, S. S. (2010). Coalescence and fragmentation of cortical networks during focal seizures. J. Neurosci. 30, 10076–10085. doi:10.1523/JNEUROSCI.6309-09.2010
Kramer, M. A., Kolaczyk, E. D., and Kirsch, H. E. (2008). Emergent network topology at seizure onset in humans. Epilepsy Res. 79, 173–186. doi:10.1016/j.eplepsyres.2008.02.002
Kramer, M. A., Truccolo, W., Eden, U. T., Lepage, K. Q., Hochberg, L. R., Eskandar, E. N., et al. (2012). Human seizures self-terminate across spatial scales via a critical transition. Proc. Natl. Acad. Sci. U.S.A. 109, 21116–21121. doi:10.1073/pnas.1210047110
Kreuz, T., Mormann, F., Andrzejak, R. G., Kraskov, A., Lehnertz, K., and Grassberger, P. (2007). Measuring synchronization in coupled model systems: a comparison of different approaches. Phys. D. 225, 29–42. doi:10.1016/j.physd.2006.09.039
Kuehn, C. (2011). A mathematical framework for critical transitions: bifurcations, fast-slow systems and stochastic dynamics. Phys. D. 240, 1020–1035. doi:10.1016/j.physd.2011.02.012
Kuhlmann, L., Freestone, D., Lai, A. L., Burkitt, A. N., Fuller, K., Grayden, D., et al. (2010). Patient-specific bivariate-synchrony-based seizure prediction for short prediction horizons. Epilepsy Res. 91, 214–231. doi:10.1016/j.eplepsyres.2010.07.014
Kuhlmann, L., Lehnertz, K., Richardson, M. P., Schelter, B., and Zaveri, H. P. (2018). Seizure prediction – ready for a new era. Nat. Rev. Neurol. 14, 618–630. doi:10.1038/s41582-018-0055-2
Kuhnert, M.-T., Bialonski, S., Noennig, N., Mai, H., Hinrichs, H., Helmstaedter, C., et al. (2013). Incidental and intentional learning of verbal episodic material differentially modifies functional brain networks. PLoS ONE 8, e80273. doi:10.1371/journal.pone.0080273
Kuhnert, M.-T., Elger, C. E., and Lehnertz, K. (2010). Long-term variability of global statistical properties of epileptic brain networks. Chaos 20, 043126. doi:10.1063/1.3504998
Kuhnert, M.-T., Geier, C., Elger, C. E., and Lehnertz, K. (2012). Identifying important nodes in weighted functional brain networks: a comparison of different centrality approaches. Chaos 22, 023142. doi:10.1063/1.4729185
Kwan, P., and Brodie, M. J. (2000). Early identification of refractory epilepsy. N. Engl. J. Med. 342, 314–319. doi:10.1056/NEJM200002033420503
Kwon, C.-S., Jacoby, A., Ali, A., Austin, J., Birbeck, G. L., Braga, P., et al. (2022). Systematic review of frequency of felt and enacted stigma in epilepsy and determining factors and attitudes toward persons living with epilepsy–Report from the International League against Epilepsy Task Force on Stigma in Epilepsy. Epilepsia 63, 573–597. doi:10.1111/epi.17135
Lacasa, L., Stramaglia, S., and Marinazzo, D. (2021). Beyond pairwise network similarity: exploring mediation and suppression between networks. Commun. Phys. 4, 136. doi:10.1038/s42005-021-00638-9
Lado, F. A., and Moshé, S. L. (2008). How do seizures stop? Epilepsia 49, 1651–1664. doi:10.1111/j.1528-1167.2008.01669.x
Lang, J., Jeschke, S., Herziger, B., Müller, R. M., Bertsche, T., Neininger, M. P., et al. (2022). Prejudices against people with epilepsy as perceived by affected people and their families. Epilepsy Behav. 127, 108535. doi:10.1016/j.yebeh.2021.108535
Larivière, S., Rodríguez-Cruces, R., Royer, J., Caligiuri, M. E., Gambardella, A., Concha, L., et al. (2020). Network-based atrophy modeling in the common epilepsies: a worldwide ENIGMA study. Sci. Adv. 6, eabc6457. doi:10.1126/sciadv.abc6457
Laufs, H. (2012). Functional imaging of seizures and epilepsy: evolution from zones to networks. Curr. Opin. Neurol. 25, 194–200. doi:10.1097/WCO.0b013e3283515db9
Lawrence, R. M., Bridgeford, E. W., Myers, P. E., Arvapalli, G. C., Ramachandran, S. C., Pisner, D. A., et al. (2021). Standardizing human brain parcellations. Sci. Data 8, 78. doi:10.1038/s41597-021-00849-3
Lee, U., Kim, S., and Jung, K.-Y. (2006). Classification of epilepsy types through global network analysis of scalp electroencephalograms. Phys. Rev. E 73, 041920. doi:10.1103/PhysRevE.73.041920
Lehnertz, H., Bröhl, T., Rings, T., Von Wrede, R., and Lehnertz, K. (2023a). Modifying functional brain networks in focal epilepsy by manual visceral-osteopathic stimulation of the vagus nerve at the abdomen. Front. Netw. Physiol. 3, 1205476. doi:10.3389/fnetp.2023.1205476
Lehnertz, K. (2021). “Predicting epileptic seizures—an update,” in Physics of biological oscillators (Springer), 345–360.
Lehnertz, K. (2023). Ordinal methods for a characterization of evolving functional brain networks. Chaos An Interdiscip. J. Nonlinear Sci. 33, 022101. doi:10.1063/5.0136181
Lehnertz, K., Ansmann, G., Bialonski, S., Dickten, H., Geier, C., and Porz, S. (2014). Evolving networks in the human epileptic brain. Phys. D. 267, 7–15. doi:10.1016/j.physd.2013.06.009
Lehnertz, K., Bröhl, T., and Rings, T. (2020). The human organism as an integrated interaction network: recent conceptual and methodological challenges. Front. Physiol. 11, 598694. doi:10.3389/fphys.2020.598694
Lehnertz, K., Bröhl, T., and von Wrede, R. (2023b). Epileptic-network-based prediction and control of seizures in humans. Neurobiol. Dis. 181, 106098. doi:10.1016/j.nbd.2023.106098
Lehnertz, K., and Dickten, H. (2015). Assessing directionality and strength of coupling through symbolic analysis: an application to epilepsy patients. Phil. Trans. R. Soc. A 373, 20140094. doi:10.1098/rsta.2014.0094
Lehnertz, K., Dickten, H., Porz, S., Helmstaedter, C., and Elger, C. E. (2016). Predictability of uncontrollable multifocal seizures – towards new treatment options. Sci. Rep. 6, 24584. doi:10.1038/srep24584
Lehnertz, K., Geier, C., Rings, T., and Stahn, K. (2017). Capturing time-varying brain dynamics. EPJ Nonlin. Biomed. Phys. 5, 2. doi:10.1051/epjnbp/2017001
Lehnertz, K., Rings, T., and Bröhl, T. (2021). Time in brain: how biological rhythms impact on EEG signals and on EEG-derived brain networks. Front. Netw. Physiol. 1, 755016. doi:10.3389/fnetp.2021.755016
Li, A., Cornelius, S. P., Liu, Y.-Y., Wang, L., and Barabási, A.-L. (2017). The fundamental advantages of temporal networks. Science 358, 1042–1046. doi:10.1126/science.aai7488
Li, R., Yang, D., Fang, F., Hong, K.-S., Reiss, A. L., and Zhang, Y. (2022). Concurrent fNIRS and EEG for brain function investigation: a systematic, methodology-focused review. Sensors 22, 5865. doi:10.3390/s22155865
Liao, H., Mariani, M. S., Medo, M., Zhang, Y.-C., and Zhou, M.-Y. (2017). Ranking in evolving complex networks. Phys. Rep. 689, 1–54. doi:10.1016/j.physrep.2017.05.001
Lignani, G., Baldelli, P., and Marra, V. (2020). Homeostatic plasticity in epilepsy. Front. Cell. Neurosci. 14, 197. doi:10.3389/fncel.2020.00197
Lopes, M. A., Perani, S., Yaakub, S. N., Richardson, M. P., Goodfellow, M., and Terry, J. R. (2019). Revealing epilepsy type using a computational analysis of interictal EEG. Sci. Rep. 9, 10169. doi:10.1038/s41598-019-46633-7
Lopes, M. A., Richardson, M. P., Abela, E., Rummel, C., Schindler, K., Goodfellow, M., et al. (2018). Elevated ictal brain network ictogenicity enables prediction of optimal seizure control. Front. Neurol. 9, 98. doi:10.3389/fneur.2018.00098
Lopes da Silva, F. H., Blanes, W., Kalitzin, S. N., Parra, J., Suffczynski, P., and Velis, D. N. (2003). Dynamical diseases of brain systems: different routes to epileptic seizures. IEEE Trans. Biomed. Eng. 50, 540–548. doi:10.1109/TBME.2003.810703
Lü, L., Chen, D., Ren, X.-L., Zhang, Q.-M., Zhang, Y.-C., and Zho, T. (2016). Vital nodes identification in complex networks. Phys. Rep. 650, 1–63. doi:10.1016/j.physrep.2016.06.007
Luat, A. F., and Chugani, H. T. (2008). Molecular and diffusion tensor imaging of epileptic networks. Epilepsia 49 (Suppl. 3), 15–22. doi:10.1111/j.1528-1167.2008.01506.x
Lüders, H. O., Turnbull, J., and Kaffashi, F. (2009). Are the dichotomies generalized versus focal epilepsies and idiopathic versus symptomatic epilepsies still valid in modern epileptology? Epilepsia 50, 1336–1343. doi:10.1111/j.1528-1167.2009.02074.x
Lütkepohl, H. (2005). New introduction to multiple time series analysis. Springer Science & Business Media.
Lytton, W. W. (2008). Computer modelling of epilepsy. Nat. Rev. Neurosci. 9, 626–637. doi:10.1038/nrn2416
Machado, A., Lina, J.-M., Tremblay, J., Lassonde, M., Nguyen, D. K., Lesage, F., et al. (2011). Detection of hemodynamic responses to epileptic activity using simultaneous Electro-EncephaloGraphy (EEG)/Near Infra Red Spectroscopy (NIRS) acquisitions. Neuroimage 56, 114–125. doi:10.1016/j.neuroimage.2010.12.026
Madole, J. W., Buchanan, C. R., Rhemtulla, M., Ritchie, S. J., Bastin, M. E., Deary, I. J., et al. (2023). Strong intercorrelations among global graph-theoretic indices of structural connectivity in the human brain. NeuroImage 275, 120160. doi:10.1016/j.neuroimage.2023.120160
Majumdar, K., Prasad, P. D., and Verma, S. (2014). Synchronization implies seizure or seizure implies synchronization? Brain Topogr. 27, 112–122. doi:10.1007/s10548-013-0284-z
Mandke, K., Meier, J., Brookes, M. J., O’Dea, R. D., Van Mieghem, P., Stam, C. J., et al. (2018). Comparing multilayer brain networks between groups: introducing graph metrics and recommendations. NeuroImage 166, 371–384. doi:10.1016/j.neuroimage.2017.11.016
Marino, A. C., Yang, G. J., Tyrtova, E., Wu, K., Zaveri, H. P., Farooque, P., et al. (2019). Resting state connectivity in neocortical epilepsy: the epilepsy network as a patient-specific biomarker. Clin. Neurophysiol. 130, 280–288. doi:10.1016/j.clinph.2018.11.016
Martínez, J. H., and Chavez, M. (2019). Comparing complex networks: in defence of the simple. New J. Phys. 21, 013033. doi:10.1088/1367-2630/ab0065
Mémoli, F. (2011). Gromov–Wasserstein distances and the metric approach to object matching. Found. Comput. Math. 11, 417–487. doi:10.1007/s10208-011-9093-5
Mercier, M. R., Dubarry, A.-S., Tadel, F., Avanzini, P., Axmacher, N., Cellier, D., et al. (2022). Advances in human intracranial electroencephalography research, guidelines and good practices. NeuroImage 260, 119438. doi:10.1016/j.neuroimage.2022.119438
Merlis, J. (1970). Proposal for an international classification of the epilepsies. Epilepsia 11, 114–119. doi:10.1111/j.1528-1157.1970.tb03873.x
Mesraoua, B., Deleu, D., Hassan, A. H., Gayane, M., Lubna, A., Ali, M. A., et al. (2020). Dramatic outcomes in epilepsy: depression, suicide, injuries, and mortality. Curr. Med. Res. Opin. 36, 1473–1480. doi:10.1080/03007995.2020.1776234
Meyer-Ortmanns, H. (2023). Heteroclinic networks for brain dynamics. Front. Netw. Physiol. 3, 1276401. doi:10.3389/fnetp.2023.1276401
Mheich, A., Wendling, F., and Hassan, M. (2020). Brain network similarity: methods and applications. Netw. Neurosci. 4, 507–527. doi:10.1162/netn_a_00133
Milanowski, P., and Suffczynski, P. (2016). Seizures start without common signatures of critical transition. Int. J. Neural Syst. 26, 1650053. doi:10.1142/S0129065716500532
Milne-Ives, M., Dunn-Henriksen, J., Blaabjerg, L., Mclean, B., Shankar, R., and Meinert, E. (2023). At home EEG monitoring technologies for people with epilepsy and intellectual disabilities: a scoping review. Seizure 110, 11–20. doi:10.1016/j.seizure.2023.05.007
Mitsis, G. D., Anastasiadou, M. N., Christodoulakis, M., Papathanasiou, E. S., Papacostas, S. S., and Hadjipapas, A. (2020). Functional brain networks of patients with epilepsy exhibit pronounced multiscale periodicities, which correlate with seizure onset. Hum. Brain Mapp. 41, 2059–2076. doi:10.1002/hbm.24930
Montes-Restrepo, V., van Mierlo, P., Strobbe, G., Staelens, S., Vandenberghe, S., and Hallez, H. (2014). Influence of skull modeling approaches on EEG source localization. Brain Topogr. 27, 95–111. doi:10.1007/s10548-013-0313-y
Mori, S., and Van Zijl, P. C. (2002). Fiber tracking: principles and strategies–a technical review. NMR Biomed. 15, 468–480. doi:10.1002/nbm.781
Mori, S., Wakana, S., Van Zijl, P. C. M., and Nagae-Poetscher, L. M. (2005). MRI atlas of human white matter. Elsevier.
Mormann, F., Elger, C. E., and Lehnertz, K. (2006). Seizure anticipation: from algorithms to clinical practice. Curr. Opin. Neurol. 19, 187–193. doi:10.1097/01.wco.0000218237.52593.bc
Mormann, F., Kreuz, T., Andrzejak, R. G., David, P., Lehnertz, K., and Elger, C. E. (2003). Epileptic seizures are preceded by a decrease in synchronization. Epilepsy Res. 53, 173–185. doi:10.1016/s0920-1211(03)00002-0
Mormann, F., Lehnertz, K., David, P., and Elger, C. E. (2000). Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients. Phys. D. 144, 358–369. doi:10.1016/S0167-2789(00)00087-7
Morrell, M. (2006). Brain stimulation for epilepsy: can scheduled or responsive neurostimulation stop seizures? Curr. Opin. Neurol. 19, 164–168. doi:10.1097/01.wco.0000218233.60217.84
Morrison, M., and Young, L.-S. (2022). Chaotic heteroclinic networks as models of switching behavior in biological systems. Chaos An Interdiscip. J. Nonlinear Sci. 32, 123102. doi:10.1063/5.0122184
Motter, A. E., Zhou, C., and Kurths, J. (2005). Enhancing complex-network synchronization. Europhys. Lett. 69, 334–340. doi:10.1209/epl/i2004-10365-4
Muehllehner, G., and Karp, J. S. (2006). Positron emission tomography. Phys. Med. Biol. 51, R117–R137. doi:10.1088/0031-9155/51/13/R08
Muldoon, S. F., and Bassett, D. S. (2016). Network and multilayer network approaches to understanding human brain dynamics. Philos. Sci. 83, 710–720. doi:10.1086/687857
Mulert, C., and Lemieux, L. (2023). EEG-fMRI: physiological basis, technique, and applications. Springer Nature.
Muskulus, M., Houweling, S., Verduyn-Lunel, S., and Daffertshofer, A. (2009). Functional similarities and distance properties. J. Neurosci. Methods 183, 31–41. doi:10.1016/j.jneumeth.2009.06.035
Mutti, C., Misirocchi, F., Zilioli, A., Rausa, F., Pizzarotti, S., Spallazzi, M., et al. (2022). Sleep and brain evolution across the human lifespan: a mutual embrace. Front. Netw. Physiol. 2, 938012. doi:10.3389/fnetp.2022.938012
Nabbout, R., and Kuchenbuch, M. (2020). Impact of predictive, preventive and precision medicine strategies in epilepsy. Nat. Rev. Neurol. 16, 674–688. doi:10.1038/s41582-020-0409-4
Newman, M. E. J. (2001). Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys. Rev. E 64, 016132. doi:10.1103/PhysRevE.64.016132
Newman, M. E. J. (2002). Assortative mixing in networks. Phys. Rev. Lett. 89, 208701. doi:10.1103/PhysRevLett.89.208701
Newman, M. E. J. (2003). Mixing patterns in networks. Phys. Rev. E 67, 026126. doi:10.1103/PhysRevE.67.026126
Newman, M. E. J. (2006). Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 74, 036104. doi:10.1103/PhysRevE.74.036104
Nguyen, D. K., Tremblay, J., Pouliot, P., Vannasing, P., Florea, O., Carmant, L., et al. (2012). Non-invasive continuous EEG-fNIRS recording of temporal lobe seizures. Epilepsy Res. 99, 112–126. doi:10.1016/j.eplepsyres.2011.10.035
Nguyen, T., Babawale, O., Kim, T., Jo, H. J., Liu, H., and Kim, J. G. (2018). Exploring brain functional connectivity in rest and sleep states: a fNIRS study. Sci. Rep. 8, 16144. doi:10.1038/s41598-018-33439-2
Nicosia, V., and Latora, V. (2015). Measuring and modeling correlations in multiplex networks. Phys. Rev. E 92, 032805. doi:10.1103/PhysRevE.92.032805
Niedermeyer, E., and Lopes da Silva, F. (2005). Electroencephalography: basic principles, clinical applications, and related fields. Philadelphia: Lippincott Williams and Williams.
Nishikawa, T., and Motter, A. E. (2010). Network synchronization landscape reveals compensatory structures, quantization, and the positive effect of negative interactions. Proc. Natl. Acad. Sci. U.S.A. 107, 10342–10347. doi:10.1073/pnas.0912444107
Niu, H., Li, Z., Liao, X., Wang, J., Zhao, T., Shu, N., et al. (2013). Test-retest reliability of graph metrics in functional brain networks: a resting-state fNIRS study. PLoS One 8, e72425. doi:10.1371/journal.pone.0072425
Noe, K. (2019). Counseling and management of the risks of living with epilepsy. CONTINUUM Lifelong Learn. Neurology 25, 477–491. doi:10.1212/CON.0000000000000708
Novelli, L., and Razi, A. (2022). A mathematical perspective on edge-centric brain functional connectivity. Nat. Commun. 13, 2693. doi:10.1038/s41467-022-29775-7
Obrig, H. (2014). NIRS in clinical neurology–a ‘promising’tool? Neuroimage 85, 535–546. doi:10.1016/j.neuroimage.2013.03.045
Osterhage, H., Mormann, F., Staniek, M., and Lehnertz, K. (2007a). Measuring synchronization in the epileptic brain: a comparison of different approaches. Int. J. Bifurc. Chaos Appl. Sci. Eng. 17, 3539–3544. doi:10.1142/s0218127407019330
Osterhage, H., Mormann, F., Wagner, T., and Lehnertz, K. (2007b). Measuring the directionality of coupling: phase versus state space dynamics and application to EEG time series. Int. J. Neural Syst. 17, 139–148. doi:10.1142/S0129065707001019
Oto, M. M. (2017). The misdiagnosis of epilepsy: appraising risks and managing uncertainty. Seizure 44, 143–146. doi:10.1016/j.seizure.2016.11.029
Paluš, M. (2007). From nonlinearity to causality: statistical testing and inference of physical mechanisms underlying complex dynamics. Contemp. Phys. 48, 307–348. doi:10.1080/00107510801959206
Paluš, M., and Vejmelka, M. (2007). Directionality of coupling from bivariate time series: how to avoid false causalities and missed connections. Phys. Rev. E 75, 056211. doi:10.1103/PhysRevE.75.056211
Palva, J. M., Wang, S. H., Palva, S., Zhigalov, A., Monto, S., Brookes, M. J., et al. (2018). Ghost interactions in MEG/EEG source space: a note of caution on inter-areal coupling measures. Neuroimage 173, 632–643. doi:10.1016/j.neuroimage.2018.02.032
Papo, D., and Buldú, J. M. (2019). Brain synchronizability, a false friend. NeuroImage 196, 195–199. doi:10.1016/j.neuroimage.2019.04.029
Papo, D., Zanin, M., Martínez, J. H., and Buldú, J. M. (2016). Beware of the small-world neuroscientist. Front. Hum. Neurosci. 10, 96. doi:10.3389/fnhum.2016.00096
Park, H.-J., and Friston, K. (2013). Structural and functional brain networks: from connections to cognition. Science 342, 1238411. doi:10.1126/science.1238411
Parvizi, J., and Kastner, S. (2018). Promises and limitations of human intracranial electroencephalography. Nat. Neurosci. 21, 474–483. doi:10.1038/s41593-018-0108-2
Pathak, A., Roy, D., and Banerjee, A. (2022). Whole-brain network models: from physics to bedside. Front. Comput. Neurosci. 16, 866517. doi:10.3389/fncom.2022.866517
Paz, J. T., and Huguenard, J. R. (2015). Microcircuits and their interactions in epilepsy: is the focus out of focus? Nat. Neurosci. 18, 351–359. doi:10.1038/nn.3950
Pedersen, M., Abbott, D. F., and Jackson, G. D. (2022). Wearable OPM-MEG: a changing landscape for epilepsy. Epilepsia 63, 2745–2753. doi:10.1111/epi.17368
Pegg, E. J., McKavanagh, A., Bracewell, R. M., Chen, Y., Das, K., Denby, C., et al. (2021). Functional network topology in drug resistant and well-controlled idiopathic generalized epilepsy: a resting state functional MRI study. Brain Commun. 3, fcab196. doi:10.1093/braincomms/fcab196
Pegg, E. J., Taylor, J. R., Keller, S. S., and Mohanraj, R. (2020). Interictal structural and functional connectivity in idiopathic generalized epilepsy: a systematic review of graph theoretical studies. Epilepsy Behav. 106, 107013. doi:10.1016/j.yebeh.2020.107013
Pelc, N. J. (2014). Recent and future directions in CT imaging. Ann. Biomed. Eng. 42, 260–268. doi:10.1007/s10439-014-0974-z
Percival, D. B., and Walden, A. T. (2000). Wavelet methods for time series analysis, 4. Cambridge University Press.
Pereda, E., Quian Quiroga, R., and Bhattacharya, J. (2005). Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 77, 1–37. doi:10.1016/j.pneurobio.2005.10.003
Perez Velazquez, J. L., Khosravani, H., Lozano, A., Bardakijan, B. L., Carlen, P. L., and Wennberg, R. (1999). Type III intermittency in human partial epilepsy. Eur. J. Neurosci. 11, 2571–2576. doi:10.1046/j.1460-9568.1999.00688.x
Phelps, M. E., and Mazziotta, J. C. (1985). Positron emission tomography: human brain function and biochemistry. Science 228, 799–809. doi:10.1126/science.2860723
Pikovsky, A. S., Rosenblum, M. G., and Kurths, J. (2001). Synchronization: a universal concept in nonlinear sciences. Cambridge, UK: Cambridge University Press. doi:10.1017/CBO9780511755743
Piper, R. J., Richardson, R. M., Worrell, G., Carmichael, D. W., Baldeweg, T., Litt, B., et al. (2022). Towards network-guided neuromodulation for epilepsy. Brain 145, 3347–3362. doi:10.1093/brain/awac234
Pisarchik, A., Grubov, V., Maksimenko, V., Lüttjohann, A., Frolov, N., Marqués-Pascual, C., et al. (2018). Extreme events in epileptic EEG of rodents after ischemic stroke. Eur. Phys. J. St. 227, 921–932. doi:10.1140/epjst/e2018-800019-1
Pisarchik, A. N., and Hramov, A. E. (2022). Multistability in physical and living systems, 2. Springer.
Pittau, F., and Vulliemoz, S. (2015). Functional brain networks in epilepsy: recent advances in noninvasive mapping. Curr. Opin. Neurol. 28, 338–343. doi:10.1097/WCO.0000000000000221
Pizzo, F., Collotta, A. D., Di Nora, A., Costanza, G., Ruggieri, M., and Falsaperla, R. (2022). Ketogenic diet in pediatric seizures: a randomized controlled trial review and meta-analysis. Expert Rev. Neurother. 22, 169–177. doi:10.1080/14737175.2022.2030220
Ponten, S. C., Bartolomei, F., and Stam, C. J. (2007). Small-world networks and epilepsy: graph theoretical analysis of intracerebrally recorded mesial temporal lobe seizures. Clin. Neurophysiol. 118, 918–927. doi:10.1016/j.clinph.2006.12.002
Ponten, S. C., Douw, L., Bartolomei, F., Reijneveld, J. C., and Stam, C. J. (2009). Indications for network regularization during absence seizures: weighted and unweighted graph theoretical analyses. Exp. Neurol. 217, 197–204. doi:10.1016/j.expneurol.2009.02.001
Porz, S., Kiel, M., and Lehnertz, K. (2014). Can spurious indications for phase synchronization due to superimposed signals be avoided? Chaos 24, 033112. doi:10.1063/1.4890568
Pourmotabbed, H., de Jongh Curry, A. L., Clarke, D. F., Tyler-Kabara, E. C., and Babajani-Feremi, A. (2022). Reproducibility of graph measures derived from resting-state MEG functional connectivity metrics in sensor and source spaces. Hum. Brain Mapp. 43, 1342–1357. doi:10.1002/hbm.25726
Presigny, C., and Fallani, F. D. V. (2022). Colloquium: multiscale modeling of brain network organization. Rev. Mod. Phys. 94, 031002. doi:10.1103/revmodphys.94.031002
Press, W. H., and Rybicki, G. B. (1989). Fast algorithm for spectral analysis of unevenly sampled data. Astrophys. J. 338, 277–280. doi:10.1086/167197
Puce, A., and Hämäläinen, M. S. (2017). A review of issues related to data acquisition and analysis in EEG/MEG studies. Brain Sci. 7, 58. doi:10.3390/brainsci7060058
Qin, Y., Xu, P., and Yao, D. (2010). A comparative study of different references for EEG default mode network: the use of the infinity reference. Clin. Neurophysiol. 121, 1981–1991. doi:10.1016/j.clinph.2010.03.056
Rammal, R., Toulouse, G., and Virasoro, M. A. (1986). Ultrametricity for physicists. Rev. Mod. Phys. 58, 765–788. doi:10.1103/RevModPhys.58.765
Rapisarda, E., Bettinardi, V., Thielemans, K., and Gilardi, M. (2010). Image-based point spread function implementation in a fully 3D OSEM reconstruction algorithm for PET. Phys. Med. Biol. 55, 4131–4151. doi:10.1088/0031-9155/55/14/012
Reijneveld, J. C., Ponten, S. C., Berendse, H. W., and Stam, C. J. (2007). The application of graph theoretical analysis to complex networks in the brain. Clin. Neurophysiol. 118, 2317–2331. doi:10.1016/j.clinph.2007.08.010
Ribeiro, P., Paredes, P., Silva, M. E., Aparicio, D., and Silva, F. (2021). A survey on subgraph counting: concepts, algorithms, and applications to network motifs and graphlets. ACM Comput. Surv. 54, 1–36. doi:10.1145/3433652
Richardson, M. (2010). Current themes in neuroimaging of epilepsy: brain networks, dynamic phenomena, and clinical relevance. Clin. Neurophysiol. 121, 1153–1175. doi:10.1016/j.clinph.2010.01.004
Richardson, M. P. (2012). Large scale brain models of epilepsy: dynamics meets connectomics. J. Neurol. Neurosurg. Psychiatry 83, 1238–1248. doi:10.1136/jnnp-2011-301944
Rings, T., Cox, R., Rüber, T., Lehnertz, K., and Fell, J. (2020). No evidence for spontaneous cross-frequency phase–phase coupling in the human hippocampus. Eur. J. Neurosci. 51, 1735–1742. doi:10.1111/ejn.14608
Rings, T., Mazarei, M., Akhshi, A., Geier, C., Tabar, M. R. R., and Lehnertz, K. (2019a). Traceability and dynamical resistance of precursor of extreme events. Sci. Rep. 9, 1744. doi:10.1038/s41598-018-38372-y
Rings, T., Von Wrede, R., Bröhl, T., Schach, S., Helmstaedter, C., and Lehnertz, K. (2021). Impact of transcutaneous auricular vagus nerve stimulation on large-scale functional brain networks: from local to global. Front. Physiol. 1328. doi:10.3389/fphys.2021.700261
Rings, T., von Wrede, R., and Lehnertz, K. (2019b). Precursors of seizures due to specific spatial-temporal modifications of evolving large-scale epileptic brain networks. Sci. Rep. 9, 10623. doi:10.1038/s41598-019-47092-w
Ritchie, P. D., Alkhayuon, H., Cox, P. M., and Wieczorek, S. (2023). Rate-induced tipping in natural and human systems. Earth Syst. Dyn. 14, 669–683. doi:10.5194/esd-14-669-2023
Rizkallah, J., Amoud, H., Fraschini, M., Wendling, F., and Hassan, M. (2020). Exploring the correlation between M/EEG source–space and fMRI networks at rest. Brain Topogr. 33, 151–160. doi:10.1007/s10548-020-00753-w
Rizzi, M., Weissberg, I., Milikovsky, D. Z., and Friedman, A. (2016). Following a potential epileptogenic insult, prolonged high rates of nonlinear dynamical regimes of intermittency type is the hallmark of epileptogenesis. Sci. Rep. 6, 31129. doi:10.1038/srep31129
Rodgers, J. L., and Nicewander, W. A. (1988). Thirteen ways to look at the correlation coefficient. Am. Stat. 42, 59–66. doi:10.1080/00031305.1988.10475524
Roine, T., Jeurissen, B., Perrone, D., Aelterman, J., Philips, W., Sijbers, J., et al. (2019). Reproducibility and intercorrelation of graph theoretical measures in structural brain connectivity networks. Med. Image Anal. 52, 56–67. doi:10.1016/j.media.2018.10.009
Roliz, A. H., and Kothare, S. (2022). The interaction between sleep and epilepsy. Curr. Neurol. Neurosci. Rep. 22, 551–563. doi:10.1007/s11910-022-01219-1
Rolle, C. E., Narayan, M., Wu, W., Toll, R., Johnson, N., Caudle, T., et al. (2022). Functional connectivity using high density EEG shows competitive reliability and agreement across test/retest sessions. J. Neurosci. Methods 367, 109424. doi:10.1016/j.jneumeth.2021.109424
Rosch, R., Baldeweg, T., Moeller, F., and Baier, G. (2018). Network dynamics in the healthy and epileptic developing brain. Netw. Neurosci. 2, 41–59. doi:10.1162/NETN_a_00026
Rosenblum, M., and Pikovsky, A. (2023). Inferring connectivity of an oscillatory network via the phase dynamics reconstruction. Front. Netw. Physiol. 3, 1298228. doi:10.3389/fnetp.2023.1298228
Rosenow, F., and Lüders, H. (2001). Presurgical evaluation of epilepsy. Brain 124, 1683–1700. doi:10.1093/brain/124.9.1683
Rossi, K. L., Budzinski, R. C., Medeiros, E. S., Boaretto, B. R., Muller, L., and Feudel, U. (2023). A unified framework of metastability in neuroscience. arXiv preprint arXiv:2305.05328.
Rothkegel, A., and Lehnertz, K. (2009). Multistability, local pattern formation, and global collective firing in a small-world network of non-leaky integrate-and-fire neurons. Chaos 19, 015109. doi:10.1063/1.3087432
Rothkegel, A., and Lehnertz, K. (2014). Irregular macroscopic dynamics due to chimera states in small-world networks of pulse-coupled oscillators. New J. Phys. 16, 055006. doi:10.1088/1367-2630/16/5/055006
Roy, C. S., and Sherrington, C. S. (1890). On the regulation of the blood-supply of the brain. J. Physiol. 11, 85–158. doi:10.1113/jphysiol.1890.sp000321
Royer, J., Bernhardt, B. C., Larivière, S., Gleichgerrcht, E., Vorderwülbecke, B. J., Vulliémoz, S., et al. (2022a). Epilepsy and brain network hubs. Epilepsia 63, 537–550. doi:10.1111/epi.17171
Royer, J., Rodríguez-Cruces, R., Tavakol, S., Larivière, S., Herholz, P., Li, Q., et al. (2022b). An open MRI dataset for multiscale neuroscience. Sci. Data 9, 569. doi:10.1038/s41597-022-01682-y
Rubinov, M., and Sporns, O. (2010). Complex network measures of brain connectivity: uses and interpretations. NeuroImage 52, 1059–1069. doi:10.1016/j.neuroimage.2009.10.003
Rummel, C., Baier, G., and Müller, M. (2007). The influence of static correlations on multivariate correlation analysis of the EEG. J. Neurosci. Methods 166, 138–157. doi:10.1016/j.jneumeth.2007.06.023
Rungratsameetaweemana, N., Lainscsek, C., Cash, S. S., Garcia, J. O., Sejnowski, T. J., and Bansal, K. (2022). Brain network dynamics codify heterogeneity in seizure evolution. Brain Commun. 4, fcac234. doi:10.1093/braincomms/fcac234
Rydin Gorjão, L., Heysel, J., Lehnertz, K., and Tabar, M. R. R. (2019). Analysis and data-driven reconstruction of bivariate jump-diffusion processes. Phys. Rev. E 100, 062127. doi:10.1103/PhysRevE.100.062127
Sadaghiani, S., Brookes, M. J., and Baillet, S. (2022). Connectomics of human electrophysiology. NeuroImage 247, 118788. doi:10.1016/j.neuroimage.2021.118788
Salami, P., Borzello, M., Kramer, M. A., Westover, M. B., and Cash, S. S. (2022). Quantifying seizure termination patterns reveals limited pathways to seizure end. Neurobiol. Dis. 165, 105645. doi:10.1016/j.nbd.2022.105645
Salcedo-Sanz, S., Casillas-Pérez, D., Del Ser, J., Casanova-Mateo, C., Cuadra, L., Piles, M., et al. (2022). Persistence in complex systems. Phys. Rep. 957, 1–73. doi:10.1016/j.physrep.2022.02.002
Sanz-Garcia, A., Rings, T., and Lehnertz, K. (2018). Impact of type of intracranial EEG sensors on link strengths of evolving functional brain networks. Physiol. Meas. 39, 074003. doi:10.1088/1361-6579/aace94
Schaworonkow, N., and Nikulin, V. V. (2022). Is sensor space analysis good enough? Spatial patterns as a tool for assessing spatial mixing of EEG/MEG rhythms. Neuroimage 253, 119093. doi:10.1016/j.neuroimage.2022.119093
Schevon, C. A., Tobochnik, S., Eissa, T., Merricks, E., Gill, B., Parrish, R. R., et al. (2019). Multiscale recordings reveal the dynamic spatial structure of human seizures. Neurobiol. Dis. 127, 303–311. doi:10.1016/j.nbd.2019.03.015
Schieber, T. A., Carpi, L., Díaz-Guilera, A., Pardalos, P. M., Masoller, C., and Ravetti, M. G. (2017). Quantification of network structural dissimilarities. Nat. Commun. 8, 13928. doi:10.1038/ncomms13928
Schindler, K., Bialonski, S., Horstmann, M.-T., Elger, C. E., and Lehnertz, K. (2008). Evolving functional network properties and synchronizability during human epileptic seizures. Chaos 18, 033119. doi:10.1063/1.2966112
Schindler, K., Elger, C. E., and Lehnertz, K. (2007a). Increasing synchronization may promote seizure termination: evidence from status epilepticus. Clin. Neurophysiol. 118, 1955–1968. doi:10.1016/j.clinph.2007.06.006
Schindler, K., Leung, H., Elger, C. E., and Lehnertz, K. (2007b). Assessing seizure dynamics by analysing the correlation structure of multichannel intracranial EEG. Brain 130, 65–77. doi:10.1093/brain/awl304
Schreiber, T. (1998). Constrained randomization of time series data. Phys. Rev. Lett. 80, 2105–2108. doi:10.1103/physrevlett.80.2105
Schreiber, T., and Schmitz, A. (2000). Surrogate time series. Phys. D. 142, 346–382. doi:10.1016/S0167-2789(00)00043-9
Schroeder, G. M., Diehl, B., Chowdhury, F. A., Duncan, J. S., De Tisi, J., Trevelyan, A. J., et al. (2020). Seizure pathways change on circadian and slower timescales in individual patients with focal epilepsy. Proc. Natl. Acad. Sci. (U.S.A.) 117, 11048–11058. doi:10.1073/pnas.1922084117
Schulze-Bonhage, A. (2019). Long-term outcome in neurostimulation of epilepsy. Epilepsy Behav. 91, 25–29. doi:10.1016/j.yebeh.2018.06.011
Seider, N. A., Adeyemo, B., Miller, R., Newbold, D. J., Hampton, J. M., Scheidter, K. M., et al. (2022). Accuracy and reliability of diffusion imaging models. NeuroImage 254, 119138. doi:10.1016/j.neuroimage.2022.119138
Seshadri, V., Zarroli, K. A., Schetlick, R. S., Massey, J. C., Reyes, J. M., Muttikal, T. J. E., et al. (2021). Dynamic FDG-PET in localization of focal epilepsy: a pilot study. Epilepsy Behav. 122, 108204. doi:10.1016/j.yebeh.2021.108204
Shine, J. M. (2019). Neuromodulatory influences on integration and segregation in the brain. Trends Cogn. Sci. 23, 572–583. doi:10.1016/j.tics.2019.04.002
Simpson, H. D., Schulze-Bonhage, A., Cascino, G. D., Fisher, R. S., Jobst, B. C., Sperling, M. R., et al. (2022). Practical considerations in epilepsy neurostimulation. Epilepsia 63, 2445–2460. doi:10.1111/epi.17329
Sinha, N., Joshi, R. B., Sandhu, M. R. S., Netoff, T. I., Zaveri, H. P., and Lehnertz, K. (2022). Perspectives on understanding aberrant brain networks in epilepsy. Front. Netw. Physiol. 2, 868092. doi:10.3389/fnetp.2022.868092
Sisodiya, S. M., Whelan, C. D., Hatton, S. N., Huynh, K., Altmann, A., Ryten, M., et al. (2022). The ENIGMA-Epilepsy working group: mapping disease from large data sets. Hum. Brain Mapp. 43, 113–128. doi:10.1002/hbm.25037
Slinger, G., Otte, W. M., Braun, K. P., and van Diessen, E. (2022). An updated systematic review and meta-analysis of brain network organization in focal epilepsy: looking back and forth. Neurosci. Biobehav. Rev. 132, 211–223. doi:10.1016/j.neubiorev.2021.11.028
Soloukey, S., Vincent, A. J., Smits, M., De Zeeuw, C. I., Koekkoek, S. K., Dirven, C. M., et al. (2023). Functional imaging of the exposed brain. Front. Neurosci. 17, 1087912. doi:10.3389/fnins.2023.1087912
Sotiropoulos, S. N., and Zalesky, A. (2019). Building connectomes using diffusion MRI: why, how and but. NMR Biomed. 32, e3752. doi:10.1002/nbm.3752
Spencer, D. C., Sun, F. T., Brown, S. N., Jobst, B. C., Fountain, N. B., Wong, V. S., et al. (2016). Circadian and ultradian patterns of epileptiform discharges differ by seizure-onset location during long-term ambulatory intracranial monitoring. Epilepsia 57, 1495–1502. doi:10.1111/epi.13455
Spencer, S. S. (2002). Neural networks in human epilepsy: evidence of and implications for treatment. Epilepsia 43, 219–227. doi:10.1046/j.1528-1157.2002.26901.x
Sporns, O. (2022). Structure and function of complex brain networks. Dialogues Clin. Neurosci. 15, 247–262. doi:10.31887/DCNS.2013.15.3/osporns
Stahn, K., and Lehnertz, K. (2017). Surrogate-assisted identification of influences of network construction on evolving weighted functional networks. Chaos 27, 123106. doi:10.1063/1.4996980
Stam, C., Tewarie, P., Van Dellen, E., Van Straaten, E., Hillebrand, A., and Van Mieghem, P. (2014). The trees and the forest: characterization of complex brain networks with minimum spanning trees. Int. J. Psychophysiol. 92, 129–138. doi:10.1016/j.ijpsycho.2014.04.001
Stam, C. J. (2014). Modern network science of neurological disorders. Nat. Rev. Neurosci. 15, 683–695. doi:10.1038/nrn3801
Stankovski, T., Duggento, A., McClintock, P. V. E., and Stefanovska, A. (2012). Inference of time-evolving coupled dynamical systems in the presence of noise. Phys. Rev. Lett. 109, 024101. doi:10.1103/PhysRevLett.109.024101
Steiger, B. K., Muller, A. M., Spirig, E., Toller, G., and Jokeit, H. (2017). Mesial temporal lobe epilepsy diminishes functional connectivity during emotion perception. Epilepsy Res. 134, 33–40. doi:10.1016/j.eplepsyres.2017.05.004
Strzelczyk, A., Aledo-Serrano, A., Coppola, A., Didelot, A., Bates, E., Sainz-Fuertes, R., et al. (2023). The impact of epilepsy on quality of life: findings from a European survey. Epilepsy Behav. 142, 109179. doi:10.1016/j.yebeh.2023.109179
Strzelczyk, A., Reese, J. P., Dodel, R., and Hamer, H. M. (2008). Cost of epilepsy: a systematic review. Pharmacoeconomics 26, 463–476. doi:10.2165/00019053-200826060-00002
Su, R.-Q., Wang, W.-X., and Lai, Y.-C. (2012). Detecting hidden nodes in complex networks from time series. Phys. Rev. E 85, 065201. doi:10.1103/PhysRevE.85.065201
Sumsky, S., and Greenfield, L. J. (2022). Network analysis of preictal iEEG reveals changes in network structure preceding seizure onset. Sci. Rep. 12, 12526. doi:10.1038/s41598-022-16877-x
Sun, J., Bollt, E. M., and Nishikawa, T. (2009). Master stability functions for coupled nearly identical dynamical systems. EPL 85, 60011. doi:10.1209/0295-5075/85/60011
Swierczek-Jereczek, J., Robinson, A., Blasco, J., Alvarez-Solas, J., and Montoya, M. (2023). Time-scale synchronisation of oscillatory responses can lead to non-monotonous R-tipping. Sci. Rep. 13, 2104. doi:10.1038/s41598-023-28771-1
Tabar, M. R. R. (2019). Analysis and data-based reconstruction of complex nonlinear dynamical systems: using the methods of stochastic processes. Cham-Switzerland: Springer. doi:10.1007/978-3-030-18472-8
Tailby, C., Kowalczyk, M. A., and Jackson, G. D. (2018). Cognitive impairment in epilepsy: the role of reduced network flexibility. Ann. Clin. Transl. Neurol. 5, 29–40. doi:10.1002/acn3.503
Takahashi, H., Takahashi, S., Kanzaki, R., and Kawai, K. (2012). State-dependent precursors of seizures in correlation-based functional networks of electrocorticograms of patients with temporal lobe epilepsy. Neurol. Sci. 33, 1355–1364. doi:10.1007/s10072-012-0949-5
Takeshita, D., Sato, Y. D., and Bahar, S. (2007). Transitions between multistable states as a model of epileptic seizure dynamics. Phys. Rev. E 75, 051925. doi:10.1103/PhysRevE.75.051925
Tauste Campo, A., Principe, A., Ley, M., Rocamora, R., and Deco, G. (2018). Degenerate time-dependent network dynamics anticipate seizures in human epileptic brain. PLoS Biol. 16, e2002580. doi:10.1371/journal.pbio.2002580
Téllez-Zenteno, J. F., Dhar, R., Hernandez-Ronquillo, L., and Wiebe, S. (2007). Long-term outcomes in epilepsy surgery: antiepileptic drugs, mortality, cognitive and psychosocial aspects. Brain 130, 334–345. doi:10.1093/brain/awl316
Téllez-Zenteno, J. F., Dhar, R., and Wiebe, S. (2005). Long-term seizure outcomes following epilepsy surgery: a systematic review and meta-analysis. Brain 128, 1188–1198. doi:10.1093/brain/awh449
Thompson, W. H., Brantefors, P., and Fransson, P. (2017). From static to temporal network theory: applications to functional brain connectivity. Netw. Neurosci. 1, 69–99. doi:10.1162/NETN_a_00011
Tognoli, E., and Kelso, J. S. (2014). The metastable brain. Neuron 81, 35–48. doi:10.1016/j.neuron.2013.12.022
Tononi, G., Sporns, O., and Edelman, G. M. (1994). A measure for brain complexity: relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. 91, 5033–5037. doi:10.1073/pnas.91.11.5033
Torricelli, A., Contini, D., Pifferi, A., Caffini, M., Re, R., Zucchelli, L., et al. (2014). Time domain functional NIRS imaging for human brain mapping. Neuroimage 85, 28–50. doi:10.1016/j.neuroimage.2013.05.106
Tousseyn, S., Dupont, P., Goffin, K., Sunaert, S., and Van Paesschen, W. (2015). Correspondence between large-scale ictal and interictal epileptic networks revealed by single photon emission computed tomography (SPECT) and electroencephalography (EEG)–functional magnetic resonance imaging (fMRI). Epilepsia 56, 382–392. doi:10.1111/epi.12910
Tudisco, F., Arrigo, F., and Gautier, A. (2018). Node and layer eigenvector centralities for multiplex networks. SIAM J. Appl. Math. 78, 853–876. doi:10.1137/17m1137668
Tufa, U., Gravitis, A., Zukotynski, K., Chinvarun, Y., Devinsky, O., Wennberg, R., et al. (2022). A peri-ictal EEG-based biomarker for sudden unexpected death in epilepsy (SUDEP) derived from brain network analysis. Front. Netw. Physiol. 2, 866540. doi:10.3389/fnetp.2022.866540
Turrigiano, G. G. (1999). Homeostatic plasticity in neuronal networks: the more things change, the more they stay the same. Trends Neurosci. 22, 221–227. doi:10.1016/s0166-2236(98)01341-1
Uchitel, J., Vidal-Rosas, E. E., Cooper, R. J., and Zhao, H. (2021). Wearable, integrated EEG–fNIRS technologies: a review. Sensors 21, 6106. doi:10.3390/s21186106
Vaiana, M., and Muldoon, S. F. (2020). Multilayer brain networks. J. Nonlinear Sci. 30, 2147–2169. doi:10.1007/s00332-017-9436-8
van Diessen, E., Diederen, S. J. H., Braun, K. P. J., Jansen, F. E., and Stam, C. J. (2013). Functional and structural brain networks in epilepsy: what have we learned? Epilepsia 54, 1855–1865. doi:10.1111/epi.12350
van Diessen, E., Otte, W. M., Stam, C. J., Braun, K. P., and Jansen, F. E. (2016). Electroencephalography based functional networks in newly diagnosed childhood epilepsies. Clin. Neurophysiol. 127, 2325–2332. doi:10.1016/j.clinph.2016.03.015
van Mierlo, P., Höller, Y., Focke, N. K., and Vulliemoz, S. (2019). Network perspectives on epilepsy using EEG/MEG source connectivity. Front. Neurol. 10, 721. doi:10.3389/fneur.2019.00721
van Mierlo, P., Papadopoulou, M., Carrette, E., Boon, P., Vandenberghe, S., Vonck, K., et al. (2014). Functional brain connectivity from EEG in epilepsy: seizure prediction and epileptogenic focus localization. Prog. Neurobiol. 121, 19–35. doi:10.1016/j.pneurobio.2014.06.004
van Wijk, B. C. M., Stam, C. J., and Daffertshofer, A. (2010). Comparing brain networks of different size and connectivity density using graph theory. PLoS ONE 5, e13701. doi:10.1371/journal.pone.0013701
Vaquero, J. J., and Kinahan, P. (2015). Positron emission tomography: current challenges and opportunities for technological advances in clinical and preclinical imaging systems. Annu. Rev. Biomed. Eng. 17, 385–414. doi:10.1146/annurev-bioeng-071114-040723
Varotto, G., Tassi, L., Franceschetti, S., Spreafico, R., and Panzica, F. (2012). Epileptogenic networks of type II focal cortical dysplasia: a stereo-EEG study. NeuroImage 61, 591–598. doi:10.1016/j.neuroimage.2012.03.090
Váša, F., and Mišić, B. (2022). Null models in network neuroscience. Nat. Rev. Neurosci. 23, 493–504. doi:10.1038/s41583-022-00601-9
Vecchio, F., Miraglia, F., Quaranta, D., Granata, G., Romanello, R., Marra, C., et al. (2016). Cortical connectivity and memory performance in cognitive decline: a study via graph theory from EEG data. Neuroscience 316, 143–150. doi:10.1016/j.neuroscience.2015.12.036
Vetkas, A., Germann, J., Elias, G., Loh, A., Boutet, A., Yamamoto, K., et al. (2022). Identifying the neural network for neuromodulation in epilepsy through connectomics and graphs. Brain Commun. 4, fcac092. doi:10.1093/braincomms/fcac092
Villringer, A., and Chance, B. (1997). Non-invasive optical spectroscopy and imaging of human brain function. Trends Neurosci. 20, 435–442. doi:10.1016/s0166-2236(97)01132-6
Vlooswijk, M. C. G., Vaessen, M. J., Jansen, J. F. A., de Krom, M. C. F. T. M., Majoie, H. J. M., Hofman, P. A. M., et al. (2011). Loss of network efficiency associated with cognitive decline in chronic epilepsy. Neurology 77, 938–944. doi:10.1212/WNL.0b013e31822cfc2f
von Helmholtz, H. (1853). Ueber einige Gesetze der Vertheilung elektrischer Ströme in körperlichen Leitern, mit Anwendung auf die thierisch-elektrischen Versuche (Schluss.). Ann. Phys. Leipz. 165, 353–377. doi:10.1002/andp.18531650702
von Wrede, R., Bröhl, T., Rings, T., Pukropski, J., Helmstaedter, C., and Lehnertz, K. (2022a). Modifications of functional human brain networks by transcutaneous auricular vagus nerve stimulation: impact of time of day. Brain Sci. 12, 546. doi:10.3390/brainsci12050546
von Wrede, R., Rings, T., Bröhl, T., Pukropski, J., Schach, S., Helmstaedter, C., et al. (2022b). Transcutaneous auricular vagus nerve stimulation differently modifies functional brain networks of subjects with different epilepsy types. Front. Hum. Neurosci. 16, 867563. doi:10.3389/fnhum.2022.867563
von Wrede, R., Rings, T., Schach, S., Helmstaedter, C., and Lehnertz, K. (2021). Transcutaneous auricular vagus nerve stimulation induces stabilizing modifications in large-scale functional brain networks: towards understanding the effects of taVNS in subjects with epilepsy. Sci. Rep. 11, 7906. doi:10.1038/s41598-021-87032-1
Vorderwülbecke, B. J., Carboni, M., Tourbier, S., Brunet, D., Seeber, M., Spinelli, L., et al. (2020). High-density electric source imaging of interictal epileptic discharges: how many electrodes and which time point? Clin. Neurophysiol. 131, 2795–2803. doi:10.1016/j.clinph.2020.09.018
Wandschneider, B., and Koepp, M. J. (2016). Pharmaco fMRI: determining the functional anatomy of the effects of medication. NeuroImage Clin. 12, 691–697. doi:10.1016/j.nicl.2016.10.002
Wang, P., Wang, J., Michael, A., Wang, Z., Klugah-Brown, B., Meng, C., et al. (2022). White matter functional connectivity in resting-state fMRI: robustness, reliability, and relationships to gray matter. Cereb. Cortex 32, 1547–1559. doi:10.1093/cercor/bhab181
Watabe, T., and Hatazawa, J. (2019). Evaluation of functional connectivity in the brain using positron emission tomography: a mini-review. Front. Neurosci. 13, 775. doi:10.3389/fnins.2019.00775
Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442. doi:10.1038/30918
Weisdorf, S., Duun-Henriksen, J., Kjeldsen, M. J., Poulsen, F. R., Gangstad, S. W., and Kjær, T. W. (2019). Ultra-long-term subcutaneous home monitoring of epilepsy—490 days of EEG from nine patients. Epilepsia 60, 2204–2214. doi:10.1111/epi.16360
Weiss, S. A., Pastore, T., Orosz, I., Rubinstein, D., Gorniak, R., Waldman, Z., et al. (2022). Graph theoretical measures of fast ripples support the epileptic network hypothesis. Brain Commun. 4, fcac101. doi:10.1093/braincomms/fcac101
Welton, T., Kent, D. A., Auer, D. P., and Dineen, R. A. (2015). Reproducibility of graph-theoretic brain network metrics: a systematic review. Brain Connect. 5, 193–202. doi:10.1089/brain.2014.0313
Wen, T., and Cheong, K. H. (2021). The fractal dimension of complex networks: a review. Inf. Fusion 73, 87–102. doi:10.1016/j.inffus.2021.02.001
Wendling, F., Ansari-Asl, K., Bartolomei, F., and Senhadji, L. (2009). From EEG signals to brain connectivity: a model-based evaluation of interdependence measures. J. Neurosci. Methods 183, 9–18. doi:10.1016/j.jneumeth.2009.04.021
Wheelock, M. D., Culver, J. P., and Eggebrecht, A. T. (2019). High-density diffuse optical tomography for imaging human brain function. Rev. Sci. Instr. 90, 051101. doi:10.1063/1.5086809
Whelan, C. D., Altmann, A., Botía, J. A., Jahanshad, N., Hibar, D. P., Absil, J., et al. (2018). Structural brain abnormalities in the common epilepsies assessed in a worldwide ENIGMA study. Brain 141, 391–408. doi:10.1093/brain/awx341
Wiedermann, M., Donges, J. F., Kurths, J., and Donner, R. V. (2016). Spatial network surrogates for disentangling complex system structure from spatial embedding of nodes. Phys. Rev. E 93, 042308. doi:10.1103/PhysRevE.93.042308
Wilkat, T., Rings, T., and Lehnertz, K. (2019). No evidence for critical slowing down prior to human epileptic seizures. Chaos 29, 091104. doi:10.1063/1.5122759
Wilke, C., Worrell, G., and He, B. (2011). Graph analysis of epileptogenic networks in human partial epilepsy. Epilepsia 52, 84–93. doi:10.1111/j.1528-1167.2010.02785.x
Woldman, W., Schmidt, H., Abela, E., Chowdhury, F. A., Pawley, A. D., Jewell, S., et al. (2020). Dynamic network properties of the interictal brain determine whether seizures appear focal or generalised. Sci. Rep. 10, 7043. doi:10.1038/s41598-020-63430-9
Wu, C., Ferreira, F., Fox, M., Harel, N., Hattangadi-Gluth, J., Horn, A., et al. (2021). Clinical applications of magnetic resonance imaging based functional and structural connectivity. Neuroimage 244, 118649. doi:10.1016/j.neuroimage.2021.118649
Wu, J., Aton, S. J., Booth, V., and Zochowski, M. (2022). Heterogeneous mechanisms for synchronization of networks of resonant neurons under different E/I balance regimes. Front. Netw. Physiol. 2, 975951. doi:10.3389/fnetp.2022.975951
Yaffe, R. B., Borger, P., Megevand, P., Groppe, D. M., Kramer, M. A., Chu, C. J., et al. (2015). Physiology of functional and effective networks in epilepsy. Clin. Neurophysiol. 126, 227–236. doi:10.1016/j.clinph.2014.09.009
Yang, H., Zhang, C., Liu, C., Yu, T., Zhang, G., Chen, N., et al. (2018). Brain network alteration in patients with temporal lobe epilepsy with cognitive impairment. Epilepsy Behav. 81, 41–48. doi:10.1016/j.yebeh.2018.01.024
Yao, D., Qin, Y., Hu, S., Dong, L., Bringas Vega, M. L., and Valdés Sosa, P. A. (2019). Which reference should we use for EEG and ERP practice? Brain Topogr. 32, 530–549. doi:10.1007/s10548-019-00707-x
Yao, D., Wang, L., Oostenveld, R., Dremstrup Nielsen, K., Arendt-Nielsen, L., and Chen, A. C. N. (2005). A comparative study of different references for EEG spectral mapping: the issue of the neutral reference and the use of the infinity reference. Physiol. Meas. 26, 173–184. doi:10.1088/0967-3334/26/3/003
Yeh, C.-H., Jones, D. K., Liang, X., Descoteaux, M., and Connelly, A. (2021). Mapping structural connectivity using diffusion MRI: challenges and opportunities. J. Magn. Reson. Imag. 53, 1666–1682. doi:10.1002/jmri.27188
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., van den Heuvel, M. P., and Breakspear, M. (2016). Connectome sensitivity or specificity: which is more important? Neuroimage 142, 407–420. doi:10.1016/j.neuroimage.2016.06.035
Zalesky, A., Fornito, A., Harding, I. H., Cocchi, L., Yücel, M., Pantelis, C., et al. (2010). Whole-brain anatomical networks: does the choice of nodes matter? NeuroImage 50, 970–983. doi:10.1016/j.neuroimage.2009.12.027
Zanin, M., Belkoura, S., Gomez, J., Alfaro, C., and Cano, J. (2018). Topological structures are consistently overestimated in functional complex networks. Sci. Rep. 8, 11980. doi:10.1038/s41598-018-30472-z
Zanin, M., Sousa, P., Papo, D., Bajo, R., Garcia-Prieto, J., del Pozo, F., et al. (2012). Optimizing functional network representation of multivariate time series. Sci. Rep. 2, 630. doi:10.1038/srep00630
Zaoli, S., Mazzarisi, P., and Lillo, F. (2021). Betweenness centrality for temporal multiplexes. Sci. Rep. 11, 4919. doi:10.1038/s41598-021-84418-z
Zaveri, H. P., Duckrow, R. B., and Spencer, S. S. (2006). On the use of bipolar montages for time-series analysis of intracranial electroencephalograms. Clin. Neurophysiol. 117, 2102–2108. doi:10.1016/j.clinph.2006.05.032
Zaveri, H. P., Pincus, S. M., Goncharova, I. I., Duckrow, R. B., Spencer, D. D., and Spencer, S. S. (2009). Localization-related epilepsy exhibits significant connectivity away from the seizure-onset area. NeuroReport 20, 891–895. doi:10.1097/WNR.0b013e32832c78e0
Zaveri, H. P., Schelter, B., Schevon, C. A., Jiruska, P., Jefferys, J. G. R., Worrell, G., et al. (2020). Controversies on the network theory of epilepsy: debates held during the ICTALS 2019 conference. Seizure 78, 78–85. doi:10.1016/j.seizure.2020.03.010
Zhang, F., Daducci, A., He, Y., Schiavi, S., Seguin, C., Smith, R. E., et al. (2022). Quantitative mapping of the brain’s structural connectivity using diffusion MRI tractography: a review. Neuroimage 249, 118870. doi:10.1016/j.neuroimage.2021.118870
Zhang, Y., and Motter, A. E. (2017). Identical synchronization of nonidentical oscillators: when only birds of different feathers flock together. Nonlinearity 31, R1–R23. doi:10.1088/1361-6544/aa8fe7
Zhang, Z., Liao, W., Chen, H., Mantini, D., Ding, J.-R., Xu, Q., et al. (2011). Altered functional-structural coupling of large-scale brain networks in idiopathic generalized epilepsy. Brain 134, 2912–2928. doi:10.1093/brain/awr223
Zhou, T. (2021). Progresses and challenges in link prediction. Iscience 24, 103217. doi:10.1016/j.isci.2021.103217
Zijlmans, M., Zweiphenning, W., and van Klink, N. (2019). Changing concepts in presurgical assessment for epilepsy surgery. Nat. Rev. Neurol. 15, 594–606. doi:10.1038/s41582-019-0224-y
Zubler, F., Gast, H., Abela, E., Rummel, C., Hauf, M., Wiest, R., et al. (2015). Detecting functional hubs of ictogenic networks. Brain Topogr. 28, 305–317. doi:10.1007/s10548-014-0370-x
Zuo, X.-N., Anderson, J. S., Bellec, P., Birn, R. M., Biswal, B. B., Blautzik, J., et al. (2014). An open science resource for establishing reliability and reproducibility in functional connectomics. Sci. Data 1, 140049. doi:10.1038/sdata.2014.49
Keywords: epilepsy, epileptic network, epileptic focus, seizure, seizure-prediction, seizure-control, electroencephalography, brain dynamics
Citation: Bröhl T, Rings T, Pukropski J, von Wrede R and Lehnertz K (2024) The time-evolving epileptic brain network: concepts, definitions, accomplishments, perspectives. Front. Netw. Physiol. 3:1338864. doi: 10.3389/fnetp.2023.1338864
Received: 15 November 2023; Accepted: 19 December 2023;
Published: 16 January 2024.
Edited by:
Cristina Masoller, Universitat Politecnica de Catalunya, SpainReviewed by:
Jan Kudlacek, Charles University, CzechiaCopyright © 2024 Bröhl, Rings, Pukropski, von Wrede and Lehnertz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Timo Bröhl, timo.broehl@uni-bonn.de
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.