Harnessing electroosmotic hybrid nanofluid dynamics in curved arteries: insights into biomedical flow enhancement

In this study, we investigated the dynamics of unsteady electroosmotic pulsatile flow involving a hybrid nanofluid within a curved artery, influenced by both stenosis and an embedded catheter. The hybrid nanofluid, a mixture of silver $(Ag)$ and aluminum oxide $(A{l}_2{O}_3)$ nanoparticles dispersed in blood, was modeled via the Carreau non-Newtonian framework to more accurately represent the intricate nature of blood flow. The electroosmotic forces introduced simulated the effect of an external electric field, while the catheter served as an additional structural constraint within the artery. To account for both the curvature of the vessel and the overlapping stenosis, we derived the governing equations for this model. Using numerical methods, particularly the finite-difference approach, we solved the nonlinear partial differential equations that govern the flow, temperature, and concentration distributions. Our findings suggest that the hybrid nanofluid demonstrates enhanced thermal and flow properties compared to standard fluids. The results showed significant influences from electroosmotic forces, curvature, and pulsatility on the velocity, temperature, and concentration profiles. Furthermore, an increase in the electroosmotic and Weissenberg parameters substantially accelerated fluid velocity by reducing viscous drag while improving mass transport. These results offer valuable insights into the behavior of blood flow in catheterized arteries and may inform future advancements in cardiovascular treatment technologies.

1 Introduction

Hybrid nanofluids, particularly those with non-Newtonian properties, have attracted significant interest lately due to their broad applications in biomedical engineering and fluid transportation. When combined with electroosmotic flow, these hybrid nanofluids exhibit additional complexities in behavior, making them well suited for use in microscale and nanoscale fluid manipulation scenarios (Sundar et al., 2013). Nanofluids and hybrid nanofluids are utilized in various disciplines, demonstrating their flexibility and potential impact. There are a variety of applications for nanofluids and hybrid nanofluids in fields such as biomedical applications, the energy sector, manufacturing, and engineering (El Kot and Abd Elmaboud, 2021; El-Masry et al., 2020; Ali et al., 2020). Abdal et al. (2021) investigated the effects of bio-convection and activation energy on the Reiner–Rivlin nanofluid flow over a rotating disk with partial slips. By deriving a system of coupled nonlinear differential equations based on the Reiner–Rivlin fluid relationships, the study explores a variety of non-Newtonian fluid models and slip coefficients for numerical analysis. Ali et al. (2022) delved into the impact of volume fraction and Coriolis and Lorentz forces on the behavior of water-based silver (Ag) nanoparticle flow toward a continuously stretching sheet.

Electroosmotic flow, influenced by applied electric fields, offers precise control over fluid movement, which is highly desirable in medical contexts such as targeted drug delivery and microfluidic systems. Wang et al. (2009) demonstrated the ability of electroosmotic pumps to precisely regulate microflow in microfluidic applications. Hybrid nanofluids, typically composed of metal-based nanoparticles dispersed in base fluids, provide enhanced thermal and flow properties, making them ideal for improving the fluid efficiency in medical systems. Sarkar et al. (2015) and Huminic and Huminic 2018() reviewed hybrid nanofluids and their improved thermal properties, emphasizing their potential in various heat transfer applications. Bhatti et al. (2024) investigated third-grade fluid motion between vertical parallel walls utilizing an electromagnetic hydrodynamic approach. The walls, oriented vertically, contain a nanofluid with sodium alginate infused with gold and iron oxide nanoparticles in a porous structure. The Darcy–Brinkman–Forchheimer model is applied, particularly in scenarios with non-Darcy media. Numerical solutions are obtained using a shooting approach for the nonlinear differential equations. The results are analyzed through graphs and tables, revealing the favorable industrial application potential of the nanoparticle combination studied. Recent research has shown that these fluids exhibit superior heat transfer capabilities, which is crucial for biomedical use cases. Sundar et al. (2014) demonstrated that hybrid nanofluids containing multiwalled carbon nanotubes (MWCNTs) and $F{e}_3{O}_4$ nanoparticles significantly improve heat transfer performance, indicating their potential in advanced thermal management systems.

The study of pulsatile flow in curved arteries with stenosis has gained importance in understanding cardiovascular health. Long et al. (2001) conducted numerical investigations on physiologically realistic pulsatile flow through arterial stenosis, providing key insights into flow patterns and wall shear stress distributions essential for understanding atherosclerosis. Pulsatile flow, which mimics the heartbeat’s rhythm, is greatly influenced by arterial curvature and stenosis (Perktold et al., 1991). Perktold et al. (1991) performed three-dimensional numerical analyses of pulsatile flow in carotid artery bifurcations, revealing that arterial geometry significantly affects flow patterns and wall shear stress, both critical factors in atherosclerosis.

Stenosis, or the narrowing of arteries, presents challenges to blood flow, increasing wall shear stress and pressure gradients, potentially leading to adverse cardiovascular events (Johnston et al., 2004). Curved arteries add to the complexity by introducing secondary flow patterns that further influence flow dynamics. Studying such systems is crucial for advancing treatments for vascular diseases (Berger et al., 1983). Berger et al. (1983) reviewed the flow in curved pipes, showing how curvature induces secondary flows that alter the shear stress distribution, which is critical in understanding vascular pathologies. Recent research underscores the importance of considering realistic arterial geometries for accurate predictions of hemodynamic forces (Morris et al., 2016) (Cheng et al., 2006). Morris et al. (2016) discussed how computational fluid dynamics modeling using patient-specific geometries improves our understanding of cardiovascular hemodynamics, aiding in diagnosis and treatment. Cheng et al. (2006) used in vivo MR angiography to quantify deformations of the superficial femoral artery. Numerical studies indicate that stenosed arteries under pulsatile flow behave differently from healthy arteries, highlighting the need for specialized treatments (Gijsen et al., 1999). Huo and Kassab (2006) developed a theoretical and experimental model of pulsatile blood flow in the coronary arterial tree, demonstrating significant differences in hemodynamic parameters in stenosed arteries compared to healthy arteries, emphasizing the need for tailored therapeutic strategies.

The finite-difference technique is widely used for numerically solving complex fluid flow problems, particularly in biomedical applications like cardiovascular treatments (Quarteroni et al., 2000). Quarteroni et al. (2000) discussed computational methods in vascular fluid dynamics and how numerical techniques like the finite difference method solve fluid–structure interaction problems in blood flow simulations. This method is highly beneficial for solving nonlinear partial differential equations, which arise in blood flow modeling, especially in stenosed and catheterized arteries. Basha et al. (2022) used finite volume methods to study the behavior of gold and copper biomagnetic blood flow in an inclined stenosed artery with varying viscosities. Haghighi et al. (2006) numerically investigated pulsatile blood flow through a stenosed elastic artery. The finite-difference method provides a stable and efficient framework for understanding the intricate interactions between blood, vessel walls, and medical devices such as stents or catheters (LaDisa et al., 2005). LaDisa et al. (2005) used computational models to predict the sites of neointimal hyperplasia after stent implantation, demonstrating the role of numerical methods in improving cardiovascular device design and patient outcomes. Studies have shown that the finite-difference method can efficiently model heat transfer and predict flow behavior in biomedical systems, leading to better clinical outcomes (Xu et al., 2009). Xu et al. (2009) reviewed mathematical modeling of skin bioheat transfer, emphasizing the role of numerical methods like the finite-difference technique in predicting thermal responses in tissues.

Mathematical modeling and analysis are essential for understanding the complex behaviors of non-Newtonian hybrid nanofluids in biomedical applications. The Carreau non-Newtonian model is a foundational mathematical framework for characterizing shear-thinning fluids, like blood, especially under pulsatile flow in stenosed and curved arteries (Apostolidis and Beris, 2014). Apostolidis and Beris (2014) provided a detailed mathematical analysis of blood rheology using the Carreau model, advancing the understanding of non-Newtonian fluid dynamics under physiological conditions. Recent studies have also explored the impact of magnetic fields on the flow of non-Newtonian fluids in stenosed arteries. The mathematical analysis of pulsatile flow in curved arteries has advanced through the use of numerical methods like the finite-difference method (Tzirtzilakis, 2005). Tzirtzilakis (2005) developed a mathematical model to study the effects of magnetic fields on blood flow using finite-difference techniques. Additionally, studies on thermophoretic effects in non-Newtonian fluid flow have provided new perspectives on heat transfer in biological systems. Pal and Mondal (2011) analyzed thermophoresis and Brownian motion effects in non-Newtonian nanofluid flow over a stretching sheet, offering mathematical models that can be applied in biomedical engineering. Hassan et al. (2024) discussed a viscoelastic three-element viscous model, comprising a spring in parallel with one dashpot and a second dashpot in series, and used it to analyze the heat and mass flow properties of the fluid across a variable-thickness sheet. Transport equations incorporating this model are solved using the numerical Runge–Kutta (RK) technique. The research highlights that viscosity exerts a more substantial influence on the outcomes than other parameters. Notably, a significant enhancement of 22$\%$ in the Nusselt number and 137$\%$ in the entropy generation rate was observed.

The main objective of this research is to analyze the unsteady electroosmotic pulsatile flow of a hybrid nanofluid through a stenosed, curved, catheterized artery using the Carreau non-Newtonian model. The study uses a numerical approach based on the finite-difference method to solve the governing equations of fluid motion, temperature, and concentration. This research is significant because it offers new insights into the behavior of hybrid nanofluids under electroosmotic forces in complex arterial geometries, which could help design more effective cardiovascular treatments and medical devices. The study results contribute to a broader understanding of hemodynamics in diseased arteries, providing valuable implications for improving patient outcomes in cardiovascular care.

2 Problem description and mathematical model

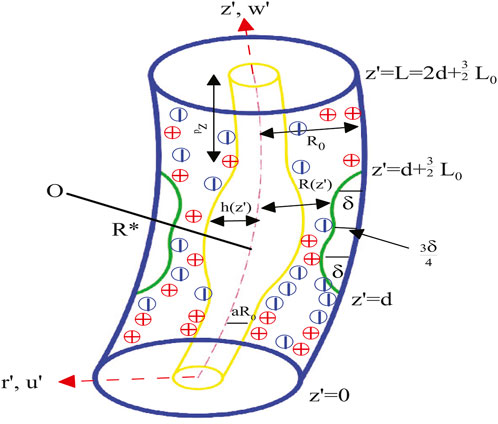
In our paper, we examine the unsteady laminar electroosmotic pulsatile flow of an incompressible Carreau non-Newtonian hybrid nanofluid ($Ag-A{l}_2{O}_3$/blood) through a curved catheterized artery with stenosis. The blood is a base fluid containing suspended nanoparticles of both Ag and aluminum oxide $(A{l}_2{O}_3)$. The artery segment with length $L$ has a mild constriction coiled in a circle with radius $R^{*}$ from the center $O$. Another solid circular cylinder balloon catheter is inserted into this curved artery. We choose a coordinate system in which $r$ aligns with the radial direction and $z$ aligns with the artery axis. We also choose $r=0$ as the axis of symmetry for the two coaxial cylinders. The fluid is subjected to an axial electric field of strength $E_z$ and an imposed magnetic field $\frac{R^{*}{B}_o}{r+R^{*}}$ in the radial direction. The temperature, concentration, and zeta potential near the arterial wall are given by $T_1$, $C_1$, and ${\zeta }_1$, respectively. The catheter wall is maintained at temperature $T_o$, concentration $C_o$, and zeta potential ${\zeta }_1$, where $T_1>T_o$, $C_1>C_o$, and ${\zeta }_1>{\zeta }_o$. We assume that the nanoparticles are uniformly dispersed within the blood and that there is no agglomeration. The thermophysical properties of the hybrid nanofluid, such as thermal conductivity and viscosity, are considered to be functions of the nanoparticle volume fraction and temperature. Viscous dissipation is taken into account to understand the conversion of kinetic energy into thermal energy due to the fluid’s viscosity. Joule heating, resulting from the interaction of the electric field with the fluid, is also considered, which affects the temperature distribution within the artery. The arterial wall geometry with overlapping stenosis and the balloon model are defined as follows (see Equations 1, 2 and Figure 1) (Chakravarty and Mandal, 1996; Pincombe and Mazumdar, 1977):

$R^{\prime }\left(z^{\prime }\right)=\left\{\begin{array}{cc}{R}_o-\frac{\delta \left(z^{\prime }-d\right)}{L_o}\left[11-\frac{94\left(z^{\prime }-d\right)}{3L_o}+\frac{32{\left(z^{\prime }-d\right)}^2}{L_o^2}-\frac{32{\left(z^{\prime }-d\right)}^3}{3L_o^3}\right]\hfill & d\le z^{\prime }\le d+\frac{3L_o}{2}\hfill \\ R_o\hfill & \text{otherwise},\hfill \end{array}\right.(1)$

$h^{\prime }\left(z^{\prime }\right)=\left\{\begin{array}{cc}{R}_o\left[a+b\exp \left(-{\pi }^2{\left(z^{\prime }-z_d-\frac{1}{2}\right)}^2\right)\right]\hfill & d\le z^{\prime }\le d+\frac{3L_o}{2}\hfill \\ a{R}_o\hfill & \text{otherwise},\hfill \end{array}\right.(2)$

where $d$ is the stenotic position, $\frac{3L_o}{2}$ is the length of the overlapping stenosis, and $R_o$ is the non-tapered artery’s radius in the non-stenotic portion. As a result, the proportion $\frac{\delta }{R_o}\ll 1$ occurs in two different locations, namely, $z^{\prime }=d+\frac{L_o}{2}$ and $z^{\prime }=d+L_o$. Here, $\delta$ represents the essential altitude of the stenosis. At $z^{\prime }=d+\frac{3L_o}{4}$, the elevation of the stenosis from the starting position is $\frac{3\delta }{4}$. For the annular inflated catheterization, it is presumed that $b$ is the catheter’s maximum height at $z^{\prime }=z_d+0.5$, $z_d$ is the balloon’s axial displacement throughout catheterization, $a{R}_o$ is the catheter’s inner radius, and $a$ seems extremely small. At any given value $z^{\prime }$, the gradient of pressure can be written as

$-\frac{d{p}^{\prime }}{d{z}^{\prime }}=A_0+A_{1}cos\left({\omega }_P{t}^{\prime }\right),(3)$

where $(A_0\&A_1)$ are the pressure gradient’s steady and pulsatile components, respectively, and ${\omega }_p=2\pi f_p$, where $f_p$ is the pulse’s frequency.

Figure 1

Figure 1. Geometrical configuration.

The conservative continuity, momentum, energy, and concentration governing equations with thermophoresis and Brownian motion are as follows (Ramanamurthy et al., 2013; El Kot and Abd Elmaboud, 2024; El-Dabe and Mostapha, 2020; Tawade et al., 2022; El Kot and Abd Elmaboud, 2023):

Continuity equation:

$\frac{\partial u^{\prime }}{\partial r^{\prime }}+\frac{u^{\prime }}{r^{\prime }+R^{*}}+\frac{R^{*}}{r^{\prime }+R^{*}}\frac{\partial w^{\prime }}{\partial z^{\prime }}=0.(4)$

Momentum equations:

$\begin{array}{cc}\hfill & {\rho }_{\mathit{hnf}}\left(\frac{\partial u^{\prime }}{\partial t^{\prime }}+u^{\prime }\frac{\partial u^{\prime }}{\partial r^{\prime }}+\frac{R^{*}}{r^{\prime }+R^{*}}{w}^{\prime }\frac{\partial u^{\prime }}{\partial z^{\prime }}-\frac{w^{\prime 2}}{r^{\prime }+R^{*}}\right)\hfill \\ \hfill & =-\frac{\partial p^{\prime }}{\partial r^{\prime }}+\frac{1}{r^{\prime }+R^{*}}\frac{\partial }{\partial r^{\prime }}\left[\left(r^{\prime }+R^{*}\right){\tau }_{rr}^{\prime }\right]+\frac{R^{*}}{r^{\prime }+R^{*}}\frac{\partial {\tau }_{rz}^{\prime }}{\partial z^{\prime }}-\frac{{\tau }_{zz}^{\prime }}{r^{\prime }+R^{*}},\hfill \end{array}(5)$

$\begin{array}{cc}\hfill & {\rho }_{\mathit{hnf}}\left(\frac{\partial w^{\prime }}{\partial t^{\prime }}+u^{\prime }\frac{\partial w^{\prime }}{\partial r^{\prime }}+\frac{R^{*}}{r^{\prime }+R^{*}}{w}^{\prime }\frac{\partial w^{\prime }}{\partial z^{\prime }}+\frac{u^{\prime }{w}^{\prime }}{r^{\prime }+R^{*}}\right)\hfill \\ \hfill & =-\frac{R^{*}}{r^{\prime }+R^{*}}\frac{\partial p^{\prime }}{\partial z^{\prime }}+\frac{1}{{\left(r^{\prime }+R^{*}\right)}^2}\frac{\partial }{\partial r^{\prime }}\left[{\left(r^{\prime }+R^{*}\right)}^2{\tau }_{rz}^{\prime }\right]+\frac{R^{*}}{r^{\prime }+R^{*}}\frac{\partial {\tau }_{zz}^{\prime }}{\partial z^{\prime }}-{\left(\frac{R^{*}}{r^{\prime }+R^{*}}\right)}^2{\sigma }_{\mathit{hnf}}{B}_o^2{w}^{\prime }\hfill \\ \hfill & +{\rho }_e^{\prime }{E}_z+{\left(\rho {\alpha }_T\right)}_{\mathit{hnf}}g\left(T^{\prime }-T_o\right)+{\left(\rho {\alpha }_C\right)}_{\mathit{hnf}}g\left(C^{\prime }-C_o\right).\hfill \end{array}(6)$

Energy equation:

$\begin{array}{cc}\hfill & {\left(\rho c_p\right)}_{\mathit{hnf}}\left(\frac{\partial T^{\prime }}{\partial t^{\prime }}+u^{\prime }\frac{\partial T^{\prime }}{\partial r^{\prime }}+\frac{R^{*}}{r^{\prime }+R^{*}}{w}^{\prime }\frac{\partial T^{\prime }}{\partial z^{\prime }}\right)=\hfill \\ \hfill & K_{\mathit{hnf}}\left[\frac{{\partial }^2{T}^{\prime }}{\partial r^{\prime 2}}+\frac{1}{r^{\prime }+R^{*}}\frac{\partial T^{\prime }}{\partial r^{\prime }}+{\left(\frac{R^{*}}{r^{\prime }+R^{*}}\right)}^2\frac{{\partial }^2{T}^{\prime }}{\partial z^{\prime 2}}\right]+{\tau }_{rr}^{\prime }\frac{\partial u^{\prime }}{\partial r^{\prime }}+{\tau }_{rz}^{\prime }\frac{\partial w^{\prime }}{\partial r^{\prime }}+{\tau }_{zr}^{\prime }\left(\frac{R^{*}}{r^{\prime }+R^{*}}\frac{\partial u^{\prime }}{\partial z^{\prime }}-\frac{w^{\prime }}{r^{\prime }+R^{*}}\right)\hfill \\ \hfill & +{\tau }_{zz}^{\prime }\left(\frac{u^{\prime }}{r^{\prime }+R^{*}}+\frac{R^{*}}{r^{\prime }+R^{*}}\frac{\partial w^{\prime }}{\partial z^{\prime }}\right)+\left(\frac{16{\sigma }_o{T}_a^3}{3k_2}\right)\frac{{\partial }^2{T}^{\prime }}{\partial r^{\prime 2}}+{\sigma }_{\mathit{hnf}}\left[E_z^2+{\left(\frac{R^{*}}{r^{\prime }+R^{*}}\right)}^2{B}_o^2{w}^{\prime 2}\right]\hfill \\ \hfill & +{\tau }_1{\left(\rho c_p\right)}_{\mathit{hnf}}\left\{D_B\left(\frac{\partial C^{\prime }}{\partial r^{\prime }}\frac{\partial T^{\prime }}{\partial r^{\prime }}+{\left(\frac{R^{*}}{r^{\prime }+R^{*}}\right)}^2\frac{\partial C^{\prime }}{\partial z^{\prime }}\frac{\partial T^{\prime }}{\partial z^{\prime }}\right)+\frac{D_T}{T_m}\left({\left(\frac{\partial T^{\prime }}{\partial r^{\prime }}\right)}^2+{\left(\frac{R^{*}}{r^{\prime }+R^{*}}\right)}^2{\left(\frac{\partial T^{\prime }}{\partial z^{\prime }}\right)}^2\right)\right\}.\hfill \end{array}(7)$

Concentration equation:

$\begin{array}{cc}\hfill & \frac{\partial C^{\prime }}{\partial t^{\prime }}+u^{\prime }\frac{\partial C^{\prime }}{\partial r^{\prime }}+\frac{R^{*}}{r^{\prime }+R^{*}}{w}^{\prime }\frac{\partial C^{\prime }}{\partial z^{\prime }}\hfill \\ \hfill & =D_B\left[\frac{{\partial }^2{C}^{\prime }}{\partial r^{\prime 2}}+\frac{1}{r^{\prime }+R_c}\frac{\partial C^{\prime }}{\partial r^{\prime }}+{\left(\frac{R^{*}}{r^{\prime }+R^{*}}\right)}^2\frac{{\partial }^2{C}^{\prime }}{\partial z^{\prime 2}}\right]+\frac{D_T}{T_m}\left[\frac{{\partial }^2{T}^{\prime }}{\partial r^{\prime 2}}+\frac{1}{r^{\prime }+R^{*}}\frac{\partial T^{\prime }}{\partial r^{\prime }}+{\left(\frac{R^{*}}{r^{\prime }+R^{*}}\right)}^2\frac{{\partial }^2{T}^{\prime }}{\partial z^{\prime 2}}\right]\hfill \\ \hfill & -K_o\left(C^{\prime }-C_o\right),\hfill \end{array}(8)$

where $(u^{\prime },w^{\prime })$ are the radial and axial velocities, respectively; ${\rho }_{\mathit{hnf}}$ is the density of the hybrid nanofluid; $t^{\prime }$ is the time; $p$ symbolizes the pressure of the fluid; ${\sigma }_{\mathit{hnf}}$ is the electrical conductivity of the hybrid nanofluid; ${\rho }_e^{\prime }$ is the total ionic charge density; $g$ is gravitational acceleration; $({\alpha }_T,{\alpha }_C)$ are coefficients of thermal and solutal expansions, respectively; $T^{\prime }$ is the fluid temperature; $c_p$ indicates specific heat at a constant pressure; $K$ indicates the heat conduction; ${\sigma }_o$ is the Stefan–Boltzmann constant; $T_a$ is the fluid’s average temperature; $k_2$ is the Rosseland absorption coefficient; ${\tau }_1$ is the effective heat capacity ratio; $D_B$ is the Brownian diffusion coefficient; $D_T$ is the diffusion coefficient for thermophoresis; $T_m$ is the medium’s temperature; $C^{\prime }$ is the concentration of the fluid; and $K_o$ is the chemical term.

Considering that the electrolyte combination $(N{a}^{+}C{l}^{-})$ is homogeneous, the Poisson–Boltzmann equation provides the electrical potential disturbance for it by (Akhtar et al., 2021)

${\mathrm{\nabla }}^2{\mathrm{\Phi }}^{\prime }=-\frac{{\rho }_e^{\prime }}{\epsilon },(9)$

where ${\mathrm{\Phi }}^{\prime }$ is the potential electricity and $\epsilon$ is the dielectric permittivity.

Ionic energy density is described as ${\rho }_e^{\prime }=e{z}^{*}(n^{+}-n^{-})$. When an overlaid double electrical layer is ignored, the cation and anion densities $(n^{+},n^{-})$ are expressed as

$n^{\pm }=n_o\exp \pm \left(\frac{e{z}^{*}{\mathrm{\Phi }}^{\prime }}{K_B{T}^{*}}\right).(10)$

Here, $n_o$ represents the concentration of ions, $e$ stands for electrical charge, $z^{*}$ reflects the charge balance, $K_B$ indicates the Boltzmann constant, and $T^{*}$ denotes the electrolytic solution’s mean temperature.

By substituting $n^{\pm }$ and ${\rho }_e^{\prime }$ for their respective values in Equation 9, and by using the Debye–Hückel approach, the Poisson–Boltzmann equation for potential electricity can be expressed as

$\frac{{\partial }^2{\mathrm{\Phi }}^{\prime }}{\partial r^{\prime 2}}+\frac{1}{r^{\prime }+R^{*}}\frac{\partial {\mathrm{\Phi }}^{\prime }}{\partial r^{\prime }}+{\left(\frac{R^{*}}{r^{\prime }+R^{*}}\right)}^2\frac{{\partial }^2{\mathrm{\Phi }}^{\prime }}{\partial z^{\prime 2}}=\frac{2n_o{\left(e{z}^{*}\right)}^2}{\epsilon K_B{T}^{*}}{\mathrm{\Phi }}^{\prime }.(11)$

The extra stress tensor for the Carreau hybrid nanofluid according to the shear rate is formulated as (Akbar and Nadeem, 2014; Rana and Liao, 2019; Wajihah and Sankar, 2021; Zaman and Khan, 2021)

${\tau }^{\prime }=\left[{\mu }_{\infty }+\left({\mu }_{\mathit{hnf}}-{\mu }_{\infty }\right){\left(1+{\left(\mathrm{\Gamma }{\dot{\xi }}^{\prime }\right)}^2\right)}^{\frac{n-1}{2}}\right]{\vartheta }^{\prime },(12)$

${\dot{\xi }}^{\prime }=\sqrt{\frac{{\mathrm{\Pi }}^{\prime }}{2}}=\sqrt{\frac{1}{2}tr{\left({\vartheta }^{\prime }\right)}^2}\mathrm{a}\mathrm{n}\mathrm{d}{\vartheta }^{\prime }=\mathrm{\nabla }{\mathbf{V}}^{\prime }+{\left(\mathrm{\nabla }{\mathbf{V}}^{\prime }\right)}^{\top },(13)$

where ${\mathit{\tau }}^{\prime }$ is the extra stress tensor, ${\mu }_{\infty }$ is the viscosity at an infinite shear rate, ${\mu }_{\mathit{hnf}}$ is the viscosity of the hybrid nanofluid, $\mathrm{\Gamma }$ is the constant of time, ${\dot{\xi }}^{\prime }$ is the shear rate, $n$ is the power-law index, ${\mathit{\vartheta }}^{\prime }$ is the first Rivlin–Ericksen tensor, ${\mathrm{\Pi }}^{\prime }$ is the strain rate tensor’s second invariant, ${\mathbf{V}}^{\prime }=(u^{\prime },0,w^{\prime })$ is the vector of velocity, and $\top$ denotes the transpose.

Except for the fluid’s thermal conductivity and viscosity, all of its physical properties should remain constant. It is hypothesized that the viscosity varies with temperature in addition to shear rate dependence and presuming $\mathrm{\Gamma }{\dot{\xi }}^{\prime }\ll 1$, ${\mu }_{\infty }=0$. Consequently, the apparent viscosity is described as follows:

${\mathit{\tau }}^{\prime }={\mu }_{\mathit{hnf}}\left[1+\left(\frac{n-1}{2}\right){\left(\mathrm{\Gamma }{\dot{\xi }}^{\prime }\right)}^2\right]{\vartheta }^{\prime }.(14)$

Here, the initial and boundary constraints are

$\begin{array}{cc}\hfill & u^{\prime }=0,w^{\prime }=0,T^{\prime }=T_o,C^{\prime }=C_0\mathrm{a}\mathrm{t}{t}^{\prime }=0,\hfill \\ \hfill & u^{\prime }=0,w^{\prime }=0,T^{\prime }=T_o,C^{\prime }=C_0,{\mathrm{\Phi }}^{\prime }={\zeta }_0\mathrm{a}\mathrm{t}{r}^{\prime }=h^{\prime }\left(z^{\prime }\right),\hfill \\ \hfill & u^{\prime }=0,w^{\prime }=0,T^{\prime }=T_1,C^{\prime }=C_1,{\mathrm{\Phi }}^{\prime }={\zeta }_1\mathrm{a}\mathrm{t}{r}^{\prime }=R^{\prime }\left(z^{\prime }\right).\hfill \end{array}(15)$

Non-dimensional variables and parameters are defined as [(El Kot and Abd Elmaboud, 2024) (El Kot and Abd Elmaboud, 2023)]

$\begin{array}{cc}\hfill & r=\frac{r^{\prime }}{R_o},z=\frac{z^{\prime }}{L_o},w=\frac{w^{\prime }}{\left(\frac{A_o{R}_o^2}{{\mu }_f}\right)},u=\frac{u^{\prime }}{\left(\frac{A_o{R}_o^2\delta }{L_o{\mu }_f}\right)},R=\frac{R^{\prime }}{R_o},t=\frac{t^{\prime }}{\left(\frac{1}{f_p}\right)},p=\frac{p^{\prime }}{A_o{L}_o},\hfill \\ \hfill & \theta =\frac{T^{\prime }-T_o}{T_1-T_o},\varphi =\frac{C^{\prime }-C_o}{C_1-C_o},\mathrm{\Phi }=\frac{{\mathrm{\Phi }}^{\prime }}{{\zeta }_1},{\rho }_e=\frac{{\rho }_e^{\prime }}{\left(-\frac{\epsilon {\zeta }_1}{R_o^2}\right)},{\tau }_{rr}=\frac{{\tau }_{rr}^{\prime }}{\left(\frac{A_o{R}_o^2}{L_o}\right)},{\tau }_{rz}=\frac{{\tau }_{rz}^{\prime }}{A_o{R}_o},\hfill \\ \hfill & {\tau }_{zr}=\frac{{\tau }_{zr}^{\prime }}{A_o{R}_o},{\tau }_{zz}=\frac{{\tau }_{zz}^{\prime }}{\left(\frac{A_o{R}_o^2}{L_o}\right)},\dot{\xi }=\frac{{\dot{\xi }}^{\prime }}{\left(\frac{A_o{R}_o}{{\mu }_f}\right)},R_c=\frac{R^{*}}{R_o},{\gamma }^2=\frac{{\rho }_f{R}_o^2{f}_p}{{\mu }_f},R_e=\frac{{\rho }_f{A}_o{R}_o^3}{{\mu }_f^2},\hfill \\ \hfill & e=\frac{A_1}{A_o},Ha=\sqrt{\frac{{\sigma }_f}{{\mu }_f}}{B}_o{R}_o,\kappa =\frac{R_o}{{\lambda }_D},{\lambda }_D={\left(\frac{2n_o{\left(e{z}^{*}\right)}^2}{\epsilon K_B{T}^{*}}\right)}^{\frac{-1}{2}},u_{HS}=\frac{-\epsilon E_z{\zeta }_1}{A_o{R}_o^2},\hfill \\ \hfill & G_r=\frac{{\left(\rho {\alpha }_T\right)}_{f}g\left(T_1-T_o\right)}{A_o},G_c=\frac{{\left(\rho {\alpha }_C\right)}_{f}g\left(C_1-C_o\right)}{A_o},W_e=\frac{\mathrm{\Gamma }{A}_o{R}_o}{{\mu }_f},P_r=\frac{c_p{\mu }_f}{K_f},\hfill \\ \hfill & R_a=\frac{16{\sigma }_o{T}_a^3}{3k_2{K}_f},S=\frac{{\sigma }_f{E}_z^2{R}_o^2}{K_f\left(T_1-T_o\right)},B_r=\frac{A_o^2{R}_o^4}{{\mu }_f\left(T_1-T_o\right)K_f},N_b=\frac{{\left(\rho c_p\right)}_f{\tau }_1{D}_B\left(C_1-C_o\right)}{K_f},\hfill \\ \hfill & N_t=\frac{{\left(\rho c_p\right)}_f{\tau }_1{D}_T\left(T_1-T_o\right)}{K_f{T}_m},S_c=\frac{{\mu }_f}{{\rho }_f{D}_B},{\beta }_c=\frac{{\rho }_f{K}_o{R}_o^2}{{\mu }_f},\hfill \end{array}(16)$

where $R_c$ is the curvature parameter, $\gamma$ is the Womersley frequency parameter, $\mathrm{R}\mathrm{e}$ is the Reynolds number, $e$ is the parameter of amplitude fluctuation, $Ha$ represents the Hartmann number, $Da$ is the Darcy number, $\kappa$ symbolizes the electroosmotic parameter, ${\lambda }_D$ is the Debye length, $u_{HS}$ is the Helmholtz–Smoluchowski velocity, $G_r$ is the thermal Grashof number, $G_c$ is the solutal Grashof number, $W_e$ is the Weissenberg number, $P_r$ is the Prandtl number, $R_a$ is the radiation parameter, $S$ is the Joule heating parameter, $B_r$ is the Brickman number, $\alpha$ is the heat source parameter, $N_b$ is the Brownian motion parameter, $N_t$ is the thermophoresis parameter, $S_c$ is the Schmidt number, and ${\beta }_c$ is the chemical parameter.

Based on the suppositions and simplifications outlined by Young (1968) for mild stenosis $\left(\frac{\delta }{R_o}\ll 1\right)$, $\left(\frac{R_o}{L_o}\sim o(1)\right)$. Applying Equation 16 and using the abovementioned presumption, the non-dimensional form of the Equations 3–15 is as follows:

$\frac{\partial w}{\partial z}=0,\frac{\partial p}{\partial r}=0,(17)$

$\frac{{\partial }^2\mathrm{\Phi }}{\partial r^2}+\frac{1}{r+R_c}\frac{\partial \mathrm{\Phi }}{\partial r}={\kappa }^2\mathrm{\Phi },(18)$

$\begin{array}{cc}\hfill & \left(\frac{{\rho }_{\mathit{hnf}}}{{\rho }_f}\right){\gamma }^2\frac{\partial w}{\partial t}=\frac{R_c}{r+R_c}\left[1+e\cos \left(2\pi t\right)\right]\hfill \\ \hfill & +\left(\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}\right)\frac{1}{{\left(r+R_c\right)}^2}\frac{\partial }{\partial r}\left[{\left(r+R_c\right)}^2\left\{\left(\frac{\partial w}{\partial r}-\frac{w}{r+R_c}\right)+W_e^2\left(\frac{n-1}{2}\right){\left(\frac{\partial w}{\partial r}-\frac{w}{r+R_c}\right)}^3\right\}\right]\left]\right\}\hfill \\ \hfill & -\left[\left(\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}\right){\left(\frac{R_c}{r+R_c}\right)}^2{H}_a^2\right]w+u_{HS}{\kappa }^2\mathrm{\Phi }+\frac{{\left(\rho {\alpha }_T\right)}_{\mathit{hnf}}}{{\left(\rho {\alpha }_T\right)}_f}{G}_r\theta +\frac{{\left(\rho {\alpha }_C\right)}_{\mathit{hnf}}}{{\left(\rho {\alpha }_C\right)}_f}{G}_C\varphi ,\hfill \end{array}(19)$

$\begin{array}{cc}\hfill & \frac{{\left(\rho c_p\right)}_{\mathit{hnf}}}{{\left(\rho c_p\right)}_f}{P}_r{\gamma }^2\frac{\partial \theta }{\partial t}=\left(\frac{K_{\mathit{hnf}}}{K_f}+R_a\right)\frac{{\partial }^2\theta }{\partial r^2}+\left(\frac{K_{\mathit{hnf}}}{K_f}\right)\frac{1}{r+R_c}\frac{\partial \theta }{\partial r}\hfill \\ \hfill & +B_r\left(\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}\right)\left\{{\left(\frac{\partial w}{\partial r}-\frac{w}{r+R_c}\right)}^2+W_e^2\left(\frac{n-1}{2}\right){\left(\frac{\partial w}{\partial r}-\frac{w}{r+R_c}\right)}^4\right\}\}+B_r\left\{\left(\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}\right){\left(\frac{R_c}{r+R_c}\right)}^2{H}_a^2\right\}\}{w}^2\hfill \\ \hfill & +\left(\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}\right)S+\frac{{\left(\rho c_p\right)}_{\mathit{hnf}}}{{\left(\rho c_p\right)}_f}\left\{N_b\left(\frac{\partial \varphi }{\partial r}\frac{\partial \theta }{\partial r}\right)+N_t{\left(\frac{\partial \theta }{\partial r}\right)}^2\right\},\hfill \end{array}(20)$

$\begin{array}{c}\hfill S_c{\gamma }^2\frac{\partial \varphi }{\partial t}=\frac{{\partial }^2\varphi }{\partial r^2}+\frac{1}{r+R_c}\frac{\partial \varphi }{\partial r}-{\beta }_c{S}_c\varphi +\left(\frac{N_t}{N_b}\right)\left(\frac{{\partial }^2\theta }{\partial r^2}+\frac{1}{r+R_c}\frac{\partial \theta }{\partial r}\right).\end{array}(21)$

The corresponding initial and boundary constraints are

$\begin{array}{cc}\hfill & w=0,\theta =0,\varphi =0\mathrm{a}\mathrm{t}t=0,\hfill \\ \hfill & w=0,\theta =0,\varphi =0,\mathrm{\Phi }=\zeta =\left(\frac{{\zeta }_o}{{\zeta }_1}\right)\mathrm{a}\mathrm{t}r=h\left(z\right),\hfill \\ \hfill & w=0,\theta =1,\varphi =1,\mathrm{\Phi }=1\mathrm{a}\mathrm{t}r=R\left(z\right),\hfill \end{array}(22)$

$R\left(z\right)=\left\{\begin{array}{cc}1-{\delta }^{*}\left(z-d^{*}\right)\left(11-\frac{94\left(z-d^{*}\right)}{3}+32{\left(z-d^{*}\right)}^2-\frac{32{\left(z-d^{*}\right)}^3}{3}\right)\hfill & d^{*}\le z\le d^{*}+\frac{3}{2}\hfill \\ 1\hfill & \text{otherwise},\hfill \end{array}\right.(23)$

$h\left(z\right)=\left\{\begin{array}{cc}a+b{e}^{-{\pi }^2{\left(z-z_d^{*}-\frac{1}{2}\right)}^2}\hfill & d^{*}\le z\le d^{*}+\frac{3}{2}\hfill \\ a\hfill & \text{otherwise},\hfill \end{array}\right.(24)$

where Equations 23, 24 are the non-dimensional walls and ${\delta }^{*}=\frac{\delta }{R_o}$, $d^{*}=\frac{d}{L_o}$, and $z_d^{*}=\frac{z_d}{L_o}$.

Comparing hybrid nanofluids to simple nanofluids, the former have shown better stability and thermal properties. In many facets of human endeavor, such as electronics, medical, power, and chemical engineering equipment, tiny concentrations of hybrid nanoparticles of metal or metal oxides are used. Tables 1, 2 list the thermal and physical characteristics of blood, silver nanoparticles, and aluminum oxide nanoparticles. In this case, the volume fraction for silver and aluminum oxide nanoparticles is denoted by ${\varphi }_1$ and ${\varphi }_2$, respectively. The solid nanoparticles of Ag, solid nanoparticles of aluminum oxide $(A{l}_2{O}_3)$, base fluid (blood), and nanoblood hybrid are denoted by the suffices $s_1$, $s_2$, $f$, and $hnf$, respectively. Specifically, if $({\varphi }_1={\varphi }_2=1)$, the hybrid nanofluid is transformed into a nanofluid (Das et al., 2021).

Table 1

Table 1. Thermal physical features of the hybrid nanoparticles.

Table 2

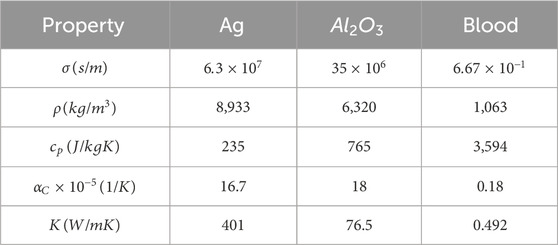
Table 2. Thermal physical properties of silver (Ag) and aluminum oxide $(A{l}_2{O}_3)$ nanoparticles and blood fluid:

3 Numerical solution technique

The unsteady electroosmotic pulsatile flow-governing equations of the hybrid nanofluid are nonlinear partial differential equations governed by continuity, momentum, energy, and species concentration. To solve these equations, the finite-difference method was used due to its effectiveness in handling complex boundary conditions typically encountered in arterial geometries. More specifically, the Crank–Nicolson scheme was chosen as it provides a good balance between computational cost and accuracy. The solution domain was discretized using a uniform grid, and a semi-implicit formulation was used to ensure convergence. The resulting algebraic equations were solved iteratively until the desired level of accuracy was achieved, ensuring reliable simulations of the flow dynamics within the stenosed, curved, and catheterized artery. We used the finite-difference method to solve the coupled nonlinear partial differential Equations 17–21 with initial and boundary conditions given by Equation 22. To proceed, the physical domain is transformed into a regular uniform domain using the transformation:

$\begin{array}{cc}\hfill t& =\tau ,\hfill \\ \hfill \eta & =\frac{r-h}{R-h}.\hfill \end{array}(25)$

Using Equation 25 in Equations 17–24, we obtain:

$\frac{1}{{\left(R-h\right)}^2}\frac{{\partial }^2\mathrm{\Phi }}{\partial {\eta }^2}+\frac{1}{\left[h+R_c+\eta \left(R-h\right)\right]\left(R-h\right)}\frac{\partial \mathrm{\Phi }}{\partial \eta }={\kappa }^2\mathrm{\Phi },(26)$

$\begin{array}{cc}\hfill & \left(\frac{{\rho }_{\mathit{hnf}}}{{\rho }_f}\right){\gamma }^2\frac{\partial w}{\partial \tau }=\frac{R_c}{\left[h+R_c+\eta \left(R-h\right)\right]}\left[1+e\cos \left(2\pi \tau \right)\right]\hfill \\ \hfill & +\left(\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}\right)\frac{1}{\left(R-h\right){\left(h+R_c+\eta \left(R-h\right)\right)}^2}\frac{\partial }{\partial \eta }\left[{\left(h+R_c+\eta \left(R-h\right)\right)}^2\left(\frac{1}{\left(R-h\right)}\frac{\partial w}{\partial \eta }-\frac{w}{\left[h+R_c+\eta \left(R-h\right)\right]}\right))\right.\hfill \\ \hfill & \left.\times \left\{1+W_e^2\left(\frac{n-1}{2}\right){\left(\frac{1}{\left(R-h\right)}\frac{\partial w}{\partial \eta }-\frac{w}{\left[h+R_c+\eta \left(R-h\right)\right]}\right)}^2\left\}\right]\right\}\right]\hfill \\ \hfill & -\left[\left(\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}\right){\left(\frac{R_c}{\left[h+R_c+\eta \left(R-h\right)\right]}\right)}^2{H}_a^2\right]w+u_{HS}{\kappa }^2\mathrm{\Phi }+\frac{{\left(\rho {\alpha }_T\right)}_{\mathit{hnf}}}{{\left(\rho {\alpha }_T\right)}_f}{G}_r\theta +\frac{{\left(\rho {\alpha }_C\right)}_{\mathit{hnf}}}{{\left(\rho {\alpha }_C\right)}_f}{G}_C\varphi ,\hfill \end{array}(27)$

$\begin{array}{cc}\hfill & \frac{{\left(\rho c_p\right)}_{\mathit{hnf}}}{{\left(\rho c_p\right)}_f}{P}_r{\gamma }^2\frac{\partial \theta }{\partial \tau }=\left(\frac{K_{\mathit{hnf}}}{K_f}+R_a\right)\frac{1}{{\left(R-h\right)}^2}\frac{{\partial }^2\theta }{\partial {\eta }^2}+\left(\frac{K_{\mathit{hnf}}}{K_f}\right)\frac{1}{\left[h+R_c+\eta \left(R-h\right)\right]\left(R-h\right)}\frac{\partial \theta }{\partial \eta }\hfill \\ \hfill & +B_r\left(\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}\right){\left(\frac{1}{\left(R-h\right)}\frac{\partial w}{\partial \eta }-\frac{w}{\left[h+R_c+\eta \left(R-h\right)\right]}\right)}^2\left\{1+W_e^2\left(\frac{n-1}{2}\right){\left(\frac{1}{\left(R-h\right)}\frac{\partial w}{\partial \eta }-\frac{w}{\left[h+R_c+\eta \left(R-h\right)\right]}\right)}^2\}\right\}\hfill \\ \hfill & +B_r\left\{\left(\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}\right){\left(\frac{R_c}{\left[h+R_c+\eta \left(R-h\right)\right]}\right)}^2{H}_a^2\}\right\}{w}^2+\left(\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}\right)S+\frac{{\left(\rho c_p\right)}_{\mathit{hnf}}}{{\left(\rho c_p\right)}_f}\frac{1}{{\left(R-h\right)}^2}\left\{N_b\left(\frac{\partial \varphi }{\partial \eta }\frac{\partial \theta }{\partial \eta }\right)+N_t{\left(\frac{\partial \theta }{\partial \eta }\right)}^2\right\},\hfill \end{array}(28)$

$\begin{array}{cc}\hfill S_c{\gamma }^2\frac{\partial \varphi }{\partial \tau }& =\frac{1}{{\left(R-h\right)}^2}\frac{{\partial }^2\varphi }{\partial {\eta }^2}+\frac{1}{\left[h+R_c+\eta \left(R-h\right)\right]\left(R-h\right)}\frac{\partial \varphi }{\partial \eta }-{\beta }_c{S}_c\varphi \hfill \\ \hfill & +\left(\frac{N_t}{N_b}\right)\left(\frac{1}{{\left(R-h\right)}^2}\frac{{\partial }^2\theta }{\partial {\eta }^2}+\frac{1}{\left[h+R_c+\eta \left(R-h\right)\right]\left(R-h\right)}\frac{\partial \theta }{\partial \eta }\right).\hfill \end{array}(29)$

The associated initial and boundary conditions are

$\begin{array}{cc}\hfill & w=0,\theta =0,\varphi =0\mathrm{a}\mathrm{t}\tau =0,\hfill \\ \hfill & w=0,\theta =0,\varphi =0,\mathrm{\Phi }=\zeta =\left(\frac{{\zeta }_o}{{\zeta }_1}\right)\mathrm{a}\mathrm{t}\eta =0,\hfill \\ \hfill & w=0,\theta =1,\varphi =1,\mathrm{\Phi }=1\mathrm{a}\mathrm{t}\eta =1.\hfill \end{array}(30)$

The finite-difference approach is used by the Crank–Nicolson semi-implicit discretization because it is unconditionally stable. Let us consider a uniform grid with spacing $\mathrm{\Delta }\eta (=\frac{1}{N_{\eta }})$ in the $\eta$ direction and time $\mathrm{\Delta }\tau (=\frac{1}{N_{\tau }})$ in the $\tau$ direction. Consider the discrete approximation of $w,\theta ,\varphi$ and $\mathrm{\Phi }$ at the grid point $i\mathrm{\Delta }\eta ,(i=\mathrm{1,2,3},\dots \dots ,N_{\eta })$ and $j\mathrm{\Delta }\tau (j=\mathrm{1,2,3},\dots \dots ,N_{\tau })$. The discretization of the above equations (Equations 26–30) will be

$\frac{1}{{\left(R-h\right)}^2}\left\{\frac{{\mathrm{\Phi }}_{i+1}^j-2{\mathrm{\Phi }}_i^j+{\mathrm{\Phi }}_{i-1}^j}{{\left(\mathrm{\Delta }\eta \right)}^2}\right\}+\frac{1}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]\left(R-h\right)}\left\{\frac{{\mathrm{\Phi }}_{i+1}^j+{\mathrm{\Phi }}_{i-1}^j}{2\mathrm{\Delta }\eta }\right\}={\kappa }^2{\mathrm{\Phi }}_i^j,(31)$

$\begin{array}{cc}\hfill & \left(\frac{{\rho }_{\mathit{hnf}}}{{\rho }_f}\right){\gamma }^2\left\{\frac{w_i^{j+1}-w_i^j}{\mathrm{\Delta }\tau }\right\}=\frac{R_c}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]}\left[1+e\cos \left(2\pi {\tau }_j\right)\right]\hfill \\ \hfill & +\left(\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}\right)\frac{1}{\left(R-h\right){\left(h+R_c+{\eta }_i\left(R-h\right)\right)}^2}\left\{\frac{{\left(h+R_c+\eta \left(R-h\right)\right)}^2}{\left(R-h\right)}\left(\frac{w_{i+1}^{j+1}-2w_i^{j+1}+w_{i-1}^{j+1}+w_{i+1}^j-2w_i^j+w_{i-1}^j}{2\mathrm{\Delta }{\eta }^2}\right)\right.\hfill \\ \hfill & \left.-\left(h+R_c+{\eta }_i\left(R-h\right)\right)\left(\frac{w_{i+1}^{j+1}-w_{i-1}^{j+1}+w_{i+1}^j-w_{i-1}^j}{4\mathrm{\Delta }\eta }\right)-\left(R-h\right)w_i^j\right\}\hfill \\ \hfill & +2\left(h+R_c+{\eta }_i\left(R-h\right)\right)\left(R-h\right)\left\{\left(\frac{w_{i+1}^{j+1}-w_{i-1}^{j+1}+w_{i+1}^j-w_{i-1}^j}{4\mathrm{\Delta }\eta }\right)-\frac{w_i^j}{\left(h+R_c+{\eta }_i\left(R-h\right)\right)}\right\}+3W_e^2\left(\frac{n-1}{2}\right)\hfill \\ \hfill & \times \left\{\left.{\left[\frac{1}{\left(R-h\right)}\left(\frac{w_{i+1}^{j+1}-w_{i-1}^{j+1}+w_{i+1}^j-w_{i-1}^j}{4\mathrm{\Delta }\eta }\right)-\frac{w_i^j}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]}]\right]}^2\right\}\}\right.\times \left\{\frac{1}{\left(R-h\right)}\left(\frac{w_{i+1}^{j+1}-2w_i^{j+1}+w_{i-1}^{j+1}+w_{i+1}^j-2w_i^j+w_{i-1}^j}{2\mathrm{\Delta }{\eta }^2}\right)-\frac{1}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]}\left(\frac{w_{i+1}^{j+1}-w_{i-1}^{j+1}+w_{i+1}^j-w_{i-1}^j}{4\mathrm{\Delta }\eta }\right)\right.\hfill \\ \hfill & \left.\left.-\frac{\left(R-h\right)w_i^j}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]}\right\}\right\}-\left[\left(\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}\right){\left(\frac{R_c}{\left[h+R_c+\eta \left(R-h\right)\right]}\right)}^2{H}_a^2\right]w_i^j\hfill \\ \hfill & +u_{HS}{\kappa }^2{\mathrm{\Phi }}_i^j+\frac{{\left(\rho {\alpha }_T\right)}_{\mathit{hnf}}}{{\left(\rho {\alpha }_T\right)}_f}{G}_r{\theta }_i^j+\frac{{\left(\rho {\alpha }_C\right)}_{\mathit{hnf}}}{{\left(\rho {\alpha }_C\right)}_f}{G}_C{\varphi }_i^j,\hfill \end{array}(32)$

$\begin{array}{cc}\hfill & \frac{{\left(\rho c_p\right)}_{\mathit{hnf}}}{{\left(\rho c_p\right)}_f}{P}_r{\gamma }^2\left\{\frac{{\theta }_i^{j+1}-{\theta }_i^j}{\mathrm{\Delta }\tau }\right\}=\left(\frac{K_{\mathit{hnf}}}{K_f}+R_a\right)\frac{1}{{\left(R-h\right)}^2}\left(\frac{{\theta }_{i+1}^{j+1}-2{\theta }_i^{j+1}+{\theta }_{i-1}^{j+1}+{\theta }_{i+1}^j-2{\theta }_i^j+{\theta }_{i-1}^j}{2\mathrm{\Delta }{\eta }^2}\right)\hfill \\ \hfill & +\left(\frac{K_{\mathit{hnf}}}{K_f}\right)\frac{1}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]\left(R-h\right)}\left(\frac{{\theta }_{i+1}^{j+1}-{\theta }_{i-1}^{j+1}+{\theta }_{i+1}^j-{\theta }_{i-1}^j}{4\mathrm{\Delta }\eta }\right)\hfill \\ \hfill & +B_r\left(\frac{{\mu }_{\mathit{hnf}}}{{\mu }_f}\right){\left(\frac{1}{\left(R-h\right)}\left(\frac{w_{i+1}^{j+1}-w_{i-1}^{j+1}+w_{i+1}^j-w_{i-1}^j}{4\mathrm{\Delta }\eta }\right)-\frac{w_i^j}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]}\right))}^2\times \left\{1+W_e^2\left(\frac{n-1}{2}\right){\left(\frac{1}{\left(R-h\right)}\left(\frac{w_{i+1}^{j+1}-w_{i-1}^{j+1}+w_{i+1}^j-w_{i-1}^j}{4\mathrm{\Delta }\eta }\right)-\frac{w_i^j}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]}\right)}^2\right\}\}\hfill \\ \hfill & +B_r\left\{\left(\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}\right){\left(\frac{R_c}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]}\right)}^2{H}_a^2\right\}\}{\left(w_i^j\right)}^2\hfill \\ \hfill & +\left(\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}\right)S+\frac{{\left(\rho c_p\right)}_{\mathit{hnf}}}{{\left(\rho c_p\right)}_f}\frac{1}{{\left(R-h\right)}^2}\left\{N_b\left(\left(\frac{{\varphi }_{i+1}^{j+1}-{\varphi }_{i-1}^{j+1}+{\varphi }_{i+1}^j-{\varphi }_{i-1}^j}{4\mathrm{\Delta }\eta }\right)\left(\frac{{\theta }_{i+1}^{j+1}-{\theta }_{i-1}^{j+1}+{\theta }_{i+1}^j-{\theta }_{i-1}^j}{4\mathrm{\Delta }\eta }\right)\right)\right.)\hfill \\ \hfill & \left.+N_t{\left(\frac{{\theta }_{i+1}^{j+1}-{\theta }_{i-1}^{j+1}+{\theta }_{i+1}^j-{\theta }_{i-1}^j}{4\mathrm{\Delta }\eta }\right)}^2\right\},\hfill \end{array}(33)$

$\begin{array}{cc}\hfill & S_c{\gamma }^2\left\{\frac{{\varphi }_i^{j+1}-{\varphi }_i^j}{\mathrm{\Delta }\tau }\right\}=\frac{1}{{\left(R-h\right)}^2}\left(\frac{{\varphi }_{i+1}^{j+1}-2{\varphi }_i^{j+1}+{\varphi }_{i-1}^{j+1}+{\varphi }_{i+1}^j-2{\varphi }_i^j+{\varphi }_{i-1}^j}{2\mathrm{\Delta }{\eta }^2}\right)\hfill \\ \hfill & +\frac{1}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]\left(R-h\right)}\left(\frac{{\varphi }_{i+1}^{j+1}-{\varphi }_{i-1}^{j+1}+{\varphi }_{i+1}^j-{\varphi }_{i-1}^j}{4\mathrm{\Delta }\eta }\right)-{\beta }_c{S}_c{\varphi }_i^j\hfill \\ \hfill & +\left(\frac{N_t}{N_b}\right)\left(\frac{1}{{\left(R-h\right)}^2}\left(\frac{{\theta }_{i+1}^{j+1}-2{\theta }_i^{j+1}+{\theta }_{i-1}^{j+1}+{\theta }_{i+1}^j-2{\theta }_i^j+{\theta }_{i-1}^j}{2\mathrm{\Delta }{\eta }^2}\right)\right.\hfill \\ \hfill & \left.+\frac{1}{\left[h+R_c+{\eta }_i\left(R-h\right)\right]\left(R-h\right)}\left(\frac{w_{i+1}^{j+1}-w_{i-1}^{j+1}+w_{i+1}^j-w_{i-1}^j}{4\mathrm{\Delta }\eta }\right)\right).\hfill \end{array}(34)$

The associated initial and boundary conditions are

$\begin{array}{cc}\hfill & w_i^0=0,{\theta }_i^0=0,{\varphi }_i^0=0,\hfill \\ \hfill & w_0^j=0,{\theta }_0^j=0,{\varphi }_0^j=0,{\mathrm{\Phi }}_0^j=\zeta ,\hfill \\ \hfill & w_{N_{\eta }}^j=0,{\theta }_{N_{\eta }}^j=1,{\varphi }_{N_{\eta }}^j=1,{\mathrm{\Phi }}_{N_{\eta }}^j=1.\hfill \end{array}(35)$

The function FindRoot in Mathematica software is used to solve the produced system of nonlinear algebraic equations (Equations 31–35) and obtain the consecutive solutions. After several cycles of this procedure, a steady state is achieved. The steady-state solution is assumed to be obtained when the absolute differences between the values of $w,\theta$ and $\varphi$ at two subsequent time steps are less than $10^{-5}$ at all grid points.

4 Results and discussions

In this section, we discuss the effects of various physical parameters on the flow, heat transfer, and mass transfer characteristics of the hybrid nanofluid through a stenosed curved artery. Specifically, the influences of electroosmotic forces, pulsatility, curvature, and nanoparticle concentration on velocity, temperature, and concentration profiles are examined. The interaction of these parameters shows significant variations in hemodynamic parameters, which may hold relevance for medical applications involving catheters. The following sections present the results in relation to the figures provided, highlighting trends and comparing the effects of different governing parameters on velocity, temperature, and concentration.

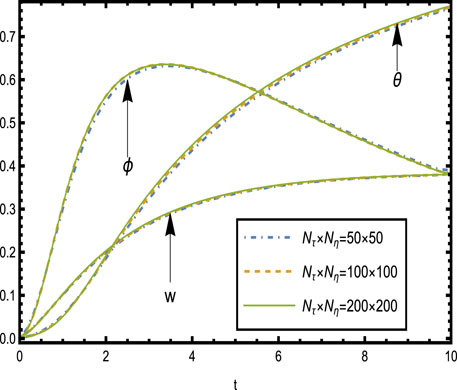
4.1 Grid independence test

The grid independence test was carried out to ensure that the solution was not dependent on the mesh size used in the numerical solution, guaranteeing credible and ensuring computational efficiency for the velocity, temperature, and concentration profiles without sacrificing accuracy. The model was solved by using grids with dimensions of $50\times 50$, $100\times 100$, and $200\times 200$. Figure 2 shows that the solutions found are always the same regardless of whether one uses a relatively small or large grid. We choose a grid size of $100\times 100$ for subsequent simulations.

Figure 2

Figure 2. Grid independence test for the velocity, heat, and concentration.

4.2 Velocity

Figures 3, 4 show the behavior of the electric potential $(\mathrm{\Phi })$ under different conditions. Figures 3A, B show the effects of the wall zeta potential $(\zeta )$ and Debye–Hückel parameter $(\kappa )$ on the electric potential distribution. As the wall zeta potential increases, the electric potential within the flow domain increases, increasing the electroosmotic effect. This results in a more uniform electric potential distribution along the artery, which enhances the electroosmotic flow and affects the velocity profile. The Debye–Hückel parameter, characterizing the thickness of the electrical double layer, also affects the electric potential distribution, with higher values causing a steeper potential gradient near the walls. Figure 4 highlights the impact of the curvature parameter $(R_c)$ on the electric potential. The results indicate that increasing the curvature enhances the asymmetry in the potential distribution, particularly near the outer wall of the curved artery segment, influencing the velocity distribution observed in subsequent figures.

Figure 3

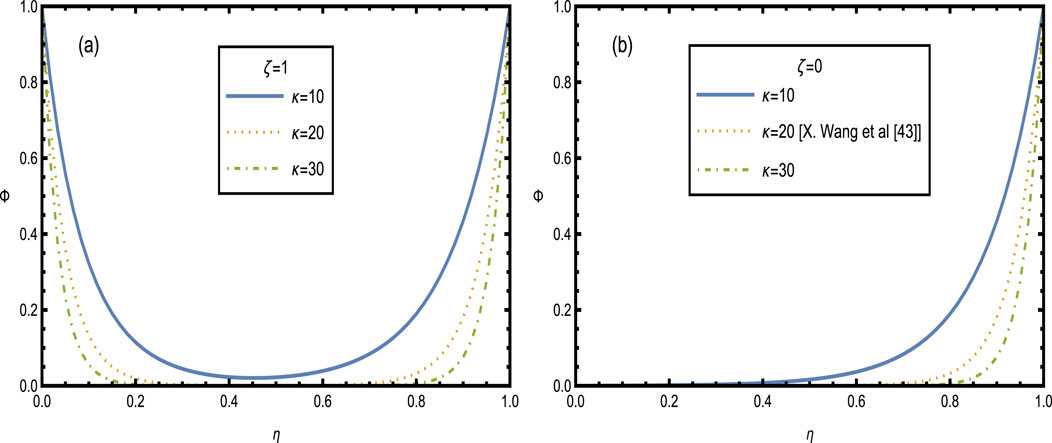
Figure 3. Potential electricity $\mathrm{\Phi }$ [Panels (A, B)] for different values of the wall zeta potential $\zeta$ and Debye–Hückel parameter $\kappa$.

Figure 4

Figure 4. Potential electricity $\mathrm{\Phi }$ for different values of the curvature parameter $R_c$.

The velocity profiles for the hybrid nanofluid are shown in Figures 5–9, illustrating the complex interaction of various physical parameters. Figure 5 shows the velocity distribution across the artery for different values of wall zeta potential $(\zeta )$ and the Weissenberg number $(W_e)$. As the wall zeta potential increases, the electroosmotic force strengthens, enhancing the overall velocity of the fluid. This is because the increased electrokinetic force reduces the resistance imposed by viscous forces. Additionally, the Weissenberg number, which characterizes the fluid’s elasticity, plays a key role. Higher values of $(W_e)$ increase the velocity peak near the artery’s central axis as the elastic properties of the Carreau fluid work to minimize viscous drag. The combined effect of the higher wall zeta potential and Weissenberg number produces a more favorable velocity distribution, enhancing mass transport, which is beneficial in medical applications involving catheterized arteries.

Figure 5

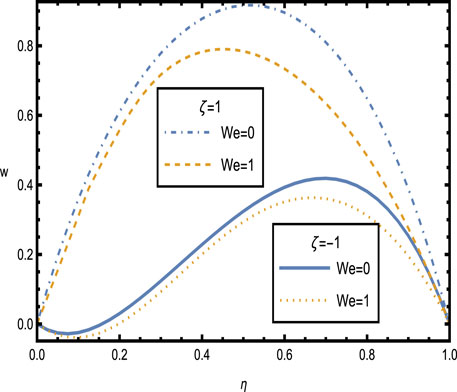
Figure 5. Velocity distributions $w$ for different values of the wall zeta potential $\zeta$ and Weissenberg number $W_e$.

Figure 6

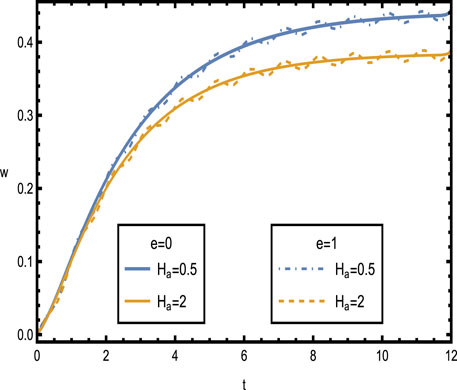
Figure 6. Velocity distributions $w$ versus the time $t$ for different values of the Hartmann number $H_a$ and fluctuation parameter $(e)$.

Figure 7

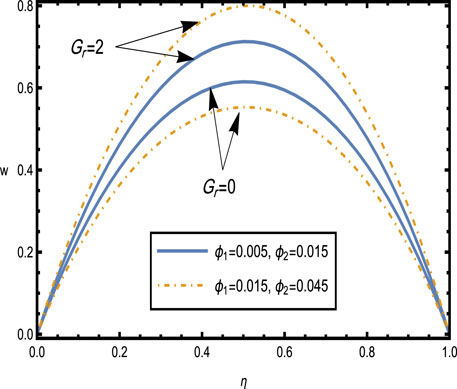
Figure 7. Velocity distributions $w$ for different values of the Grashof number $G_r$ and volume concentrations ${\varphi }_1,{\varphi }_2$.

Figure 8

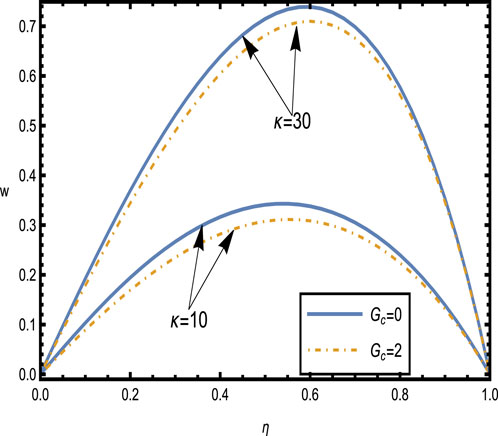
Figure 8. Velocity distributions $w$ for different values of the electroosmotic parameter $\kappa$ and solutal Grashof number $G_c$.

Figure 9

Figure 9. Velocity distributions $w$ versus the time $t$ for different values of the curvature parameter $R_c$.

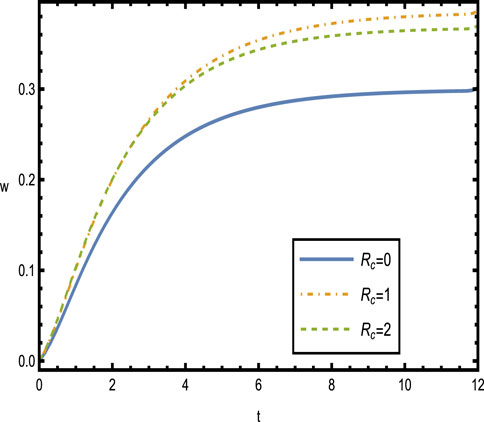
Figure 6 shows the velocity distributions over time $t$ for different values of the Hartmann number $(H_a)$ and the fluctuation parameter $(e)$. The Hartmann number reflects the influence of the magnetic field on the flow, with higher values corresponding to a stronger magnetic field. As $H_a$ increases, the velocity decreases, indicating that the magnetic field exerts a damping effect on fluid motion, reducing the overall velocity. This magnetic damping effect is critical for controlling blood flow in biomedical applications where precise modulation is needed. In contrast, the fluctuation parameter $(e)$, representing the amplitude of the pulsatile flow, causes more pronounced oscillations in the velocity profile with higher values, reflecting the increased impact of pulsatility on flow dynamics. The interplay between $(H_a)$ and $(e)$ reveals that although the magnetic field lowers the peak velocity, the pulsatile nature of the flow can counterbalance this effect, maintaining a dynamic and controlled flow environment.

Figure 7 shows the velocity distributions for different values of the Grashof number $(G_r)$ and volume concentrations $({\varphi }_1,{\varphi }_2)$. The Grashof number represents the ratio of buoyancy to viscous forces, and as $(G_r)$ increases, the velocity profile exhibits a notable enhancement due to the increased buoyant force acting on the fluid. This buoyant force helps overcome the resistance of the arterial walls, thus increasing the flow rate. The volume concentrations of hybrid nanoparticles $({\varphi }_1,{\varphi }_2)$ also significantly influence the velocity. Higher concentrations lead to improved thermal conductivity and reduced effective viscosity, resulting in a more pronounced velocity peak. The combined effect of an increased Grashof number and higher nanoparticle concentration significantly enhances the overall velocity, which can help improve blood flow in stenosed arteries.

Figure 8 shows the velocity distributions for different values of the electroosmotic parameter $(\kappa )$ and solutal Grashof number $(G_c)$. The electroosmotic parameter $(\kappa )$ influences the electrokinetic flow within the artery, and as its value increases, the overall fluid velocity increases due to the enhanced electroosmotic force, providing additional driving support for the flow. The solutal Grashof number $(G_c)$, which represents the ratio of solutal buoyancy forces to viscous forces, also significantly affects the velocity profile. Higher $G_c$ values increase the buoyant force, enhancing fluid velocity, particularly in the core region of the artery. The combined effects of $(\kappa )$ and $(G_c)$ contribute to a more efficient flow, crucial for optimizing mass transport in biomedical applications involving stenosed arteries.

Figure 9 presents the velocity distributions over time $t$ for different values of the curvature parameter $(R_c)$. The curvature parameter strongly influences the velocity profile due to the centrifugal forces generated by the artery’s curved geometry. As $R_c$ increases, the velocity near the outer wall of the artery increases, leading to an asymmetric velocity distribution. This effect is due to centrifugal forces pushing the fluid toward the outer curvature, increasing the velocity in that region while reducing it near the inner wall. The pulsatile nature of the flow further modulates these effects, with peak velocity occurring during the systolic phase, especially in regions affected by a higher curvature. This interaction between the curvature and pulsatility is critical for understanding hemodynamics in curved arterial segments, particularly in the presence of stenosis or catheterization.

4.3 Heat and concentration distribution

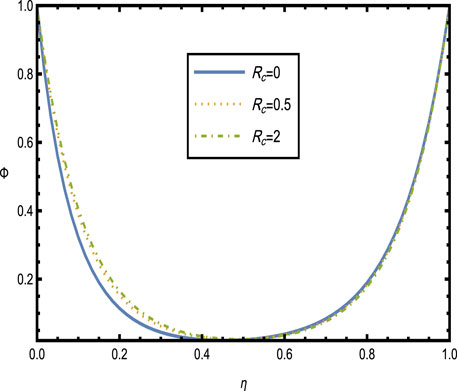
Figure 10 shows the distribution of temperature and concentration for different values of the curvature parameter $(R_c)$ and radiation parameter $(R_a)$. Panel (a) shows the temperature distribution, which is significantly influenced by the artery’s curvature. As $R_c$ increases, the temperature distribution becomes more asymmetric, with higher temperatures near the artery’s outer curvature. This asymmetry is attributed to enhanced convective heat transfer driven by centrifugal forces that push the fluid carrying thermal energy toward the outer wall. The radiation parameter $(R_a)$ also plays an important role; higher $R_a$ values increase radiative heat flux, leading to a more uniform temperature profile across the artery, which is crucial for maintaining stable thermal conditions. Panel (b) shows the concentration distribution for various values of $(R_c)$ and $(R_a)$. Similar to the temperature distribution, the concentration profile is influenced by curvature and radiation effects. Higher $R_c$ values result in an asymmetric concentration profile, with more concentration near the artery’s outer wall. $(R_a)$ enhances mass diffusion, leading to a more uniform concentration distribution. The combination of curvature and radiation parameters is crucial in optimizing both heat and mass transfer, making it valuable for biomedical applications like targeted drug delivery and thermal therapies.

Figure 10

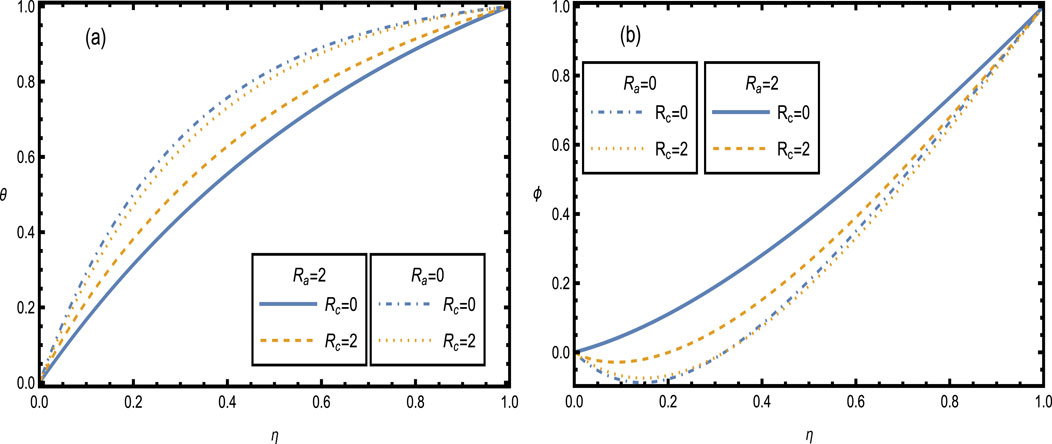
Figure 10. Heat and concentration distributions [Panels (A, B)] for different values of the curvature parameter $R_c$ and radiation parameter $R_a$.

Figure 11 shows the heat and concentration distributions for different values of the thermophoresis parameter $(N_t)$. Panel (a) shows how the temperature distribution is significantly affected by the thermophoresis effect. As $N_t$ increases, the temperature gradient becomes steeper, enhancing heat transfer from regions of higher temperature to lower temperature. This effect is particularly important in applications where maintaining a controlled temperature gradient is essential, such as in hyperthermia treatments. Panel (b) shows the concentration distribution for different $(N_t)$ values. The thermophoresis effect causes particles to move from hot to cold regions, leading to a decrease in the concentration in the hotter areas and an increase in the cooler areas. As $N_t$ increases, the concentration distribution becomes more uniform, reflecting enhanced mass transfer and more effective diffusion of nanoparticles within the fluid. Generally, a decrease in the concentration in hotter regions and an increase in the concentration in cooler areas align with thermophoresis, which drives movement from hot to cold. However, achieving a more consistent concentration across the entire domain or a uniform reduction suggests a balanced distribution, which is beneficial in biomedical applications like targeted drug delivery, where a homogeneous distribution is often desired for optimal therapeutic outcomes.

Figure 11

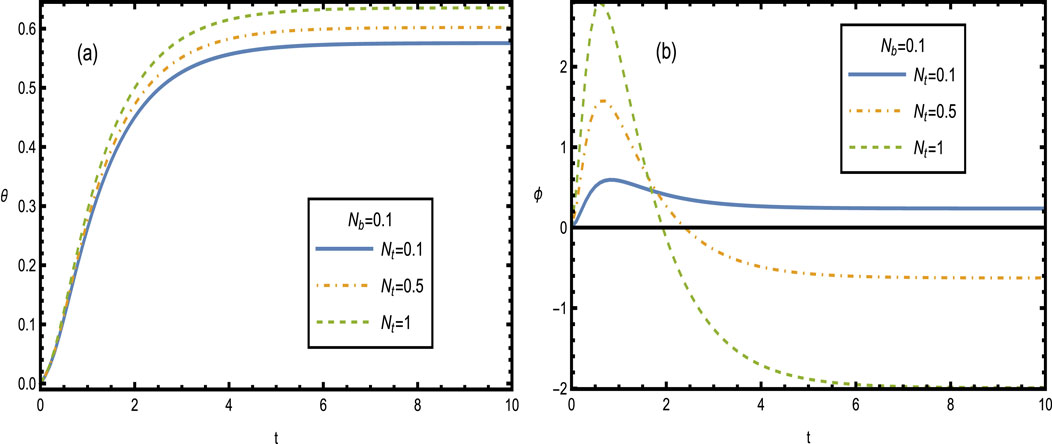
Figure 11. Heat and concentration distributions [Panels (A, B)] for different values of the thermophoresis parameter $N_t$.

Figure 12 shows the heat and concentration distributions for different values of the Brownian motion parameter $(N_b)$ at a fixed thermophoresis parameter $(N_t)$ value. Panel (a) illustrates that the Brownian motion parameter significantly affects the temperature distribution. Panel (b) shows the concentration distribution for different values of the Brownian motion parameter $(N_b)$. The concentration distribution is highly sensitive to the Brownian motion at the beginning of the time interval; this sensitivity decreases as time increases, and the concentration goes to its steady state.

Figure 12

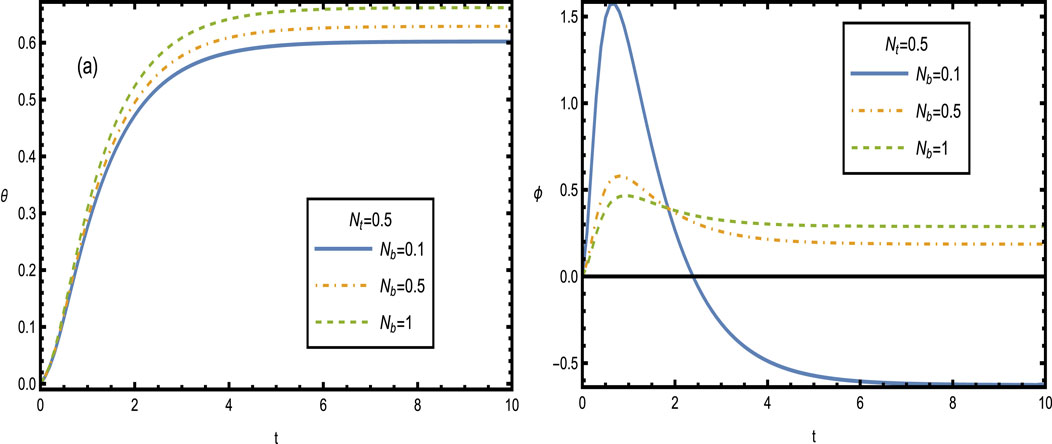
Figure 12. Heat and concentration distributions [Panels (A, B)] for different values of the Brownian motion parameter $N_b$.

Figure 13 shows the impact of the Schmidt number $(S_c)$ and chemical parameter $({\beta }_c)$ on the concentration distribution. Panel (a) and Panel (b) illustrate that the Schmidt number $(S_c)$ and chemical parameter $({\beta }_c)$ significantly affect the concentration distribution. Furthermore, the concentration distribution is reduced by increasing Schmidt number $(S_c)$ and chemical parameter $({\beta }_c)$. Physically, a thicker hydrodynamic layer compared to the mass transfer layer is indicated by a greater Schmidt number, which causes the concentration to diffuse more slowly. In processes like chemical reactors or environmental engineering, where regulated mass transfer is sought, this is essential.

Figure 13

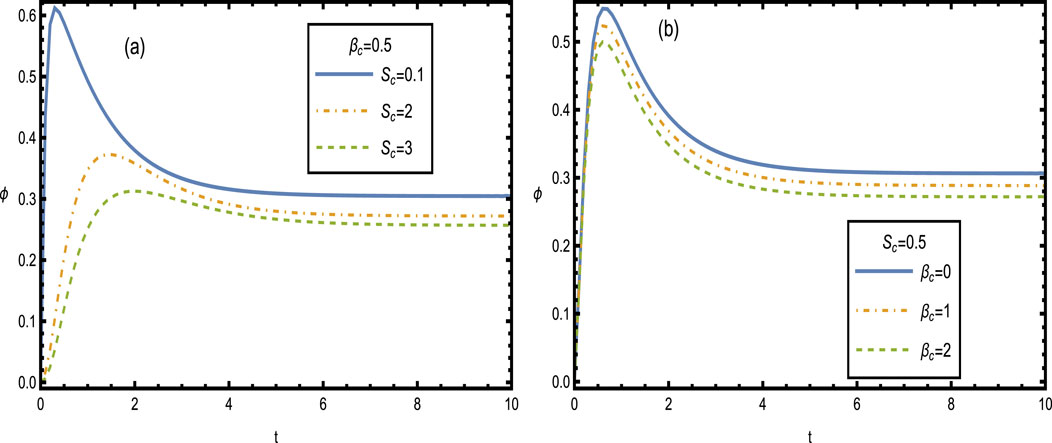
Figure 13. Concentration distributions $\varphi$ versus time $t$ for different values of the Schmidt number $S_c$ and chemical parameter ${\beta }_c$ [Panels (A, B)].

5 Conclusion

The flow of hybrid nanofluid through a stenosed, curved, and catheterized artery was treated as unsteady electroosmotic pulsatile flow using the Carreau non-Newtonian model. The characteristics of the velocity, temperature, and concentration distributions were analyzed for various representative physical parameters. The main findings are as follows.

• The results of the dimensionless potential distribution shown in Figure 2B match the results obtained by Wang et al. (2020).

• Numerical analysis of the hybrid nanofluid flow within a stenosed, curved, and catheterized artery showed significant influences of electroosmotic forces, curvature, and pulsatility on velocity, temperature, and concentration profiles.

• Increases in the electroosmotic and Weissenberg parameters substantially accelerated fluid velocity by reducing viscous drag while improving mass transport.

• The curvature parameter and radiation effects played a crucial role in creating asymmetric heat and concentration distributions, optimizing thermal and mass transport.

• The thermophoresis parameter influenced temperature and concentration distributions by promoting uniformity, which is beneficial in biomedical applications for efficient mass diffusion.

• The fluctuating patterns imply that the concentration distribution is extremely responsive to the parameter of Brownian motion. In procedures requiring exact concentration control, such as chemical reactions or material creation, this might be extremely important.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

ME: conceptualization, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. AA: conceptualization, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. YA: conceptualization, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. SA: conceptualization, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

Abdullah Alsharif acknowledges Taif University, Saudi Arabia, for supporting this work through the project number TU-DSPP-2024-185. Sara I. Abdelsalam acknowledges Fundación Mujeres por África for supporting this work through the fellowship awarded to her.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdal, S., Mariam, A., Ali, B., Younas, S., Ali, L., and Habib, D. (2021). Implications of bioconvection and activation energy on Reiner-Rivlin nanofluid transportation over a disk in rotation with partial slip. Chin. J. Phys. 73, 672–683. doi:10.1016/j.cjph.2021.07.022

CrossRef Full Text | Google Scholar

Akbar, N. S., and Nadeem, S. (2014). Carreau fluid model for blood flow through atapered artery with a stenosis. Ain Shams Eng. J. 5, 1307–1316. doi:10.1016/j.asej.2014.05.010

CrossRef Full Text | Google Scholar

Akhtar, S., McCash, L. B., Nadeem, S., Saleem, S., and Issakhov, A. (2021). Mechanics of non-Newtonian blood flow in an artery having multiple stenosis and electroosmotic effects. Sci. Prog. 104 (3), 368504211031693–15. doi:10.1177/00368504211031693

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, B., Siddique, I., Ahmadian, A., Senu, N., Ali, L., and Haider, A. (2022). Significance of Lorentz and Coriolis forces on dynamics of water based silver tiny particles via finite element simulation. Ain Shams Eng. J. 13 (2), 101572. doi:10.1016/j.asej.2021.08.014

CrossRef Full Text | Google Scholar

Ali, L., Liu, X., and Ali, B. (2020). Finite element analysis of variable viscosity impact on MHD flow and heat transfer of nanofluid using the cattaneo-christov model. Coatings 10 (4), 395. doi:10.3390/coatings10040395

CrossRef Full Text | Google Scholar

Apostolidis, A. J., and Beris, A. N. (2014). Modeling of the blood rheology in steady-state shear flows. J. Rheology 58 (3), 607–633. doi:10.1122/1.4866296

CrossRef Full Text | Google Scholar

Basha, H. T., Rajagopal, K., Ahammad, N. A., Sathish, S., and Gunakala, S. R. (2022). Finite difference computation of Au-Cu/Magneto-bio-hybrid nanofluid flow in an inclined uneven stenosis artery. Complexity 2022 (1), 2078372–18. doi:10.1155/2022/2078372

CrossRef Full Text | Google Scholar

Berger, S. A., Talbot, L., and Yao, L. S. (1983). Flow in curved pipes. Annu. Rev. Fluid Mech. 15 (1), 461–512. doi:10.1146/annurev.fl.15.010183.002333

CrossRef Full Text | Google Scholar

Bhatti, M. M., Abbas, M. A., and Muhammad, S. (2024). “Optimizing fluid flow efficiency: third-grade hybrid nanofluid flow with electro-magneto-hydrodynamics in confined vertical spaces,” in Nanofluids (Elsevier), 243–275. doi:10.1016/b978-0-443-13625-2.00012-7

CrossRef Full Text | Google Scholar

Chakravarty, S., and Mandal, P. (1996). A nonlinear two dimensional model of blood flow in an overlapping arterial stenosis subjected to body acceleration. Math. Comput. Model. 24 (1), 43–58. doi:10.1016/0895-7177(96)00079-9

CrossRef Full Text | Google Scholar

Cheng, C. P., Wilson, N. M., Hallett, R. L., Herfkens, R. J., and Taylor, C. A. (2006). In vivo MR angiographic quantification of axial and twisting deformations of the superficial femoral artery resulting from maximum hip and knee flexion. J. Vasc. Interventional Radiology 17 (6), 979–987. doi:10.1097/01.rvi.0000220367.62137.e8

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, S., Barman, B., Jana, R. N., and Makinde, O. D. (2021). Hall and ion slip currents impact on electromagnetic blood flow conveying hybrid nanoparticles through an endoscope with peristaltic waves. Bio Nanosci. 11, 770–792. doi:10.1007/s12668-021-00873-y

CrossRef Full Text | Google Scholar

El-Dabe, N. T. M., and Mostapha, D. R. (2020). Hall current and Joule heating effects on peristaltic flow of a Sisko fluid with mild stenosis through a porous medium in a tapered artery with slip and convective boundary conditions. Sains Malays. 49 (5), 1175–1190. doi:10.17576/jsm-2020-4905-23

CrossRef Full Text | Google Scholar

El Kot, M. A., and Abd Elmaboud, Y. (2021). Hybrid nanofluid flows through a vertical diseased coronary artery with heat transfer. J. Mech. Med. Biol. 21 (02), 2150012. doi:10.1142/s0219519421500123

CrossRef Full Text | Google Scholar

El Kot, M. A., and Abd Elmaboud, Y. (2023). Model of LDL-C concentration of blood flow through a vertical porous microchannel with multiple stenoses: computational simulation. J. Taibah Univ. Sci. 17 (1), 2176194. doi:10.1080/16583655.2023.2176194

CrossRef Full Text | Google Scholar

El Kot, M. A., and Abd Elmaboud, Y. (2024). Numerical simulation of electroosmotic sutterby hybrid nanofluid flowing through an irregularly mild stenotic artery with an aneurysm. Arabian J. Sci. Eng. 49, 2483–2498. doi:10.1007/s13369-023-08257-y

CrossRef Full Text | Google Scholar

El-Masry, Y. A. S., Abd Elmaboud, Y., and Abdel-Sattar, M. A. (2020). Direct current/alternating current magnetohydrodynamic micropump of a hybrid nanofluid through a vertical annulus with heat transfer. J. Therm. Sci. Eng. Appl. 12 (4). doi:10.1115/1.4046058

PubMed Abstract | CrossRef Full Text | Google Scholar

Gijsen, F. J. H., van de Vosse, F. N., and Janssen, J. D. (1999). The influence of the non-Newtonian properties of blood on the flow in large arteries: steady flow in a carotid bifurcation model. J. Biomechanics 32 (6), 601–608. doi:10.1016/S0021-9290(99)00015-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Haghighi, A. R., Kabdool, A. A., Asl, M. S., and Kiyatsatfar, M. C. (2006). Numerical investigation of pulsatile blood flow in stenosed artery. Int. J. Appl. Comput. Math. 2, 649–662. doi:10.1007/s40819-015-0084-0

CrossRef Full Text | Google Scholar

Hassan, M., Chunwei, Z., Firdous, A., and Bhatti, M. M. (2024). Viscoelastic fluid flow on variable thickness sheets using a three-element viscous model. Int. J. Model. Simul., 1–12. doi:10.1080/02286203.2024.2338583

CrossRef Full Text | Google Scholar

Huminic, G., and Huminic, A. (2018). Hybrid nanofluids for heat transfer applications - a state-of-the-art review. Int. J. Heat Mass Transf. 125, 82–103. doi:10.1016/j.ijheatmasstransfer.2018.04.059

CrossRef Full Text | Google Scholar

Huo, Y., and Kassab, G. S. (2006). Pulsatile blood flow in the entire coronary arterial tree: theory and experiment. Am. J. Physiology-Heart Circulatory Physiology 302 (6), H1074–H1087. doi:10.1152/ajpheart.00200.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnston, B. M., Johnston, P. R., Corney, S., and Kilpatrick, D. (2004). Non-Newtonian blood flow in human right coronary arteries: steady state simulations. J. Biomechanics 37 (5), 709–720. doi:10.1016/j.jbiomech.2003.09.016

PubMed Abstract | CrossRef Full Text | Google Scholar

LaDisa, J. F., Olson, L. E., Molthen, R. C., Hettrick, D. A., Pratt, P. F., Hardel, M. D., et al. (2005). Alterations in wall shear stress predict sites of neointimal hyperplasia after stent implantation in rabbit iliac arteries. Am. J. Physiology-Heart Circulatory Physiology 288 (5), H2465–H2475. doi:10.1152/ajpheart.01107.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, Q., Xu, X. Y., Ramnarine, K. V., and Hoskins, P. (2001). Numerical investigation of physiologically realistic pulsatile flow through arterial stenosis. J. Biomechanics 34 (10), 1229–1242. doi:10.1016/s0021-9290(01)00100-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Morris, P. D., Narracott, A., von Tengg-Kobligk, H., Silva Soto, D. A., Hsiao, S., Lungu, A., et al. (2016). Computational fluid dynamics modelling in cardiovascular medicine. Heart 102 (1), 18–28. doi:10.1136/heartjnl-2015-308044

PubMed Abstract | CrossRef Full Text | Google Scholar

Pal, D., and Mondal, H. (2011). Effects of Soret, Dufour, chemical reaction, and thermal radiation on MHD non-Darcy unsteady mixed convective heat and mass transfer over a stretching sheet. Commun. Nonlinear Sci. Numer. Simul. 16 (4), 1942–1958. doi:10.1016/j.cnsns.2010.08.033

CrossRef Full Text | Google Scholar

Perktold, K., Resch, M., and Peter, R. O. (1991). Three-dimensional numerical analysis of pulsatile flow and wall shear stress in the carotid artery bifurcation. J. Biomechanics 24 (6), 409–420. doi:10.1016/0021-9290(91)90029-M

PubMed Abstract | CrossRef Full Text | Google Scholar

Pincombe, B., and Mazumdar, J. (1977). The effects of post-stenotic dilatations on the flow of a blood analogue through stenosed coronary arteries. Math. Comput. Model. 25 (6), 57–70. doi:10.1016/S0895-7177(97)00039-3

CrossRef Full Text | Google Scholar

Quarteroni, A., Tuveri, M., and Veneziani, A. (2000). Computational vascular fluid dynamics: problems, models and methods. Comput. Vis. Sci. 2 (4), 163–197. doi:10.1007/s007910050039

CrossRef Full Text | Google Scholar

Ramanamurthy, J. V., Prasad, K. M., and Narla, V. K. (2013). Unsteady peristaltic transport in curved channels. Phys. Fluids 25, 1903–1909. doi:10.1063/1.4821355

CrossRef Full Text | Google Scholar

Rana, J., and Liao, S. (2019). A general analytical approach to study solute dispersion in non-Newtonian fluid flow. Eur. J. Mech. - B/Fluids 77, 183–200. doi:10.1016/j.euromechflu.2019.04.013

CrossRef Full Text | Google Scholar

Sarkar, J., Ghosh, P., and Adil, A. (2015). A review on hybrid nanofluids: recent research, development and applications. Renew. Sustain. Energy Rev. 43, 164–177. doi:10.1016/j.rser.2014.11.023

CrossRef Full Text | Google Scholar

Sundar, L. S., Farooky, Md. H., Sarada, S. N., and Singh, M. K. (2013). Experimental thermal conductivity of ethylene glycol and water mixture based low volume concentration of Al₂O₃ and CuO nanofluids. Int. Commun. Heat Mass Transf. 41, 41–46. doi:10.1016/j.icheatmasstransfer.2012.11.004

CrossRef Full Text | Google Scholar

Sundar, L. S., Singh, M. K., and Sousa, A. C. M. (2014). Enhanced heat transfer and friction factor of MWCNTF e₃O₄/water hybrid nanofluids. Int. Commun. Heat Mass Transf. 52, 73–83. doi:10.1016/j.icheatmasstransfer.2014.01.012

CrossRef Full Text | Google Scholar

Tawade, J. V., Guled, C. N., Noeiaghdam, S., Fernandez-Gamiz, U., Govindan, V., and Balamuralitharan, S. (2022). Effects of thermophoresis and Brownian motion for thermal and chemically reacting Casson nanofluid flow over a linearly stretching sheet. Results Eng. 15, 100448. doi:10.1016/j.rineng.2022.100448

CrossRef Full Text | Google Scholar

Tzirtzilakis, E. E. (2005). A mathematical model for blood flow in magnetic field. Phys. Fluids 17 (7), 077103. doi:10.1063/1.1978807

CrossRef Full Text | Google Scholar

Wajihah, S. A., and Sankar, D. S. (2021). Effects of porosity in four-layered non-linear blood rheology in constricted narrow arteries with clinical applications. Comput. Methods Programs Biomed. 199, 105907. doi:10.1016/j.cmpb.2020.105907

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Cheng, C., Wang, S., and Liu, S. (2009). Electroosmotic pumps and their applications in microfluidic systems. Microfluid. Nanofluidics 6 (2), 145–162. doi:10.1007/s10404-008-0399-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Jiang, Y., Qiao, Y., Xu, H., and Qi, H. (2020). Numerical study of electroosmotic slip flow of fractional Oldroyd-B fluids at high zeta potentials. ELECTROPHORESIS 41 (10-11), 769–777. doi:10.1002/elps.201900370

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, F., Lu, T. J., Seffen, K. A., and Ng, E. (2009). Mathematical modeling of skin bioheat transfer. Appl. Mech. Rev. 62 (5). doi:10.1115/1.3124646

CrossRef Full Text | Google Scholar

Young, D. F. (1968). Effect of a time-dependent stenosis on flow through a tube. J. Eng. Industrial Trans. ASME 90 (2), 248–254. doi:10.1115/1.3604621

CrossRef Full Text | Google Scholar

Zaman, A., and Khan, A. A. (2021). Time dependent non-Newtonian nano-fluid (blood) flow in w-shape stenosed channel; with curvature effects. Math. Comput. Simul. 181, 82–97. doi:10.1016/j.matcom.2020.09.017

CrossRef Full Text | Google Scholar