Mechanisms of cage noise generation in machine tool bearings

Cage instability in ball bearings can lead to torque fluctuations and significant noise. In machine tool spindles, which require high rotational precision, outer ring-guided cages are often preferred over common ball-guided cages. While outer ring-guided cages suppress instability modes caused by sliding friction between the cage and balls, increased interaction between the cage and outer ring can introduce other instability modes, leading to noise. Despite the critical implications of these findings, prior research into this specific type of cage instability, incorporating both experimental and analytical perspectives, remains limited. Therefore, in this study, we utilized a high-speed camera system to conduct visualization tests on cage behavior in grease-lubricated angular contact ball bearings used in machine tools. Through detailed image-processing of the results, we identified specific behaviors associated with cage noise. To facilitate the optimal design of the cage to stabilize these behaviors, we developed a dynamic analysis model focusing on the friction between the cage and the outer ring under grease lubrication, considering fluid pressure effects. The validity of this model was confirmed through experiments at various rotational speeds. This analytical model enabled us to elucidate the underlying mechanisms driving cage instability. The insights gained from this research are expected to significantly enhance the fundamental understanding of cage design principles aimed at eliminating cage noise.

1 Introduction

In typical rolling bearings, a cage is utilized to maintain equal spacing among the rolling elements. Interaction occurs between the rolling elements and the cage, where sliding friction between these elements and the rotating cage can induce cage whirl (Kingsbury, 1965). This whirl, when occurring at high speeds, may lead to collisions with the rolling elements, causing deviations from their equidistant arrangements. Such non-repetitive runout compromises the rotational accuracy of the bearing, which is critical in machine tool spindles that require high precision. To mitigate this issue, bearings are often designed with an outer ring-guided cage. This design integrates two distinct types of clearance, as shown in Figure 1. However, challenges arise when the pocket clearance ($c_p$) exceeds the guide clearance ($c_g$), causing the interaction between the cage and outer ring to become dominant. This results in a cage whirl along the shoulder of the outer ring owing to increased sliding friction (Nogi et al., 2018). This whirl is a primary source of severe noise, commonly referred to as cage noise, which significantly degrades the quality of the bearing.

Figure 1

Figure 1. Schematic of cage clearance in outer ring-guided type.

To address and mitigate cage instability, extensive research has been conducted through both experimental (Kingsbury, 1965; Stevens, 1980; Gupta et al., 1986; Boesiger et al., 1992; Kingsbury and Walker, 1994; Stacke and Fritzson, 2001; Servais et al., 2013; Palladino et al., 2017; Chen et al., 2019; Choe et al., 2019; Schwarz et al., 2021; Gao et al., 2022a; Gao et al., 2022b; Liao et al., 2023; Russell, 2023) and analytical methods (Walter, 1971; Kannel and Bupara, 1978; Meeks, 1985; Meeks and Ng, 1985; Gupta et al., 1986; Boesiger et al., 1992; Stacke et al., 1999; Ghaisas et al., 2004; Weinzapfel and Sadeghi, 2009; Ashtekar and Sadeghi, 2012; Nogi et al., 2018; Niu, 2019; Schwarz et al., 2021; Gao et al., 2022a; Gao et al., 2022b; Liao et al., 2023; Russell, 2023). Kingsbury (1965) and Kingsbury and Walker (1994) explored the influence of cage instability on torque variation in rolling bearings. They highlighted the rigid body motion of the cage owing to the sliding friction between the ball and cage as a primary factor causing torque variations. Walter (1971) utilized Euler’s equations of motion to describe the non-steady-state dynamics of ball bearings. Kannel and Bupara (1978) investigated the evolution of the cage’s rigid body motion without temporal integration, assuming no sliding between the ball and raceways and neglecting the out-of-plane motion of the cage. Their results aligned with the experimental findings of Kingsbury (1965).

Further, Meeks (1985) and Meeks and Ng (1985) performed dynamic analyses on the six degrees of freedom of the cage, assessing the effect of clearance on cage stability. Gupta et al. (1986) developed a comprehensive dynamic analysis program that modeled all the components of a rolling bearing with six degrees of freedom. Boesiger et al. (1992) investigated the impact of a biased cage and operational conditions on cage instability using both experimental and analytical methods. They conducted a dynamic analysis of the rigid-body motion of the cage, considering only planar motion, and confirmed a strong correlation between these results and the experimental results. Ashtekar and Sadeghi (2012) integrated a three-dimensional finite-element model of the cage into a general six-degree-of-freedom bearing dynamics model to examine the effect of elastic deformation of the cage. Servais et al. (2013) developed a method to evaluate cage materials that could potentially reduce cage instability, utilizing the stability map constructed from the coefficients of restitution and friction between the ball and cage.

Choe et al. (2019) conducted an experimental study on the dynamic behavior of a ball bearing cage with mass imbalance in cryogenic environments. Their findings underscore the significant impact of mass imbalance on whirling motion and wear, which align with existing literature. The study also highlights the role of hydraulic forces and suggests that future research should explore the combined effects of mass imbalance and hydraulic forces to enhance understanding of bearing performance. Gao et al. (2022a) developed an advanced dynamic model focusing on cage flexibility and three-dimensional whirling motion in angular contact ball bearings. The model, which neglects fluid pressure effects, divides the self-lubricated cage into segments to assess flexibility and uses multiple coordinate systems to describe ball-cage interactions. The study highlights the need to consider cage flexibility and motion and suggests that future research should address lubricating modes and the impact of varying lubricant amounts on cage behavior. Additionally, Gao et al. (2022b) developed the KH-TEHD model to analyze bearing skidding and cage whirling behavior, incorporating advanced factors such as thermal deformation and elasto-hydrodynamic lubrication, which enhance predictive accuracy in dynamic simulations. This model provides more detailed insights into cage dynamics, particularly under varying operational conditions. However, experimental validation of the cage whirling behavior remains a future research priority to fully confirm the model’s effectiveness. Russell (2023) presents an innovative study on the lubrication mechanisms of deep groove ball bearing cages. He introduces the Bearing Cage Friction Test Rig, enabling detailed measurements of friction and lubrication under realistic conditions. The research notably includes a comprehensive model for cage lubrication that addresses cage pocket starvation and varying lubrication environments. Russell’s work incorporates extensive computational fluid dynamics (CFD) simulations to analyze lubricant flow and fluid drag within ball bearings, revealing the impact of cage shape on performance. Future challenges include refining lubrication models for high-speed applications and integrating thermal effects into CFD analyses. Nogi et al. (2018) further refined the understanding of cage instability by establishing a critical friction coefficient that determines its occurrence. In addition, it asserts that cage instability could manifest as positive whirl (cage whirls in the direction of its rotation) when $c_p<c_g$ owing to sliding friction with the rolling elements or as negative whirl (cage whirls opposite to its rotation) when $c_p>c_g$ owing to sliding friction with the outer ring.

To optimally design cages that effectively suppress noise in machine tool spindles, it is crucial to utilize a bearing dynamic analysis model that accurately replicates real-world phenomena. Previous research on the generation mechanisms of cage instability, particularly negative whirl in outer ring-guided cages, has been limited. Moreover, these studies have rarely employed a combination of experimental and analytical methods. This study focuses on grease lubrication, where fluid pressure effects are non-negligible, and includes the experimental validation of a friction model between the cage and the outer ring, which had not been sufficiently verified previously. We intend to achieve this by conducting visualization tests to observe cage behavior directly and applying dynamic analysis.

2 Visualization test of cage behavior

2.1 Test method

Figure 2 presents a schematic of the testing apparatus used in this study. The apparatus employed an open-type angular contact ball bearing as the test bearing, specified by the bearing dimension series 70. The cage’s dimensions include an outer diameter of 110 mm, an inner diameter of 70 mm, and a width of 20 mm. The cage material is phenolic resin with a density of 1,250 kg/m³ and Young’s modulus of 9.61 GPa. The cage is a cylindrical type guided by the outer ring, with pocket clearance $c_p$ of 0.555 mm and guide clearance $c_g$ of 0.427 mm. The lubrication was provided by extreme pressure grease, comprising 2.6 g of barium complex soap thickener and mineral oil with a kinematic viscosity of 105 mm²/s at 313 K and 12 mm²/s at 373 K.

Figure 2

Figure 2. Schematic of experimental apparatus.

The inner ring was mounted on a shaft supported by an angular contact ball bearing of the same series. The outer ring was secured in a fixed housing to restrict its movement. Noise measurement was conducted using a microphone positioned 40 mm from the housing’s end face, while a high-speed camera coaxially aligned with the shaft visualized the cage’s rigid body motion. High-intensity LED lighting ensured adequate exposure for the camera. An air cylinder attached to the housing exerted a constant axial load ($F_a$), and a motor provided a constant angular velocity (${\omega }_z$).

After a 2 h break-in period, sound pressure levels recorded by the microphone and optical images captured by the high-speed camera were synchronously documented. The recording spanned at least 50 shaft rotations, with the camera operating at up to 12,800 frames per second. The recorded area was a 93.75 mm square, equivalent to the diameter of the outer ring shoulder, with an image resolution of 1,024 × 1,024 pixels. This study analyzes results under test conditions of $F_{\mathrm{a}}$ = 687 N and ${\omega }_z$ ranging from 50 to 8,000 rpm.

It should be noted that, given that the tests were conducted with grease lubrication, the results may be influenced by the characteristics of the grease, such as its viscosity, consistency, and distribution. Therefore, approximately five trials per condition were performed to obtain the data reported in this paper. Within the same test, the occurrence and disappearance of cage noise were repeated, leading to some variability in the frequency of these occurrences. However, it was confirmed that the sound pressure levels during the occurrence of cage noise and the cage whirl velocities, as detailed in Section 2.3, remained relatively consistent under the same conditions. Consequently, this paper presents the most reliable data, including average values and ranges, for comparison with the computational results.

2.2 Trajectory of the cage center

To determine the trajectory of the cage center from the test results, image-processing techniques were applied to multiple optical images captured by the high-speed camera. The cage’s center of gravity, calculated from its contour in each image, was used to establish the cage’s center. This method provided the trajectory data depicted in Figure 3. For each cage rotation, between 200 and 660 optical images were processed. The contour extraction involved binarization, setting a constant brightness threshold for each pixel to ensure the area of the cage contour remained consistent across different frames.

Figure 3

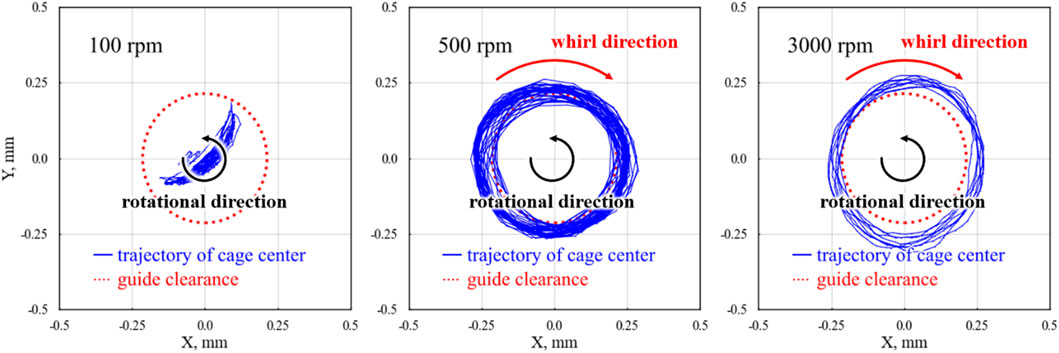
Figure 3. Trajectories of cage center during one rotation at $F_{\mathrm{a}}$ = 687 N and ${\omega }_z$ = 100, 500, and 3,000 rpm in experiment.

In Figure 3, the radial directions of the cage center’s inertial coordinates are represented on the vertical and horizontal axes. This presentation shows the results over a single rotation of the cage, including a circle representing the guide clearance diameter. In the present tests, where the rotational speed (${\omega }_z$) was incrementally increased in steps, no cage noise was observed at speeds below 100 rpm, whereas cage noise was observed at speeds above 500 rpm. Therefore, the trajectories for conditions at rotational speeds of 100, 500, and 3,000 rpm are shown as representative samples. Notably, the reference origin for each condition is the center of gravity coordinates of the cage trajectory rather than the center of the shaft, considering the convenience of the image-processing technique used.

The observed trajectories suggest that the cage center can exceed the guide clearance owing to the elastic deformation caused by centrifugal forces because of the orbital motion of the cage. At ${\omega }_z$ = 100 rpm, the cage center exhibits a wobbling motion, forming a crescent-shaped trajectory without generating any detectable noise. At higher speeds, ${\omega }_z$ = 500 and 3,000 rpm, the cage performs a circular motion within the guide clearance. During one cage rotation, multiple revolutions of orbital motion occurred, with the orbital direction opposite to the rotation direction, indicating negative whirl. Noise associated with the cage was detected under these conditions.

The forces acting on the cage include contact and friction from the rolling elements and outer ring, as well as gravity. In particular, when the relationship between pocket clearance $c_p$ and guide clearance $c_g$ is $c_p>c_g$, the interaction with the outer ring becomes dominant. At ${\omega }_z$ = 100 rpm, the cage’s wobbling is interpreted to center around an equilibrium position where the friction force from the outer ring counterbalances gravity acting in the negative y-axis direction. The wobble radius closely aligns with half of the guide clearance $\left(c_g/2\right)$, suggesting it wobbles along the outer ring shoulder. At ${\omega }_z$ = 500 and 3,000 rpm, similar forces act, but increased centrifugal force at higher rotational speeds increases the contact and friction forces from the outer ring, thereby making the friction force predominant over gravity, resulting in negative whirl.

2.3 Effect of cage whirl on cage noise

Analysis of Figure 3 involved calculating the angle between the time-varying cage center coordinates and the origin. The derivative of this angle with respect to time was then used to compute the cage’s whirl velocity. These calculations allowed us to determine the time-averaged whirl velocity and time-averaged sound pressure during a single rotation of the cage, as shown in Figure 4. The graph plots time-averaged whirl velocity on the horizontal axis against time-averaged sound pressure on the vertical axis. Positive whirl velocity values indicate the cage orbiting in the same direction as its rotation, whereas negative values indicate an orbit in the opposite direction. Data points are marked with an “x” for cases where cage noise was audibly detected and with an “o” where noise was absent. Given the intermittent nature of the cage noise observed, data points at the beginning, middle, and end of each test condition were plotted.

Figure 4

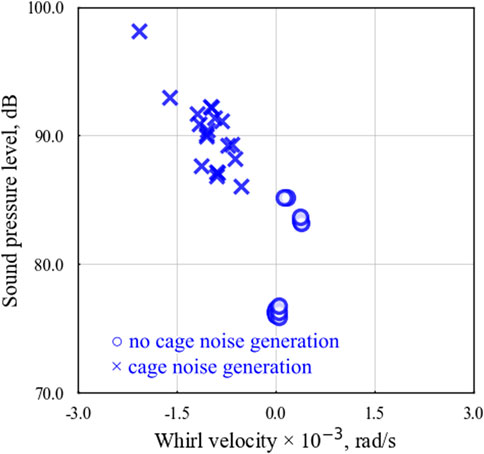
Figure 4. Relationship between cage whirl velocity and sound pressure level by microphone at ${\omega }_z$ = 50–8,000 rpm in experiment.

From the data represented in Figure 4, test results can be categorized into two distinct types of cage behavior, detailed in Table 1. This categorization has allowed for the clear identification that negative whirl significantly contributes to the generation of cage noise. For a representative condition where negative whirl was observed, we further analyzed the time variations of whirl velocity and sound pressure. These findings are illustrated in Figure 5, where the upper panel shows the time variation of the whirl velocity, and the lower panel shows the corresponding sound pressure variations. The timing of fluctuations in these two measurements generally aligns, corroborating that negative whirl is a principal factor in the generation of cage noise.

Table 1

Table 1. Definition of two types of cage motion in this experiment.

Figure 5

Figure 5. Comparison between temporal changes in whirl velocity (first row) and sound pressure level (second row) at ${\omega }_z$ = 3,000 rpm (negative whirl generation) in experiment.

3 Analytical method

3.1 Equations of motion

This section outlines the analytical model developed to replicate the negative whirl observed in experimental settings, effectively capturing the essence of the phenomenon. This approach is instrumental in fundamentally addressing cage noise. To simplify the understanding of the phenomenon and reduce computational costs, a streamlined mechanical model comprising minimal elements is employed. For dynamic analysis of bearing focusing on cage behavior, Kannel and Bupara (1978) and Boesiger et al. (1992) investigated the in-plane motion of a rigid cage, validating this assumption through experimental data. According to Nogi et al. (2018), negative whirl primarily results from sliding friction between the cage and the outer ring. Therefore, this study focuses on the in-plane motion of a rigid cage, disregarding the interaction between the rolling elements and the raceways, with each rolling element theoretically orbiting at equal intervals. Thus, the equations of motion are confined to those of the cage.

The motion of a rigid cage, with two degrees of freedom for translation and one for rotation, is governed by the following equations based on Newton’s laws:

$m\ddot{x}=F_x,(1)$

$m\ddot{y}=F_y,(2)$

$I_z\ddot{\theta }=M_z,(3)$

where $m$ is the mass of the cage, $I_z$ is the moment of inertia about its rotational axis, $F_x$ and $F_y$ are the resultant forces in the x and y directions, respectively, and $M_z$ is the resultant moment about the axis of rotation.

A moving coordinate system, fixed at the cage center, facilitates analysis of the forces acting on the cage. The direction of cage eccentricity is denoted as the $\epsilon$-axis, while the orthogonal direction is termed the $\phi$-axis. The transformation from the moving coordinate system to the inertial coordinate system is expressed by the following Equation 4 for the rotation matrix:

$\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=\left[\begin{array}{cc}\cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{array}\right]\left[\begin{array}{c}{F}_{\epsilon }\\ F_{\phi }\end{array}\right],(4)$

where $\phi$ is the angle between the $\epsilon$-axis and the y-axis ($0<\phi <2\pi$).

Figure 6 shows the forces acting on the cage, encompassing contact and friction forces from the rolling elements and outer ring, as well as gravity, as outlined in Section 2.2.

Figure 6

Figure 6. Schematic of forces on cage.

3.2 Interaction between the cage and rolling elements

The contact state between the cage and rolling elements is effectively modeled by a series connection of the contact stiffness, as determined by Hertzian contact theory, and the deflection stiffness of the cage (Boesiger et al., 1992). Given that the contact stiffness substantially exceeds the deflection stiffness, only the latter is considered significant. A linear Voigt model, consisting of a spring and a dashpot in parallel, is employed as the contact model. The Coulomb friction model is used for the friction calculations.

3.3 Interaction between the cage and the outer ring

When examining the interaction between the cage and the outer ring, relying solely on solid contact and Coulomb friction was found to predict a negative whirl velocity approximately ten times greater than what was observed experimentally. Furthermore, to induce negative whirl using a solid friction model, an unrealistically high Coulomb friction coefficient of at least 0.6 was required. Thus, the impact of fluid friction in this interaction cannot be ignored. As shown in Figure 7, the case where the cage center is eccentrically displaced by $\epsilon$ is considered. Given the study’s focus on grease lubrication, it is not assumed that the clearance is consistently filled with grease. It is assumed that a uniform thickness, $h_L$, of lubricant exists on the shoulder of the outer ring, with $h_L$ treated as a constant input value. This model does not account for changes in film thickness due to side leakage or scooping. The presence of lubricant subjects the cage to film pressure and shear force, assumed to act within the geometrically contactable region between the cage and the lubricant (from $\angle POQ$ to $\angle PO{Q}^{\prime }$). To simplify the representation of cavitation, the film pressure is considered zero in regions of negative pressure.

Figure 7

Figure 7. Schematic of lubricant forces on cage/race (balls were excluded for visibility).

The analysis also necessitates addressing collision phenomena. The pressure dependency of viscosity in the fluid lubrication model is described by the following equation (Barus, 1893):

$\eta ={\eta }_0\exp \left(\alpha P\right),(5)$

where ${\eta }_0$ is the base oil viscosity, and $\alpha$ is the pressure-viscosity coefficient. Furthermore, owing to potential interference between the cage and the outer ring, contact and friction models are adapted based on the cage’s eccentricity, $\epsilon$. Given that both solid contact and fluid lubrication can occur owing to the surface roughness of the cage, the metal contact ratio ${\lambda }_r$, as defined by Aihara (1987), is employed in the following Equation 6:

${\lambda }_{\mathrm{r}}=1-\exp \left(1.8{\mathrm{\Lambda }}^{1.2}\right),(6)$

where $\mathrm{\Lambda }$ represents the film thickness ratio, calculated as the minimum film thickness between the cage and the outer ring divided by the surface roughness.

Table 2 outlines the friction model between the cage and the outer ring, considering the following three contact states:

1. When $c_{\mathrm{g}}/2-h_L\ge \epsilon$:

Table 2

Table 2. Constructed friction model on cage/race.

In this pattern, the cage and lubricant do not geometrically contact, resulting in no interaction between the cage and the outer ring.

2. When $\epsilon >c_{\mathrm{g}}/2-h_L$ and $\mathrm{\Lambda }>0$:

This scenario involves geometric contact between the cage and lubricant where the film thickness ratio $\mathrm{\Lambda }>0$. Here, both solid contact and fluid lubrication occur owing to the surface roughness of the cage, linked via the metal contact ratio ${\lambda }_{\mathrm{r}}$.

3. When $\epsilon >c_{\mathrm{g}}/2-h_L$ and $\mathrm{\Lambda }\le 0$:

This signifies geometric contact with a film thickness ratio $\mathrm{\Lambda }\le 0$, indicating interference between the rigid cage and the outer ring. This is considered a transient state where only solid contact is modeled.

The forces acting on the cage, as delineated in Table 2, are formulated under various conditions. Under solid contact, the Voigt model and Coulomb friction, as outlined in Section 3.2, are applied. For fluid lubrication scenarios, the forces derive from Reynolds’ equation, considering the dominance of axial flow due to the cage width being typically less than one-fourth of the outer diameter. This scenario applies the theory of short-width journal bearings. The validity of this approach was confirmed through point contact elastohydrodynamic lubrication analysis, focusing on the interaction between the cage and the outer ring, which demonstrated that oil film pressure and tangential forces due to shear do not significantly affect the results.

The Reynolds equation is derived under this assumption, based on Cameron (1971), in the following Equations 7 and 8:

$\frac{\partial }{\partial y}\left(\frac{h^3}{\eta }\frac{\partial p}{\partial y}\right)=6\left(u_1+u_2\right)\frac{\partial h}{\partial x}+12\frac{\partial h}{\partial t},(7)$

$h=C\left(1+\epsilon \cos \theta \right),(8)$

where $h$ is the oil film thickness, $u_1$ and $u_2$ are the surface velocities of the cage and outer ring, $C$ is half the guide clearance, and $\epsilon$ is the eccentricity, respectively.

Assuming η as defined in Equation 5, Equation 7 cannot be solved algebraically using the approach for short-width journal bearings. Based on Cameron (1971), we apply Equation 9 to transform Equation 7. This transformation necessitates the case distinctions described in Equation 10, but the resulting modified Reynolds Equation 11 can then be solved algebraically.

$q=\left(1-e^{-\alpha p}\right)/\alpha .(9)$

$p=\left\{\begin{array}{c}-\frac{1}{\mathrm{\alpha }}\ln \left(1-\alpha q\right)\text{\hspace{0.17em}at\hspace{0.5em}}q<1/\alpha \\ q\text{\hspace{0.17em}at\hspace{0.5em}}q\ge 1/\alpha \end{array}\right.(10)$

$\frac{{\partial }^{2}q}{\partial y^2}=\frac{6{\eta }_0}{h^3}\left(\left(u_1+u_2\right)\frac{\partial h}{\partial x}+2\frac{\partial h}{\partial t}\right).(11)$

Integrating Equation 11 with boundary conditions from Equation 12 yields Equation 13.

$p\left(L/2\right)=p\left(-L/2\right)=0(12)$

$q=-\frac{3{\eta }_0}{h^3}\left(\left(u_1+u_2\right)\frac{\partial h}{\partial x}+2\frac{\partial h}{\partial t}\right)\left(\frac{L^2}{4}-y^2\right)(13)$

To simplify the representation of cavitation, the pressure is set to zero in regions of negative pressure. From Equations 10, 13, the oil film pressure is derived as

$p=\left\{\begin{array}{c}\max \left[0,-\frac{1}{\alpha }\ln \left(1+\frac{3{\alpha \eta }_0}{h^3}\left(\left(u_1+u_2\right)\frac{\partial h}{\partial x}+2\frac{\partial h}{\partial t}\right)\left(\frac{L^2}{4}-y^2\right)\right)\right]\text{\hspace{0.17em}at\hspace{0.5em}}q<1/\alpha \\ \max \left[0,-\frac{3{\eta }_0}{h^3}\left(\left(u_1+u_2\right)\frac{\partial h}{\partial x}+2\frac{\partial h}{\partial t}\right)\left(\frac{L^2}{4}-y^2\right)\right]\text{\hspace{0.17em}at\hspace{0.5em}}q\ge 1/\alpha \end{array}\right..(14)$

Pressure-induced forces $F_{P-\epsilon }$ and $F_{P-\phi }$ acting on the cage center are calculated from the following Equations 15 and 16:

$F_{\mathrm{P}-\epsilon }=R{\displaystyle \underset{-L/2}{\overset{L/2}{\int }}}{\displaystyle \underset{\pi -{\theta }_c}{\overset{\pi +{\theta }_c}{\int }}}p\cos \theta \mathrm{d}\theta \mathrm{d}y,(15)$

$F_{\mathrm{P}-\phi }=R{\displaystyle \underset{-L/2}{\overset{L/2}{\int }}}{\displaystyle \underset{\pi -{\theta }_c}{\overset{\pi +{\theta }_c}{\int }}}p\sin \theta \mathrm{d}\theta \mathrm{d}y,(16)$

where ${\theta }_c$ is $\angle \text{POQ}$ in Figure 7.

The shear force acting on the cage is calculated based on journal bearing theory (Cameron, 1971), as shown by Equations 17–20. Here, $F_S$ and $M_S$ represent the forces and moments acting on the cage center, respectively. It is important to note that the parameter $p$, which appears in Equation 17, is defined in Equation 14. Consequently, the calculations for Equations 18–20 necessarily require numerical integration.

$\tau =\frac{\partial p}{\partial x}\frac{h}{2}+\frac{\eta \left(u_1-u_2\right)}{h}(17)$

$F_{\mathrm{S}-\epsilon }=R{\displaystyle \underset{-L/2}{\overset{L/2}{\int }}}{\displaystyle \underset{\pi -{\theta }_c}{\overset{\pi +{\theta }_c}{\int }}}\tau \sin \theta \mathrm{d}\theta \mathrm{d}y(18)$

$F_{\mathrm{S}-\phi }=R{\displaystyle \underset{-L/2}{\overset{L/2}{\int }}}{\displaystyle \underset{\pi -{\theta }_c}{\overset{\pi +{\theta }_c}{\int }}}\tau \cos \theta \mathrm{d}\theta \mathrm{d}y(19)$

$M_{\mathrm{S}}=R^2{\displaystyle \underset{-L/2}{\overset{L/2}{\int }}}{\displaystyle \underset{\pi -{\theta }_c}{\overset{\pi +{\theta }_c}{\int }}}\tau \mathrm{d}\theta \mathrm{d}y(20)$

Thus, the resultant forces acting on the cage from the interaction with the outer ring are detailed in Equations 21, 22.

$F_{\epsilon }={\lambda }_{\mathrm{r}}\left(F_{\mathrm{P}-\epsilon }+F_{\mathrm{S}-\epsilon }\right)+\left(1-{\lambda }_{\mathrm{r}}\right)F_{\mathrm{D}C}(21)$

$F_{\phi }={\lambda }_{\mathrm{r}}\left(F_{\mathrm{P}-\phi }+F_{\mathrm{S}-\phi }\right)+\left(1-{\lambda }_{\mathrm{r}}\right)F_{\mathrm{D}F}(22)$

Here, $F_{DC}$ and $F_{DF}$ represent the contact and friction forces under solid contact, respectively.

3.4 Analytical conditions

Table 3 lists the analytical conditions, which correspond to those under which negative whirl was observed in the experiments described in Section 2. Here, the angular velocities of ball rotation and orbit are set to values corresponding to an inner ring rotational speed of ${\omega }_z$ = 3,000 rpm. The initial conditions are set with the cage center at coordinates $x=0$, $y=0$ and the cage’s angular velocity at 142.5 rad/s. The analysis period is defined as 100 ms, within which the cage’s behavior is expected to stabilize. During this interval, the cage completes approximately 4.5 rotations.

Table 3

Table 3. Analytical conditions.

The simulation addresses the dynamic problem of the cage’s contact or non-contact with the rolling elements and the outer ring, which varies over time. This variability renders Equations 1–3 as stiff differential equations. To effectively manage these, the LSODA (Petzold, 1983) numerical integration algorithm was utilized. LSODA is an algorithm that automatically switches between the Adams method and the BDF method depending on the stiffness of the ODE, allowing for efficient and accurate solutions to ODEs. It is important to note that although the BDF method selects the optimal scheme to ensure the accuracy and stability of the solution, higher-order schemes are known to increase numerical errors. Therefore, we compared the analysis results obtained using LSODA with those obtained using the Radau method, which is considered less susceptible to errors under similar conditions, and confirmed their consistency. In this study, we adopted LSODA, which has a proven track record in similar bearing dynamic analyses (e.g., Boesiger et al., 1992).

4 Analytical results

4.1 Cage motion

Figure 8 illustrates the trajectory of the cage center and the temporal changes in cage whirl velocity. It also shows the maximum and minimum whirl velocities observed during negative whirl events, as detailed in the visualization tests described in Section 2. The trajectory of the cage center reveals orbital motion, with trends broadly matching the experimental results shown in Figure 3 (right). The orbital radius remains consistently within the guide clearance, suggesting that the cage stays in contact with the outer ring via the lubricant. It is important to note that this analysis assumes a rigid cage; thus, unlike the experimental results, the cage center does not exceed the guide clearance due to elastic deformation caused by centrifugal force. From 25 ms onward, the whirl velocity remains generally constant and negative, signifying a steady-state condition characterized by continuous negative whirl. A comparative analysis between experimental and analytical whirl velocities indicates a discrepancy ranging from approximately 1.2–2.3 times. In contrast, an analysis based solely on solid contact and Coulomb friction between the cage and the outer ring resulted in a whirl velocity approximately ten times higher than the experimental value, indicating significant enhancements achieved with the analytical model introduced in Section 3.

Figure 8

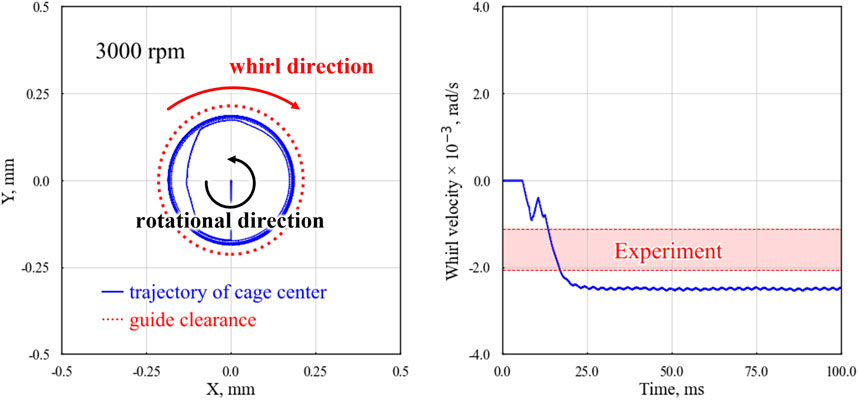
Figure 8. Trajectory of cage center (left column) and temporal change in cage whirl velocity (right column) in analysis.

The model expansion to include more degrees of freedom provides a nuanced representation of the forces driving the cage, encompassing contact, friction, and inertia. While the model discussed in Section 3 initially considered only the radial plane motion of a two-dimensional cage, extending this model to three dimensions allows for the resolution of the driving forces in the axial direction as well. This extension is expected to reduce the absolute value of the whirl velocity, which has been primarily determined within the radial plane, thereby aligning it more closely with the experimental findings.

4.2 Forces acting on the cage

Figure 9 shows the time variation of the tangential force $F_{\phi }$ acting on the cage center. Under the current analytical conditions, there was no solid contact between the cage and the outer ring; thus, only fluid forces were involved. The force $F_{\phi }$ is critical in inducing cage whirl, leading to positive whirl when positive and negative whirl when negative. Specifically, the oil film pressure force $F_{P-\phi }$ tends to induce positive whirl, whereas the shear force $F_{S-\phi }$ tends to induce negative whirl. The mechanism by which $F_{S-\phi }$ induces negative whirl is linked to the direction of the shear force, which opposes the sliding velocity of the cage. This sliding velocity, determined by the rotational and translational speeds of the cage, predominantly aligns with the cage’s rotation direction. $F_{S-\phi }$ acts in the opposite direction thereby inducing negative whirl.

Figure 9

Figure 9. Temporal changes in fluid forces on cage/race in tangential direction in analysis.

The positive whirl induced by $F_{P-\phi }$ can be elucidated by Figure 7, where the steady-state oil film pressure is influenced by the wedge effect. This effect generates positive pressure on the entry side and negative pressure on the exit side of the cage. Given the consideration of cavitation, the oil film pressure on the exit side is effectively zero. By integrating the oil film pressure along the arc from Q to P, the resultant force aligns with the direction of cage rotation, causing $F_{P-\phi }$ to induce positive whirl.

Figure 8 reveals that for $t>25$ ms, a consistent negative whirl velocity occurs, and the forces acting on the cage reach equilibrium. However, focusing on $t\le 25$ ms in Figure 9, $F_{S-\phi }$ (inducing negative whirl) rises earlier than $F_{P-\phi }$ (which counters negative whirl), indicating the initial cause of negative whirl.

In the steady state at $t>25$ ms, the average value of the resultant force, as shown in Figure 9, is marginally negative. This suggests the presence of a counteracting force that moderates an increase in negative whirl. Figure 10 shows the time variation of the tangential force resulting from the interactions between the outer ring and the cage and between the rolling elements and the cage. The interaction with the rolling elements generates a tangential force that induces positive whirl, effectively balancing the tangential force that induces negative whirl owing to the interaction with the outer ring for $t>25$ ms.

Figure 10

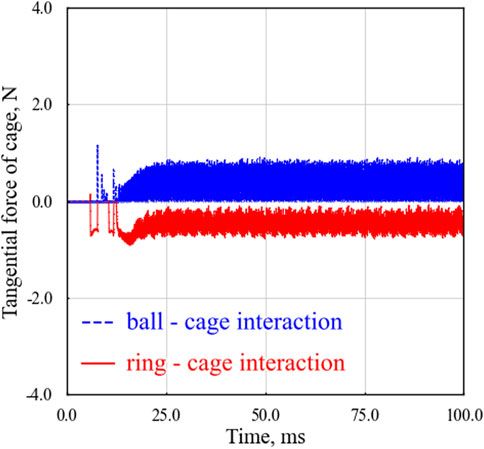
Figure 10. Temporal changes in tangential forces of cage by ball/cage interaction and ring/cage interaction in analysis.

4.3 Effect of rotational speed on cage instability

In the content up to Section 4.2, we constructed and validated an analytical model capable of reproducing the negative whirl observed in the 3,000 rpm experiment. In this section, to examine the applicability of this model to other rotational speeds, we evaluated the rotational speed dependency of cage whirl. The analytical conditions were based on those shown in Table 3, with only the angular velocity of ball rotation and orbit adjusted to match the inner ring rotational speed. In the experiment described in Section 2, the cooling effect was not expected due to the influence of grease lubrication, and it is considered that the guide surface experienced heating as the rotational speed increased, potentially leading to a decrease in the viscosity of the base oil on the guide surface. Here, two analytical conditions regarding the base oil temperature were set to identify the parameters needed to reproduce the cage behavior observed in the experiment. Specifically, one condition set a constant temperature regardless of rotational speed, and the other allowed the temperature to vary depending on the rotational speed. It should be noted that the base oil temperatures used in the analysis are reference values, as the guide surface temperatures were not measured in the experiments described in Section 2. The relationship between temperature and viscosity was considered using Walther’s equation (ASTM International, 1993).

The analytical results are shown in Figure 11. The left side of the figure shows the rotational speed dependency of the whirl velocity, with the experimental results also included. For each condition, the average values are plotted, and error bars indicating the upper and lower bounds are shown. Regarding the temperature settings in the analysis, the condition of constant temperature used 313 K, as in the content up to Section 4.2, while for the condition where temperature varies with rotational speed, the temperature was explored through trial and error to reproduce the cage behavior observed in the experiment. The right side of the figure shows the base oil temperatures determined for each rotational speed.

Figure 11

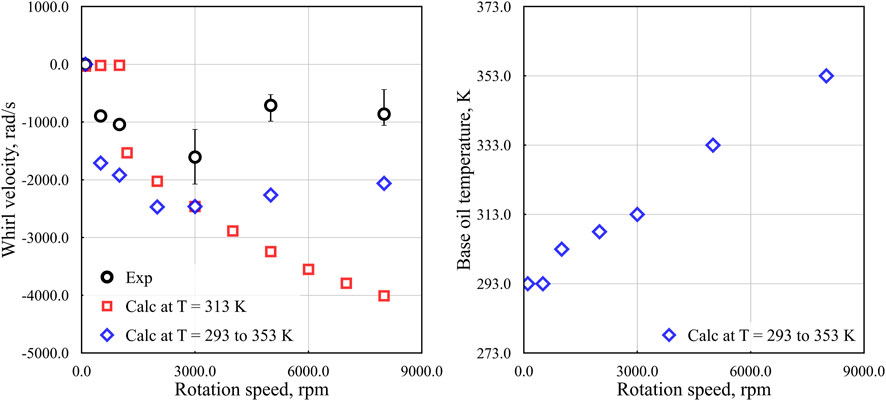
Figure 11. Effect of rotational speed on whirl velocity (left column) and base oil temperature used in analysis (right column).

The analysis with the base oil temperature fixed at 313 K showed that the cage exhibited stable behavior at rotational speeds below N < 1,100 rpm, while negative whirl occurred at N ≥ 1,100 rpm. The absolute value of the whirl velocity also tended to increase with increasing rotational speed. However, this result qualitatively differs from the experimental findings, suggesting that the analytical model requires further refinement.

On the other hand, the analysis with the base oil temperature adjusted for each rotational speed indicated that the cage behavior qualitatively matched the experimental results when the temperature increase was determined through trial-and-error adjustments. This observation suggests that the base oil temperature had a significant impact on the experimental outcomes described in Section 2, underscoring the necessity of considering this factor when assessing cage instability in grease-lubricated systems. Additionally, while shear thinning is often considered in the modeling of grease lubrication, it was concluded that this effect could be neglected in this analysis due to the oil film thickness being on the order of tens of micrometers. However, this conclusion may lack sufficient supporting evidence. Therefore, future research should focus on measuring the guide surface temperature, visualizing the lubrication state during testing, and measuring the torque exclusively on the guide surface. These approaches are expected to provide a deeper understanding of cage behavior.

5 Conclusion

This study aimed to elucidate the mechanism of cage noise generation in outer ring-guided cages of machine tool spindles. Through visualization tests and bearing dynamic analysis, it was revealed that negative whirl—where the cage whirls in the opposite direction of its rotation—is a significant contributor to cage noise. These visualization tests showed clear evidence of this phenomenon during noise-generation events.

To accurately simulate this behavior, friction models between the cage and the outer ring, identified as the primary cause of negative whirl, were examined and integrated into a bearing dynamic analysis model. This model successfully replicated cage behaviors that qualitatively matched experimental observations and was validated under various rotational speeds by accounting for the effects of base oil temperature. Furthermore, an examination of the time variation of forces acting on the cage clarified the specific mechanisms responsible for the generation of negative whirl. Understanding these mechanisms enhances the fundamental comprehension of cage design and its implications for noise reduction in machine tool spindles.

Additionally, advancements in analytical methods are expected to reduce prototyping costs and lower environmental impact. The ease of conducting parametric studies is a notable feature of this approach, which could also contribute to shortened development times. These advancements are anticipated to address fundamental issues and enhance the maintainability of the developed bearings.

However, this study focused solely on the in-plane motion of a rigid cage. In practical applications, the three-dimensional motion of the cage, including its deformation and tilt motion, plays a critical role. To achieve higher precision in future analyses, these factors should be incorporated, which can provide a more comprehensive understanding of cage dynamics. For example, as noted in previous research (Ashtekar and Sadeghi, 2012; Gao et al., 2022a; Gao et al., 2022b), treating the cage as an elastic body allows for the consideration of deformation due to centrifugal forces. This approach enables the representation of reduced contact pressure on the guide surface and a decrease in the effective eccentricity of the cage. By integrating this approach with the analytical method proposed in this paper, not only can the friction on the cage guide surface be calculated with greater precision, but this method may also prove to be a powerful tool for investigating the impact of cage material on cage instability.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

KT: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Writing–original draft. KM: Conceptualization, Data curation, Investigation, Methodology, Project administration, Software, Validation, Visualization, Writing–review and editing. KI: Supervision, Writing–review and editing. SO: Supervision, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors KT, KM, SO, and KI were employed by NSK Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aihara, S. (1987). A new running torque formula for tapered roller bearings under axial load. J. Tribol. 109 (7), 471–477. doi:10.1115/1.3261475

CrossRef Full Text | Google Scholar

Ashtekar, A., and Sadeghi, F. (2012). A new approach for including cage flexibility in dynamic bearing models by using combined explicit finite and discrete element methods. ASME J. Tribol. 134 (10), 041502. doi:10.1115/1.4007348

CrossRef Full Text | Google Scholar

ASTM International (1993). Standard practice for viscosity-temperature charts for liquid petroleum products, ASTM d341-93. West Conshohocken, PA: ASTM International.

Google Scholar

Barus, C. (1893). Isothermals, isopiestics and isometrics relative to viscosity. Am. J. Sci. 266 (2)–87. doi:10.2475/ajs.s3-45.266.87

CrossRef Full Text | Google Scholar

Boesiger, E. A., Donley, A. D., and Loewenthal, S. (1992). An analytical and experimental investigation of ball bearing retainer instabilities, ASME J. Tribology 114 (7)–531. doi:10.1115/1.2920915

CrossRef Full Text | Google Scholar

Cameron, A. (1971). Basic lubrication theory. London, United Kingdom: Longman.

Google Scholar

Chen, S., Chen, X., Zhang, T., Li, Q., and Gu, J. (2019). Cage motion analysis in coupling influences of ring guidance mode and rotation mode. Jpn. Soc. Mech. Eng. 13, JAMDSM0054. doi:10.1299/jamdsm.2019jamdsm0054

CrossRef Full Text | Google Scholar

Choe, B., Kwak, W., Jeon, D., and Lee, Y. (2019). Experimental study on dynamic behavior of ball bearing cage in cryogenic environments, Part II: effects of cage mass imbalance. Mech. Syst. Signal Process. 116, 25–39. doi:10.1016/j.ymssp.2018.06.034

CrossRef Full Text | Google Scholar

Gao, S., Chatterton, S., Pennacchi, P., Han, Q., and Chu, F. (2022a). Skidding and cage whirling of angular contact ball bearings: kinematic-Hertzian contact-thermal-elasto-hydrodynamic model with thermal expansion and experimental validation. Mech. Syst. Signal Process. 166, 108427. doi:10.1016/j.ymssp.2021.108427

CrossRef Full Text | Google Scholar

Gao, S., Han, Q., Zhou, N., Pennacchi, P., Chatterton, S., Qing, T., et al. (2022b). Experimental and theoretical approaches for determining cage motion dynamic characteristics of angular contact ball bearings considering whirling and overall skidding behaviors. Mech. Syst. Signal Process. 168, 108704. doi:10.1016/j.ymssp.2021.108704

CrossRef Full Text | Google Scholar

Ghaisas, N., Wassgren, C. R., and Sadeghi, F. (2004). Cage instabilities in cylindrical roller bearings, ASME J. Tribology 126 (10)–681. doi:10.1115/1.1792674

CrossRef Full Text | Google Scholar

Gupta, P. K., Dill, J. F., Artuso, J. W., and Forster, N. H. (1986). Ball bearing response to cage unbalance. ASLE Trans. 30 (1)–55. doi:10.1115/1.3261240

CrossRef Full Text | Google Scholar

Kannel, J. W., and Bupara, S. S. (1978). A simplified model of cage motion in angular contact bearings operating in the EHD lubrication regime. ASME J. Tribol. 100 (7), 395–403. doi:10.1115/1.3453196

CrossRef Full Text | Google Scholar

Kingsbury, E., and Walker, R. (1994). Motions of an unstable retainer in an instrument ball bearing, ASME J. Tribology 116 (4)–203. doi:10.1115/1.2927197

CrossRef Full Text | Google Scholar

Kingsbury, E. P. (1965). Torque variations in instrument ball bearings. ASLE Trans. 8, 435–441. doi:10.1080/05698196508972113

CrossRef Full Text | Google Scholar

Liao, H., Xie, P., Deng, S., Zhang, W., Shi, L., and Zhao, S. (2023). Investigation of dynamic characteristics experiments and stability evaluation criterion of space ball bearing cage. Tribol. Trans. 66 (3), 453–465. doi:10.1080/10402004.2022.2163015

CrossRef Full Text | Google Scholar

Meeks, C. R. (1985). The dynamics of ball separators in ball bearings - Part II: results of optimization study. ASLE Trans. 28 (3), 288–295. doi:10.1080/05698198508981623

CrossRef Full Text | Google Scholar

Meeks, C. R., and Ng, K. O. (1985). The dynamics of ball separators in ball bearings - Part I: analysis. ASLE Trans. 28 (3), 277–287. doi:10.1080/05698198508981622

CrossRef Full Text | Google Scholar

Niu, L. (2019). A simulation study on the effects of race surface waviness on cage dynamics in high-speed ball bearings. ASME J. Tribol. 141 (5), 051101. doi:10.1115/1.4042656

CrossRef Full Text | Google Scholar

Nogi, T., Maniwa, K., and Matsuoka, N. (2018). A dynamic analysis of cage instability in ball bearings. ASME J. Tribol. 140 (11), 011101. doi:10.1115/1.4036451

CrossRef Full Text | Google Scholar

Palladino, M., Neglia, S. G., and Wygachiewicz, M. (2017). Analysis and monitoring of cage dynamics in ball bearings for space applications. Procs ESMATS.

Google Scholar

Petzold, L. R. (1983). Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations. SIAM J. Sci. Stat. Comput. 4 (1), 136–148. doi:10.1137/0904010

CrossRef Full Text | Google Scholar

Russell, T. C. (2023) Investigation into the lubrication mechanism of the ball bearing cage. West Lafayette, Indiana: Purdue University ProQuest Dissertations and Theses. 30741226.

Google Scholar

Schwarz, S., Grillenberger, H., Tremmel, S., and Wartzack, S. (2021), Investigations on the rolling bearing cage dynamics with regard to different operating conditions and cage properties, IOP Conf. Ser. Mater. Sci. Eng. 1097, 012009. doi:10.1088/1757-899x/1097/1/012009

CrossRef Full Text | Google Scholar

Servais, C., Duquenne, M., and Bozet, J.-L. (2013). Influence of tribology of cage material on ball bearing cage instability. ESMATS 9.

Google Scholar

Stacke, L. E., and Fritzson, D. (2001). Dynamic behaviour of rolling bearings: simulations and experiments. Proc. Instn Mech. Engrs 215 (Part J), 499–508. doi:10.1243/1350650011543754

CrossRef Full Text | Google Scholar

Stacke, L. E., Fritzson, D., and Nordling, P. (1999). BEAST - a rolling bearing simulation tool. Proc. Instn Mech. Engrs 213 (Part K), 63–71. doi:10.1243/1464419991544063

CrossRef Full Text | Google Scholar

Stevens, K. T. (1980). Experimental observations on torque variation caused by ball bearing cage instabilities, 105. ESA SP-158.

Google Scholar

Walter, C. T. (1971). The dynamics of ball bearings. ASME J. Lubr. 93 (1), 1–10. doi:10.1115/1.3451516

CrossRef Full Text | Google Scholar

Weinzapfel, N., and Sadeghi, F. (2009). A discrete element approach for modeling cage flexibility in ball bearing dynamics simulations. ASME J. Tribol. 131 (4), 021102. doi:10.1115/1.3063817

CrossRef Full Text | Google Scholar