- 1Mechanical Engineering Department, School of Engineering, Institute of Technology, Nirma University, Ahmedabad, Gujarat, India
- 2Department of Mechanical Engineering, School of Engineering and Technology, JECRC University, Jaipur, Rajasthan, India
- 3Department of Electronics and Communication Engineering, School of Engineering and Technology, JECRC University, Jaipur, Rajasthan, India
- 4Department of Orthodontics, Faculty of Dental Sciences, SGT University, Gurugram, India
- 5Department of Mechanical and Industrial Engineering, Manipal Institute of Technology, Manipal Academy of Higher Education, Udupi, India
- 6Department of Mechatronics, Manipal Institute of Technology, Manipal Academy of Higher Education, Udupi, India
Robots are becoming integral to society and industries due to their enormous advantages. Among the various categories of mobile robots, including wheeled robot, tracked robot, and legged robots, the latter stands out as a better choice for most field applications due to their adaptability across various terrains. The purpose of this review is to study the locomotion capabilities of quadruped robots and judge their suitability for climbing applications as most unexplored applications of automation and robotics are required to climb. This review explores the locomotion capabilities of quadruped robots. It covers different aspects of quadruped robots like types of legs, leg design, gait patterns, and their mathematical formulations, and types of motions like omnidirectional motion and body sway motion. It also emphasizes its fault-tolerant gait, adaptability, and reliability. The paper also focuses on slope and stair climbing, outlining design requirements and applications. The study includes an examination of the applicability of various gaits under different conditions and the methods for increasing stability without compromising speed. Overall, the review serves as a valuable resource for future research in this field.
1 Introduction
Robots are becoming integral to society and industries due to their enormous advantages. Industrial robotic manipulators have already secured their position in many automobile and electronic industries and are growing in numbers every year. Mobile robots, which have pros in mobility and maneuverability, are also used in many applications like interplanetary missions and nuclear power plants (Takano, 1990; Driewer et al., 2005; Shiroma et al., 2005). Quadruped robots have a high load carrying capacity and better stability than biped or humanoid robots. Compared with multi-legged systems, they have broader leg space, less mechanism redundancy, and a lower level of complexity but also lower stability. Due to the emergence of AI and machine vision, the applicability of mobile robots is increasing significantly. Mobile robots can be classified into wheeled robots, tracked robots, and legged robots. Even after many technological advancements in wheeled and tracked vehicles, their mobility is limited to plain and less rough terrains. Even if we develop one robot capable of traveling in rough terrain, speed must be compromised heavily (Sintov et al., 2011; Pfotzer et al., 2017; Sun et al., 2017; Zhao et al., 2018). To resolve the problem, we can look into the solution in nature. All animals and humans can access much of Earth’s landmass with their legs. Although it is less stable, slower, and needs a complex blend of features, it has been the locomotion of almost all creatures due to its phenomenal advantages. A legged robot has a bionic structure, proven to be most efficient in theory, and due to this reason, researchers have started exploring this domain since the 1960s (Menon and Sitti, 2005; Zhang et al., 2014; Xu et al., 2019; Zhang et al., 2019).
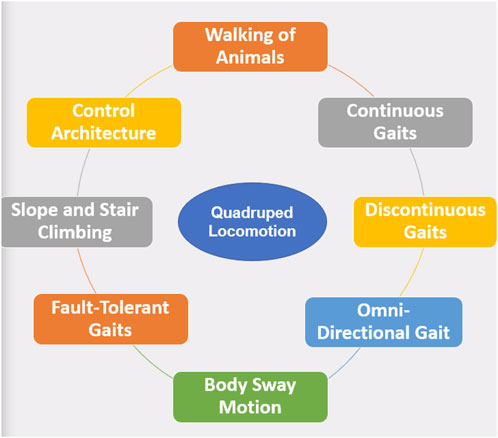
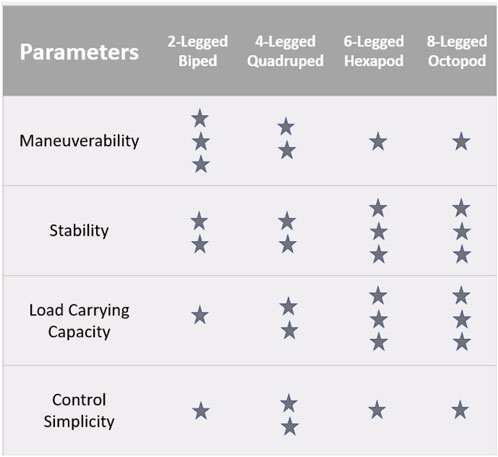
Even though many path-breaking experiments and simulations have been carried out, the technology has not reached the mark to be used extensively in prospective applications like defense, nuclear plants, and assistance for people with disabilities. The reason behind this lag is due to its complex system design. Although the legged robot can have two, six, or more legs, the four-leg system is a good trade-off between stability and complexity (Sun et al., 2017; Digumarti et al., 2014; Suzumori and Faudzi, 2018). One of the pioneer scientists who conducted research on legged robots, Shigeo Hirose, reported that the “Quadruped robot is the best form of legged robots from the aspects of stability, control difficulty, and manufacturing cost.” Quadrupeds are logically a better choice for most applications regarding stability and control. Decreasing legs results in instability issues, and increasing portions makes control critical (Pongas et al., 2007; Tsukagoshi et al., 2014; Chen et al., 2015; Li, 2017). Figure 1 shows the different locomotion patterns available for quadruped robots in research and development.
Quadruped locomotion is classified into categories of statically stable and dynamically stable. The former is suitable for rough terrain, where speed is to be compromised, but the actual purpose of a legged robot, i.e., maneuverability, can effectively be explored. The basic principle of the statically stable robot is that the vertical projection of the center of gravity of the robot on horizontal ground must always fall inside the support polygon formed by the supporting legs. Researchers have designed many kinds of such walks, i.e., wave, discontinuous, body sway, zigzag, crab, spinning, turning, and omnidirectional, sophisticatedly keeping this criterion. In dynamics walk, the robot is not stable at every instant. Still, in a run cycle, it is made stable dynamically by keeping the center of pressure, i.e., the resultant of all the forces inside the support polygon (Gor et al., 2013; Gülhan and Erbatur, 2018). When animals like tigers and leopards run, they follow this dynamic gait in which speed can highly be increased.
In this study, statically stable gait is considered, and its applicability under different conditions and the possibility of increasing stability without compromising speed are explored. Section 2 highlights the various legs and gait patterns for a quadruped robot. Section 3 discusses the mathematical formulation of different gaits for motion requirements. The design requirements for the climbing application are discussed in Section 4. Section 5 highlights the various applications of a quadruped climber robot. Discussion and recommendations are included in Section 6, and concluding remarks, along with the future directions, are presented in Section 7.
2 Design of legs and gait pattern for a quadruped robot
The varieties of leg designs that can be incorporated for quadruped robots are presented in Section 2.1. The gait pattern is the most crucial parameter for a mobile robot. Different gait patterns for a quadruped robot are discussed in Section 2.2.
2.1 Various quadruped legs
The leg design of a quadruped robot is a crucial factor that directly impacts its locomotion, stability, adaptability, and overall performance. There are several leg design options for quadruped robots, and the choice depends on the specific application and requirements, some of which are discussed as follows.
• Rigid legs: Rigid legs are the simplest leg design and consist of solid links connected by joints (usually rotary joints). They are sturdy and straightforward, making them suitable for applications with relatively flat terrain (Tedeschi and Carbone, 2014).
• Articulated legs: Articulated legs have multiple segments connected by joints, allowing more degrees of freedom. These legs provide enhanced flexibility and can navigate uneven terrains and obstacles effectively (Tsitsimpelis et al., 2019).
• Parallel mechanism legs: Parallel mechanism legs use multiple linkages connected in parallel, providing increased stability and load-carrying capacity. These legs are often used in heavy-duty applications or scenarios where stability is critical (Wang et al., 2013).
• Insect-like legs: Inspired by insect locomotion, insect-like legs have joints and segments that mimic the movements of real insects. They offer high agility and adaptability to complex terrains (Roennau et al., 2013).
• Multi-degrees of freedom (DOF) legs: Multi-DOF legs have more than three degrees of freedom, enabling sophisticated movements and better grasping capabilities. These legs are often used in research and advanced robotics applications (Hashimoto, 2017).
• Spring-loaded legs: Spring-loaded legs use mechanical springs to absorb shocks and vibrations during locomotion. They are suitable for rough terrains and can provide smoother movements (Mooney and Johnson, 2014).
• Hydraulic/pneumatic legs: Some hexapod robots use hydraulic or pneumatic actuators in their legs for enhanced power and load capacity. These legs are commonly found in heavy-duty industrial applications (Suzumori and Faudzi, 2018).
• Passive compliance leg: Passive compliance legs use flexible materials or mechanisms to allow a certain level of compliance during environmental interactions. This compliance helps prevent damage to the robot and enhances safety.
• Bio-inspired legs: Biomimetic or bio-inspired legs take inspiration from the anatomy and movement of animals, such as mammals or arthropods. These legs often improve performance in specific environments, such as climbing or swimming (Vidoni and Gasparetto, 2011).
• Wheeled–leg hybrid: Some hexapod robots feature legs with integrated wheels, providing both legged and wheeled locomotion options. This design allows the robot to switch between walking and rolling modes based on the terrain (Sun et al., 2017; Bai et al., 2018).
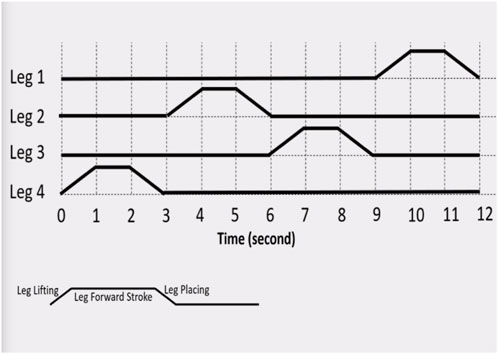
The selection of the leg design depends on factors such as the application, terrain, payload capacity, speed requirements, power source, and cost constraints. Each leg design has its advantages and limitations, and researchers and engineers often choose or design leg configurations that best suit the specific needs of the intended tasks of the hexapod robots. Figure 3 shows the continuous gait pattern.
2.2 Varieties of quadruped gaits
Quadruped robots, or quadrupeds, use different gaits for locomotion, each offering unique advantages and characteristics. A comparison of various quadruped gaits is presented as follows.
• Walking gait: In the walking gait, the quadruped moves, each leg coordinated, mimicking the walking pattern of animals like dogs and cats. This gait provides stability and is energy-efficient, making it suitable for slow and steady movements (Yang, 2008a).
• Trotting gait: The trotting gait involves diagonal pairs of legs moving together, while the other diagonal pair moves together alternately. For example, the front left and back right legs move together, while the front right and back left legs move together. Trotting allows for faster locomotion than walking while maintaining stability (Yang, 2008a).
• Pacing gait: The pacing gait is similar to the trotting gait, but the legs on the same side of the quadruped move together. For instance, both left legs move together, followed by both right legs. Pacing offers increased speed compared to trotting but may sacrifice some stability (Article, 2015).
• Bounding gait: In the bounding gait, the quadruped combines walking or trotting, followed by a period of suspension or flight, during which all four legs are off the ground. This gait provides high speed and agility, but it requires more energy (Article, 2015).
• Galloping gait: The gait is characterized by a sequence of one hind leg, followed by the other back leg and the front legs moving together. Galloping allows for high-speed locomotion but can be less stable than other gaits.
• Crawling gait: In the crawling gait, the quadruped moves with its body close to the ground, using its legs to crawl forward. This gait is suitable for navigating tight spaces and rough terrains (Suzumori and Faudzi, 2018).
• Climbing gait: Quadrupeds can employ specialized climbing gaits when moving on vertical or inclined surfaces. These gaits involve alternating movements of the legs to maintain stability during climbing (Zoppi and Molfino, 2006).
• Prancing gait: The prancing gait is high-stepping, where the quadruped raises its legs higher than usual during each step. This gait is often seen in certain breeds of dogs and can be used for playful or showy movement.
The choice of gait for a quadruped robot depends on its intended application and environment. For example, walking or trotting gaits are preferred for stability and energy efficiency in rough terrains, while bounding or galloping gaits are used for higher speeds in more open areas. Quadruped robots can often adapt their gaits to different situations, utilizing patterns based on the specific task or user input.
3 Various quadruped motions
A rigorous literature review was carried out on different aspects of quadruped locomotion. To start from the “Walking of Animals,” mathematical formulations of different walking patterns like continuous and discontinuous gait are studied. Then, the efforts to increase stability using different body sway motions are investigated, and omnidirectional walking using basic gaits is reviewed. Apart from these, when robots undergo kinematic failure, the coping strategies discovered by researchers, named fault-tolerance gaits, are studied in detail. Then, control architects designed for different quadruped robots are reviewed. Figure 2 shows the control capabilities of the different-legged robots.
The scientific study of the motion of a legged robot was initiated in 1957, when researchers started analyzing the movement of different animals. The first studies observed the walking patterns of quadruped animals highlighted by Muybridge and Hirose (Animals in Motion, 1957; Symmetrical Gaits of Horses). Using a slow-motion camera, they captured the walking of different quadrupeds like ox, goat, tiger, lion, cat, elephant, and dog. They identified various walking (gait) patterns like trot, walk, pace, rack, amble, gallop, and leap.
3.1 Continuous and discontinuous gait
This section includes the mathematical modeling of continuous and discontinuous gaits.
3.1.1 Mathematical formulations of continuous gaits
Based on identifications of “Animals in Motion,” 1957; “Symmetrical Gaits of Horses,” one of the pioneer researchers of the domain, McGhee, worked on mathematical formulations of quadruped gait planning (Mcghee and Fkask, 1968). His significant contribution was to give terminologies to various locomotion properties, i.e., stride, stroke, duty factor, phase, and stability margin. During these formulations, they studied the stability aspects extensively and gave the formulations of the static stability margin. In the stability computation for different gaits, they found that, out of the possible leg-swing sequences for a four-legged system, only six are suitable for statically stable gait. Out of those six, only one has a maximum stability margin. Furthermore, surprisingly, it is the same as that used by natural quadrupeds while walking at slow speed. This gait is denoted as the creep or wave gait. This unique optimal gait and its generation method are stated in the paper. In these studies, the motion is straightforward, and the terrain is assumed to be flat and obstacle-free.
Another pioneering researcher, Hirose, presented key aspects of gait control for rough terrain (Hirose, 1084). The theory of adaptive gait control that he proposed can accommodate the key irregularity of the terrain. He explained the theory with an analogy of an “Artificial Horse,” for which the controller provides general instructions on direction and pace, but the horse (machine) realizes the terrain irregularities and obstacles by its own algorithms. A quadruped walking vehicle is expected to attain the same level of intelligence.
Regarding this, all the work for quadruped locomotion was for generating a standard, straightforward gait. The procedure to generate a crab gait, i.e., walking at some predefined angle, was demonstrated by Lee and Shih (1986). From this stage onward, the need for a three-degrees-of-freedom leg becomes necessary because, in a two-degrees-of-freedom leg, the workspace of the foot tip will be only a line, which will not be sufficient for displacing the foot tip at some angle to move the robot at a crab angle. Majithiya and Dave (2021a) developed an algorithm to produce a circular gait to rotate the robot about an arbitrary point, i.e., turning center on the ground. This turning center can be placed at an infinite distance to produce a straightforward gait. In such a way, the same gait algorithm can produce any standard gait demonstrated until that time. This gait is considered a generalized standard gait for many future studies.
3.2.2 Mathematical formulations of discontinuous gaits
Until now, all the formulations and experiments are carried out based on the types of continuous gait, mainly wave gait, in which all the legs, as well as the body, are in motion at the same time, which means that the body will be in motion when one of the legs is lifted. This gait is reasonably appropriate to start the study as it was selected by nature for animals to walk at a slow speed. However, it was also observed that when animals walk in difficult terrain conditions, and when it becomes difficult to maintain stability, they use intermittent body motion instead of continuous motion. This observation led researchers to consider applying the same walking pattern to artificial walking machines. This kind of gait, named discontinuous gaits, became famous as it inherently enhances stability by allowing controlled stable adjustment during the maneuvering of complex terrains. This decreases the chance of destabilization over uneven terrain.
Majithiya and Dave (2021b) and Majithiya and Dave (2022) discussed a basic discontinuous gait and, for a straightforward crab, turning walk, and systematically compared them with continuous gait in terms of maximum achievable velocity and stability. Energy requirements and the control scheme are also discussed in brief. The significant difference in this discontinuous gait was that the body moves only when all four legs are in the support phase. One of the main advantages of using this kind of gait is that it is much easier to implement. In terms of performance, it produces a better longitudinal stability margin than wave gait and can walk at a higher velocity in medium and large duty factors. The wave gait was initially designed for flat terrain, but practically, each terrain has some level of irregularity, which makes the wave gait less effective. However, this discontinuous gait can handle slight irregularities easily. Furthermore, in continuous gait, all the legs, i.e., all the actuators, are in motion every instant, whereas in discontinuous gait, only a few actuators work at a time.
It is a fundamental understanding that the lesser the number of instantaneous powered actuators, the lesser is the power consumption. In this regard, in discontinuous gait, the body moves during a very small cycle duration, when all the actuators will be required to provide power. Hence, at all other times, only one leg moves at a time. Due to this, instantaneous powered actuators are much less than continuous gait. Furthermore, the higher the power requirement, the more the weight of the power source, which directly affects the efficiency of any mobile robot. In addition, if we can apply a break to the non-moving actuators, power consumption can be further reduced. Figures 4A, B show the discontinuous gait pattern in the time frame for normal surfaces and uneven terrain.
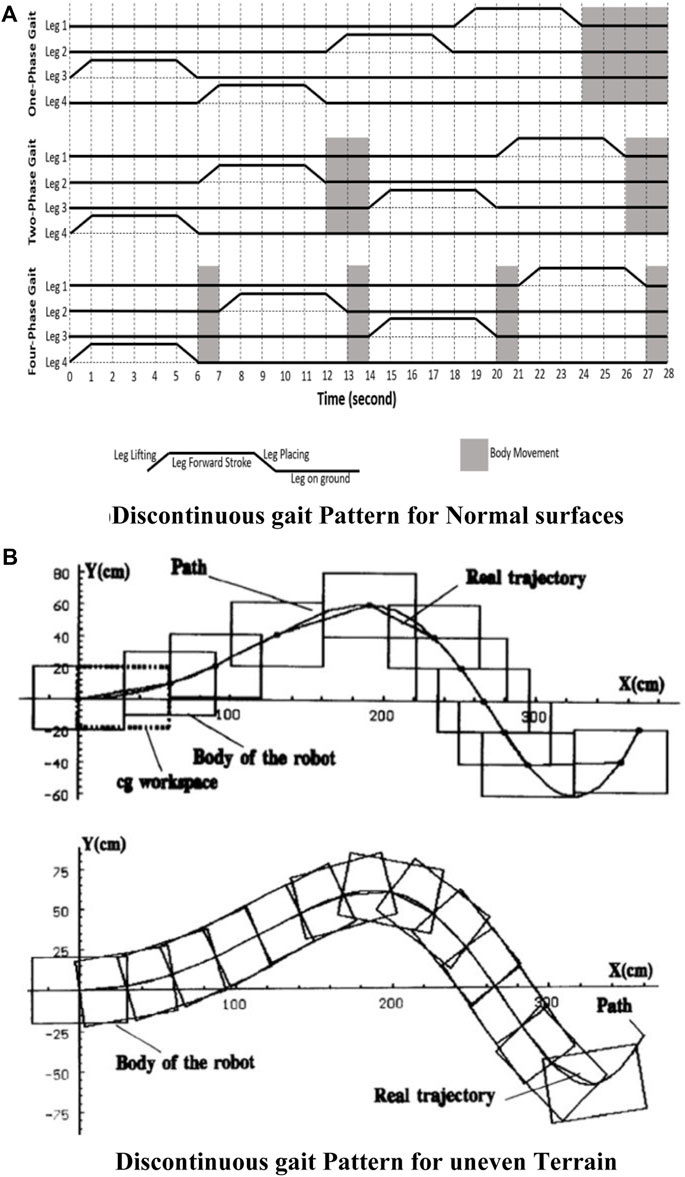
Figure 4. Discontinuous gait (De Santos and Jimenez, 1995). (A) Discontinuous gait pattern for Normal Surfaces (B) Discontinuous gait pattern for uneven terrain.
There are two options to follow in the predefined path for implementing discontinuous gait and its different variations like crab, spinning, and turning for path planning. In the first option, the body orientation remains the same and keeps following the path by keeping the longitudinal axis of the robot constant. This means the body does not spin about its axis. In the second way, the body keeps rotating about its axis and always keeps its longitudinal axis tangent to the defined path. De Santos and Jimenez (1995) studied a path following an arbitrary trajectory with discontinuous gait and proposed its solutions. It has also been implemented on the RIMHO robot. The results of the experiments showed that discontinuous gaits are efficient in terms of energy consumption. The control architect was designed in such a way that the leg, during its transfer phase, stops only when it touches the ground, which makes the walking adaptive to minor irregularities of the terrain.
In the above-stated discontinuous gaits, two-phase and four-phase gaits are shown, in which the body moves two and four times, respectively, in one locomotion cycle. Banos et al. (1992) attempted to simplify the gait planning of quadruped robots. A novel gait with only one center-of-gravity movement (COCM) in a cycle is proposed, and its reliability and stability were verified in the THU-WL robot. The initial foothold pattern, leg swing sequence, foothold lift, and placement positions are derived considering the omnidirectional stability margin. This gait reduces complexity and is easier to apply than all previously proposed gaits. However, the stride is to be compromised. In simulations and experiments with the THU-WL robot, this gait plan proved reliable and stable and is considered a remarkable simplification of the creeping gait. Furthermore, a systematic analysis was conducted on the geometrical model, and few conclusions were deduced based on that. One important inference was that, for improving stability, the length-to-width ratio of a quadruped robot should be near one, and the reachable area of the leg should be as close as possible to the center of gravity of the robot body.
3.2 Omni-directional gait control
Using the above standard gaits, a gait scheme for omni-directional travel is proposed, which uses successive gait transitions and standing posture transformation to plan the walk in any direction in the least possible steps and time (Liu et al., 2013; Hu et al., 2015; Zhang et al., 2004). Figure 5 shows an omnidirectional gait pattern.
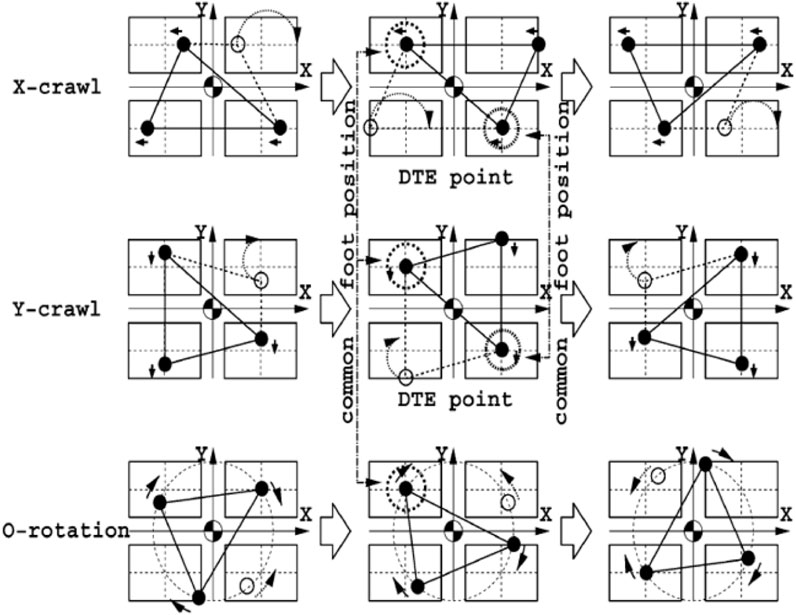
Figure 5. Omni-directional gait (Zhang et al., 2004).
3.3 Body sway motion
All the continuous and discontinuous gaits discussed so far have unidirectional body motion, i.e., the body will travel in a straight line, inclined line, or spin around an arbitrary point. Calculation of the stability and maximum possible stride (distance traveled in a cycle) are discussed in previous studies. However, the search for a more stable gait led researchers to discover some novel gaits that may not be biologically inspired and found in nature but might be more suitable for the robots. The basic idea was to keep the COG of the robot at the most stable position in the support triangle. It needed to move the robot in a lateral direction, known as COG adjustment or body sway motion, which increases the stability. It also proposes solutions for the straightforward gait and solutions for the turning gait. This method of gait planning is validated by an experiment with a TITAN VII robot while walking on a 15-degree slope. Figure 6 highlights the body sway motion pattern.
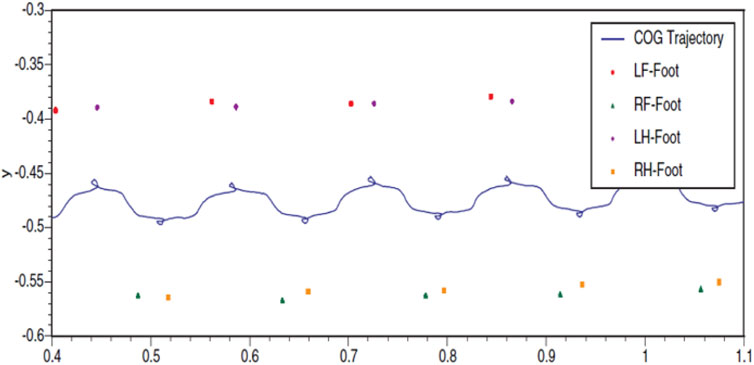
Figure 6. Body sway motion (Zhang et al., 2005).
A crocodile inspires the performance of the quadruped robot on a static walk gait pattern. Novel algorithms are proposed by Messuri and Klein (2015), who first demonstrated the benefits of body sway motion, i.e., body movement in the lateral direction. The gait planning shown in this paper is based on a regular wave gait. It can be used on a slope and flat terrain to considerably increase stability with the same configuration without losing speed. One of the methods is Y-sway motion, in which the y-component of COG is always taken to the y-component of the center of the support polygon without worrying about the stability margin.
In contrast, in E-sway motion, considering the energy stability margin, the y-component of COG is brought to the point where energy stability is equal. The former is easier to implement and generates a better stable walk than regular wave gaits, and the latter provides extra stability. Both the planning methods are simple enough to be implemented in a robot in real time and are validated through simulations for their effectiveness on even and slope terrain.
The advantages of quadruped robots increase with the roughness of the terrain. It becomes important to generate a smooth walking pattern even in a rocky environment with continuous velocity and acceleration profiles. Pongas et al. (2007) demonstrated a flexible walking pattern generation, which moves the body like the number 8 by implementing sinusoidal sway in lateral and longitudinal directions using fifth-order spline curves. The algorithm is tested in the LittleDog robot and is proven to have enough balance, as well as smooth movement.
To compensate for the decrease in the stability of periodic gait, researchers worked on different gaits (intermittent crawl gait [Tsukagoshi et al., 2014], E-sway [Gülhan and Erbatur, 2018], and zigzag gait [Tsitsimpelis et al., 2019]). Even after applying these gaits, a similar level of motion was not attained as that of the animals. Furthermore, one of the main reasons for this was the use of the waist joint in animals to revolve their front and rear parts concerning each other as per the requirement. Cherig et al. (1999) added a passive one-degree-of-freedom joint in the box, and the COG and waist joint relationship is studied. Furthermore, the proposed discontinuous zigzag gait was implemented in a simulation environment and on an ELIRO-II robot, and its superiority against a single-body robot, in terms of extra stride and higher stability, is demonstrated on a flat surface. Figure 7 shows the discontinuous zigzag gait.
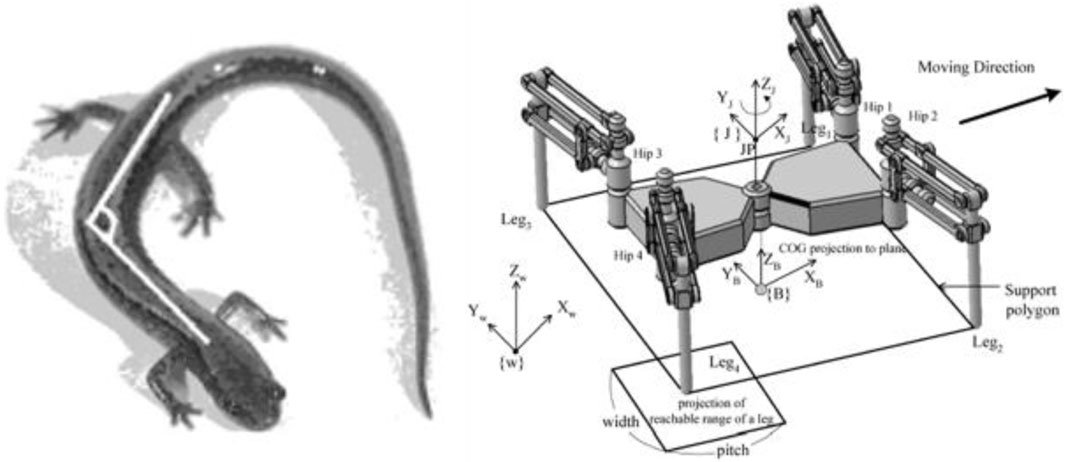
Figure 7. Discontinuous zigzag gait (Taylor et al., 2012).
Taylor et al. (2012) generated a COG trajectory based on the ZMP stability criterion, represented as a series of quintic spline segments, and COG trajectory generation was formulated as an optimization problem to minimize the squared acceleration along the trajectory, subject to continuity and ZMP stability constraints.
Systematic gait planning is one of the most important facets of controlling a quadruped robot on various terrains and under different conditions. Several COG adjustment techniques have been implemented previously. The method shown is involves planning in which continuous velocity and acceleration profiles are guaranteed on a rough terrain. Kalakrishnan et al. (2010), using this planning method, divided the COG movement into two parts. During leg swing, the COG follows a straight line to avoid extra acceleration and jerks. During the supporting phase, which is named the “COG adjustment stage,” COG follows a quantic curve for maintaining a continuous acceleration at the starting and ending points of the adjustment stage. In this real-time planning method, constant velocity and acceleration profiles are observed in the simulation results, and the stability margin is more than or equal to the minimum predefined value.
Different researchers proposed various adjustment strategies, but in all of them, either the stability margin is reduced or the body retrieval, i.e., movement of the body in the opposite to forward direction, takes place, which ultimately reduces the forward speed and increases the energy consumption that leads to a decrease in the efficiency of the robot. Zhang et al. (2015) proposed a discontinuous crawl gait, which is good for irregular terrain with grass or asphalts. In this method, the duty factor is more than 0.75, and the body only moves when all four legs are on the ground, similar to the traits of ordinary discontinuous gait. The only difference is that the direction of movement of the body and the stability criterion will be different as per the next swing leg. Before the front legs swing, the body moves sideways and reaches the point per the modified longitudinal stability margin criterion. On account of this, when the next supporting swing leg is on the hind side, the body moves forward following the static stability margin criterion. This planning method is sophisticatedly designed to avoid the retrieval of COG and maintain maximum stability.
Li (2017) proposed an optimized discontinuous crawl gait, in which the movement of the COG is divided into two types. When making a lateral motion, the COG searches for a minimal distance in the lateral direction, which can ensure a stability margin, and while in forward motion, it searches for the maximum moving distance in the forward direction. This improves the forward velocity by reducing unnecessary lateral movement. The proposed method is validated in the simulation environment of websites, and it has proven to be faster than the previous method while maintaining a predefined stability margin value.
3.4 Fault-tolerant gaits
Tolerating the fault is one of the prime aspects of control of the legged system, especially while working in a hazardous environment like volcanic explorations and prospective interplanetary missions, where repairing or replacing a failed component is impractical. Two types of kinematic failures are possible in a leg. In the first type, the joint cannot tolerate any load, and the leg loses its support capacity. In the second type, one of the joints of a leg is locked and fails to change its angular position further. Initial works on fault-tolerant gaits are started for the hexapod robot and then further implemented on quadrupeds.
Xin et al. (2016) proposed a standard straightforward and crab gait having fault-tolerant capability for regular terrain, and based on that, Yang and Kim (1998) proposed a gait scheme that makes the hexapod capable of walking on a two-dimensional irregular terrain with forbidden areas where foot placement is not possible. The fault considered in these studies is the one in which legs are prevented from being maintained by the supporting state, either due to a failure of the kinematic part of a leg or a communication failure. The proposed gait is for an uneven terrain but was also applied on even terrain and proven to be more efficient in terms of double stride length and fewer body adjustment steps. For uneven terrain, the proposed gait is based on a discontinuous follow-the-leader (FLT) gait, in which the hind legs place the feet at the same points where the front feet are kept, reducing the efforts to find possible foot placement areas within the forbidden region. Computer simulations are carried out to validate the effectiveness of the proposed method on the even and uneven terrain. Hjalmarsson and Juditsky (2000) compared the rectangular model and hexagonal model of the hexapod robot for fault tolerance on even terrain and the mathematical relation between these two models. Studies show that the hexagonal model has better turning ability, higher stability margin, and greater stride length under certain conditions.
All the above studies are for type 1 failure of the quadruped robot. For type 2, i.e., locked joint failure of the quadruped, extensive study has been done, and mathematical solutions for different gaits have been proposed by Chu and Pang (2002), Yang (2005), Yang (2006a), Yang et al. (2006), and Yang (2009).
In the quadruped robot, gait planning with type 1 failure is practically impossible if one leg loses its capacity to be used as a supporting leg. Only two legs will be in support when the third leg is in the transfer phase, which makes the system kinematically unstable. So, all the studies on fault-tolerant gait planning are for the type 2 failure, i.e., locked joint failure.
Yang (2008b) reported that even though three degrees of freedom are required in each leg for omnidirectional movement, a stable walk can also be achieved if one of the degrees of freedom is reduced from the system. Based on this fact, a fault-tolerant gait for the legged robot is proposed, first on the quadruped robot, which can easily be applied further to a robot having more than four legs. The workspace of the leg, a joint that is at fault, is reduced, which becomes a critical aspect in designing a walking algorithm with the reduced movement of that leg. This study became a starting point for this kind of control planning of quadruped robots. It uses discontinuous gait for better stability. In this systematic study, first, the type of failure and behavior of the robot with the locked joint of joints 1, 2, and 3 are explained, and then, the gait algorithm is proposed. This basic work assumes that the robot moves in a straight line and on even terrain. In the end, the scheme is applied to a traditional wave gait to verify the effectiveness of the proposed algorithm. It is proven applicable and capable of maneuvering the robot under such conditions.
Based on the planning scheme proposed in previous research, crab gait planning is presented by Yang (2002) for a robot having one locked joint failure. As the workspace of the leg is constrained, once one of the joints is locked, the planning procedure becomes critical in maintaining static stability and maximizing the possible stride. In this paper, first, the locked angle range is derived to achieve the foothold position to follow the specific foot trajectory. If the locked angle is out of range, the body height can be changed to get it inside the range. Then, a strategy of gait planning is proposed, in which the motion will be of a discontinuous type, and the failed leg will be in the supporting phase, while the remaining three legs are in the transfer phase one after another. Then, the failed leg is lifted, and the body propels, while the other three legs are in the supporting phase. As a case, a periodic wave gait is taken, and the fault-tolerance gait is implemented between wave gaits. Furthermore, an adjustment procedure for changing the leg configuration from wave gait to the proposed fault-tolerant gait is explained. The initial and final positions and stride lengths of the legs are calculated analytically. The proposed leg is stable and has the maximum stride in a cycle.
The author’s previous work proposed fault-tolerant quadruped gaits, straightforward (Yang, 2006a) and crab walking (Yang et al., 2006). In both solutions, dead-lock conditions are defined, for which the direct solutions of gait planning are unavailable and post-failure walking could not be realized. Yang (2012) proposed an amended fault-tolerant gait scheme to avoid the dead-lock kinematic constraint. In this method, the walking pattern can be generated under any condition without any constraints. The motion trajectory of the failed leg changes so that the available foot points can be obtained on the trajectory of the robot motion. Furthermore, to gain a non-zero stability margin, the trajectory of the opposite leg is changed as well. Here, the body trajectory is the same, and there is no compromise in walking speed than the previously proposed fault-tolerant gait planning.
Yang (2008a) stated that, in the gaits mentioned above, the performance of the gait was not up to the mark in terms of speed, terrain adaptability, and stability as those are based on one-phase discontinuous gait, i.e., the body moves only once during the cycle. Furthermore, the above studies are not appropriate for irregular terrain, which is one of the main focuses for the legged robot and in which the probability of failure is more. In this study, the two-phase discontinuous gait is used as a fault-tolerant gait, and its better performance is shown using simulation. For walking on irregular terrain, one of the cases of ditch crossing and avoidance is taken, and an algorithm is developed for it using the gait proposed in this paper and previous papers of the author. The effectiveness of both ditch crossing and avoidance is validated using a simulation study. The study of fault-tolerant gait was upgraded from the flat terrain to constant slope terrain (Yang, 2006b).
In fault-tolerant gait planning proposed in the literature so far, the geometry of the robot is used to maintain static stability by always keeping the projection of COG inside the support polygon, but as the irregularity of the terrain increases, the need for a higher stability margin increases, which is constrained to the speed of the vehicle. If we increase the margin, the leg stride decreases, ultimately reducing the vehicle speed. In all the above studies, the COG of the robot is assumed at the geometric center of its body. Yang (2005) and Pana et al. (2008) proposed a novel idea, in which a moving appendage was placed on the robot body, which changes the position of COG as per the requirement, and solutions of the gait scheme for straight and crab walking are discussed. The proposed robot model has proven to deliver a more stable walk without compromising the vehicle speed. Figure 8 shows the fault-tolerant gait.
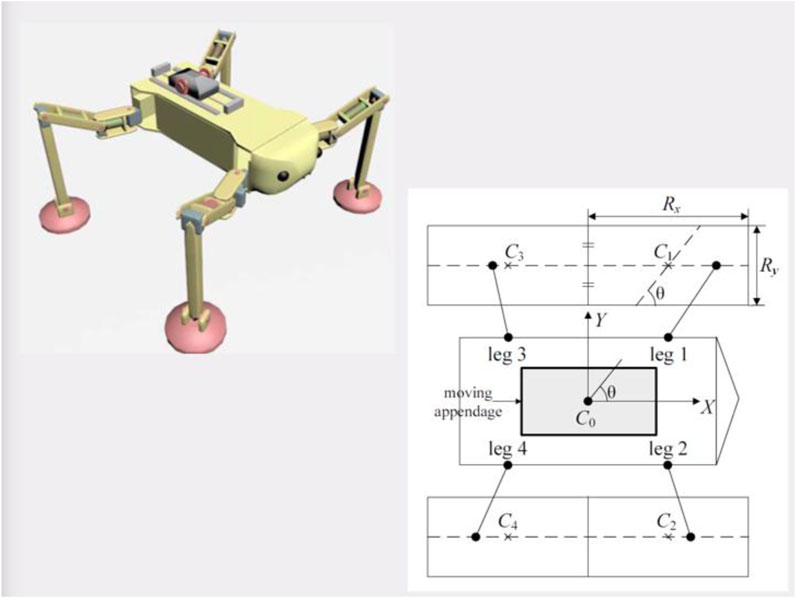
Figure 8. Fault-tolerance gait (Krishnan et al., 2011).
Apart from articulated legs, fault-tolerant gait for hydraulic legs was proposed by Yang and Kwak (2013) and Chen et al. (2015). In the discussed motion planning, failure up to two joints in two different legs is tolerated as well.
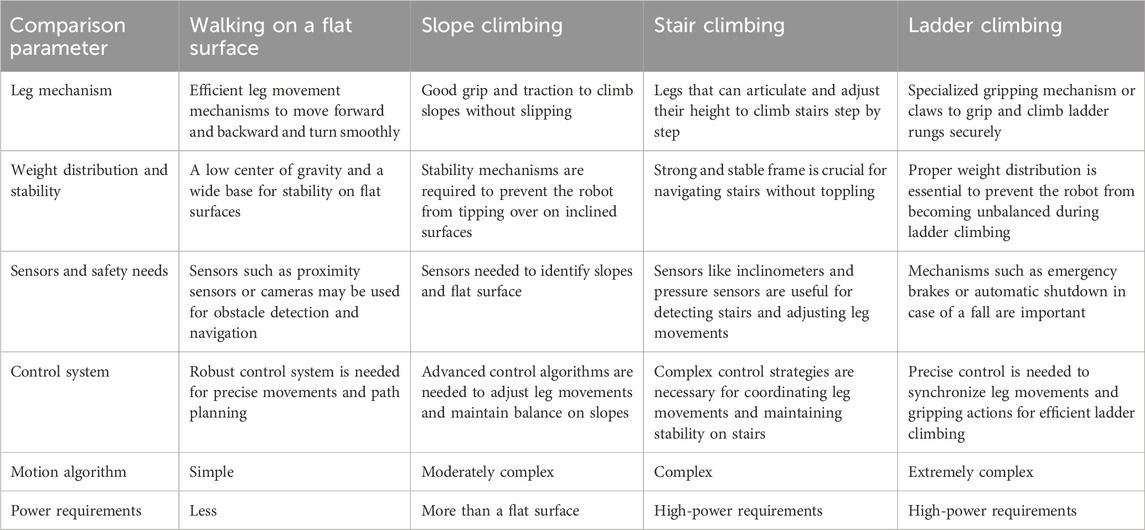
3.5 Slope and stair and ladder climbing
The stability margin criteria, like static stability margin and longitudinal stability margin based on geometry, are applicable for flat terrain only, whereas for sloped locomotion, the criteria of the COG being nearest to the center of the support polygon are not the most stable position. For that, Zhang et al. (2005) proposed the energy stability margin, which provides the most stable position for the given configuration. Based on that, Chen et al. (2014) proposed a normalized stability margin, which provides the tool to find the most desirable posture even in rough inclined terrain. Majithia et al. proposed a stable static gait for climbing slope (Majithiya and Dave, 2021a). It is very important to climb up on the slope with payload and without tilting the torso of the robot. Figure 9 shows the slope climbing solution.
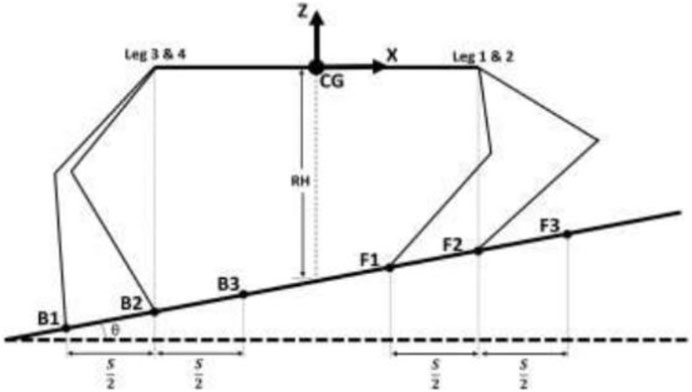
Figure 9. Stable slope-climbing gait (Majithiya and Dave, 2021a).
Considering this idea while following the static or longitudinal stability margin criterion in locomotion on a slope, there will be an imbalance in the energy on both sides of the robot as these criteria only consider the vertical projection of COG on the horizontal ground. Furthermore, as the slope angle increases, the effectiveness of these criteria decreases. Hence, based on the energy stability margin (Liu et al., 2013), a new intermittent crawl gait is proposed by Tsukagoshi et al. (2014) because energy balance on both sides can be maintained equally. Hirose and Yoneda (2001) proposed adaptive gait for slope maneuvering, in which the slope angle need not be known, and it is automatically calculated based on the contact force sensed from the force sensor attached to the feet. The effect of slope on the COG position is incorporated by the term SCOG, i.e., substantial center of gravity. Some studies (Zhang et al., 2004; Hu et al., 2015) proposed omnidirectional walking on a slope using successive gait transitions.
One of the novel ideas for sloped locomotion was proposed by Konno et al. (2003), who added a vertical waist joint to the robot body. There are two fundamental ways of sloped maneuvering, i.e., either keeping the body parallel to the slope or keeping it horizontal. The former has a higher stride and lower stability, whereas the latter has a softer stride and higher stability. To achieve an advantage in both the parameters, i.e., stride and stability, this waist joint is added, which keeps the front portion parallel to the slope and the hind portion horizontal. Using computer simulations, slope traversing up to 20° was demonstrated. Figure 10 shows the quadruped locomotion for climbing a slope.
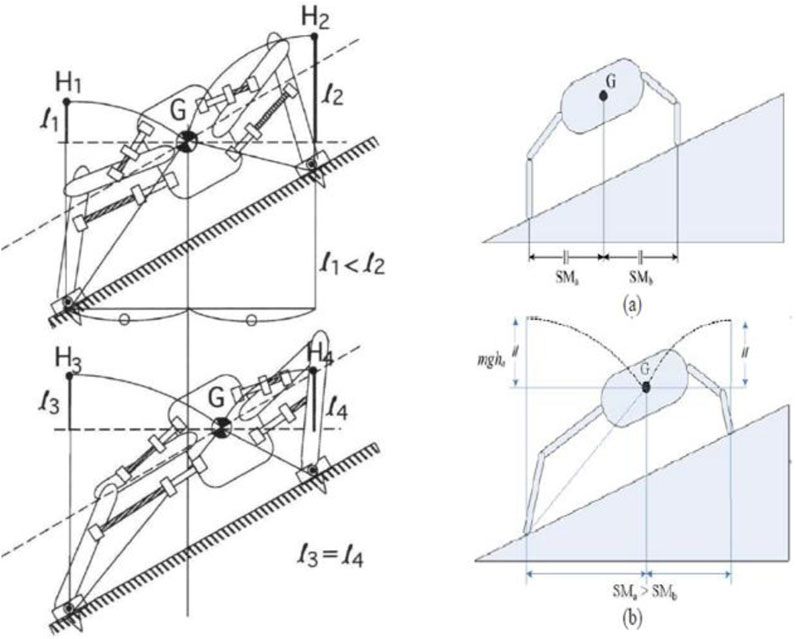
Figure 10. Locomotion for slope climbing by a quadruped (Konno et al., 2003)
Park and Lee (2022) proposed a concept of a walking chair, in which, based on a quadruped platform, straight-line, turning, and stair-climbing gait schemes are proposed, with the constraint of always keeping the body horizontal, due to its application. In one of two stair-climbing methods, the robot advances one stair in a cycle and, in the second, two stairs in a cycle. The work was extended for different geometries by Wang et al. (2013) and Yang (2006a) Figures 11, 12 show the stair-climbing quadruped robot.
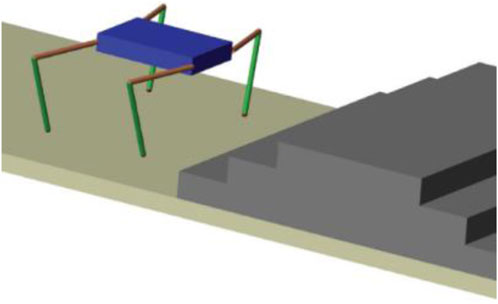
Figure 11. Stair-climbing quadruped gait (Majithiya and Dave, 2022)
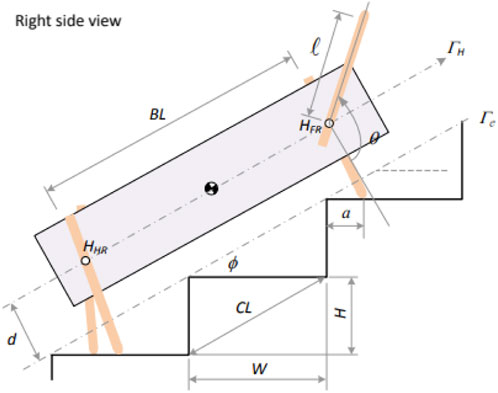
Figure 12. Stair-climbing quadruped (Zhang and Song, 1989).
Using the above standard gaits, systematic control schemes are designed for quadruped robots, especially rough terrain, with hierarchical structures (Kolter et al., 2008; Chen et al., 2012).
Climbing vertical towers, masts, pipes, and poles is again a difficult task. The ladders attached to the poles are perfectly vertical. Robots climbing ladders are subject to stability issues. These climbing solutions are highly desired as many industrial applications require ladder-climbing robots (Goel et al., 2015; Shah et al., 2022a). Ladder-climbing robots for inspections of telecom towers are highlighted in Figure 13.
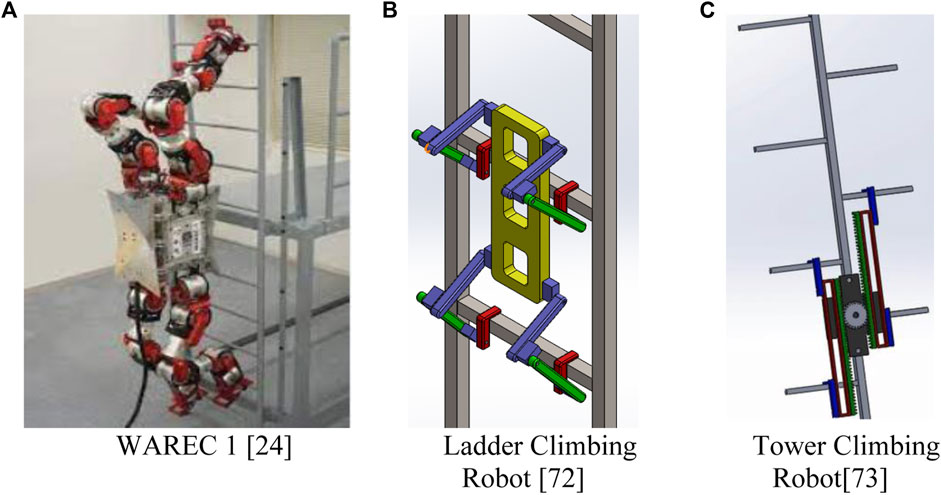
Figure 13. Ladder-climbing robot for vertical tower applications. (A) WAREC-1 (Hashimoto, 2017). (B) Ladder-climbing robot (Goel et al., 2015). (C) Tower-climbing robot (Shah et al., 2022a).
4 Design requirements for climbing
Quadruped robots designed for climbing applications are highly specialized and equipped to navigate vertical or inclined surfaces. Many industrial applications require stable climbing on walls and vertical ladders. Applications where climbing robots are important are highlighted by Shah et al. (2021), Shah et al. (2022b), and Shah and Dave (2023). These robots often feature advanced locomotion and gripping mechanisms to ensure stability and traction during climbing. Design and controlling algorithms mostly depend on the applications, sources of power available, and environment and safety considerations. Signature verification, organic farming, and line follower robot control strategy are the emerging areas for robotics applications. For climbing on uneven surfaces, an intelligent controlling algorithm is needed (Ramya et al., 2021; Darshita Shah et al., 2022; Mahalakshmi et al., 2022; Shaik et al., 2022). Some key features and considerations for quadruped robots used in climbing applications are as follows:
• Climbing mechanism: Climbing quadruped robots have specialized gripping mechanisms allowing them to adhere to various surfaces securely. These mechanisms can include retractable claws, adhesive pads, or suction cups to ensure a reliable grip on different climbing surfaces (Jerril Gilda and Jose Anand, 2023).
• Leg design: The leg design is crucial for climbing robots. Legs with multiple degrees of freedom and flexible joints allow the robot to adapt to irregular surfaces and negotiate obstacles during climbing (Toussaint et al., 2009).
• Limb actuation: Quadruped climbing robots often utilize powerful and precise actuators for limb movement. High-torque motors with position and force control capabilities are commonly used to provide the necessary force for climbing and maintain stability (Batayneh et al., 2010).
• Sensor suite: Climbing robots require a range of sensors for feedback and navigation. These may include cameras, depth sensors, and contact sensors on the feet to detect surface irregularities and ensure proper grip (Silva et al., 2008).
• Stability control: Climbing robots must maintain stability during vertical ascents. Advanced control algorithms are used to adjust the posture and limb movements to ensure a balanced and stable climbing motion (Widanagamage et al., 2014).
• Adaptive gait control: Climbing quadrupeds may use specialized climbing gaits that adapt to the terrain and surface conditions. These gaits allow the robot to adjust its leg movements for optimal climbing performance (Zoppi and Molfino, 2006).
• Power and energy efficiency: Climbing robots must be designed for energy efficiency as climbing often requires more power than walking on a leveled ground. Efficient actuators and lightweight materials are used to maximize battery life and climbing duration.
• Safety mechanisms: Safety is critical for climbing robots, especially when operating at heights or on unstable surfaces. Emergency stop features, fail-safe mechanisms, and collision detection systems are integrated to prevent accidents and protect the robot.
• Remote operation and autonomy: Climbing robots may be remotely operated for certain tasks, especially in hazardous environments. However, they can also have varying degrees of autonomy for autonomous exploration and navigation.
• Application-specific modifications: Depending on the specific climbing application, quadruped robots may be customized with additional tools or sensors. For example, robots used for inspection tasks may have cameras or sensors for data collection.
Climbing quadruped robots have applications in a wide range of industries, including inspection and maintenance of infrastructure, search and rescue missions in disaster-stricken areas, exploration of rugged terrains, and even space exploration on planetary bodies. Their ability to navigate challenging environments makes them valuable assets in various climbing-related tasks.
5 Applications of a quadruped climbing robot
Quadruped climbing robots are versatile machines capable of performing various tasks in challenging environments. Some of the functions that can be accomplished with quadruped climbing robots include the following:
• Inspection and maintenance: Climbing robots can be used for inspecting and maintaining infrastructure such as bridges (Tsukagoshi et al., 2014), dams, buildings (Majithiya and Dave, 2022), and towers (Zhang and Song, 1989). They can access difficult-to-reach areas and perform visual inspections, structural assessments, and repairs (Schmidt and Berns, 2013; Wang and Kawamura, 2015; Hinderer et al., 2017; Gecko Robotics, 2020).
• Search and rescue: Quadruped climbing robots are valuable for search and rescue missions, especially in disaster-stricken areas. They can navigate through debris and rubble, searching for survivors or assessing the structural integrity of collapsed buildings (Richardson et al., 2013; Saputra et al., 2019; Ito et al., 2020; Melenbrink et al., 2020). These robots are specially equipped with sensors to search for people stuck in a disaster-struck environment.
• Exploration and surveying: Climbing robots can be deployed in exploration missions to collect data in rugged terrains, caves, or areas with challenging access. They can survey geological formations, collect samples, and provide valuable information for scientific research (Majithiya and Dave, 2022; Liu et al., 2020; Sakuhara et al., 2020).
• Environmental monitoring: Quadruped climbing robots equipped with sensors can be used for environmental monitoring in remote or hazardous locations. They can collect data on air quality, temperature, humidity, and wildlife, aiding in environmental research and conservation efforts (Wang and Kawamura, 2015; Cai et al., 2019; Sharma and Doriya, 2021).
• Industrial inspections: Climbing robots are utilized in industrial settings to inspect equipment, pipelines, and tall structures. They can assess the condition of industrial assets and identify potential maintenance issues (Driewer et al., 2005; Lee and Shih, 1986; Sakuhara et al., 2020; Dürr et al., 2019; Gerdes et al., 2020).
• Surveillance and security: Quadruped climbing robots can be used for surveillance and security purposes in both indoor and outdoor environments. They can patrol areas, monitor activity, and provide real-time video feeds to operators (Karimov et al., 2019).
• Agriculture: Climbing robots are used for crop monitoring, pesticide application, and harvesting. They can navigate through fields and provide data on crop health and yield (Zoppi and Molfino, 2006; Schmidt and Berns, 2013; Osswald and Iida, 2013).
• Entertainment and performances: Climbing robots are sometimes used in the entertainment industry for robotic performances, art installations, and interactive displays.
• Research and development: Climbing robots serve as valuable platforms for research in robotics, artificial intelligence, and bio-inspired locomotion. Researchers use them to explore new algorithms, control strategies, and advanced locomotion techniques.
• Space exploration: Climbing robots have potential applications in space exploration, assisting in planetary exploration missions, such as on Mars or other celestial bodies, where they can navigate rough and challenging terrains.
These tasks highlight the versatility and adaptability of quadruped climbing robots. Their ability to navigate complex environments and reach locations that are difficult for other robots or humans to access makes them valuable tools in a wide range of applications.
6 Discussion and recommendations
Quadruped robots are most popular nowadays for their versatile application in agriculture, space applications, services, and more. The purpose of this review is to identify the present locomotion capabilities of the quadruped robot and explore new ways to impart locomotion to quadrupeds (Xiao and Wang, 2015; Sun, 2019; Ajeil et al., 2020; Buchanan et al., 2021). An exhaustive literature review helped identify the future research directions in the locomotion of quadruped robots, which are as follows:
• Mammal-type fault tolerance for locked joint failure
Very little literature reports have highlighted locomotion capabilities in the case of locked joint failure in mammal-type fault-tolerance gait patterns.
• Walking after the failure of the whole leg
The ability to walk after leg failure is a very important feature while the quadrupeds perform operations in the field. Possibilities of walking after one-leg failure are very rare in the literature.
•Scope of increasing stability by deliberately planning a body sway gait scheme
The stability of the robot highly depends on the terrain. Legged locomotion can travel through uneven or rough terrain. It is found through the literature that the strength of a quadruped robot compromises in the uneven terrain.
• Scope of better planning stair and slope climbing
An essential feature of a legged robot in the application is to climb stairs or slopes. The robot must be static and dynamically stable while moving through the stair or a slope. Very less literature studies focus on the motion dynamics while climbing (Vidoni and Gasparetto, 2011; Wang et al., 2017). Very few literature studies highlight climbing solutions on vertical ladders. Certain applications like inspections of towers of electricity, telecommunication, and light mast climbing seem to be the future scopes for quadruped climbing robots.
The quadruped robots capable of navigating varied terrains require a combination of mechanical design, sensing technologies, control algorithms, and power management to ensure stability, mobility, and safety in each scenario. A comparison of design requirements for varieties of terrains is given in Table 1. The comparison provided in Table 1 is only the variations in the design parameters based on the motion type that are recommended for the development of quadruped robots for applications.
The above discussion provided an insight into further research directions like determining the gait pattern in the case of failure of any joint or a whole leg. The dynamic stability analysis is highly important for precision-controlled motion in uneven terrain and stair and slope surfaces (T. climbing Robots, 2008).
The climbing robots available in the literature have certain limitations regarding certain specific aspects. The design must accommodate mountings of sophisticated mechatronics components, manufacturing aspects, and material considerations (Davim, 2011; Zhang, 2013). Developing a quadruped robot for climbing applications is a multi-disciplinary task that requires proper integration of hardware and software with safety and stability (Davim, 2012). The precise motion control algorithm, coordination of sensors and actuators, and design of a robot with space and environmental constraints are important parameters for quadruped robot development for climbing applications (Davim and Habib, 2013; Pawar et al., 2023).
Compared to wheeled and tracked mobile robots, legged mobile robots are selected due to their challenging locomotion planning and phenomenal advantages in maneuvering different terrains (Bhole et al., 2023). Furthermore, out of 2, 4, 6, and 8-legged robots, the 4-legged robot, i.e., quadruped, is selected as it has good stability and complexity. Different aspects of the quadruped, like fault tolerance, stability improvement, and stair and slope climbing, have many scopes of enhancement, and many novel ideas can be incorporated into the design and gait planning, which can ultimately result in the superior performance of the quadruped robot.
7 Conclusion
In the era of Industry 5.0, the industrial world is shifting towards robotics and artificial intelligence. Around three million industrial robotic manipulators in the world suggest the huge advantage of this technology. Still, the domain of mobile robots has not reached that level, even though it can be proven more beneficial in thousands of applications. The research in the field of mobile robotics is going on in many domains like kinematic design, navigation, and path planning, which is one of the best domains to contribute to research.
This review provided a comprehensive overview of the locomotion capabilities of quadruped robots. The paper showcased the significance of design considerations, such as leg structure and gait patterns, and elucidated the variety of legs and gaits available for different scenarios. The exploration of slope and stair climbing spotlighted the practical applications of quadruped climbing robots in real-world scenarios. As we move forward, it is evident that this field holds enormous potential for addressing challenges in fields as diverse as search and rescue, inspection, and exploration.
Some key research findings including research gaps and future suggestions from the study are as follows:
• Having higher stability and control than wheeled and tracked robots, the quadruped robot is an ideal choice for climbing applications.
• The dynamic gait patterns are more suitable for plain terrain, whereas for climbing operations, static gait, especially discontinuous static gaits, becomes superior due to higher stability.
• Fault tolerance in the quadruped robot is a critical area of research as the probability of failure is higher due to a greater number of actuators. Most of the gaits presented by different researchers can be modified to fault-tolerant gaits to improve the performance of the robot.
• The sway motion of the robot significantly improves stability, which can be applied to different gait patterns.
The recommendations outlined in this paper offer valuable insights for researchers and engineers to further advance the capabilities of quadruped robots, making them more versatile and effective in climbing applications. The prospects for the continued development of quadruped robots remain promising, with ample room for innovation and progress.
Author contributions
AM: conceptualization, investigation, and writing–original draft. DS: conceptualization, methodology, supervision, and writing–review and editing. JD: conceptualization, methodology, supervision, and writing–review and editing. AK: conceptualization, methodology, supervision, visualization, and writing–original draft. SR: conceptualization, supervision, validation, and writing–review and editing. ND: conceptualization, investigation, methodology, and writing–review and editing. HV: conceptualization, methodology, and writing–review and editing. DC: conceptualization, investigation, methodology, and writing–review and editing. SH: conceptualization, methodology, and writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ajeil, F. H., Ibraheem, I. K., Sahib, M. A., and Humaidi, A. J. (2020). Multi-objective path planning of an autonomous mobile robot using hybrid PSO-MFB optimization algorithm. Appl. Soft Comput. J. 89, 106076. doi:10.1016/j.asoc.2020.106076
Bai, L., Guan, J., Chen, X., Hou, J., and Duan, W. (2018). An optional passive/active transformable wheel-legged mobility concept for search and rescue robots. Rob. Auton. Syst. 107, 145–155. doi:10.1016/j.robot.2018.06.005
Banos, A., Jimenez, M. A., and Gonzalez de Santos, P. (1992). “Dynamic simulation of a four-legged gait,” in Proceedings 1992 IEEE international conference on systems, man, and cybernetics, 498–503.
Batayneh, W., Hayajneh, M., and Rasras, Z. (2010). C1979E design and implementation of climbing service and maintenance robot along tubular structures.
Bhole, K. S., Kale, B., Bhole, D., and Oak, S. (2023). Design methodology for development of experimental setup for fabrication of controlled micro and meso fractals. Procedia CIRP 119, 501–507. doi:10.1016/j.procir.2023.03.112
Buchanan, R., Wellhausen, L., Bjelonic, M., Bandyopadhyay, T., Kottege, N., and Hutter, M. (2021). Perceptive whole-body planning for multilegged robots in confined spaces. J. F. Robot. 38 (1), 68–84. doi:10.1002/rob.21974
Cai, S., Ma, Z., Skibniewski, M. J., and Bao, S. (2019). Construction automation and robotics for high-rise buildings over the past decades: a comprehensive review. Adv. Eng. Inf. 42 (May), 100989. doi:10.1016/j.aei.2019.100989
Chen, S. C., Ko, C. C., Li, C. H., and Lin, P. C. (2012). Stair climbing in a quadruped robot. Int. J. Autom. Smart Technol. 2 (1), 11–20. doi:10.5875/ausmt.v2i1.77
Chen, X., Gao, F., Qi, C., Tian, X., and Wei, L. (2015). Kinematic analysis and motion planning of a quadruped robot with partially faulty actuators. MAMT 94, 64–79. doi:10.1016/j.mechmachtheory.2015.05.010
Chen, X., Qi, C., Gao, F., Tian, X., Zhao, X., and Yu, H. (2014). Fault-tolerant gait for a quadruped robot with partially Fault legs.
Cherig, F., Lee, H., and Oriri, D. E. (1999). Increasing the locomotive stability margin of multilegged vehicles definitions of various stabil-ity margins constructing the loci of CG for equal energy stability, 1708–1714.
Chu, S. K., and Pang, G. K. (2002). Comparison between different model of hexapod robot in fault-tolerant gait. IEEE Trans. Syst. Man. Cybern. A 32 (6), 752–756. doi:10.1109/tsmca.2002.807066
Darshita Shah, P. J., Dave, J., and Patel, A. (2022). “Design of climbing robot for inspection of telecom tower,” in 3rd international conference on robotics, intelligent automation and control technologies (RIACT 2022), 1–9.
J. P. Davim (2011). Mechatronics (Wiley). Available at: https://www.wiley.com/en-gb/Mechatronics-p-9781848213081.
J. P. Davim (2012). Mechatronics and manufacturing engineering, elsevier (Elsevier). Available at: https://www.wiley.com/en-gb/Mechatronics-p-9781848213081.
De Santos, P. G., and Jimenez, M. A. (1995). Generation of discontinuous gaits for quadruped walking vehicles. J. Robot. Syst. 2 (9), 599–611. doi:10.1002/rob.4620120903
Digumarti, K. M., Gehring, C., Coros, S., Hwangbo, J., and Siegwart, R. (2014). Concurrent optimization of mechanical design and locomotion control of a legged robot. in Mob. Serv. Robot. Proc. 17th Int. Conf. Climbing Walk. Robot. Support Technol. Mob. Mach., 315–323.
Driewer, F., Baier, H., and Schilling, K. (2005). Robot-human rescue teams: a user requirements analysis. Adv. Robot. 19 (8), 819–838. doi:10.1163/1568553055011519
Dürr, V., Arena, P. P., Cruse, H., Dallmann, C. J., Drimus, A., Hoinville, T., et al. (2019). Integrative biomimetics of autonomous hexapedal locomotion. Front. Neurorobot. 13 (October), 1–32. doi:10.3389/fnbot.2019.00088
Gecko Robotics (2020). Gecko robotics: wall climbing robot for industrial inspections. Available at: https://www.wevolver.com/article/gecko-robotics-wall-climbing-robot-for-industrial-inspections.
Gerdes, L., Azkarate, M., Sánchez-Ibáñez, J. R., Joudrier, L., and Perez-del-Pulgar, C. J. (2020). Efficient autonomous navigation for planetary rovers with limited resources. J. F. Robot. 37 (7), 1153–1170. doi:10.1002/rob.21981
Goel, D., Pareekutty, N., and Shah, S. (2015). Implementation of gaits for achieving omnidirectional walking in a quadruped robot.
Gor, M. M., Pathak, P. M., Yang, J. M., Samantaray, A. K., and Kwak, S. W. (2013). Dynamic modeling and simulation of compliant legged quadruped robot. in 1st Int. 16th Natl. Conf. Mach. Mech. Ina. 2013, 7–16.
Gülhan, M. M., and Erbatur, K. (2018). Kinematic arrangement optimization of a quadruped robot with genetic algorithms. Meas. Control (United Kingdom) 51 (9–10), 406–416. doi:10.1177/0020294018795640
Hashimoto, K. (2017). “WAREC-1 - a four-limbed robot having high locomotion ability with versatility in locomotion styles,” in Ssrr 2017 - 15th IEEE int. Symp. Safety, secur. Rescue Robot. Conf., 172–178.
Hinderer, M., Friedrich, P., and Wolf, B. (2017). An autonomous stair-climbing wheelchair. Rob. Auton. Syst. 94, 219–225. doi:10.1016/j.robot.2017.04.015
Hirose, S. (1084). A study of design and control of a quadruped walking vehicle. Int. J. 3, 113–133. doi:10.1177/027836498400300210
Hirose, S., and Yoneda, K. (2001). Normalized energy stability margin and its contour of walking vehicles on rough terrain, 181–186.
Hjalmarsson, H., and Juditsky, A. (2000). a fault tolerant gait for a hexapod robot over uneven terrain. IEEE Trans. Syst. Man. Cybern. B 30 (1), 172–180. doi:10.1109/3477.826957
Hu, X., Wang, H., Sang, L., Gu, Q., and Yuan, L. (2015). The quadruped/biped reconfigurable walking Chair mechanism introduction of walking Chair, 562–571.
Ito, K., Homma, Y., and Rossiter, J. (2020). The soft multi-legged robot inspired by octopus: climbing various columnar objects. Adv. Robot. 34 (17), 1096–1109. doi:10.1080/01691864.2020.1753570
Jerril Gilda, S., and Jose Anand, A. (2023). “Implementation of intelligent control techniques applied on a line follower vehicle controller,” in 2nd int. Conf. Autom. Comput. Renew. Syst. ICACRS 2023, 46–53.
Kalakrishnan, M., Buchli, J., Pastor, P., Mistry, M., and Schaal, S. (2010). Fast, robust quadruped locomotion over challenging terrain, 2665–2670.
Karimov, A. I., Kopets, E. E., Rybin, V. G., Leonov, S. V., Voroshilova, A. I., and Butusov, D. N. (2019). Advanced tone rendition technique for a painting robot. Rob. Auton. Syst. 115, 17–27. doi:10.1016/j.robot.2019.02.009
Kolter, J. Z., Rodgers, M. P., and Ng, A. Y. (2008). A control architecture for quadruped locomotion over rough terrain, 811–818.
Konno, A., Ogasawara, K., Hwang, Y., Inohua, E., and Uchiyama, M. (2003). An adaptive gait for quadruped robots to walk on a slope, 589–594.
Krishnan, V. L., Pathak, P. M., Jain, S. C., and Samantaray, A. K. (2011). Reconfiguration of four-legged walking robot for actuator faults. Proc. Inst. Mech. Eng. Part I: J. Syst. Control Eng. 226, 11–26. doi:10.1177/0959651811410257
Liu, F., Wu, D., Chen, K., Liu, F., Wu, D., and Chen, K. (2013). The simplest creeping gait for a quadruped robot. Proc. Institution Mech. Eng. Part C J. Mech. Eng. Sci. 227, 170–177. doi:10.1177/0954406212444987
Liu, G., Yuan, Z., Qiu, Z., Feng, S., Xie, Y., Leng, D., et al. (2020). A brief review of bio-inspired surface technology and application toward underwater drag reduction. Ocean. Eng. 199 (February), 106962. doi:10.1016/j.oceaneng.2020.106962
Mahalakshmi, S., Rajeswari, C., Jose Anand, A., and Rahul, A. V. (2022). Client authentication by signature verification method using robotic process automation (RPA). in 2022 Int. Conf. Data Sci. Agents Artif. Intell. ICDSAAI, 1–5.
Majithiya, A., and Dave, J. (2021a). Static gait scheme for horizontal posture slope climbing with quadruped robot. J. Phys. Conf. Ser. 2115 (1), 012005. doi:10.1088/1742-6596/2115/1/012005
Majithiya, A., and Dave, J. (2021b). Comparing the performance of one-phase, two-phase, and four-phase discontinuous static gait for a quadruped robot. in ACM Int. Conf. Proceeding Series, 1–5.
Majithiya, A., and Dave, J. (2022). Discontinuous gait for statically stable stair climbing and descending of quadruped robot with horizontal body posture. Aust. J. Mech. Eng. 00 (00), 79–94. doi:10.1080/14484846.2022.2066839
Mcghee, R. B., and Fkask, A. A. (1968). On the stability properties of quadruped creeping gaits. Mathematical Biosci. 3, 331–351. doi:10.1016/0025-5564(68)90090-4
Melenbrink, N., Werfel, J., and Menges, A. (2020). On-site autonomous construction robots: towards unsupervised building. Autom. Constr. 119 (February), 103312. doi:10.1016/j.autcon.2020.103312
Menon, C., and Sitti, M. (2005). Biologically inspired adhesion based surface climbing robots. Proc. - IEEE Int. Conf. Robot. Autom. 2005 (April), 2715–2720. doi:10.1109/ROBOT.2005.1570524
Messuri, D., and Klein, C. (2015). Automatic body regulation for maintaining stability of a legged vehicle during rough-terrain locomotion. IEEE J. Robot. Auto. 3, 132–141. doi:10.1109/JRA.1985.1087012
Mooney, G., and Johnson, E. N. (2014). A comparison of automatic nap-of-the-earth guidance strategies for helicopters. J. F. Robot. 33 (1), 637–653. doi:10.1002/rob.21514
Osswald, M., and Iida, F. (2013). Design and control of a climbing robot based on hot melt adhesion. Rob. Auton. Syst. 61 (6), 616–625. doi:10.1016/j.robot.2013.02.004
Pana, C. F., Resceanu, I. C., and Patrascu, D. M. (2008). Fault-tolerant gaits of quadruped robot on a constant-slope terrain, 1–4.
Park, S., and Lee, Y. (2022). Gait analysis of a quadruped walking robot with vertical waist-joint on slope. IFAC 42 (13), 507–512. doi:10.3182/20090819-3-PL-3002.00088
Pawar, U., Chavan, S. G., Bhole, K. S., Rathod, M., Bhole, D., Oza, A. D., et al. (2023). Modeling and analysis of multi-functional self-healing material using Runge-Kutta Method for investigation of aircraft wing structure. Adv. Mat. Process. Technol. 00 (00), 1–17. doi:10.1080/2374068X.2023.2264577
Pfotzer, L., Klemm, S., Roennau, A., Zöllner, J. M., and Dillmann, R. (2017). Autonomous navigation for reconfigurable snake-like robots in challenging, unknown environments. Rob. Auton. Syst. 89, 123–135. doi:10.1016/j.robot.2016.11.010
Pongas, D., Mistry, M., and Schaal, S. (2007). A robust quadruped walking gait for traversing rough terrain, 10–14.
Ramya, E., Anand, J., Renugha Devi, R., Issac, N. A., and Roshni Prasenth, K. (2021). “Solar grass cutter with water spraying vehicle,” in 2021 int. Conf. Adv. Electr. Electron. Commun. Comput. Autom. ICAECA 2021, 3–9.
Richardson, A. N., Whitehead Scoutek, R. S., Ng, T. C., and Hawass, Z. (2013). The ‘djedi’ robot exploration of the southern shaft of the queen’s chamber in the great pyramid of giza, Egypt. J. F. Robot. (1), 323–349. doi:10.1002/rob
Roennau, A., Heppner, G., Pfotzer, L., and Dillmann, R. (2013). LAURON V: optimized leg configuration for the design of a bio-inspired walking robot. Nature-Inspired Mob. Robot., 563–570. doi:10.1142/9789814525534_0071
Sakuhara, Y., Shimizu, H., and Ito, K. (2020). “Climbing soft robot inspired by Octopus,” in 2020 IEEE 10th int. Conf. Intell. Syst. IS 2020, 463–468.
Saputra, A. A., Toda, Y., Takesue, N., and Kubota, N. (2019). A novel capabilities of quadruped robot moving through vertical ladder without handrail support. IEEE Int. Conf. Intell. Robot. Syst., 1448–1453. doi:10.1109/IROS40897.2019.8968175
Schmidt, D., and Berns, K. (2013). Climbing robots for maintenance and inspections of vertical structures - a survey of design aspects and technologies. Rob. Auton. Syst. 61 (12), 1288–1305.
Shah, D., and Dave, J. (2023). A comprehensive review on deploying robotics application in telecom network tower’s field maintenance: challenges with current practices and feasibility analysis for robotics implementation. J. F. Robot. 40, 1860–1883. doi:10.1002/rob.22223
Shah, D., Dave, J., chauhan, M., and Modi, B. A. (2022a). Ladder climbing robot. Available at: https://search.ipindia.gov.in/DesignSearch/DESIGNSEARCH/Searchtility?page=1.
Shah, D., Dave, J., chauhan, M., and Modi, B. A. (2022b). Telecom tower climbing robot. Available at: https://search.ipindia.gov.in/DesignSearch/DESIGNSEARCH/Searchtility?page=1.
Shah, D., Dave, J., Majithiya, A., and Patel, Y. (2021). Conceptual design and analysis of pipe climbing robot. J. Phys. Conf. Ser. 2115 (1), 012004. doi:10.1088/1742-6596/2115/1/012004
Shaik, A., Badruzaman, N., Gajendran, D., Geethalakshmi, M., and Anand, J. (2022). Organic farming in drainage systems with advanced automation through robotics and IoT. in 2022 1st Int. Conf. Comput. Power Commun. ICCPC 2022 - Proc., 592–597.
Sharma, K., and Doriya, R. (2021). Coordination of multi-robot path planning for warehouse application using smart approach for identifying destinations. Intell. Serv. Robot. 14 (2), 313–325. doi:10.1007/s11370-021-00363-w
Shiroma, N., Chiu, Y. U. H., Sato, N., and Matsuno, F. (2005). Cooperative task excecution of a search and rescue mission by a multi-robot team. Adv. Robot. 19 (3), 311–329. doi:10.1163/1568553053583670
Silva, M. F., Tenreiro Machado, J. A., and Tar, J. K. (2008). A Survey of Technologies for climbing robots adhesion to surfaces. in ICCC 2008 - IEEE 6th Int. Conf. Comput. Cybern. Proc., 127–132.
Sintov, A., Avramovich, T., and Shapiro, A. (2011). Design and motion planning of an autonomous climbing robot with claws. Rob. Auton. Syst. 59 (11), 1008–1019. doi:10.1016/j.robot.2011.06.003
Sun, T., Xiang, X., Su, W., Wu, H., and Song, Y. (2017). A transformable wheel-legged mobile robot: design, analysis and experiment. Rob. Auton. Syst. 98, 30–41. doi:10.1016/j.robot.2017.09.008
Sun, X. (2019). Error compensation system with proximity sensors for vertical ladder climbing of the robot ‘WAREC-1. in 2018-Novem. IEEE-RAS Int. Conf. Humanoid Robot, 40–46.
Suzumori, K., and Faudzi, A. A. (2018). Trends in hydraulic actuators and components in legged and tough robots: a review. Adv. Robot. 32 (9), 458–476. doi:10.1080/01691864.2018.1455606
Takano, M. (1990). Mechanism of an autonomous mobile robot and its control. Adv. Robot. 4 (3), 187–202. doi:10.1163/156855390X00242
Taylor, P., Park, S., and Lee, Y., (2012). Discontinuous zigzag gait planning of a quadruped walking robot with a waist-joint, pp. 37–41. doi:10.1163/156855307779293733
Tedeschi, F., and Carbone, G. (2014). Design issues for hexapod walking robots. Robotics 3 (2), 181–206. doi:10.3390/robotics3020181
Toussaint, K., Pouliot, N., and Montambault, S. (2009). Transmission line maintenance robots capable of crossing obstacles: state-of-the-art review and challenges ahead. J. F. Robot. 26 (5), 477–499. doi:10.1002/rob.20295
Tsitsimpelis, I., Taylor, C. J., Lennox, B., and Joyce, M. J. (2019). A review of ground-based robotic systems for the characterization of nuclear environments. Prog. Nucl. Energy 111 (October 2018), 109–124. doi:10.1016/j.pnucene.2018.10.023
Tsukagoshi, H., Hirose, S., and Yoneda, K. (2014). Maneuvering operations of a quadruped walking robot on a slope. Adv. Robot. 11, 359–375. doi:10.1163/156855397X00371
Vidoni, R., and Gasparetto, A. (2011). Efficient force distribution and leg posture for a bio-inspired spider robot. Rob. Auton. Syst. 59 (2), 142–150. doi:10.1016/j.robot.2010.10.001
Wang, F., Liu, Y., and Guo, L. (2017). Modeling and steady holding strategy of a climbing robot. in Proceedings of the 2017 2nd International Conference on Electrical, Automation and Mechanical Engineering (EAME 2017), 321–325.
Wang, H., Fang, D., Sang, L., Wang, Y., Wen, Y., and Chen, N. (2013). Gait P lanning of the quadruped walking Chair robot with parallel leg mechanism, 1–5.
Wang, R., and Kawamura, Y. (2015). A magnetic climbing robot for steel bridge inspection. Proc. World Congr. Intell. Control Autom. 2015, 3303–3308. doi:10.1109/WCICA.2014.7053262
Widanagamage, B. C., Gallege, T. N., Salgado, S., and Wijayakulasooriya, J. (2014). Treebot: an autonomous tree climbing robot utilizing four bar linkage system. in Research Symposium Engineering Advancements, 181–185.
Xiao, J., and Wang, H. (2015). Advances in climbing robots. Contemp. Issues Syst. Sci. Eng., 737–766. doi:10.1002/9781119036821.ch22
Xin, Y., Li, B., Hong, Z., and Li, Y. (2016). A combined COG adjustment approach of the crawl gait for quadruped robot. in 2016 Chinese Control Decis Conf, 6851–6856.
Xu, F., Jia, Y., Jia, Z., Chen, H., Guan, X., and Shi, Q. (2019). Research on gait control algorithm of bionic hexapod robot system based on adams and matlab. IOP Conf. Ser. Earth Environ. Sci. 332 (4), 042036. doi:10.1088/1755-1315/332/4/042036
Yang, J. (2002). Fault-tolerant gaits of quadruped robots for locked joint failures. IEEE Trans. Syst. Man. Cybern. C 32 (4), 507–516. doi:10.1109/tsmcc.2002.807274
Yang, J. (2005). Gait synthesis for hexapod robots with a locked joint failure. Robotica, Gait synthesis hexapod robots a locked Jt. Fail. 23, 701–708. doi:10.1017/S0263574705001578
Yang, J. M., Park, Y. K., and Kim, J. G. (2006). Fault-tolerant gait planning of multi-legged robots. doi:10.5772/4739
Yang, J. (2006a). Fault-tolerant crab gaits and turning gaits for a hexapod robot. Robotica, Fault-tolerant crab gaits Turn. gaits a hexapod robot 24, 269–270. doi:10.1017/S0263574705002237
Yang, J. (2006b). Kinematic constraints on Fault-Tolerant gaits for a locked joint failure, 323–342. doi:10.1007/s10846-006-9054-4
Yang, J. (2008a). Two-phase discontinuous gaits for quadruped walking machines with a failed leg. Rob. Auton. Syst. 56, 728–737. doi:10.1016/j.robot.2008.01.002
Yang, J. (2008b). Omnidirectional walking of legged robots with a failed leg. Math. Comput. Model. 47, 1372–1388. doi:10.1016/j.mcm.2007.08.006
Yang, J. (2009). Fault-tolerant gait planning for a hexapod robot walking over rough terrain. Terrain 54, 613–627. doi:10.1007/s10846-008-9282-x
Yang, J. (2012). Crab walking of quadruped robots with a locked joint failure. Adv. Robot. 17, 863–878. doi:10.1163/156855303770558660
Yang, J., and Kim, J. (1998). Fault-tolerant locomotion of the hexapod robot. IEEE Trans. Syst. Man. Cybern. B 28 (1), 109–116. doi:10.1109/3477.658585
Yang, J. M., and Kwak, S. W., (2013). Fault tolerant crab gaits of a quadruped robot: the use of moving appendage. 69–74. doi:10.2316/P.2013.799-070
Zhang, H., Liu, Y., Zhao, J., Chen, J., and Yan, J. (2014). Development of a bionic hexapod robot for walking on unstructured terrain. J. Bionic Eng. 11 (2), 176–187. doi:10.1016/S1672-6529(14)60041-X
Zhang, L., Ma, S., Honda, Y., and Inoue, K. (2004). Omni-directional walking of a quadruped robot on a slope, 268–273.
Zhang, L., Ma, S., Inoue, K., and Honda, Y. (2005). Omni-directional walking of a quadruped robot with optimal body postures on a slope, 76–81.
Zhang, S., Rong, X., Li, Y., and Li, B., (2015). A composite COG trajectory planning method for the quadruped robot walking on rough terrain. Int. J. Control Automation 8, 101–118. doi:10.14257/ijca.2015.8.9.11
Zhang, Y. (2013). Motion planning of ladder climbing for humanoid robots. IEEE Conf. Technol. Pract. Robot. Appl. TePRA, 1218534. doi:10.1109/TePRA.2013.6556364
Zhang, Z., Li, X., Yu, X., Chai, H., Li, Y., Wu, H., et al. (2019). Magnetic actuation bionic robotic gripper with bistable morphing structure. Compos. Struct. 229 (June), 111422. doi:10.1016/j.compstruct.2019.111422
Zhang, C. D., and Song, S. M. (1989). Gaits and geometry of a walking for the disabled. J. Terramech. 26, 211–233. doi:10.1016/0022-4898(89)90037-2
Zhao, Y., Chai, X., Gao, F., and Qi, C. (2018). Obstacle avoidance and motion planning scheme for a hexapod robot Octopus-III. Rob. Auton. Syst. 103, 199–212. doi:10.1016/j.robot.2018.01.007
Keywords: quadruped robot, climbing robot, legged robot, fault-tolerant design, gait planning, dynamic analysis
Citation: Majithia A, Shah D, Dave J, Kumar A, Rathee S, Dogra N, H. M. V, Chiniwar DS and Hiremath S (2024) Design, motions, capabilities, and applications of quadruped robots: a comprehensive review. Front. Mech. Eng. 10:1448681. doi: 10.3389/fmech.2024.1448681
Received: 13 June 2024; Accepted: 16 July 2024;
Published: 06 August 2024.
Edited by:
Kanak Kalita, Vel Tech Dr. RR & Dr. SR Technical University, IndiaReviewed by:
V. B. Murali Krishna, National Institute of Technology, IndiaGaydaa AlZohbi, Prince Mohammad bin Fahd University, Saudi Arabia
Copyright © 2024 Majithia, Shah, Dave, Kumar, Rathee, Dogra, H. M., Chiniwar and Hiremath. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ajay Kumar, YWpheS5rdW1hcjMwODg2QGdtYWlsLmNvbQ==; Vishwanatha H. M., dmlzaHdhbmF0aGEuaG1AbWFuaXBhbC5lZHU=; Dundesh S. Chiniwar, ZHVuZGVzaC5zY0BtYW5pcGFsLmVkdQ==; Shivashankarayya Hiremath, c3MuaGlyZW1hdGhAbWFuaXBhbC5lZHU=
 Ashish Majithia1
Ashish Majithia1 Darshita Shah
Darshita Shah Ajay Kumar
Ajay Kumar Vishwanatha H. M.
Vishwanatha H. M.