Blending physics with data using an efficient Gaussian process regression with soft inequality and monotonicity constraints

In this work, we propose a new Gaussian process (GP) regression framework that enforces the physical constraints in a probabilistic manner. Specifically, we focus on inequality and monotonicity constraints. This GP model is trained by the quantum-inspired Hamiltonian Monte Carlo (QHMC) algorithm, which is an efficient way to sample from a broad class of distributions by allowing a particle to have a random mass matrix with a probability distribution. Integrating the QHMC into the inequality and monotonicity constrained GP regression in the probabilistic sense, our approach enhances the accuracy and reduces the variance in the resulting GP model. Additionally, the probabilistic aspect of the method leads to reduced computational expenses and execution time. Further, we present an adaptive learning algorithm that guides the selection of constraint locations. The accuracy and efficiency of the method are demonstrated in estimating the hyperparameter of high-dimensional GP models under noisy conditions, reconstructing the sparsely observed state of a steady state heat transport problem, and learning a conservative tracer distribution from sparse tracer concentration measurements.

1 Introduction

In many real-world applications, measuring complex systems or evaluating computational models can be time-consuming, costly or computationally intensive. Gaussian process (GP) regression is one of the Bayesian techniques that addresses this problem by building a surrogate model. It is a supervised machine learning framework that has been widely used in regression and classification tasks. A GP can be interpreted as a suitable probability distribution on a set of functions, which can be conditioned on observations using Bayes’ rule (Lange-Hegermann, 2021). GP regression has found applications in various challenging practical problems including multi-target regression problems Nabati et al. (2022), biomedical applications Dürichen et al. (2014), Pimentel et al. (2013), robotics Williams and Rasmussen (2006) and mechanical engineering applications Song et al. (2021), Li et al. (2023), etc. The recent research demonstrate that a GP regression model can make predictions incorporating prior information (kernels) and generate uncertainty measures over predictions. However, prior knowledge often includes physical laws, and using the standard GP regression framework may lead to an unbounded model in which some points can take infeasible values that violate physical laws (Lange-Hegermann, 2021). For example, non-negativity is a requirement for various physical properties such as temperature, density and viscosity (Pensoneault et al., 2020). Incorporating physical information in GP framework can regularize the behaviour of the model and provide more realistic uncertainties, since the approach concurrently evaluates problem data and physical models (Swiler et al., 2020; Ezati et al., 2024).

A significant amount of research has been conducted to incorporate physical information in GP framework, resulting in various techniques and methodologies (Swiler et al., 2020). For example, a probit model for the likelihood of derivative information can be employed to enforce monotonicity constraints (Riihimäki and Vehtari, 2010). Although this approach can also be used to enforce convexity in one dimension, an additional requirement on Hessian is incorporated for higher dimensions (Da Veiga and Marrel, 2012). In (López-Lopera et al., 2022) an additive GP approach is introduced to account for monotonicity constraints. Although posterior sampling step can be challenging, the additive GP framework enables to satisfy the constraints everywhere in the input space, and it is scalable to higher dimensions. The work presented in Gulian et al. (2022) presents a framework in which spectral decomposition covariance kernels and differential equation constraints are used in a co-kriging setup to perform GP regression constrained by boundary value problems. With their inherent advantages, physics-informed GP models that incorporate physical constraints has applications in diverse areas, such as manufacturing Qiang et al. (2023), forecasting in power grids Mao et al. (2020) or urban flooding models Kohanpur et al. (2023), mimicing drivers’ behavior Wang et al. (2021), monitoring intelligent tire systems Barbosa et al. (2021), predicting fuel flow rate Chati and Balakrishnan (2017), designing wind turbines Wilkie and Galasso (2021), etc. Due to their flexibility, physics-informed GP models can be combined with several approaches to enhance the accuracy of model predictions. These works show that integrating physical knowledge into the prediction process provides accurate results.

Enforcing inequality constraints into a GP is typically challenging as the conditional process, subject to these constraints, does not retain the properties of a GP (Maatouk and Bay, 2017). One of the approaches to handle thi s problem is a data augmentation approach in which the inequality constraints are enforced at various locations and approximate samples are drawn from the predictive distribution (Abrahamsen and Benth, 2001), or using a block covariance kernel (Raissi et al., 2017). Implicitly constrained GP regression method proposed in (Salzmann and Urtasun, 2010) shows that the mean prediction of a GP implicitly satisfies linear constraints, if the constraints are satisfied by the training data. A similar approach shows that when we impose linear inequality constraints on a finite set of points in the domain, the resulting process is a compound Gaussian Process with a truncated Gaussian mean (Agrell, 2019). Most of the approaches assume that the inequalities are satisfied on a finite set of input locations. Based on that assumption, the methods approximate the posterior distribution given those constraint input points. The approach introduced in (Da Veiga and Marrel, 2012) is an example of these methods, where maximum likelihood estimation of GP hyperparameters are investigated under the constraint assumptions. In practice, this should also limit the number of constraint points needed for an effective discrete-location approximation. In addition, the method is not efficient on high-dimensional datasets as it takes a large amount of time to train the GP model.

To the best of our knowlege, the first Gaussian method that satisfies certain inequalities at all the input space is proposed by Maatouk and Bay (2017). The GP approximation of the samples are performed in the finite-dimensional space functions, and a rejection sampling method is used for approximating the posterior. The convergence properties of the method is investigated in (Maatouk et al., 2015). Although using the rejection sampling to obtain posterior helps convergence, it might be computationally expensive. Similar to the previous approaches in which a set of inputs satisfy the constraints, this method also suffers from the curse of dimensionality. Later, the truncated Gaussian approach (López-Lopera et al., 2018) extends the framework in (Maatouk and Bay, 2017) to general sets of linear inequalities. Building upon the approaches in (Maatouk and Bay, 2017; Maatouk et al., 2015), the work presented in (López-Lopera et al., 2018) introduces a finite-dimensional approach that incorporates inequalities for both data interpolation and covariance parameter estimation. In this work, the posterior distribution is expressed as a truncated multinormal distribution. The method uses different Markov Chain Monte Carlo (MCMC) methods and exact sampling methods to obtain the posterior distribution. Among the various MCMC sampling techniques including Gibbs, Metropolis-Hastings (MH) and Hamiltonian Monte Carlo (HMC), the results indicate that HMC sampling is the most efficient one. The truncated Gaussian approaches offer several advantages, including the ability to achieve high accuracy and the flexibility in satisfying multiple inequality conditions. However, although those types of methods address the limitations in (Maatouk and Bay, 2017), they might be time consuming particularly in applications with large datasets or high-dimensional spaces.

In this work, we use QHMC algorithm to train the GP model, and enforce the inequality and monotonicity constraints in a probabilistic manner. Our work addresses the computational limitations caused by high dimensions or large datasets. Unlike truncated Gaussian methods in (López-Lopera et al., 2018) for inequality constraints, or additive GP (López-Lopera et al., 2022) with monotonicity constraints, the proposed method can maintain its efficiency on higher dimensions. Further, we adopt an adaptive learning algorithm that selects the constraint locations. The efficiency and accuracy of the QHMC algorithms are demonstrated on inequality and monotonicity constrained problems. Inequality constrained examples include lower and higher dimensional synthetic problems, a conservative tracer distribution from sparse tracer concentration measurements and a three-dimensional heat transfer problem, while monotonicity constrained examples provide lower and higher dimensional synthetic problems. Our contributions can be summarized in three key points: i) QHMC reduces difference between posterior mean and the ground truth, ii) utilizing QHMC in a probabilistic sense decreases variance and uncertainty, and iii) the proposed algorithm is a robust, efficient and flexible method applicable to a wide range of problems. We implemented QHMC sampling in the truncated Gaussian approach to enhance accuracy and efficiency while working with the QHMC algorithm.

2 Gaussian process under inequality constraints

2.1 Standard GP regression framework

Suppose we have a target function represented by values $\mathbf{y}={(y^{(1)},y^{(2)},\dots ,y^{(T)})}^N$, where $y^{(i)}\in \mathbb{R}$ are observations at locations $\mathbf{X}={\{x^{(i)}\}}_{i=1}^N$. Here, $x^{(i)}$ represents $d$-dimensional vectors in the domain $\mathcal{D}\in {\mathbb{R}}^d$. Using the framework provided in Kuss and Rasmussen (2003), we approximate the target function by a GP, denoted as $Y(.,.):D\times \mathrm{\Omega }\to \mathrm{R}$. We can express $Y$ as

$Y\left(x\right)≔GP\left[\mu \left(x\right),K\left(x,x^{\prime }\right)\right],(1)$

where $\mu (.)$ is the mean function and $K(x,x^{\prime })$ is the covariance and mean functions in Equation 1 are defined as

$\mu \left(x\right)=\mathbb{E}\left[Y\left(x\right)\right],\text{and}K\left(x,x^{\prime }\right)=\mathbb{E}\left[Y\left(x\right)-\mu \left(x\right)\right]\left[Y\left(x^{\prime }\right)-\mu \left(x^{\prime }\right)\right](2)$

Typically, the standard squared exponential covariance kernel can be used as a kernel function in Equation 2:

$K\left(x,x^{\prime }\right)={\sigma }^2\exp \left(-\frac{\Vert x-x^{\prime }{\Vert }_2^2}{2l^2}\right)+{\sigma }_n^2{\delta }_{x,x^{\prime }},(3)$

where ${\sigma }^2$ is the signal variance, ${\delta }_{x,x^{\prime }}$ is the Kronecker delta function and $l$ is the length-scale. We then assume that the observation includes an additive independent identically distributed (i.i.d.) Gaussian noise term $ϵ$ and having zero mean and variance ${\sigma }_n^2$. We denote the hyperparameters in Equation 3 by $\mathit{\theta }=(\sigma ,l,{\sigma }_n)$, and estimate them using the training data. The parameters can be estimated by minimizing the negative marginal log-likelihood Kuss and Rasmussen (2003), Stein (1988), Zhang (2004):

$-\log \left[p\left(\mathbf{Y}|\mathbf{X},\theta \right)\right]=\frac{1}{2}\left[{\left(\mathbf{y}-\mathit{\mu }\right)}^{\text{T}}{K}^{-1}\left(\mathbf{y}-\mathit{\mu }\right)+\log |K|+N\log \left(2\pi \right)\right].(4)$

The following section shows how the parameter updates are performed using the QHMC method.

2.2 Quantum-inspired Hamiltonian Monte Carlo

QHMC is an enhanced version of the HMC algorithm that incorporates a random mass matrix for the particles, following a probability distribution. In conventional HMC, the position is represented by the original variables $(x)$, while Gaussian momentum is represented by auxiliary variables $(q)$. Utilizing the energy-time uncertainty relation of quantum mechanics, QHMC allows a particle to have a random mass matrix with a probability distribution. Consequently, in addition to the position and momentum variables, a mass variable $(m)$ is introduced within the QHMC framework. Having a third variable offers the advantage of exploring various landscapes in the state-space. As a result, unlike standard HMC or conventional sampling methods such as MH and Gibbs, QHMC can perform well on discontinuous, non-smooth and spiky distributions Barbu and Zhu (2020), Liu and Zhang (2019). In particular, while the performance of HMC and MH sampling degrade when the distribution is ill-conditioned or multi-modal, the performance of QHMC does not have these limitations. Moreover, QHMC maintains its performance with almost zero additional cost of resampling the mass variable. Due to its efficiency and adaptibility, QHMC can easily integrate with other techniques, or be modified to enhance its performance based on specific objectives and applications. For example, stochastic versions of QHMC can yield accurate solutions with increased efficiency, and the approach is applicable to various scenarios involving missing data Liu and Zhang (2019), Kochan et al. (2022).

The quantum nature of QHMC can be understood by considering a one-dimensional harmonic oscillator example provided in Liu and Zhang (2019). Let us consider a ball with a fixed mass $m$ attached to a spring at the origin. Assuming $x$ is the displacement, the magnitude of the restoring force that pulls back the ball to the origin is $F=-kx$, and the ball oscillates around the origin with period $T=2\pi \sqrt{\frac{m}{k}}$. In contrast to standard HMC where the mass $m$ is fixed at 1, QHMC incorporates a time-varying mass, allowing the ball to experience acceleration and explore various distribution landscapes. That is, QHMC has the capability to employ a short time period $T$, corresponding to a small mass $m$, to efficiently explore broad but flat regions. Conversely, in spiky regions, it can switch to a larger time period $T$, i.e., larger $m$, to ensure thorough exploration of all corners of the landscape Liu and Zhang (2019).

The implementation of QHMC is straightforward: i) construct a stochastic process $M(t)$ for the mass, and at each time $t$, ii) sample $M(t)$ from a distribution $P_M(M)$. Resampling the positive-definite mass matrix is the only additional step to the standard HMC procedure. In practice, assuming that $P_M(M)$ is independent of $x$ and $q$, a mass density function $P_M(M)$ with mean ${\mu }_m$ and variance ${\sigma }_m^2$ can be where $I$ is the identity matrix. QHMC framework simulates the following dynamical system:

$d\left(\begin{array}{c}\hfill x\hfill \\ \hfill q\hfill \end{array}\right)=dt\left(\begin{array}{c}\hfill M{\left(t\right)}^{-1}q\hfill \\ \hfill -\nabla U\left(x\right)\hfill \end{array}\right).(5)$

In this setting, the potential energy function of the QHMC system is $U(x)=-\log [p(\mathbf{Y}|\mathbf{X},\theta )]$, i.e., the negative of marginal log-likelihood. Algorithm 1 summarizes the steps of QHMC sampling, and, here, we consider the location variables ${\{x^{(i)}\}}_{i=1}^N$ in GP model as the position variables $x$ in Algorithm 1. The method evolves the QHMC dynamics in Equation 5 to update the locations $x$. In this work, we implement the QHMC method for inequality constrained GP regression in a probabilistic manner.

2.3 Proposed method

Instead of enforcing all constraints strictly, the approach introduced in Pensoneault et al. (2020) minimizes the negative marginal log-likelihood function in Equation 4 while allowing constraint violations with a small probability. For example, for non-negativity constraints, the following requirement is imposed to the problem:

$P\left[\left(\mathbf{Y}\left(x\right)|x,\theta \right)<0\right]\le \eta ,\text{for\hspace{0.17em}all}x\in \mathcal{D},(6)$

where $0<\eta \ll 1$.

In contrast to enforcing the constraint via truncated Gaussian assumption Maatouk and Bay (2017) or performing inference based on the Laplace approximation and expectation propagation Jensen et al. (2013), the proposed method preserves the Gaussian posterior of the standard GP regression. The method uses a slight modification of the existing cost function. Given a model that follows a Gaussian distribution, the constraint in Equation 6 can be re-expressed by the posterior mean and posterior standard deviation:

$y^{*}\left(x\right)+{\varphi }^{-1}\left(\eta \right)s\left(x\right)\ge 0,\text{for\hspace{0.17em}all}x\in \mathcal{D},(7)$

where $y*(x)$ stands for the posterior mean, $s$ is the standard deviation and $\varphi$ is the cumulative distribution function of a Gaussian random variable. Following the work in Pensoneault et al. (2020), in this study $\eta$ was set to $2.2\%$ for demonstration purposes. As a result, ${\varphi }^{-1}(\eta )=-2$, indicating that two standard deviations below the mean is still nonnegative. Then, using Equation 7 the formulation of the optimization problem is given as

$\begin{array}{cc}\hfill {\mathrm{arg\; min}}_{\theta }& -\log \left[p\left(\mathbf{Y}|\mathbf{X},\theta \right)\right]\text{such\hspace{0.17em}that}\hfill \\ \hfill & y^{*}\left(x\right)-2s\left(x\right)\ge 0.\hfill \end{array}(8)$

In this particular form of the optimization problem, a functional constraint described by Equation 8 is existent. It can be prohibitive or impossible to satisfy this constraint at all points across the entire domain. Therefore, we adopt a strategy where Equation 8 is enforced only on a selected set of $m$ constraint points denoted as ${\mathbf{X}}_c={x_c^{(i)}}_{i=1}^m$. The optimization problem can be reformulated as

$\begin{array}{cc}\hfill {\mathrm{arg\; min}}_{\theta }& -\log \left[p\left(\mathbf{Y}|\mathbf{X},\theta \right)\right]\text{such\hspace{0.17em}that}\hfill \\ \hfill & y^{*}\left(x_c^{\left(i\right)}\right)-2s\left(x_c^{\left(i\right)}\right)\ge 0\text{for\hspace{0.17em}all}i=\mathrm{1,2},\dots ,m,\hfill \end{array}(9)$

where hyperparameters are estimated to enforce bounds. Solving this optimization problem can be very challenging, and hence, in Pensoneault et al. (2020) additional regularization terms are added. Rather than directly solving the optimization problem, this work adopts the soft-QHMC method, which introduces inequality constraints with a high probability (e.g., 95%) by selecting a specific set of $m$ constraint points in the domain. Then non-negativity on the posterior GP is enforced at these selected points. The log-likelihood in Equation 4 is minimized using the QHMC algorithm. Leveraging the Bayesian estimation Gelman et al. (2014), we can approximate the posterior distribution by log-likelihood function and prior probability distribution as shown in the following:

$p\left(\mathbf{X},\theta |\mathbf{Y}\right)\propto p\left(\mathbf{X},\theta ,\mathbf{Y}\right)=p\left(\theta \right)p\left(\mathbf{X}|\theta \right)p\left(\mathbf{Y}|\mathbf{X},\theta \right).(10)$

The QHMC training flow starts with the Bayesian learning shown in Equation 10 this Bayesian learning and proceeds with an MCMC procedure for drawing samples generated by the Bayesian framework. A general sampling procedure at step $t$ is given as

$\begin{array}{cc}\hfill X^{\left(t+1\right)}& \sim \pi \left(X|\theta \right)=p\left(X|{\theta }^{\left(t\right)},Y\right),\hfill \\ \hfill {\theta }^{\left(t+1\right)}& \sim \pi \left(\theta |X\right)=p\left(\theta |X^{\left(t+1\right)},Y\right).\hfill \end{array}(11)$

The workflow of soft inequality-constrained GP regression with the sampling procedure in Equation 11 is summarized in Algorithm 2, where QHMC sampling (provided in Algorithm 1) is used as a GP training method. In this version of non-negativity enforced GP regression, the constraint points are located where the posterior variance is highest.

Algorithm 1.QHMC Training for GP with Inequality Constraints.

Input: Initial point $x_0$, step size $ϵ$, number of       simulation steps $L$, mass distribution       parameters ${\mu }_m$ and ${\sigma }_m$.

1: for $t=\mathrm{1,2},\dots$ do

2:   Resample $M_t\sim P_M(M)$

     Resample $q_t\sim N(0,M_t)$

     $(x_0,q_0)=(x^{(t)},q^{(t)})$

     $q_0\leftarrow q_0-\frac{ϵ}{2}\nabla U(x_0)$

3:  for $i=\mathrm{1,2},\dots ,L-1$ do

4:    $x_i\leftarrow x_{i-1}+ϵM_t^{-1}{q}_{i-1}$

      $q_i\leftarrow q_{i-1}-\frac{ϵ}{2}\nabla U(x_i)$

5:  end for

   $x_L\leftarrow x_{L-1}+ϵM_t^{-1}{q}_{L-1}$

   $q_L\leftarrow q_{L-1}-\frac{ϵ}{2}\nabla U(x_L)$

   $(\widehat{x},\widehat{q})=(x_L,q_L)$

   MH step: $u\sim$ Uniform[0,1];

   $\rho =e^{-H(\widehat{x},\widehat{q})+H(x^{(t)},q^{(t)})}$;

6:  if $u<\min (1,\rho )$ then

7:   $(x^{(t+1)},q^{(t+1)})=(\widehat{x},\widehat{q})$

8:  else

9:     $(x^{(t+1)},q^{(t+1)}=(x^{(t)},q^{(t)})$

10:  end if

11: end for

    Output: $\{x^{(1)},x^{(2)},\dots \}$

Algorithm 2.Soft Inequality-constrained GP Regression.

1: Specify $m$ constraint points denoted by ${\mathbf{X}}_c={x_c^{(i)}}_{i=1}^m$, where corresponding observation $y^{*}{(x_c)}^{(i)}$.

2: for $i=\mathrm{1,2},\dots ,m$ do

3:  Compute the MSE of $s^2(x_c^{(i)})$ of MLE prediction    $y^{*}(x_c)$ for $x_c\in \mathcal{D}$.

    Obtain observation $y^{*}{(x_c)}^{(i)}$ at $x_c^{(i)}$

    Locate $x_c^{(i+1)}$ for the maximum of $s^2(x_c^{(i)})$ for

    $x_c\in \mathcal{D}$.

4: end for

   Construct the MLE prediction of $y^{*}(x)$ using   QHMC training.

2.3.1 Enforcing monotonicity constraints

Monotonicity constraints on a GP can be enforced using the likelihood of derivative observations. After the selection of active constraints, non-negativity constraints are incorporated in the partial derivative, i.e.,

$\frac{\partial f}{\partial x_i}\left({\mathbf{x}}_{\mathbf{i}}\right)\ge 0,(12)$

where $f$ is a vector of $N$ latent values. In the soft-constrained GP method, we introduce the non-negativity information in Equation 12 on a set of selected points, and apply the same procedure as in Equation 9.

Since the derivative is also a GP with mean and covariance matrix Riihimäki and Vehtari (2010):

$\mu \left(x^{\prime }\right)=\mathbb{E}\left[\frac{\partial Y\left(x\right)}{\partial x_i}\right],\text{and}K\left(x,x^{\prime }\right)=\frac{\partial }{\partial x_i}\frac{\partial }{\partial x_i^{\prime }}K\left(x,x^{\prime }\right),(13)$

the new posterior distribution using the parameters in Equation 13 is given as

$\begin{array}{cc}\hfill & p\left({\mathbf{y}}^{*},\theta |\mathbf{y},\mathbf{x},{\mathbf{x}}^{*}\right)=\int p\left({\mathbf{y}}^{*},\theta |f^{*}\right)p\left(f^{*}|\mathbf{y},\mathbf{x},{\mathbf{x}}^{*}\right)df,\hfill \\ \hfill & p\left(f^{*}|\mathbf{y},\mathbf{x},{\mathbf{x}}^{*}\right)=\int \int p\left(f^{*}|{\mathbf{x}}^{*},f,f^{\prime }\right)p\left(f,f^{\prime }|\mathbf{x},\mathbf{y}\right)dfd{f}^{\prime },\hfill \end{array}(14)$

where ${\mathbf{y}}^{*}$ and ${\mathbf{f}}^{*}$ denote the predictions at location ${\mathbf{x}}^{*}$. The general sampling procedure for the posterior distribution in Equation 14 is the same as in Equation 11.

3 Theoretical analysis of the method

In this section, employing Bayes’ Theorem, we demonstrate how QHMC is capable of producing a steady-state distribution that approximates the actual posterior distribution. Then, we examine the convergence characteristics of the probabilistic approach on the optimization problem outlined in Equation 9.

3.1 Convergence of QHMC training

The study presented in Liu and Zhang (2019) demonstrates that the QHMC framework can effectively capture a correct steady-state distribution that describes the desired posterior distribution $p(x)\propto \exp (-U(x))$ via Bayes’ rule. The joint probability density of $(x,q,M)$ can be calculated by Bayesian theorem:

$p\left(x,q,M\right)=p\left(x,q|M\right)P_M\left(M\right),(15)$

The conditional distribution in Equation 15 is approximated as follows:

$p\left(x,q|M\right)\propto \exp \left(-U\left(x\right)-K\left(q\right)\right)=\exp \left(-U\left(x\right)\right)\exp \left(-\frac{1}{2}{q}^T{M}^{-1}q\right),(16)$

Then, using Equation 16, $p(x)$ can be written as

$p\left(x\right)={\int }_q{\int }_{M}dqdMp\left(x,q,M\right)\propto \exp \left(-U\left(x\right)\right).(17)$

Equation 17 shows that the marginal steady distribution approaches the true posterior distribution Liu and Zhang (2019).

3.2 Convergence properties of probabilistic approach

In this section, we show that satisfying the constraints on a set of locations $x$ in the domain $\mathcal{D}$ preserves convergence. Recall the following inequality-constrained optimization problem:

$\begin{array}{cc}\hfill {\mathrm{arg\; min}}_{\theta }& -\log \left[p\left(\mathbf{Y}|\mathbf{X},\theta \right)\right]\text{such\hspace{0.17em}that}\hfill \\ \hfill & y^{*}\left(x_c^{\left(i\right)}\right)-2s\left(x_c^{\left(i\right)}\right)\ge 0\text{for\hspace{0.17em}all}i=\mathrm{1,2},\dots ,m.\hfill \end{array}(18)$

Now, it is necessary to demonstrate that the result obtained by using the selected set of input locations as in Equation 18 converge to the value of the regression model’s output. This convergence ensures that probabilistic approach will eventually result in a model that satisfy the desired conditions.

Note that throughout the proof, it is assumed that $\mathcal{D}$ is finite. The proof can be constructed for the cases whether the domain is countable or uncountable.

(i) Assume that the domain $\mathcal{D}$ is a countable set containing $N$ elements. Then, select a subset ${\mathcal{D}}_m\in \mathcal{D}$ with $m$ points, where $x_c^{(1)},x_c^{(2)},\dots ,x_c^{(m)}\in {\mathcal{D}}_m$. For each point $x\in \mathcal{D}$, there exists a Gaussian probability distribution. The set of distributions associated with $x\in \mathcal{D}$ is denoted as $\mathcal{P}$. For the constraint points $x\in {\mathcal{D}}_m$, there are $m$ constraints and their corresponding probability distributions, which can be defined as ${\mathcal{P}}_m$. Additionally, we introduce a set $H(x)$ such that

$H\left(x\right)≔\left\{\theta |p\left(\mathbf{Y}|\mathbf{X},\theta \right)<0\right\},(19)$

which covers the locations where the non-negativity constraint is violated. For each fixed $x\in \mathcal{D}$, define

$\begin{array}{cc}\hfill v\left(x\right)& ≔\underset{P\in \mathcal{P}}{\inf }P\left(\mathbf{Y}|\mathbf{X},\theta \right)<0\equiv \underset{P\in \mathcal{P}}{\inf }P\left(H\left(x\right)\right),\text{and}\hfill \\ \hfill v_m\left(x\right)& ≔\underset{P\in {\mathcal{P}}_m}{\inf }P\left(\mathbf{Y}|\mathbf{X},\theta \right)<0\equiv \underset{P\in {\mathcal{P}}_m}{\inf }P\left(H\left(x\right)\right).\hfill \end{array}(20)$

(ii) Assume that the domain $\mathcal{D}$ is a finite but uncountable set. In this case, a countable subset $\tilde{\mathcal{D}}$ with $x\in \tilde{\mathcal{D}}$ can be constructed. The set of probability distributions are defined as in case (i). Since $\mathcal{D}$ is finite, the set $\mathcal{D}\cup \{x\}$ is also finite. Consequently, the sets $H(x),v(x)$ and $v_m(x)$ can be constructed as in the first case, (Equations 19, 20). Next steps establish a convergence of $v_m$ over $v$ as ${\mathcal{P}}_m$ converges to $\mathcal{P}$.

First, let us provide distance metrics used throughout the proof. Following the definitions in Guo et al. (2015), let

$d\left(x,A\right)≔\underset{x^{\prime }\in A}{\inf }\Vert x-x^{\prime }\Vert (21)$

denote the distance from a point $x$ to a set $A$. Then, the distance of two compact sets $A$ and $B$ can be defined as

$\mathbb{D}\left(A,B\right)≔\underset{x\in A}{\sup }d\left(x,B\right).(22)$

Then, using the definitions in Equations 21, 22, the Hausddorff distance between $A$ and $B$ is defined as $\mathbb{H}(A,B)≔\max \{\mathbb{D}(A,B),\mathbb{D}(B,A)\}$. Finally, we define a pseudo-metric $\mathbf{d}$ to describe the distance between two probability distributions $P$ and $\tilde{P}$ as

$\mathbf{d}\left(P,\tilde{P}\right)≔\underset{x\in \mathcal{D}}{\sup }|P\left(H\left(x\right)\right)-\tilde{P}\left(H\left(x\right)\right)|,(23)$

where $\mathcal{D}$ is the domain specified in Section 3.2.

Assumption 1. Suppose that the probability distributions $\mathcal{P}$ and ${\mathcal{P}}_m$ satisfy the following conditions:

1. There exists a weakly compact set $\tilde{\mathcal{P}}$ such that $\mathcal{P}\subset \tilde{\mathcal{P}}$ and ${\mathcal{P}}_m\subset \tilde{\mathcal{P}}$.

2. $\underset{m\to N}{\lim }\mathbf{d}(\mathcal{P},{\mathcal{P}}_m)=0$, with probability 1.

3. $\underset{m\to N}{\lim }\mathbf{d}({\mathcal{P}}_m,\mathcal{P})=0$, with probability 1.

Now, we show that Theorem 1 holds under the assumptions in Assumption 1. Recall that we have

$\mathbb{H}\left(\text{conv}V,\text{conv}{V}_m\right)=\max \left\{\left|\underset{P\in {\mathcal{P}}_m}{\sup }P\left(H\left(x\right)\right)-\underset{P\in \mathcal{P}}{\sup }P\left(H\left(x\right)\right)\right|,\left|\underset{P\in {\mathcal{P}}_m}{\inf }P\left(H\left(x\right)\right)-\underset{P\in \mathcal{P}}{\inf }P\left(H\left(x\right)\right)\right|\right\}.$

Based on the definition and property of Hausdorff distance Hess (1999) we also have

$\mathbb{H}\left(\text{conv}V,\text{conv}{V}_m\right)\le \mathbb{H}\left(V,V_m\right)\le \max \left\{\mathbb{D}\left(V,V_m\right),\mathbb{D}\left(V_m,V\right)\right\}.(24)$

Consider the distance of two sets:

$\begin{array}{cc}\hfill \mathbb{D}\left(V,V_m\right)& =\underset{v\in V}{\sup }\underset{v^{\prime }\in V_m}{\inf }\Vert v-v^{\prime }\Vert \hfill \\ \hfill & =\underset{P\in \mathcal{P}}{\sup }\underset{\tilde{P}\in {\mathcal{P}}_m}{\inf }\Vert P\left(H\left(x\right)\right)-\tilde{P}\left(H\left(x\right)\right)\Vert \hfill \\ \hfill & \le \underset{P\in \mathcal{P}}{\sup }\underset{\tilde{P}\in {\mathcal{P}}_m}{\inf }\underset{x\in \mathcal{D}}{\sup }\Vert P\left(H\left(x\right)\right)-\tilde{P}\left(H\left(x\right)\right)\Vert \hfill \\ \hfill & =\mathbf{d}\left(\mathcal{P},{\mathcal{P}}_m\right),\hfill \end{array}(25)$

where d is defined in Equation 23 and apply the same procedures as in Equations 24, 25 to obtain $\mathbb{D}(V_m,V)\le \mathbf{d}({\mathcal{P}}_m,\mathcal{P})$. Hence,

$\mathbb{H}\left(\text{conv}V,\text{conv}{V}_m\right)\le \mathbb{H}\left(V,V_m\right)\le \mathbb{H}\left({\mathcal{P}}_m,\mathcal{P}\right).(26)$

Consequently from Equation 26, we obtain

$\begin{array}{cc}\hfill |v_m\left(x\right)-v\left(x\right)|& \le \left|\underset{P\in {\mathcal{P}}_m}{\inf }P\left(H\left(x\right)\right)-\underset{P\in \mathcal{P}}{\inf }P\left(H\left(x\right)\right)\right|\hfill \\ \hfill & \le \mathbb{H}\left(\text{conv}V,\text{conv}{V}_m\right)\hfill \\ \hfill & \le \mathbb{H}\left({\mathcal{P}}_m,\mathcal{P}\right).\hfill \end{array}(27)$

Theorem 1. $v_m$ converges to $v$ as ${\mathcal{P}}_m$ converges to $\mathcal{P}$, that is

$\underset{m\to N}{\lim }\underset{x\in \mathcal{D}}{\sup }|v_m\left(x\right)-v\left(x\right)|=0.$

Proof.Let us assume that $x\in \mathcal{D}$ is fixed, and define

$V≔\left\{P\left(H\left(x\right)\right):P\in \text{cl}\mathcal{P}\right\},\text{and},V_m≔\left\{P\left(H\left(x\right)\right):P\in \text{cl}{\mathcal{P}}_m\right\},(28)$

where cl represents the closure. Note that both $V$ and $V_m$ are bounded subsets in ${\mathbb{R}}^d$. Let us define $a,b,a_m$ and $b_m$ such that

$a≔\underset{v\in V}{\inf }v,b≔\underset{v\in V}{\sup }v,a_m≔\underset{v\in V_m}{\inf }v,b_m≔\underset{v\in V_m}{\sup }v,(29)$

The Hausdorff distance between convex hulls (conv) of the sets $V$ and $V_m$ are calculated as Hess (1999).

$\mathbb{H}\left(\text{conv}V,\text{conv}{V}_m\right)=\max \left\{|b_m-b|,|a-a_m|\right\}.(30)$

Since we know that

$b_m-b=\underset{v\in V_m}{\sup }v-\underset{v\in V}{\sup }v,\text{and}{a}_m-a=\underset{v\in V_m}{\inf }v-\underset{v\in V}{\inf }v,(31)$

combining the result in Equation 27, and the definitions in Equations 28–31

$\mathbb{H}\left(\text{conv}V,\text{conv}{V}_m\right)=\max \left\{\left|\underset{P\in {\mathcal{P}}_m}{\sup }P\left(H\left(x\right)\right)-\underset{P\in \mathcal{P}}{\sup }P\left(H\left(x\right)\right)\right|,\left|\underset{P\in {\mathcal{P}}_m}{\inf }P\left(H\left(x\right)\right)-\underset{P\in \mathcal{P}}{\inf }P\left(H\left(x\right)\right)\right|\right\}(32)$

Based on the Equation 32 and the definition and property of Hausdorff distance Hess (1999) we have

$\mathbb{H}\left(\text{conv}V,\text{conv}{V}_m\right)\le \mathbb{H}\left(V,V_m\right),(33)$

The inequality in Equation 33 yields Guo et al. (2015).

$|v_m\left(x\right)-v\left(x\right)|\le \mathbb{H}\left(V,V_m\right)\le \mathbb{H}\left(\mathcal{P},{\mathcal{P}}_m\right).(34)$

In this setting, $x$ can be any point in $\mathcal{D}$, and the right hand side of the inequality is independent of $x$. The proof can be completed by taking the supremum of each side in Equation 34 with respect to $x$ Guo et al. (2015).

4 Numerical examples

In this section, we evaluate the performance of the proposed algorithms on various examples including synthetic and real data. The evaluations consider the size and dimension of the datasets. Several versions of QHMC algorithms are introduced and compared depending on the selection of constraint point locations and probabilistic approach.

Rather than randomly locating $m$ constraint points, the algorithm starts with an empty constraint set and determine the locations of the constraint points one by one adaptively. Throughout this process, various strategies are employed to add constraints. The specific approaches are outlined as follows:

1. Constraint-adaptive approach: While constructing the set of constraint points, this approach evaluates whether the constraint is satisfied at a given location. The function value at that point is calculated, and if the constraint is found to be violated, a constraint point is added to indicate this violation. This helps track areas where the constraint is not met and allows for adjustments to be made accordingly.

2. Variance-adaptive approach: This approach calculates the prediction variance in the test set. Constraint points are identified at the positions where the variance values are highest. As outlined in Algorithm 2, new constraints are located at the maxima of $s(x)$. The goal here is basically to reduce the variance in predictions and increase the stability.

3. Combination of constraint and variance adaption: In this approach, a threshold value (e.g., 0.20) is determined for the variance, and the algorithm locates constraint points to the locations where the highest prediction variance is observed. Once the variance reduces to the threshold value, the algorithm switches to the first strategy, in which it locates constraint points where the violation occurs.

We represent the constraint-adaptive, hard-constrained approach as QHMCad and its soft-constrained counterpart as QHMCsoftad. Similarly, QHMCvar refers to the method focusing on variance, while QHMCsoftvar corresponds to its soft-constrained version. The combination of the two approaches with hard and soft constraints are denoted by QHMCboth and QHMCsoftboth, respectively. For the sake of comparison, truncated Gaussian algorithms using an HMC sampler (tnHMC) and a QHMC sampler (tnQHMC) for inequality-constrained examples are implemented, while additive GP (additiveGP) algorithm is adapted for monotonicity-constrained examples.

For the synthetic examples, the time and accuracy performances of the algorithms are evaluated while simultaneously changing the dataset size and noise level in the data. Following Pensoneault et al. (2020), as our metric, we calculate the relative $l_2$ error between the posterior mean $y^{*}$ and the true value of the target function $f(x)$ on a set of test points ${\mathbf{X}}_t={\{x_T^{(i)}\}}_{i=1}^{N_t}$:

$E=\sqrt{\frac{{\displaystyle \sum _{i=1}^{N_t}}{\left[y^{*}\left(x_T^{\left(i\right)}\right)-f\left(\underset{T}{\overset{\left(i\right)}{x}}\right)\right]}^2}{{\displaystyle \sum _{i=1}^{N_t}}f{\left(x_T^{\left(i\right)}\right)}^2}}.(35)$

We solve the log-likelihood minimization problem in MATLAB, using the GPML package Rasmussen and Nickisch (2010). For the constrained optimization, we use the fmincon from the MATLAB Optimization Toolbox based on the built-in interior point algorithm. Additionally, in order to highlight the advantage of QHMC over HMC, the proposed approach is implemented with using the standard HMC procedure. The relative error, (calculated as in Equation 35), posterior variance and execution time of each version of QHMC and HMC algorithms are presented.

4.1 Inequaltiy constraints

This section provides two synthetic examples and two real-life application examples to demonstrate the effectiveness of QHMC algorithms on inequality constraints. Synthetic examples compare the performance QHMC approach with truncated Gaussian methods for a 2-dimensional and a 10-dimensional problems. For the 2-dimensional example, the primary focus is on enforcing the non-negativity constraints within the GP model. In the case of the 10-dimensional example, we generalize our analysis to satisfy a different inequality constraint, and evaluate the performances of truncated Gaussian, QHMC and soft-QHMC methods. Third example considers conservative transport in a steady-state velocity field in heterogeneous porous media. Despite being a two-dimensional problem, the non-homogeneous structure of the solute concentration introduces complexity and increases the level of difficulty. The last example is a 3-dimensional heat transfer problem in a hallow sphere.

4.1.1 Example 1

Consider the following 2D function under non-negativity constraints:

$f\left(x\right)=\arctan 5x_1+\arctan x_2,(36)$

where $\{x_1,x_2\}\in {[\mathrm{0,1}]}^2$. In this example, the GP model is trained via QHMC over 20 randomly selected locations.

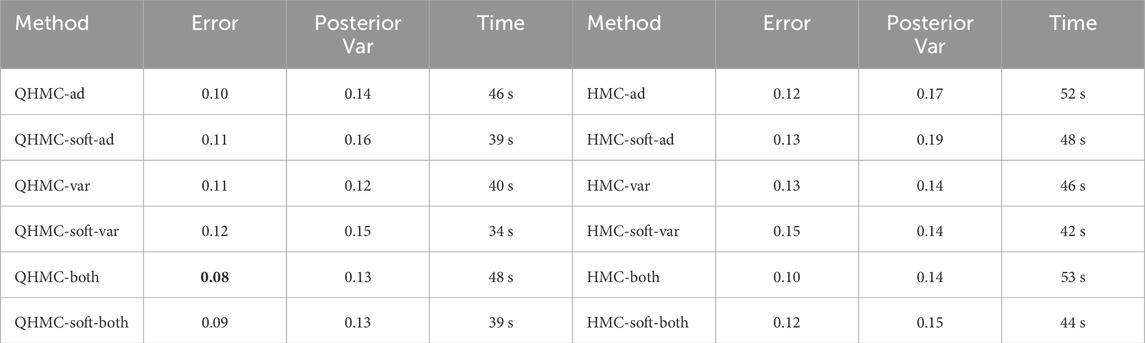
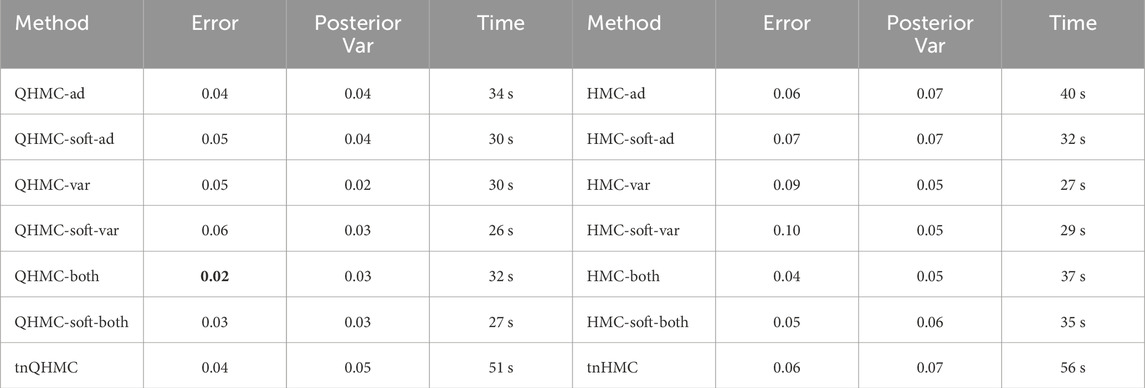
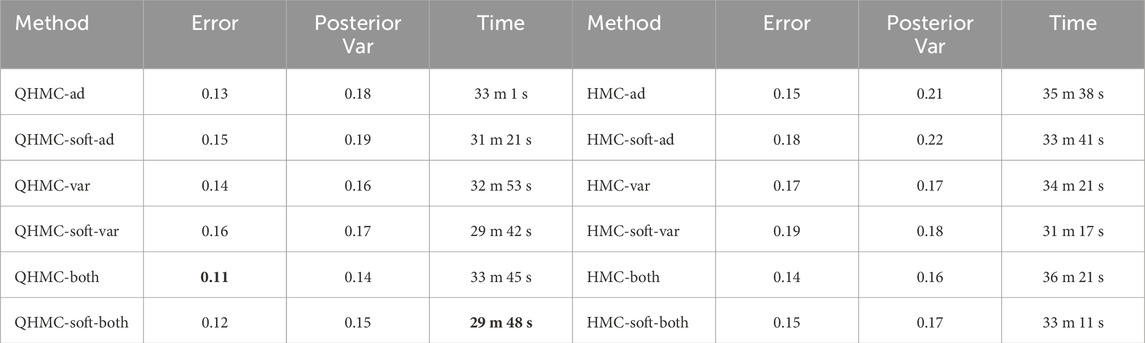
In Table 1, the comparison between QHMC and HMC algorithms with a dataset size of 200 is presented. The relative error values indicate that QHMC yields approximately $20\%$ more accurate results than HMC, and it achieves this with a shorter processing time. Consequently, QHMC demonstrates both higher accuracy and efficiency compared to HMC.

Table 1

Table 1. Comparison of QHMC and HMC on 2D, inequality.

Figure 1 presents the relative error values of the algorithms with respect to two parameters: the size of the dataset and signal-to-noise ratio (SNR). It can be seen that the most accurate results without adding any noise are provided by QHMCboth and tnQHMC algorithms with around $10\%$ relative error. However, upon introducing the noise to the data and increasing its magnitude, a distinct pattern is observed. The QHMC methods exhibit relative error values of approximately $15\%$ within the SNR range of $15\%$ to $20\%$. In contrast, the relative error of the truncated Gaussian methods increases to $25\%$ within the same noise range. This pattern demonstrates that QHMC methods can tolerate noise and maintain higher accuracy under these conditions.

Figure 1

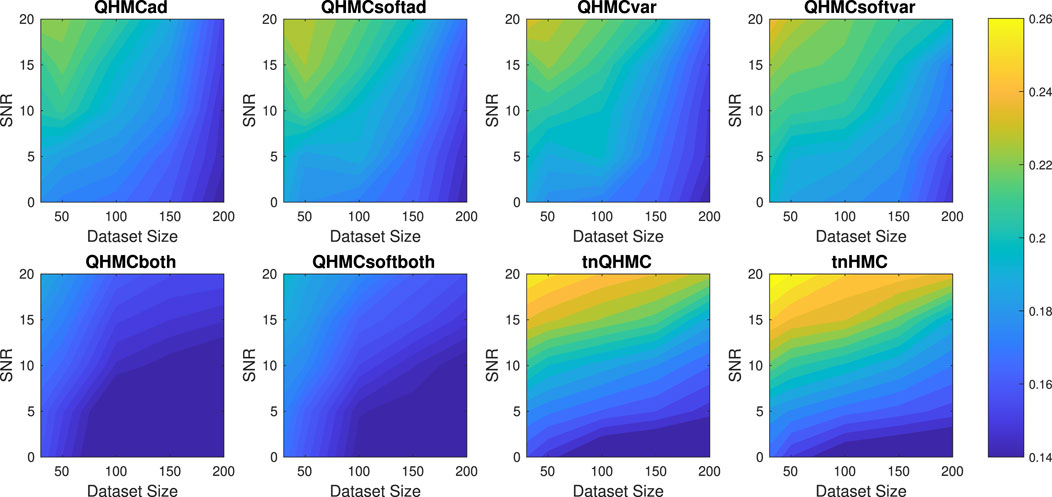
Figure 1. Relative error of the algorithms with different SNR and data sizes for Example 1 (2D), inequality.

Further, we compare the time performances of the algorithms in Figure 2 which demonstrates that QHMC methods, especially the probabilistic QHMC approaches can perform much faster than the truncated Gaussian methods. In this simple 2D problem in Equation 36, the presence of noise does not significantly impact the running times of the QHMC algorithms. In contrast, truncated Gaussian algorithms are slower under noisy environment even when the dataset size is small. Additionally, it can be observed in Figure 3 that the QHMC algorithms, especially QHMCvar and QHMCboth are the most robust ones, as their small relative error comes with a small posterior variance. In contrast, the posterior variance values of the truncated Gaussian methods are higher than QHMC posterior variances even when there is no noise, and gets higher along with the relative error (see Figure 1) when the SNR levels increase. Combining all of these experiments, the inference is that QHMC methods achieve higher accuracy within a shorter time frame. Consequently, these methods prove to be more efficient and robust as they can effectively tolerate changes in parameters. Additionally, it is worth noting that a slight improvement is achieved in the performance of truncated Gaussian algorithms by implementing tnQHMC. Based on the numerical results obtained by tnQHMC, it can be concluded that employing tnQHMC not only yields higher accuracy but also saves some computational time compared to tnHMC.

Figure 2

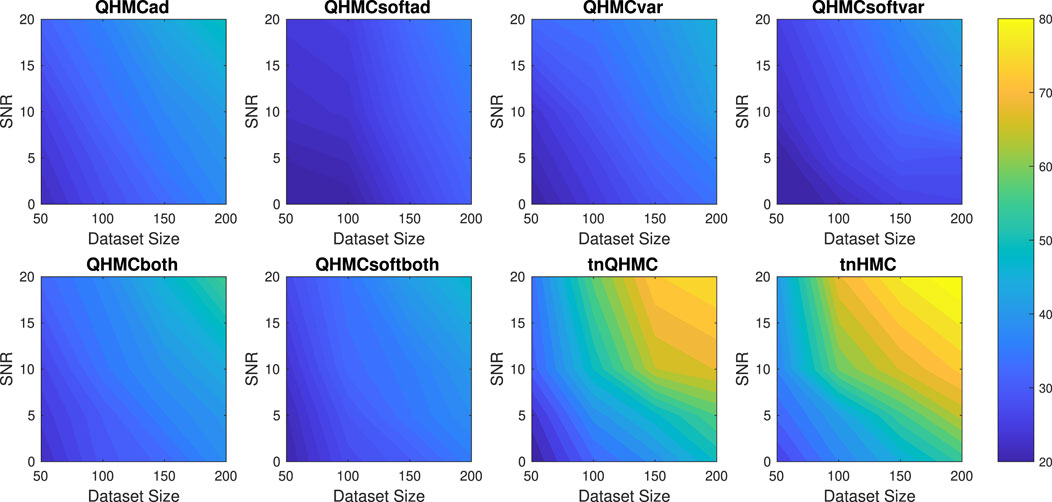
Figure 2. Execution times (in seconds) of the algorithms with different SNR and datasizes for Example 1 (2D), inequality.

Figure 3

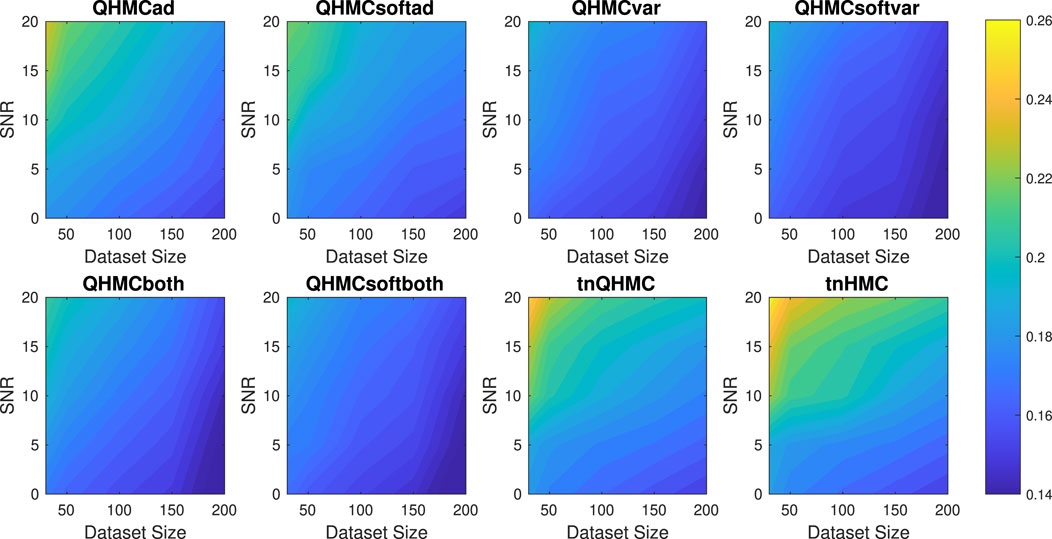
Figure 3. Posterior variances of the algorithms with different SNR and datasizes for Example 1 (2D), inequality.

4.1.2 Example 2

Consider the 10D Ackley function Eriksson and Poloczek (2021) defined as follows:

$f\left(x\right)=-a\exp \left(-b\sqrt{\frac{1}{d}{\displaystyle \sum _{i=1}^d}{x}_i^2}\right)-\exp \left(-b\sqrt{\frac{1}{d}{\displaystyle \sum _{i=1}^d}\cos c{x}_i}\right)+a+\exp 1,(37)$

where $d=10$, $a=20$, $b=0.2$ and $c=2\pi$. We study the performance of the algorithms on the domain ${[-\mathrm{10,10}]}^{10}$ while enforcing the function in Equation 37 to be greater than 5. Table 2 shows the comparison between QHMC and HMC algorithms with 200 data points. Similar to the previous example, the results indicate that QHMC yields approximately 20% more accurate results than HMC in a shorter amount of time.

Table 2

Table 2. Comparison of QHMC and HMC on 10D, inequality.

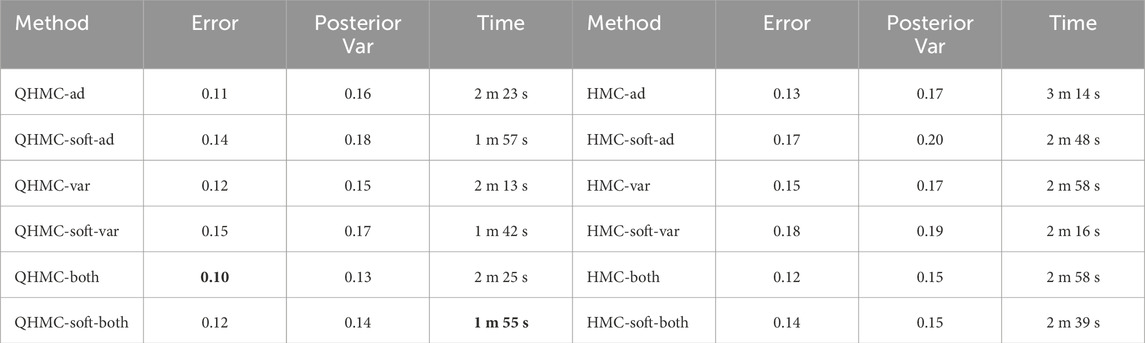
Figure 4 illustrates that QHMCboth, QHMCsoftboth and truncated Gaussian algorithms yield the lowest error when there is no noise in the data. However, as the noise level increases, truncated Gaussian methods fall behind all QHMC approaches. Specifically, both the QHMCboth and QHMCsofthboth algorithms demonstrate the ability to tolerate noise levels up to $15\%$ with an associated relative error of approximately $15\%$. However, other variants of QHMC methods display greater noise tolerance when dealing with larger datasets. With fewer than 100 data points, the error rate reaches around $25\%$, but it decreases to $15-20\%$ when the number of data points exceeds 100.

Figure 4

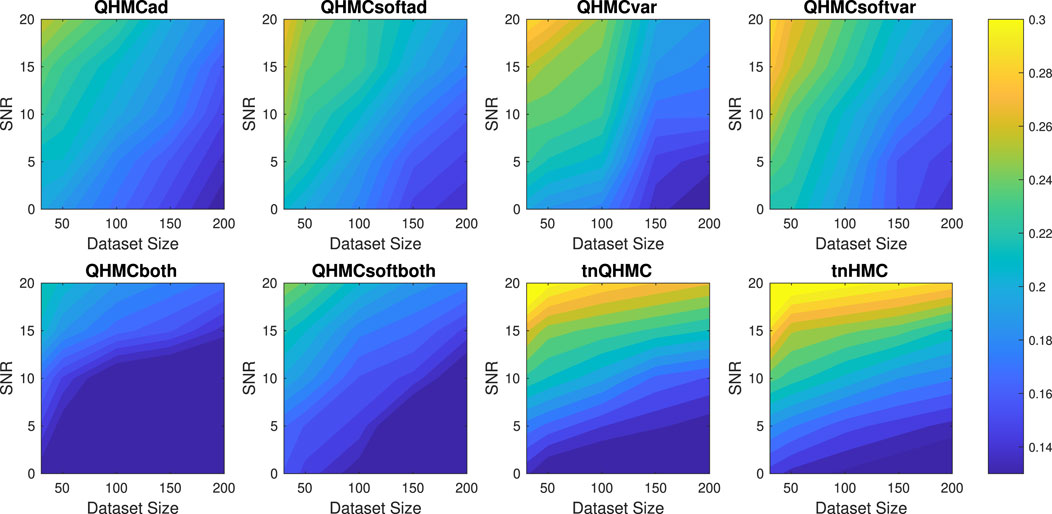
Figure 4. Relative error of the algorithms with different SNR and data sizes for Example 2 (10D), inequality.

Figure 5 illustrates the time comparison of the algorithms, where QHMC methods provide around $30-35\%$ time efficiency for the datasets larger than a size of 150. Combining this time advantage with the higher accuracy of QHMC indicates that both soft and hard constrained QHMC algorithms outperform truncated Gaussian methods across various criteria. QHMC methods offer the flexibility to employ one of the algorithms depending on the priority of the experiments. For example, if speed is the primary consideration, QHMCsoftvar is the fastest method while maintaining a good level of accuracy. If accuracy is the most important metric, employing QHMCboth would be a wiser choice, as it still offers significant time savings compared to other methods.

Figure 5

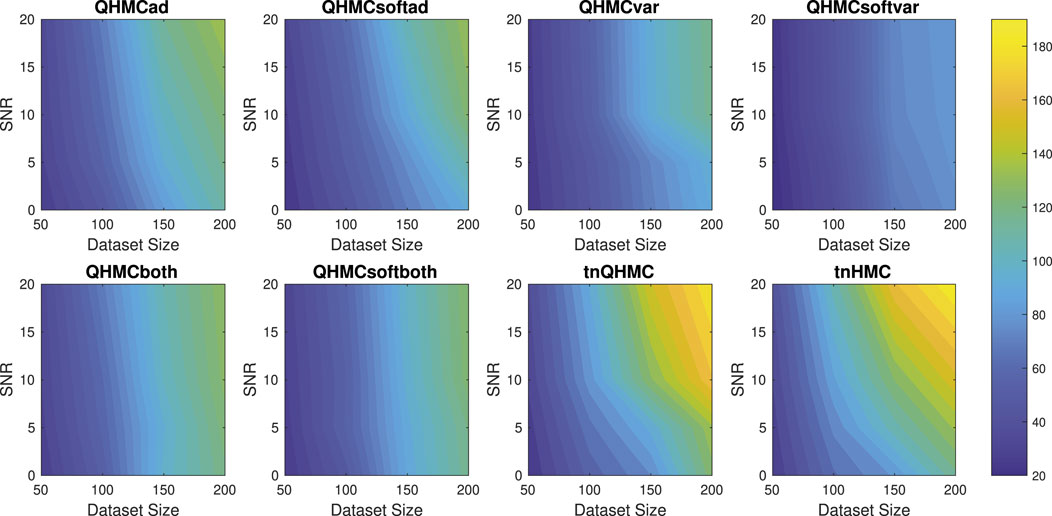
Figure 5. Execution times (in minutes) of the algorithms with different SNR and datasizes for Example 2 (10D), inequality.

Figure 6 presents that the posterior variance values of truncated Gaussian methods are significantly higher than that of the QHMC algorithms, especially when the noise levels are higher than $5\%$. As expected, QHMCvar and QHMCsoftvar algorithms offer the lowest variance, while QHMCboth and QHMCsoftboth follow them. A clear pattern is shown in the figure, in which QHMC approaches can tolerate higher noise levels especially when the dataset is large. It is notable that our method demonstrates a significant increase in efficiency as the dimension increases. When comparing this 10D example to the 2D case, the execution times of the truncated Gaussian methods are notably impacted by the dimension, even in the absence of noise in the datasets. Although their relative error levels can remain low without noise, it takes 1.5 times longer than the QHMC methods to offer those accuracy. Additionally, this observation holds only for cases where the data is noise-free. As soon as noise is present, the accuracy of truncated Gaussian methods deteriorates, whereas QHMC methods can withstand the noise and yield good results in a shorter time span. In all tables, bold values indicate the best performance in each metric.

Figure 6

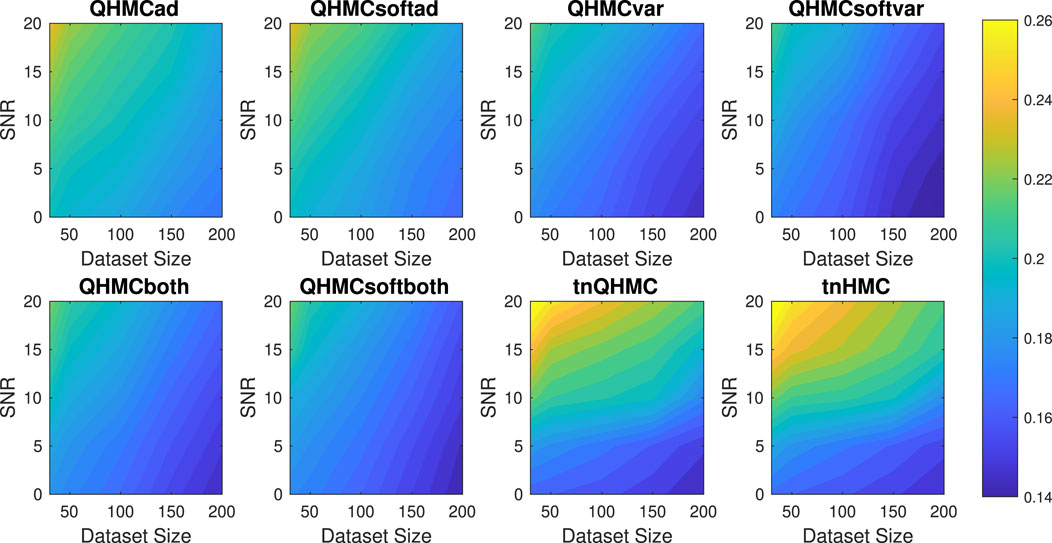
Figure 6. Posterior variances of the algorithms with different SNR and datasizes for Example 2 (10D), inequality.

4.1.3 Example 3: solute transport in heterogeneous porous media

Following the example in Yang et al. (2019), we examine conservative transport within a constant velocity field in heterogeneous porous media. Let us denote the solute concentration by $C(\mathbf{x},t)(\mathbf{x}={(x,y)}^{\text{T}})$, and suppose that the measurements of $C(\mathbf{x},t)$ are available at various locations at different times. Conservation laws can be used to describe the processes of flow and transport. Specifically, Darcy flow equation describes the flow by Yang et al. (2019).

$\left\{\begin{array}{cc}\nabla \cdot \left(K\nabla h\right)=0,\hfill & \mathbf{x}\in \mathbb{D},\hfill \\ \frac{\partial h}{\partial \mathbf{n}}=0,\hfill & y=0\text{\hspace{0.17em}or\hspace{0.17em}}y=L_2,\hfill \\ h=H_1,\hfill & x=0,\hfill \\ h=H_2,\hfill & x=L_1,\hfill \end{array}\right.(38)$

where $h(\mathbf{x},w)$ is the hydraulic head, $\mathbb{D}=[0,L_1]\times [0,L_2]$ is the simulation domain with $L_1=256$ and $L_2=128$, $H_1$ and $H_2$ are known boundary head values and $K(\mathbf{x},w)$ is the unknown hydraulic conductivity field. The field is represented as a stochastic process, with the distribution of values described by a log-normal distribution. Specifically, it is expressed as $K(\mathbf{x},w)=\exp Z(\mathbf{x},w)$, where is a second-order stationary GP with a known exponential covariance function, $\text{Cov}\{Z(\mathbf{x}),Z({\mathbf{x}}^{\prime })\}={\sigma }_Z^2\exp (-|\mathbf{x}-{\mathbf{x}}^{\prime }|/l_z)$ where variance ${\sigma }_Z^2=2$ and correlation length $l_z=5$. The solute transport by the advection-dispersion equation Emmanuel and Berkowitz (2005), Lin and Tartakovsky (2009), Yang et al. (2019) can be described by

$\left\{\begin{array}{cc}\frac{\partial C}{\partial t}+\nabla \cdot \left(v\mathbf{C}\right)=\nabla \cdot \left(\frac{D_w}{\tau }+\alpha \Vert \mathbf{v}{\Vert }_2\right)\nabla C,\hfill & \mathbf{x}\text{\hspace{0.17em}in\hspace{0.17em}}\mathbb{D},\hfill \\ C=Q\delta \left(\mathbf{x}-{\mathbf{x}}^{*}\right),\hfill & t=0,\hfill \\ \frac{\partial C}{\partial \mathbf{n}}=0,\hfill & y=0\text{\hspace{0.17em}or\hspace{0.17em}}y=L_2\text{\hspace{0.17em}or\hspace{0.17em}}x=L_1,\hfill \\ C=0,\hfill & x=0.\hfill \end{array}\right.(39)$

In this context, $C(\mathbf{x},t;w)$ represents the solute concentration defined over $\mathbb{D}\times [0,T]\times \mathrm{\Omega }$, $\mathbf{v}$ denotes the fluid velocity given by $\mathbf{v}(\mathbf{x};w)=-K(\mathbf{x};\omega )\nabla h(\mathbf{x},\omega )/\varphi$ with $\varphi$ being porosity; $D_w$ is the diffusion coefficient, $\tau$ stands for the tortuosity, and $\alpha$ is the dispersivity tensor, with diagonal components ${\alpha }_L$ and ${\alpha }_T$. In this study, the transport parameters for Equations 38, 39 are defined as: $\varphi =0.317,\tau ={\varphi }^{1/3},D_w=2.5\times 10^{-5},{\alpha }_L=5$ and ${\alpha }_T=0.5$. Lastly, the solute is instantaneously injected at $\mathbf{x}*=(\mathrm{50,64})$ at $t=0$ with the intensity $Q=1$ Yang et al. (2019). In Figure 7, the ground truth with observation locations and constraint locations are presented to provide an insight into the structure of solute concentration.

Figure 7

Figure 7. Observation locations (black squares) and constraint locations (black stars).

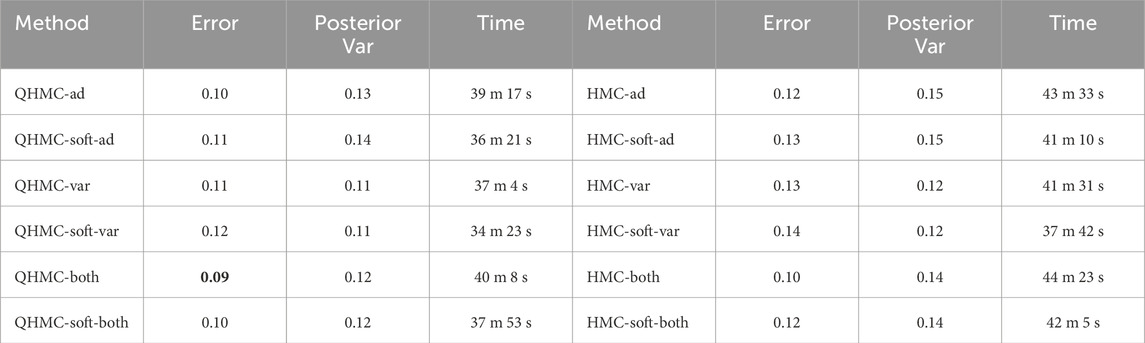
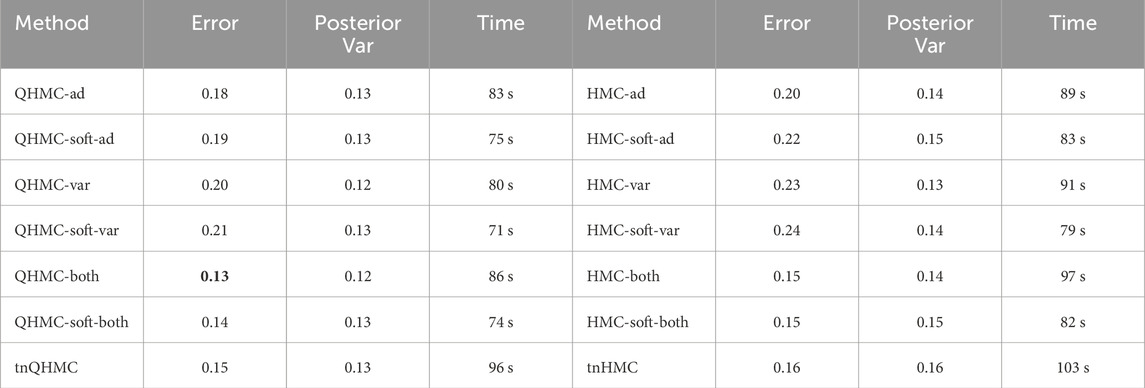
Table 3 presents a comparison of all versions of QHMC and HMC methods, along with the truncated Gaussian algorithms. Similar to the results observed with synthetic examples, the QHMCboth, QHMCsoftboth, and tnQHMC algorithms demonstrate the most accurate predictions with a relative error of $13-15\%$. Notably, QHMCsoftboth emerges as the fastest among the methods while achieving higher accuracy. For instance, the error value obtained by QHMCsoftboth is 0.14, whereas tnQHMC’s error is 0.15. However, QHMCsoftboth delivers a $20\%$ time efficiency gain with slightly superior accuracy. In Figure 8, a comprehensive comparison of the algorithms is presented. The decrease in relative error values is noticeable as constraints are gradually added, following the adopted adaptive approach. Initially, the error is 0.5 and gradually decreases to approximately 0.13. Furthermore, it is evident that the QHMCboth and QHMCsoftboth methods consistently deliver the most accurate results at each step, whereas the performance of the QHMCsoftvar method is outperformed by other approaches.

Table 3

Table 3. Comparison of QHMC and HMC on solute transport with nonnegativity.

Figure 8

Figure 8. The change in relative error while adding constraints, solute transport.

4.1.4 Example 4: heat transfer in a hallow sphere

This 3-dimensional example considers a heat transfer problem in a hallow sphere. Let $B_r(0)$ represent a ball centered at 0 with radius $r$. Defining the hallow sphere as $D=B_4(0)-B_2(0)$, the equations are given as Yang et al. (2021).

$\left\{\begin{array}{cc}\frac{\partial u\left(\mathbf{x},t\right)}{\partial t}-\nabla \cdot \left(\kappa \nabla u\left(\mathbf{x},t\right)\right)=0,\hfill & \mathbf{x}\in D,\hfill \\ \kappa \frac{\partial u\left(\mathbf{x},t\right)}{\partial \mathbf{n}}={\theta }^2{\left(\pi -\theta \right)}^2{\varphi }^2{\left(\pi -\varphi \right)}^2,\hfill & \text{if\hspace{0.17em}}\Vert \mathbf{x}{|}_2=4\text{\hspace{0.17em}and\hspace{0.17em}}\varphi \ge 0,\hfill \\ \kappa \frac{\partial u\left(\mathbf{x},t\right)}{\partial \mathbf{n}}=0,\hfill & \text{if\hspace{0.17em}}\Vert \mathbf{x}{\Vert }_2=4\text{\hspace{0.17em}and\hspace{0.17em}}\varphi <0,\hfill \\ u\left(\mathbf{x},t\right)=0,\hfill & \text{if\hspace{0.17em}}\Vert \mathbf{x}{\Vert }_2=2.\hfill \end{array}\right.(40)$

In this context, $\mathbf{n}$ denotes the normal vector pointing outward, while $\theta$ and $\varphi$ represent the azimuthal and elevation angles, respectively, of points within the sphere. We determine the precise heat conductivity in Equation 40 using $\kappa =1.0+\exp (0.05u)$. The quadratic elements with 12,854 degrees of freedom are employed, and we set $y(\mathbf{x})=u(\mathbf{x},10)$ to solve the partial differential equations (PDE). Starting with 6 initial locations at 0 on the surface, 6 new constraint locations are introduced based on the active learning approach of the QHMC version. In Figure 9, the decrease is evident in relative error while the constraints are added step by step. In addition, Figure 10 shows the ground truth and the GP result obtained by QHMCsoftboth algorithm, where QHMCsoftboth $y*(x)$ matches the reference model. The constraint locations of the result are shown in Figure 11. Moreover, its posterior variance is small based on the results shown in Table 2. The table also provides the error, posterior variance and time performances of QHMC and HMC algorithms, where the advantages of QHMC over HMC in all categories, even with the truncated Gaussian algorithm are observed. Although all of the algorithms complete the GP regression in less than 1 min, comparing the truncated Gaussian method with QHMC-based algorithms, $40-60\%$ time efficiency along with compatible accuracy of QHMC algorithms is achieved. In addition to the time and accuracy performances, it is shown that the posterior variance values are smallest with QHMCvar and QHMCboth approaches, followed by tnQHMC and QHMCad approaches. Using HMC sampling in all methods generates larger posterior variances.

Figure 9

Figure 9. The change in relative error while adding constraints, heat equation.

Figure 10

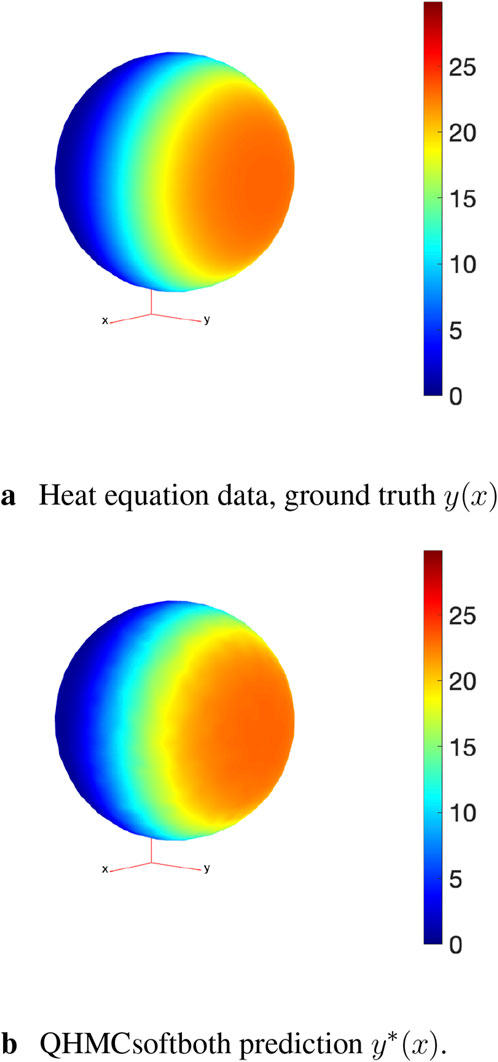
Figure 10. Comparison of the ground truth and QHMCsoftboth result. (A) Heat equation data, ground truth y(x). (B) QHMCsoftboth prediction y*(x).

Figure 11

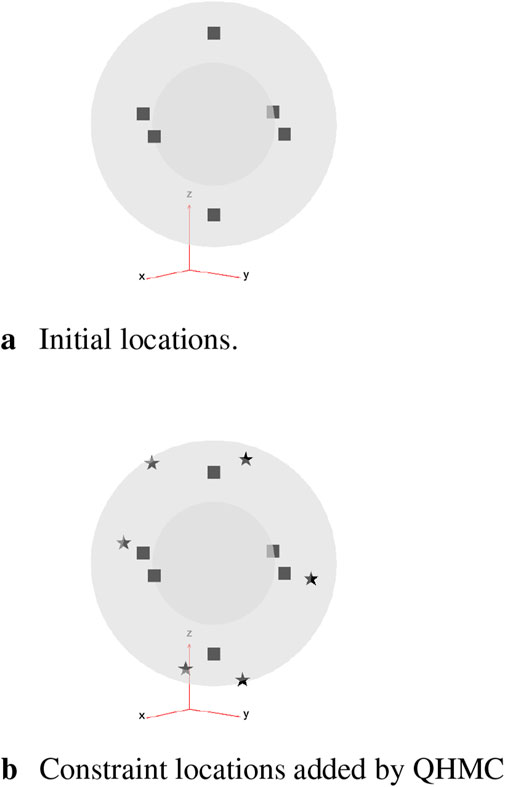
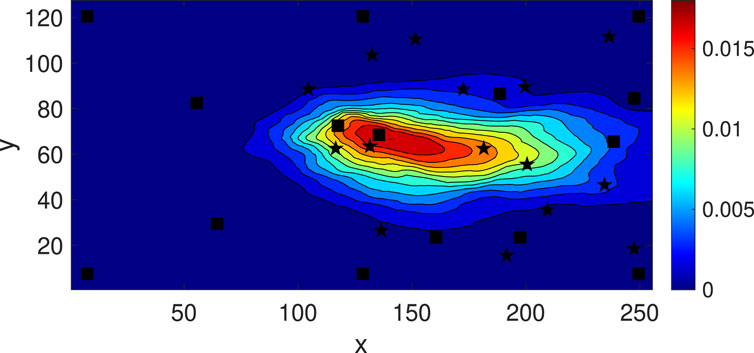
Figure 11. Initial locations (squares) and adaptively added constraint locations (stars). (A) Initial locations. (B) Constraint locations added by QHMC.

4.2 Monotonicity constraints

This section provides two numerical examples to investigate the effectiveness of our algorithms on monotonicity constraints. As stated in Section 2.3.1, the monotonicity constraints are enforced in the direction of active variables. Similar to the comparisons in previous section, we illustrate the advantages of QHMC over HMC, and then compare the performance of QHMC algorithms with additive GP approach introduced in López-Lopera et al. (2022) with respect to the same criteria as in the previous section.

4.2.1 Example 1

Consider the following 5D function with monotonicity constraints López-Lopera et al. (2022):

$f\left(x\right)=\arctan \left(5x_1\right)+\arctan \left(2x_2\right)+x_3+2x_4^2+\frac{2}{1+\exp -10\left(x_5-\frac{1}{2}\right)}.(41)$

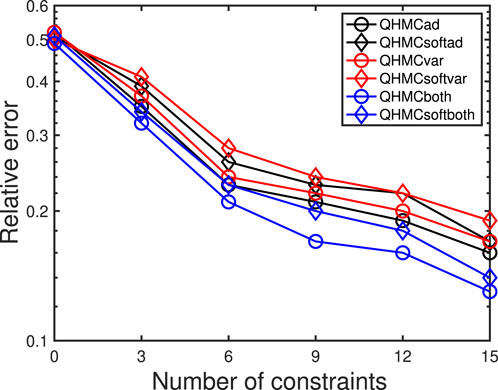
In this example, we enforce the function in Equation 41 to be non-decreasing with x ∈ [0, 1]^5. Table 5 shows the performances of HMC and QHMC algorithms, where we observe that QHMC achieves higher accuracy with lower variance in a shorter amount of time. The comparison proves that each version of QHMC is more efficient than HMC In addition, Figure 12 shows the relative error values of QHMC and additive GP algorithms with respect to the change in SNR and dataset size. Based on the results, it is clear that QHMCboth and QHMCsoftboth provide the most accurate results under every different condition, while the difference is more remarkable for the cases in which noise is higher. Although QHMCboth and QHMCsoftboth provides the most accurate results, other QHMC versions also generate more accurate results then additive GP method. Moreover, Figure 13 shows that the soft-constrained QHMC approaches are faster than the hard-constrained QHMC, while hard-constrained QHMC versions are still faster than additive GP algorithm. Additionally, we can see in Figure 14 that QHMC, both hard and soft constrained versions, can reduce the posterior variance. Unlike the additiveGP method, QHMC approaches generate small variances even under high noise.

Figure 12

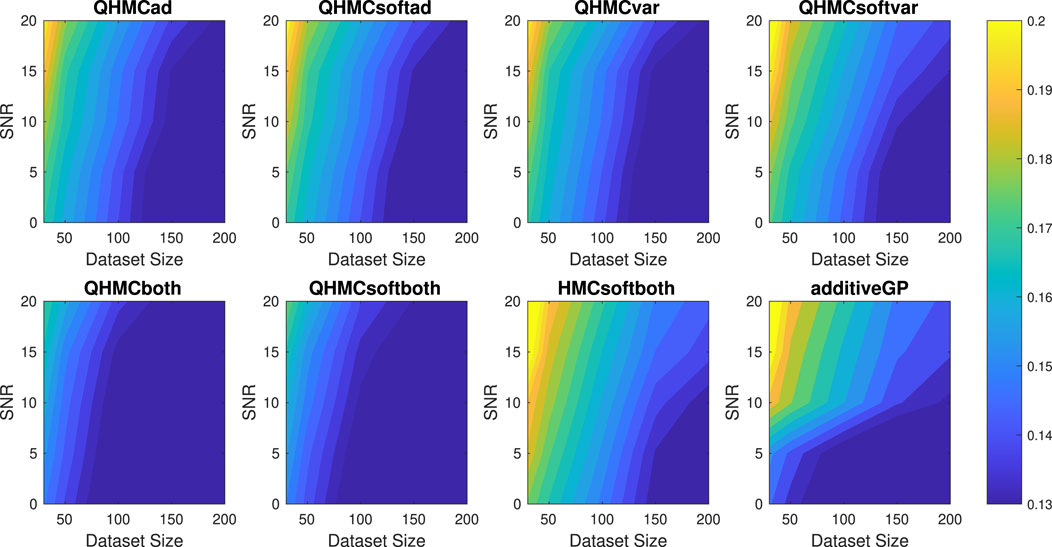
Figure 12. Relative error of the algorithms with different SNR and data sizes for Example 1 (5D), monotonicity.

Figure 13

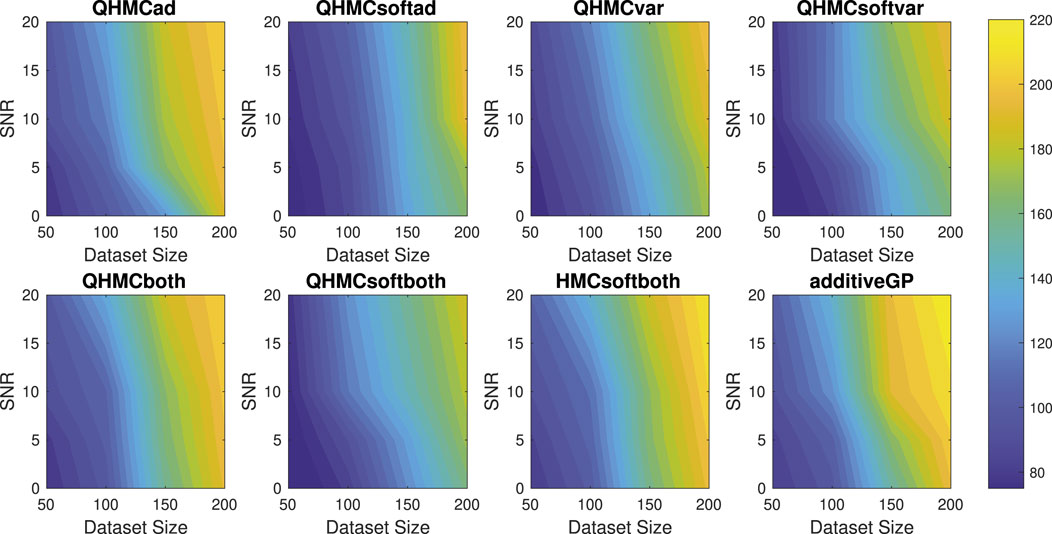
Figure 13. Execution times (in seconds) of the algorithms with different SNR and data sizes for Example 1 (5D), monotonicity.

Figure 14

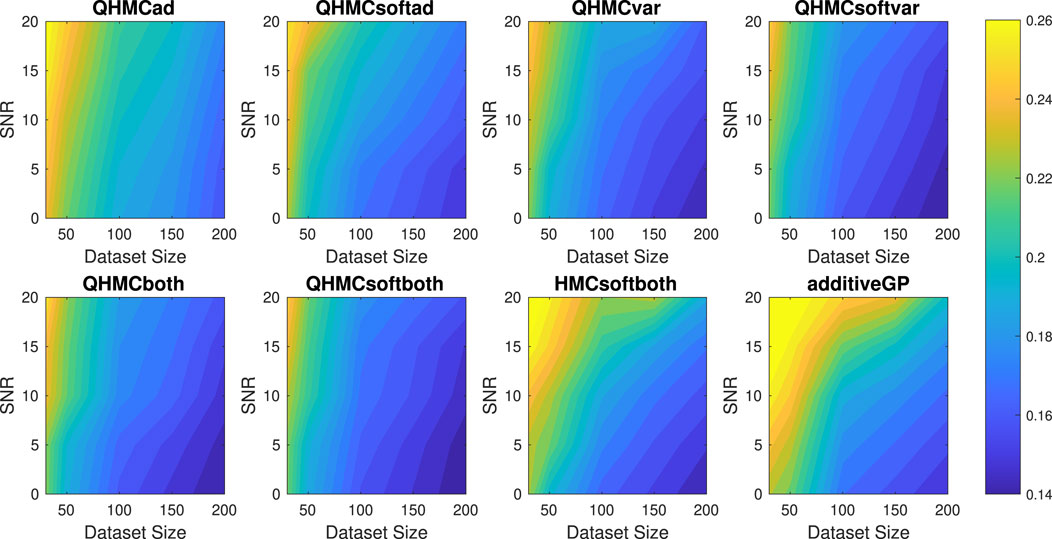
Figure 14. Posterior variances of the algorithms with different SNR and data sizes for Example 1 (5D), monotonicity.

4.2.2 Example 2

We provide a 20-dimensional example to indicate the applicability and effectiveness of QHMC algorithms on higher dimensions with monotonicity constraint. We consider the target function used in López-Lopera et al. (2022), Bachoc et al. (2022).

$f\left(x_1,x_2,\dots ,x_d\right)={\displaystyle \sum _{i=1}^d}\arctan 5\left[1-\frac{i}{d+1}\right]x_i(42)$

with $d=20$. We enforce monotonicity constraint on the 20D function in Equation 42.

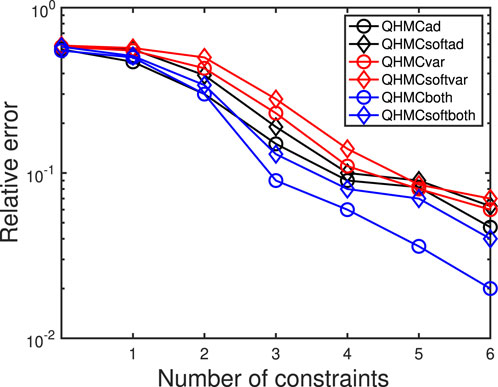
Table 6 illustrates accuracy and time advantages of QHMC over HMC. For each version of QHMC and HMC, using QHMC sampling in a specific version accelerates the process while increasing the accuracy. Overall comparison shows that among all versions with QHMC and HMC sampling, QHMCboth is the most accurate approach, while QHMCsoftboth is the fastest and ranked second in accuracy. Figures 15, 16 show the relative error and time performances of QHMC-based algorithms, HMCsoftboth and additive GP algorithm, respectively. In this final example with the highest dimension, the same phenomenon is observed as in previous results: soft-constrained versions demonstrate greater efficiency, while hard-constrained QHMC approaches remain faster than additive GP across different conditions, including high noise levels. Based on Figure 15, QHMCboth can tolerate noise levels up to $10\%$ with the smallest error, and it can still provide good accuracy (error is around 0.15) even when the SNR is higher than $10\%$. It is also worth to mention that although the error values generated by HMCsoftboth and additiveGP are pretty close, HMCsoftboth performs faster than additiveGP, especially when the dataset is larger and noise level is higher. Furthermore, QHMC reduces the posterior variance as in shown in Figure 17. The behavior of the algorithms follows the same trend as 5-dimensional example, where the methods can tolerate the noise in the data, especially with larger datasets.

Figure 15

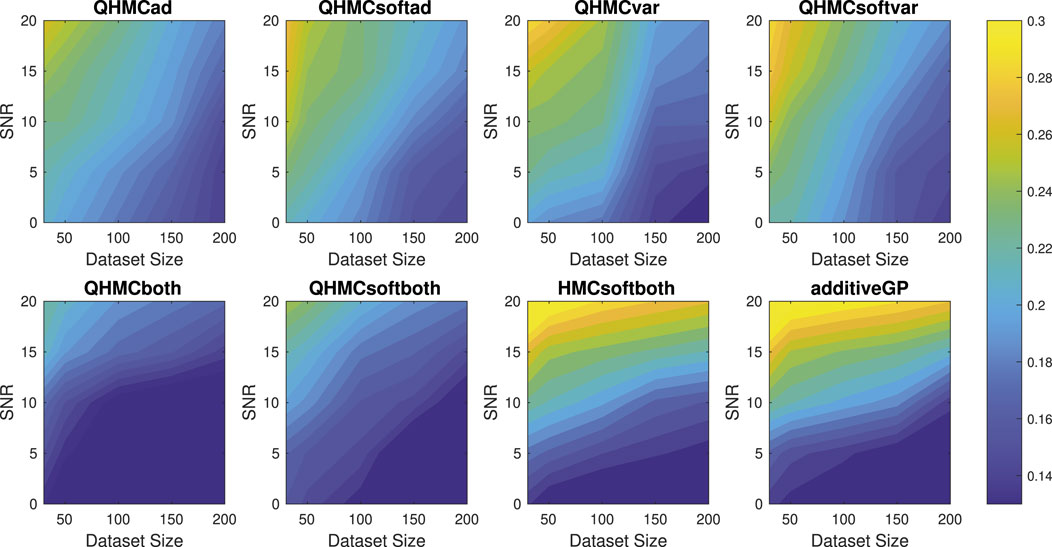
Figure 15. Relative error of the algorithms with different SNR and data sizes for Example 2 (20D), monotonicity.

Figure 16

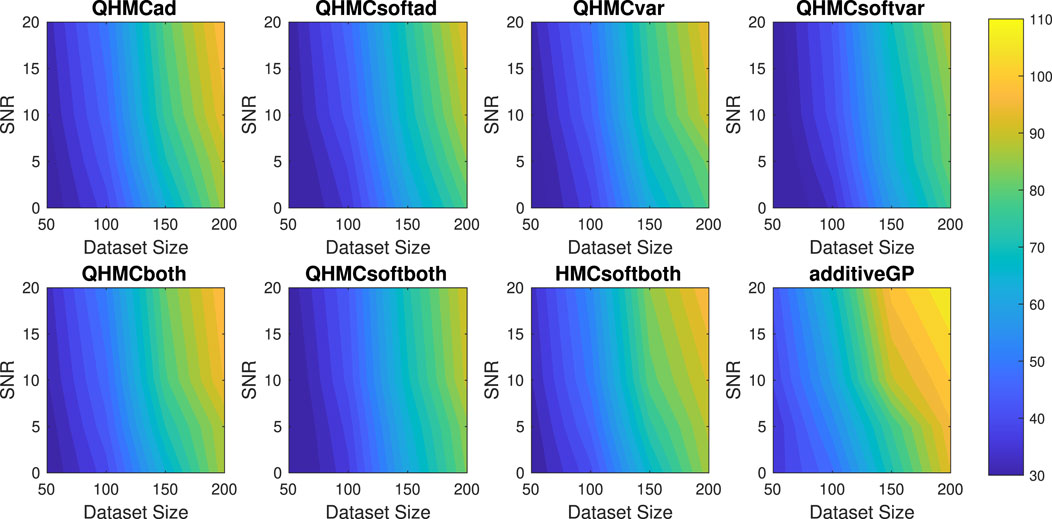
Figure 16. Execution times (in minutes) of the algorithms with different SNR and data sizes for Example 2 (20D), monotonicity.

Figure 17

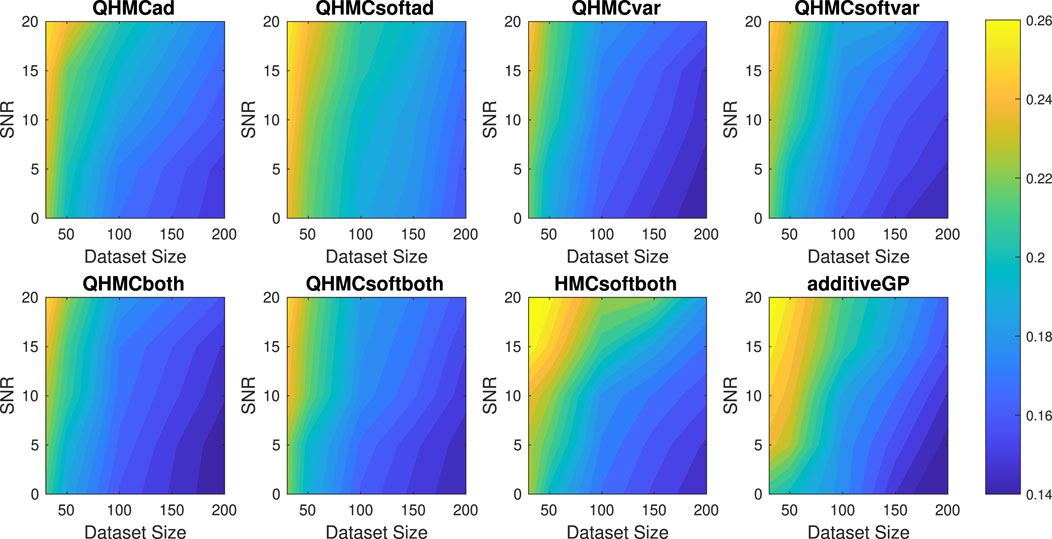
Figure 17. Posterior variances of the algorithms with different SNR and data sizes for Example 2 (20D), monotonicity.

4.3 Discussion

In the scope of the proposed QHMC-based method, this work investigates the advantages and disadvantages of using soft-constrained approach on physics-informed GP regression. The comparison of modified versions of proposed algorithm along with a recent method is further performed to validate the superiority of the approach. The significant findings and the corresponding possible reasons are summarized as follows:

1. Synthetic examples are designed to highlight the robustness and efficiency of proposed method. In one example, considering two criteria: dataset size and SNR. The QHMC-based algorithms are evaluated in an environment with a range of $0-20\%$ SNR, and results provided in Figures 1, 4, 12, 15 have shown that both soft and hard-constrained versions of proposed method tolerate the noise in the data, especially if it is less then $10\%$. In addition, the methods are more tolerant when the dataset size increases. This part of the experiments for each synthetic example proved the robustness of the proposed method.

2. Additionally, the numerical results of synthetic examples include the execution times for when the SNR and dataset size increase in each example. The goal is to underscore the effectiveness of the proposed algorithm. Figures 2, 5, 13, 16 show the time advantages of the algorithms, especially for the soft-constrained versions.

3. The dimensions of synthetic examples are selected to verify that the robustness and efficiency of the algorithms remain for higher dimensions. For inequality-constrained scenarios, evaluations are performed on 2D and 10D problems, while for monotonicity-constrained algorithms evaluations are performed on 5D and 20D problems. The results have verified that the performance of proposed methods can maintain the accuracy for higher-dimensional cases in a relatively short amount of times.

4. The real-life applications are chosen to verify that the proposed method is promising to generalize different type of problems. The solute concentration example is a 2D problem with non-homogeneous structure, while heat transfer problem is a 3D problem that requires PDE solving. On the contrary of synthetic examples, in this set of experiments, the dataset size is fixed and there is no injected Gaussian noise in the data. We present a comprehensive comparison of all methods along with the truncated Gaussian algorithm. Step by step decrease in the error is presented in Figures 8, 9, where the success of all versions are verified.

5. The proposed method is a combination of QHMC algorithm and a probabilistic approach for phiysics-informed GP. QHMC training provides accuracy due to its broad state space exploration, while probabilistic approach lowers the variance. In each case, we start with the experiments conducted with fixed dataset size and zero SNR to demonstrate the superiority of QHMC over HMC. The HMC versions of the proposed methods are implemented and compared to the corresponding QHMC algorithms in Tables 1, 3–6. The findings for every single case confirm that QHMC enhances the accuracy, robustness and efficiency. After demonstrating the superiority of QHMC method, a comprehensive evaluation is performed for QHMC-based methods in different scenarios. Again, for the sake of verification of efficiency of soft-constrained QHMC, we implemented the hard constrained versions by choosing the violation probability as 0.005. The findings indicate that the soft-constrained approaches reduce computational expenses while maintaining accuracy comparable to that of the hard-constrained counterparts. Releasing the constraints by a probabilistic sense has brought efficiency, while decreasing the posterior variance.

6. We should also note that while the numerical results indicate that the current approach is a robust and efficient QHMC algorithm, the impact of the probability of constraint violation should be further investigated. The experiments were conducted with a relatively low probability of releasing the constraints (around $5\%$) and the accuracy was maintained under these conditions. However, allowing for more violations may pose limitations. In addition, the performance of the proposed approach on different type of constrained optimization problems, including those involving equality constraints, can be more challenging. Addressing these challenges can be both a limitation and a potential future work for QHMC-based, physics-informed GP regression.

7. While our examples demonstrate the efficiency of the proposed approach in higher dimensions (up to 20), evaluating the performance of the algorithms in much higher dimensions, such as 100 or more, remains a subject for future work. Based on the current results, we expect that the QHMC will outperform HMC, due to its sampling advantages. For example, in Liu and Zhang (2019) a stochastic version of QHMC approach is efficiently applied to train a two-layer neural network for classifying the MNIST dataset, where the weight matrices have dimensions of $784\times 200$ and $200\times 10$. Similarly, a stochastic QHMC approach in Kochan et al. (2022) is employed for image reconstruction on MNIST data, treating the dataset as a $\mathrm{60,000}\times 784$ matrix. However for constrained GP problems, the algorithm might need further improvements to effectively address the challenges posed by the curse of dimensionality in more demanding scenarios.

Table 4

Table 4. Comparison of QHMC and HMC on heat transfer with nonnegativity.

Table 5

Table 5. Comparison of QHMC and HMC on 5D, monotonicity.

Table 6

Table 6. Comparison of QHMC and HMC on 20D, monotonicity.

5 Conclusion

Leveraging the accuracy of QHMC training and the efficiency of probabilistic approach, this work introduced a soft-constrained QHMC algorithm to enforce inequality and monotonicity constraints on the GP. The proposed algorithm reduces the difference between ground truth and the posterior mean in the resulting GP model, while increasing the efficiency by attaining the accurate results in a short amount of time. To further enhance the performance of the QHMC algorithms across various scenarios, modified versions of QHMC are implemented adopting adaptive learning. These versions provide flexibility in selecting the most suitable algorithm based on the specific priorities of a given problem.

We provided the convergence of QHMC by showing that its steady-state distribution approach the true posterior density, and theoretically justified that the probabilistic approach preserves convergence. Finally, we have implemented our methods to solve several types of optimization problems. Each experiment initially outlined the benefits of QHMC sampling in comparison to HMC sampling. These advantages remained consistent across all cases, resulting in approximately a $20\%$ time-saving and $15\%$ higher accuracy. Having demonstrated the advantages of QHMC sampling, further evaluation on the performances of the algorithms across various scenarios was performed. The examples cover higher-dimensional problems featuring both inequality and monotonicity constraints. Furthermore, the evaluations include real-world applications where injecting physical properties is essential, particularly in cases involving inequality constraints.

In the context of inequality-constrained Gaussian processes (GPs), we explored 2-dimensional and 10-dimensional synthetic problems, along with two real applications involving 2-dimensional and 3-dimensional data. For synthetic examples, the relative error, posterior variance and execution time of the algorithms were compared while gradually increasing the noise level and dataset size. Overall, QHMC-based algorithms outperformed the truncated Gaussian methods. Although the truncated Gaussian methods provide high accuracy in the absence of noise and are compatible with QHMC approaches, their relative error and posterior variances increase as the noise appeared and increased. Moreover, the advantages of soft-constrained QHMC became more evident, particularly in higher-dimensional cases, when compared to truncated Gaussian and even hard-constrained QHMC. The time comparison of the algorithms underscores that the truncated Gaussian methods are significantly impacted by the curse of dimensionality and large datasets, exhibiting slower performance under these conditions. In real-world application scenarios featuring 2-dimensional and 3-dimensional data, the findings were consistent with those observed in the synthetic examples. Although the accuracy level may not reach the highest levels observed in the synthetic examples and 3-dimensional heat equation problem, the observed trend remains consistent. The lower accuracy observed in the latter problem can be attributed to the non-homogeneous structure of solute concentration.

In the case of monotonicity-constrained GP, we addressed 5-dimensional and 20-dimensional examples, utilizing the same configuration as employed for inequality-constrained GP. A comprehensive comparison was conducted between all versions of QHMC algorithms and the additive GP method. The results indicate that QHMC-based approaches hold a notable advantage, particularly in scenarios involving noise and large datasets. While additive GP proves to be a strong method suitable for high-dimensional cases, QHMC algorithms performed faster and yielded lower variances.

In conclusion, the work has demonstrated that soft-constrained QHMC is a robust, efficient and flexible method that can be applicable to higher dimensional cases and large datasets. Numerical results have shown that soft-constrained QHMC is promising to be generalized to various applications with different physical properties.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: Datasets are from author’s one of the previous papers. Requests to access these datasets should be directed to DK, ZGlrMzE4QGxlaGlnaC5lZHU=.

Author contributions

DK: Formal Analysis, Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. XY: Formal Analysis, Methodology, Project administration, Resources, Supervision, Writing–review and editing, Funding acquisition.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the NSF CAREER DMS-2143915.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abrahamsen, P., and Benth, F. E. (2001). Kriging with inequality constraints. Math. Geol. 33, 719–744. doi:10.1023/a:1011078716252

CrossRef Full Text | Google Scholar

Agrell, C. (2019). Gaussian processes with linear operator inequality constraints. arXiv Prepr. arXiv:1901, 03134.

Google Scholar

Bachoc, F., López-Lopera, A. F., and Roustant, O. (2022). Sequential construction and dimension reduction of Gaussian processes under inequality constraints. SIAM J. Math. Data Sci. 4, 772–800. doi:10.1137/21m1407513

CrossRef Full Text | Google Scholar

Barbosa, B. H. G., Xu, N., Askari, H., and Khajepour, A. (2021). Lateral force prediction using Gaussian process regression for intelligent tire systems. IEEE Trans. Syst. Man, Cybern. Syst. 52, 5332–5343. doi:10.1109/tsmc.2021.3123310

CrossRef Full Text | Google Scholar

Barbu, A., and Zhu, S.-C. (2020) Monte Carlo methods, 35. Springer.

Google Scholar

Chati, Y. S., and Balakrishnan, H. (2017). “A Gaussian process regression approach to model aircraft engine fuel flow rate,” in Proceedings of the 8th international conference on cyber-physical systems, 131–140.

Google Scholar

Da Veiga, S., and Marrel, A. (2012). Gaussian process modeling with inequality constraints. Ann. la Fac. Sci. Toulouse Mathématiques 21, 529–555. doi:10.5802/afst.1344

CrossRef Full Text | Google Scholar

Dürichen, R., Pimentel, M. A., Clifton, L., Schweikard, A., and Clifton, D. A. (2014). “Multi-task Gaussian process models for biomedical applications,” in IEEE-EMBS international Conference on Biomedical and health informatics (BHI) (IEEE), 492–495.

Google Scholar

Emmanuel, S., and Berkowitz, B. (2005). Mixing-induced precipitation and porosity evolution in porous media. Adv. water Resour. 28, 337–344. doi:10.1016/j.advwatres.2004.11.010

CrossRef Full Text | Google Scholar

Eriksson, D., and Poloczek, M. (2021). Scalable constrained Bayesian optimization, In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics (PMLR 130:730–738, 2021), 730–738606.

Google Scholar

Ezati, M., Esmaeilbeigi, M., and Kamandi, A. (2024). Novel approaches for hyper-parameter tuning of physics-informed Gaussian processes: application to parametric pdes. Eng. Comput. 40, 3175–3194. doi:10.1007/s00366-024-01970-8

CrossRef Full Text | Google Scholar

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B. (2014). Bayesian data analysis. Philadelphia, Pennsylvania: Tyler & Francis Group, Inc.

Google Scholar

Gulian, M., Frankel, A., and Swiler, L. (2022). Gaussian process regression constrained by boundary value problems. Comput. Methods Appl. Mech. Eng. 388, 114117. doi:10.1016/j.cma.2021.114117

CrossRef Full Text | Google Scholar

Guo, S., Xu, H., and Zhang, L. (2015). Convergence analysis for mathematical programs with distributionally robust chance constraint. SIAM J. Optim. 27, 784–816. (to appear). doi:10.1137/15m1036592

CrossRef Full Text | Google Scholar

Hess, C. (1999). Conditional expectation and martingales of random sets. Pattern Recognit. 32, 1543–1567. doi:10.1016/s0031-3203(99)00020-5

CrossRef Full Text | Google Scholar

Jensen, B. S., Nielsen, J. B., and Larsen, J. (2013). “Bounded Gaussian process regression,” in 2013 IEEE international workshop on machine learning for signal processing (MLSP) (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Kochan, D., Zhang, Z., and Yang, X. (2022). “A quantum-inspired Hamiltonian Monte Carlo method for missing data imputation,” in Mathematical and scientific machine learning (PMLR), 17–32.

Google Scholar

Kohanpur, A. H., Saksena, S., Dey, S., Johnson, J. M., Riasi, M. S., Yeghiazarian, L., et al. (2023). Urban flood modeling: uncertainty quantification and physics-informed Gaussian processes regression forecasting. Water Resour. Res. 59, e2022WR033939. doi:10.1029/2022wr033939

CrossRef Full Text | Google Scholar

Kuss, M., and Rasmussen, C. (2003). Gaussian processes in reinforcement learning. Adv. neural Inf. Process. Syst. 16.

Google Scholar

Lange-Hegermann, M. (2021). Linearly constrained Gaussian processes with boundary conditions. In Proceedings of The 24th International Conference on Artificial Intelligence and Statistics (PMLR628 130: 1090–1098).

Google Scholar

Li, X.-Q., Song, L.-K., Choy, Y.-S., and Bai, G.-C. (2023). Fatigue reliability analysis of aeroengine blade-disc systems using physics-informed ensemble learning. Philosophical Trans. R. Soc. A 381, 20220384. doi:10.1098/rsta.2022.0384

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, G., and Tartakovsky, A. M. (2009). An efficient, high-order probabilistic collocation method on sparse grids for three-dimensional flow and solute transport in randomly heterogeneous porous media. Adv. Water Resour. 32, 712–722. doi:10.1016/j.advwatres.2008.09.003

CrossRef Full Text | Google Scholar

Liu, Z., and Zhang, Z. (2019). Quantum-inspired Hamiltonian Monte Carlo for bayesian sampling. arXiv Prepr. arXiv:1912.01937.

Google Scholar

López-Lopera, A., Bachoc, F., and Roustant, O. (2022). High-dimensional additive Gaussian processes under monotonicity constraints. Adv. Neural Inf. Process. Syst. 35, 8041–8053.

Google Scholar

López-Lopera, A. F., Bachoc, F., Durrande, N., and Roustant, O. (2018). Finite-dimensional Gaussian approximation with linear inequality constraints. SIAM/ASA J. Uncertain. Quantification 6, 1224–1255. doi:10.1137/17m1153157

CrossRef Full Text | Google Scholar

Maatouk, H., and Bay, X. (2017). Gaussian process emulators for computer experiments with inequality constraints. Math. Geosci. 49, 557–582. doi:10.1007/s11004-017-9673-2

CrossRef Full Text | Google Scholar

Maatouk, H., Roustant, O., and Richet, Y. (2015). Cross-validation estimations of hyper-parameters of Gaussian processes with inequality constraints. Procedia Environ. Sci. 27, 38–44. doi:10.1016/j.proenv.2015.07.105

CrossRef Full Text | Google Scholar

Mao, Z., Jagtap, A. D., and Karniadakis, G. E. (2020). Physics-informed neural networks for high-speed flows. Comput. Methods Appl. Mech. Eng. 360, 112789. doi:10.1016/j.cma.2019.112789

CrossRef Full Text | Google Scholar

Nabati, M., Ghorashi, S. A., and Shahbazian, R. (2022). Jgpr: a computationally efficient multi-target Gaussian process regression algorithm. Mach. Learn. 111, 1987–2010. doi:10.1007/s10994-022-06170-3

CrossRef Full Text | Google Scholar

Pensoneault, A., Yang, X., and Zhu, X. (2020). Nonnegativity-enforced Gaussian process regression. Theor. Appl. Mech. Lett. 10, 182–187. doi:10.1016/j.taml.2020.01.036

CrossRef Full Text | Google Scholar

Pimentel, M. A., Clifton, D. A., Clifton, L., and Tarassenko, L. (2013). “Probabilistic estimation of respiratory rate using Gaussian processes,” in 2013 35th annual international conference of the IEEE engineering in medicine and biology society (EMBC) (IEEE), 2902–2905.

CrossRef Full Text | Google Scholar

Qiang, B., Shi, K., Liu, N., Ren, J., and Shi, Y. (2023). Integrating physics-informed recurrent Gaussian process regression into instance transfer for predicting tool wear in milling process. J. Manuf. Syst. 68, 42–55. doi:10.1016/j.jmsy.2023.02.019

CrossRef Full Text | Google Scholar

Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2017). Machine learning of linear differential equations using Gaussian processes. J. Comput. Phys. 348, 683–693. doi:10.1016/j.jcp.2017.07.050

CrossRef Full Text | Google Scholar

Rasmussen, C. E., and Nickisch, H. (2010). Gaussian processes for machine learning (gpml) toolbox. J. Mach. Learn. Res. 11, 3011–3015.

Google Scholar

Riihimäki, J., and Vehtari, A. (2010). “Gaussian processes with monotonicity information,” in Proceedings of the thirteenth international conference on artificial intelligence andf statistics (JMLR Workshop and Conference Proceedings), 645–652.

Google Scholar

Salzmann, M., and Urtasun, R. (2010). Implicitly constrained Gaussian process regression for monocular non-rigid pose estimation. Adv. neural Inf. Process. Syst. 23.

Google Scholar

Song, F., Shi, K., and Li, K. (2021). “A nonlinear finite element-based supervised machine learning approach for efficiently predicting collapse resistance of wireline tool housings subjected to combined loads,” in ASME International Mechanical Engineering Congress and Exposition (American Society of Mechanical Engineers). doi:10.1115/imece2021-7222285680V012T12A057

CrossRef Full Text | Google Scholar

Stein, M. L. (1988). Asymptotically efficient prediction of a random field with a misspecified covariance function. Ann. Statistics 16, 55–63. doi:10.1214/aos/1176350690

CrossRef Full Text | Google Scholar

Swiler, L. P., Gulian, M., Frankel, A. L., Safta, C., and Jakeman, J. D. (2020). A survey of constrained Gaussian process regression: approaches and implementation challenges. J. Mach. Learn. Model. Comput. 1, 119–156. doi:10.1615/jmachlearnmodelcomput.2020035155

CrossRef Full Text | Google Scholar

Wang, Y., Wang, Z., Han, K., Tiwari, P., and Work, D. B. (2021). “Personalized adaptive cruise control via Gaussian process regression,” in 2021 IEEE international intelligent transportation systems conference (ITSC) (IEEE), 1496–1502.

CrossRef Full Text | Google Scholar

Wilkie, D., and Galasso, C. (2021). Gaussian process regression for fatigue reliability analysis of offshore wind turbines. Struct. Saf. 88, 102020. doi:10.1016/j.strusafe.2020.102020

CrossRef Full Text | Google Scholar

Williams, C. K., and Rasmussen, C. E. (2006). Gaussian Processes for Machine Learning 2. MA: MIT press Cambridge.

Google Scholar

Yang, X., Barajas-Solano, D., Tartakovsky, G., and Tartakovsky, A. M. (2019). Physics-informed cokriging: a Gaussian-process-regression-based multifidelity method for data-model convergence. J. Comput. Phys. 395, 410–431. doi:10.1016/j.jcp.2019.06.041

CrossRef Full Text | Google Scholar

Yang, X., Tartakovsky, G., and Tartakovsky, A. M. (2021). Physics information aided kriging using stochastic simulation models. SIAM J. Sci. Comput. 43, A3862–A3891. doi:10.1137/20m1331585

CrossRef Full Text | Google Scholar

Zhang, H. (2004). Inconsistent estimation and asymptotically equal interpolations in model-based geostatistics. J. Am. Stat. Assoc. 99, 250–261. doi:10.1198/016214504000000241

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

additiveGP Additive Gaussian Process method

GP Gaussian Process

HMC Hamiltonian Monte Carlo

HMCad Hard-constrained Hamiltonian Monte Carlo with adaptivity

HMCboth Hard-constrained Hamiltonian Monte Carlo with both adaptivity and variance

HMCsoftad Soft-constrained Hamiltonian Monte Carlo with adaptivity

HMCsoftboth Soft-constrained Hamiltonian Monte Carlo with both adaptivity and variance

HMCsoftvar Soft-constrained Hamiltonian Monte Carlo with variance

HMCvar Hard-constrained Hamiltonian Monte Carlo with variance

MCMC Markov chain Monte Carlo

MH Metropolis-Hastings

PDE Partial differential equations

QHMC Quantum-inspired Hamiltonian Monte Carlo

QHMCad Hard-constrained Quantum-inspired Hamiltonian Monte Carlo with adaptivity

QHMCboth Hard-constrained Quantum-inspired Hamiltonian Monte Carlo with adaptivity and variance

QHMCsoftad Soft-constrained Quantum-inspired Hamiltonian Monte Carlo with adaptivity

QHMCsoftboth Soft-constrained Quantum-inspired Hamiltonian Monte Carlo with both adaptivity and variance

QHMCsoftvar Soft-constrained Quantum-inspired Hamiltonian Monte Carlo with variance

QHMCvar Hard-constrained Quantum-inspired Hamiltonian Monte Carlo with variance

SNR Signal-to-noise ratio

tnHMC Truncated Gaussian method with Hamiltonian Monte Carlo sampling

tnQHMC Truncated Gaussian method with Quantum-inspired Hamiltonian Monte Carlo sampling

Symbols

${\delta }_{x,x^{\prime }}$ Kronecker Delta

${\sigma }^2$ Signal variance

$\theta$ Hyperparameters of Gaussian model

$l$ Length-scale