Particle swarm optimization based neural network automatic controller for stability steering control of four-wheel drive electric vehicle

In addressing the steering stability issues of four-wheel-drive electric vehicles on surfaces such as wet, slippery, frozen, and soft terrains, a novel control method based on particle swarm optimization for neural networks is proposed in this study. The approach integrates the advantages of Proportional-Integral-Derivative control, particle swarm optimization, and neural networks. By constructing a neural network model with input, hidden, and output layers, the study introduces particle swarm optimization algorithm for weight and structure optimization. Fuzzy logic and slip control theory are integrated into the steering stability control. The results demonstrated that, under wet and slippery road conditions, the model exhibited a system response time of 15 ms with a steering prediction accuracy of up to 92%. On frozen road surfaces, the model showed a system response time of 18 ms, with a steering prediction accuracy reaching 90%. Compared to other models, it significantly demonstrated superior steering stability control. This suggests that the designed model performs well in handling complex driving environments, indicating high application potential in the field of electric vehicle steering stability control.

1 Introduction

In the course of the modern automotive industry, due to the needs of environmental protection and technological advancement, electric vehicles have become a crucial component of cutting-edge technology. Simultaneously, for enhancing driving safety and comfort, the four-wheel-drive electric vehicle system has garnered widespread attention. This is because the four-wheel-drive system can provide better traction and stability in various road conditions. However, the presence of challenging road surface conditions necessitates the implementation of intelligent control for steering systems to ensure the stability and maneuverability of vehicles (Guo et al., 2022; Najjari et al., 2022; Venkitaraman and Kosuru, 2022). To meet these demands, intelligent control technology is essential, and neural networks excel in handling nonlinear problems, serving as an effective tool for complex system control. However, traditional neural networks may encounter issues such as local optima and overfitting during design, limiting their application potential in four-wheel-drive electric vehicle stability control systems (Powell et al., 2022; Qiu et al., 2022; Safayatullah et al., 2022). In recent years, the Particle Swarm Optimization (PSO) algorithm has gained significant attention as a global optimization strategy due to its simplicity, ease of implementation, and rapid convergence to excellent solutions. Combining the PSO with neural networks allows the construction of an automatic controller that leverages the nonlinear mapping capabilities of neural networks and achieves globally optimal control effects (Cao et al., 2022; Shami et al., 2022; Gheisari et al., 2023). Therefore, this study aims to design a PSO-based neural network automatic controller specifically for the road stability steering of four-wheel-drive electric vehicles. The research is divided into four parts. The first part outlines the research objectives. The second part designs the road stability steering control model for four-wheel-drive electric vehicles. The third part analyzes the experimental effects of the model. The fourth part derives research conclusions.

2 Literature review

With the recent development of electric vehicles, research on the stability aspects of electric vehicles has been steadily increasing. The team led by Liu H applied a highly efficient algorithm based on the Pontryagin’s minimum principle and multiple optimization objectives to validate the practicality of the proposed algorithm. Through hardware testing in circuits, it was determined that in surfaces with reduced friction coefficients, this series of strategies demonstrated significant advantages in improving vehicle handling stability compared to the sole application of the Torque Vectoring Control (TVC) solution, and it exhibited higher efficiency (Liu et al., 2022). The approach introduced by the team led by Jeong Y transformed the problem of path tracking into a controlled yaw rate tracking problem. By employing an integrated control allocation method and combining the results of vehicle simulation software testing, the team empirically demonstrated the significant performance of this strategy in enhancing path tracking efficiency (Jeong and Yim, 2022). The team led by Jin X designed a nonlinear robust controller method applicable to autonomous electric vehicles. The proposed strategy aimed to address uncertainties in parameters, inherent nonlinear issues in the system, and potential external disturbances. The results showed that the novel controller outperformed traditional linear quadratic regulation and robust H-∞ state feedback control systems in terms of vehicle trajectory tracking (Jin et al., 2023). The team led by Ti Y introduced an innovative Internal Model Controller (IMC) with a fractional-order filter. Completed by scholars such as Tan Yan and Zheng Kangcheng, this study actively applied IMC theory and fractional-order thinking. The researchers used a quantum genetic algorithm to optimize time parameters and fractional-order characteristics, thereby enhancing the vehicle’s path tracking performance. Simulation experiment results indicated that this new controller demonstrated significant robustness in adjusting front and rear wheel steering angles to optimize path tracking capability (Ti et al., 2022).

The application areas of algorithms continue to expand. The Gad A G’s team comprehensively assessed various applications of the PSO algorithm, including algorithmic methods, application domains, unresolved issues, and future perspectives. They conducted a detailed analysis of the real-world applications of the PSO algorithm (Gad, 2022). The Pawan Y V R N team proposed two new PSO models based on deep learning, utilizing Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTM) networks to predict the inertial weights of particles, aiming to enhance optimization performance. The results indicated that the newly proposed models outperformed existing inertia-weight-based PSO models in terms of performance (Pawan et al., 2022). Allugunti V R employed deep learning techniques for skin disease classification, specifically focusing on the diagnosis of melanoma. The research team introduced a novel model that utilized deep learning and non-parametric machine learning methods, such as CNNs, for the identification and classification of melanomas. Experimental results demonstrated that this deep learning-based diagnostic approach outperformed existing state-of-the-art technologies in diagnostic accuracy (Allugunti, 2022). Shuraiji A L’s team compared the application of fuzzy logic control and Proportional-Integral-Derivative (PID) controllers in brushless permanent magnet DC motors. The research findings revealed that motors controlled by fuzzy logic exhibited significantly better characteristic responses compared to traditional PID controllers. The study particularly emphasized that for nonlinear systems, the adoption of fuzzy logic control methods was more recommended (Shuraiji and Shneen, 2022).

Additionally, the Wei H’s team proposed a Direct Yaw moment Control (DYC) strategy based on Deep Reinforcement Learning (DRL), which constructs the DYC problem as a Markov decision process and establishes a state set based on observation signals and external yaw moments. On this basis, the deep deterministic strategy gradient algorithm was used to ensure the stability of the algorithm learning process. This method effectively improved the stability of vehicle lateral steering (Wei et al., 2022). The Fan J’s team adopted the Trust Region Policy Optimization (TRPO) method to select the optimal frontier for robot tracking path planning, and determined the optimality and shorter path length of the path planner. The proposed method was validated through simulation and compared with classical and state-of-the-art methods. The results indicated that compared to traditional Deep Q-networks (DQN), the algorithm designed in this study had a faster training speed (Fan et al., 2023). Fan J et al. proposed a cloud computing-based optimization driving method for parallel hybrid electric vehicles to optimize fuel consumption and driving speed. The driving optimization problem was transformed into a spatial domain and appropriately discretized. The performance of this method was studied through real scene simulation, and the results showed that it can achieve real-time energy management of hybrid vehicles (Fan et al., 2019). Fan J and Ou Y et al. described the Markov characteristics of driver power demand and designed an optimized energy management strategy for plug-in hybrid electric vehicles based on the Markov decision process. This strategy could combine the driver’s power demand to switch the deterministic state of the power system, and solve the optimization problem through iterative strategies (Fan et al., 2020).

In summary, in the field of electric vehicle stability research, the current trend is towards designing efficient optimization algorithms and controllers to achieve better vehicle handling stability. The strategies are primarily focused on optimizing issues related to path tracking and control of active front-wheel steering systems. In this study, the combination of PSO algorithm and neural networks is proposed to address stability issues encountered by four-wheel-drive electric vehicles during steering, with the expectation of improving their stability performance.

3 PSO neural network steering stability automatic control model design

This paper proposes a Particle Swarm Optimization Neural Network-based Proportional-Integral-Derivative (PSO-N-PID) control method for vehicle steering, combining the nonlinear mapping capability of neural networks with the simplicity and efficiency of PID control. The method introduces the PSO algorithm for the optimization of weights and structure, demonstrating fast convergence and adaptability to global optimization problems.

3.1 PSO neural network steering control model design

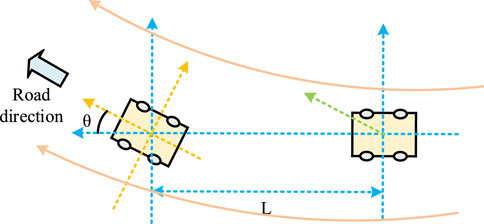
In the context of electric vehicle travel, a reliable and stable steering system is essential. For four-wheel independently driven electric vehicles, independent wheel drive enhances steering stability (Indu and Aswatha Kumar, 2023; Guan et al., 2024). A neural network PID method is designed, integrating the nonlinear mapping capability of neural networks with the efficiency and simplicity of PID control. The study incorporates the PSO algorithm to optimize the neural network’s weights and structure. The advantages of this design include fast convergence, practicality, and applicability to global optimization problems. The model construction begins with establishing a neural network comprising input, hidden, and output layers. The input layer receives external input signals, representing the vehicle’s steering state. The hidden layer processes input signals, potentially containing multiple hidden layers and neurons per layer. The output layer reflects the network’s response, with the output used to adjust PID controller parameters. The vehicle steering model is illustrated in Figure 1.

Figure 1

Figure 1. Vehicle steering model.

The activation function for the hidden layer is defined by Formula 1.

$f\left(x\right)=\frac{e^x-e^{-x}}{e^x+e^{-x}}(1)$

The activation function for the output layer is defined by Formula 2.

$g\left(x\right)=\frac{e^x}{e^x+e^{-x}}(2)$

Gradient descent is employed to adjust the weights in the neural network. This method involves computing the local gradient of the given function and gradually optimizing the weights along this gradient direction, aiming to minimize network error. The weight adjustment formula is represented by Formula 3.

$\Delta w_{mi}\left(n\right)=-\eta \frac{\mathit{\partial }e\left(n\right)}{\mathit{\partial }{w}_{mi}\left(n\right)}(3)$

In Formula 3, $\frac{\mathit{\partial }e\left(n\right)}{\mathit{\partial }w}$ denotes the partial derivative of the error with respect to the weights, and $\eta$ represents the learning rate. The iterative error signal is defined by Formula 4.

$e_j\left(n\right)=d_j\left(n\right)+Y_j\left(n\right)(4)$

Formula 4 represents the network’s expected output, where $d_j\left(n\right)$ signifies the network’s anticipated output, and $Y_j\left(n\right)$ represents the actual output. When the working signal propagates forward, the weighted sum of the input to the hidden layer neurons is given by Formula 5.

$u_I^i\left(n\right)={\displaystyle \sum _{m=1}^3}{\omega }_{mi}\left(n\right){v_M}^m\left(n\right)(5)$

In Formula 5, $I$ represents the hidden layer vector field, ${\omega }_{mi}$ denotes the weight values, $M$ is the vector length of the input layer, and $v_M^m\left(n\right)$ represents the local gradient. Error backpropagation is described by Formula 6.

$\Delta {\omega }_{ij}\left(n\right)=-\eta \frac{\mathit{\partial }e\left(n\right)}{\mathit{\partial }{\omega }_{ij}\left(n\right)}(6)$

Formula 6 introduces ${\omega }_{ij}$ for output layer weights and $\frac{\mathit{\partial }e\left(n\right)}{\mathit{\partial }{\omega }_{ij}\left(n\right)}$ for the gradient of the error with respect to the weights. The study addresses the slow convergence of neural networks by improving them, incorporating parameters to adjust the weights. The algorithmic learning formula is presented in Formula 7.

$\Delta w\left(n\right)=-\eta \left(1-\beta \right)\frac{\mathit{\partial }e\left(n\right)}{\mathit{\partial }{w}_{mi}\left(n\right)}+\beta \Delta w\left(n-1\right)(7)$

In Formula 7, $\beta \Delta w\left(n-1\right)$ is the parameter added, where $\beta$ is the momentum factor, and $\Delta w\left(n-1\right)$ represents the change in weights from the previous step. The addition of correction parameters enhances the step size of weight updates when the direction of weight update is consistent, accelerating convergence. Conversely, when the direction is inconsistent, indicating the presence of a local minimum, the correction parameters reduce the step size, preventing overshooting of the minimum. The process is detailed in Formula 8.

$\eta \left(n+1\right)=\left\{\begin{array}{l}\frac{1}{a}{\eta }^{\prime }\left(n\right),e\left(n+1\right)<e\left(n\right)\\ a\eta \left(n\right),e\left(n+1\right)>e\left(n\right)\end{array}\right.,0.5<a<1.0(8)$

Formula 8 introduces $a$ as the learning rate reduction factor and ${\mu }^{\prime }$ as the learning rate increase factor. The next weight update is determined by Formula 9.

$\Delta w\left(n+1\right)=-{\eta }^{\prime }\left(n+1\right)\left(1-\beta \right)\frac{\mathit{\partial }e\left(n\right)}{\mathit{\partial }{w}_{mi}\left(n\right)}+\beta \Delta w\left(n\right)(9)$

Formula 9 incorporates ${\eta }^{\prime }\left(n+1\right)$, representing the adjusted learning rate. However, this optimization method can sometimes result in slow network learning or convergence to local minima. To address this, the PSO algorithm is introduced to optimize weight adjustments, enhancing the network’s global search capability for faster convergence, as illustrated in Figure 2.

Figure 2

Figure 2. Weight adjustment process.

The iterative rules for particle individual velocities are given by Formula 10.

$v_{id}=\omega v_{id}+c_1\cdot \mathit{ran}{d}_{1d}\cdot \left(pBes{t}_i-x_{id}\right)+c_2\cdot \mathit{ran}{d}_{2d}\cdot \left(nBes{t}_i-x_{id}\right)(10)$

In Formula 10, $\omega$ represents the inertia weight. $c_1$ and $c_2$ are acceleration factors. $\mathit{ran}{d}_{1d}$ 1 and $\mathit{ran}{d}_{2d}$ are constant weights. $nBest$ is the particle’s best position. $pBes{t}_i$ B is the individual’s best position. $x_{id}$ represents the particle’s position. The position update rule is detailed in Formula 11.

$x_{id}=x_{id}+v_{id}(11)$

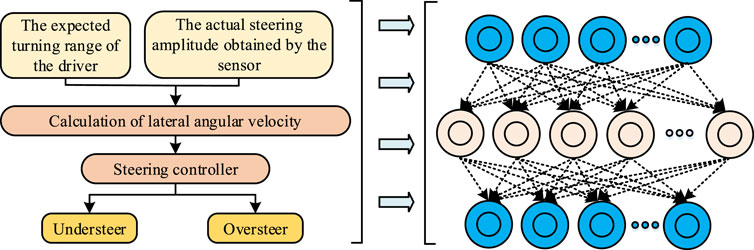
For the engineering implementation of the control system, the system initially collects various data information about the current car state, such as changes in slip angle and slip ratio. Subsequently, the system utilizes this data for dynamic prediction of vehicle behavior, generating a series of control signals. These signals, through the specific actions of the vehicle’s internal execution devices, adjust the vehicle’s yaw rate and wheel speed to achieve precise control of vehicle stability. The study comprehensively evaluates the performance of this control model by contrasting it with the expected vehicle behavior. The interconnected structure of the model is depicted in Figure 3.

Figure 3

Figure 3. Model linkage structure.

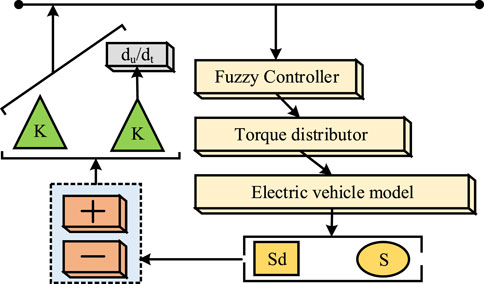
In the development process, continuous calibration and optimization of the automated control module are crucial. Considering the inherent dynamic properties of vehicles and the variability of driving scenarios, developers should incorporate a wide range of unforeseen factors to enhance the stability and reliability of the system. In addition, rapid responsiveness of the system is indispensable to ensure prompt adjustments in response to environmental changes and provide appropriate operational signals. The control model architecture is illustrated in Figure 4.

Figure 4

Figure 4. Model control architecture.

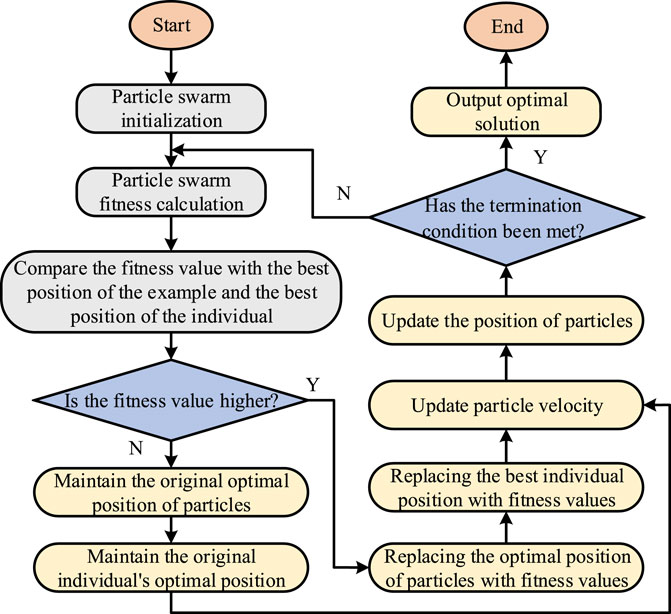
The neural network PID control scheme optimized based on the PSO algorithm involves the following steps in the tuning process: Neural Network Deployment (selecting a reasonable number of neurons and a hierarchical structure to ensure sufficient complexity for simulating control behavior); Particle Swarm Setup (defining the total number of particles, initial positions and velocities, and determining key parameters such as weights and acceleration constants); Data Collection (gathering real vehicle or simulated driving data, covering dynamic indicators such as angular velocity, slip ratio, etc.); Network Training (training the neural network based on collected data, implementing forward prediction and backward error correction, and comprehensively optimizing weights and network architecture using the particle swarm strategy); Continuous Optimization Cycle (repeating the training steps until the system output is stable and accurate or reaches a maximum number of iterations); Dynamic Real-time Calibration (implementing the well-trained network into the vehicle control unit and dynamically fine-tuning PID parameters based on real-time data, completing the closed-loop control process).

In the selection of model domain parameters, the neural network includes an input layer, a hidden layer, and an output layer. The input vehicle state includes state data such as side slip angle change rate, sliding ratio, yaw rate, longitudinal speed, and front wheel angle. The hidden layer adopts a structure of three hidden layers, each containing 20 neurons. The output layer is mainly used to generate signals for adjusting the parameters of the PID controller.

In this study, the number of super-particles is determined to be 40, and the inertia value is usually between 0.4 and 0.9, with an empirical value of 0.7. The acceleration factor is set to two according to the usual situation.

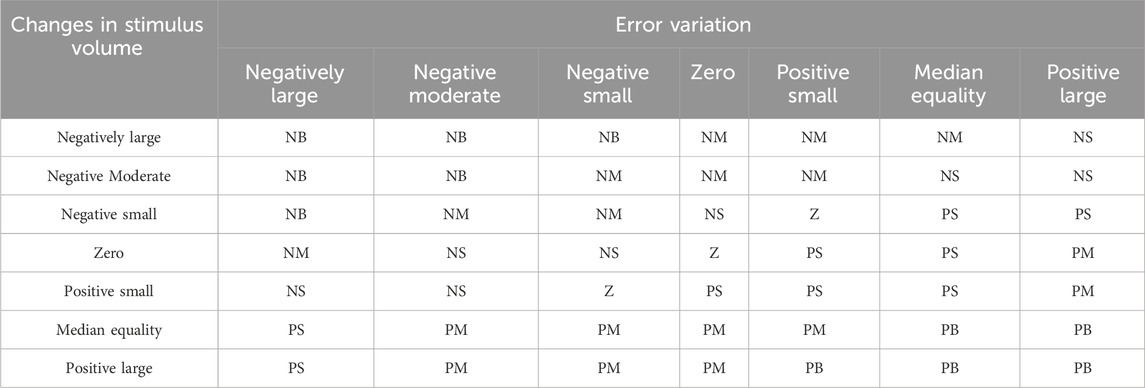
The standard for selecting PID control parameters is to adjust the proportional coefficient (K_p), integral coefficient (K_i), and differential coefficient (K_d) through experiments, in order to find the optimal balance point between stability and response speed.

3.2 Fuzzy control stabilization controller design

The steering stability controller contributes to ensuring vehicle stability during external disturbances. The key to designing the steering stability controller is to control the longitudinal yaw rate and lateral sliding phenomenon when the lateral angle of the car is small (Bartfai et al., 2024). To meet this requirement, a combination of artificial neural networks and particle swarm evolution is employed, incorporating fuzzy control methods. The neural network-based PID control is suitable for controlling the lateral rotational torque, while fuzzy control rules can manage slip ratio. The stability control structure is depicted in Figure 5.

Figure 5

Figure 5. Stability control structure.

Assuming the car is regarded as a two-degree-of-freedom dynamic system model, this model can simplify the dynamic behavior of a real car while maintaining accuracy in analysis. The simplified state equation is represented by Formula 12.

$\left[\begin{array}{l}\dot{\beta }\\ \dot{\gamma }\end{array}\right]=A\left[\begin{array}{l}\beta \\ \gamma \end{array}\right]+B{\delta }_f(12)$

In Formula 12, $\beta$ represents the lateral deviation angle of the center of mass, and $\gamma$ represents the yaw angular velocity. The ideal yaw angular velocity is then given by Formula 13.

${\gamma }_{des}=\frac{v_x}{R}=\frac{v_x}{L+k}{\delta }_f(13)$

In Formula 13, $v_x$ represents the longitudinal velocity, ${\delta }_f$ represents the front wheel steering angle, $L$ represents the wheelbase, and $k$ represents a constant coefficient. The goal of the model is to find an ideal longitudinal yaw angular velocity. Subsequently, corresponding control rules are set to ensure that the real yaw angle quickly catches up with this ideal value. During the actual design process, it is necessary to calculate the ideal yaw angular velocity while considering the influence of real road conditions on the car’s yaw angular velocity. Especially in situations with insufficient road grip, forcibly tracking the ideal throttle yaw angular velocity may lead to vehicle side slip. Therefore, dynamic correction of the ideal longitudinal yaw angular velocity is required based on the road grip conditions. The relationship between the ideal yaw angular velocity, vehicle speed, and front wheel is described by Formula 14.

${\gamma }_d=\left\{\begin{array}{l}{\gamma }_{des},\left|{\gamma }_{des}\right|\le 0.85\frac{\mu g}{v_x}\\ 0.85\frac{\mu g}{v_x}\text{sgn}\left({\gamma }_{des}\right),{\gamma }_{des}>0.85\frac{\mu g}{v_x}\end{array}\right.(14)$

In the development of a neural network controller, the use of PSO is explored to enhance the weight setting in the neural network. This aims to accelerate the learning speed of the network and avoid obtaining only locally optimal results. The initial steps involve setting the neural network weights and determining the total amount of weight and, acceleration coefficient, inertia constraint, and the maximum number of weight adjustment cycles. Subsequently, the calculation of weight efficiency is performed, wherein the input error signal is treated as the optimization goal, specifically the deviation of the vehicle’s yaw velocity. Subsequently, the particle swarm characteristics are updated, adjusting the rate of weight changes and positions to find the optimal strategy. The termination conditions are then checked. If the change in the optimization value of the weights is minimal, it is considered that the best solution has been obtained. Subsequently, the ideal parameters for the PID controller are derived using the determined optimal weights and a specific formula, involving proportional, integral, and derivative control elements to determine the optimal distribution of lateral dynamics. The fitness of neural network weight adaptation uses the yaw angular velocity error as the target function, and the total error is represented by Formula 15.

$g_{v_i}=\frac{1}{2}{\displaystyle \sum _{j=1}^3}{e}_j^2\left(n\right)(15)$

In Formula 15, $e_j$ represents the yaw angular velocity error corresponding to the input. To prevent the car from slipping, precise control of slip ratio is essential. The application of fuzzy logic control to regulate slip ratio is studied, as this technique demonstrates excellent control effectiveness when dealing with nonlinear systems. In designing the fuzzy logic control device, the initial step involves obtaining the difference between the slip ratio target and the actual value. This difference and its rate of change become factors for the controller input, and the output becomes the adjustment torque for the four-wheel slip ratio. By describing these factors using fuzzy sets such as narrow, medium, wide, positive, and negative, the continuous composite control task is simplified into a discrete and intuitive task. The slip ratio adjustment torque derived from the fuzzy control unit must fall within the torque output range of the motor. To achieve this, seven fuzzy sets are defined. Based on knowledge of the variation in the car’s slip ratio, a series of control rules are established to adapt the relationship between input and output more appropriately. The fuzzy logic is detailed in Table 1.

Table 1

Table 1. Fuzzy logic.

In addition to integrating neural networks and fuzzy logic controllers, the management of vehicle roll torque has also begun to emphasize the use of sliding mode control strategies. In the design process of sliding mode controller, the sliding surface is the expression of the actual and expected difference in roll angle speed. The focus of controller design is to make the sliding surface approach infinitesimal, with the goal of continuously fine-tuning and improving parameters.

4 Evaluation of the performance of PSO-N-PID stable steering automatic control model

In the study of testing the effectiveness of the PSO-N-PID stable steering automatic control model, various specialized scenarios were tested, including sinusoidal and serpentine steering angles. Subsequently, the effects under different external environmental disturbances were analyzed.

4.1 Analysis of effects under different steering scenarios

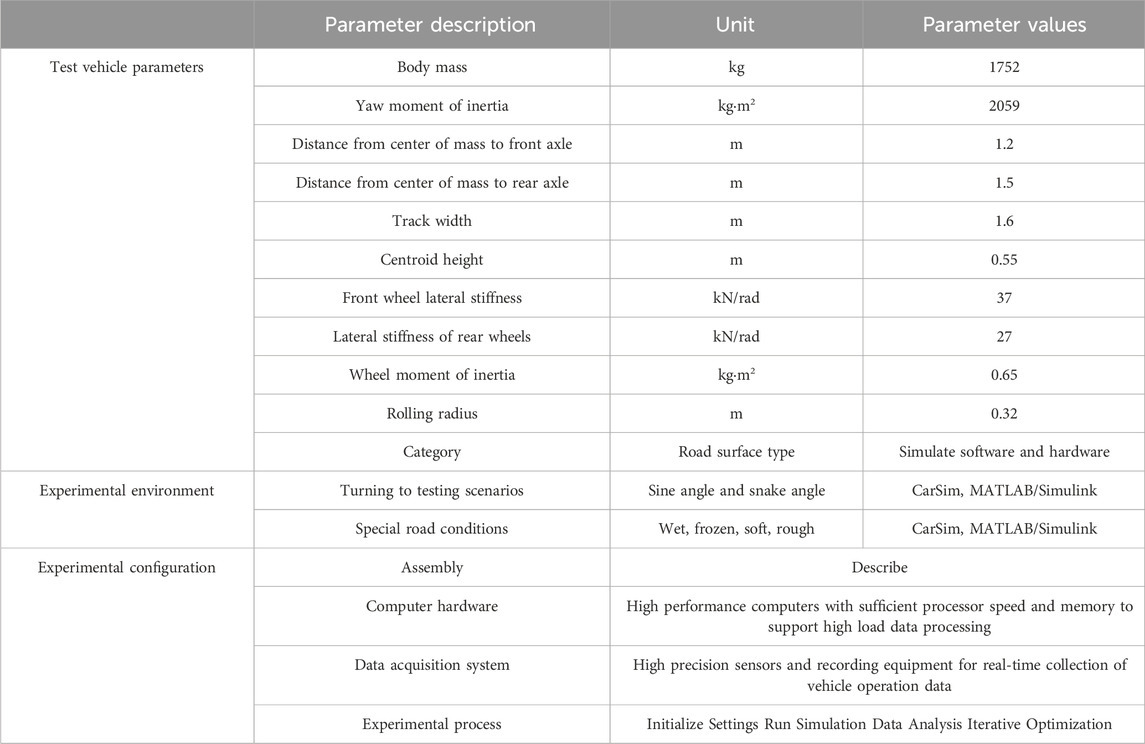
In this entire vehicle simulation experiment, the study involved configuring the parameters of the entire vehicle body to establish a foundation for the overall vehicle performance, ensuring the accuracy of the experimental results. The specific experimental settings for the entire vehicle parameters are presented in Table 2.

Table 2

Table 2. Experimental setup.

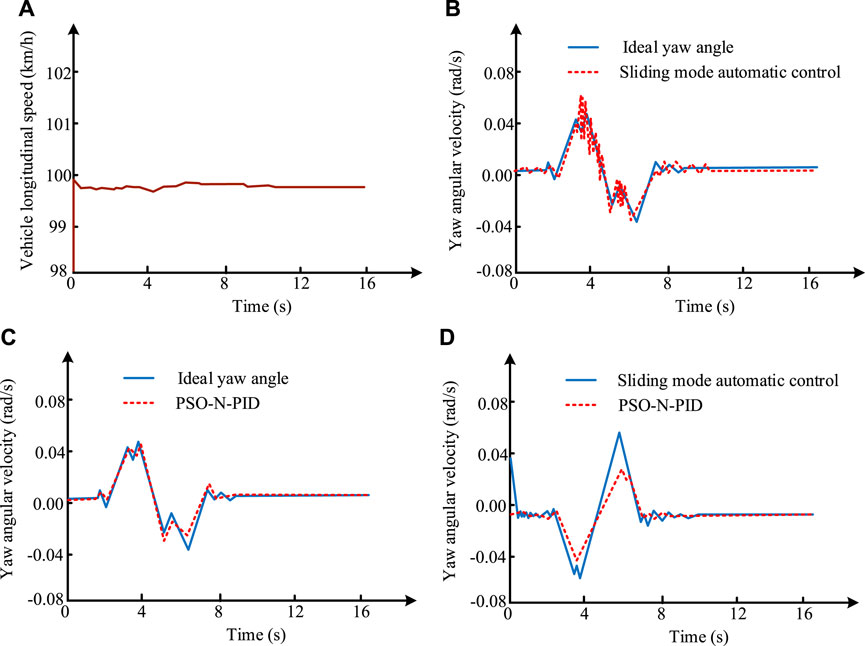
Table 2 illustrates that the adopted entire vehicle model had a mass of 1752 kg. The yaw moment of inertia of the vehicle model was adjusted to 2059 kgm², facilitating the simulation of the dynamic response of actual vehicles. The distances of the vehicle’s center of gravity relative to the front and rear axles were 1.2 m and 1.5 m, respectively, with a track width set at 1.6 m. The effects under sinusoidal steering conditions are shown in Figure 6.

Figure 6

Figure 6. Sine angle working condition effect.

As shown in Figure 6, the yaw rate obtained by Sliding mode automatic control and PSO-N-PID control is consistent with the Ideal yaw angle, but PSO-N-PID control has better and smoother performance, and the vehicle speed is always maintained within the range of 99.8-100 km per hour. In Figure 6A, the variation in the positive maximum yaw angle for sliding mode control was extremely abrupt, with data values ranging from 0.059 to 0.06° per second. In Figure 6B, the PSO-N-PID model prevented system oscillations and addressed the issue of traditional PID algorithms easily falling into local optimal solutions. The maximum yaw angle values were between 0.042–0.043° per second, representing favorable data. In Figure 6C, the lateral displacement amplitude of the PSO-N-PID model decreased by 0.032°, increasing the vehicle’s controllability by 47.2%. The effects under serpentine steering conditions are illustrated in Figure 7.

Figure 7

Figure 7. Effect of snake shaped corner working condition.

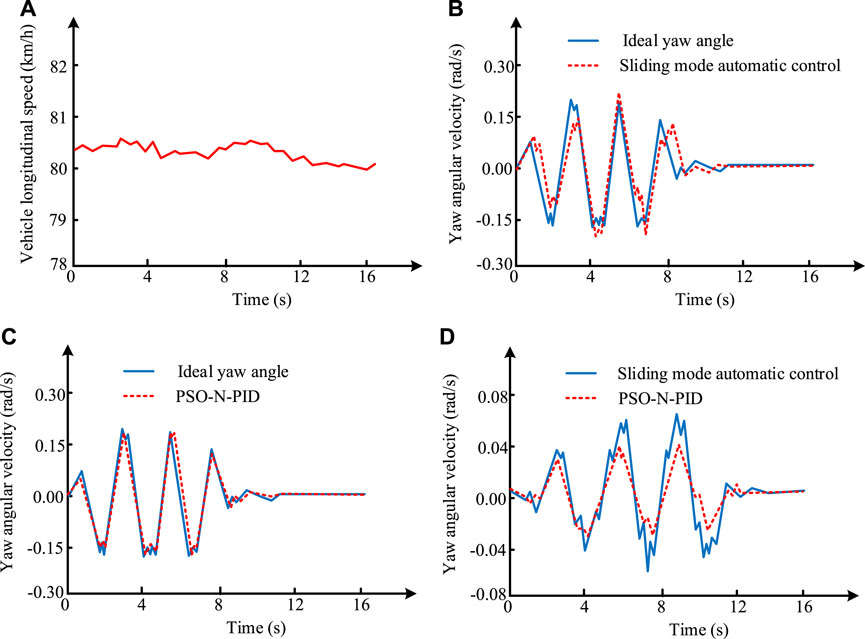
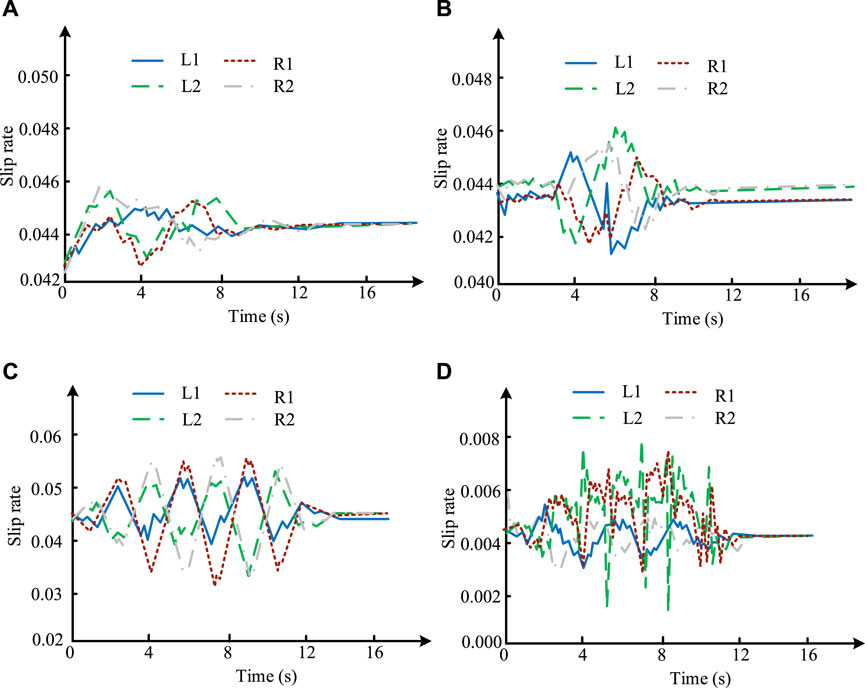
As shown in Figure 7, the yaw rate controlled by Sliding mode automatic control and PSO-N-PID is consistent with the Ideal yaw angle. Overall, the fluctuation of the line in Sliding mode automatic control is greater than that in PSO-N-PID, indicating a stronger control capability of PSO-N-PID. Figure 7A shows a relatively stable speed curve. Figure 7B exhibits pronounced oscillations on the response curve for the sliding mode control method, with the maximum yaw rate measurement ranging from 0.19 to 0.21. Figure 7C demonstrates that the optimized BP-PID algorithm avoids such oscillation issues and significantly reduces the likelihood of being trapped in local optimal solutions. This optimization allows the vehicle to almost eliminate oscillations, improve synchronicity, and successfully control the error values within a lower range of 0.09–0.1 radians per second. In Figure 7D, the PSO-N-PID model’s lateral deviation angle of the vehicle’s center of gravity also exhibits a smaller amplitude. The variation in slip ratio is depicted in Figure 8.

Figure 8

Figure 8. Change in slip rate.

L1, L2, R1, and R2 respectively represent the left front wheel, left rear wheel, right front wheel, and right rear wheel. As shown in Figure 8, in the sinusoidal cornering environment, the slip ratios of both control strategies remained below 0.05, demonstrating a high level of lateral stability. However, it is noteworthy that under sliding mode control, the slip ratio of the vehicle’s tires exhibited significant fluctuations. Under the PSO-N-PID model control, this risk decreased by approximately 3.8%. Moreover, in comparison with sliding mode control, the new optimization strategy reduced the vehicle’s yaw rate by about 27.1%. On the other hand, in the serpentine cornering environment, the slip ratios of the four tires were also analyzed under these control strategies. The slip ratios under both control strategies remained below 0.083, indicating good lateral stability during steering. However, under sliding mode control, the slip ratio reached 0.085 with severe oscillations, confirming the advantages of the new optimization solution. It controlled the slip ratio at 0.054, with a reduction of nearly 36.4% compared to sliding mode control. Additionally, the maximum yaw rate under this algorithmic control also decreased by 42.8%, which is crucial for stability in serpentine conditions.

4.2 Effect analysis under external interference

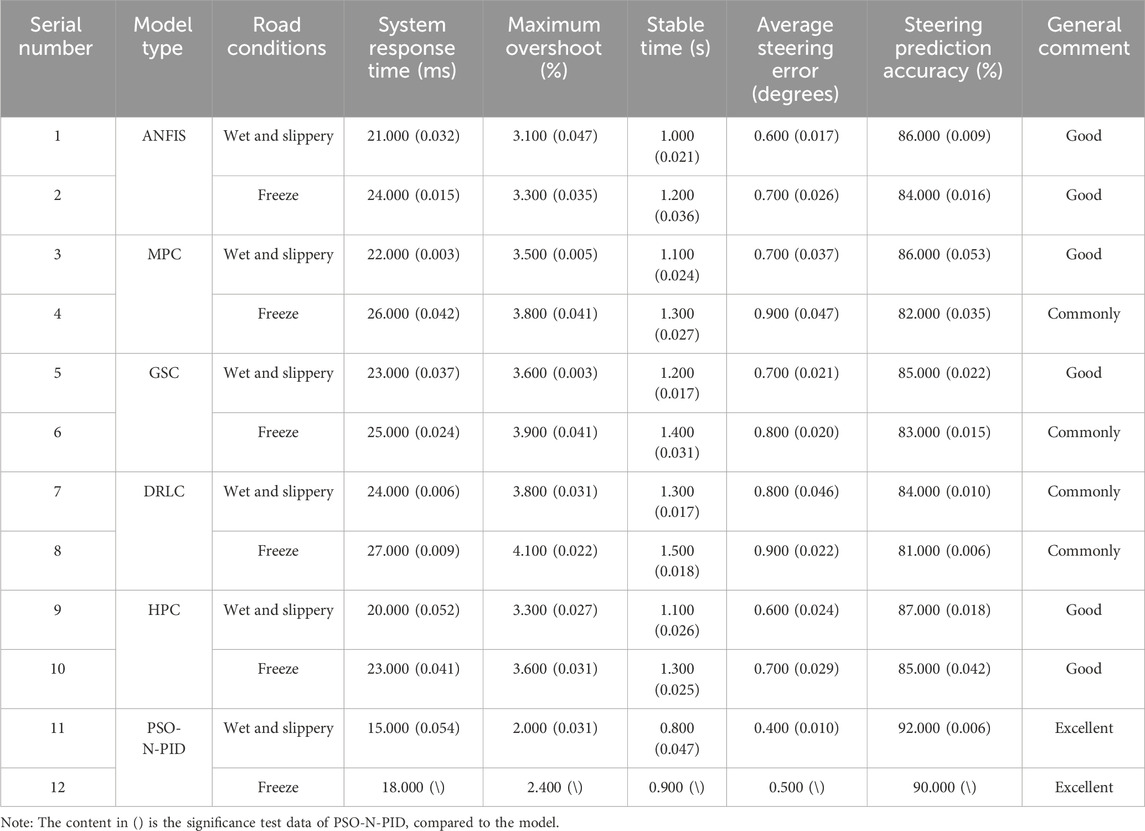
By comparing the performance of six different advanced fusion controller models under typical road conditions, namely, wet and icy surfaces, the compared models are the Adaptive Neuro-Fuzzy Inference System (ANFIS), Model Predictive Controller (MPC), Generalized Sliding Mode Controller (GSC), Deep Reinforcement Learning Controller (DRLC), and Hybrid Power Controller (HPC). The performance under wet and icy road conditions is summarized in Table 3.

Table 3

Table 3. Effect under wet and frozen road conditions.

Table 3 presents the performance under wet and slippery road conditions. The PSO-N-PID model exhibited the fastest system response time at 15 milliseconds and the highest steering prediction accuracy at 92%. It also maintained lower maximum overshoot (2%) and average steering error (0.4°) compared to other models. This indicates that the PSO-N-PID model possesses rapid and accurate control capabilities, along with excellent adaptability to environmental conditions, providing outstanding stability for electric vehicles. Similarly, under freezing road conditions, the PSO-N-PID model demonstrated optimal performance with the lowest system response time (18 milliseconds) and the highest steering prediction accuracy (90%). Despite a slight increase in maximum overshoot and average steering error, it remained ahead of other models. In summary, the PSO-N-PID model held a significant advantage in road steering stability for electric vehicles due to its excellent overall performance.

The data advantages of the research models are significant. Overall, firstly, the research model can effectively improve driving safety. Its superior prediction accuracy and response time compared to other models mean that the model can predict and analyze road conditions more quickly, improving driving safety. Secondly, the low overshoot and steering error of the model can ensure smoother driving of the vehicle, providing users with higher comfort. Finally, this model can help vehicles maintain stability in complex road conditions such as slippery and icy conditions, reducing the incidence of accidents.

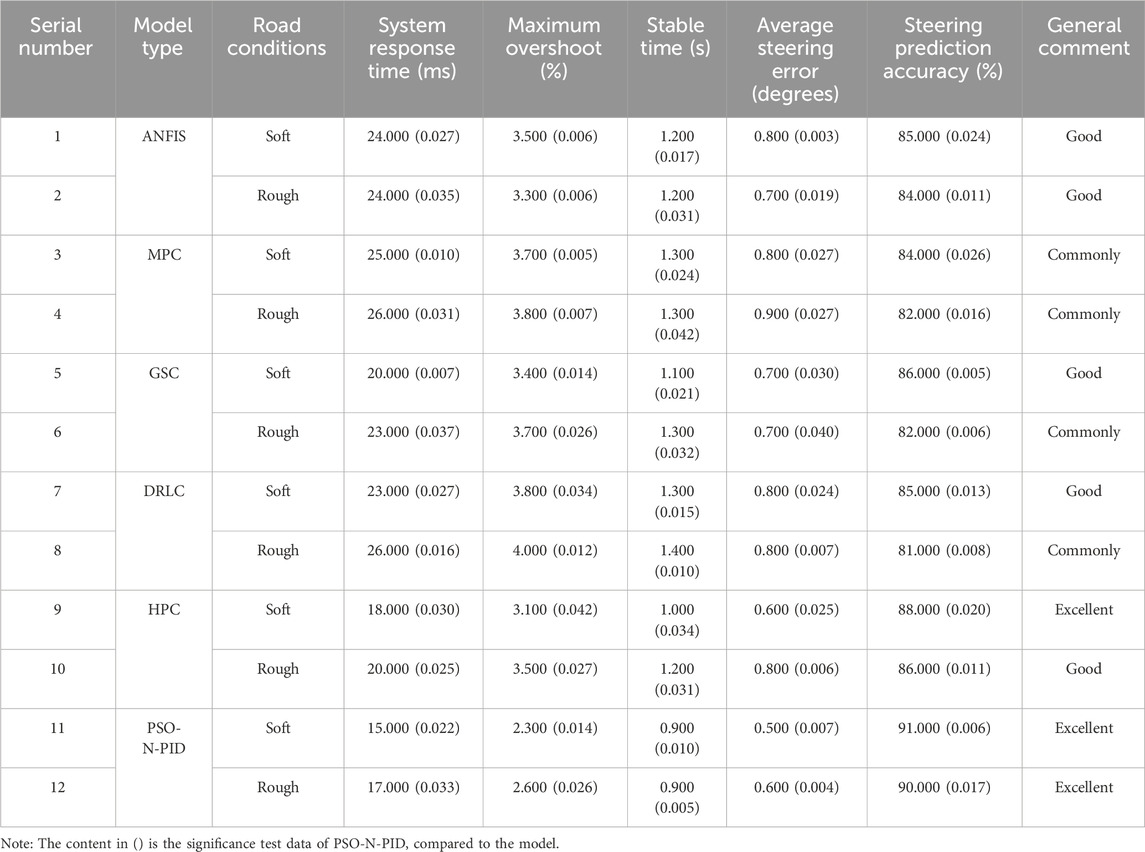
The results for soft and rough road conditions are shown in Table 4.

Table 4

Table 4. Effect under soft and rough road conditions.

In Table 4, under soft road conditions, the PSO-N-PID model exhibited the fastest system response time among all controllers, at only 15 milliseconds, which is 3 milliseconds faster than the next fastest HPC. Additionally, the maximum overshoot for PSO-N-PID was 2.3%, significantly lower than other models, indicating smaller fluctuations when adjusting to the target path and providing a smoother driving experience. The average steering error was only 0.5°, showing high-precision steering control. Furthermore, its steering prediction accuracy reached 91%, surpassing all other models, reflecting the model’s high reliability on soft road surfaces. For rough road conditions, the PSO-N-PID also demonstrated optimal performance with a response time of 17 milliseconds, maintaining the fastest level. The maximum overshoot was 2.6%, consistently kept at a lower level to ensure smooth steering actions. The system settling time remained at 0.9 s, indicating that PSO-N-PID could quickly achieve stability even on harsh, rough road surfaces. The average steering error was 0.6°, similar to soft road conditions, demonstrating consistent and precise control. The steering prediction accuracy remained high at 90%, showing excellent predictive and control capabilities in such complex and slippery road conditions.

The designed model has significant performance data advantages compared to other models. The designed model still performs well under soft and rugged road conditions. It exhibits faster response speed, lower overshoot, and can reach a stable state in a shorter time, with lower steering error and higher steering prediction accuracy. From this, under complex road conditions, the research model can provide stable and accurate control for vehicles, improving the user’s driving experience.

To verify the stability of the model, three scenarios were introduced: wind interference, road obstacles, and sudden braking. The robustness tests were conducted to verify the robustness of the model in different unique scenarios.

Table 5 shows that the model still has performance advantages in three situations: wind interference, road obstacles, and sudden braking, indicating that the model has excellent robustness.

Table 5

Table 5. Robustness check.

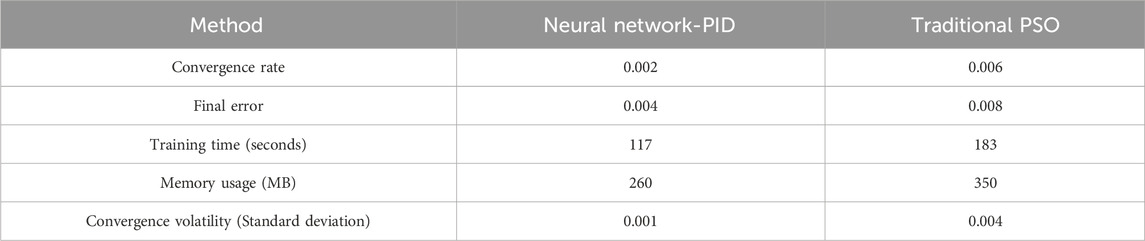
Through comparison, Table 6 shows that the designed model has faster convergence speed, shorter training time, and occupies less memory, resulting in better processing speed. From a stability perspective, the final error of the model is smaller, and the convergence fluctuation is also smaller, reflecting higher stability.

Table 6

Table 6. Model performance comparison.

Firstly, the diversity of climate and geographical environment necessitates that the system be capable of operating stably under a variety of weather and road conditions, requiring a high degree of robustness. Secondly, differences in infrastructure and road quality can also have a significant impact on the system. Finally, electric vehicle technology will be strongly influenced by policies and regulations, and will also affect the product needs of users. Targeted optimization without interruption is necessary to effectively overcome these obstacles and improve the performance of electric vehicles.

5 Conclusion

In the application of modern electric vehicles, enhancing the stability and steering performance under various road conditions and driving scenarios is a crucial issue. To address this concern, the study designed a stable steering control strategy for electric vehicles based on PSO-N-PID control. This approach integrated fuzzy control theory and sliding mode control strategy for a comprehensive stability control. The results indicated that, when the vehicle speed was between 99.8 and 100 km/h, employing PSO-N-PID for stable control maintained the maximum yaw rate of the vehicle at 0.042–0.043° per second, showing a significant improvement over traditional sliding mode control. Under wet and slippery road conditions, the model’s system response time was only 15 ms, achieving a steering prediction accuracy of 92%. The overshoot was only 2%, and the average steering error was a low value of 0.4°. In frozen road conditions, the model’s system response time was 18 ms, and the steering prediction accuracy reached 90%. Comparative testing with other control models such as ANFIS, MPC, GSC, DRLC, and HPC revealed that the PSO-N-PID model demonstrated outstanding performance in both system response time and control accuracy, showing its practical application value.

Although the study yielded practical conclusions, the model is designed for conventional situations. However, the accuracy of the model may also be affected under extreme climate and road conditions. Therefore, designing additional modules for extreme weather and road conditions is the future research direction.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YL: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allugunti, V. R. (2022). A machine learning model for skin disease classification using convolution neural network. Int. J. Comput. Program. Database Manag. 3 (1), 141–147. doi:10.33545/27076636.2022.v3.i1b.53

CrossRef Full Text | Google Scholar

Bartfai, A., Voros, I., and Takacs, D. (2024). Stability analysis of a digital hierarchical steering controller of autonomous vehicles with multiple time delays. J. Vib. Control 30 (1-2), 330–341. doi:10.1177/10775463221146624

CrossRef Full Text | Google Scholar

Cao, Y., Chen, Z., Belkin, M., and Gu, Q. (2022). Benign overfitting in two-layer convolutional neural networks. Adv. neural Inf. Process. Syst. 35, 25237–25250. doi:10.48550/arXiv.2202.06526

CrossRef Full Text | Google Scholar

Fan, J., Ou, Y., Wang, P., Xu, L., Li, Z., Zhu, H. G., et al. (2020). Markov decision process of optimal energy management for plug-in hybrid electric vehicle and its solution via policy iteration. J. Phys. Conf. Ser. IOP Publ. 1550 (4), 042011. doi:10.1088/1742-6596/1550/4/042011

CrossRef Full Text | Google Scholar

Fan, J., Zhang, X., and Zou, Y. (2023). Hierarchical path planner for unknown space exploration using reinforcement learning-based intelligent frontier selection. Expert Syst. Appl. 230, 120630. doi:10.1016/j.eswa.2023.120630

CrossRef Full Text | Google Scholar

Fan, J., Zou, Y., Kong, Z., and Heide, L. (2019). Cloud computing based optimal driving for a parallel hybrid electric vehicle. J. Beijing Inst. Technol. 28 (1), 155–161. doi:10.15918/j.jbit1004-0579.17160

CrossRef Full Text | Google Scholar

Gad, A. G. (2022). Particle swarm optimization algorithm and its applications: a systematic review. Arch. Comput. Method Eng. 29 (5), 2531–2561. doi:10.1007/s11831-021-09694-4

CrossRef Full Text | Google Scholar

Gheisari, M., Hamidpour, H., Liu, Y., Saedi, P., Raza, A., Jalili, A., et al. (2023). Data mining techniques for web mining: a survey. Artif. Intell. Appl. 1 (1), 3–10. doi:10.47852/bonviewaia2202290

CrossRef Full Text | Google Scholar

Guan, X., Zhang, Y. N., Lu, P. P., Duan, C. G., and Zhan, J. (2024). The control strategy of the electric power steering system for steering feel control. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 238 (2-3), 347–357. doi:10.1177/09544070221132131

CrossRef Full Text | Google Scholar

Guo, N., Zhang, X., and Zou, Y. (2022). Real-time predictive control of path following to stabilize autonomous electric vehicles under extreme drive conditions. Automot. Innov. 5 (4), 453–470. doi:10.1007/s42154-022-00202-3

CrossRef Full Text | Google Scholar

Indu, K., and Aswatha Kumar, M. (2023). Electric vehicle control and driving safety systems: a review. IETE J. Res. 69 (1), 482–498. doi:10.1080/03772063.2020.1830862

CrossRef Full Text | Google Scholar

Jeong, Y., and Yim, S. (2022). Path tracking control with four-wheel independent steering, driving and braking systems for autonomous electric vehicles. IEEE Access 10, 74733–74746. doi:10.1109/access.2022.3190955

CrossRef Full Text | Google Scholar

Jin, X., Wang, Q., Yan, Z., and Yang, H. (2023). Nonlinear robust control of trajectory-following for autonomous ground electric vehicles with active front steering system. AIMS Math. 8 (5), 11151–11179. doi:10.3934/math.2023565

CrossRef Full Text | Google Scholar

Liu, H., Zhang, L., Wang, P., and Chen, H. (2022). A real-time NMPC strategy for electric vehicle stability improvement combining torque vectoring with rear-wheel steering. IEEE Trans. Transp. Electrif. 8 (3), 3825–3835. doi:10.1109/tte.2022.3153388

CrossRef Full Text | Google Scholar

Najjari, B., Mirzaei, M., and Tahouni, A. (2022). Decentralized integration of constrained active steering and torque vectoring systems to energy-efficient stability control of electric vehicles. J. Frankl. Inst.-Eng. Appl. Math. 359 (16), 8713–8741. doi:10.1016/j.jfranklin.2022.08.035

CrossRef Full Text | Google Scholar

Pawan, Y. V. R. N., Prakash, K. B., Chowdhury, S., and Hu, Y. C. (2022). Particle swarm optimization performance improvement using deep learning techniques. Multimed. Tools Appl. 81 (19), 27949–27968. doi:10.1007/s11042-022-12966-1

CrossRef Full Text | Google Scholar

Powell, S., Cezar, G. V., Min, L., InêsAzevedo, M. L., and Rajagopal, R. (2022). Charging infrastructure access and operation to reduce the grid impacts of deep electric vehicle adoption. Nat. Energy 7 (10), 932–945. doi:10.1038/s41560-022-01105-7

CrossRef Full Text | Google Scholar

Qiu, W., Hao, Q., Annamareddy, S. H. K., Xu, B., Guo, Z., and Jiang, Q. (2022). Electric vehicle revolution and implications: ion battery and energy. Eng. Sci. 20, 100–109. doi:10.30919/es8d772

CrossRef Full Text | Google Scholar

Safayatullah, M., Elrais, M. T., Ghosh, S., Reza, R., and Batarseh, I. (2022). A comprehensive review of power converter topologies and control methods for electric vehicle fast charging applications. IEEE Access 10, 40753–40793. doi:10.1109/access.2022.3166935

CrossRef Full Text | Google Scholar

Shami, T. M., El-Saleh, A. A., Alswaitti, M., Gu, Q., Summakieh, M. A., and Mirjalili, S. (2022). Particle swarm optimization: a comprehensive survey. IEEE Access 10, 10031–10061. doi:10.1109/access.2022.3142859

CrossRef Full Text | Google Scholar

Shuraiji, A. L., and Shneen, S. W. (2022). Fuzzy logic control and PID controller for brushless permanent magnetic Direct current motor: a comparative study. J. Robot. Control (JRC) 3 (6), 762–768. doi:10.18196/jrc.v3i6.15974

CrossRef Full Text | Google Scholar

Ti, Y., Zheng, K., Zhao, W., and Song, T. (2022). A novel IMC-FOF design for four wheel steering systems of distributed drive electric vehicles. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 236 (5), 842–856. doi:10.1177/09544070211031415

CrossRef Full Text | Google Scholar

Venkitaraman, A. K., and Kosuru, V. S. R. (2022). A review on autonomous electric vehicle communication networks-progress, methods and challenges. World J. Adv. Res. Rev. 16 (3), 013–024. doi:10.30574/wjarr.2022.16.3.1309

CrossRef Full Text | Google Scholar

Wei, H., Zhao, W., Ai, Q., Zhang, Y., and Huang, T. (2022). Deep reinforcement learning based active safety control for distributed drive electric vehicles. IET Intell. Transp. Syst. 16 (6), 813–824. doi:10.1049/itr2.12176

CrossRef Full Text | Google Scholar