- School of Civil Engineering, Hefei University of Technology, Hefei, China
Although the instability of graded elastic cylinders has been analyzed by many researchers, most of them focused on the core-shell cylinders and film-substrate structures with inhomogeneous Young’s modulus. For a radially graded elastic cylinder subjected to the axial compression, the variation of Poisson’s ratio may result in the radial and circumferential stresses and thereby affects the critical condition of instability. By assuming linear elasticity with nonlinear kinematics, the governing equation for the incremental stress field is developed for instability analysis of the cylinder with radially graded material properties (Young’s modulus and Poisson’s ratio). Considering the arbitrariness of material properties, the state space technique is implemented and a semi-analytical solution is acquired. The obtained solution is validated by the finite element results. Numerical examples show that the critical condition of instability for graded elastic cylinders is related to whether Poisson’s ratio is assumed to be constant.
1 Introduction
The morphology characteristics caused by surface instability are often observed in nature and biological tissues, such as fruits, vegetables, animal brains, human guts (Dai and Liu, 2014; Budday et al., 2014; Balbi et al., 2015), and have been exploited for a broad range of applications, e.g., testing of mechanical properties for ultrathin films (Stafford et al., 2004), active surfaces (Tokarev and Minko, 2009), micro-optics (Harrison et al., 2004), microfluidic devices (Sugiura et al., 2007), and soft electronics and actuators (Rogers, et al., 2010; Yang et al., 2010). Due to curiosity about the natural phenomena and motivation of the development and utilization based on these configurations, the intrinsic mechanism of surface instability has attracted much attention of a large number of researchers over the last decades.
For the surface wrinkling instability, there are many previous works on core-shell cylinders and film-substrate structures. The pioneering work on film-substrate structures originated from the delamination analysis of such systems with a large unbounded flaw under compressive stress (Evans and Hutchinson, 1984; Hutchinson and Suo, 1992). The instability of an elastic film on a viscous substrate was then studied profoundly (Sridhar, et al., 2001; Huang and Suo, 2002a; Huang and Suo, 2002b). The relevant analyses of stiff films on compliant substrates were later presented ceaselessly in a large numbers. Huang et al. (2005) provided a nonlinear analysis of a film bonded to a substrate with finite thickness. Using the finite deformation theory, Song et al. (2008) studied the mechanics of thin buckled films on compliant substrates and obtained an analytical solution. Jia et al. (2012) investigated the wrinkling problem of a bilayer film on a soft substrate via theoretical analysis and finite element simulations. Xu et al. (2015) studied the occurrence and evolution of 3D instability patterns in thin films on hyperelastic substrates based on a fully nonlinear 3D finite element model. In comparison with the film-substrate structure, the stability analysis of cylindrical shells with soft cores was considered earlier by Seide (1962) using Donnell’s equations. About the same time a theoretical solution for the determination of buckling characteristics was presented for a long cylinder shell with a solid or elastic soft core under axial compression with the sinusoidal buckling assumption (Yao, 1962). Inspired by optimization of natural structures, Karam and Gibson (1995) theoretically analyzed the buckling of core-shell structures and found that the buckling resistance of a hollow cylindrical shell could be improved significantly by infilling a compliant elastic core. Hutchinson and He (2000) addressed the buckling of cylindrical sandwich shells with foamed metal cores for the optimal design for structural weight and carrying capacity, and a similar comprehensive analysis was provided by Dawson and Gibson (2007). By energy method, Arani et al. (2007) studied the elastic axisymmetric buckling of a thin simply supported cylindrical shell with an elastic core under axial compression. To further investigate the effect of the filled core rigidity and thickness on the buckling behavior, Ye et al. (2011) developed a simple formula to predict the critical buckling stress by using the Rayleigh–Ritz approximation. Based on the nonlinear Donnell-Mushtari-Vlassov shell theory, Zhao et al. (2014) investigated surface wrinkling of a core-shell cylinder along the axial and circumferential directions. Recently, the axisymmetric and non-axisymmetric mode transitions in the post-buckling regime in axially compressed core–shell cylinders were investigated based on a nonlinear 3D finite element model (Xu and Potier-Ferry, 2016) and nonlinear shell finite element (Lavrencic et al., 2020).
The aforementioned literature only involves the film-substrate and core-shell systems with uniform substrates and cores. In nature and some engineering problems, the material properties of substrates and cores are commonly inhomogeneous, and thus the surface wrinkling of such systems is necessary to be studied. However, the inhomogeneity of materials makes it difficult to obtain a completely analytical solution. In the past few years, some theoretical researches on surface instability have been devoted to graded elastic materials. Cao et al. (2012a) derived the critical condition of wrinkling for a stiff thin layer on a semi-infinite substrate with the power-law and exponential grading moduli, respectively. For elastic layers with material properties varying from the surface to the interior, a semi-analytical solution was obtained by the theoretical analysis combined with the finite element method (Lee et al., 2008) and the state space method (Wu et al., 2014); similar semi-analytical solutions for onset of surface instability of elastic cylinders with radially graded Young’s modulus were performed by Jia et al. (2014) and Han et al. (2017). Based on Floquet’s principle, most recently an explicit semi-analytical isogeometric analysis method was suggested for predicting wrinkling instability of a stiff film on a graded compliant cylinder (Li et al., 2020). We note in the existing studies that Poisson’s ratio in graded elastic layers and cylinders was commonly assumed to be a constant. In practice, however, for a radially graded elastic cylinder subjected to the axial compression, the variation of Poisson’s ratio may result in radial and circumferential stresses, which must affect the critical condition of instability.
In addition to be directly subjected to compression, surface instability of film-substrate or core-shell systems may be induced by swelling or growing, and surface stability of soft elastic layers may be also influenced by surface tension (Kang and Huang, 2010a; Wang, 2020). Upon swelling in a solvent, the surface of thin hydrogel layers on rigid substrates may become unstable and further evolves into various morphologies (Guvendiren et al., 2009; Guvendiren et al., 2010; Kang and Huang, 2010b; Wu et al., 2017). The tubular organ of animals, such as esophagus, can be seen as cylindrical bilayers with the stiffer outer layer (muscle) and softer inner layer (mucosa). When the inner mucosa grows, the outer muscle restricts its expansion, eventually leading to wrinkling, folding or creasing on the inner surface of mucosa (Jin et al., 2011; Li et al., 2011; Razavi et al., 2016). Similar instability was also found on the outer surface of core-shell cylinders as the outer shell grows or swells on a stiff core Cao et al. (2012b). The surface instability related to growth and swelling has been adequately studied in the past 10 years.
In this paper, we focus on an inhomogeneous elastic cylinder and assume that both Young’s modulus and Poisson’s ratio vary arbitrarily in the radial direction. A state space method is employed to investigate the onset of wrinkling for elastic cylinders under axial compression. The effects of the variation of Poisson’s ratio on stress distribution and critical condition of instability are discussed. The rest of this paper is arranged as follows. In Section 2, the instability theory of elastic cylinders is introduced. The solution of stress field in fundamental state is obtained by using the state space method in Section 3. In Section 4, the instability analysis for elastic cylinders with material properties varying arbitrarily in the radial direction is carried out and the critical condition of instability is presented. Two instability examples, a cylinder covered by a bilayer and a homogeneous cylinder with a linearly graded stiff layer, are discussed in Section 5. Concluding remarks are presented in Section 6.
2 Instability Theory of Elastic Cylinders
An elastic hollow inhomogeneous cylinder with traction free surfaces is considered as shown in Figure 1A, where a Cartesian coordinate system is set up with the reference coordinates X1 and X2 at one cross-section and X3 along the axis of the cylinder. The inner and outer radii of the cylinder in the stress-free state are A and B, respectively. When subjected to an axial compression, the compressive stress inside the cylinder may cause surface or internal instability of the cylinder. Prior to surface or internal instability, the compressed cylinder is seen as in the fundamental state with the inner and outer radii a and b (Figure 1B), and the corresponding current coordinates are denoted as (x1, x2, x3).
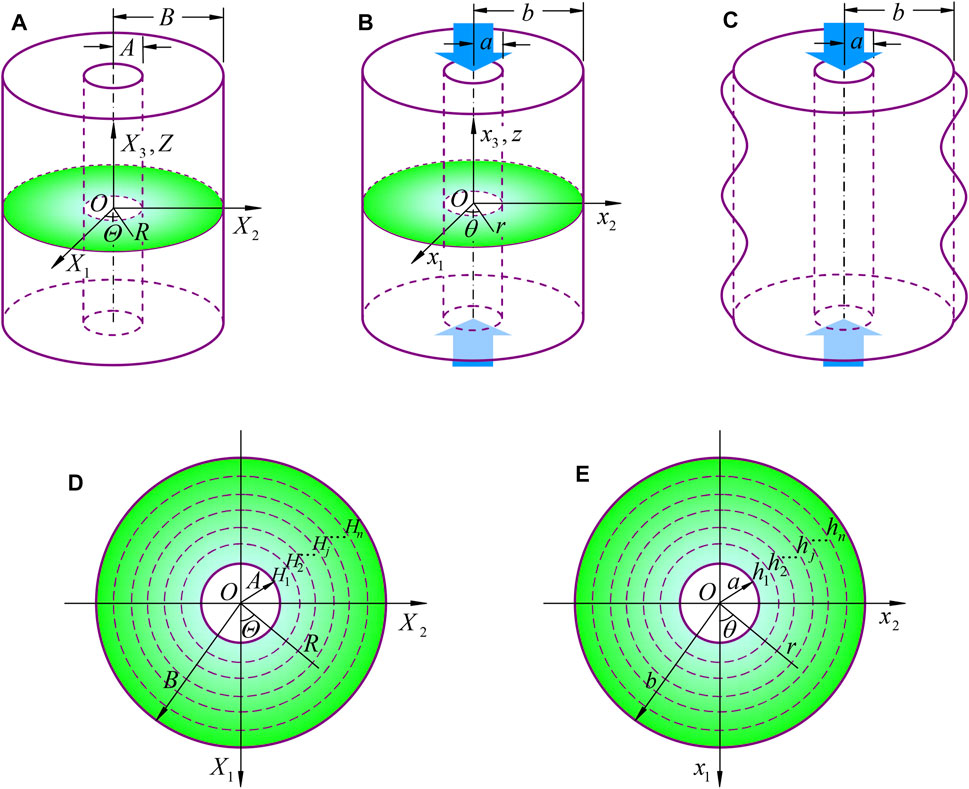
FIGURE 1. Schematic illustrations for an elastic hollow cylinder: (A) in the stress-free reference state; (B) in the fundamental state subjected to axial compression; (C) in the axial wrinkling state; (D) and (E) divided into n cylindrical subshells in the reference and fundamental states for the state space analysis.
In the present study, we consider an elastic cylinder with material properties varying in the radial direction, especially emphasizing the influence of Poisson’s ratio on stress distribution and structural stability. The material is assumed to be linear elastic and isotropic with a quadratic strain energy density function in terms of Green-Lagrange strain:
where EIJ = (FkIFkJ − δIJ)/2, FkJ = ∂xk/∂XJ, δIJ is the Kronecker delta, and the elastic modulus CIJKL is a function of X1 and X2 and possesses the isotropic symmetry. The first and second Piola–Kirchhoff stresses PiJ and SIJ are accordingly in the Cartesian coordinate system as (Wu et al., 2014)
In the fundamental state, the equilibrium equation is
and the boundary conditions at the inner and outer surfaces are
where the notation ( ),J stands for differentiation with respect to XJ in the reference state, NJ represents the direction cosine of the outer normal relative to the coordinate XJ; the Einstein summation convention is implied over repeated indices unless noted otherwise.
Under the axial compression, the imposed axial nominal strain ε0 = F33–1 is identical everywhere in the fundamental state. In the process of instability analysis, it is assumed that an incremental displacement Δui (i = 1, 2, 3) occurs from the fundamental state, then the corresponding incremental stress field must satisfy the following equilibrium equation and boundary conditions:
where
Assuming that the strain in the fundamental state is small, we have
where ( ),j denotes differentiation with respect to xj in the current state, and nj represents the direction cosine of the outer normal relative to the coordinate xj.
Considering axisymmetry of the problem, the cylindrical coordinates in the reference state (R, Θ, Z) and in the current state (r, θ, z) are applied as shown in Figure 1. With the coordinate transformation from the Cartesian coordinates to the cylindrical coordinates, the equilibrium Eq. 3 in the fundamental state for radially graded elastic cylinders can be converted into the following form:
where
with uR representing the radial displacement component. The axial stress in the fundamental state is then determined by
The boundary condition (4) becomes
In general, Poisson’s ratio changes with the change of Young’s modulus of graded elastic materials. Poisson’s ratio commonly changes very little and thus it is often approximated as a constant for convenience. When the radially graded elastic cylinder is subjected to axial compression, the axial compressive stress is generated definitely. However, the radial and circumferential stresses do not necessarily occur, which depend on Poisson’s ratio. If Poisson’s ratio remains constant in the radial direction, transversely homogeneous strain generates and no radial and circumferential stresses occur. In contrast, if Poisson’s ratio varies in the radial direction, the radial and circumferential strains are inhomogeneous and corresponding stresses must be produced, which will inevitably affect the axial and circumferential stabilities of cylindrical structures. The instability analysis for Poisson’s ratio fixed as a constant has been carried out by many researchers (Jia et al., 2014; Han et al., 2017). In the present study, we assume that Poisson’s ratio varies in the radial direction as that of Young’s modulus. By the coordinate transformation, the equilibrium equation of the incremental stress field in Eq. 7 can be converted into the following form in the cylindrical coordinate system:
where
The boundary condition of the incremental stress field in Eq. 8 becomes
Equations 9–12 and Eqs 14–25 constitute the governing equations of instability analysis for radially graded elastic cylinders, which together with the boundary conditions (13) and (26) lead to an eigenvalue problem. If there is a nontrivial solution for the incremental displacement field, the critical condition for onset of instability is obtained successfully.
It should be noted that if the cylindrical structure is a solid cylinder, the boundary condition (13) at R = A needs to be replaced with
and the boundary condition (26) at r = a replaced with
3 Solution of Stress Field in Fundamental State
Considering arbitrariness of the material properties varying in the radial direction, it is impossible to obtain the analytical solution of stress field in the cylinder, and the state space technique is thereby employed in this paper.
From Eq. 10, we have
Substituting Eq. 29 into Eq. 11 and then into Eq. 9, we get
and the circumferential and axial nominal stresses are, respectively,
where λ and μ are Lame’s constants of isotropic elasticity, relating to Young’s modulus E and Poisson’s ratio ν as follows:
Combining Eqs 29, 30, a set of inhomogeneous differential equations are obtained in a matrix form as
where the coefficient matrix D and the inhomogeneous item K are, respectively,
Since the coefficient matrix and inhomogeneous item in Eq. 35 contain the radial coordinate R and the radially varying material parameters, the analytical solution to Eq. 34 cannot be obtained directly. For this reason, we first divide the hollow cylinder into n subshells and number them from the inner subshell to the outer subshell. The thickness of the ith subshell is denoted by Hi (
The relation between the state vectors at outer surface and the inner surface of the ith subshell is determined as
Thanks to the continuity of the state vector across all interfaces between the adjacent subshells, the relationship between the state vectors at the outer and inner surfaces of the cylinder can be acquired as
By using the boundary condition (13), i.e.
or Eq. 27 together with Eq. 13 at R = B, i.e.
the state variables at the inner and outer surfaces are subsequently obtained as functions of the axial strain ε0, and uRi and PrRi (
4 Instability Analysis
To acquire the critical condition of instability for cylinders with material properties varying arbitrarily in the radial direction, the virtual dividing model in the prior section is still demanded in the following solving process.
From Eqs 14–25, we can get the differentiations of incremental displacements and stresses with respect to the radial coordinate r as follows:
With the assumption of small strain in the fundamental state, we have
where ω1 and ω2 refer to the wave number along the circumferential and axial directions, respectively. Substituting Eqs 47, 48 into Eqs 41–46, we obtain a set of homogeneous differential equations in the matrix form as
where the state vector G(r) = [Ur(r) Uθ(r) Uz(r) Tr(r) Tθ(r) Tz(r)]T, and M is a 6×6 coefficient matrix with the following nonzero elements:
Taking
Integrating two sides of Eq. 50, the state vector of the outer surface relating to that of the inner surface is derived as
By means of the continuity of the state vector across all interfaces, the relationship between the state vectors for the outer and inner surfaces of the whole cylinder is determined as
where
Corresponding to Eq. 52, the boundary condition Eqs 26, 28 can be rewritten as that
and
Since the coefficient matrix Mi includes the wave numbers ω1 and ω2, and the stress components PrRi, PθΘi, and PzZi (
5 Results and Discussion
For a validation of the present study, we first analyze the stress distribution for a graded elastic cylinder under axial compression, and then discuss the critical condition of instability for a soft homogeneous cylinder covered by a bilayer or including a linearly graded stiff layer, respectively. The numerical simulation is computed by the finite element analysis code ABAQUS. The stress field and the critical condition of instability for graded elastic cylinders with a varied Poisson’s ratio are addressed and compared to that with a fixed Poisson’s ratio.
5.1 Validation of Stress Field in Fundamental State
For a radially graded elastic cylinder subjected to axial compression, from the theoretical analysis we know that the radial and circumferential stresses will be induced due to the variation of Poisson’s ratio. Consider a solid cylinder with the outer radius B = 100 mm, both Young’s modulus and Poisson’s ratio are assumed to vary linearly in the radial direction, i.e.
where y stands for Young’s modulus E or Poisson’s ratio ν, y0 and yB represent E or ν at R = 0 and B, respectively.
Figure 2 depicts the radial displacement uR, radial stress PrR, circumferential stress PθΘ, and axial stress PzZ as functions of the radial coordinate R for a solid cylinder with E0 = 1 MPa and EB = 100 MPa, comparing with the numerical results by ABAQUS. From Figure 2, it is observed that the present results are in excellent agreement with the results by ABAQUS. Figures 2A,D reveal that both the varied Poisson’s ratio (ν0 = 0.45 and νB = 0.35) and the fixed one (ν0 = 0.4 and νB = 0.4) have little effectiveness on the radial displacement and the axial stress. However, the variation of Poisson’s ratios has significant influence on the radial and circumferential stresses (Figures 2B,C). When Poisson’s ratio is varied and ranges from 0.45 to 0.35, the radial and circumferential compressive stresses increase firstly and then decrease in the radial direction. The radial stress is consistently compressive within the cylinder and equal to zero at the surface, satisfying the traction free boundary condition, whereas the circumferential stress turns to be tensile as
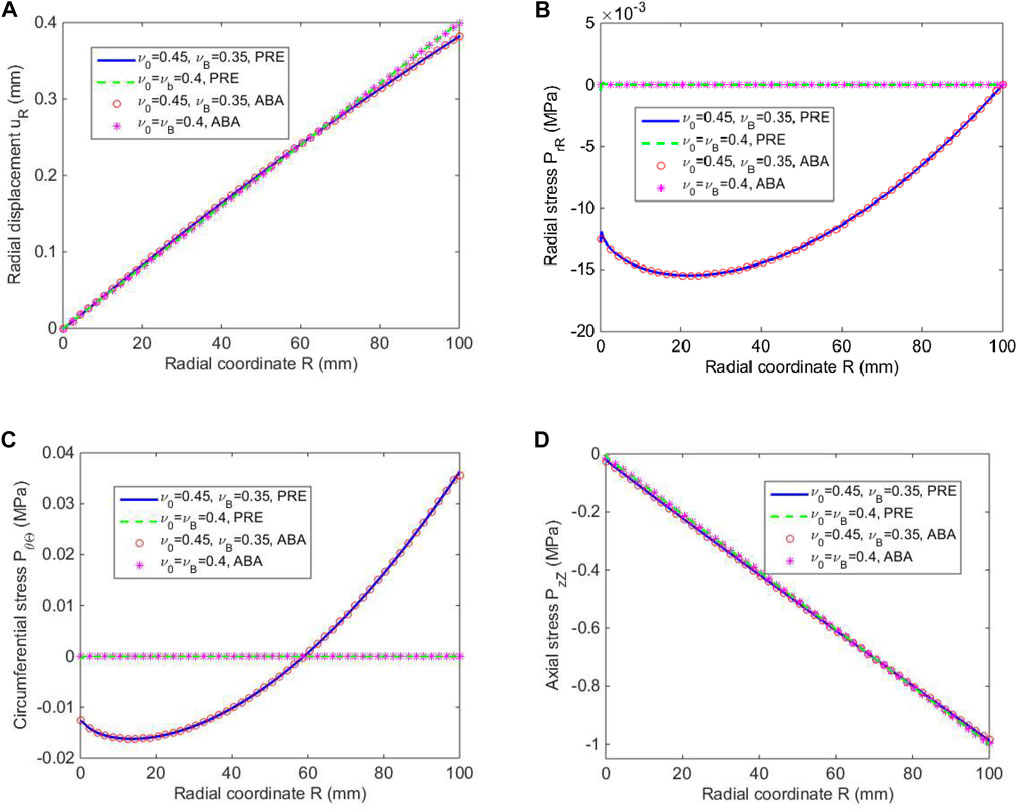
FIGURE 2. (A) Radial displacement, (B) radial stress, (C) circumferential stress, and (D) axial stress varying in the radial direction, obtained by the present method (PRE), for a solid cylinder under an axial strain ε0 = −0.01, in comparison with the results by ABAQUS (ABA).
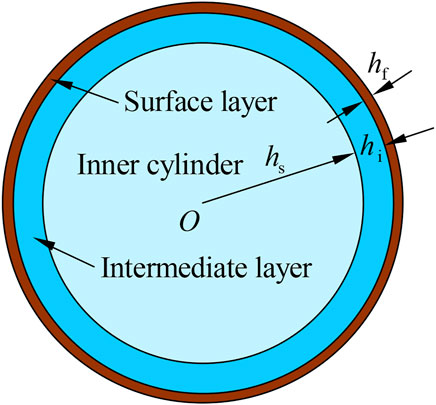
5.2 Surface Instability for a Cylinder Covered by a Bilayer
As an example for surface instability analysis for a graded elastic cylinder, we consider a soft cylinder covered by a bilayer as shown in Figure 3. Similar to the example in Jia et al. (2014) and Han et al. (2017), the radius of the inner soft cylinder is hs = 90 mm, the thicknesses of the surface shell and the intermediate shell are hf = 1 mm and hi = 10 mm, respectively. Young’s moduli for the surface shell and the inner cylinder are Ef = 1 GPa and Es = 1 MPa. However, in this paper Poisson’s ratios for three different layers are not fixed as 0.4. We here assume that Poisson’s ratios for the surface shell and the inner cylinder to be νf = 0.4 and νs = 0.48, and that for the intermediate shell varies with its Young’s modulus and is given by
where Ei is Young’s module for the intermediate shell.
The critical strain for onset of surface instability εc and the corresponding wavelength
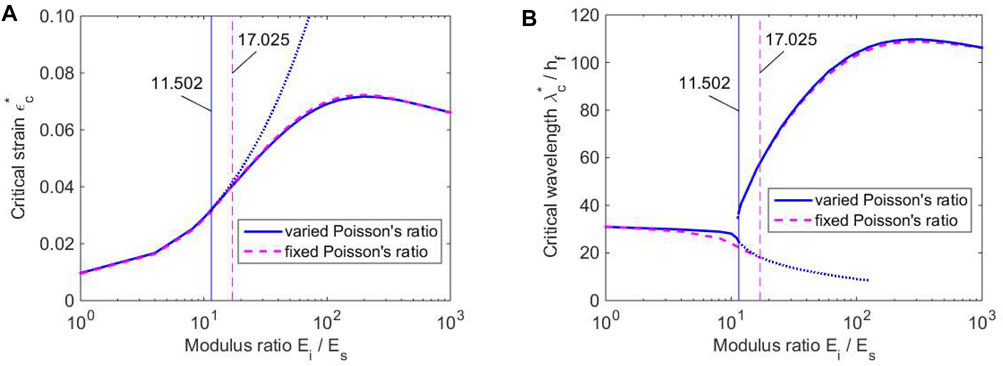
FIGURE 4. (A) The critical strain and (B) the corresponding wavelength for a soft cylinder covered by a bilayer with a varied Poisson’s ratio in the intermediate shell, in comparison with the results with a fixed Poisson’s ratio (Han et al., 2017).
It should be noted that during searching for the critical stain, there are two local minimums for the candidate of the critical strain εc, corresponding to a short wavelength and a long wavelength (see Han et al., 2017). The smaller local minimum strain and the corresponding wavelength are the true critical strain and critical wavelength. The dotted lines in Figures 4A,B illustrate the bigger local minimum strain and the corresponding wavelength for the system with varied Poisson’s ratio at a possible metastable state of surface instability.
To verify the correctness of the theoretical solution, we select two computation models with two different lengths for numerical simulation: one has the length 162.8 mm with a varied Poisson’s ratio, equivalent to four times of the wavelength at Ei/Es = 12.0; the other has 175.28 mm with a fixed Poisson’s ratio, equivalent to three times of the wavelength at Ei/Es = 17.5. Figures 5A,B present the surface wrinkling patterns for the cylinder with a varied Poisson’s ratio, and their modulus ratios are Ei/Es = 11.0 and 12.0, respectively. Figures 5C,D provide the surface wrinkling patterns for the cylinder with a fixed Poisson’s ratio and their Ei/Es = 16.5 and 17.5. It can be found that the wave numbers are 6.5 in Figures 5A, 4 in Figure 5B, respectively, indicating that the modulus ratio for critical wavelength switching must be within 11.0 and 12.0 for the varied Poisson’s ratio. In Figures 5C,D, the wave numbers are 8.5 and 3, respectively, illustrating that the modulus ratio for critical wavelength switching is within 16.5 and 17.5 for the fixed Poisson’s ratio. The numerical simulation manifests that the modulus ratios 11.502 and 17.025, predicted for critical wavelength switching by the theoretical analysis, are correct and enough accurate.
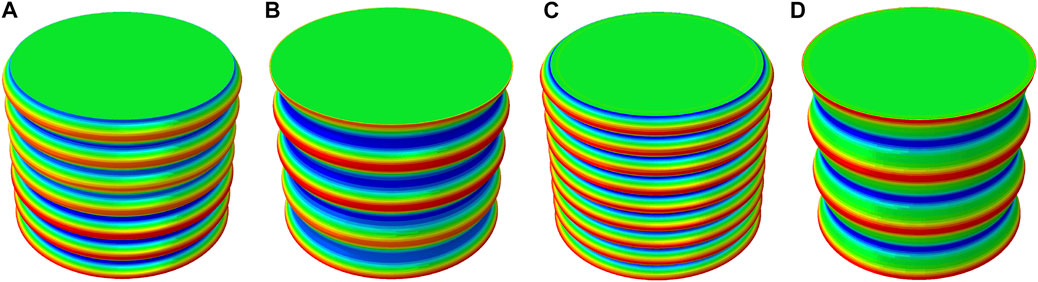
FIGURE 5. Wrinkling patterns for a soft cylinder covered by a bilayer: (A) and (B) for the system with a varied Poisson’s ratio and the modulus ratios Ei/Es = 11.0 and 12.0, respectively; (C) and (D) for the system with a fixed Poisson’s ratio and Ei/Es = 16.5 and 17.5, respectively.
5.3 Instability of a Homogeneous Cylinder With a Linearly Graded Stiff Layer
Next we consider a homogeneous soft hollow cylinder containing a linearly graded stiff layer with the thickness hg = 1 mm as shown in Figure 6. The inner and outer radii of the cylinder are A = 40 mm and B = 100 mm, Young’s modulus and Poisson’s ratio are Eh = 1 MPa and νh = 0.48 for the homogeneous soft material, respectively. Young’s modulus and Poisson’s ratio of the stiff layer are assumed to be linear in the radial direction, and the maximum Young’s modulus is denoted as Em, corresponding Poisson’s ratio as νm. In the numerical analysis, the stiff layer is considered to be the inner layer (Figure 6A), the middle layer (Figure 6B), and the outer layer (Figure 6C) of the cylinder, respectively. For the first case, Young’s modulus and Poisson’s ratio of the stiff layer vary linearly from Em and νm at R = 40 mm to Eh and νh at R = 41 mm; for the second case, from Eh and νh at R = 69.5 mm to Em and νm at R = 70 mm, and then to Eh and νh at R = 70.5 mm; for the third case, from Eh and νh at R = 99 mm to Em and νm at R = 100 mm.
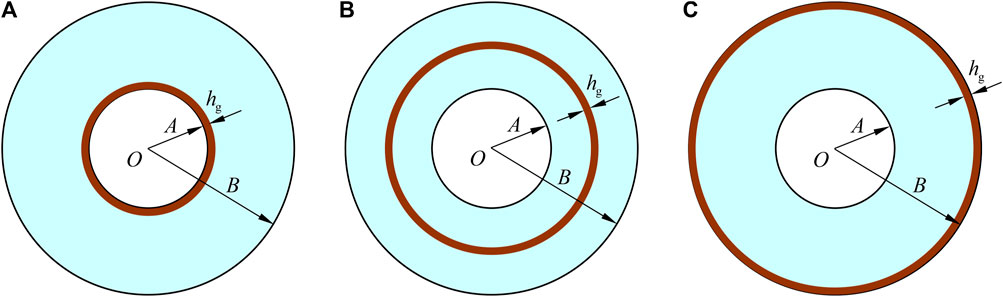
FIGURE 6. Cross-sections of a homogeneous soft hollow cylinder containing a linearly graded stiff (A) inner layer, (B) middle layer, and (C) outer layer with the thickness hg.
Figure 7 presents the critical strain and the corresponding wavelength versus the modulus ratio Em/Eh ranging from 102 to 105 for soft cylinders with an inner, a middle, and an outer stiff layers. νm = 0.4 and νm = νh = 0.48 are used for the stiff layer with the varied Poisson’s ratio and fixed Poisson’s ratio, respectively. It is seen that the critical strains for the stiff cylinder with varied and fixed Poisson’s ratios are very close to each other in each case and even indistinguishable, while the critical wavelength for varied Poisson’s ratio is obviously less than that for the fixed Poisson’s ratio, showing that the change of Poisson’s ratio mainly affects the critical wavelength. In addition, from the results for the three different cases we can find that the critical strain of the cylinder with an outer stiff layer is always less than that with an inner or a middle stiff layer, and the corresponding wavelength is greater than that of the other two cases overall. For the cylinders with an inner stiff layer and a middle one, there is an intersection point for both the critical strain and the corresponding wavelength.
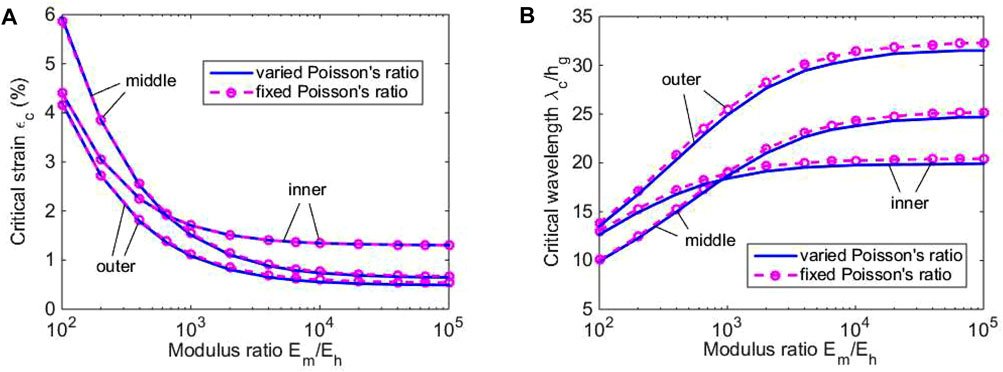
FIGURE 7. (A) The critical strain and (B) the corresponding wavelength for soft cylinders with a linearly graded stiff layer as the inner, the middle, and the outer layers.
Finally we provide three numerical simulations for the homogeneous hollow cylinders with an inner, a middle, and an outer stiff layers, respectively, as shown in Figure 8. As predicted in Figure 7B, there is an intersection point near the modulus ratio Em/Eh = 103 for the critical wavelengths of the first and second cases. The exact dimensionless wavelengths at Em/Eh = 103 for the three cases are 18.41, 18.68, and 24.91, respectively. Thus, there is an approximate common multiple for the three wavelengths, such as 74.73. In the numerical simulation, the lengths of cylinders are selected as 74.73 mm, equivalent to about three times the critical wavelength for the cylinder with an outer stiff layer, four times for the cylinder with an inner stiff layer or a middle one. From the profiles of the numerical simulations in Figure 8, it can be clearly identified that there are four, four, and three wave numbers at the inner surface, middle face, and outer surface of the cylinder.
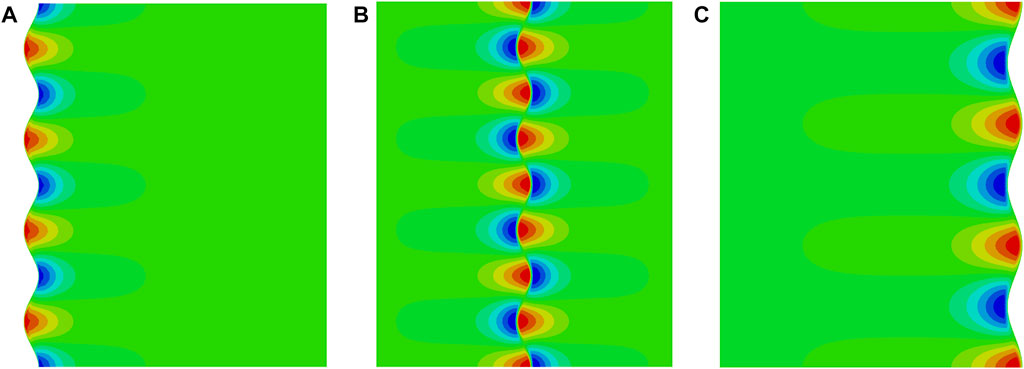
FIGURE 8. Numerical simulations of instability for a hollow soft cylinder with: (A) an inner stiff layer, (B) a middle stiff layer, and (C) an outer stiff layer. The modulus ratio of the stiff layer Em/Eh = 103, and Poisson’s ratio νm = 0.4 and νh = 0.48.
It should be mentioned that in the above example analyses, the circumferential instability has not been found. In the practical numerical calculation, the critical strains for axial and circumferential instabilities are obtained by taking wave number ω1 = 0 and ω2 = 0 in Eq. 55, respectively. The critical strain for onset of circumferential instibility is found to be much greater than that of axial instability. Therefore, axial instability always occurs earlier than circumferential instability for the cylinder subjected to axial compression. We note that the circumferential instability has been investigated in Zhao et al. (2014) and Xu and Potier-Ferry (2016) for a stiff film on a soft cylinder. In their works, the postbuckling was analyzed and the circumferential instability was found to commonly occur after the formation of axial wrinkling. By further analysis, we can realize that when the cylinder wrinkles, the circumferential compressive stress at the trough of the axial wrinkling turns to be larger and larger with increasing of the axial deformation. Hence, it is not hard to understand that the circumferential instability always starts at the trough of the axial wrinkling. The relative postbuckling analysis for graded elastic cylnders is left for further studies.
6 Concluding Remarks
The critical condition for onset of instability of elastic cylinders was analyzed for their Young’s modulus and Poisson’s ratio varying in the radial direction. When the cylinder is subjected to an axial loading, the radial and circumferential stresses will be produced simultaneously due to the variation of Poisson’s ratio, and thus both the axial and the circumferential instabilities may be caused individually. A semi-analytical solution was obtained for the prediction of instability in both the axial and the circumferential directions. The critical strain for onset of the circumferential instability is much greater than that of the axial instability, and consequently the axial wrinkling often occurs before the circumferential instability. For a soft cylinder covered by a bilayer with varied and fixed Poisson’s ratios, the numerical results manifest that their critical strains are very close to each other, but their modulus ratios for critical wavelength switching are different obviously. For the soft cylinder with a linearly graded stiff layer, the critical wavelength for the varied Poisson’s ratio is slightly smaller than that for the fixed one. Numerical examples show that the critical condition is different for the radially graded elastic cylinder as its Poisson’s ratio is assumed to be varied or fixed as a constant. The results obtained may provide valuable reference for the design and evaluation of the relevant cylindrical structures.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
ZW contributed to the conception and design of the study. CZ performed the numerical analysis and prepared the first draft of the manuscript. All authors equally contributed to the manuscript revision, reading, and approved the submitted version.
Funding
This work is financed by the National Natural Science Foundation of China (Grant No. 11572108).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
ZW and CZ gratefully acknowledge Prof. Rui Huang of the University of Texas at Austin for the insightful discussions.
References
Arani, A. G., Golabi, S., Loghman, A., and Daneshi, H. (2007). Investigating Elastic Stability of Cylindrical Shell with an Elastic Core under Axial Compression by Energy Method. J. Mech. Sci. Technol. 21 (7), 983–996. doi:10.1007/BF03027648
Balbi, V., Kuhl, E., and Ciarletta, P. (2015). Morphoelastic Control of Gastro-Intestinal Organogenesis: Theoretical Predictions and Numerical Insights. J. Mech. Phys. Solids 78, 493–510. doi:10.1016/j.jmps.2015.02.016
Budday, S., Steinmann, P., and Kuhl, E. (2014). The Role of Mechanics during Brain Development. J. Mech. Phys. Solids 72, 75–92. doi:10.1016/j.jmps.2014.07.010
Cao, Y.-P., Jia, F., Zhao, Y., Feng, X.-Q., and Yu, S.-W. (2012a). Buckling and Post-buckling of a Stiff Film Resting on an Elastic Graded Substrate. Int. J. Solids Struct. 49 (13), 1656–1664. doi:10.1016/j.ijsolstr.2012.03.004
Cao, Y.-P., Li, B., and Feng, X.-Q. (2012b). Surface Wrinkling and Folding of Core-Shell Soft Cylinders. Soft Matter 8 (2), 556–562. doi:10.1039/c1sm06354e
Dai, H.-H., and Liu, Y. (2014). Critical Thickness Ratio for Buckled and Wrinkled Fruits and Vegetables. Epl 108 (4), 44003. doi:10.1209/0295-5075/108/44003
Dawson, M. A., and Gibson, L. J. (2007). Optimization of Cylindrical Shells with Compliant Cores. Int. J. Solids Struct. 44 (3−4), 1145–1160. doi:10.1016/j.ijsolstr.2006.06.009
Evans, A. G., and Hutchinson, J. W. (1984). On the Mechanics of Delamination and Spalling in Compressed Films. Int. J. Solids Struct. 20, 455–466. doi:10.1016/0020-7683(84)90012-x
Guvendiren, M., Burdick, J. A., and Yang, S. (2010). Solvent Induced Transition from Wrinkles to Creases in Thin Film Gels with Depth-wise Crosslinking Gradients. Soft Matter 6 (22), 5795–5801. doi:10.1039/c0sm00317d
Guvendiren, M., Yang, S., and Burdick, J. A. (2009). Swelling-induced Surface Patterns in Hydrogels with Gradient Crosslinking Density. Adv. Funct. Mat. 19 (19), 3038–3045. doi:10.1002/adfm.200900622
Han, L., Zhan, C., Liu, Y., and Wu, Z. (2017). A State Space Solution for Onset of Surface Instability of Elastic Cylinders with Radially Graded Young's Modulus. Int. J. Solids Struct. 126-127, 8–16. doi:10.1016/j.ijsolstr.2017.07.025
Harrison, C., Stafford, C. M., Zhang, W., and Karim, A. (2004). Sinusoidal Phase Grating Created by a Tunably Buckled Surface. Appl. Phys. Lett. 85 (18), 4016–4018. doi:10.1063/1.1809281
Huang, R., and Suo, Z. (2002b). Instability of a Compressed Elastic Film on a Viscous Layer. Int. J. Solids Struct. 39 (7), 1791–1802. doi:10.1016/S0020-7683(02)00011-2
Huang, R., and Suo, Z. (2002a). Wrinkling of a Compressed Elastic Film on a Viscous Layer. J. Appl. Phys. 91 (3), 1135–1142. doi:10.1063/1.1427407
Huang, Z. Y., Hong, W., and Suo, Z. (2005). Nonlinear Analyses of Wrinkles in a Film Bonded to a Compliant Substrate. J. Mech. Phys. Solids 53 (9), 2101–2118. doi:10.1016/j.jmps.2005.03.007
Hutchinson, J. W., and He, M. Y. (2000). Buckling of Cylindrical Sandwich Shells with Metal Foam Cores. Int. J. Solids Struct. 37 (46−47), 6777–6694. doi:10.1016/S0020-7683(99)00314-5
Hutchinson, J. W., and Suo, Z. (1992). Mixed Mode Cracking in Layered Materials. Adv. Appl. Mech. 29, 63. doi:10.1016/S0065-2156(08)70164-9
Jia, F., Cao, Y.-P., Liu, T.-S., Jiang, Y., Feng, X.-Q., and Yu, S.-W. (2012). Wrinkling of a Bilayer Resting on a Soft Substrate under In-Plane Compression. Philos. Mag. 92 (12), 1554–1568. doi:10.1080/14786435.2011.652691
Jia, F., Cao, Y.-P., Zhao, Y., and Feng, X.-Q. (2014). Buckling and Surface Wrinkling of an Elastic Graded Cylinder with Elastic Modulus Arbitrarily Varying along Radial Direction. Int. J. Appl. Mech. 06, 1450003. doi:10.1142/S1758825114500033
Jin, L., Cai, S., and Suo, Z. (2011). Creases in Soft Tissues Generated by Growth. Epl 95 (6), 64002. doi:10.1209/0295-5075/95/64002
Kang, M. K., and Huang, R. (2010a). Effect of Surface Tension on Swell-Induced Surface Instability of Substrate-Confined Hydrogel Layers. Soft Matter 6 (22), 5736–5742. doi:10.1039/c0sm00335b
Kang, M. K., and Huang, R. (2010b). Swell-induced Surface Instability of Confined Hydrogel Layers on Substrates. J. Mech. Phys. Solids 58, 1582–1598. doi:10.1016/j.jmps.2010.07.008
Karam, G. N., and Gibson, L. J. (1995). Elastic Buckling of Cylindrical Shells with Elastic Cores-I. Analysis. Int. J. Solids Struct. 32, 1259–1283. doi:10.1016/0020-7683(94)00147-o
Lavrenčič, M., Brank, B., and Brojan, M. (2020). Multiple Wrinkling Mode Transitions in Axially Compressed Cylindrical Shell-Substrate in Dynamics. Thin-Walled Struct. 150, 106700. doi:10.1016/j.tws.2020.106700
Lee, D., Triantafyllidis, N., Barber, J. R., and Thouless, M. D. (2008). Surface Instability of an Elastic Half Space with Material Properties Varying with Depth. J. Mech. Phys. Solids 56 (3), 858–868. doi:10.1016/j.jmps.2007.06.010
Li, B., Cao, Y.-P., Feng, X.-Q., and Gao, H. (2011). Surface Wrinkling of Mucosa Induced by Volumetric Growth: Theory, Simulation and Experiment. J. Mech. Phys. Solids 59 (4), 758–774. doi:10.1016/j.jmps.2011.01.010
Li, C., Han, Q., and Wang, Z. (2020). Semi-analytical Isogeometric Analysis for Wrinkling Instability of Stiff Films Bonded to Cylindrical Modulus-Graded Compliant Substrates. Compos. Struct. 235, 111787. doi:10.1016/j.compstruct.2019.111787
Razavi, M. J., Pidaparti, R., and Wang, X. (2016). Surface and Interfacial Creases in a Bilayer Tubular Soft Tissue. Phys. Rev. E 94 (2), 022405. doi:10.1103/PhysRevE.94.022405
Rogers, J. A., Someya, T., and Huang, Y. (2010). Materials and Mechanics for Stretchable Electronics. Science 327, 1603–1607. doi:10.1126/science.1182383
Seide, P. (1962). The Stability under Axial Compression and Lateral Pressure of Circular-Cylindrical Shells with a Soft Elastic Core. J. Aerosp. Sci. 29, 851–862. doi:10.2514/8.9619
Song, J., Jiang, H., Liu, Z. J., Khang, D. Y., Huang, Y., Rogers, J. A., et al. (2008). Buckling of a Stiff Thin Film on a Compliant Substrate in Large Deformation. Int. J. Solids Struct. 45 (10), 3107–3121. doi:10.1016/j.ijsolstr.2008.01.023
Sridhar, N., Srolovitz, D. J., and Suo, Z. (2001). Kinetics of Buckling of a Compressed Film on a Viscous Substrate. Appl. Phys. Lett. 78, 2482–2484. doi:10.1063/1.1368180
Stafford, C. M., Harrison, C., Beers, K. L., Karim, A., Amis, E. J., Vanlandingham, M. R., et al. (2004). A Buckling-Based Metrology for Measuring the Elastic Moduli of Polymeric Thin Films. Nat. Mater 3 (8), 545–550. doi:10.1038/nmat117510.1038/nmat1175
Sugiura, S., Sumaru, K., Ohi, K., Hiroki, K., Takagi, T., and Kanamori, T. (2007). Photoresponsive Polymer Gel Microvalves Controlled by Local Light Irradiation. Sensors Actuators A Phys. 140 (2), 176–184. doi:10.1016/j.sna.2007.06.024
Tokarev, I., and Minko, S. (2009). Stimuli-responsive Hydrogel Thin Films. Soft matter 5 (3), 511–524. doi:10.1039/b813827c
Wang, L. (2020). Axisymmetric Instability of Soft Elastic Tubes under Axial Load and Surface Tension. Int. J. Solids Struct. 191-192, 341–350. doi:10.1016/j.ijsolstr.2020.01.015
Wu, Z., Bouklas, N., Liu, Y., and Huang, R. (2017). Onset of Swell-Induced Surface Instability of Hydrogel Layers with Depth-wise Graded Material Properties. Mech. Mater. 105, 138–147. doi:10.1016/j.mechmat.2016.11.005
Wu, Z., Meng, J., Liu, Y., Li, H., and Huang, R. (2014). A State Space Method for Surface Instability of Elastic Layers with Material Properties Varying in Thickness Direction. J. Appl. Mech. 81 (8), 081003. doi:10.1115/1.4027464
Xu, F., Koutsawa, Y., Potier-Ferry, M., and Belouettar, S. (2015). Instabilities in Thin Films on Hyperelastic Substrates by 3D Finite Elements. Int. J. Solids Struct. 69-70, 71–85. doi:10.1016/j.ijsolstr.2015.06.007
Xu, F., and Potier-Ferry, M. (2016). On Axisymmetric/diamond-like Mode Transitions in Axially Compressed Core-Shell Cylinders. J. Mech. Phys. Solids 94, 68–87. doi:10.1016/j.jmps.2016.04.025
Yang, S., Khare, K., and Lin, P.-C. (2010). Harnessing Surface Wrinkle Patterns in Soft Matter. Adv. Funct. Mat. 20 (16), 2550–2564. doi:10.1002/adfm.201000034
Yao, J. C. (1962). Buckling of Axially Compressed Long Cylindrical Shell with Elastic Core. J. Appl. Mech. 29 (2), 329–334. doi:10.1115/1.3640550
Ye, L., Lu, G., and Ong, L. S. (2011). Buckling of a Thin-Walled Cylindrical Shell with Foam Core under Axial Compression. Thin-Walled Struct. 49 (1), 106–111. doi:10.1016/j.tws.2010.08.011
Keywords: wrinkling, instability, cylinder, graded material, Poisson’s ratio
Citation: Zhan C, Wang M, Li H and Wu Z (2022) Wrinkling of Elastic Cylinders With Material Properties Varying in Radial Direction. Front. Mech. Eng 8:911570. doi: 10.3389/fmech.2022.911570
Received: 02 April 2022; Accepted: 27 April 2022;
Published: 16 June 2022.
Edited by:
Liu Wang, Massachusetts Institute of Technology, United StatesReviewed by:
Shaoting Lin, Massachusetts Institute of Technology, United StatesYue Zheng, University of Southern California, United States
Copyright © 2022 Zhan, Wang, Li and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhigen Wu, emhpZ2Vud3VAaGZ1dC5lZHUuY24=
 Chunxiao Zhan
Chunxiao Zhan Zhigen Wu
Zhigen Wu