Fundamental Frequency Decomposition of Slender Structures on a Self-Tandem Dual Satellite

In order to make full use of the carrying capacity of the rocket and reduce the invalid mass of the satellite, the first-order fundamental frequency of the self-tandem dual satellite should be effectively decomposed into the designed fundamental frequency of each satellite. In this article, the fundamental frequency of the self-tandem dual satellite is analyzed based on the beam theory of slender structure arranged in the tandem and Rayleigh–Ritz theory. The influence of stiffness ratio, mass ratio, and size ratio on the first-order fundamental frequency of the dual satellite is also discussed. Based on the results, the decomposition method of the first-order fundamental frequency index of the self-tandem dual satellite is proposed, taking into consideration of the influence of manufacturing error and the joint stiffness between satellites. The numerical simulation is verified against experiments, setting the dual satellite on the same platform and different platforms. The results show that the decomposition method can effectively decompose the first-order fundamental frequency of a self-tandem dual satellite. The result is within the required error range, and the error is less than 6.5%. The calculation can effectively improve the specific stiffness and functional density of the satellite, reducing the overall development risk.

Introduction

In the field of deep space exploration, separable modules are generally designed to perform different tasks such as orbital transfer, orbital entry, and scientific experiments. Constrained by the limited carrier-envelope space, the multimodule self-tandem slender structure has become a typical form of deep space exploration spacecraft (Yu et al., 2016). Typical examples of modular tandem slender structures include the “Magellan” Venus probe, the Lunar Atmosphere and Dust Environment probe of the United States, the combination of “Forbes” and “Yinghuo-1” Mars probe jointly developed by Russia and China, and the Chinese Mars probe “Tianwen-1” (Yu et al., 2016; Liu et al., 2019).

In order to reduce the launch cost and make full use of the carrying capacity, launching two medium–high orbit satellites in the form of the tandem dual satellite is widely employed for international commercial satellites at present (Zhang et al., 2014; Li et al., 2019). Successful representatives of launch vehicles for tandem dual satellites are, among others, ARIANE’s SPELDA (supporting from outside payload fairing) and SYLDA (supporting from inside payload fairing) (ESA, 2004), as well as the external supporting structure of China’s Z-3A series that launch Beidou navigation dual satellite (Zhang et al., 2014). But both internal and external support structures consume the effective carrying capacity. Therefore, another scheme is proposed, which is called “self-tandem.” The main idea is to connect the two satellites without the installation of external supporting structures. Instead, the two satellites are connected by slender structures that belong to the two satellites (Fan et al., 2012; Feuerbornl and Neary, 2013; Zhang et al., 2014).

The most basic mechanical requirement of the launch vehicles for the satellite is its first-order fundamental frequency. The self-tandem dual satellite can be regarded as a whole to face the mechanical environment and requirements during the launch process. The design difficulty of the self-tandem state of the dual satellite is mainly reflected in how to effectively decompose the first-order fundamental frequency requirements of the dual satellite combination to each satellite, so as to ensure that each satellite has a clear design boundary, reasonable allocation of overall design resources, an accurate optimization design direction, and a clear fault handling interface, etc. During the development of the satellite, how to effectively decompose the indicators from top-level design and realize the optimization and control of the dynamic characteristics of the whole satellite have always been a technical problem to be solved urgently (Yu et al., 2016). Therefore, this article is aimed to derive a theoretical model and propose the optimization method based on the simulation results, taking into consideration of the carrier’s requirement for the first-order fundamental frequency requirements of the dual satellite and the characteristics of the slender structure. The innovations of this article are as follows. First, based on the theoretical analysis model established by tandem cantilever beam theory and Rayleigh–Ritz theory, the mathematical relationship between the stiffness ratio, mass ratio, size ratio, and the first-order fundamental frequency of the combination is established and analyzed theoretically. Moreover, a first-order fundamental frequency index decomposition method for self-tandem dual satellites is proposed, considering the interface stiffness of point connection between satellites. Its effectiveness is also proved by simulation and experiment. In order to achieve this, a theoretical model (Peng et al., 2018) for the fundamental frequency analysis of self-tandem dual satellites is first established, based on the beam theory and Rayleigh–Ritz theory (Smith et al., 2003; Lin et al., 2017). For simplicity, we assume the satellite as a continuous homogeneous beam with a uniform cross-section, which deforms in a quasistatic manner. The connection between the satellite is also simplified to spring with infinite (Section 2) or finite (Section 3) stiffness. The fundamental frequency characteristics of the self-tandem dual satellite are then discussed. Based on the results, a method to assign the fundamental frequency of self-tandem dual satellites between the satellites is proposed, considering the influence of interface stiffness on the whole fundamental frequency of the pointed joint between the satellites. Lastly, the numerical results are verified against the experiment and good agreement is obtained.

Theoretical Model of Fundamental Frequency Analysis

The form of one-rocket-carrying-two-satellites increases the launch difficulty due to high centroid and low frequency, which also seriously affects the reliability of launch flight. Therefore, higher requirements are put forward for the structural design of satellites with high specific stiffness. Under the premise that the carrier has a clear overall design target for the tandem dual satellite, the key to this problem is how to identify the contribution from each satellite/connection to the overall stiffness of the combination. And, the stiffness should be allocated (Gladwell, 1964; Gladwell, 1986; Chen et al., 2015) to each component at the early stage of satellite development to ensure that the overall mechanical properties of tandem dual satellites are optimal, without wasted resources and redundant design cycles.

Lin et al. (2017) has studied the multisatellite launch system with the frequency allocation method, sectional stiffness allocation method, staggered frequency method, and deformation index method. They have also verified the theoretical results against ground tests (Lin et al., 2017). The stiffness allocation method was proposed by Bijlaard (1951) as early as 1952 to solve the deflection, critical load, and fundamental frequency of sandwich plate/beam. In 1985, Hu (1985) proposed a constrained substructure method based on the stiffness distribution method and stated that the former offers a more feasible way to decompose stiffness. They also proposed a joint method that combined constrained substructure and decomposition stiffness method (Richard, 1971; Hu, 1985; Chen et al., 2015). In the work of Xia et al. (Xia and Jin, 2002), a hierarchical optimization method based on the stiffness distribution principle was proposed to optimize the dynamic characteristics of satellite structure subdivision design, which enhanced the realizability and reliability of engineering design (Rubin, 1975; Xia and Jin, 2002). Yang et al. (2016) studied the stiffness allocation method with the 30 m telescope three-mirror system as the object and presented a simplified stiffness allocation estimation formula (Yang et al., 2016). In the work of Yu et al. (2016) and Cai et al. (2020), the fundamental frequency of a tandem cantilever beam structure was analytically solved and analyzed and simplified to an ideal model with three extreme cases. They analyzed the fundamental frequency error between the ideal model and the actual model and discussed the feasibility of engineering application of the simplified method for the fundamental frequency decomposition on tandem dual satellites (Yu et al., 2016; Cai et al., 2020).

In this section, a theoretical model for the fundamental frequency analysis based on the beam theory of slender structure arranged in tandem and Rayleigh–Ritz theory will be given, taking into consideration of characteristics of the slender structure of self-tandem dual satellite. The fundamental frequency characteristics of the self-tandem dual satellite are then analyzed based on the model.

Theoretical Model

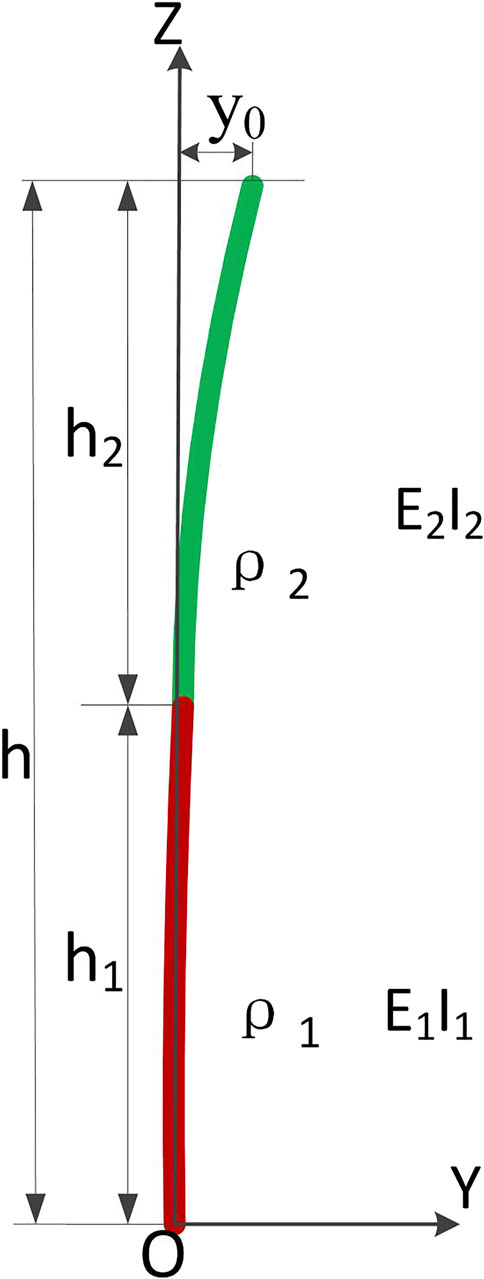
The configuration of the self-tandem dual satellite is shown in Figure 1, which includes satellite A (located on the bottom, connected with the carrier), satellite B (located on the top, connected with A), and a point joint device between the satellites. Compared with the surface connection device, the point joint is to connect two satellites through the contact point, and its joint is more like the bolt joint connecting the explosive bolt into the punched hole at the connection interface between two satellites.

FIGURE 1

FIGURE 1. The launch configuration of the self-tandem dual satellite.

The self-tandem dual satellite is assumed as two cantilevers (Chawda and Murugan, 2020) connected in tandem. Thus, an analytical solution can be obtained (Yu et al., 2016). The simplified model is shown in Figure 2, with beams 1 and 2 representing satellites A and B, respectively. $h_1$, ${\rho }_1$, and $E_1{I}_1$ are the length, the equivalent linear density, and the equivalent bending stiffness of beam 1, respectively. Similarly, $h_2$, ${\rho }_2$, and $E_2{I}_2$ are the length, the equivalent linear density, and the equivalent bending stiffness of beam 2. In addition, $h$ is the natural total length of the cantilever beam in tandem, and $y_0$ is the displacement of the cantilever beam end.

FIGURE 2

FIGURE 2. The tandem cantilever beam model.

Let $y^{\prime }$ denote the generalized displacement array of self-tandem dual satellite, which can take any value in the vibration mode space $H$, and ${\omega }_{0 }$ is the fundamental natural frequency. According to Rayleigh–Ritz theory,

${\omega }_0^2=\begin{array}{c}\text{min}\\ y^{\prime }\in H\end{array}\frac{U\left(y^{\prime },y^{\prime }\right)}{T\left(y^{\prime },y^{\prime }\right)}(1)$

where $U\left(y^{\prime },y^{\prime }\right)$ and $T\left(y^{\prime },y^{\prime }\right)$ represent the potential energy and kinetic energy at $y^{\prime }$ displacement, respectively, and satisfy the following relation:

$y^{\prime }={\displaystyle \sum _{i=1}^n{y}_i^{\prime },y_i^{\prime }\in H}(2)$

$U\left(y^{\prime },y^{\prime }\right)={\displaystyle \sum _{i=1}^{n}U\left(y_i^{\prime },y_i^{\prime }\right)}(3)$

$\frac{1}{{\omega }_0^2}\le {\displaystyle \sum _{i=1}^n\frac{1}{{\omega }_i^2}}(4)$

${\omega }_i^{\mathrm{2}}=\begin{array}{c}min\\ y_i^{\prime }\in H_i\end{array}\frac{U\left(y_i^{\prime },y_i^{\prime }\right)}{T\left(y_i^{\prime },y_i^{\prime }\right)}(5)$

At launch state, the self-tandem dual satellite can be considered to be fixed at the bottom, and $U\left(y_i^{\prime },y_i^{\prime }\right)$ and $T\left(y_i^{\prime },y_i^{\prime }\right)$ can be considered as positive definite functionals containing positive definite symmetric stiffness matrix and mass matrix. Note, the notation of $U\left(y^{\prime },y^{\prime }\right)$ rather than $U\left(y^{\prime }\right)$ is because the two independent variables in the bracket can represent the potential energy arising from two different displacements $\left(y^{\prime \left(1\right)},y^{\prime \left(2\right)}\right)$, e.g., two different modes. The same argument applies for $T\left(y^{\prime },y^{\prime }\right)$.

Based on the assumption that the beam is homogeneous and continuous with equal cross-section, we obtained

$U_{max}={\displaystyle \underset{0}{\overset{h_1}{\int }}\frac{E_1{I}_1}{2}{\left(\frac{d^{2}y}{d{z}^2}\right)}^{2}dz}+{\displaystyle \underset{h_1}{\overset{h_2}{\int }}\frac{E_2{I}_2}{2}{\left(\frac{d^{2}y}{d{z}^2}\right)}^{2}dz}(6)$

$T_{max}={\displaystyle \underset{0}{\overset{h_1}{\int }}\frac{{\rho }_1}{2}{\omega }^2{y}^{2}dz}+{\displaystyle \underset{h_1}{\overset{h_2}{\int }}\frac{{\rho }_2}{2}{\omega }^2{y}^{2}dz}(7)$

An error will arise from the assumption of the static deformation of the cantilever beam (Yu et al., 2016; Cai et al., 2020), but it does not hinder the acquisition of a relatively accurate and reliable analytical solution. Substituting (6-7) into 5) and assuming a rigid connection (infinite stiffness) between the beams, we can obtain the fundamental frequency as

$\omega =\frac{{\displaystyle {\int }_0^{h_1}{E}_1{I}_1{\left(\frac{d^{2}y}{d{z}^2}\right)}^{2}dz}\mathrm{+}{\displaystyle {\int }_{h_1}^{h_2}{E}_2{I}_2{\left(\frac{d^{2}y}{d{z}^2}\right)}^{2}dz}}{{\displaystyle {\int }_0^{h_1}{\rho }_1{\omega }^2{y}^{2}dz}+{\displaystyle {\int }_{h_1}^{h_2}{\rho }_2{\omega }^2{y}^{2}dz}}\mathrm{=}\sqrt{\frac{\delta }{\epsilon }}\cdot \sqrt{\frac{E_1{I}_1}{{\rho }_2}}(8)$

In Eq. 8, $\delta$ and $\epsilon$ are defined as

$\delta =2.268h_2^3{\alpha }^2+11.34h_1{h}_2^3\alpha +22.68h_1^2{h}_2^1\alpha +15.12h_1^3\alpha +7.56h_1^3\alpha \beta +11.34h_1^3\gamma \alpha \beta +2.268h_1^3{\gamma }^2\alpha {\beta }^2,(9)$

$\begin{array}{l}\epsilon =0.182h_1^7{\gamma }^2\alpha {\beta }^3+0.42h_1^6{h}_2^1\alpha {\beta }^2+1.584h_1^7\alpha {\beta }^2+1.638h_1^7\gamma \alpha {\beta }^2+0.546h_1^3{h}_2^4{\alpha }^2\\ \beta +0.567h_1^4{h}_2^3{\alpha }^2\beta +2.52h_1^4{h}_2^3\alpha \beta +7.812h_1^5{h}_2^2\alpha \beta +9.828h_1^6{h}_2\alpha \beta +4.968h_1^7\alpha \\ \beta +0.182h_2^7{\alpha }^3+1.638h_1{h}_2^6{\alpha }^2+2.772h_1^2{h}_2^5{\alpha }^2+1.512h_1^3{h}_2^4{\alpha }^2+3.78h_1^2{h}_2^5\alpha \\ +13.23h_1^3{h}_2^4\alpha +19.845h_1^4{h}_2^3\alpha +15.12h_1^5{h}_2^2\alpha +5.04h_1^6{h}_2\alpha ,\end{array}(10)$

where $\text{α}$, $\text{β}$, and $\text{γ}$ are

$\alpha =\frac{E_1{I}_1}{E_2{I}_2}\mathrm{，}\beta =\frac{{\rho }_1}{{\rho }_2}\mathrm{，}\gamma =\frac{h_1}{h_2}.(11)$

Equations 8–10 are the analytical solution of a tandem cantilever beam for simulating a self-tandem dual satellite. In the derivation, we assume the connection stiffness is infinite for simplification, but we will consider a finite connection stiffness later in Section 3.

Characteristic Analysis

The fundamental frequency calculation model based on the Rayleigh method describe above has higher accuracy than the simplified model from the literature (Yu et al., 2016; Cai et al., 2020). In this section, the influence of $\alpha$, $\beta$, and $\gamma$ on the first-order fundamental frequency of the system will be analyzed based on the model without simplification.

We use a series of equivalent parameter estimates of a self-tandem dual satellite as cantilever beam design inputs, assigning $\alpha$, $\beta$, and $\gamma$ from 0.1 to 10 (for convenience, when a single parameter is varied, the other two parameters are assigned as 1), respectively. In this way, the first-order fundamental frequency of the system will be calculated, and the characteristics of the first-order fundamental frequency of the tandem cantilever beam varying with the stiffness ratio, mass ratio, and size ratio of the tandem beam are obtained, as shown in Figure 3.

FIGURE 3

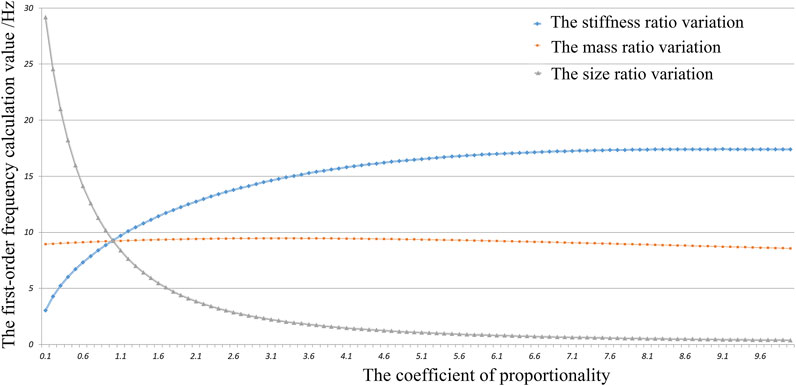
FIGURE 3. The characteristics of the proportion of stiffness, mass, and size on the first-order fundamental frequency of the system.

From Figure 3, we come to the following conclusions:

(1) With regard to the stiffness ratio of tandem beams, the first-order fundamental frequency of the system increases with the increased stiffness of the A-satellite, and the increasing rate decreases gradually.

(2) With regard to the mass ratio, the first-order fundamental frequency of the system increases first and then decreases with the increasing mass of the A-satellite. The mass ratio of dual satellites corresponding to the highest fundamental frequency is about 3.2. The curve of independent stiffness ratio variation is shown in Figure 4.

(3) With regard to the size ratio, the first-order fundamental frequency of the system decreases with the increasing height of the A-satellite, and the decreasing rate is gradually reduced.

(4) There is an intersection point of the three change curves, at which the corresponding ratios of stiffness, mass, and size of the dual satellite are all 1.

FIGURE 4

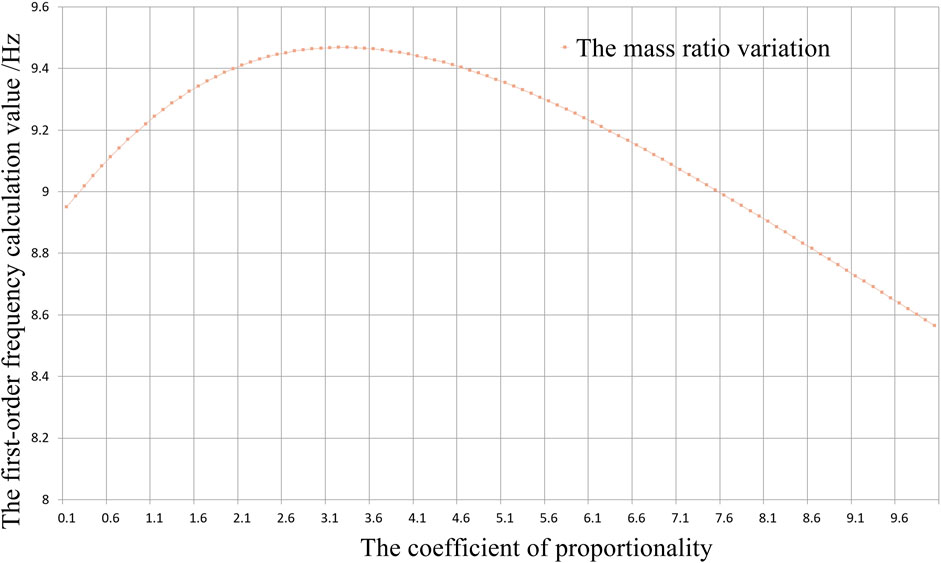
FIGURE 4. The influence of mass ratio variation of the self-tandem dual satellite on the first-order fundamental frequency of the system.

Decomposition Method of Fundamental Frequency and Its Verification

The analytical solution derived in the last section based on the tandem cantilever beam theory and Rayleigh–Ritz method has high accuracy in calculating the low-order fundamental frequency value. However, the actual fundamental frequency value will be lower than the theoretical analysis value, due to the disregard for tandem interface stiffness. Moreover, the difference between the theoretical beam model and the real model of the self-tandem dual satellite should also be considered, and the theoretical results should be correctly translated into engineering-informed values. Therefore, it is necessary to adapt the decomposition method of the fundamental frequency to an engineering environment.

Decomposition Process of Fundamental Frequency

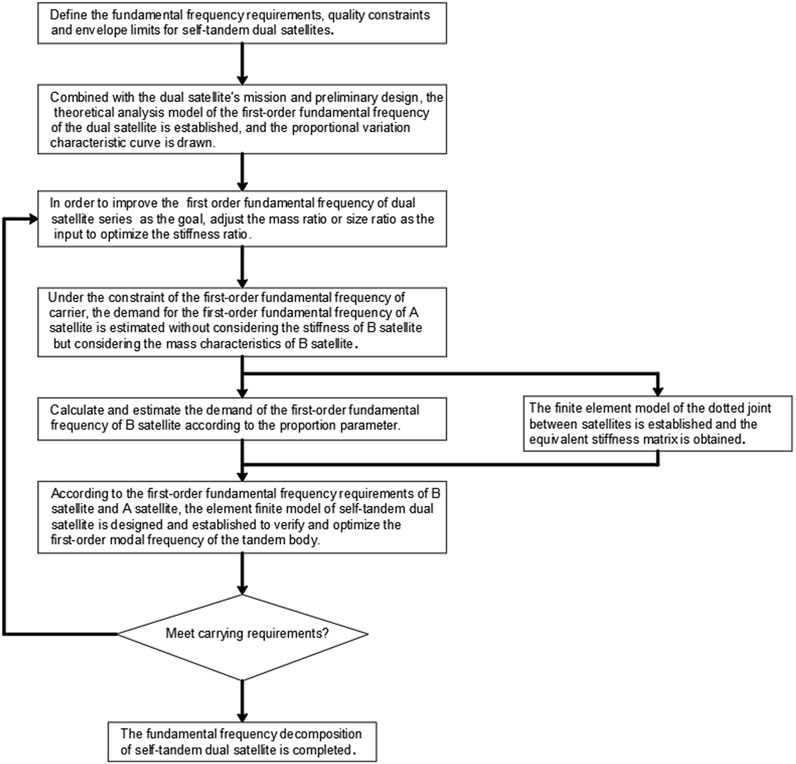
To facilitate the implementation of the fundamental frequency decomposition of tandem dual satellite, the stiffness of satellite A is first estimated from theoretical analysis. Then, the influence of connection stiffness between satellites is also taken into consideration. The decomposed fundamental frequency and allocated mass and size ratios of the self-tandem dual satellite are thus been preliminarily determined, which are further validated by finite element simulation. The flow chart of the decomposition process of the fundamental frequency is shown in Figure 5.

FIGURE 5

FIGURE 5. The flow chart of fundamental frequency decomposition of the self-tandem dual satellite.

It should be noted that if the component between satellites is designed as an independent component, we may only consider the contribution of the mass of the component and disregard its stiffness because the stiffness ratio and mass ratio between the intersatellite component and the satellite are sufficiently small (Yu et al., 2016). Nevertheless, the stiffness matrix of intersatellite connection still exists, especially for point joints with a limited number of connection points. We can use spring elements assigned with equivalent stiffness to simulate these connections (Shi et al., 2016).

Numerical Simulation and Its Experimental Verification

Following the flow chart in Section 2.1, we simulate a typical self-tandem dual satellite and consider two cases: 1) the two satellites from the dual system share the same platform and have similar mass and size, and 2) the two satellites put on different platforms and have different masses and sizes.

Case 1

Two satellites in self-tandem are put on the same satellite platform, of which one satellite is on the top and the other on the bottom. Based on the satellite design, there are the following constraints:

(i) Carrying constraints: the total mass of the dual satellite shall not exceed 5400kg, and the size shall fulfill the envelope requirement.

(ii) The first-order transverse fundamental frequency of the self-tandem dual satellite shall not be below 10 Hz.

The numerical model is built based on the parameters from the preliminary design of the satellite. The fundamental frequency varying with dual satellite characteristics is given in Figure 3.

Since the two satellites are put on the same platform, despite the different load configurations, the sizes of the two satellites cannot vary too much. Therefore, we set $\gamma$ = 1 for simplicity.

According to the preliminary design, the mass of the satellite on the top is set as 2400 kg (including the mass of the component between the satellites). Furthermore, based on the characteristic curve and carrying constraints from Figure 4, we take $\beta =1.25$ (estimated value, without mass optimization to increase specific stiffness) to improve the fundamental frequency of the whole satellite.

Taking the allowed error as 15% is selected for the stiffness ratio.

The satellites are connected by point joints, whose equivalent bending stiffness is set as 1.5E+9N mm/rad. The value is chosen by analyzing the relationship between interface stiffness and the number of the joints.

The first-order transverse fundamental frequency of the self-tandem dual satellite shall not be below 10 Hz. In order to simplify the process, we can treat the upper satellite as a pure rigid body ($E2$ which tends to infinity, but its mass cannot be disregarded) (Yu et al., 2016; Cai et al., 2020) to estimate the first-order fundamental frequency demand of the lower satellite. Under the foregoing assumptions, we set $h=2h_1$, $\gamma =1$, $\beta =1.25$, and $\alpha =0$, and substitute it into Eq. 8, yielding $f_0=0.559\sqrt{\frac{E_1{I}_1}{{\rho }_2{h}^4}}\ge 10\text{Hz}$. The first-order fundamental frequency of the satellite at the bottom is $f_1=0.559\sqrt{\frac{E_1{I}_1}{{\rho }_2{\left(h_1\right)}^4}}\ge 40\text{Hz}$. Consequently, the first-order fundamental frequency constraint of the satellite on the top is $f_2=f_1/\alpha \ge 26.67\text{Hz}$.

Based on these requirements, the design analysis and model test are carried out, and the results are shown in Figure 6.

FIGURE 6

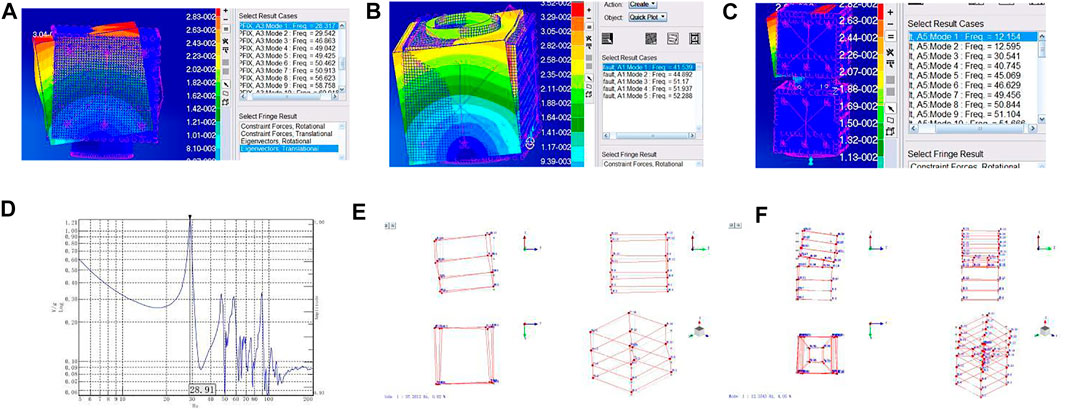
FIGURE 6. The modal analysis and experimental results of a self-tandem dual satellite. (A) The upper satellite modal analysis (the first-order 28.3 Hz). (B) The lower satellite modal analysis (the first-order 41.5Hz). (C) The modal analysis of combination (the first-order 12.2Hz). (D) The results of the upper satellite frequency sweep mode test (the first-order 28.9Hz). (E) The lower satellite mode test results (the first-order 37.3Hz). (F) The combination modal test results (the first-order 12.4Hz).

The numerical results show good agreement with the designed first-order fundamental frequency of the self-tandem dual satellite, which is $12.3\text{Hz}$. This is 6.5% different from the targeted value, which meets the carrying requirements with a sufficient margin for error. Although there is a certain deviation of the numerical results from experimental results for the satellite at the bottom due to a mass difference of the satellite at the bottom between the design and the experiment, the first-order fundamental frequency deviation is still less than 15%. As for the dual satellite as a whole, the first-order fundamental frequency is almost the same as that in the experiments. It is thus concluded that, in general, the fundamental frequency decomposition method derived in this article can effectively solve the first-order fundamental frequency of the dual satellite, whose deviation from the experimental result is within 0.02%.

The goal of the fundamental frequency decomposition process developed in this paper is to optimize the specific stiffness of the dual satellite, with emphasis on the specific stiffness improvement of the satellite at the bottom. However, if the centroid of the dual satellite is located too high to adjust the specific stiffness of the lower satellite to meet the requirements, the carbon fiber laminate can be employed.

Case 2

Two satellites in self-tandem are put on different satellite platforms. Based on the design principle of the satellite, there are the following constraints and limitations:

(i) Carrying constraints: the total mass of the dual satellite shall not exceed 600kg, and the size shall meet the envelope requirements.

(ii) The first-order transverse fundamental frequency of the self-tandem dual satellite shall not be below 13 Hz.

Parameters from the preliminary design requirements of the satellite are implemented in a numerical model. The fundamental frequency varying with dual satellite characteristics is given in Figure 3.

According to the preliminary design, the mass of satellites A and B are 400 and 200 kg, respectively, which yields $\beta =2$. In order to improve the fundamental frequency of tandem dual satellite, given the actual situation, we set $\gamma =1.5$. Moreover, we incorporate the target to maximize the specific stiffness of the satellite structure as much as possible (reduce the invalid mass of the structure), and a 15% allowed error, $\alpha =1.5$, is selected for the stiffness ratio.

The satellites are connected by point joints, whose equivalent bending stiffness is set as 8.2E+8N mm/rad. Again, the value is chosen from analyzing the relationship between interface stiffness and the number of joints.

Now, we consider the constraint that the first-order transverse fundamental frequency of a self-tandem dual satellite shall not be below 13 Hz. Due to the same reason as in case 1, satellite B is considered a rigid body (the mass cannot be disregarded) (Bijlaard, 1951). Therefore, $f_0=0.559\sqrt{\frac{E_1{I}_1}{{\rho }_2{h}^4}}\ge 13\text{Hz}$, and the estimated first-order fundamental frequency of satellite A is $f_1=0.559\sqrt{\frac{E_1{I}_1}{{\rho }_2{\left(h_1\right)}^4}}\ge 36.1\text{Hz}.$ Finally, the first-order fundamental frequency constraint of satellite B is $f_2=f_1/\alpha \ge 25.8\text{Hz}$.

Based on these requirements, the preliminary design is given and the finite element model is established. The analysis results are shown in Figure 7.

FIGURE 7

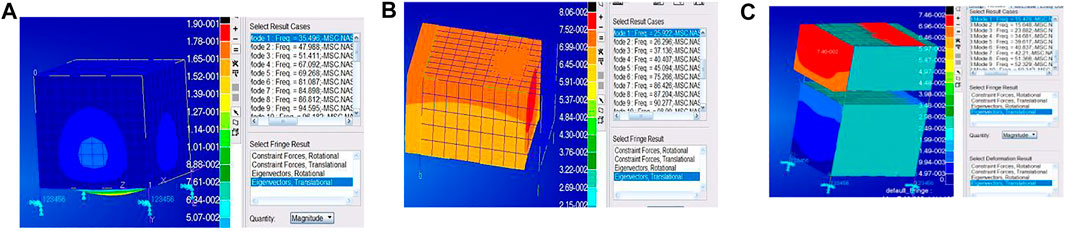
FIGURE 7. The modal analysis of a self-tandem dual satellite. (A) A satellite modal analysis (the first-order 35.5Hz). (B) B satellite modal analysis (the first-order 35.5Hz). (C) The modal analysis of dual satellite combination (the first-order 15.4Hz).

The results show that the first-order fundamental frequency of the dual satellite is 15.4 Hz, which is 3.5% different from the targeted frequency and meets the carrying requirements with a sufficient margin for error. Given that the mass deviation of the satellites and the bending stiffness of point connection between satellites are closely related to the manufacturing process, the implementation of the parameters from the actual situation can greatly improve the reliability of the fundamental frequency decomposition process in this paper.

Conclusion

This article has studied the decomposition method of the first-order fundamental frequency of the self-tandem dual satellite and derived an analytical solution based on the beam theory and Rayleigh–Ritz method. Based on the solution, we discussed the influence of stiffness ratio, mass ratio, and size ratio of a self-tandem dual satellite on the first-order fundamental frequency of the system and proposed a method of decomposition of the first-order fundamental frequency for self-tandem dual satellite, which took into consideration of the error and the connection stiffness of the pointed joint between satellites. Through theoretical analysis and experimental verification, the results show this, the fundamental frequency decomposition method can effectively decompose the frequency of the self-tandem dual satellite. Moreover, the first-order fundamental frequency of the dual satellite meets the targeted frequency with an error of no more than 6.5%. It can effectively improve the specific stiffness and development efficiency of the satellite and reduce the risk of engineering development. Furthermore, the decomposition method of the fundamental frequency is also beneficial to the overall design of mass, size, and fundamental frequency allocation at the initial stage of developing a related self-tandem dual satellite.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

GJ designed the overall structure of the whole article together with BL, JL. KL, and JY established the specific theoretical model, and analyzed the satellite’s characteristics. YZ has made a great contribution in simulating and verifying the decomposition method by experiments. The original manuscript was written by JL and reviewed and revised by GJ.

Funding

YZ was supported by Shanghai Sailing Program (project no. 20YF1452300), the National Natural Science Foundation of China (project no. 12102305), and the Fundamental Research Funds for the Central Universities.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bijlaard, P. P. (1951). Analysis of the Elastic and Plastic Stability of Sand wich Plates by the Method of Split Rigidities [J]. J. Aeronaut. Sci. 19 (7), 502–503. doi:10.2514/8.2120

CrossRef Full Text | Google Scholar

Cai, Y. B., Du, D., Kong, X. H., Hu, M. Y., and Tao, J. M. (2020). Fundamental Frequency Decomposition Technology for Tandem-Module Spacecraft [J]. Spacecraft Eng. 29 (2), 67–72. (Chinese). doi:10.3969/j.issn.1673-8748.2020.02.010

CrossRef Full Text | Google Scholar

Chawda, D., and Murugan, S. (2020). Dynamic Response of a Cantilevered Beam Under Combined Moving Moment, Torque and Force [J]. Int. J. Struct. Stab. Dyn. 20, 2050065. doi:10.1142/S0219455420500650

CrossRef Full Text | Google Scholar

Chen, G., Wang, H., Lin, Z., and Lai, X. (2015). The Principal Axes Decomposition of Spatial Stiffness Matrices. IEEE Trans. Robot. 31 (1), 191–207. doi:10.1109/tro.2015.2389415

CrossRef Full Text | Google Scholar

ESA (2004). Ariane 5 User's Manual Issue 5 Revision 3 [M].. Arianespace Group.

Google Scholar

Fan, R. X., Tang, J. G., and Lei, K. (2012). Separation Technology of Dual Satellite for Internal Carrying Layout [J]. Missiles and Space Vehicles 41 (2), 1–4. (Chinese). doi:10.3969/j.issn.1004-7182.2012.04.001

CrossRef Full Text | Google Scholar

Feuerbornl, S. A., and Neary, D. A. (2013). “Finding Away: Boeing’s “All Electric Propulsion Satellite” [C],” in 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Washington DC, 1–5.

Google Scholar

Gladwell, G. M. L. (1964). Branch Mode Analysis of Vibrating Systems. J. Sound Vibration 1 (1), 41–59. doi:10.1016/0022-460x(64)90006-9

CrossRef Full Text | Google Scholar

Gladwell, G. M. L. (1986). Inverse Problems in Vibration[M]. Dordrecht: Martinus Noordhoff Publisher.

Google Scholar

Hu, H. C. (1985). Lower Bounds of the Fundamental Natural Frequencies and the Critical Loads by the Method of Split Rigidities [J]. Acta Mechanica Solida Sinica 6 (2), 142–150. (Chinese).

Google Scholar

Li, W.-J., Cheng, D.-Y., Liu, X.-G., Wang, Y.-B., Shi, W.-H., Tang, Z.-X., et al. (2019). On-Orbit Service (OOS) of Spacecraft: A Review of Engineering Developments. Prog. Aerospace Sci. 108 (2), 32–120. doi:10.1016/j.paerosci.2019.01.004

CrossRef Full Text | Google Scholar

Lin, H., Zhang, X. Y., Peng, H. L., Chen, Y., Pan, Z. W., and Xu, Q. H. (2017). Determination of Stiffness Distribution for Muli-Payload Mission [J]. Struct. Environ. Eng. 44 (1), 36–42. (Chinese). doi:10.19447/j.cnki.11-1773/v.2017.01.006

CrossRef Full Text | Google Scholar

Liu, H. W., Li, W. J., Tian, B. Y., Ding, J. F., Zeng, F. M., Wang, Y. B., et al. (2019). Development and Application of Modular Deep-Space Probe Based on On-Orbit Assembly and Maintenance [J]. J. Deep Space Exploration 6 (6), 595–602. (Chinese). doi:10.15982/j.issn.2095-7777.2019.06.011

CrossRef Full Text | Google Scholar

Peng, X., Shi, X. P., and Gong, Y. P. (2018). Integerated Modeling of Spacecraft Relative Motion Dynamics Using Dual Quaternion[J]. Syst. Eng. Elect. 19 (2), 367–377. doi:10.21629/JSEE.2018.02.17

CrossRef Full Text | Google Scholar

Richard, M. (1971). A Hybrid Method of Component Mode Synthesis[J]. Comput. Structures 1 (4), 581–601.

Google Scholar

Rubin, S. (1975). Improved Component-Mode Representation for Structural Dynamic Analysis. AIAA J. 13 (8), 995–1006. doi:10.2514/3.60497

CrossRef Full Text | Google Scholar

Shi, C. Q., Zhou, X. B., Zhang, Y. T., Du, D., and Li, H. (2016). Modal Analysis of Spacecraft with Dotted Joints Based on Equivalent Stiffness. Spacecraft Eng. 25 (1), 31–39. (Chinese). doi:10.3969/j.issn.1673-8748.2016.01.005

CrossRef Full Text | Google Scholar

Smith, S. T., Bradford, M. A., and Oehlers, D. J. (2003). Inelastic Bucking of Rectangular Steel Plates Using a Rayleigh-Ritz Method[J]. Int. J. Struct. Stab. Dyn. 3 (4), 503–521. doi:10.1142/s0219455403001026

CrossRef Full Text | Google Scholar

Xia, L. J., and Jin, X. D. (2002). Study on the Global Dynamic Optimum Design of the Satellite Structure [D]. Shang Hai, China: Shanghai Jiao Tong University. (Chinese).

Google Scholar

Yang, F., Liu, G. J., Zhao, H. C., and Zhang, J. X. (2016). Stiffness Allocation and Analysis of TMT M3S [J]. Opt. Precision Eng. 24 (1), 152–159. (Chinese). doi:10.3788/ope.20162401.0152

CrossRef Full Text | Google Scholar

Yu, D. Y., Zhang, Y. H., Chu, Y. Z., Li, H., Wang, J. W., and Du, D. (2016). Structure Dynamics Analysis of Modularzed Deep Space Detector [J]. J. Deep Space Exploration 3 (3), 268–274. (Chinese). doi:10.15982/j.issn.2095-7777.2016.03.011

CrossRef Full Text | Google Scholar

Zhang, T., Wu, Y. T., Hu, W., Cheng, X., and Lu, S. T. (2014). Current Situation and Prospect of Dual Launch Technologies of the LM-3A Series Launch Vehicle ’s Structure Overall Design [J]. Missiles and Space Vehicles 43 (4), 1–4. (Chinese). doi:10.7654/j.issn.1004-7182.20140401

CrossRef Full Text | Google Scholar