Investigation on the micromechanical damage mechanism of cement-stabilized macadam after multiple freeze-thaw cycles

Cement-stabilized macadam is widely used in railway subgrade in cold regions. However, various diseases have occurred. In order to study the microscopic damage of cement-stabilized macadam after multiple cycles of freeze-thaw, the stress-strain curves were calculated by freeze-thaw tests in this paper. The discrete element model of cement-stabilized macadam constructed on the basis of discrete element theory was verified to be reasonable. After solving the linear/non-linear process of damage of cement-stabilized macadam, the relationship between the total damage variable and strain was obtained. The results show that as the number of freeze-thaw cycles increases, the initial damage variable increases. The results show that the more freeze-thaw cycles, the greater the initial damage variable. The damage variable formed after 20 freeze-thaw cycles is similar to that formed after 30 cycles. As the number of freeze-thaw cycles increases, the peak stress and particle contact area also decrease. The force chains are most numerous at the 215° position, and the number of force chains during the early stages of particle loading exceeds that in the later stages. The distribution of tangential and normal contact forces is symmetrical, with tangential stress distributed in an “∞” shape and normal contact force distributed in an “8” shape.

1 Introduction

In traditional research on cement-stabilized macadam, it is typically considered a homogeneous/continuous elastic body. Cement-stabilized macadam is a quintessential quasi-brittle material, composed internally of various aggregates, cement, and stone dust, thereby constituting a heterogeneous/discontinuous structure. The internal complex structure of cement-stabilized macadam significantly differs from its macroscopic properties (Fursa et al., 2016; Wang and Cui, 2018a). To enhance the performance of cement-stabilized macadam, many experts have conducted research on the damage of cement-stabilized macadam under freeze-thaw cycles based on discrete element theory. This research not only aims to improve the performance of cement-stabilized macadam but also to reveal the internal damage mechanisms, which is highly significant for the construction and design of railway subgrades (Yarbasi et al., 2007; Zhang et al., 2016).

Numerous experts have made significant contributions to the field. Xiao et al. (2024) investigated the freeze-thaw damage characteristics of cement-stabilized macadam. The strength of cement-stabilized macadam specimens decreases in a parabolic shape after cyclic freeze-thaw. As the freeze-thaw period increases, the rate of substrate quality loss increases and the ultrasonic wave transmission speed decreases. Lu et al. (2023) studied the mechanical properties and microscopic changes of soil-rock mixed fill materials at different freezing temperatures and cycles by using indoor testing methods. The results show that the strength of the specimens decreased linearly as the number of freeze-thaw cycles increased. The inside of the specimen gradually changed from dense to loose and the fracture mode changed from ductile to brittle fracture. In order to improve the frost resistance of subgrade soil, Zhao et al. (2023) studied the influence of freeze-thaw cycle on subgrade soil by adding calcium carbide slag and coal gangue to subgrade soil. The results show that calcium carbide slag and coal gangue stabilized soil has good freeze resistance, dry shrinkage slightly better than lime stabilized soil and excellent temperature shrinkage. Du et al. (2019) researched the feasibility of using sandstone as an aggregate for cement-stabilized macadam through unconfined compressive strength tests, split tests, and freeze-thaw cycle tests. The results showed that as temperature increased, the indirect tensile strength and frost resistance of the specimens also improved, with cement content, aggregate type, and curing time being critical factors in the experiments. Xu et al. (2021) studied the impact of curing temperature on the strength and moisture content of cement-stabilized macadam, evaluating its mechanical and pavement performance through tests. The results indicated that unconfined compressive strength, split tensile strength, and resilient modulus increased with the cement content, and the thermal shrinkage coefficient was approximately 15% of that of cement concrete. Sagidullina et al. (2022a) examined the mechanical properties of ordinary Portland cement-stabilized soil, conducting freeze-thaw cycles, unconfined compressive strength tests, and ultrasonic pulse velocity tests after curing the soil samples for 3, 7, and 14 days. The findings showed a declining trend in strength and pulse velocity values with an increase in freeze-thaw cycles, noting that the cement content could improve soil properties. Li et al. (2023) investigated the damage to rocks under freeze-thaw cycles by analyzing P-wave velocity, freeze-thaw cycle tests, and uniaxial compression tests to understand the mechanical properties and microstructural evolution of rocks. The research indicated that under freeze-thaw conditions, fine pores and cracks progressively developed, expanded, and permeated, reducing the interparticle bonding force, with the Box-counting method used to quantitatively describe the degradation of rock’s fine structure. Under the combined effect of freeze-thaw cycles and impact loads, Li et al. (2019) studied the fractal characteristics and energy dissipation of cement concrete by conducting freeze-thaw cycle tests at −20°C/20°C, establishing a relationship between energy consumption density and fractal dimension, revealing the coupling mechanism of freeze-thaw action and strain rate on fractal features and energy consumption. Huang et al. (2023) researched the energy dissipation and strength characteristics of cement soil under different freeze-thaw cycles through impact compression tests. The results showed that both the number of freeze-thaw cycles and impact pressure significantly affected the fractal dimension, strength, and absorbed energy of the cement soil. With increasing freeze-thaw cycles, the strength and energy absorption gradually decreased, with the effects diminishing when the number of cycles exceeded six. Lei et al. (2023) explored the mechanical properties of recycled coarse aggregates using freeze-thaw cycles and repeated loads to simulate damage during the breaking process. The results indicated that as the number of freeze-thaw cycles/repeated loads increased, both the compressive and tensile strengths of the recycled coarse aggregates declined, with internal damage primarily occurring as spalling and external damage manifesting as macroscopic cracks, while the tensile strength and elastic modulus linearly decreased with the number of freeze-thaw cycles.

In conclusion, most experts study the mechanical properties of cement-stabilized macadam from a macro perspective, with a single angle of research and a lack of mechanistic analysis, while research on internal particle damage is minimal. Since cement-stabilized macadam is a heterogeneous/discontinuous material, this paper builds a discrete element model of cement-stabilized macadam based on the theory of discrete elements. Through freeze-thaw tests (stress-strain curves), the micromechanical parameters of the cement-stabilized macadam discrete element model are obtained. The paper analyzes the micromechanical damage mechanisms of cement-stabilized macadam and studies the mechanical behavior between particles. Therefore, this paper has significant research and practical value.

2 Cement-stabilized macadam test

According to the “QCR9602-2015 Technical Specification for Construction of High-Speed Railway Subgrade Engineering,” specimens are prepared as shown in Figure 1. The specimens are 150 mm in diameter and 150 mm in height. The gradation of the cement-stabilized macadam material is shown in Table 1. The specimens are standardly cured for 28 days. Multiple freeze-thaw cycle tests are conducted on the cement-stabilized macadam specimens as depicted in Figure 2. Ultimately, the cement-stabilized macadam specimens undergo a uniaxial compression test as illustrated in Figure 3, with strain gauges attached to the surface of the specimens.

Figure 1

Figure 1. Cement-stabilized macadam specimen.

Table 1

Table 1. Gradation of cement-stabilized macadam material.

Figure 2

Figure 2. High and low temperature alternating test chamber.

Figure 3

Figure 3. Uniaxial compression test.

The detailed procedure of the test is as follows: The cement-stabilized macadam specimen is placed in a high and low temperature test chamber with a temperature range of −20°C–20°C. 24 h is a complete freeze-thaw cycle, 12 h freezing at −20°C, 12 h thawing at 20°C. The number of freeze-thaw cycles is 0, 10, 20, 30 and 40 times respectively. To ensure close contact between the loading plate and the specimen surface, the specimen is pre-pressed twice. Finally, the press continuously and uniformly applies a load at a rate of 1 mm/min until the specimen is destroyed.

3 Construction of discrete element model for cement-stabilized macadam

3.1 Model construction

Based on the discrete element theory, a cement-stabilized macadam model is constructed (Figure 4). When constructing a discrete element model for cement-stabilized macadam typical irregular particles are first selected to form an aggregate reservoir. For ease of calculation, particles greater than or equal to 4.75 mm are used as irregular aggregates (coarse aggregates) and particles less than 4.75 mm are used as round aggregates. The contact between particles is set as parallel bonded contact, and the upper/lower ends are set as loading plates. The interaction between the loading plates and the particles is modeled with a linear contact model. The gradation of the cement-stabilized macadam discrete element model is the same as the experiment. The upper and lower walls are subjected to a certain speed to simulate the uniaxial compression test (Yang et al., 2021; Yang et al., 2020; Wang and Cui, 2018b).

Figure 4

Figure 4. Cement-stabilized macadam discrete element model.

3.2 Evolution of damage in cement-stabilized macadam

Under the effect of cyclic freeze-thaw, a large number of mesoscopic cracks are generated inside the cement-stabilized macadam. The quantity of these cracks is closely related to the damage of the cement-stabilized macadam. These cracks are distributed randomly. It is assumed that the damage to the cement-stabilized macadam follows a Weibull probability distribution function (Chen et al., 2022; Nguyen et al., 2019; Jumassultan et al., 2021).

$p\left(\epsilon \right)=\frac{\beta }{\eta }{\left(\frac{\epsilon }{\eta }\right)}^{\beta -1}\exp \left[-{\left(\frac{\epsilon }{\eta }\right)}^{\beta }\right](1)$

where, β is the shape parameter, η is the scale parameter, and ε is the strain.

The variable for damage is:

$D=\frac{n}{N}=\frac{{\int }_0^{\epsilon }p\left(x\right)Ndx}{N}=1-\exp \left[-{\left(\frac{\epsilon }{\eta }\right)}^{\beta }\right](2)$

where, N refers to the total number of microelements in the specimen; n is the number of microelements that have been damaged.

Considering that the cement-stabilized macadam undergoes freeze-thaw cycles and uniaxial compression together, the relationship between the total damage variable and the constitutive is as follows.

$D_{total}=1-\frac{E_t}{E_0}\exp \left[-{\left(\frac{\epsilon }{{\eta }_t}\right)}^{{\beta }_t}\right](3)$

$\sigma =E_t\epsilon \exp \left[-{\left(\frac{\epsilon }{{\eta }_t}\right)}^{{\beta }_t}\right](4)$

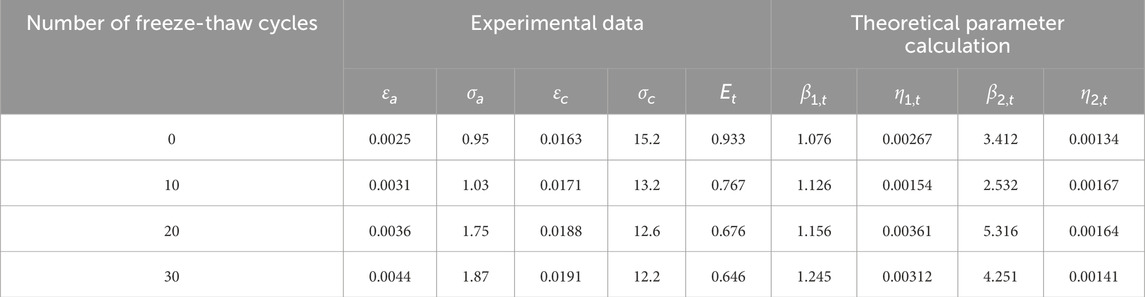
where, E_t is the modulus of elasticity measured in the test after t cycles of freezing-thawing.

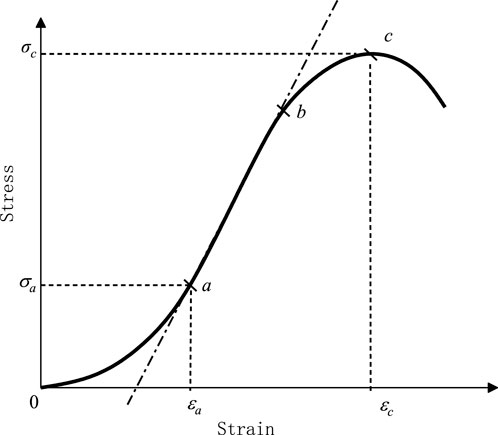
The typical stress-strain curve of cement-stabilized macadam under freeze-thaw cycles and uniaxial compression is shown in Figure 5. Where the 0a segment represents the pore compression phase, a-b is the elastic deformation phase, and b-c is the nonlinear compression phase (Xia et al., 2023; Kong et al., 2024; Sagidullina et al., 2022b).

Figure 5

Figure 5. Typical stress-strain curve for uniaxial compression.

Therefore, the total damage is obtained as Equation 5:

$\sigma =\left\{\begin{array}{l}{E}_t\epsilon \left\{1-\exp \left[-{\left(\frac{\epsilon }{{\eta }_{1,t}}\right)}^{{\beta }_{1,t}}\right]\right\}\left(\epsilon \le {\epsilon }_{a,t}\right)\\ E_t\left(\epsilon -{\epsilon }_{a,t}\right)\exp \left[-{\left(\frac{\epsilon -{\epsilon }_{a,t}}{{\eta }_{2,t}}\right)}^{{\beta }_{2,t}}\right]+{\sigma }_{a,t}\left(\epsilon >{\epsilon }_{a,t}\right)\end{array}\right.(5)$

where, σ_a,t and ε_a,t are the stress and strain at point a after t freeze-thaw cycles. η_t and β_t are the scale and shape parameters after t freeze-thaw cycles, respectively.

Then the total damage can be divided into two states.

$D_{total}=\left\{\begin{array}{l}1-\frac{E_t}{E_0}\left(\epsilon \le {\epsilon }_{a,t}\right)\\ 1-\frac{E_t}{E_0}\exp \left[-{\left(\frac{\epsilon -{\epsilon }_{a,t}}{{\eta }_{2,t}}\right)}^{{\beta }_{2,t}}\right]\left(\epsilon >{\epsilon }_{a,t}\right)\end{array}\right.(6)$

When the specimen is loaded to point C,

${\sigma }_{c,t}=\sigma {|}_{\epsilon ={\epsilon }_{c,t}}(7)$

Differentiating,

$\left.\frac{d\sigma }{d\epsilon }\right|{ }_{\epsilon ={\epsilon }_{c,t}}=0(8)$

When $\epsilon >{\epsilon }_{a,t}$

${\beta }_{2,t}=\frac{1}{\ln \left[\frac{E_t\left({\epsilon }_{c,t}-{\epsilon }_{a,t}\right)}{{\sigma }_{c,t}-{\sigma }_{a,t}}\right]}(9)$

${\eta }_{2,t}=\left({\epsilon }_{c,t}-{\epsilon }_{a,t}\right){{\beta }_{2,t}}^{\frac{1}{{\beta }_{2,t}}}(10)$

Similarly, when $\epsilon \le {\epsilon }_{a,t}$

${\beta }_{1,t}=\frac{\left(1-\frac{1}{1-\frac{{\sigma }_{a,t}}{{\epsilon }_{a,t}{E}_t}}\right)}{\ln \left(1-\frac{{\sigma }_{a,t}}{{\epsilon }_{a,t}{E}_t}\right)}=\frac{\frac{{\sigma }_{a,t}}{{\sigma }_{a,t}-{\epsilon }_{a,t}{E}_t}}{\ln \left(1-\frac{{\sigma }_{a,t}}{{\epsilon }_{a,t}{E}_t}\right)}(11)$

${\eta }_{1,t}={\epsilon }_{a,t}{\left[-\ln \left(\frac{{\sigma }_{a,t}}{{\sigma }_{a,t}-{\epsilon }_{a,t}{E}_t}\right)\right]}^{-\frac{1}{{\beta }_{1,t}}}(12)$

The experimental and theoretical analysis data for cement-stabilized macadam can be found in Table 2.

Table 2

Table 2. Experimental data and theoretical analysis parameters.

4 Model verification

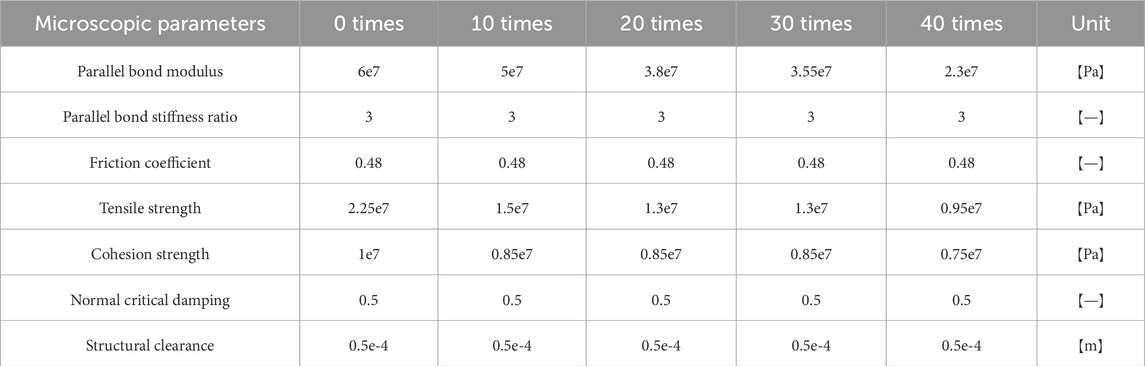
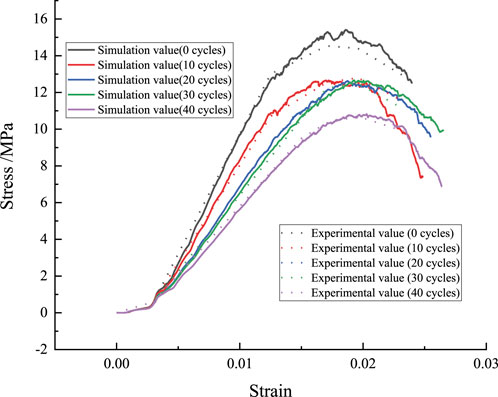
In order to verify the rationality of the discrete element model of cement-stabilized macadam, the mesoscopic parameters of cement-stabilized macadam were obtained using the “trial and error method”. After multiple calculations, the mesoscopic parameters of cement-stabilized macadam are shown in Table 3. The stress-strain curve of the cement-stabilized macadam discrete element model/experiment is shown in Figure 6.

Table 3

Table 3. Calibration values of mesoscopic parameters.

Figure 6

Figure 6. Comparison of stress-strain curves between simulation data and experimental data.

When comparing the stress-strain curves (experimental/simulation data), the maximum error in stress/strain is less than 10% (Figure 6), which indicates that the cement-stabilized macadam discrete element model is reasonably accurate.

5 Calculation results and analysis

5.1 Total damage variable and strain relationship

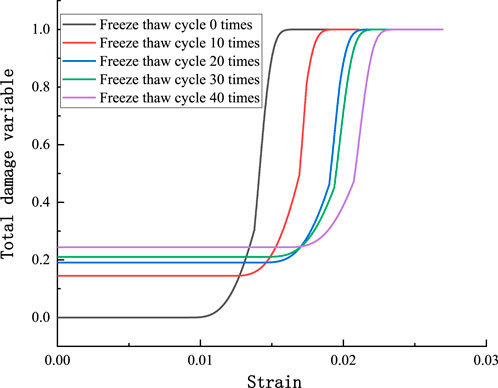
The total damage variable of cement-stabilized macadam in relation to strain is shown in Figure 7.

Figure 7

Figure 7. Relationship between total damage variable and strain.

The initial damage variables for 0, 10, 20, 30, and 40 freeze-thaw cycles are 0, 0.1449, 0.1908, 0.2091, and 0.2262 respectively (Figure 7). The initial damage variable increases with the number of freeze-thaw cycles. The damage formed after 20 cycles is close to that after 30 cycles.

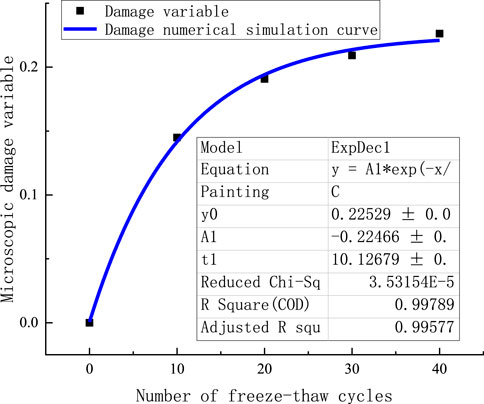
Assuming that the freeze-thaw cycle damage factor D_t and the number of freeze-thaw cycles satisfy the relationship D_t = ae (-t/b)+c, the microscopic damage variable and the number of cycles are shown in Figure 8, from which the functional relationship is obtained.

$y=0.225-0.224e^{-0.0987x}(13)$

Figure 8

Figure 8. Relationship between detailed damage variables and number of cycles.

When the coefficient of determination is R² = 0.997, the fitting effect is good.

5.2 Relationship between peak strain and freeze-thaw cycle times

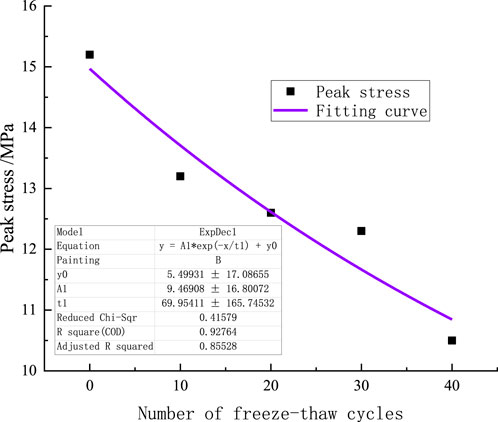
As the number of freeze-thaw cycles increases, the peak stress shows an overall decreasing trend (Figure 9). The fitted curve is calculated using formula 14.

$y=9.469e^{\frac{-x}{69.954}}+5.499(14)$

Figure 9

Figure 9. Relationship between peak stress and number of freeze-thaw cycles.

After 10 cycles of freeze-thaw, the peak stress decreased significantly (Figure 9). During 20–30 cycles of freeze-thaw, the decrease in peak stress is relatively small. However, after 40 freeze-thaw cycles, the peak stress decreased the most.

5.3 Particle contact area versus number of freeze-thaw cycles

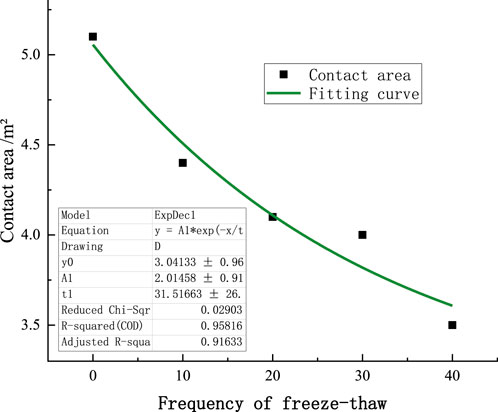
As the number of freeze-thaw cycles increases, the contact area between the particles shows a decreasing trend (Figure 10). The formula used to fit the curve is Formula 15.

$y=2.0146e^{\frac{-x}{31.517}}+3.0413(15)$

Figure 10

Figure 10. Relationship between contact area and number of freeze-thaw cycles.

After 10 freeze-thaw cycles, the contact area between particles decreased significantly (Figure 10). During 20–30 freeze-thaw cycles, the decrease in contact area between particles is relatively small. However, 40 freeze-thaw cycles caused the greatest reduction in inter-particle contact area.

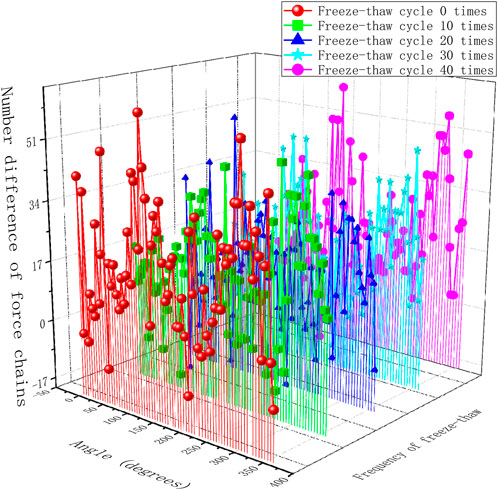
5.4 Analysis of the number/orientation of force chains between particles

The number of force chains varies with different freeze-thaw cycles (Figure 11). The orange line represents the number and angle of the force chains of cement-stabilized macadam before loading, and the purple dash line represents the number and angle of the force chains after loading. The highest number of force chains occurs at 215°, and the lowest at 265°. There are also relatively more force chains at 50° and 85°. The number of force chains in the early stages of particle loading is greater than in the later stages.

Figure 11

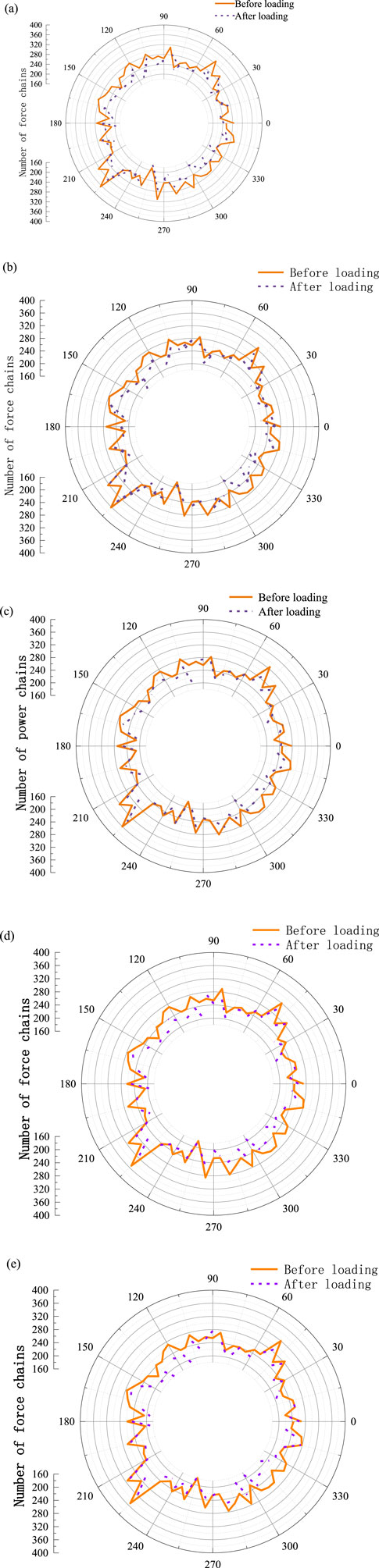
Figure 11. Changes in the number of force chains under different numbers of freeze-thaw cycles. (A) Freeze-thaw cycle 0 times. (B) Freeze-thaw cycle 10 times. (C) Freeze-thaw cycle 20 times. (D) Freeze-thaw cycle 30 times. (E) Freeze-thaw cycle 40 times.

To analyze the force chains in cement-stabilized macadam before and after loading, a differential map of the number of force chains before and after loading is established (Figure 12). There is significant fluctuation at 120° and 300°. With zero freeze-thaw cycles, the specimen shows a difference of 62 chains at 125°. After 10 freeze-thaw cycles, the largest difference occurs at 180° with a value of 46 chains. After 20 freeze-thaw cycles, the largest difference occurs at 100° with a value of 54 chains. And after 30 freeze-thaw cycles, the largest difference occurs at 345° with a value of 48 chains.

Figure 12

Figure 12. Difference in the number of force chains before and after loading.

5.5 Distribution patterns of tangential and normal contact forces

There is a certain pattern in the distribution of tangential and normal contact forces over different freeze-thaw cycles (Figure 13). It is evident that both tangential and normal contact force distributions exhibit symmetry. The tangential stresses are greater around 30°, 150°, 210°, and 330° (±15°), forming an “infinity” (∞) shape distribution; the normal contact forces are greater around 90° and 270° (±15°), forming a figure-eight (“8″) shape distribution.

Figure 13

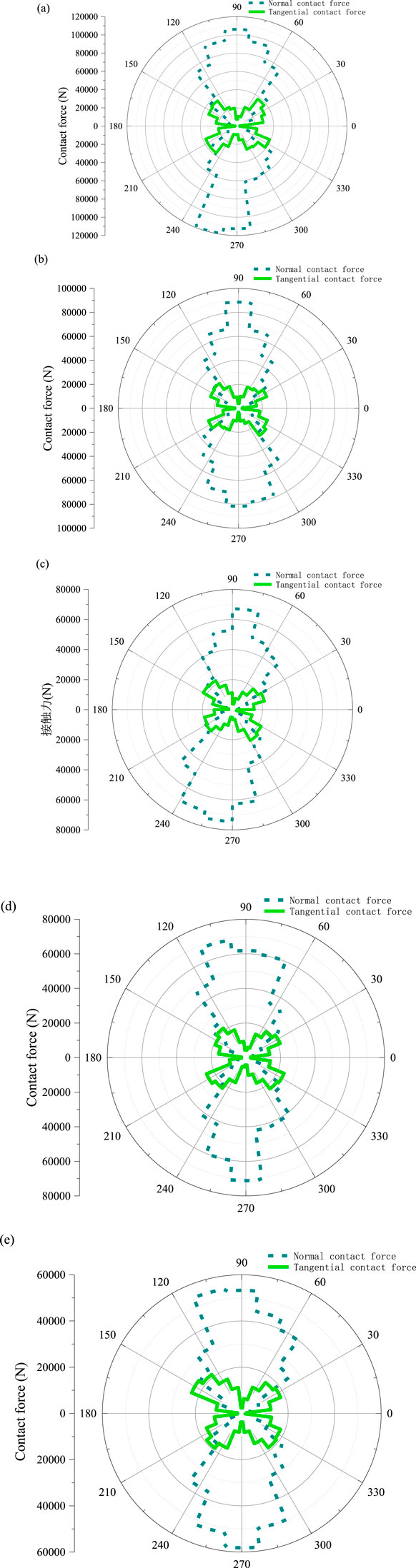
Figure 13. Distribution of tangential and normal contact forces under different freeze-thaw cycles. (A) Freeze-thaw cycle 0 times. (B) Freeze-thaw cycle 10 times. (C) Freeze-thaw cycle 20 times. (D) Freeze-thaw cycle 30 times. (E) Freeze-thaw cycle 40 times.

6 Conclusion

The more the number of freeze-thaw cycles, the larger the initial damage variable, with the damage formed after 20 cycles being close to that after 30 cycles.

As the number of freeze-thaw cycles increases, the peak stress becomes lower, and the contact area between particles also decreases.

The highest number of force chains occurs at 215°, while the lowest occurs at 265°; the number of force chains in the early stages of particle loading is greater than in the later stages.

The distribution of tangential and normal contact forces shows symmetry; the overall distribution of tangential stress forms an “∞” shape, and the overall distribution of normal contact forces forms an “8” shape.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XS: Data curation, Investigation, Writing–original draft. XW: Supervision, Writing–review and editing. GZ: Writing–review and editing, Data curation, Funding acquisition, Software, Validation. ZY: Funding acquisition, Writing–review and editing, Methodology.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by Science and Technology Research and Development Program of China National Railway Group Co., Ltd. (K2023G004), Overseas Scholar Program in the Hebei Province (C20190514), Science and Technology Project of Hebei Province (15457605D, 144576106D), National Natural Science Foundation of China (12072205), and Hebei Vocational University of Industry and Technology Campus level Project Funding (zy202402). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Author XW was employed by Shijiazhuang Fangzhou Highway Engineering Experiment and Testing Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, S. F., Hou, X. K., Luo, T., Yu, Y. T., and Jin, L. (2022). Effects of MgO nanoparticles on dynamic shear modulus of loess subjected to freeze-thaw cycles. J. Mater. Res. Technology-Jmr&T 18, 5019–5031. doi:10.1016/j.jmrt.2022.05.013

CrossRef Full Text | Google Scholar

Du, Q., Pan, T., Lv, J., Zhou, J., Ma, Q. W., and Sun, Q. (2019). Mechanical properties of sandstone cement-stabilized macadam. Appl. Sciences-Basel 9 (17), 3460. doi:10.3390/app9173460

CrossRef Full Text | Google Scholar

Fursa, T. V., Dann, D. D., and Osipov, K. Y. (2016). Evaluation of freeze-thaw damage in concrete by the parameters of electric response under impact excitation. Constr. Build. Mater. 102, 182–189. doi:10.1016/j.conbuildmat.2015.10.180

CrossRef Full Text | Google Scholar

Huang, K., Wang, H., and Huang, K. (2023). Freeze-thaw cycle effects on the energy dissipation and strength characteristics of alkali metakaolin-modified cement soil under impact loading. Water 15 (4), 730. doi:10.3390/w15040730

CrossRef Full Text | Google Scholar

Jumassultan, A., Sagidullina, N., Kim, J., Ku, T., and Moon, S. W. (2021). Performance of cement-stabilized sand subjected to freeze-thaw cycles. Geomechanics Eng. 25 (1), 41–48. doi:10.12989/gae.2021.25.1.041

CrossRef Full Text | Google Scholar

Kong, T. Y., Kothari, C., Qamhia, I. I. A., Tutumluer, E., Garg, N., Peters, T., et al. (2024). Freeze-thaw performance trends of short-term cured cement-stabilized aggregate quarry by-product materials. Transp. Res. Rec. 2678, 991–1003. doi:10.1177/03611981241236183

CrossRef Full Text | Google Scholar

Lei, B., Yu, L. J., Chen, T. Y., Lv, Z. T., Zaland, S., and Tang, Z. (2023). Experimental study on the initial damage and mechanical property evolution of recycled coarse aggregates under freeze-thaw cycles and repeated loads. Constr. Build. Mater. 375, 130972. doi:10.1016/j.conbuildmat.2023.130972

CrossRef Full Text | Google Scholar

Li, J. L., Tan, S. J., Yang, C., Chen, H., and Lin, Y. (2023). Analysis of damage characteristics for skarn subjected to freeze-thaw cycles based on fractal theory. Fractal Fract. 7 (5), 354. doi:10.3390/fractalfract7050354

CrossRef Full Text | Google Scholar

Li, Y., Zhai, Y., Liu, X. Y., and Liang, W. B. (2019). Research on fractal characteristics and energy dissipation of concrete suffered freeze-thaw cycle action and impact loading. Materials 12 (16), 2585. doi:10.3390/ma12162585

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, X., Tu, L. X., Tian, Y., Zhou, W., Zhao, X. J., and Yang, Y. Q. (2023). Experimental study of the freeze-thaw damage of alpine surface coal mine roads based on geopolymer materials. Water 15 (22), 3903. doi:10.3390/w15223903

CrossRef Full Text | Google Scholar

Nguyen, T. T. H., Cui, Y. J., Ferber, V., Herrier, G., Ozturk, T., Plier, F., et al. (2019). Effect of freeze-thaw cycles on mechanical strength of lime-treated fine-grained soils. Transp. Geotech. 21, 100281. doi:10.1016/j.trgeo.2019.100281

CrossRef Full Text | Google Scholar

Sagidullina, N., Abdialim, S., Kim, J., Satyanaga, A., and Moon, S. W. (2022a). Influence of freeze-thaw cycles on physical and mechanical properties of cement-treated silty sand. Sustainability 14 (12), 7000. doi:10.3390/su14127000

CrossRef Full Text | Google Scholar

Sagidullina, N., Abdialim, S., Kim, J., Satyanaga, A., and Moon, S. W. (2022b). Influence of freeze-thaw cycles on physical and mechanical properties of cement-treated silty sand. Sustainability 14 (12), 7000. doi:10.3390/su14127000

CrossRef Full Text | Google Scholar

Wang, Q., and Cui, J. Y. (2018a). Study on strength characteristics of solidified contaminated soil under freeze-thaw cycle conditions. Adv. Civ. Eng. 2018, 1–5. doi:10.1155/2018/8654368

CrossRef Full Text | Google Scholar

Wang, Q., and Cui, J. Y. (2018b). Study on strength characteristics of solidified contaminated soil under freeze-thaw cycle conditions. Adv. Civ. Eng. 2018, 1–5. doi:10.1155/2018/8654368

CrossRef Full Text | Google Scholar

Xia, W. T., Wang, Q., Yu, Q. B., Yao, M., Sun, D., Liu, J., et al. (2023). Experimental investigation of the mechanical properties of hydrophobic polymer-modified soil subjected to freeze-thaw cycles. Acta Geotech. 18 (7), 3623–3642. doi:10.1007/s11440-023-01804-9

CrossRef Full Text | Google Scholar

Xiao, R., An, B. P., Wu, F., Wang, W. S., Sui, Y., and Wang, Y. H. (2024). Freeze-thaw damage characterization of cement-stabilized crushed stone base with skeleton dense gradation. Material 17 (6), 1228. doi:10.3390/ma17061228

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, N., Chen, Z. D., Gao, H. J., Dong, D. M., Wu, Y. J., Lu, G. H., et al. (2021). Experimental investigation of the technical performances of SRX-stabilized graded macadam. Adv. Mater. Sci. Eng. 2021. doi:10.1155/2021/9959834

CrossRef Full Text | Google Scholar

Yang, Z. P., Li, X. Y., Li, D. H., Wang, Y., and Liu, X. R. (2020). Effects of long-term repeated freeze-thaw cycles on the engineering properties of compound solidified/stabilized Pb-contaminated soil: deterioration characteristics and mechanisms. Int. J. Environ. Res. Public Health 17 (5), 1798. doi:10.3390/ijerph17051798

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z. P., Yao, W., Li, X. Y., Ren, S. P., Hui, X., and Chang, J. Z. (2021). The effect of long-term freeze-thaw cycles on the stabilization of lead in compound solidified/stabilized lead-contaminated soil. Environ. Sci. Pollut. Res. 28 (28), 37413–37423. doi:10.1007/s11356-021-13401-y

CrossRef Full Text | Google Scholar

Yarbasi, N., Kalkan, E., and Akbulut, S. (2007). Modification of the geotechnical properties, as influenced by freeze-thaw, of granular soils with waste additives. Cold Regions Sci. Technol. 48 (1), 44–54. doi:10.1016/j.coldregions.2006.09.009

CrossRef Full Text | Google Scholar

Zhang, Y., Johnson, A. E., and White, D. J. (2016). Laboratory freeze-thaw assessment of cement, fly ash, and fiber stabilized pavement foundation materials. Cold Regions Sci. Technol. 122, 50–57. doi:10.1016/j.coldregions.2015.11.005

CrossRef Full Text | Google Scholar

Zhao, Q. M., Liu, J. S., Wu, L., Lu, X. J., Li, H., Hu, W. J., et al. (2023). Frost resistance and shrinkage characteristics of soil stabilized by carbide slag and coal gangue powder. Sustainability 15 (3), 2249. doi:10.3390/su15032249

CrossRef Full Text | Google Scholar