- 1School of Transportation and Civil Engineering, Architecture, Foshan University, Foshan, China
- 2China Construction Fourth Engineering Division Corp., Ltd., Guangzhou, China
The arch is a common structural form in bridge engineering; its collapse is often caused by instability. In this article, in-plane nonlinear instability of pin-ended functionally graded material (FGM) arches with two cross-sectional types under local radial loads is studied. New analytical solutions to nonlinear equilibrium paths, limit point instability, bifurcation instability, and multiple limit point instability of pin-ended FGM arches under local radial load are obtained. Modified slenderness corresponding to different instability patterns of FGM arches is also derived. Comparison with the numerical results of ANSYS demonstrates that the analytical solution is accurate. The results show that cross-sectional types of FGM arches have a great influence on limit-point instability and bifurcation instability. Localized parameters increase lead-to-limit point instability load and bifurcation instability load increases, while increasing the modified slenderness ratio results in decreased limit point instability load and bifurcation instability load. In addition, a material proportion coefficient and power law index increase can also lead to limit point instability load and bifurcation instability load decrease.
1 Introduction
Functionally graded material (FGM) pin-ended arches are usually subjected to local radial forms of load, and they also may be composed of a variety of materials. The forms of load on arches are generally local, such as local pedestrian and local vehicle load. However, these local loads may lead to instability and damage to arches. This article investigates the nonlinear instability of pin-ended FGM arches with locally uniform radial loads. The instability of arches is being researched by many scholars at present. Most research has found that the multiple forms of loading acting on arches may lead to their loss of stability. Accordingly, much of the literature is concerned with arches under different forms of load or different conditions. The stability of arches is an important problem in theoretical analysis, which can be termed the “classical buckling theory” (Timoshenk et al., 1962; Simitses George et al., 1976). However, this theory assumes that nonlinearity and deformation are not relevant in the pre-buckling of shallow arches. Pi et al. (2002) adopted an energy method to solve the theoretical solution of the in-plane buckling loads of arches with a radial uniformly distributed load on the whole arch axis, thus avoiding the classical buckling theory without consideringthe influence of deformation on pre-buckling. Bradford et al. (2002) analyzed the in-plane elastic stability of arches with a central concentrated load using a virtual work formulation that considers the effect of nonlinearity and deformation on pre-buckling. It has also been found that the stiffness of the end rotational restraints of arches greatly influences the buckling load (Pi et al., 2007). The buckling and post-buckling research of shallow circular arches with elastic rotational end-restraints has been studied by Pi et al. (2009). Cai et al. (2010) studied the nonlinear pre-buckling of parabolic shallow arches with elastic supports, finding that the rotational stiffness of elastic braces has a great influence on the buckling load. The in-plane stability of shallow arches under vertical uniform load and temperature variation has been studied (Cai et al., 2012). The post-buckling differential equilibrium equations of arches in horizontal and vertical directions are established through the principle of virtual work (Cai et al., 2013). Based on principles of virtual variational calculus and displacement, research on the governing equilibrium equation and the boundary conditions of circular shallow arches was conducted by Bateni et al. (2014) and Bateni et al. (2016). Han et al. (2016) addressed three limit shallowness values and the critical flexibility of the arch for elastic horizontal support to distinguish buckling patterns. Pi et al. (2017) analyzed instability and the in-plane nonlinear equilibrium of the arch with an arbitrary radial point load. Liu et al. (2017) investigated analytical solutions for the limit points and instability of arches subjected to an arbitrary radial concentrated load. Yan et al. (2017) applied the equilibrium equation of non-uniform shallow arches using the least potential energy principle. Lu et al. (2018) presented a novel theoretical solution for limit point, non-linear equilibrium, and bifurcation instability of arches subjected to locally uniform radial load by analyzing large amounts of data from finite element analyses. The out-of-plane buckling theory of doubly symmetric I-section arches with different parameters has been tested, with the theoretical solution agreeing with the experimental results (Lu et al., 2019a). Lu et al. (2019b) studied the transverse flexural buckling of an elastic steel circular arch with boundary rotation constraints under locally uniform radial load, conduced the pre-buckling shear force, axial force, and bending moment of the circular arch, and the analytical solution to the critical value of local uniform radial load under flexural and torsional buckling of the elastic steel arches.
The instability of the homogeneous cross-sectional materials of arches was discussed in the previous paragraph. At present, many scholars are studying the instability of FGM arches. FGMs are a new kind of material, with material changes that continuously reduce the concentration stress of materials and improve their properties and function. FGMs are being used in various fields (e.g., automotive, aerospace, and bridges). Lu et al. (2021a) researched the non-linear buckling of FGM arches of three materials with different cross-sectional materials under locally uniformly distributed radial loads. The multiple equilibrium and buckling of FG-GPLRC pinned-fixed arches under central point load were analyzed, and the nonlinear equilibrium path and buckling load of FG-GPLRC pinned-fixed arches were derived (Yang et al., 2020). Yang et al. (2022) assumed that the nanofillers were uniformly dispersed and the porosity coefficient varied along the direction of the arches’ thickness. The analytical solutions of the dynamic buckling loads of FG-GPLRC arches were derived by using an energy-based method (Yang et al., 2021). Lu et al. (2021b) analyzed the non-linear stability of the axial compression characteristics of graphene nanoplatelet random-reinforced composites. A new model was established to decouple the elastic properties of single-walled boron nitride nanotubes and their material thickness, and the physical significance of the thickness determination process and scale parameters of one-atom-thick materials was clarified (Yan et al., 2022a). Yan et al. (2022b) researched the mechanical bistability properties and analyzed the stable configuration and transformation process of bistable graphene under distributed compressive and uniformly out-of-plane loads according to a multi-scale computational framework. Rastgo et al. (2016) derived an instability equation for FGM curved beams. The properties of the material are identified as a power function of thickness in the analysis of the FGM arches (Song et al., 2008). Bateni et al. (2014) examined the in-plane nonlinear instability of FGM arches and also determined the existence of secondary equilibrium paths. Asgari et al. (2014) researched an analytical solution to primary equilibrium paths for FGM arches. Two-dimensional FGMs were used to explore the buckling of beams subjected to various boundaries (Şimşek et al., 2016). The finite element formulation of the general FGM plate and shell structure is given by using the theory of high-order shear deformation (Moita et al., 2018). Li et al. (2019) explored the buckling behavior of FGM arches under pressure and temperature loading. Lanc et al. (2016) analyzed the nonlinear instability of FGM thin-walled beams, obtaining numerical results of responses under lateral and flexural torsional instability loads. Some analytical studies on the nonlinear instability of pin-ended FGM arches with locally uniformly distributed radial loads can be found in previous articles.
In order to discuss the instability of arches under the local load of pedestrians and vehicles, this article studies the in-plane instability of pin-ended FGM arches with local radial loads. In order to analyze the in-plane instability behavior of FGM arches, two different types of materials are studied. New analytical solutions are offered to the nonlinear equilibrium path, limit point instability, and bifurcation instability of pin-ended FGM arches under local radial load. A modified slenderness ratio of FGM arches instability mode is here obtained. The localized parameter, modified slenderness ratio, material proportion coefficient, and power law index p also are researched in this article. Additionally, the analytical solution is accurate according to the finite limit element of shell element SHELL181, compared with the results of ANSYS. The results illustrate that the analytical solution to the FGM arches of the limit-point instability load and bifurcation instability load is accurate.
2 Materials Analysis
In this section, two types of cross-sectional material distributions are studied. The FGM pin-ended arches are made of metal Al and ceramic Al2O3. It is assumed that the material property of pin-ended FGM arches through the wall thickness is a continuous gradient change, which can be stated as
with Λc and Λm being the properties of Al2O3 and Al, respectively, where Vc and Vm are the volume fractions of Al2O3 and Al, which satisfy
Two material distribution modes for the cross-section of pin-ended FGM arches are studied in this paper, shown in Figures 1A,B, respectively, where metal (Al) is pure cyan and ceramic (Al2O3) is pure blue. In Figure 1A, Type 1 has three layers: the first and third layers are symmetrical at the top and bottom of the cross-section. The second is the middle layer, which is a pure ceramic (Al2O3) layer with thickness αh. The top surface of the first layer is made of metal (Al) and the bottom surface of the first layer is of ceramic (Al2O3). In the first layer, the cross-sectional material distribution of the ceramic (Al2O3) mass fraction of the layer decreases gradually from the bottom surface to the top surface, while the metal (Al) mass fraction increases gradually from the bottom surface to the top. In the third layer, the cross-sectional material distribution of the metal (Al) mass fraction of the layer decreases gradually from the bottom to the top surface, while the ceramic (Al2O3) mass fraction increases gradually from the bottom surface to the top surface. In Figure 1B, Type 2 has four layers. The first and fourth layers are pure ceramic (Al2O3) layers with thickness αh/2. The second layer is from αh/2 to the midline of the cross-section. The second and third layers are two middle layers and are symmetrical in the middle of the cross-section. The second layer is made of ceramic (Al2O3) material on its top and metal (Al) material on its bottom. The second layer with a material distribution of metal (Al) mass fraction of the layer increases gradually from the top to bottom surface in this layer, while the ceramic (Al2O3) mass fraction decreases gradually from top to bottom in this layer.
In Figure 1, based on the power law function, the volume fractions Vc of the two distribution modes are determined by
and
where α is the proportional coefficient of the uniform ceramic (Al2O3) layer and p is the power law index. Therefore, the elastic modulus of pin-ended FGM arches can be expressed as (Lanc et al., 2016):
where Em is the Young’s modulus of metal (Al) and Ec is the Young’s modulus of ceramic (Al2O3).
In order to analyze the in-plane instability of pin-ended FGM arches, the related stiffness parameters of the materials are calculated. A1k, B2k, and D3k are the stiffness parameters of the pin-ended FGM arches, respectively, which are defined as
Case 1. When the material distribution is subjected to Type 1, the stiffness parameters A1k, B2k, and D3k of pin-ended FGM arches can be respectively established as
Case 2. When the material distribution is subjected to Type 2, the stiffness parameters A1k, B2k, and D3k of pin-ended FGM arches can be respectively established as
3 Non-Linear Equilibrium Analysis
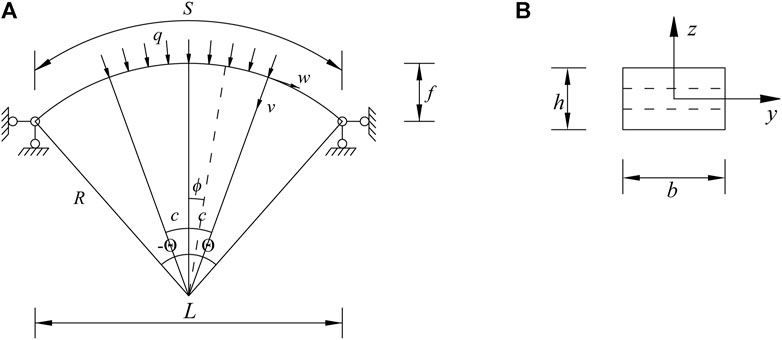
In the polar coordinates of Figure 2A, the center of the pin-ended FGM arch is the original point. The central angle 2Θ, arc length S, radius R of the pin-end FGM arches, and the load q are also respectively shown in Figure 2A, where w and v are the axial and radial displacements and 2c is the load regional angle for the pin-ended FGM arches under the locally distributed radial loads. In addition, b and h represent the width and thickness of the cross-section, respectively, as shown in Figure 2B.
The longitudinal normal strain of pin-ended FGM arches under locally distributed radial loads can be stated as
where
where
By substituting Eq. 13 into Eq. 14 and performing variational analysis, the variation of total potential energy can be stated as
where M and N represent the bending moment and the axial force of the pin-ended FGM arches, respectively, which can be written as
with A1k, B2k, and D3k being the stiffness parameters of the pin-ended FGM arches obtained from Eqs 7–12. The bending moment M can then be rewritten by substituting Eq. 18 into Eq. 17 as
For the nonlinear equilibrium of the pin-ended FGM arches, the variation of the total potential energy should vanish, which results in
and
Hence, the second order differential equations for solving radial displacement can be derived by substituting Eqs 19–21 into Eq. 22 as
with ϖ being dimensionless axial force parameter and γ being the equivalent stiffness, which can be respectively given by
In addition, one of the displacements at a pin support should be relaxed to allow displacement in an outer direction. However, this paper focuses on in-plane instability of the FGM arch, and so the boundary conditions for the out-of-plane displacement are not expressed. Therefore, the following essential boundary conditions of the pin-ended FGM arches can be expressed as
The non-dimensional radial displacement can be solved by substituting the boundary conditions obtained from Eq. 24 into Eq. 22 as
where β1 = ϖΘ, β2 = ϖc and
The non-dimensional load P can be expressed as
Equation 25 shows that the dimensionless radial displacement
Considering the essential boundary conditions
Substituting Eq. 25 into Eq. 28 and integrating it over the entire pin-ended FGM arches results in a quadratic equation of equilibrium between P and β1 as
with the coefficients a1, b1, and c1 being respectively given by
where the modified geometric slenderness λs is
The equivalent slenderness λ can comprehensively consider the influence of the cross-section of composite structures, which can be given by (Lu et al., 2021a)
with equivalent radius of rotation
By substituting Eq. 34 into Eq. 32, Eq. 32 can be rewritten as
According to Eqs 29–31 and Eq. 26, when β1, β2 and the equivalent slenderness λ are given, the non-dimensional force parameter P can be solved by the quadratic equation of equilibrium given by Eq. 29.
4 Instability Analysis
4.1 Limit Point Instability
According to Lu et al. (2018), a pin-ended arch subjected to a locally distributed radial load can lose its stability in a limit point instability pattern. At limit points, the equilibrium equation can be given by
where
Thus, by solving Eqs 29, 37 at the same time, the limit point instability loads can be obtained. By considering the proportional coefficient α and the power law index p of homogeneous layer and the types of cross-section, the limit point instability loads and the limit point instability equilibrium paths for pin-ended FGM arches under locally distributed radial loads are studied as follows.
According to Eqs 29, 37, the limit-point instability load and the equilibrium path of limit-point instability of pin-ended FGM arches are solved. The nonlinear behavior of pin-ended FGM arches subjected to locally distributed radial loads having different types of cross-section (i.e., Types 1 and 2) is shown in Figure 3A as variations of v/f with Q/(2NEc2Θ) and in Figure 3B as variations of N/NEc2 with Q/(2NEc2Θ)), where v/f represents the dimensionless central displacement, N/NEc2 represents the dimensionless axial force, and Q/(2NEc2Θ) represents the dimensionless locally distributed radial load. In these figures, the modified geometric slenderness λs = 4, S/h = 100, η = c/Θ = 0.5, α = 0.2, p = 1 of the pin-ended FGM arch.
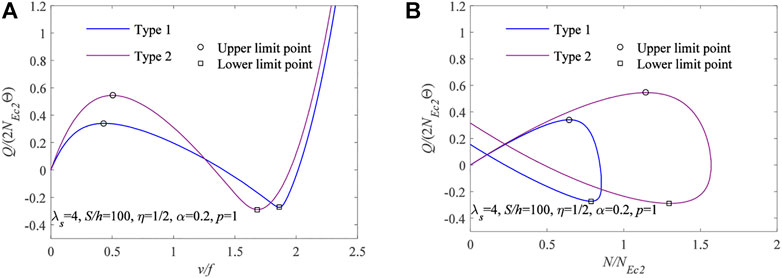
FIGURE 3. Equilibrium paths of limit point instability for pin-ended FGM arches using different types of cross-section: (A) v/f − Q/(2NEc2Θ) curves. (B) N/NEc2 − Q/(2NEc2Θ) curves.
Figure 3 shows that this point on the equilibrium path snaps through the remote point on the equilibrium path; pin-ended FGM arches then occur to the point where the instability reaches its upper limit, called “limit point instability loads”. In addition, different types of cross-section have a great effect on the limit point instability load and the limit point instability equilibrium path. The limit point instability load of the cross-section of Type 2 is higher than that of Type 1, which illustrates that the material with high stiffness distributed on the cross-sectional surface can effectively reduce the in-plane instability of pin-ended FGM arches.
Also investigated were the influence of the type, the power-law index of material distributions and the proportional coefficient of homogeneous layer, the modified geometric slenderness λs of pin-ended FGM arches, and the localized parameter η on the limit point instability load of pin-ended FGM arches. The c/Θ − Q/(2NEc2Θ) curves are shown in Figure 4A with pin-ended FGM arches using a different material type section (Type 1, Type 2), in Figure 4B for pin-ended FGM arches using the different modified geometric slenderness λs (λs = 3, 4, 5), in Figure 4C for pin-ended FGM arches using the different power-law index of material distributions p (p = 0.5, 1, 2), and in Figure 4D for pin-ended FGM arches using the different proportional coefficient of homogeneous ceramic layer α (α = 0.1, 0.2, 0.4). Figure 4 shows that, when the localized parameter c/Θ, proportional coefficient of homogeneous layer α and the modified geometric slenderness λs increases, the limit point instability load Q/(2NEc2Θ) also increases. In Figure 4A, the limit point instability load of Type 2 is greater than the limit point instability load of Type 1. In Figure 4C, the limit point instability load Q/(2NEc2Θ) decreases with the increase of the power-law index p.
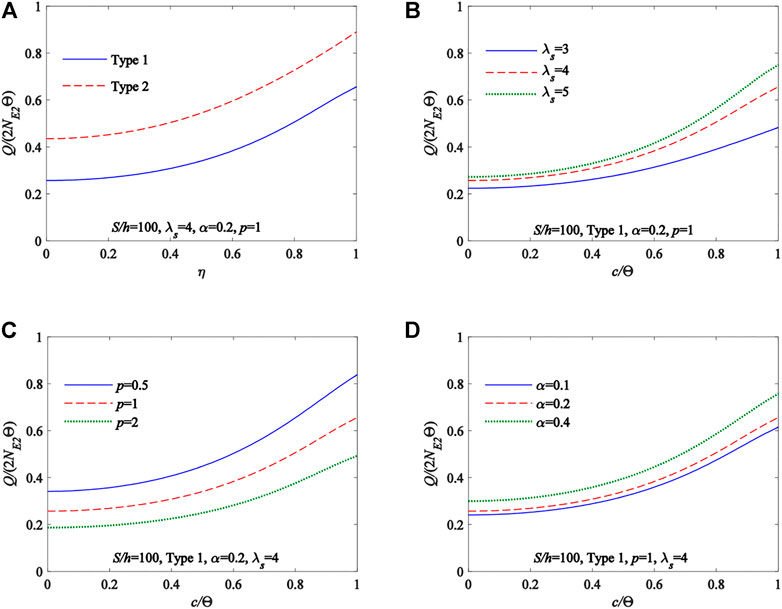
FIGURE 4. Effects of different parameters on the limit point instability load of the pin-ended FGM arches: (A) Material type. (B) Modified geometric slenderness λs. (C) Power-law index p. (D) Proportional coefficient of homogeneous ceramic layer α.
4.2 Lowest Limit Point Instability
The fixed FGM arch subjected to a locally distributed radial load can buckle in the lowest limit point instability pattern, while the arch, having the equivalent slenderness λ, is given (Lu et al., 2021b). Homoplastically, a pin-ended arch subjected to a locally distributed radial load can also buckle in the lowest limit point instability pattern, while an arch having the equivalent slenderness λ is given. Referring to the limit point instability theory of pin-ended homogeneous arches subjected to central point load (i.e., c → 0) (Lu et al., 2019a), the axial force parameters βb1 for arches buckling in lowest limit point instability pattern can be expressed as
By substituting Eq. 39 into Eq. 29, the non-dimensional load P for arches buckling in lowest limit point instability pattern can be given by
The above theory of homogeneous arches can be used for this analysis: the central displacement
with
According to Eq. 46, the central displacement
Hence, the equivalent slenderness for an arch buckling in the lowest limit point instability pattern can be expressed as
The nonlinear behavior of pin-ended FGM arches with locally distributed radial loads having different types of cross-section (i.e., Type 1 and Type 2) is shown in Figure 5A as the v/f − Q/(2NEc2Θ) curves, and in Figure 5B as the N/NEc2 − Q/(2NEc2Θ) curves. In Figure 5, there is an inflection point in the equilibrium path for a pin-ended FGM arch having equivalent slenderness. When there is an inflection point in the equilibrium path and no limit point in the equilibrium path, the load corresponding to this inflection point can be called the “lowest limit point instability load”. According to Figure 5, the lowest limit point instability load of a cross-section of Type 2 is higher than that of Type 1.
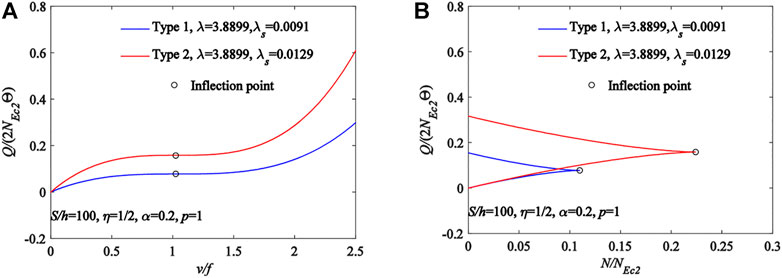
FIGURE 5. Inflection point of limit point instability for pin-ended FGM arches using different types of cross-section: (A) v/f − Q/(2NEc2Θ) curves. (B) N/NEc2 − Q/(2NEc2Θ) curves.
4.3 Multiple Limit Point Instability
A pin-ended arch with a central point load can buckle in a multiple limit point instability patterns (i.e., the number of limit points
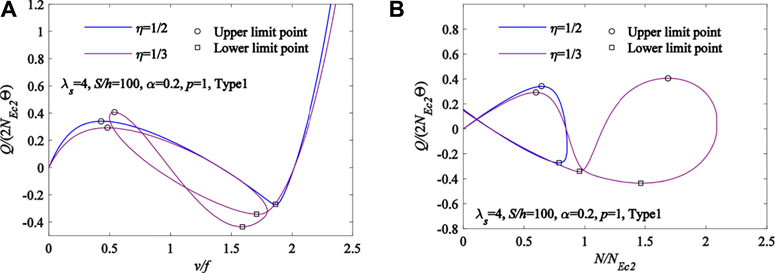
FIGURE 6. Multiple limit point instability for pin-ended FGM arches using different localized parameters: (A) v/f − Q/(2NEc2Θ) curves. (B) N/NEc2 − Q/(2NEc2Θ) curves.
Analogously, the v/f − Q/(2NEc2Θ) curves are shown in Figure 7A with the FGM arches using different equivalent slenderness λ(λ = 8, λ = 16), where η = 1/3, S/h = 100, α = 0.2, p = 1, material type section is Type 1, and the N/NEc2 − Q/(2NEc2Θ) curves are shown in Figure 7B. In Figure 7, it is found that the equivalent slenderness λ has a great influence on the limit point instability load and the equilibrium path of pin-ended FGM arches. In particular, as the equivalent slenderness λ augments from λ = 8 to λ = 16, the number of the limit point instability changes. When the modified geometric slenderness λ = 16, the multiple limit point instability particularly appears.
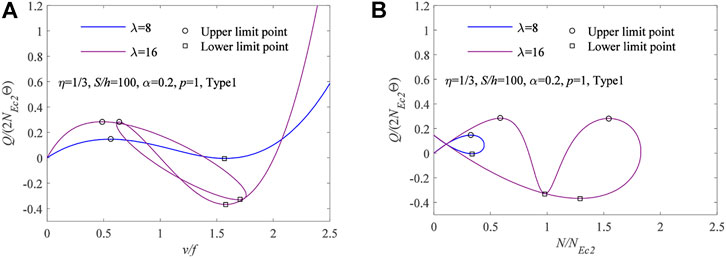
FIGURE 7. Multiple limit point instability for pin-ended FGM arches using different equivalent slenderness: (A) v/f − Q/(2NEc2Θ) curves. (B) N/NEc2 − Q/(2NEc2Θ) curves.
Figures 6, 7 indicate that a pin-ended FGM arch under locally distributed radial loads can buckle in a multiple limit points instability pattern, while the arch has a certain localized parameter η and equivalent slenderness λ. Referring to the multiple limit points instability theory of pin-ended homogeneous arches under central point load (i.e., c → 0) (Lu et al., 2019a), the axial force parameters βbk for arches buckling in the lowest limit point pattern (i.e., k = 1) and the multiple limit points instability patterns (i.e., k = 3, 5, 7, …, odd) can be expressed as
By substituting Eq. 45 into Eq. 29, the non-dimensional load P for arches buckling in the multiple limit points instability patterns can be given by
The above theory of homogeneous arches can be used for this analysis; the central displacement for a pin-ended FGM arch buckling in the multiple limit point instability pattern is given by substituting Eqs 45, 46 into Eq. 26 and performing limit analysis, as
with
According to Eq. 46, there is a solution for the central displacement
Hence, the equivalent slenderness for an arch buckling in the multiple limit point instability pattern can be expressed as
The condition for Eq. 45 has a solution only when
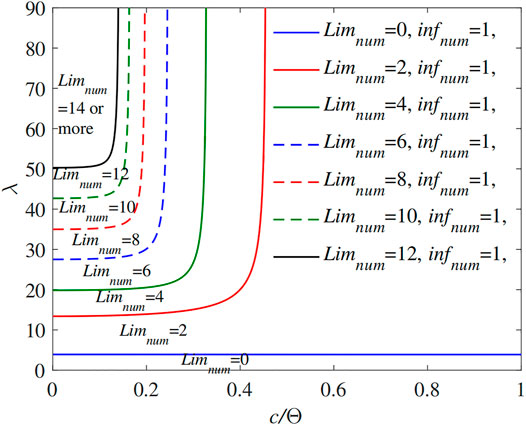
In order to discuss the relationship between the number of limit points and parameters (i.e., equivalent slenderness λ, localized parameter η), the c/Θ − λ variations are shown in Figure 8 for the pin-ended FGM arch having a different number of limit points (e.g., number = 0, 2, 4, 6, 8, 10, 12, 14, or more). According to Figure 8, it can be seen from Figure 8 that the number of multiple limit points augment an increase in equivalent slenderness λ and a decrease of the localized parameter η.
4.4 Bifurcation Instability
Instability of the pin-ended FGM arches also occurs in a bifurcation pattern. The radial equilibrium differential equation of the FGM arches in the initial equilibrium state is given by Eq. 22, while the radial equilibrium differential equation of the FGM arches in the infinitesimal closed bifurcation equilibrium state can similarly be attainted as
Combining Eq. 22 and above Eq. 52, the bifurcation equilibrium differential equation of pin-ended FGM arches becomes
These equations show that the equilibrium of the bifurcation mode is same as that of homogeneous arches (Lu et al., 2021a). Similarly, referring to the theory of homogeneous pin-ended arches with locally distributed radial loads, the axial force parameters βb1 and the axial force N of FGM arches are
The parameter βb2 of the bifurcation mode is expressed as
Substituting Eqs 54, 55 into Eq. 53, the bifurcation instability equation can be given by
The bifurcation instability load of pin-ended FGM arches with locally uniform radial loads will be obtained by giving the local parameter.
The equivalent slenderness λ solved from Eq. 59 can make pin-ended FGM arches buckle in the bifurcation buckling mode. The equivalent slenderness λb1 can be expressed as
When instability emerges in the pin-ended FGM arches in the bifurcation buckling dominant pattern, the modified geometric slenderness
This section studies when pin-ended FGM arches are under local uniformly distributed radial loads, the localized parameter η, bifurcation instability load, and the bifurcation instability equilibrium path. When pin-ended FGM arches have different localized parameters η, the bifurcation instability load and bifurcation instability equilibrium path are shown in Figure 9A for v/f vs. Q/(2NEc2Θ) and in Figure 9B for N/2NEc2 vs. Q/(2NEc2Θ), where λs = 4, S/h = 100, λ = 0.2, p = 1, and material type section is Type 1. According to Figure 9, the upper bifurcation instability points are located on the primary equilibrium path and the bifurcation instability equilibrium path. When the pin-ended FGM arch is under the bifurcation instability equilibrium path between the upper and lower bifurcation instability points, the dimensionless axial force parameter N/2NEc2 remains constant. When the instability equilibrium is at a lower bifurcation instability point, the equilibrium path of arches from the bifurcation instability equilibrium path is back to the primary equilibrium path. It was also found that the localized parameter η has an important influence on the bifurcation instability equilibrium path and the bifurcation instability load. The local bifurcation instability load augments the localized parameter η; FGM arches bifurcation instability are more likely to occur when the localized parameters η become larger.
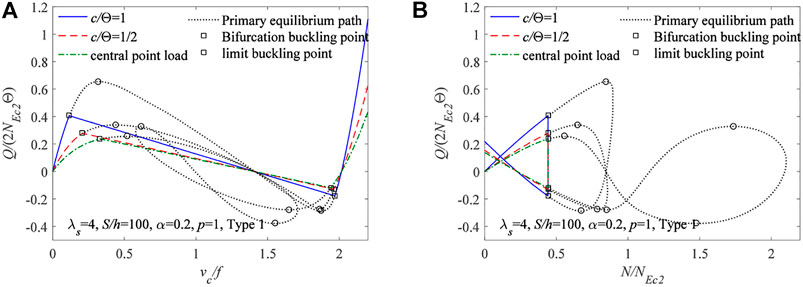
FIGURE 9. Equilibrium paths of limit point instability for pin-ended FGM arches using different localized parameters: (A) v/f − Q/(2NEc2Θ) curves. (B) N/NEc2 − Q/(2NEc2Θ) curves.
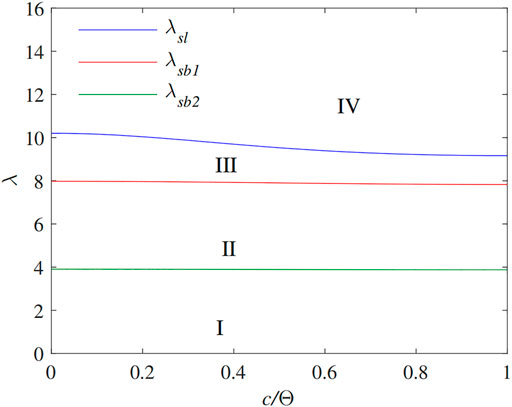
The c/Θ − λ curves of pin-ended FGM arches are shown in Figure 10. The instability pattern of the pin-ended FGM arches is obviously influenced by the equivalent slenderness λ and localized parameter c/Θ. In Figure 10, the instability pattern of the pin-ended FGM arches can be divided into four areas: Area I is the case of no instability, Area II is the case of limit point instability, Area III is the case of the lowest bifurcation instability, and Area IV is the case of dominant bifurcation instability. In addition, Figure 10 shows that the equivalent slenderness (i.e., λsl, λsb1, λsb2) increases with the decrease of the localized parameter c/Θ.
Also researched was the influence of the localized parameter c/Θ and the equivalent slenderness λ for the instability load of the pin-ended FGM arches. The λ − Q/(2NEc2Θ) curves are shown in Figure 11 for pin-ended FGM arches using the different localized parameters c/Θ (i.e., c/Θ = 1/4, c/Θ = 1/2, c/Θ = 3/4). The localized parameter c/Θ and the equivalent slenderness λ also have an important effect on the limit instability load and the bifurcation instability load of the pin-ended FGM arches. The instability load increases with an increase in equivalent slenderness λ and the localized parameter c/Θ.
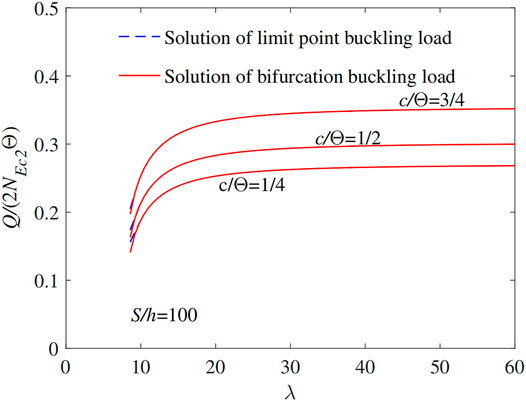
FIGURE 11. The limit point instability and bifurcation for pin-ended FGM arches having different localized parameters.
5 Comparisons of ANSYS Results
Adopting Donnell’s shallow shell theory, the Young’s modulus of metal (Al) and ceramic (Al2O3) are 70 and 380 GPa in the model of ANSYS, respectively. FGM arches’ geometrical parameters are shown in Figure 2A and the rectangular section is shown in Figure 2B, where geometric slenderness S/h = 100, total thickness h = 0.07 m, width b = 0.14 m, the proportional coefficient of homogeneous ceramic (Al2O3) layer α = 0.2, and the power-law index p = 1.
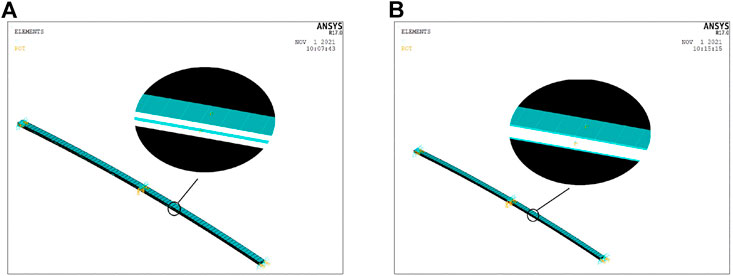
Multilayer ceramic (Al2O3) was used to simulate the properties of continuous gradient material. When the number of ceramic (Al2O3) layers is large enough, the results of simulating the properties of continuous gradient material are accurate. This section investigates the nonlinear instability of pin-ended FGM arches under locally distributed radial loads, with two section types (Type 1 and Type 2) as shown in Figure 1. In the ANSYS model, material distributions of Type 1 have 201 layers: Layers 1 to 100 are a gradient from metal (Al) to ceramic (Al2O3), Layer 101 is a pure ceramic (Al2O3) layer, and Layers 102 to 200 are a gradient from ceramic (Al2O3) to metal (Al). The boundary of FGM arches adopts the pin-ended pattern, as shown in Figure 12A. Analogously, material distributions of Type 2 have 202 layers: Layer 1 is pure ceramic (Al2O3), Layers 2 to 101 are a gradient from ceramic (Al2O3) to metal (Al), Layers 102 to 201 are a gradient from metal (Al) to ceramic (Al2O3), Layer 202 is pure ceramic (Al2O3), and the boundary of the FGM arches adopts a pin-ended pattern, as shown in Figure 12B.
ANSYS finite element analysis results verify that the theoretical solution of the bifurcation instability load, the limit instability point, and the instability equilibrium path for pin-ended FGM arches under locally distributed radial loads is correct. SHELL181 of ANSYS is used to research the convergence; the results show that all 80 elements can produce convergence results. Hence, it is reasonable to use 80 SHELL181 units to simulate pin-ended FGM arches.
The comparison of the theoretical solution of Eqs 33, 53 of the bifurcated instability equilibrium path and bifurcated instability load and corresponding ANSYS results are shown in Figure 13, where λs = 4, S/h = 100, η = 1/2, α = 0.2, and p = 1. The v/f − Q/(2NEc2Θ) curves are shown in Figure 13A with the FGM arches using Type 1 of the material section. The v/f − Q/(2NEc2Θ) curves are shown in Figure 13B with the FGM arches using Type 2 of the material section. In Figures 13A,B, the theoretical solution to the limit instability point load of the FGM arches and corresponding ANSYS results are highly consistent.
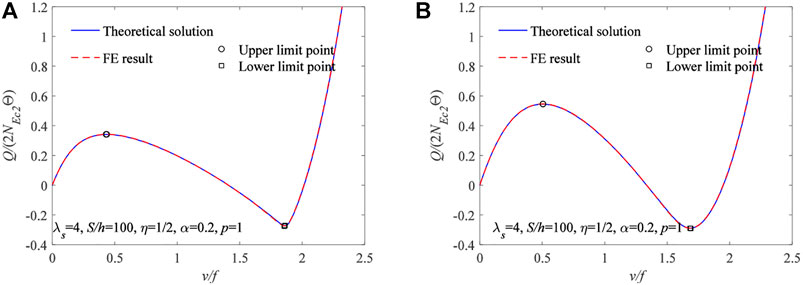
FIGURE 13. ANSYS result and theoretical result of limit point instability for pin-ended FGM arches having different types of cross-section: (A) Type 1. (B) Type 2.
Comparison of the theoretical solution of Eqs 33, 53 of the bifurcated instability equilibrium path and bifurcated instability load with the corresponding ANSYS results are shown in Figure 14, where λs = 4, S/h = 100, η = 1/3, α = 0.2, and p = 1. The v/f − Q/(2NEc2Θ) curves are shown in Figure 14A with the FGM arches using Type 1 of the material section. The v/f − Q/(2NEc2Θ) curves are shown in Figure 14B with the FGM arches using Type 2 of the material section. In Figures 14A,B, the theoretical solution of the limit instability point load of the FGM arches and corresponding ANSYS results are highly consistent.
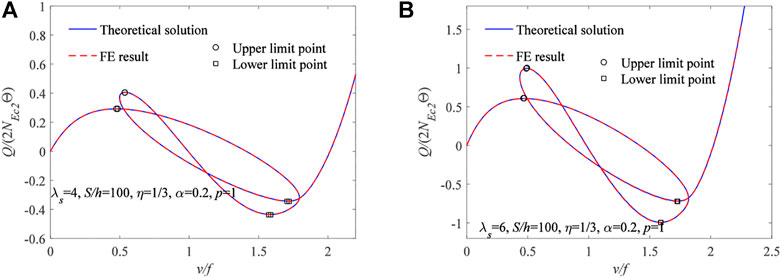
FIGURE 14. ANSYS result and theoretical result of multiple limit point instability for pin-ended FGM arches having different types of cross-section: (A) Type 1. (B) Type 2.
Comparison of the theoretical solution of Eqs 33, 53 of the bifurcated instability equilibrium path and bifurcated instability load and the corresponding ANSYS results are shown in Figure 15, where λs = 4, S/h = 100, η = 1/3, α = 0.2, and p = 1. The v/f − Q/(2NEc2Θ) curves are shown in Figure 15A with the FGM arches using Type 1 of the material section. The v/f − Q/(2NEc2Θ) curves are shown in Figure 15B with the FGM arches using Type 2 of the material section. In Figures 15A,B, the theoretical solution of the bifurcation instability load, primary equilibrium path, bifurcation instability equilibrium path of the FGM arches, and corresponding ANSYS results are highly consistent.
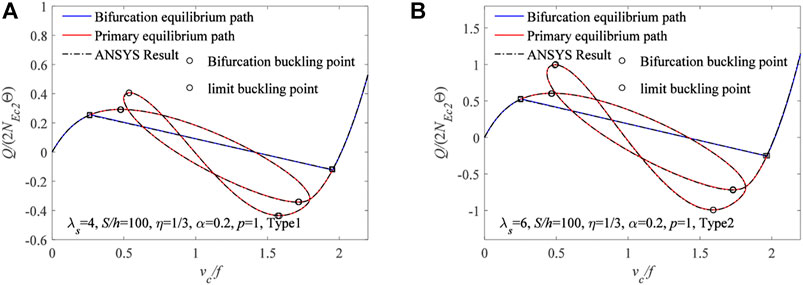
FIGURE 15. ANSYS result and theoretical result of bifurcated instability load for pin-ended FGM arches having different types of cross-section: (A) Type 1. (B) Type 2.
6 Conclusion
This paper discussed the nonlinear instability analysis of pin-ended FGM arches with locally distributed radial loads. It was assumed that the two cross-section components of the arch are graded according to a power law function along the thickness direction. New analytical solutions of limit point instability for pin-ended boundary conditions, lowest limit point instability, multiple limit point instability, and bifurcation instability were discussed. In conclusion, it was found that:
(1) FGM arches material distribution results in property changes. For arches of cross-section Types 1 and 2, the material with high stiffness distributed on the cross-sectional surface can effectively improve the in-plane stability of the pin-ended FGM arch.
(2) Analysis of the parameters of material type, modified geometric slenderness, power-law index, and the proportional coefficient of the homogeneous layer of the pin-ended FGM arch shows that the load point monotonically varies with these parameters.
(3) In a loading process, the number of multiple limit points augment an increase of the equivalent slenderness and a decrease of the localized parameter.
(4) The instability pattern of division under conditions of equivalent slenderness and the localized parameter found that the case of the dominant bifurcation instability is the largest part of the four areas.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding authors.
Author Contributions
JZ: formal analysis, validation, and writing—review and editing. GL: formal analysis, investigation, methodology, and writing—original draft. HL: data curation, formal analysis, investigation, methodology, software, visualization, and writing—review and editing. ZC: methodology, software, visualization, and writing—review and editing. ZP: data curation, formal analysis, and investigation. JZ: project administration.
Funding
This research was funded by the National Natural Science Foundation of China (Grant no. 51908146) and the graduate student Free Exploration Foundation project of Foshan University (Grant no. 2021ZYTS02).
Conflict of Interest
GL was employed by China Construction Fourth Engineering Division Corp. Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Asgari, H., Bateni, M., Kiani, Y., and Eslami, M. R. (2014). Non-linear Thermo-Elastic and Buckling Analysis of FGM Shallow Arches. Compos. Struct. 109, 75. doi:10.1016/j.compstruct.2013.10.045
Bateni, M., and Eslami, M. R. (2016). Non-linear In-Plane Stability Analysis of FG Circular Shallow Arches under Uniform Radial Pressure. Thin-Walled Struct. 94, 302. doi:10.1016/j.tws.2015.04.019
Bateni, M., and Eslami, M. R. (2014). Non-linear In-Plane Stability Analysis of FGM Circular Shallow Arches under Central Concentrated Force. Int. J. Non-Linear Mech. 60, 58. doi:10.1016/j.ijnonlinmec.2014.01.001
Bradford, M. A., Uy, B., and Pi, Y.-L. (2002). In-Plane Elastic Stability of Arches under a Central Concentrated Load. J. Eng. Mech. 128 (7). doi:10.1061/(asce)0733-9399(2002)128:7(710)
Cai, J. G., and Feng, J. (2010). Buckling of Parabolic Shallow Arches when Support Stiffens under Compression. Mech. Res. Commun. 37 (5), 467. doi:10.1016/j.mechrescom.2010.05.004
Cai, J. G., Xu, Y. X., Feng, J., and Zhang, J. (2012). In-Plane Elastic Buckling of Shallow Parabolic Arches under an External Load and Temperature Changes. J. Struct. Eng. 138 (11). doi:10.1061/(asce)st.1943-541x.0000570
Cai, J. G., Zhou, Y., and Feng, J. (2013). Post-buckling Behavior of a Fixed Arch for Variable Geometry Structures. Mech. Res. Commun. 52, 74. doi:10.1016/j.mechrescom.2013.07.002
Han, Q. H., Cheng, Y. H., Lu, Y., Li, T., and Lu, P. (2016). Nonlinear Buckling Analysis of Shallow Arches with Elastic Horizontal Supports. Thin-Walled Struct. 109, 88. doi:10.1016/j.tws.2016.09.016
Lanc, D., Turkalj, G., Vo, T. P., and Brnic, J. (2016). Nonlinear Buckling Behaviours of Thin-Walled Functionally Graded Open Section Beams. Compos. Struct. 152, 829. doi:10.1016/j.compstruct.2016.06.023
Li, Z. C., Zheng, J. X., Zhang, Z., and He, H. T. (2019). Nonlinear Stability and Buckling Analysis of Composite Functionally Graded Arches Subjected to External Pressure and Temperature Loading. Eng. Struct. 199, 109606. doi:10.1016/j.engstruct.2019.109606
Liu, A. R., Bradford, M. A., and Pi, Y.-L. (2017). In-plane Nonlinear Multiple Equilibria and Switches of Equilibria of Pinned–Fixed Arches under an Arbitrary Radial Concentrated Load. Archive Appl. Mech. 87 (11), 1909. doi:10.1007/s00419-017-1300-7
Lu, H. W., Liu, A. R., Pi, Y.-L., and Bradford, M. A. (2019a). Experimental Investigation of Out-Of-Plane Buckling of Circular Arches under a Central Radial Point Load. Thin-Walled Struct. 148, 106198. doi:10.1016/j.tws.2019.106198
Lu, H. W., Liu, A. R., Pi, Y.-L., Bradford, M. A., Fu, J. Y., and Huang, Y. H. (2018). Localized Loading and Nonlinear Instability and Post-instability of Fixed Arches. Thin-Walled Struct. 131, 165. doi:10.1016/j.tws.2018.06.019
Lu, H. W., Liu, A. R., Pi, Y.-L., Huang, Y. H., and Mark, A. (2019b). Flexural-Torsional Buckling of Steel Arches under a Localized Uniform Radial-Load Incorporating Shear Deformations. J. Struct. Eng. 145 (10). doi:10.1061/(asce)st.1943-541x.0002407
Lu, H., Zhou, J., Sahmani, S., and Safaei, B. (2021a). Nonlinear Stability of Axially Compressed Couple Stress-Based Composite Micropanels Reinforced with Random Checkerboard Nanofillers. Phys. Screen. 96 (12), 125703. doi:10.1088/1402-4896/ac1d7f
Lu, H., Zhou, J., Yang, Z., Liu, A., and Zhu, J. (2021b). Nonlinear Buckling of Fixed Functionally Graded Material Arches under a Locally Uniformly Distributed Radial Load. Front. Mat. 8, 731627. doi:10.3389/fmats.2021.731627
Moita, J. S., Araújo, A. L., Correia, V. F., Soares, C. M. M., and Herskovits, J. (2018). Material Distribution and Sizing Optimization of Functionally Graded Plate-Shell Structures. Compos. Part B 142, 263. doi:10.1016/j.compositesb.2018.01.023
Nguyen, T. T., Thang, P. T., and Lee, J. (2017). Lateral Buckling Analysis of Thin-Walled Functionally Graded Open-Section Beams. Compos. Struct. 160, 952–963. doi:10.1016/j.compstruct.2016.10.017
Pi, Y.-L., Bradford, M. A., and Liu, A. R. (2017). Nonlinear Equilibrium and Buckling of Fixed Shallow Arches Subjected to an Arbitrary Radial Concentrated Load. Int. J. Struct. Stab. Dyn. 17 (8). doi:10.1142/s0219455417500821
Pi, Y.-L., and Bradford, M. A. (2009). Non-linear In-Plane Postbuckling of Arches with Rotational End Restraints under Uniform Radial Loading. Int. J. Non-Linear Mech. 44 (9), 975. doi:10.1016/j.ijnonlinmec.2009.07.003
Pi, Y.-L., Bradford, M. A., and Tin-Loi, F. (2007). Non-linear In-Plane Buckling of Rotationally Restrained Shallow Arches under a Central Concentrated Load. Int. J. Non-Linear Mech. 43 (1), 1. doi:10.1016/j.ijnonlinmec.2007.03.013
Pi, Y.-L., Bradford, M. A., and Uy, B. (2002). In-plane Stability of Arches. Int. J. Solids Struct. 39 (1), 710. doi:10.1016/s0020-7683(01)00209-8
Rastgo, A., Shafie, H., and Allahverdizadeh, A. (2016). Instability of Curved Beams Made of Functionally Graded Material under Thermal Loading. Int. J. Mech. Mater. Des. 2 (1-2), 117. doi:10.1007/s10999-005-4446-3
Simitses George, J., and Hutchinson, J. W. (1976). An Introduction to the Elastic Stability of Structures. J. Appl. Mech. 43 (2). doi:10.1115/1.3423874
Şimşek, M. (2016). Buckling of Timoshenko Beams Composed of Two-Dimensional Functionally Graded Material (2D-FGM) Having Different Boundary Conditions. Compos. Struct. 149, 304. doi:10.1016/j.compstruct.2016.04.034
Song, X., and Li, S. R. (2008). Nonlinear Stability of Fixed-Fixed FGM Arches Subjected to Mechanical and Thermal Loads. Adv. Mater. Res. 29. doi:10.4028/www.scientific.net/amr.33-37.699
Timoshenk, S. P., Gere, J. M., and Prager, W. (1962). Theory of Elastic Stability, Second Edition. J. Appl. Mech. 29 (1). doi:10.1115/1.3636481
Yan, J. W., Xiong, M., Tong, L. H., Ding, H. B., and Lei, Z. (2022b). Spontaneous Arched Graphene under Uniaxial Compression and Bistable Interswitch Behaviors of Single-Layer Graphene. J. Vib. Eng. Technol. 10, 445. doi:10.1007/s42417-021-00360-4
Yan, J. W., Zhu, J. H., Li, C., Zhao, X. S., and Lim, C. W. (2022a). Decoupling the Effects of Material Thickness and Size Scale on the Transverse Free Vibration of BNNTs Based on Beam Models. Mech. Syst. Signal Process. 166, 108440. doi:10.1016/j.ymssp.2021.108440
Yan, S.-T., Shen, X., Chen, Z., and Jin, Z. (2017). On Buckling of Non-uniform Shallow Arch under a Central Concentrated Load. Int. J. Mech. Sci. 133, 330–343. doi:10.1016/j.ijmecsci.2017.08.046
Yang, Z. C., Liu, A. R., Lai, S. K., Safaei, B., Lv, J. G., Huang, Y. H., et al. (2022). Thermally Induced Instability on Asymmetric Buckling Analysis of Pinned-Fixed FG-GPLRC Arches. Eng. Struct. 250, 113243.
Yang, Z. C., Xu, J. M., Lu, H. W., Lv, J. G., Liu, A. R., and Fu, J. Y. (2020). Multiple Equilibria and Buckling of Functionally Graded Graphene Nanoplatelet-Reinforced Composite Arches with Pinned-Fixed End. Crystals 10, 1003. doi:10.3390/cryst10111003
Keywords: pin-ended arches, functionally graded materials, non-linear instability, limit point instability, locally distributed radial loads
Citation: Zhou J, Li G, Lu H, Chen Z, Pan Z and Zhu J (2022) Non-Linear Instability of Pin-Ended Functionally Graded Material Arches Under Locally Distributed Radial Loads. Front. Mater. 9:900437. doi: 10.3389/fmats.2022.900437
Received: 20 March 2022; Accepted: 17 May 2022;
Published: 06 September 2022.
Edited by:
S. K. Lai, Hong Kong Polytechnic University, Hong Kong SAR, ChinaReviewed by:
C. W. Lim, City University of Hong Kong, Hong Kong SAR, ChinaLihong Tong, East China Jiaotong University, China
Copyright © 2022 Zhou, Li, Lu, Chen, Pan and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hanwen Lu, bHVoYW53ZW5AZm9zdS5lZHUuY24=; Jian Zhu, emh1amlhbkBmb3N1LmVkdS5jbg==
 Jinman Zhou
Jinman Zhou Guangjun Li
Guangjun Li Hanwen Lu
Hanwen Lu Zhou Chen
Zhou Chen Zhenyu Pan
Zhenyu Pan Jian Zhu
Jian Zhu