Broadband Polarization Manipulation Based on W-Shaped Metasurface

Xu, Guangyuan; Gao, Lei; Chen, Yongqiang; Ding, Yaqiong; Wang, Jun; Fang, Yu; Wu, Xingzhi; Sun, Yong

doi:10.3389/fmats.2022.850020

ORIGINAL RESEARCH article

Front. Mater., 15 March 2022

Sec. Metamaterials

Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.850020

This article is part of the Research Topic Optical Hyperbolic Metamaterials View all 6 articles

Broadband Polarization Manipulation Based on W-Shaped Metasurface

Guangyuan Xu¹

Lei Gao¹

Yongqiang Chen¹*

Yaqiong Ding²

Jun Wang¹

Yu Fang¹

Xingzhi Wu¹

Yong Sun³*

¹Key Laboratory of Micro and Nano Heat Fluid Flow Technology and Energy Application, School of Physical Science and Technology, Suzhou University of Science and Technology, Suzhou, China
²College of Science, University of Shanghai for Science and Technology, Shanghai, China
³Key Laboratory of Advanced Micro-structure Materials, Ministry of Education, School of Physics Science and Engineering, Tongji University, Shanghai, China

We present a metasurface consisting of W-shaped resonators to realize broadband reflective linear and circular polarization conversions. We find that the cross polarization conversion ratio for normal incidence is over 0.95 from 9.2 to 18.7 GHz, covering 68.1% of the central frequency. We also show that, the conversion performance is almost insensitive to the angle of incident waves. Furthermore, by simply adjusting the geometrical parameters of the W-shaped metasurface, the broadband circular polarization conversion is also achieved. We emphasize that the bandwidth of axis ratio less than 3.0 dB covers from 10.1 to 17.7 GHz, equivalent to 54.7% relative bandwidth. Due to these broadband and high-efficiency polarization conversion features, our proposal may have a wide application prospect.

Introduction

Polarization is an important property of electromagnetic (EM) waves. The manipulate of polarization state of EM waves is critical in practical applications, such as quarter and half-wave plates, anomalous reflection, holograms, and so on (Yu et al., 2011; Larouche et al., 2012; Yu et al., 2012; Pfeiffer and Grbic, 2013; Xu et al., 2013; He et al., 2014; Jiang et al., 2014). Conventional polarization conversion devices can be achieved by using optical gratings and dichroic crystals (Chen et al., 2003; Masson and Gallot, 2006). However, long propagation distance, huge device size and limited bandwidth may impede the application and the integration of polarization conversion devices. Especially, in the microwave band, where the corresponding wavelength is large. Therefore, in order to effectively control the polarization state, it is necessary to introduce functional EM materials that can provide abundant means of EM waves regulation and make devices miniaturized.

Metamaterials are artificial subwavelength materials with unique properties not attainable in nature. In the past decades, metamaterials have been a hotspot research owing to their great power of tailoring the phase and wavefront of the propagating EM waves. Several exotic physical phenomena and fascinating functional applications are negative refraction, perfect imaging, EM cloaking, and so on (Pendry, 2000; Shelby et al., 2001; Smith et al., 2004; Fang et al., 2005; Schurig et al., 2006; Liu et al., 2007; Shalaev, 2007; Valentine et al., 2008; Ye et al., 2021; Guo et al., 2021). Recently, researchers also demonstrate that the function of bulky metamaterials can even be realized by their quasi-two-dimensional version of metasurfaces. Metasurfaces open up a new way for designing thinner, lighter, and wider polarization converters than that of the conventional technologies. Some high-efficiency linear to linear and linear to circular polarization converters have been demonstrated in microwave, terahertz, and optical frequency bands (Zhou et al., 2003; Fedotov et al., 2006; Feng et al., 2013; Cheng et al., 2014; Li et al., 2014; Zheng et al., 2014; Shi et al., 2014; Guo et al., 2015; Li et al., 2015; Yin et al., 2015; Han et al., 2016; Zhang L. et al., 2016; Zhang Z. et al., 2016; Zhao and Cheng, 2016; Zhao and Cheng, 2017; Zhang et al., 2017; Li et al., 2019; Liu et al., 2019). But so far, realizing bandwidth expansion, efficiency improvement, angle insensitivity, and functionality extension simultaneously within a simple design is still insufficient.

In this paper, a metasurface based on metal-dielectric-metal configuration is proposed to realize broadband reflective linear and circular polarization conversions. The top layer is sub-wavelength W-shaped metallic strips and a continuous metal film is attached to the bottom of the substrate. In one unit, two W-shaped strips is placed asymmetric along x-axis and y-axis. The x polarized incident wave is chosen for analysis and discussion. The results show that the cross polarization conversion ratio (PCR) for normal incidence is over 0.95 from 9.2 to 18.7 GHz, covering 68.1% of the central frequency. Importantly, the conversion performance is almost insensitive to the angle of incident waves. Further studies indicate that, by simply adjusting the geometrical parameters of the W-shaped metasurface, the broadband circular polarization conversion is also achieved. The results reveal that the axis ratio (AR) is less than 3.0 dB in the range of 10.1–17.7 GHz, equivalent to 54.7% relative bandwidth. Owing to these broadband and high-efficiency features, our proposal may facilitate further researches on matematerials-enabled polarization manipulation.

Model Design

The proposed reflective metasurface with a unit cell is shown in Figure 1. A two W-shaped metallic strips is mounted upon a 2.6-mm-thickness FR-4 substrate. A copper layer is attached to the bottom of the substrate, which ensures that most of the incident waves are reflected. The dielectric constant and loss tangent of the FR-4 substrate are 4.2 and 0.015, respectively. The two W-shaped copper strips is placed symmetrically along u-axis, and the distance between them is d = 3.6 mm. The linewidth of the copper strips are w = 0.5 mm. The lengths of the copper strips are a₁ = a₂ = a₃ = a₄ = 1.9 mm. The periods in both x and y directions are p = 9 mm. The combination of two W-shaped metallic strips can excite multiple resonances, which are essential to broadband property and high efficiency. The structure is asymmetric along x-axis and y-axis, and hence we choose the x polarized incident wave for analysis and discussion. By controlling the amplitude and phase of the two orthogonal components of the reflected wave, the broadband polarization manipulation can be realized. We take the CST Microwave Studio for all numerical simulations.

FIGURE 1

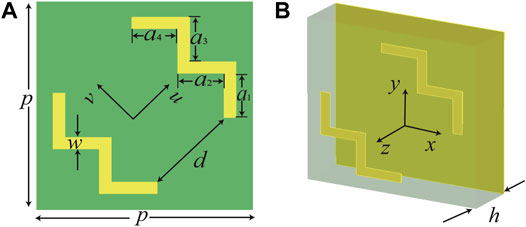
FIGURE 1. Schematic configuration of the designed reflective metasurface with a unit cell from (A) front and (B) perspective views.

Results and Discussion

Firstly, the simulated reflectivity, reflection phase and PCR of the reflective W-shaped metasurface are provided in Figure 2. Figure 2A shows the reflectivity when the x-polarized EM wave is incident along the negative direction of the z-axis. The results depict that |R_yx|² is greater than 0.8 but |R_xx|² is less than 0.1 over a broadband frequency range from 9.2 to 18.7 GHz. Here, R_xx = |E_xr/E_xi| is defined as the reflectance of x to x polarization conversion, whereas R_yx = |E_yr/E_xi| is the reflectance of x to y polarization conversion. Thus, the R_xx is called as co-polarization reflectance and the R_yx is termed as cross-polarization reflectance. In the above formulas, E represents the electric field, while subscripts i and r are for the incidence and reflection of EM waves, respectively. Moreover, the absorptivity (A) is less than 0.1 over this frequency range, as the red doted line shown in Figure 2A. Hence, the x-polarized incident EM wave converts to nearly pure y-polarized one. Figure 2B shows the reflection phase of R_xx and R_yx. Both of them are frequency dependent and the phase difference is equal to about 90⁰ over the above large frequency range, which satisfy the condition of circular polarized wave. However, the reflectivity |R_xx|² is much smaller than |R_yx|², the polarization state of the reflected wave is indeed completely linearly polarized. Furthermore, the PCR is also calculated and presented in Figure 2C. Here, PCR is defined as $R_{y x}^{2} / (R_{y x}^{2} + R_{x x}^{2})$ . At three resonant frequencies 10.0, 13.8 and 17.4 GHz, the PCR is up to 100%. From 9.2 to 18.7 GHz, the PCR is always higher than that of 0.95, confirming that a high-efficiency broadband cross-polarization conversion is successfully achieved. For comparison, the PCR of a sample with only one W-shaped metallic strip within a unit is also given as blue dashed line in Figure 2C. Obviously, the two W-shaped model provides more power in extending the bandwidth of polarization conversion ratio. Furthermore, the conversion performance for different angles of incident EM waves are illustrated in Figure 2D. It can be seen that, the increase in incident angles has not led to a considerable decrease of bandwidth and a drastic reduction of conversion efficiency. Such insensitivity to the incident angle is highly desired in practical applications but difficult to achieve in reality.

FIGURE 2

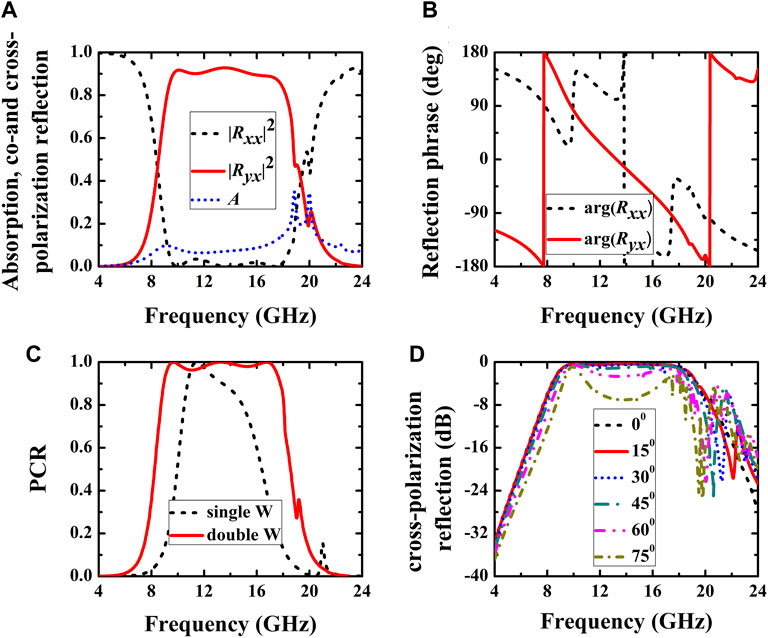
FIGURE 2. Simulated results of the reflective metasurface. (A) co-polarization reflection|R_xx|², cross-polarization reflection |R_yx|² and absorption A. (B) Reflection phase. (C) PCR. (D) The conversion performance with respect to the incident angle.

To dig deeper into the physical mechanism of broadband cross-polarization transformation, the reflection phases of the proposed metasurface for u and v polarized incident EM waves are investigated and given in Figure 3. It is apparent that the reflection phase difference between u and v polarized incident waves is equal to approximately 180⁰ over a wide frequency range from 8.7 to 18.1 GHz. That is to say, when x or y polarized EM waves are normal incident, the amplitudes of the reflected orthogonal (u and v) components are the same but the phase difference equals 180⁰. Hence, the rotation angle of the reflected linear polarized wave is 90⁰ to the incident linear polarized wave, and the incident EM wave rotates to its cross-polarized one over this frequency band. Besides, we have noticed that the phase differences of the reflected waves are ± 90⁰ at 8.4 and 19.4 GHz, respectively. It means that the metasurface can convert the linear polarized incident EM wave to a circular polarized reflected wave at this two frequencies. However, the narrow-band conversion is quite limited in practical application. Thus, broadband circular polarizer based on the presented structure is also expected.

FIGURE 3

FIGURE 3. The reflection phase for u and v polarized incident EM waves.

As follows, the magnetic field distributions in the reflective metasurface under x-polarization at three resonant frequencies of 10.0, 13.8 and 17.4 GHz are also calculated and given in Figure 4. For the resonant frequency of 10.0 GHz case in Figure 4A, it is evident that the direction of the induced magnetic field is lower-right. That means the x component of magnetic field H_x is induced. The induced magnetic field H_x can generate an electric field perpendicular to the incident electric field, which leads to a x-to-y polarization conversion. For the two other resonant frequencies of 13.8 and 17.4 GHz case in Figures 4B,C, the similar physical mechanism takes place in the W-shaped resonators. The induced magnetic field H_x plays a vital role in the cross-polarization conversion.

FIGURE 4

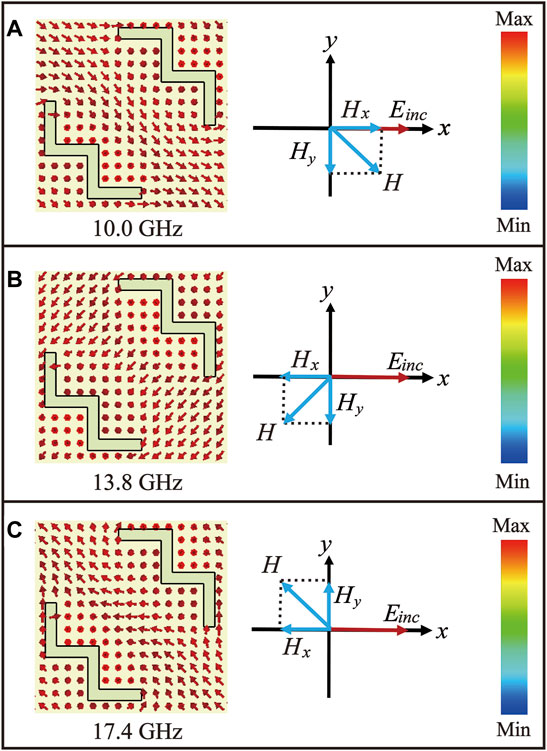
FIGURE 4. The simulated magnetic field distributions under x-polarization at frequencies of (A) 10.0 GHz, (B) 13.8 GHz, (C) 17.4 GHz.

Furthermore, we demonstrate that the broadband circular polarizer can even be realized by simply optimizing the geometrical parameters of the above presented metasurface. Here, we choose a₁ = 2.0 mm, a₂ = 2.5 mm, a₃ = 2.6 mm, and a₄ = 2 mm. The periods in both x and y directions are changed to 10 mm. The dielectric constant and thickness of FR-4 substrate are set to 2.65 and 3.7 mm, respectively. The distance between the two W-shaped metallic strips along u-axis is fixed as 3.6 mm. The width of the copper strips are maintained as 0.5 mm. Under such conditions, the reflectivity and reflection phase of the metasurface are simulated and presented in Figure 5. For x-polarized incident wave propagating along the negative direction of z-axis, the reflectivity of co-polarized and cross-polarized reflected waves are almost the same in the range of 10.1–17.7 GHz, as shown in Figure 5A. Figure 5B describes the reflection phase of R_xx and R_yx, it is clear that the phase difference is equal to 90⁰ over the above frequency range. In addition, the ellipticity and AR are also calculated and depicted in the Figure 5C and Figure 5D, respectively. Here, ellipticity is defined as $χ = 0.5 \arcsin (\frac{2 R \sin (Δ φ)}{1 + R^{2}})$ and $| \frac{1}{\tan χ} |$ is adopted as AR, where $R = \frac{| R_{y x} |}{| R_{x x} |}$ and $Δ φ = \arg (R_{y x}) - \arg (R_{x x})$ . The results reveal that the AR is less than 3.0 dB in the range of 10.1–17.7 GHz, equivalent to 54.7% relative bandwidth. This indicate that the reflected wave is a typical circular polarized wave within the above frequency range. To illustrate the conversion performance, the AR for different angles of incident EM waves are also calculated and given in Figure 5D. It is clearly that, the AR gradually increased from zero but is always smaller than 3.0 dB as the incident angles varied from 0⁰ to 30⁰. Such tolerance can help make a difference to the practical application.

FIGURE 5

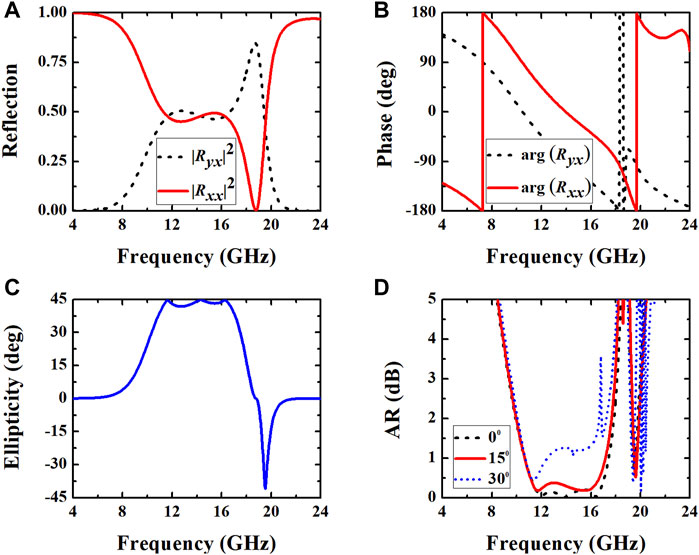
FIGURE 5. Simulated (A) reflectivity, (B) reflection phase, (C) ellipticity, and (D) AR under x-polarized incident EM waves.

In the following, the polarization ellipses at five characteristic frequencies of the broadband circular polarizer are calculated and plotted in Figure 6. The polarization azimuth angle is calculated as $ψ = 0.5 \arctan (\frac{2 R \cos (Δ φ)}{1 - R^{2}})$ . The purpose here is to illustrate the polarization state of reflected wave. For the lower band-edge frequency 10.1 GHz, the ellipticity is 26.4⁰, AR is 3.0 dB, and polarization azimuth angle is 1.3⁰. The determined reflected wave is right-handed elliptical polarized wave and the major axis of ellipse is close to x-axis. For the other two working frequencies 14.3 and 16.3 GHz, polarization azimuth angle are 49.3⁰ and 53.5⁰, the determined reflected wave are also the right-handed circular polarized waves. For the upper band-edge frequency 17.7 GHz, the ellipticity is 26.6⁰, AR is 3.0 dB, and polarization azimuth angle is 87.3⁰. The determined reflected wave is right-handed elliptical polarized wave and now the major axis of ellipse turns to y-axis. Note here that the polarization state of the reflected circular polarized wave depends on the incident wave. If a y-polarized EM wave incident, the polarization state of reflected wave will shift to a left-handed circular polarized wave. From this point of view, the W-shaped metasurface provides a flexible platform for polarization manipulation.

FIGURE 6

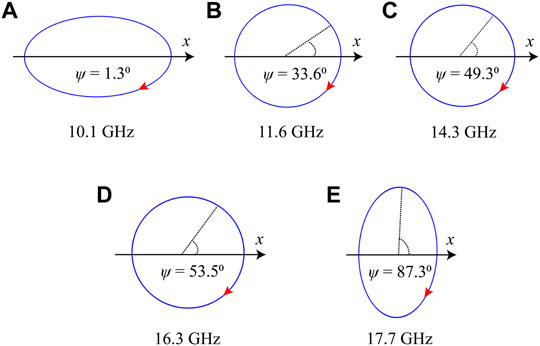
FIGURE 6. The polarization ellipses of the broadband circular polarizer at five characteristic frequencies. (A) 10.1 GHz. (B) 11.6 GHz. (C) 14.3 GHz. (D) 16.3 GHz. (E) 17.73 GHz.

Conclusion

In conclusion, we have numerically demonstrated the broadband reflective linear and circular polarization conversions in a simple W-shaped metasurface. For cross polarization conversion, the PCR for normal incidence is over 0.95 from 9.2 to 18.7 GHz, covering 68.1% of the central frequency. The conversion performance is almost insensitive to the angle of incident waves. The magnetic field distributions of working frequencies confirm that the induced magnetic field paralleled to incident electric field is crucial to a cross polarization conversion. For circular polarization conversion, the AR is less than 3.0 dB in the range of 10.1–17.7 GHz, equivalent to 54.7% relative bandwidth. The polarization ellipses of band-edge and operating frequencies show the changing process of polarization state. The above broadband and high-efficiency characteristics of our design will be conducive to the development of metamaterials-enabled communication devices.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

GX and LG conceived the research. YC and YS supervised the project. GX performed the theoretical calculation and analysis. YD, JW, YF, and XW contributed to perform the analysis with constructive discussions. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grants Nos 91850206, 51607119, and 11974261), the Natural Science Research of the Jiangsu Higher Education Institutions of China (Grant No. 18KJA470004), and the Postgraduate Research and Practice Innovation Program of Jiangsu Province (Grant No. KYCX21_3011).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, C.-Y., Tsai, T.-R., Pan, C.-L., and Pan, R.-P. (2003). Room Temperature Terahertz Phase Shifter Based on Magnetically Controlled Birefringence in Liquid Crystals. Appl. Phys. Lett. 83 (22), 4497–4499. doi:10.1063/1.1631064