Investigations on Strong-Tuned Magnetocaloric Effect in La0.5Ca0.1Ag0.4MnO3

The magnetocaloric effect (MCE) of La_0.5Ca_0.1Ag_0.4MnO₃ (LCAMO) is simulated using a phenomenological model (PM). The LCAMO MCE parameters are calculated as the results of simulations for magnetization vs. temperature at different values of external magnetic field (H_ext). The temperature range of MCE in LCAMO grew as the variation in H_ext increased, eventually covering the room temperature at high H_ext values. The MCE of LCAMO is tunable with the variation of H_ext, proving that LCAMO is practically more helpful as a magnetocaloric (MC) material for the development of magnetic refrigerators in an extensive temperature range, including room temperature and lower and higher ones. The MCE parameters of LCAMO are practically greater than those of some MC samples in earlier works.

Introduction

The need to solve the problem of emission of hazard gases, which come out of conventional vapor refrigerators, results in increased interest in functioning magnetic refrigerator (MR), the idea of which depends on functioning magnetocaloric effect (MCE) (Dhahri et al., 2014; El-Sayed and Hamad, 2019a; El-Sayed and Hamad, 2019b; Ahmed et al., 2021a, Ahmed et al., 2021b; Hamad et al., 2021; Jebari et al., 2021), because the MR provides high efficiency for cooling without any negative impact on the environment and has low energy consumption, availability of mechanical stability, and fewer noise events during cooling operation (Dhahri et al., 2015; Hamad, 2015a; ErchidiElyacoubi et al., 2018a, ErchidiElyacoubi et al., 2018b; Hamad et al., 2020; Sharma et al., 2020; Belhamra et al., 2021). MCE is described as a change in magnetic entropy (∆S_M) with a variation in the external magnetic field (H_ext) exerted on the material, causing a change in temperature (Masrour et al., 2016; ErchidiElyacoubi et al., 2018c; Kadim et al., 2020, Kadim et al., 2021a, Kadim et al., 2021b). Numerous research over decades have studied various magnetic materials to discover their suitability as magnetocaloric (MC) materials suitable for the MR industry (Hamad, 2015b; Masrour et al., 2017; Jebari et al., 2021; Labidi et al., 2021). It is preferable to use MC materials that have a magnetic transition type of the second degree with a suitable Curie temperature (${\theta }_C$) as appropriate for use in a wide temperature range, including room temperature (Choura-Maatar et al., 2020; Henchiri et al., 2020; Laajimi et al., 2020). The current efforts are directed towards the use of manganite as an effective substance in MRs due to its great chemical stability during frequent use, lack of eddy current, ease of preparation, high electrical resistance, and the possibility of improving their properties through doping and changing the oxygen content (Alzahrani et al., 2020; Choura-Maatar et al., 2020; Henchiri et al., 2020; Laajimi et al., 2020). Felhi et al. prepared La_0.5Ca_0.1Ag_0.4MnO₃ (LCAMO) via the ceramic method and reported an increase in H_ext and an increase in broad ferromagnetic (FM) phase transition of LCAMO covering room temperature under high H_ext (Jeddi et al., 2020). These results motivate us to investigate the MCE of LCAMO, expecting that the MCE of LCAMO covers a large range of temperatures, especially cryogenic temperature and room temperature. Furthermore, it is believed that LCAMO, as a manganite, has low material processing costs, high chemical stability, and high resistivity, which are advantageous for reducing the overall eddy current heating. In this research, the MCE of LCAMO is studied using a phenomenological model (PM) to simulate the isofield magnetization vs. temperature curves, concluding with simulated ∆S_M, heat capacity change ($\Delta C_{P,H}$), and relative cooling power (RCP).

Theoretical Considerations

According to PM, as described in Hamad (2012, 2015c, 2015d), the magnetization (M) vs. temperature is simulated by:

$M\left(T\right)=\left(\frac{M_i-M_f}{2}\right)\left[\tanh \left(\alpha \left({\theta }_C-T\right)\right)\right]+\beta \left(T-{\theta }_C\right)+\left(\frac{M_i+M_f}{2}\right)(1)$

where $M_i$ and $M_f$ are values of magnetization at the onset and finalization of the FM paramagnetic transition as pointed out in Figure 1, respectively.

$\alpha =\frac{2\left(\beta -\gamma \right)}{M_i-M_f}(2)$

where $\gamma ={\left(\frac{dM}{dT}\right)}_{T={\theta }_C}$.

$\beta ={\left(\frac{dM}{dT}\right)}_{average}\text{ for FM phase}(3)$

FIGURE 1

FIGURE 1. Isofield magnetization vs. temperature.

The numerical evaluation of ∆S_M of LCAMO under H_ext variation (ΔH) can be derived from Maxwell’s relation and derived from Eq. 1 as follows:

$\Delta S_M={\displaystyle \underset{0}{\overset{H_{\max }}{\int }}{\left(\frac{\partial M}{\partial T}\right)}_{H}dH=\left(-\left(\beta -\gamma \right){\text{ sech}}^2\left(\alpha \left({\theta }_C-T\right)\right)+\beta \right)\Delta H}.(4)$

From Eq. 4, we can easily calculate ΔS_M(T) by determining the M_i, M_f, θ_c, β, and γ from isofield M(T) curves. Moreover, a maximum value of ∆S_M($\Delta S_{Max}$), where $T={\theta }_C$, can be assessed according to the following equation:

$\Delta S_{Max}=\gamma \Delta H(5)$

The full-width at half-maximum ($\delta {\text{T}}_{\text{FWHM}}$) of LCAMO can be given as follows:

$\delta {\text{T}}_{\text{FWHM}}=\frac{2}{\alpha }{\text{cosh}}^{-1}\left(\left|\sqrt{\frac{2\alpha (M_i-M_f)}{\alpha (M_i-M_f)+2\beta }}\right|\right)(6)$

A magnetic cooling efficiency of LCAMO is expected by considering the magnitude of $\left|\Delta S_{Max}\left(T,H_{\max }\right)\right|$ and $\delta {\text{T}}_{\text{FWHM}}$ (Hamad, 2012). RCP is calculated as follows:

$\text{RCP}=\delta {\text{T}}_{\text{FWHM}}\times \left|\Delta S_{Max}\left(T,H_{\max }\right)\right|(7)$

The $\Delta C_{P,H}$ of LCAMO can be given as follows (Hamad, 2012):

$\mathrm{\Delta }{C}_{P,H}=-\mathrm{\Delta }H{\alpha }^{2}T\left(M_i-M_f\right)\tanh \left(\alpha \left({\theta }_c-T\right)\right){\text{sech}}^2\left(\alpha \left({\theta }_c-T\right)\right)\text{.}(8)$

Results and Discussion

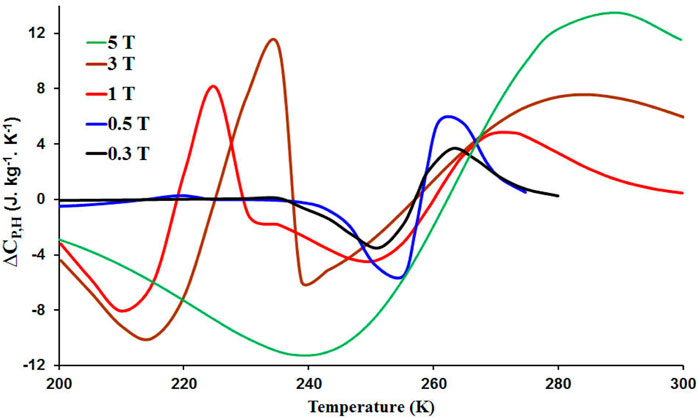
At values of H_ext <5 T, there are two magnetic transitions of LCAMO, as can be observed in Figure 2, at two different temperatufvariation, which is about 57% of the correspondingres. It is possible that this is due to the presence of a canted FM phase in the FM matrix, which can be attributed to the additional Ag content (Jeddi et al., 2020), thus expecting two peaks in the ΔS_M curves. However, at H_ext = 5 T, it seems like a single magnetic transition of LCAMO, expecting a single peak in the ΔS_M curve. It is possible that this is due to the presence of a strong interatomic double exchange interaction at H_ext = 5 T. To simulate the MCE of LCAMO, the PM parameters (M_i, M_f, ɵ_c, β, and α) of LCAMO for each magnetic transition were determined directly from experimental data (isofield magnetization vs. temperature) as in Jeddi et al. (2020). We can see from Figure 2 that there is a good agreement between the experimental and theoretical results of M(T), confirming the good fit of this model for simulating the MCE of LCAMO. This work demonstrates the good coincidence between the experimental data and the continuous curves given by PM, indicating that this model allows us to predict the MCE for LCAMO under different magnetic fields. The M(T) curves of LCAMO demonstrate the magnetic transition from the FM phase to a paramagnetic one under different magnetic fields. The ${\theta }_C$ increases as H_ext increases due to the increased alignment of the local spins, resulting in an increase in the interatomic double exchange interaction. As shown in Figure 3A, there are two peaks in the ΔS_M(T) curves when H_ext <5 T. However, at H_ext = 5 T, there is a single peak in the ΔS_M curve due to the large interatomic double exchange. ∆S_M reaches a peak of 2.75 J/kg K. Though the maximum ∆S_M is 2.75 J/kg K upon 5T applied field variation, which is about 57% of the corresponding value of the compound that belongs to the same system as La_0.5Ca_0.2Ag_0.3MnO₃ (∆S_Max = 4.8 J/kg K upon 5 T), the value of RCP (273.5 J/kg upon 5 T) is larger, and the ∆S_M distribution of LCAMO is much more broad than that of La_0.5Ca_0.2Ag_0.3MnO₃ (RCP = 168 J/kg $\delta {\text{T}}_{\text{FWHM}}$ = 35 upon 5 T), covering a wider range of temperature (Felhi et al., 2019). Figure 3B shows that ∆S_M(T) was calculated by Maxwell relation from experimental isothermal magnetization as a function of H in Ref. 31, and ∆S_M(T) was calculated by PM, ranging between 240 and 270 K and covering the highest temperature transition. There is a good agreement and approach between the calculated results of both Maxwell relation and PM. Therefore, these results confirm that Eq. 4 still holds at ΔH of 0.5, 1, 3, and 5 T.

FIGURE 2

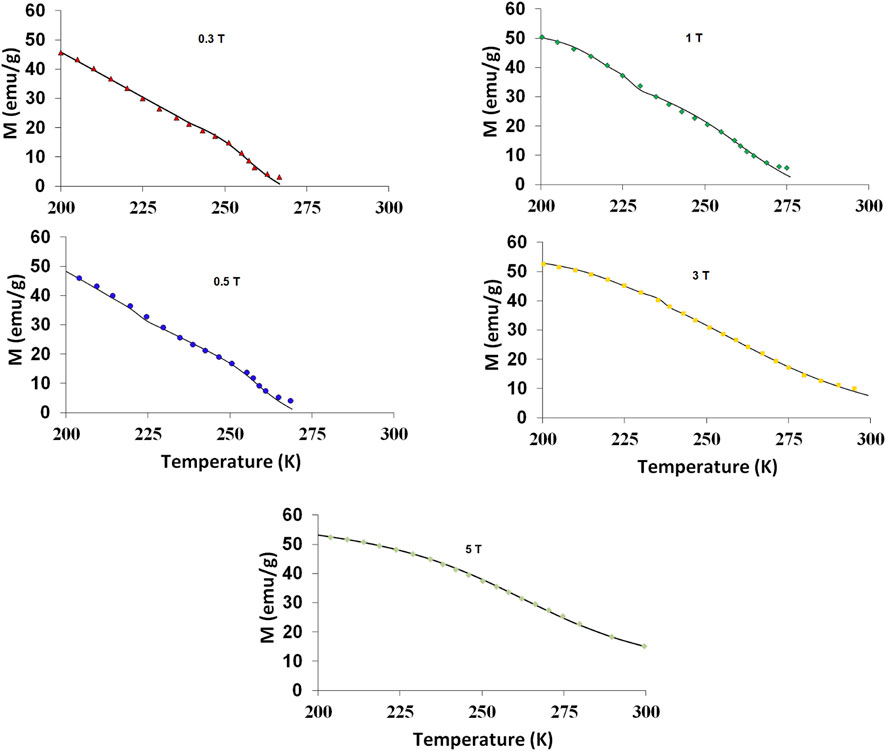
FIGURE 2. Magnetization vs. temperature for La_0.5Ca_0.1Ag_0.4MnO₃. The dashed curves are modeled results, and the symbols represent experimental data from Jeddi et al. (2020).

FIGURE 3

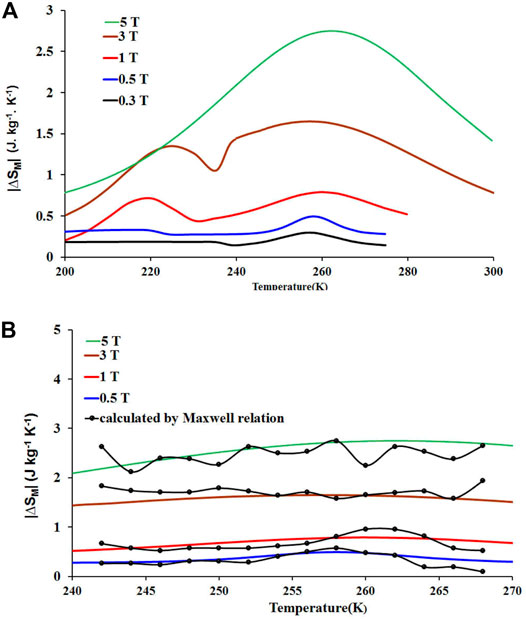
FIGURE 3. (A) ∆S_M and (B) ∆S_M(T) was calculated by Maxwell relation, and ∆S_M(T) was calculated by a phenomenological model.

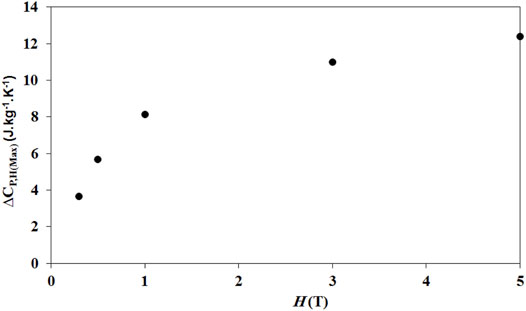
Figure 4 shows that ∆C_P,H(T) has an inverse change from a negative change to a positive one at around ${\theta }_C$ for each magnetic transition, causing a modification in the total specific heat. This oscillating temperature dependence of ∆C_P,H(T) at different temperatures is a reflection of ΔS_M(T) behavior. The behavior of |∆S_M| and ∆C_P,H(T) curves suggests how the range of temperature for functioning LCAMO in the MR can be expanded. It is clear that the |∆S_M| and ∆C_P,H peaks of LCAMO extend over a large temperature range. This temperature range of |∆S_M| and ∆C_P,H expanded with increasing variation in H_ext, i.e., the peaks broaden, covering room temperature upon high values of ∆H. This indicates that larger |∆S_M| and ∆CP, H are expected at higher values of ∆H. Moreover, the variation of H_ext allows the tuning of ${\theta }_C$ of LCAMO. This tunable ${\theta }_C$ makes LCAMO practically more helpful for the development of MRs.

FIGURE 4

FIGURE 4. ∆C_P,H vs. temperature for La_0.5Ca_0.1Ag_0.4MnO₃.

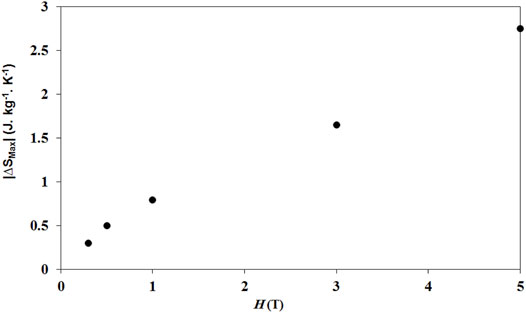
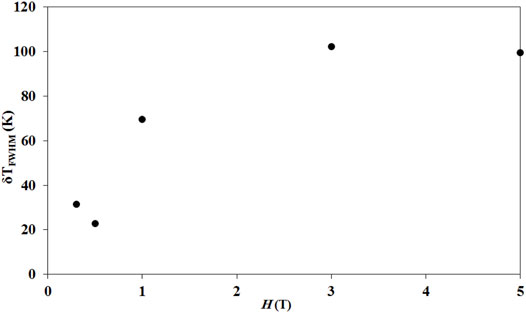
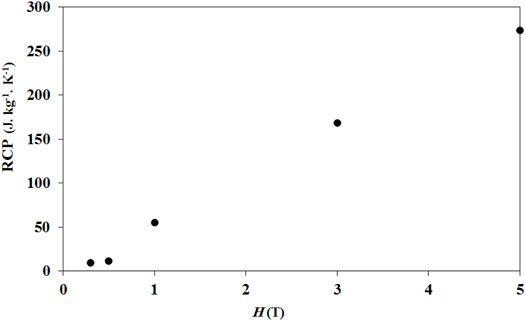
Figures 5–8 show the values of |∆S_Max|, δT_FWHM, RCP, and ∆C_P,H(Max) (maximum value of ∆C_P,H) for LCAMO, respectively. It is clear that |∆S_Max|, RCP, and ∆C_P,H(max) show a general increase with an increase in ∆H due to enhancing the variations of alignment in the local spins with an increase in ∆H, resulting in an increase in MC properties.

FIGURE 5

FIGURE 5. |∆S_Max| vs. ∆H for La_0.5Ca_0.1Ag_0.4MnO₃.

FIGURE 6

FIGURE 6. δT_FWHM vs. ∆H for La_0.5Ca_0.1Ag_0.4MnO₃.

FIGURE 7

FIGURE 7. Relative cooling power vs. ∆H for La_0.5Ca_0.1Ag_0.4MnO₃.

FIGURE 8

FIGURE 8. ∆C_P,H(max) vs. ∆H for La_0.5Ca_0.1Ag_0.4MnO₃.

These large values of |∆S_Max|, δT_FWHM, RCP, and ∆C_P,H(Max) in LCAMO prevailed as well in perovskite manganite due to the strong coupling between spin and lattice (Dhahri et al., 2008). Since lattice change is associated to magnetic transition in the manganite, this caused a further change in the magnetism of manganite (Dhahri et al., 2008). Furthermore, the bond distance of <Mn–O> plus bond angle <Mn–O–Mn> changes to favor the spin ordering with a high value of H_ext, leading to enhanced |∆S_Max|, δT_FWHM, RCP, and ∆C_P,H(Max) in LCAMO (Radaelli et al., 1995; Hamad, 2015b).

Table 1 gives a comparative importance of the MCE parameters of LCAMO with those of various materials in terms of the high values of ΔH in previous works (Álvarez-Alonso et al., 2013; Hamad, 2013; Saadaoui et al., 2013; Ho et al., 2014; Bhumireddi et al., 2015; Boutahar et al., 2015; Jerbi et al., 2015; Gupta and Poddar, 2016; Mansouri et al., 2016; Oubla et al., 2016; Long et al., 2018; Biswal et al., 2019; El Boubekri et al., 2020). The MCE parameters of LCAMO are significantly larger than some MCE parameters of MC samples in the corresponding values of ΔH and the higher ones. From this comparative image, we conclude that LCAMO can function as a favorable MC magnet for the MR.

TABLE 1

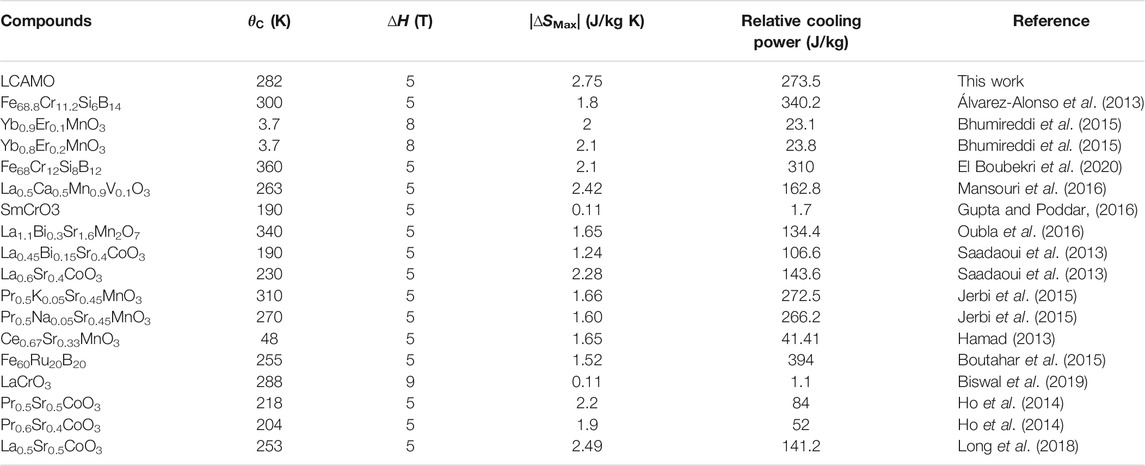
TABLE 1. The comparison of magnetocaloric effect parameters for La_0.5Ca_0.1Ag_0.4MnO₃ (LCAMO) with corresponding ones of various magnetocaloric effect materials in high ∆H.

Conclusion

Based on thermodynamic calculation via PM, the MCE of LCAMO is simulated under different values of variation in H_ext. The MCE of LCAMO is strongly tunable with the value of the variation of H_ext. Therefore, LCAMO can be used over a wide temperature range as an effective material for MR, covering a large range of temperatures, including room temperature and lower and higher ones. The MCE of LCAMO is tunable with the variation of H_ext, proving that LCAMO is practically more helpful as a MC magnet for the development of MRs in an extensive temperature range, including room temperature. The values of the MCE parameters of LCAMO are practically greater than the MCE ones of some MC samples in earlier works.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Ahmed, E. M., Alamri, H. R., Elghnam, S. M., Eldarawi, O., Tawfik, T. E., Mahmoud, A. M., et al. (2021). Tuning Magnetocaloric Properties for La1 - xSrxCoO3. Phys. Solid State. doi:10.1134/S1063783421100024

CrossRef Full Text | Google Scholar

Ahmed, E. M., Hemeda, O. M., Alamri, H. R., Elghnam, S. M., and Hamad, M. A. (2021). Investigation of Thermomagnetic Properties in Ca3Co2O6 over Cryogenic Temperature between 0 and 100 K. Phase Transitions. 94, 835–841. doi:10.1080/01411594.2021.1975706

CrossRef Full Text | Google Scholar

Álvarez-Alonso, P., Santos, J. D., Pérez, M. J., Sánchez-Valdes, C. F., Sánchez, J. L., and Gorria, P. (2013). The Substitution Effect of Chromium on the Magnetic Properties of (Fe1− xCrx) 80Si6B14 Metallic Glasses (0.02≤ X≤ 0.14). J.Magn.Magn.Mater. 347, 75–78.

Google Scholar

Alzahrani, B., Hsini, M., Hcini, S., Boudard, M., Dhahri, A., and Bouazizi, M. L. (2020). Study of the Magnetocaloric Effect by Means of Theoretical Models in La0.6Ca0.2Na0.2MnO3 Manganite Compound. J. Low Temp Phys. 200, 26–39. doi:10.1007/s10909-020-02455-w

CrossRef Full Text | Google Scholar

Belhamra, S., Masrour, R., Jabar, A., and Hlil, E. K. (2021). A Comparative Study of the Structural, Electronic, Magnetic Properties and Magnetocaloric Effect of Perovskite LaRO3 (R = Mn, Cr and Fe). Polyhedron. 193, 114891. doi:10.1016/j.poly.2020.114891

CrossRef Full Text | Google Scholar

Bhumireddi, S., Bhatnagar, A. K., Singh, D., Rayaprol, S., Das, D., and Ganesan, V. (2015). Specific Heat and Magnetocaloric Studies of Hexagonal Yb1−xErxMnO3. Mater. Lett. 161, 419–422. doi:10.1016/j.matlet.2015.08.151

CrossRef Full Text | Google Scholar

Biswal, H., Singh, V., Nath, R., Angappane, S., and Sahu, J. R. (2019). Magnetic and Magnetocaloric Properties of LaCr1-xMnxO3 (X = 0, 0.05, 0.1). Ceramics Int. 45, 22731–22736. doi:10.1016/j.ceramint.2019.07.311

CrossRef Full Text | Google Scholar

Boutahar, A., Lassri, H., and Hlil, E. K. (2015). Magnetic, Magnetocaloric Properties and Phenomenological Model in Amorphous Fe60Ru20B20 Alloy. Solid State. Commun. 221, 9–13. doi:10.1016/j.ssc.2015.08.002

CrossRef Full Text | Google Scholar

Choura-Maatar, S., Nofal, M. M., M’nassri, R., Cheikhrouhou-Koubaa, W., Chniba-Boudjada, N., and Cheikhrouhou, A. (2020). Enhancement of the Magnetic and Magnetocaloric Properties by Na Substitution for Ca of La0.8Ca0.2MnO3 Manganite Prepared via the Pechini-type Sol-Gel Process. J. Mater. Sci. Mater. Electron. 31, 1634–1645. doi:10.1007/s10854-019-02680-4

CrossRef Full Text | Google Scholar

Dhahri, A., Dhahri, E., and Hlil, E. K. (2014). Structural Characterization, Magnetic Properties and Magnetocaloric Effects of La0.75Sr0.25Mn1-X Cr X O3 (X = 0.15, 0.20, and 0.25). Appl. Phys. A. 116, 2077–2085. doi:10.1007/s00339-014-8404-5

CrossRef Full Text | Google Scholar

Dhahri, A., Jemmali, M., Dhahri, E., and Valente, M. A. (2015). Structural Characterization, Magnetic, Magnetocaloric Properties and Phenomenological Model in Manganite La0.75 Sr0.1Ca0.15 MnO3 Compound. J. Alloys Compounds. 638, 221–227. doi:10.1016/j.jallcom.2015.01.314

CrossRef Full Text | Google Scholar

Dhahri, J., Dhahri, A., Oumezzine, M., and Dhahri, E. (2008). Effect of Sn-Doping on the Structural, Magnetic and Magnetocaloric Properties of La0.67Ba0.33Mn1−xSnxO3 Compounds. J. Magnetism Magn. Mater. 320, 2613–2617. ‏. doi:10.1016/j.jmmm.2008.05.030

CrossRef Full Text | Google Scholar

El Boubekri, A., Tillaoui, S., Sajieddine, M., Sahlaoui, M., Lassri, H., Hlil, E. K., et al. (2020). Magnetic and Magnetocaloric Properties of Fe68+Cr12−Si8B12 Ribbons. J. Magnetism Magn. Mater. 507, 166819. doi:10.1016/j.jmmm.2020.166819

CrossRef Full Text | Google Scholar

El-Sayed, A. H., and Hamad, M. A. (2019a). Nickle Concentration Effect on Low Magnetic Field Magnetocaloric Properties for Ni2+xMn1−xGe. J. Supercond. Nov. Magn. 32, 1447–1450. doi:10.1007/s10948-018-4855-9

CrossRef Full Text | Google Scholar

El-Sayed, A. H., and Hamad, M. A. (2019b). Tailoring Thermomagnetic Properties in Pb(Zr0.52Ti0.48)O3-Ni(1−x)ZnxFe2O4. Phase Transitions. 92, 517–524. doi:10.1080/01411594.2019.1597096

CrossRef Full Text | Google Scholar

ErchidiElyacoubi, A. S., Masrour, R., and Jabar, A. (2018a). Surface Effects on the Magnetocaloric Properties of Perovskites Ferromagnetic Thin Films: A Monte Carlo Study. Appl. Surf. Sci. 459, 537–543. ‏. doi:10.1016/j.apsusc.2018.08.020

CrossRef Full Text | Google Scholar

ErchidiElyacoubi, A. S., Masrour, R., and Jabar, A. (2018b). Magnetocaloric Effect and Magnetic Properties in SmFe1-xMnxO3 Perovskite: Monte Carlo Simulations. Solid State. Commun. 271, 39–43. ‏. doi:10.1016/j.ssc.2017.12.015

CrossRef Full Text | Google Scholar

Erchidi Elyacoubi, A. S., Masrour, R., Jabar, A., Ellouze, M., and Hlil, E. K. (2018c). Magnetic Properties and Magnetocaloric Effect in Double Sr2FeMoO6 Perovskites. Mater. Res. Bull. 99, 132–135. doi:10.1016/j.materresbull.2017.10.037

CrossRef Full Text | Google Scholar

Felhi, H., Dhahri, R., Smari, M., Dhahri, E., and Hlil, E. K. (2019). Magnetocaloric Effect and Critical Behaviour of La0.5Ca0.2Ag0.3MnO3 Compound. Chem. Phys. Lett. 733, 136632. doi:10.1016/j.cplett.2019.136632

CrossRef Full Text | Google Scholar

Gupta, P., and Poddar, P. (2016). Study of Magnetic and thermal Properties of SmCrO3 Polycrystallites. RSC Adv. 6, 82014–82023. doi:10.1039/c6ra17203b

CrossRef Full Text | Google Scholar

Hamad, M. A. (2012). Prediction of Thermomagnetic Properties of La0.67Ca0.33MnO3and La0.67Sr0.33MnO3. Phase Transitions 85, 106–112. doi:10.1080/01411594.2011.605027

CrossRef Full Text | Google Scholar

Hamad, M. A. (2013). Magnetocaloric Effect of Perovskite Manganites Ce0.67Sr0.33MnO3. J. Supercond Nov Magn. 26, 2981–2984. doi:10.1007/s10948-013-2124-5

CrossRef Full Text | Google Scholar

Hamad, M. A. (2015a). Lanthanum Concentration Effect of Magnetocaloric Properties in La_x MnO_3−δ. J. Supercond Nov Magn. 28, 173. doi:10.1007/s10948-014-2834-3

CrossRef Full Text | Google Scholar

Hamad, M. A. (2015b). Magnetocaloric Effect in Sr2FeMoO6/Ag Composites. Process. Appl. Ceram. 9, 11. doi:10.2298/PAC1501011H

CrossRef Full Text | Google Scholar

Hamad, M. A. (2015c). Effects of Addition of Rare Earth on Magnetocaloric Effect in Fe82Nb2 B 14. J. Supercond. Nov. Magn. 28, 3111–3115. doi:10.1007/s10948-015-3140-4

CrossRef Full Text | Google Scholar

Hamad, M. A. (2015d). Magnetocaloric Effect in La1-X Ce X MnO3. J. Adv. Ceram. 4, 206–210. doi:10.1007/s40145-015-0150-4

CrossRef Full Text | Google Scholar

Hamad, M. A., Hemeda, O. M., and Mohamed, A. M. (2020). Investigations on Enhancing Thermomagnetic Properties in Co_xZn_1−xFe₂O₄. J. Supercond. Nov. Magn. 33, 2753–2757. doi:10.1007/s10948-020-05503-4

CrossRef Full Text | Google Scholar

Hamad, M. A., Hemeda, O. M., Alamri, H. R., and Mohamed, A. M. (2021). Investigations on Thermomagnetic Properties of YbFe2As2. J. Low Temp Phys. 202, 121–127. ‏. doi:10.1007/s10909-020-02528-w

CrossRef Full Text | Google Scholar

Henchiri, C., Mnasri, T., Benali, A., Hamdi, R., Dhahri, E., Valente, M. A., et al. (2020). Structural Study and Large Magnetocaloric Entropy Change at Room Temperature of La1−x□xMnO3 Compounds. RSC Adv. 10, 8352–8363. ‏doi:10.1039/c9ra10469k

CrossRef Full Text | Google Scholar

Ho, T. A., Thanh, T. D., Ho, T. O., Tran, Q. T., Phan, T. L., and Yu, S. C. (2014). Critical Behavior and Magnetocaloric Effect of Pr_1-xSr_xCoO₃. IEEE Trans. Magn. 50, 2505104. doi:10.1109/tmag.2014.2322906

CrossRef Full Text | Google Scholar

Jebari, H., Tahiri, N., Boujnah, M., El Bounagui, O., Taibi, M., and Ez-Zahraouy, H. (2021). Theoretical Investigation of Electronic, Magnetic and Magnetocaloric Properties of Bi25FeO40 Compound. Phase Transitions. 94, 147–158. doi:10.1080/01411594.2021.1931690

CrossRef Full Text | Google Scholar

Jeddi, M., Gharsallah, H., Bekri, M., Dhahri, E., and Hlil, E. K. (2020). Phenomenological Modeling of Magnetocaloric Properties in 0.75La0.6Ca0.4MnO3/0.25La0.6Sr0.4MnO3 Nanocomposite Manganite. J. Low Temp Phys. 198, 135–144. doi:10.1007/s10909-019-02256-w

CrossRef Full Text | Google Scholar

Jerbi, A., Krichene, A., Chniba-Boudjada, N., and Boujelben, W. (2015). Magnetic and Magnetocaloric Study of Manganite Compounds Pr0.5A0.05Sr0.45MnO3 (A=Na and K) and Composite. Physica B: Condensed Matter 477, 75–82. doi:10.1016/j.physb.2015.08.022

CrossRef Full Text | Google Scholar

Kadim, G., Masrour, R., and Jabar, A. (2020). Large Magnetocaloric Effect, Magnetic and Electronic Properties in Ho3Pd2 Compound: Ab Initio Calculations and Monte Carlo Simulations. J. Magnetism Magn. Mater. 499, 166263. ‏. doi:10.1016/j.jmmm.2019.166263

CrossRef Full Text | Google Scholar

Kadim, G., Masrour, R., Jabar, A., and Hlil, E. K. (2021a). Room-Temperature Large Magnetocaloric, Electronic and Magnetic Properties in La0.75Sr0.25MnO3 Manganite: Ab Initio Calculations and Monte Carlo Simulations. Physica A: Stat. Mech. its Appl. 573‏, 125936. doi:10.1016/j.physa.2021.125936

CrossRef Full Text | Google Scholar

Kadim, G., Masrour, R., and Jabar, A. (2021b). Magnetocaloric Effect, Electronic and Magnetic Properties of Ba1-xSrxFeO3 Barium-Strontium Ferrites: Monte Carlo Simulations and Comparative Study between TB-mBJ and GGA+U. Mater. Today Commun. 26, 102071. doi:10.1016/j.mtcomm.2021.102071

CrossRef Full Text | Google Scholar

Laajimi, K., Khlifi, M., Hlil, E. K., Gazzah, M. H., Ayed, M. B., Belmabrouk, H., et al. (2020). Influence of Sr Substitution on Structural, Magnetic and Magnetocaloric Properties in La0.67Ca0.33−xSrxMn0.98Ni0.02O3 Manganites. J. Mater. Sci. Mater. Electron. 31, 15322–15335. ‏. doi:10.1007/s10854-020-04096-x

CrossRef Full Text | Google Scholar

Labidi, S., Masrour, R., Jabar, A., and Ellouze, M. (2021). Mechanical, Electronic and Magnetic Properties of Double Sr2FeMoO6 Perovskite: Density Functional Theory and Monte Carlo Simulation. J. Magnetism Magn. Mater. 523, 167594. ‏. doi:10.1016/j.jmmm.2020.167594

CrossRef Full Text | Google Scholar

Long, P. T., Manh, T. V., Ho, T. A., Dongquoc, V., Zhang, P., and Yu, S. C. (2018). Magnetocaloric Effect in La1-xSrxCoO3 Undergoing a Second-Order Phase Transition. Ceramics Int. 44, 15542–15549. doi:10.1016/j.ceramint.2018.05.216

CrossRef Full Text | Google Scholar

Mansouri, M., Omrani, H., Cheikhrouhou-Koubaa, W., Koubaa, M., Madouri, A., and Cheikhrouhou, A. (2016). Effect of Vanadium Doping on Structural, Magnetic and Magnetocaloric Properties of La 0.5 Ca 0.5 MnO 3. J. Magnetism Magn. Mater. 401, 593–599. doi:10.1016/j.jmmm.2015.10.066

CrossRef Full Text | Google Scholar

Masrour, R., Jabar, A., Benyoussef, A., Hamedoun, M., and Hlil, E. K. (2016). Monte Carlo Simulation Study of Magnetocaloric Effect in NdMnO 3 Perovskite. J. Magnetism Magn. Mater. 401, 91–95. ‏. doi:10.1016/j.jmmm.2015.10.019

CrossRef Full Text | Google Scholar

Masrour, R., Jabar, A., Khlif, H., Jemaa, F. B., Ellouze, M., and Hlil, E. K. (2017). Experiment, Mean Field Theory and Monte Carlo Simulations of the Magnetocaloric Effect in La 0.67 Ba 0.22 Sr 0.11 MnO 3 Compound. Solid State. Commun. 268, 64–69. ‏. doi:10.1016/j.ssc.2017.10.003

CrossRef Full Text | Google Scholar

Oubla, M., Lamire, M., Boutahar, A., Lassri, H., Manoun, B., and Hlil, E. K. (2016). Structural, Magnetic and Magnetocaloric Properties of Layered Perovskite La1.1Bi0.3Sr1.6Mn2O7. J. Magnetism Magn. Mater. 403, 114–117. doi:10.1016/j.jmmm.2015.11.076

CrossRef Full Text | Google Scholar

Radaelli, P. G., Cox, D. E., Marezio, M., Cheong, S.-W., Schiffer, P. E., and Ramirez, A. P. (1995). Simultaneous Structural, Magnetic, and Electronic Transitions inLa1−xCaxMnO3withx=0.25 and 0.50. Phys. Rev. Lett. 75, 4488–4491. doi:10.1103/physrevlett.75.4488

PubMed Abstract | CrossRef Full Text | Google Scholar

Saadaoui, F., Koubaa, M., Cheikhrouhou-Koubaa, W., and Cheikhrouhou, A. (2013). Effects of Bismuth Doping on the Physical Properties of La0.6−x Bi X Sr0.4CoO3 (0≤x≤0.15) Cobaltites. J. Supercond. Nov. Magn. 26, 3043–3047. doi:10.1007/s10948-013-2122-7

CrossRef Full Text | Google Scholar

Sharma, P., Masrour, R., Jabar, A., Fan, J., Kumar, A., Ling, L., et al. (2020). Structural and Magnetocaloric Properties of Rare-Earth Orthoferrite Perovskite: TmFeO3. Chem. Phys. Lett. 740, 137057. ‏. doi:10.1016/j.cplett.2019.137057

CrossRef Full Text | Google Scholar