Influence of doubly-hydrogenated oxygen vacancy on the TID effect of MOS devices

The total ionizing dose (TID) effect is one of the main causes of the performance degradation/failure of semiconductor devices under high-energy γ-ray irradiation. In special, the concentration of doubly-hydrogenated oxygen vacancy (a case study of $V_{\mathrm{o}\gamma }{H}_2$) in the oxide layer seriously exacerbates the TID effect. Therefore, we developed a dynamic model of mobile particles and fixed defects by solving the rate equations and Poisson’s equation simultaneously, to reveal the contribution and influence mechanisms of $V_{\mathrm{o}\gamma }{H}_2$ on the TID effect of MOS devices. We found that $V_{o\gamma }{H}_{\mathit{2}}$ can directly and indirectly promote the formation of $V_{o\gamma }^{+}$ and $V_{o\gamma }{H}^{+}$, respectively, which can increase the electric field near the Si/SiO₂ interface and reduce the threshold voltage of silicon MOS devices accordingly. Controlling $V_{o\gamma }{H}_{\mathit{2}}$ with a concentration below 10¹⁴ cm⁻³ can suppress the adverse TID effects. The results are much helpful for analyzing the microscopic mechanisms of the TID effect and designing new MOS devices with high radiation-hardening.

Introduction

More and more new semiconductor materials are widely used as the core electronic components of sensors, detectors, radar and so on. In extreme service environments, semiconductor devices are inevitably affected by harsh radiation effects. All kinds of high-energy particles will cause serious ionization or displacement damage to semiconductors, then lead to the degradation/failure of the electrical performance of semiconductor devices, and pose adverse effects on the safety and lifetime of the entire electronic systems (Benton and Benton, 2001).

As early as 1964, Hughes and Giroux conducted a preliminary study (Hughes and Giroux, 1964) on the performance degradation of semiconductor devices (MOS) under the total ionizing dose (TID). They found that TID-induced performance degradation is due to the additional charge generated in the oxide layer (SiO₂) rather than on the surface. In subsequent decades, a large number of experimental studies of ionizing irradiation showed that the key mechanism of the performance degradation induced by the TID is the formation of oxide charged defects (N_ot) in the gate oxide region (Hughes, 1965a; Hughes, 1965b; Kooi, 1965; Zaininger, 1966). Therefore, identification of neutral defects in SiO₂ before irradiation and exploration of the evolution of charged defects after irradiation are the basis for studying the TID effect of MOS devices.

In 1956, Robert used electron paramagnetic resonance (EPR) for the first time to measure radiation-induced defects in crystalline or amorphous SiO₂ (Weeks, 1963) and found two basic types of oxygen vacancies in SiO₂, including deep ($V_{o\gamma }$) and shallow ($V_{o\delta }$) level defects. In the 1980s, these methods have been used to study possible chemical reactions and free radical formation in thermal oxides of MOS devices during irradiation (Blöchl, 2000). Several kinds of defects that existed in the oxide layer before and after irradiation were thus determined. The existing initial defects in the oxide layer (SiO₂) of the device before irradiation include oxygen vacancy ($V_{o\gamma }$ and $V_{\mathrm{o}\delta }$), singly-hydrogenated oxygen vacancy ($V_{\mathrm{o}\delta }H$ and $V_{\mathrm{o}\gamma }H$) and doubly-hydrogenated oxygen vacancy ($V_{\mathrm{o}\delta }{H}_2$ and $V_{\mathrm{o}\gamma }{H}_2$) defects (Conley and Lenahan, 1993; Walle and Tuttle, 2000). Whereas, after irradiation, defects generated in the oxide layer of the device are mainly oxide charged defects ($V_{\mathrm{o}\delta }^{+}$, $V_{\mathrm{o}\delta }{H}^{+}$, $V_{\mathrm{o}\delta }{H}_2^{+}$, $V_{\mathrm{o}\gamma }^{+}$, $V_{\mathrm{o}\gamma }{H}^{+}$ and $V_{\mathrm{o}\gamma }{H}_2^{+}$) (Lenahan and Dressendorfer, 1984).

The pre-existing concentration of defects in SiO₂ is still known little. Density functional theory (DFT) calculations suggest that relative concentrations of different pre-existing trap species, and order of magnitude estimates of the actual concentration of defects have been suggested by etch-back experiments of irradiated oxides (Devine et al., 1993). It is found that the initial concentration of doubly-hydrogenated oxygen vacancy before irradiation is relatively high, while its charged concentration after irradiation is the lowest among the oxide charged defects (Rowsey et al., 2011a). In the process of ionizing irradiation, the evolution process of doubly-hydrogenated oxygen vacancy and its specific contribution to the TID effect are still unclear. It is thus urgent to establish a dynamic model of the TID effect that includes the dynamic of doubly-hydrogenated oxygen vacancy to reveal their influence mechanism.

In this paper, a one-dimensional (1-D) dynamics model of mobile particles and fixed defects in the oxide layer (SiO₂) of typical silicon MOS devices is developed to systematically study the influence of doubly-hydrogenated oxygen vacancy on the TID effect. This work provides theoretical guidance by controlling the concentration of doubly-hydrogenated oxygen vacancy for the radiation-hardening-by-design (RHBD) techniques of semiconductor devices.

Simulation methods

Dynamics model

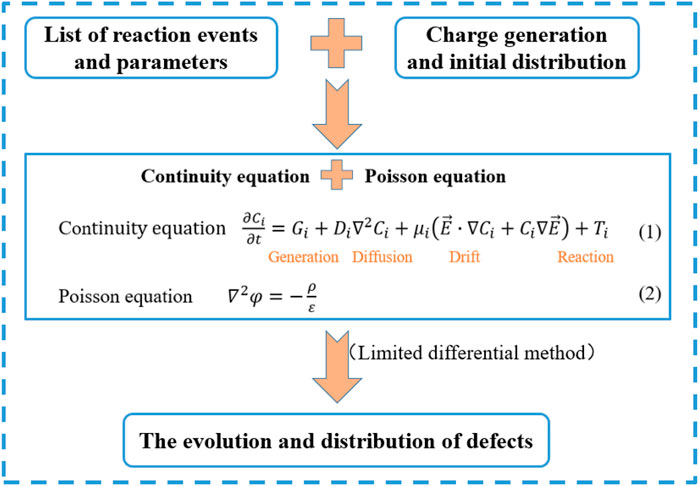
The model framework is shown in Figure 1. First, the initial distribution of defects can be determined by EPR measurements (Lenahan and Conley, 1998; Lu et al., 2002). The reaction events and rate coefficients between mobile particles and defects are mainly given by the DFT calculations (Rowsey et al., 2011a; Rowsey et al., 2011b). Then, with this information, the continuity equations of mobile particles and fixed defects can be described based on the rate theory. In addition, the Poisson equation is established to determine the spatial electric field distribution. Finally, the finite difference method is employed to solve the ordinary differential equations (ODEs). The evolution and distribution of oxide charged defects and electric fields can thus be obtained by this model.

FIGURE 1

FIGURE 1. Diagram framework of the dynamic model.

Continuity equation

$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{u}\mathrm{i}\mathrm{t}\mathrm{y}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\frac{\partial c_i}{\partial \mathrm{t}}=G_i+D_i{\nabla }^2{C}_i+{\mu }_i\left(\overrightarrow{E}\cdot \nabla C_i+C_i\nabla \overrightarrow{E}\right)+T_i(1)$

$\mathrm{P}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}{\mathit{\nabla }}^2\phi =-\frac{\rho }{ϵ}(2)$

The continuity Eq. 1 in Figure 1, where $C_{\mathrm{i}}$ represents the concentration of particle i at a certain position at a certain time. $G_{\mathrm{i}}$ and $T_{\mathrm{i}}$ represent the generation (only for electron/hole) and reaction (with other defects) rates of the particle i, respectively. ${\mu }_{\mathrm{i}}$ represents the mobility of mobile charged particles, $D_{\mathrm{i}}={\mu }_{\mathrm{i}}{k}_{B}T/q$ represents the diffusion coefficients of mobile particles, and E represents the electric field.

The generation rate of e-h pairs induced by ionizing irradiation is given as follows (Oldham, 2000),

$G_{\mathrm{e}/\mathrm{h}}=Y\cdot G_0\cdot R,(3)$

where G₀ represents the density of e-h pairs per unit ionizing dose, Y is the survival rate of the e-h pairs after initial recombination, which is set to be 0.01 for SiO₂ under γ-ray irradiation (Shaneyfelt et al., 1991), and R is the dose rate (rad/s).

The reaction rates of mobile particles with fixed defects are determined by the rate theory, which is proportional to the reactant concentrations. Comprehensively considering all reaction events, the total reaction rate of the particle i is given by (Xu et al., 2018),

$T_{\mathrm{i}}=-{\displaystyle \sum }_{\mathrm{j}}\alpha C_{\mathrm{i}}{C}_{\mathrm{j}}+{\displaystyle \sum }_{\mathrm{m}+\mathrm{n}\to \mathrm{i}}\beta C_{\mathrm{m}}{C}_{\mathrm{n}},(4)$

where the j, m and n are termed as the other reactants, and the α and β represent the forward and reverse reaction rate coefficients, respectively.

Since the fixed defect is immobile and has no additional generation, the continuity equation includes only the reaction term ($T_{\mathrm{i}}$), given in Eq. 4. For the continuity equation of mobile particles, the drift-diffusion term should be considered. Especially for electrons/holes, the generation term ($G_{\mathrm{e}/\mathrm{h}}$) should also be introduced, given in Eq. 1.

Reaction events and coefficients

Since deep- and shallow-level defects cannot be transformed into each other, we only consider the dynamics of deep-level defects ($V_{\mathrm{o}\gamma }$, $V_{\mathrm{o}\gamma }H$ and $V_{\mathrm{o}\gamma }{H}_2$) in the model. This simplification will not affect the purpose of exploring the influence of doubly-hydrogenated oxygen vacancy on the TID effect.

For oxygen vacancy ($V_{\mathrm{o}\gamma }$), singly-hydrogenated oxygen vacancy ($V_{\mathrm{o}\gamma }H$) and doubly-hydrogenated oxygen vacancy ($V_{\mathrm{o}\gamma }{H}_2$) formed during high-temperature processing steps (Hughart et al., 2009; Tuttle et al., 2010), first principles results indicate that the initial concentration of defects are approximately 10¹⁵ cm⁻³, 10¹⁴ cm⁻³ and 10¹⁶ cm⁻³, respectively (Rowsey et al., 2011a; Rowsey et al., 2011b). All three first capture a hole to form positively charged defects, then $V_{\mathrm{o}\gamma }^{+}$ split hydrogen molecular (H₂) to release a proton (H⁺), $V_{\mathrm{o}\gamma }{H}^{+}$ directly release a H⁺, $V_{\mathrm{o}\gamma }{H}_2^{+}$ can directly release a H⁺ or directly dissociate into H₂ (Hughart et al., 2012). All three of these charged defects can also capture electrons as the recombination center (Rowsey et al., 2011a; Xu et al., 2018). The above chemical reaction and rate coefficients are given in Table 1.

TABLE 1

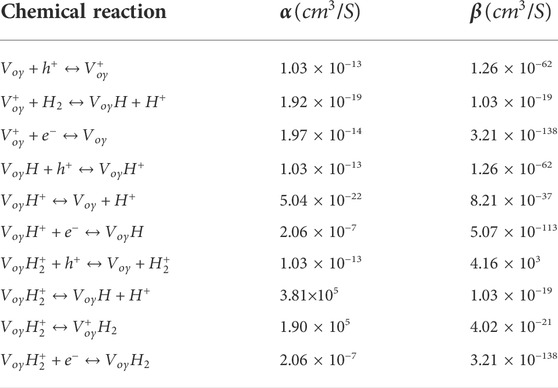
TABLE 1. Chemical reaction and rate coefficients (Bunson et al., 2000; Rowsey et al., 2012; Patrick et al., 2015; Sharov et al., 2022).

The accumulation of the charged defects results in the formation of a built-in electric field in the oxide layer. The electric field can be solved by Poisson’s equation as below (Esqueda et al., 2012; Jafari et al., 2015),

$\nabla \cdot \overrightarrow{E}=\frac{\rho }{{\epsilon }_{\mathrm{o}\mathrm{x}}{\epsilon }_0}(5)$

$\rho =e_{\mathrm{c}}\left(C_{{\mathrm{h}}^{+}}+C_{{\mathrm{H}}^{+}}+C_{{\mathrm{V}}_{o\gamma }^{+}}+C_{{\mathrm{V}}_{o\gamma }{\mathrm{H}}^{+}}+C_{{\mathrm{V}}_{o\gamma }{\mathrm{H}}_2^{+}}-C_{e^{-}}\right)(6)$

where, $\rho$ is the total charge density in the oxide layer, ${\epsilon }_{\mathrm{o}\mathrm{x}}=3.9$ is the relative permittivity of SiO₂, and ${\epsilon }_0$ is the permittivity in a vacuum.

An important parameter is the density of N_ot, with units of cm⁻², which can be integrated from the distribution of each oxide charged defect as (Esqueda et al., 2011),

$C_{\mathrm{N}\mathrm{o}\mathrm{t}}={\int }_0^{L_{\mathrm{o}\mathrm{x}}}\frac{x}{L_{\mathrm{o}\mathrm{x}}}\left({\mathrm{C}}_{{\mathrm{V}}_{\mathrm{o}\gamma }^{+}}+{\mathrm{C}}_{{\mathrm{V}}_{\mathrm{o}\gamma }{\mathrm{H}}^{+}}+{\mathrm{C}}_{{\mathrm{V}}_{\mathrm{o}\gamma }{\mathrm{H}}_2^{+}}\right)dx(7)$

where L_ox is the thickness of the oxide layer, and x refers to the distance from the Gate.

Numerical method

The finite difference method with a uniform spatial grid is adopted for solving the partial differential equations (PDEs). Here the lsoda solver of the C version (Whitbeck, 1991) is employed to solve the corresponding ODEs. The key to using the finite difference method to solve the above time and space related problems is the setting of appropriate initial values and boundary conditions. The initial concentration of charged defects and charged particles is set to 0. In the 1-D model, there are two boundaries of Gate/SiO₂ and Si/SiO₂ in contact with the SiO₂ layer. The mobile particles can flow freely at both boundaries, so the first kind of boundary conditions are adopted. In addition, we specify that the electrostatic potential is continuous at all boundaries (Xu et al., 2018).

Results and discussions

This section presents the evolution and distribution of defects in the SiO₂ layer of an NPN-type MOS capacitor (L_ox = 200 nm) irradiated by γ-rays of $G_{\mathit{0}}=\mathit{8.1}\times {\mathit{10}}^{\mathit{12}}{cm}^{-\mathit{3}}\cdot {\mathrm{r}\mathrm{a}\mathrm{d}}^{-\mathit{1}}$ uniformly for the whole SiO₂ layer (Esqueda et al., 2011). The mobility of electrons and holes in SiO₂ are 20 and ${\mathit{10}}^{-\mathit{6}}{cm}^{\mathit{2}}\cdot V^{-\mathit{1}}\cdot s^{-\mathit{1}}$ (Hughart et al., 2011), respectively. The diffusion coefficients of H₂ and H⁺ in SiO₂ are 10⁻⁹ and ${\mathit{10}}^{-\mathit{10}}{cm}^{\mathit{2}}\cdot s^{-\mathit{1}}$, respectively (Rowsey et al., 2011b).

Validation and verification

The simulated density of oxide charged defects (N_ot) is compared with the experimental ones (Tuttle et al., 2010) to verify our model. Figure 2 shows the time evolution of the density of N_ot, under the time of $\mathit{1.5}\times {\mathit{10}}^{\mathit{4}}s$ with the dose rate of 20 rad/s at 300 K. The Capacitance-Gate voltage curves of the irradiated devices under three different TIDs were measured to determine the average densities of N_ot. Typically, N_ot increase gradually with irradiation time and tend to saturation. The simulation results are consistent with the experimental ones well. The little differences may be caused by the model approximations and measurement errors. Thus, our model should be reasonable enough for simulating the TID effect.

FIGURE 2

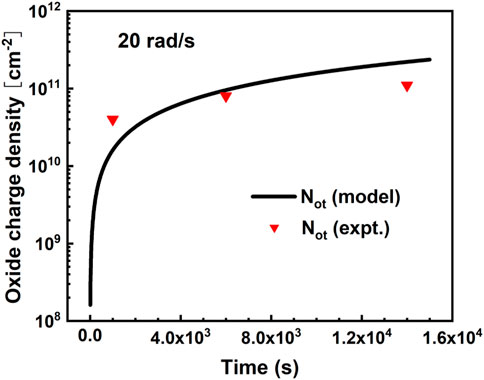
FIGURE 2. Comparison of the evolution of N_ot with the experiment for the MOS capacitor with a 200 nm SiO₂ layer under 5 V bias.

The influence of $V_{\mathrm{o}\gamma }{H}_2$ on $V_{\mathrm{o}\gamma }^{+}$ and $V_{\mathrm{o}\gamma }{H}^{+}$

In the following, we studied the key factors of the oxide charged defects for the TID effect, such as their composition, distribution and evolution. Figure 3A shows the distributions of different oxide charged defects under the TID of 10 krad with the dose rate of 10 rad/s at 300 K. $V_{\mathrm{o}\gamma }^{+}$ is the main component of the oxide charged defects, while the initial density of $V_{o\gamma }{H}_{\mathit{2}}$ is the highest in the oxide layer. We also simulated the evolutions of $V_{o\gamma }{H}_{\mathit{2}}^{+}$ and $V_{\mathrm{o}\gamma }{H}_2$ under the dose rate of 10 rad/s at 300 K. As shown in Figure 3B, the densities of $V_{\mathrm{o}\gamma }{H}_2^{+}$ and $V_{\mathrm{o}\gamma }{H}_2$ decrease with increasing TID. This means that $V_{o\gamma }{H}_{\mathit{2}}^{+}$ formed by the hole capture of $V_{o\gamma }{H}_{\mathit{2}}$ will not exist stably but continue to be dissociated. Thus, $V_{\mathrm{o}\gamma }{H}_2^{+}$ has the lowest density, while $V_{\mathrm{o}\gamma }{H}_2$ can promote the formation of $V_{\mathrm{o}\gamma }^{+}$ and $V_{\mathrm{o}\gamma }{H}^{+}$.

FIGURE 3

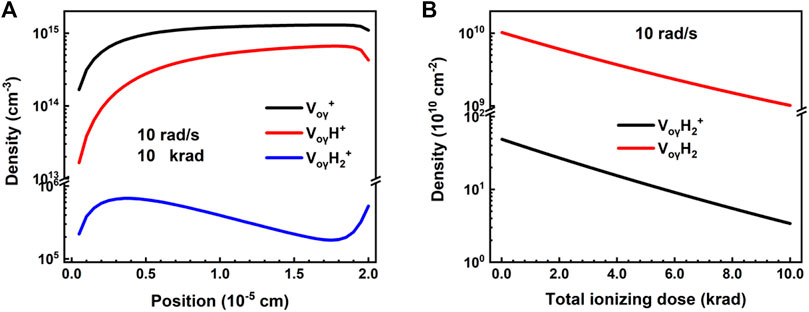
FIGURE 3. Distributions of (A) different oxide charged defects under the TID of 10 krad, and (B) evolution of $V_{\mathrm{o}\gamma }{H}_2^{+}$ and $V_{\mathrm{o}\gamma }{H}_2$ with the dose rate of 10 rad/s at 300 K.

Also as shown in Figure 3A, with increasing the distance from the Gate, the densities of $V_{\mathrm{o}\gamma }^{+}$ and $V_{\mathrm{o}\gamma }{H}^{+}$ slowly increase in the oxide layer but decrease at the boundaries, because the reaction particles (holes) of $V_{\mathrm{o}\gamma }{H}_2$ flow out at the boundaries, the density of holes decrease near the Si/SiO₂ interface. With increasing the distance from the Gate, the density of $V_{\mathrm{o}\gamma }{H}_2^{+}$ first increase and then decrease, and rise again near (about 30 nm) the Si/SiO₂ boundary. In the first rise range, the reaction of $V_{\mathrm{o}\gamma }{H}_2$ capturing holes is dominant, but they are unstable and dissociate easily. So in the latter range, the reaction releasing H⁺/H₂ forms $V_{\mathrm{o}\gamma }{H}^{+}$ or $V_{\mathrm{o}\gamma }{H}_2^{+}$ is dominant.

As given above, $V_{\mathrm{o}\gamma }{H}_2$ promote the formation of $V_{\mathrm{o}\gamma }^{+}$ and $V_{\mathrm{o}\gamma }{H}^{+}$. However, through what transformation mechanism does $V_{\mathrm{o}\gamma }{H}_2$ promote the generation of $V_{o\gamma }^{+}$ and $V_{o\gamma }{H}^{+}$, we further explored the transformation mechanism that $V_{o\gamma }{H}_{\mathit{2}}$ promotes the generation of $V_{o\gamma }^{+}$ and $V_{o\gamma }{H}^{+}$. We simulated the densities of $V_{o\gamma }$, $V_{o\gamma }^{+}$ and $V_{o\gamma }+V_{o\gamma }^{+}$ as a function of TID with and without $V_{o\gamma }{H}_{\mathit{2}}$, under the TID of 10 krad with the dose rate of 10 rad/s at room temperature. As shown in Figure 4A, with $V_{o\gamma }{H}_{\mathit{2}}$, the density of $V_{o\gamma }+V_{o\gamma }^{+}$ increases with increasing TID, and approaches to saturation. Thus, there are other channels that can produce $V_{\mathrm{o}\gamma }$ or $V_{\mathrm{o}\gamma }^{+}$. As shown in Figure 4B, without $V_{\mathrm{o}\gamma }{H}_2$, the density of $V_{\mathrm{o}\gamma }+V_{\mathrm{o}\gamma }^{+}$ is constant, which means there’s no other reaction to form $V_{\mathrm{o}\gamma }$ or $V_{\mathrm{o}\gamma }^{+}$. Compare Figures 4A,B, the density of $V_{\mathrm{o}\gamma }+V_{\mathrm{o}\gamma }^{+}$ with $V_{\mathrm{o}\gamma }{H}_2$ is always higher than that without $V_{\mathrm{o}\gamma }{H}_2$, and the increase up to 30% when the TID is 10 krad. Therefore, the increase of $V_{\mathrm{o}\gamma }+V_{\mathrm{o}\gamma }^{+}$ only comes from $V_{\mathrm{o}\gamma }{H}_2$ through $V_{\mathrm{o}\gamma }{H}_2^{+}\leftrightarrow V_{\mathrm{o}\gamma }^{+}+{\mathrm{H}}_2$, and the reason why the increase of $V_{\mathrm{o}\gamma }+V_{\mathrm{o}\gamma }^{+}$ becomes slow is that the density of $V_{\mathrm{o}\gamma }{H}_2$ decreases with increasing TID. In addition, the density of $V_{\mathrm{o}\gamma }$ with $V_{\mathrm{o}\gamma }{H}_2$ is almost no different from that without $V_{\mathrm{o}\gamma }{H}_2$ during the ionizing process, while the density of $V_{\mathrm{o}\gamma }^{+}$ with $V_{\mathrm{o}\gamma }{H}_2$ is obviously higher than that without $V_{\mathrm{o}\gamma }{H}_2$. Therefore, the $V_{\mathrm{o}\gamma }{H}_2$ directly promotes the formation of $V_{\mathrm{o}\gamma }^{+}$ through releasing H₂.

FIGURE 4

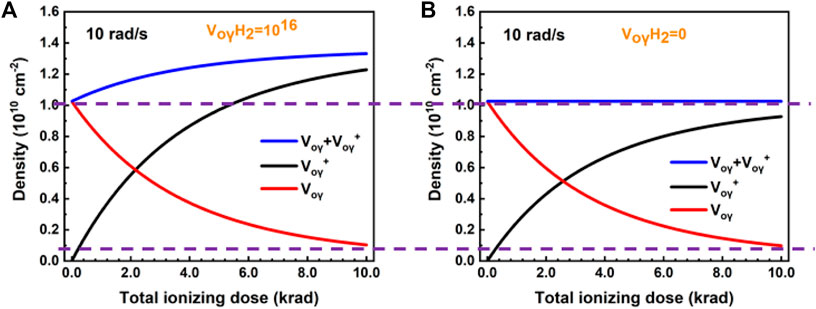
FIGURE 4. Evolution of $V_{\mathrm{o}\gamma }^{+}$, $V_{\mathrm{o}\gamma }$ and $V_{\mathrm{o}\gamma }^{+}+V_{\mathrm{o}\gamma }$ (A) with and (B) without $V_{\mathrm{o}\gamma }{H}_2$ as a function of TID at the dose rate of 10 rad/s at 300K.

We also simulated the densities of $V_{\mathrm{o}\gamma }{H}^{+}+V_{\mathrm{o}\gamma }H$, $V_{\mathrm{o}\gamma }{H}^{+}$ and $V_{\mathrm{o}\gamma }H$ as a function of TID with and without $V_{\mathrm{o}\gamma }{H}_2$, under the TID of 10 krad with the dose rate of 10 rad/s at room temperature. As shown in Figure 5A, with $V_{\mathrm{o}\gamma }{H}_2$, the density of $V_{\mathrm{o}\gamma }{H}^{+}+V_{\mathrm{o}\gamma }H$ increases with increasing TID, and the growth rate is gradually slow, which is similar to the evolution of $V_{\mathrm{o}\gamma }+V_{\mathrm{o}\gamma }^{+}$. It also means that there are other channels that can produce $V_{\mathrm{o}\gamma }{H}^{+}+V_{\mathrm{o}\gamma }H$. As shown in Figure 5B, without $V_{\mathrm{o}\gamma }{H}_2$, the density of $V_{\mathrm{o}\gamma }{H}^{+}+V_{\mathrm{o}\gamma }H$ is constant that means there’s no other reaction to form $V_{\mathrm{o}\gamma }{H}^{+}$ or $V_{\mathrm{o}\gamma }H$. Compare Figures 5A,B, the density of $V_{\mathrm{o}\gamma }{H}^{+}+V_{\mathrm{o}\gamma }H$ with $V_{\mathrm{o}\gamma }{H}_2$ is always higher than that without $V_{\mathrm{o}\gamma }{H}_2$, and the increment is up to 6 times when the TID is 10 krad. Thus, the increase only comes from $V_{\mathrm{o}\gamma }{H}_2$ though $V_{\mathrm{o}\gamma }{H}_2^{+}\leftrightarrow V_{\mathrm{o}\gamma }H+{\mathrm{H}}^{+}$, with the density increases slowly due to the decreases of $V_{\mathrm{o}\gamma }{H}_2$ with increasing TID. In addition, the density of $V_{\mathrm{o}\gamma }H$ decreases with increasing TID without $V_{\mathrm{o}\gamma }{H}_2$, for the $V_{\mathrm{o}\gamma }H$ is constantly transformed into $V_{\mathrm{o}\gamma }{H}^{+}$ during the ionizing process. The density of $V_{\mathrm{o}\gamma }H$ increases from 0 to 3.0 krad and then decreases with increasing TID with $V_{\mathrm{o}\gamma }{H}_2$. The $V_{\mathrm{o}\gamma }H$ increases because the rate at which $V_{\mathrm{o}\gamma }{H}_2$ is converted to $V_{\mathrm{o}\gamma }H$ is higher than the rate at which $V_{\mathrm{o}\gamma }H$ is converted to $V_{\mathrm{o}\gamma }{H}^{+}$during the ionizing process. The decrease of $V_{\mathrm{o}\gamma }H$ from 3.0 to 10.0 krad is due to that $V_{\mathrm{o}\gamma }H$convert to $V_{\mathrm{o}\gamma }{H}^{+}$ faster than $V_{\mathrm{o}\gamma }{H}_2$ convert to $V_{\mathrm{o}\gamma }H$. The density of $V_{\mathrm{o}\gamma }H$ with $V_{\mathrm{o}\gamma }{H}_2$ is always higher than that without $V_{\mathrm{o}\gamma }{H}_2$, and the density of $V_{\mathrm{o}\gamma }H$ decreases with increasing TID without $V_{\mathrm{o}\gamma }{H}_2$. Therefore, the $V_{\mathrm{o}\gamma }{H}_2$ directly promotes the formation of $V_{\mathrm{o}\gamma }H$ through releasing H⁺, then promotes the formation of $V_{\mathrm{o}\gamma }{H}^{+}$ through capturing holes.

FIGURE 5

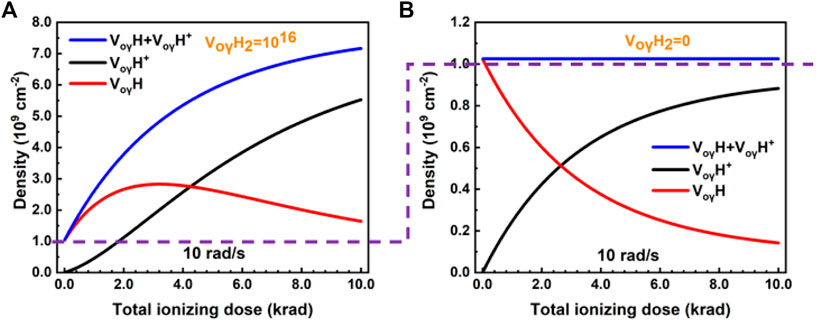
FIGURE 5. Evolution of $V_{\mathrm{o}\gamma }{H}^{+}$, $V_{\mathrm{o}\gamma }H$ and $V_{\mathrm{o}\gamma }{H}^{+}+V_{\mathrm{o}\gamma }H$ (A) with and (B) without $V_{\mathrm{o}\gamma }{H}_2$ as a function of TID at the dose rate of 10 rad/s at 300K.

It has been known that the TID effect of devices is closely related to the electric field near the Si/SiO₂ interface ($E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$) of the oxide layer, which $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ can be simply described as follows,

$E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}=E_{\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{d}}+E_{\mathrm{b}\mathrm{u}\mathrm{i}\mathrm{l}\mathrm{t}-\mathrm{i}\mathrm{n}}=V_{\mathrm{g}}/L_{\mathrm{o}\mathrm{x}}+{\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}/{\epsilon }_0{\epsilon }_{\mathrm{o}\mathrm{x}}.(8)$

According to Eq. 8, when the gate voltage ($V_{\mathrm{g}}$), the thickness ($L_{\mathrm{o}\mathrm{x}}$) and the permittivity (${\epsilon }_{\mathrm{o}\mathrm{x}}$) of oxide layer are fixed, the relationship of $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ with the total charge density (${\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}$) follows $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}\propto {\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}$. Changing the concentration of $V_{\mathrm{o}\gamma }{H}_2$ corresponds to changing the ${\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}$ after irradiation. As shown in Figure 6, we simulated the $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ with increasing the concentration of $V_{\mathrm{o}\gamma }{H}_2$ ($C_{V_{\mathrm{o}\gamma }{H}_2}$) under the TID of 10 krad with the dose rate of 10 rad/s at 300 K. We found that, $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ does not change with $C_{V_{\mathrm{o}\gamma }{H}_2}$ before irradiation. After irradiation, when $C_{V_{\mathrm{o}\gamma }{H}_2}$ is lower than about 10¹⁴ cm⁻³, $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ almost does not change with the increase of $C_{V_{\mathrm{o}\gamma }{H}_2}$, but when $C_{V_{\mathrm{o}\gamma }{H}_2}$ is higher than about 10¹⁵ cm⁻³, $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ increases rapidly with increasing $C_{V_{\mathrm{o}\gamma }{H}_2}$, following $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}\propto C_{V_{\mathrm{o}\gamma }{H}_2}$. This means that $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ is mainly contributed by $E_{\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{d}}$ when $C_{V_{\mathrm{o}\gamma }{H}_2}$ less than about 10¹⁴ cm⁻³ and $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ is affected by $V_{\mathrm{o}\gamma }{H}_2$ over about 10¹⁵ cm⁻³. $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ at 10¹⁶ cm⁻³ of $C_{V_{\mathrm{o}\gamma }{H}_2}$ is about 1.7 times as high as $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$at 10¹⁴ cm⁻³ of $C_{V_{\mathrm{o}\gamma }{H}_2}$. This means that when the concentration of $V_{\mathrm{o}\gamma }{H}_2$ is lower than that of about 10¹⁴ cm⁻³, $V_{\mathrm{o}\gamma }{H}_2$ has almost no influence on the TID effect, while when the concentration of $V_{\mathrm{o}\gamma }{H}_2$ is higher than 10¹⁵ cm⁻³, $V_{\mathrm{o}\gamma }{H}_2$ has a more obvious influence on the TID effect. The results show that the irradiation resistance of the device can be improved by controlling the concentration of $V_{\mathrm{o}\gamma }{H}_2$ below 10¹⁴ cm⁻³ when fabricating the oxide layer of the MOS device. Although the quantitative relationship between the density of $V_{\mathrm{o}\gamma }{H}_2$ and $E_{{\mathrm{S}\mathrm{i}/\mathrm{S}\mathrm{i}\mathrm{O}}_2}$ cannot be given in current experiments, it has important guiding significance for future experimental development and device anti-radiation design.

FIGURE 6

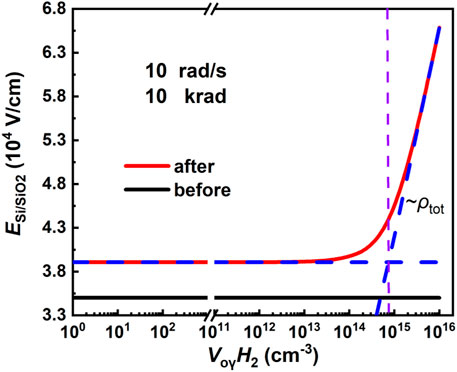
FIGURE 6. Electric fields at the Si/SiO₂ interface with increasing the density of $V_{\mathrm{o}\gamma }{H}_2$ under the TID of 10 krad with the dose rate of 10 rad/s at 300 K.

Conclusion

In summary, $V_{\mathrm{o}\gamma }^{+}$ is the main component of the oxide charged defects, and the contribution of $V_{\mathrm{o}\gamma }{H}_2$ is crucial, high concentration of $V_{\mathrm{o}\gamma }{H}_2$ can intensify the TID effect of MOS devices. The $V_{\mathrm{o}\gamma }{H}_2$ can directly promote the formation of $V_{\mathrm{o}\gamma }^{+}$, and $V_{\mathrm{o}\gamma }{H}_2$ first promotes the formation of $V_{\mathrm{o}\gamma }H$, then indirectly promotes the formation of $V_{\mathrm{o}\gamma }{H}^{+}$. $V_{\mathrm{o}\gamma }{H}_2$with concentration higher than 10¹⁴ cm⁻³ can enhance the negative TID effect. This finding provides a new idea that controlling $V_{\mathrm{o}\gamma }{H}_2$ in the oxide layer with concentration below 10¹⁴ cm⁻³ are more conducive to the design of anti-irradiation to the TID effect.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

GL: Methodology, Software, Data Curation, Formal analysis, Writing—Original Draft. JL: Methodology, Formal analysis, Software, Writing—Review and; Editing. QZ: Writing—Review and; Editing. YL: Formal analysis, Writing—Review and; Editing, Funding acquisition.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 11975018), the National MCF Energy R&D Program (Grant No. 2018YEF0308100), and the Outstanding member of Youth Innovation Promotion Association CAS (Grant No. Y202087). Some of the calculations were performed at the Center for Computational Science of CASHIPS, the ScGrid of Supercomputing Center, and the Computer Network Information Center of the Chinese Academy of Sciences. This research work was also supported by the Tianhe-2JK computing time award of the Beijing Computational Science Research Center (CSRC).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Benton, E. R., and Benton, E. V. (2001). Space radiation dosimetry in low-Earth orbit and beyond. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 184, 255–294. doi:10.1016/s0168-583x(01)00748-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Blöchl, P. E. (2000). First-principles calculations of defects in oxygen-deficient silica exposed to hydrogen. Phys. Rev. B 62, 6158–6179. doi:10.1103/physrevb.62.6158

CrossRef Full Text | Google Scholar

Bunson, P. E., Ventra, M. D., Pantelides, S. T., Fleetwood, D. M., and Schrimpf, R. D. (2000). Hydrogen-related defects in irradiated SiO₂. IEEE Trans. Nucl. Sci. 47, 2289–2296. doi:10.1109/23.903767

CrossRef Full Text | Google Scholar

Conley, J. F., and Lenahan, P. M. (1993). Room temperature reactions involving silicon dangling bond centers and molecular hydrogen in amorphous SiO₂ thin films on silicon. Appl. Phys. Lett. 62, 40–42. doi:10.1063/1.108812

CrossRef Full Text | Google Scholar

Devine, R. A. B., Mathiot, D., Warren, W. L., Fleetwood, D. M., and Aspar, B. (1993). Point defect generation during high temperature annealing of the Si-SiO₂ interface. Appl. Phys. Lett. 63, 2926–2928. doi:10.1063/1.110275

CrossRef Full Text | Google Scholar

Esqueda, I. S., Barnaby, H. J., and Adell, P. C. (2012). Modeling the effects of hydrogen on the mechanisms of dose rate sensitivity. IEEE Trans. Nucl. Sci. 59, 701–706. doi:10.1109/tns.2012.2195201

CrossRef Full Text | Google Scholar

Esqueda, I. S., Barnaby, H. J., Adell, P. C., Rax, B. G., Hjalmarson, H. P., McLain, M. L., et al. (2011). Modeling low dose rate effects in shallow trench isolation oxides. IEEE Trans. Nucl. Sci. 58, 2945–2952. doi:10.1109/tns.2011.2168569

CrossRef Full Text | Google Scholar

Hughart, D. R., Schrimpf, R. D., Fleeteood, D. M., Rowsey, N. L., Law, M. E., Tuttle, B. R., et al. (2012). The effects of proton-defect interactions on radiation-induced interface-trap formation and annealing. IEEE Trans. Nucl. Sci. 59, 3087–3092. doi:10.1109/tns.2012.2220982

CrossRef Full Text | Google Scholar

Hughart, D. R., Schrimpf, R. D., Fleetwood, D. M., Chen, X. J., Barnaby, H. J., Holbert, K. E., et al. (2009). The effects of aging and hydrogen on the radiation response of gated lateral PNP bipolar transistors. IEEE Trans. Nucl. Sci. 56, 3361–3366. doi:10.1109/tns.2009.2034151

CrossRef Full Text | Google Scholar

Hughart, D. R., Schrimpf, R. D., Fleetwood, D. M., Tuttle, B. R., and Pantelides, S. T. (2011). Mechanisms of interface trap buildup and annealing during elevated temperature irradiation. IEEE Trans. Nucl. Sci. 58, 2930–2936. doi:10.1109/tns.2011.2171364

CrossRef Full Text | Google Scholar

Hughes, H. L., and Giroux, R. R. (1964). Space radiation affects MOSFET’s. Electronics 37, 58–60.

Google Scholar

Hughes, H. L. (1965). Radiation effects on evacuated and gas encapsulated commercially available silicon planar transistors. Bull. Am. Phys. Soc. 9, 655.

Google Scholar

Hughes, H. L. (1965). Surface effects of space radiation on silicon devices. IEEE Trans. Nucl. Sci. 12, 53–63. doi:10.1109/tns.1965.4323924

CrossRef Full Text | Google Scholar

Jafari, H., Feghhi, S. A. H., and Boorboor, S. (2015). The effect of interface trapped charge on threshold voltage shift estimation for gamma irradiated MOS device. Radiat. Meas. 73, 69–77. doi:10.1016/j.radmeas.2014.12.008

CrossRef Full Text | Google Scholar

Kooi, E. (1965). Influence of X-ray irradiations on the charge distribution of metal-oxide-silicon structures. Philips Res. Rept. 20, 306.

Google Scholar

Lenahan, P. M., and Conley, J. F. (1998). What can electron paramagnetic resonance tell us about the Si/SiO2 system. J. Vac. Sci. Technol. B 16, 2134–2153. doi:10.1116/1.590301

CrossRef Full Text | Google Scholar

Lenahan, P. M., and Dressendorfer, P. V. (1984). Hole traps and trivalent silicon centers in metal/oxide/silicon devices. J. Appl. Phys. 55, 3495–3499. doi:10.1063/1.332937

CrossRef Full Text | Google Scholar

Lu, Z. Y., Nicklaw, C. J., Fleetwood, D. M., Schrimpf, R. D., and Pantelides, S. T. (2002). Structure, properties, and dynamics of oxygen vacancies in amorphous SiO₂. Phys. Rev. Lett. 89, 285505. doi:10.1103/physrevlett.89.285505

PubMed Abstract | CrossRef Full Text | Google Scholar

Oldham, T. R. (2000). Ionizing radiation effects in MOS oxides. World Scientific Programming. Singapore.

Google Scholar

Patrick, E., Rowsey, N., and Law, M. E. (2015). Total dose radiation damage: A simulation framework. IEEE Trans. Nucl. Sci. 62, 1650–1657. doi:10.1109/tns.2015.2425226

CrossRef Full Text | Google Scholar

Rowsey, N. L., Law, M. E., Schrimpf, R. D., Fleetwood, D. M., Tuttle, B. R., and Pantelides, S. T. (2011). A quantitative model for ELDRS and H₂ degradation effects in irradiated oxides based on first principles calculations. IEEE Trans. Nucl. Sci. 58, 2937–2944. doi:10.1109/tns.2011.2169458

CrossRef Full Text | Google Scholar

Rowsey, N. L., Law, M. E., Schrimpf, R. D., Fleetwood, D. M., Tuttle, B. R., and Pantelides, S. T. (2011). Radiation-induced oxide charge in low- and high-H₂ environments. IEEE Trans. Nucl. Sci. 59, 51–53. doi:10.1109/TNS.2012.2183889

CrossRef Full Text | Google Scholar

Rowsey, N. L., Law, M. E., Schrimpf, R. D., Fleetwood, D. M., Tuttle, B. R., and Pantelides, S. T. (2012). Radiation-induced oxide charge in low- and high-H₂ environments. IEEE Trans. Nucl. Sci. 59, 755–759. doi:10.1109/tns.2012.2183889

CrossRef Full Text | Google Scholar

Shaneyfelt, M. R., Fleetwood, D. M., and Hughes, K. L. (1991). Charge yield for cobalt-60 and 10-keV X-ray irradiations of MOS devices. IEEE Trans. Nucl. Sci. 38, 1187–1194. doi:10.1109/23.124092

CrossRef Full Text | Google Scholar

Sharov, F. V., Moxim, S. J., Haase, G. S., Hughart, D. R., McKay, C. G., and Lenahan, P. M. (2022). Probing the atomic scale mechanisms of time dependent dielectric breakdown in Si/SiO₂ MOSFETs. IEEE Trans. Device Mate. Reliab. 22, 322–331. doi:10.1109/TDMR.2022.3186232

CrossRef Full Text | Google Scholar

Tuttle, B. R., Hughart, D. R., Schrimpf, R. D., Fleetwood, D. M., and Pantelides, S. T. (2010). Defect interactions of H₂ in SiO₂: Implications for ELDRS and latent interface trap buildup. IEEE Trans. Nucl. Sci. 57, 3046–3053. doi:10.1109/TNS.2010.2086076

CrossRef Full Text | Google Scholar

Walle, C. G. V., and Tuttle, B. R. (2000). Microscopic theory of hydrogen in silicon devices. IEEE Trans. Electron Devices 47, 1779–1786. doi:10.1109/16.870547

CrossRef Full Text | Google Scholar

Weeks, R. A. (1963). Paramagnetic spectra of E₀₂ centers in crystalline quartz. Phys. Rev. 130, 570–576. doi:10.1103/physrev.130.570

CrossRef Full Text | Google Scholar

Whitbeck, M. (1991). React - Program to solve kinetic equations for chemical systems. Desert Research Institute.Reno, Nevada.

Google Scholar

Xu, J. J., Ma, Z. C., Li, H. L., Song, Y., Zhang, L. B., and Lu, B. Z. (2018). A multi-time-step finite element algorithm for 3-D simulation of coupled drift-diffusion reaction process in total ionizing dose effect. IEEE Trans. Semicond. Manufact. 31, 183–189. doi:10.1109/tsm.2017.2779058

CrossRef Full Text | Google Scholar

Zaininger, K. H. (1966). Electron bombardment of MOS capacitors. Appl. Phys. Lett. 8, 140–142. doi:10.1063/1.1754525

CrossRef Full Text | Google Scholar