Geometric and Electronic Properties of Monolayer HfX2 (X = S, Se, or Te): A First-Principles Calculation

The essential properties of monolayer HfX₂ (X = S, Se, or Te) are fully explored by first-principles calculations. The optimal lattice symmetries, sublattice buckling, electronic energy spectra, and density of states are systematically investigated. Monolayer HfS₂, HfSe_2, and HfTe_2, respectively, belong to middle-gap semiconductor, narrow-gap one and semimetal, with various energy dispersions. Moreover, the van Hove singularities (vHs) mainly arise from the band-edge states, and their special structures in the density of states strongly depend on their two or three-dimensional structures and the critical points in the energy-wave-vector space. The above-mentioned theoretical predictions are attributed to the multi-orbital hybridizations of [$d_{x^2-y^2}$, d_xy, d_yz, d_zx, $d_{z^2}$]–[s, p_x, p_y, p_z] in the Hf-X chemical bonds. The diversified physical phenomena clearly indicate a high potential for applications, as observed in MoS₂-related emergent materials ions.

Introduction

In recent decades, two-dimensional (2D) materials, including metals, semiconductors, and insulators, emerged as a focus of the scientific community because of a wide range of properties (Novoselov et al., 2016). They can often present essential differences of properties compared to their bulk phase (Kolobov, 2016). Since graphene was isolated from graphite in 2004, it has become an interesting and unique material, which is a gapless semiconductor (Balandin et al., 2008; Castro Neto et al., 2009; Das et al., 2015; Novoselov et al., 2016). Graphene exhibits noticeably essential properties, such as quantum Hall effect (Ma et al., 2009; Zhang et al., 2011), magnetic quantization (Guinea et al., 2006; Huang et al., 2014; Lin et al., 2015) and devoured optical selection (Chung et al., 2011). In order to extend the applications, 2D materials based on graphene have been investigated and offer a significant number of potential candidates (Fiori et al., 2014; Das et al., 2015; Kim et al., 2015; Novoselov et al., 2016; Zhou et al., 2018). Among these materials, 2D transition metal dichalcogenides (2D-TMDs) recently covered a number of applications in optical and electronic devices (Lebègue et al., 2013; Kaul, 2014; McDonnell and Wallace, 2016; Novoselov et al., 2016; Zhou et al., 2018). Although the bulk of TMDs that have been constructed and explored (Kolobov, 2016) show various properties, the electronic properties of layered TMDs are dominated by quantum confinement. It should be noted that the geometry and the electron count play an essential role in their electronic properties (Kolobov, 2016).

HfX₂ (X = S, Se, or Te) is a class in the group IV chalcogenides of the 2D-TMDs family whose general properties were reported in previous studies (Hussain Reshak and Auluck, 2005; Jiang, 2011; Abdulsalam and Joubert, 2016; Toh et al., 2016; Cheng et al., 2018; Salavati, 2018). Experimental investigations (Roubi and Carlone, 1988; Aretouli et al., 2015; Yue et al., 2015; Aminalragia-Giamini et al., 2016; Kanazawa et al., 2016; Yin et al., 2016; Mangelsen et al., 2017; Mleczko et al., 2017; Tsai et al., 2018) on Hf-based have been conducted in bulk and monolayer. HfS₂ is anticipated to have high electron mobility and sheet current density, proposing a candidate for electronic devices (Fiori et al., 2014; Zhang et al., 2014). Moreover, HfS₂ was experimentally investigated in a flake form as promising for use in transistors (Roubi and Carlone, 1988; Traving et al., 2001; Xu et al., 2015; Kanazawa et al., 2016; Mirabelli et al., 2016; Nie et al., 2017). Monolayer and bilayer HfSe₂, exhibit low lattice thermal conductivity, suggesting a great potential for thermoelectric devices (Aretouli et al., 2015; Kang et al., 2015; Yue et al., 2015; Mirabelli et al., 2016; Yin et al., 2016; Mleczko et al., 2017). Epitaxial thin films of HfTe₂ are grown in AlN substrates using angle-resolved photoemission spectroscopy provided that HfTe₂/AlN is an epitaxial topological semimetal (Aminalragia-Giamini et al., 2016).

Moreover, theoretical studies via first-principles calculations on HfS₂ show a slow increase in the bandgap with increasing tensile strain and thickness (Kreis et al., 2003; Wu et al., 2017; Salavati, 2018). Similar electronic characteristics are also observed in HfSe₂ (Yun et al., 2012; Setiyawati et al., 2019). In-depth investigations of the electronic band structures of HfS₂ and HfSe₂, reveal that sulfur and selenium atoms have a primary effect on the valence band, while the hafnium atoms play a dominant role in the conduction band (Zhao et al., 2017). The 1T phase structures are found in among the possible phases HfX₂ could exist in, predict that T phase is the most favorable phase (Hussain Reshak and Auluck, 2005; Jiang, 2011; Abdulsalam and Joubert, 2016; Ding et al., 2016; Wu et al., 2017; Zhao et al., 2017; Nakata et al., 2019; Yan et al., 2019). Previous studies show that monolayer 1T-HfTe₂ are metallic (Sun and Wang, 2017), while those of 1T-HfS₂ (Abdulsalam and Joubert, 2016; Wu et al., 2017; Zhao et al., 2017) and 1T-HfSe₂(Abdulsalam and Joubert, 2016; Ding et al., 2016; Zhao et al., 2017; Setiyawati et al., 2019; Yan et al., 2019) are indirect-gap semiconductors.

From a theoretical point of view, the first-principles calculations for layered materials pose challenges in investigating structural properties because of interactions between layers that are dominated by van der Waals force. Furthermore, the intra-layer chemical bonding (M-X bonding), which is mainly covalent in nature, predicts that the interactions play important roles in the structural features (Kumar and Ahluwalia, 2012). Even though many three-dimensional TMDs have been reported and numerous research papers published on 2D-TMDs, especially MoS₂ (Xiao et al., 2012; Zeng et al., 2012; He et al., 2014; Jiang et al., 2014; Zeng and Cui, 2015; Kang et al., 2016; Kolobov, 2016; Lin et al., 2016; Mirabelli et al., 2016; Hu et al., 2019), the available information on geometric and electronic properties of layered group IV chalcogenides, especially monolayer HfX₂, severely limited. While most numbers of the HfX₂ family that have been constructed to date show promise for applications, but the detailed characteristics might be lacking.

In this work, the geometric and electronic properties of layered HfX₂ (X = S, Se, or Te) are investigated in the T and H phases using first-principles calculations. The optimal lattice symmetries, sublattice buckling, electronic energy spectra, and the density of states are systematically calculated. HfS₂, HfSe₂, and HfTe₂ are respectively middle-gap semiconductor, narrow-gap one and semimetal, with various energy dispersions. The electronic properties strongly depends on the geometry and the multi-orbital hybridizations in the Hf-X bondings. Besides, the van Hove singularities mainly arise from the band-edges state. These physical phenomena clearly indicate a high potential for applications.

Method

The first-principles calculations based on the density functional theory (DFT) framework (Hohenberg and Kohn, 1964) are implemented in the Vienna Ab initio Simulation Package (VASP) (Kresse and Hafner, 1993) emerged as a dominant method in quantum mechanics simulation. In this work, the essential properties are investigated by DFT using VASP with the generalized gradient approximation (GGA) (Perdew et al., 1993; Perdew and Wang, 2018) of the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional (Ernzerhof and Scuseria, 1999) and projector-augmented-wave (PAW) potentials (Kresse and Joubert, 1999). The kinetic energy cutoff is set to 400 eV. A vacuum of 15 Å is added along the z-direction to avoid interactions between layers due to the periodic boundary condition. The structures are relaxed until the residual force is less than 0.001 eV/Å, and the self-consistent electronic convergence criterion is set at 10⁻⁶ eV. The Brillouin zone is sampled by 21 × 21 × 1 within the Gamma scheme for geometric optimizations and further calculations on electronic structures.

Results and Discussion

Optimized Crystal Structures

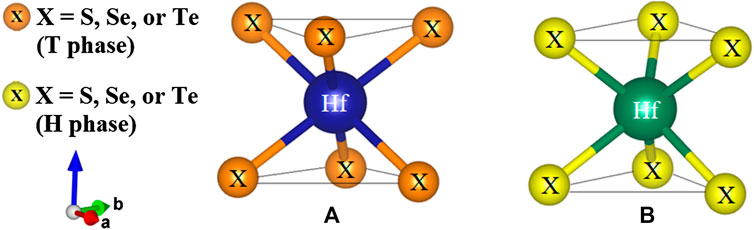
Two-dimensional TMDs are characterized by layered structures forming a hexagonal packing in which each layer has a sandwich-like structure of transition metal and chalcogen atoms (Kolobov, 2016). Metal atoms are six-fold coordinated, as shown in Figure 1. Depending on the relative position of the chalcogen atoms, the coordination can be octahedral or trigonal prismatic exhibiting various polymorphs. In their bulk phase, more than 16 polytypes have been defined (Kolobov, 2016; Zhou et al., 2018), which suggests versatile and flexible applications. In the two kinds of symmetry coordination, the two chalcogen planes form a stagger in the octahedral arrangement (Figure 1A), while a slab is directly stacked above each other in the trigonal prismatic arrangement (Figure 1B). As a result, the cleavage properties are caused by the lopsided coordination around the chalcogens, which is perpendicular to the hexagonal or trigonal symmetry axis. Furthermore, the dangling bonds are absent, which leads to the surface is very stable and nonreactive.

FIGURE 1

FIGURE 1. The local coordination of the two types (A) octahedral and (B) trigonal prismatic.

Monolayer TMDs have only two polymorphs, namely the T and H phases (Kolobov, 2016), depending on their hexagonal or trigonal prismatic coordination. In Figure 2, the crystal optimization for three compounds in the monolayer HfX₂ family is performed with the top (xy plane) and side (yz plane) views. Hafnium (Hf) and two chalcogen atoms (X) form the X-Hf-X layered unit per unit cell, where the Hf atom is sandwiched between two X atoms referred to as a monolayer. In other words, each layer consists of three atomic planes that include one hafnium plane and two chalcogen planes through ionic-covalent interaction (see side view). From the top view, the spatial position of the chalcogen atoms is additionally filled with the light yellow triangles that show the different stacking in the two forms. The structural arrangements are constructed in the T and H phases with the period layer and trigonal symmetry being formulated by the octahedrally-coordinated stacking.

FIGURE 2

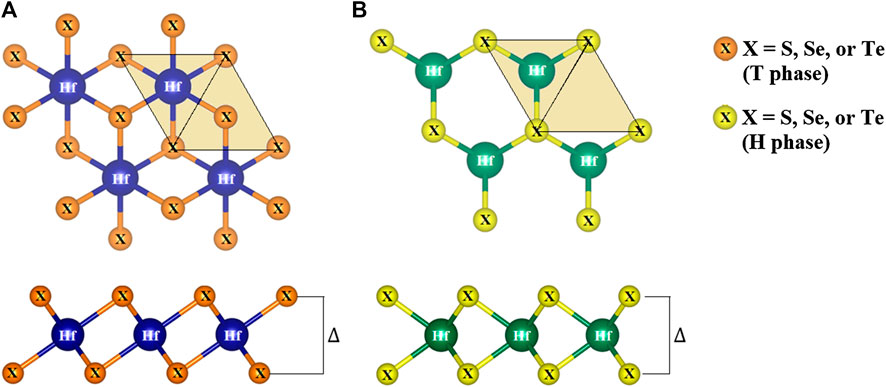
FIGURE 2. The top (xy plane) and side (yz plane) views of HfX₂ (X = S, Se, or Te) in the (A) T phase and (B) H phase.

The formation energy is calculated using Eq. 1

$E_f=E_{tot}-n_{Hf}{\mu }_{Hf}-n_X{\mu }_X(1)$

where $E_f$ is the formation energy; $E_{tot}$ is the total energy of monolayer HfX₂ (see in Table 1); $n_{Hf}$ and $n_X$ are, respectively, the number of atoms of hafnium and chalcogen atoms per unit cell; ${\mu }_{Hf}$ and ${\mu }_X$ are, respectively, the chemical potential of hafnium and chalcogen atoms in their bulk phases. As shown in Table 1 and Figure 3, the formation energy of the T phase is slightly smaller than that of the H phase; this indicates that the T phase structures are stable, while the H phase structures are metastable. This finding is in good agreement with experimental studies (Roubi and Carlone, 1988; Xu et al., 2015; Yue et al., 2015; Aminalragia-Giamini et al., 2016; Kanazawa et al., 2016; Yin et al., 2016; Mleczko et al., 2017; Tsai et al., 2018; Nakata et al., 2019) that reveal most monolayer HfX₂ exist in the T phase. To give further information, we have calculated the formation energy of monolayer MoS₂ in both T and H phases (shown in Table 1). In contrast to our materials, the total and formation energies in the T phase are larger than the H phase shows that the H phase is probably more stable. In addition, all formation energies of both materials are negative indicating the probability to construct them experimentally.

TABLE 1

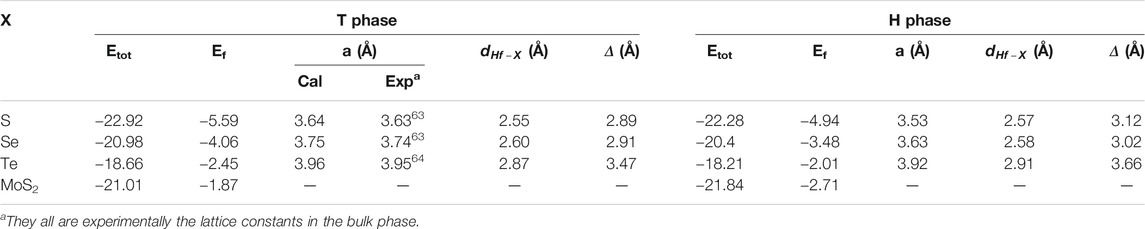
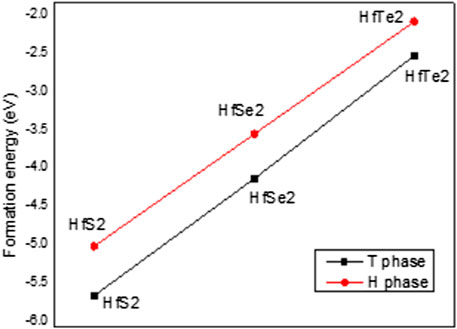
TABLE 1. Total energy (E_tot, eV), formation energy (E_f, eV), the lattice constant (a, Å), chemical bonding between hafnium and chalcogen atoms ($d_{Hf-X}$, Å), buckling ($\Delta$, Å) of monolayer HfX₂ in the T and H phases.

FIGURE 3

FIGURE 3. Formation energy of HfX₂ in the T (black line) and H (red line) phases.

The calculated lattice constant, bond length, and buckling of monolayer T and H phases are also shown in Table 1. As shown in this table, the lattice constants of HfS₂, HfSe₂, and HfTe₂ are, respectively, 3.64, 3.75, 3.96 $\mathrm{Å}$ in the T phase, and 3.55, 3.63, 3.92 $\mathrm{Å}$in the H phase. These parameters in the T phase are lightly larger than those of the H phase. Compared to the experimental lattice constants in previous studies (Greenaway and Nitsche, 1965; Bayliss and Liang, 1982) which are listed in Table 1, the structure is changed from bulk to monolayer by adding the vacuum, the lattice constant is insignificantly change. The electronic configuration of Hf is 5d²6s², and that of the chalcogens S, Se, and Te are respectively 3s (Kolobov, 2016), 3p⁴, 4s²4p⁴, and 5s (Kolobov, 2016), 5p⁴. The formal charge of +4 and −2 can be respectively ascribed to the transition metal and chalcogens. To fully fill the valence shell, the relatively ionic Hf-X bond forces the four valence electrons of the Hafnium atom to transfer to the two chalcogen atoms. The bond lengths are, respectively, 2.55, 2.60, 2.87 $\mathrm{Å}$ in the T phase and 2.57, 2.58, 2.91 $\mathrm{Å}$ in the H phase for HfS₂, HfSe₂, and HfTe₂. With varying the chalcogen atoms going from sulfur to selenium and tellurium, respectively, there is a gradation of increasing bond lengths that anticipates the features of electronegativity and orbital radii. The chalcogen pure p-orbital takes part in forming these bonds and suggests that the lone-pair electrons (Kolobov, 2016) are located on the sp (Balandin et al., 2008)-hybridized orbitals. In addition, the d-orbital in hafnium plays an essential role in the energy band, which is discussed in the electronic properties section. Compared to graphene (Castro Neto et al., 2009), the distance between hafnium atoms is larger than that of carbon atoms; it is Hf-X interaction that suppresses the height fluctuation of hafnium atoms. The chalcogen-metal (Hf-X) bonds are mainly determined by both hafnium and chalcogen atoms.

Furthermore, monolayer HfX₂ exists in a bucked form ($\Delta$) (see Figure 2) of approximate 2.89, 2.91, and 3.47 $\mathrm{Å}$, respectively, for monolayer HfS₂, HfSe₂, and HfTe₂ in the T phase. With the H phase, for HfS₂, HfSe₂, and HfTe₂, these values are respectively 3.12, 3.02, and 3.66 $\mathrm{Å}$. The Hf-X interaction suppresses the height fluctuation of the hafnium atom in these monolayers. As a result, the buckling in monolayer HfX₂ is sharper than in silicene (Meng et al., 2013), which can be attributed to the sandwiched structure of these materials. Notice that the height fluctuations (buckling) are presented at equilibrium that provides the broad distribution of height displacement. This phenomenon predicts the phenomenological theories of thermal fluctuations in flexible membranes.

Electronic Properties

In the Brillouin zone, the electronic band structures have been calculated along with the high symmetry point Γ-M-K-Γ belonging to the hexagonal lattice. The system band gaps of monolayer HfX₂ with the T and H phases are shown in Table 2. Both HfS₂ and HfSe₂ are semi-conducting with each material exhibiting distinct properties. HfS₂ shows a middle-gap of 1.2 and 0.92 eV in the T and H phases, respectively. HfSe₂ with these phases remains semi-conducting and belongs to a narrow-gap of 0.86 and 0.4 eV, respectively. In contrast, HfTe₂ is semi-metallic. The values of approximately zero reveal it to be a gapless semimetal similar to graphene (Castro Neto et al., 2009). The experimental gaps of the monolayer T phase are also listed in Table 2. However, these values are smaller than the calculated band gaps, in which respectively exists a difference of approximate 0.6 and 0.3 eV for HfS₂ and HfSe₂. In this work, the band gaps are obtained from PBE functional, which notes that the approaches in calculating might cause the differences that are significant when comparing them to experimental values. Because most members of group IV (Ti, Zr, and Hf) TMDs are experimentally found in the T phase (Greenaway and Nitsche, 1965; Terashima and Imai, 1987), there is no recorded measurement for making a comparison for the H phase in this work.

TABLE 2

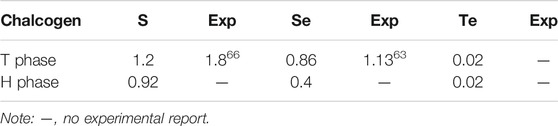
TABLE 2. The calculated band gap (E_g, eV) of monolayer HfX₂ with the T and H phases and experimental values of the bandgap in the T phase monolayer.

The system band energy spectra of monolayer HfX₂ are shown in Figure 4, which presents the atom dominances of hafnium and chalcogens. The left panel (Figures 4A–C) describes the system band of the T phase structures, and the right panel (Figures 4D–F) shows the system band of the H phase. All three materials share as a common feature that the valence band maximum (VBM) is located at Γ point (k = 0, 0, 0) and the conduction band minimum (CBM) is at M point (k = ½, 0, 0) of the high symmetry k-points in the T phase. While those of the H phase have a VBM between K and Γ point corresponding to the CBM is located between Γ and M point. The unoccupied conduction bands are asymmetric to the occupied valence bands about the Fermi level. Most energy bands have a strong dispersion relation, with the parabolic dispersion being exhibited in both the conduction and the valence bands. However, each material is predicted to have an unusual energy band. There are many distinguishing features between the T and H phases in the electronic band structures that are discussed below.

FIGURE 4

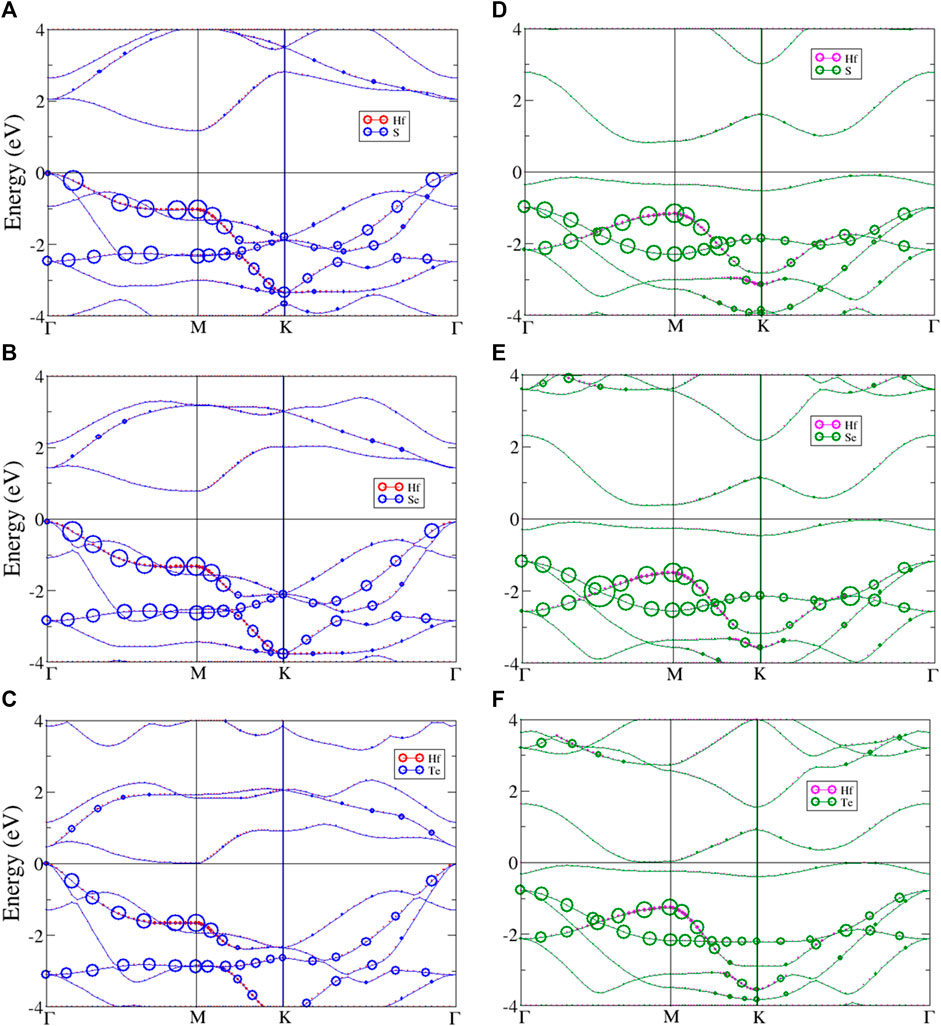
FIGURE 4. The band energy spectrum of monolayer (A) HfS₂, (B) HfSe₂, (C) HfTe₂ with T phase, and (D) HfS₂, (E) HfSe₂, (F) HfTe₂ with H phase. The red, magenta, blue, and green circles describe the atom dominant in the band for Hf and chalcogen atoms in T and H phase, respectively.

As previously mentioned, monolayer HfX₂ (X = S, Se, or Te) are constructed with two phases that reveal distinct properties. The electronic bands of the T phase with atom dominance are described in Figures 4A–C (left panel). The red and blue circles respectively represent the hafnium and chalcogen atoms. They all show an indirect bandgap with the direction of the gap shifted from Γ point to M point. The occupied hole band is strongly asymmetric to the unoccupied electron band. The low-lying valence bands exhibit valleys between Γ and M point, as well as K and Γ point. The low-lying valence bands also change into parabolic bands. The parabolic dispersions have band-edge states at M point belonging to saddle points, which results in van Hove singularities (vHs). In Figure 4A, the $\sigma$ and ${\sigma }^{\ast }$ bands (in the valence and conduction bands) of HfS₂ initiate from Γ point at −2.5, 0 and 2 eV, while the $\sigma$ and ${\sigma }^{\ast }$ bands of HfSe₂ are at −3, 0 and 1.5 eV (Figure 4B). The energy band of HfTe₂ reveals contrasting features compared to HfS₂ and HfSe₂, as shown in Figure 4C. A semi-metallic property of HfTe₂ has been shown, which is investigated by the pressure-dependence conductivity and Hall coefficient (Aminalragia-Giamini et al., 2016). Apart from the special valleys located in the low-lying valence band that is similar to HfS₂ and HfSe₂, there exist flat bands in the low-lying valence bands. There are $\sigma$ and ${\sigma }^{\ast }$ bands that initiate from Γ point at −3, 0, and 0.5 eV. The difference between HfTe₂ and both HfS₂ and HfSe₂ is that all of the VBMs and CBMs are nearly at the Fermi level, which presents a gapless material. With regard to atom dominance in bands, the chalcogen atoms in all structures dominate in valence band ranging from 0 to −4 eV, while the contribution of hafnium atoms is smaller than in this band. In contrast, hafnium contributes to the conduction band more than the valence band. In valence band, this atom dominates in bands of a scale of 0 to −2 eV. Both hafnium and chalcogens contribute to the whole band with ranges from −4 to 4 eV, but chalcogens show a sharper dominance compared to hafnium.

In order to compare with the T phase structures, the band energy spectra of the H phase are presented in Figures 4D–F (right panel). The green and magenta circles represent chalcogen and hafnium atoms. The occupied valence band and the unoccupied conduction band are asymmetric. Both HfS₂ and HfSe₂ still exhibit semiconducting with narrow-indirect gaps, but the direction is shifted from between K and Γ point to the point near M point. Similar to the T phase, HfTe₂ remains semimetal with the same bandgap value (see Table 2). All the H phase structures exist in approximate flat bands near the Fermi level while the degeneracy lies below it, this leads to additional valleys in the low-lying valence bands. In Figure 4D, two $\sigma$ bands of HfS₂ initiate from Γ point at -1 and -2 eV in the valence band, while the $\sigma$ and ${\sigma }^{\ast }$ bands of HfSe₂ and HfTe₂, respectively, are located at −1, −2.5, 3.5 eV and −0.8, −2.2, 3.2 eV. Furthermore, all materials in the H phase show the crossing dispersion in the valence band, which is between Γ and M point. The most important atom dominances are at low-lying valence bands, while those of the T phase is at the edges of the valence band. The chalcogen atoms also dominate in valence bands like in the T phase, but they contribute in a lower energy range from −1 to −2 eV. In the conduction band, the dominance of chalcogen atoms is almost absent, while hafnium exists in both the valence and conduction bands. Although all of the chalcogens control the valence bands, they the different contributions in each band. The tellurium atom in HfTe₂ has the smallest contribution, followed by Se and S.

In general, the band energy spectra exhibit a lot of asymmetric peaks and few symmetric ones due to the parabolic form of energy bands. A pair of asymmetric peaks exists near the Fermi level that defines the indirect energy gaps. The bandgap opening is associated with the quantum confinement effect. Although all three materials are members of the same chalcogen group, HfS₂, HfSe₂, and HfTe₂ are different in their low-lying peaks and degenerate with varying the stacking configuration between the two phases. Moreover, most van Hove singularities (vHs) come from the parabolic energy dispersions. The peaks near the Fermi level are found to arise from the band-edge states mainly. These peaks could be a signature feature unique to vHs.

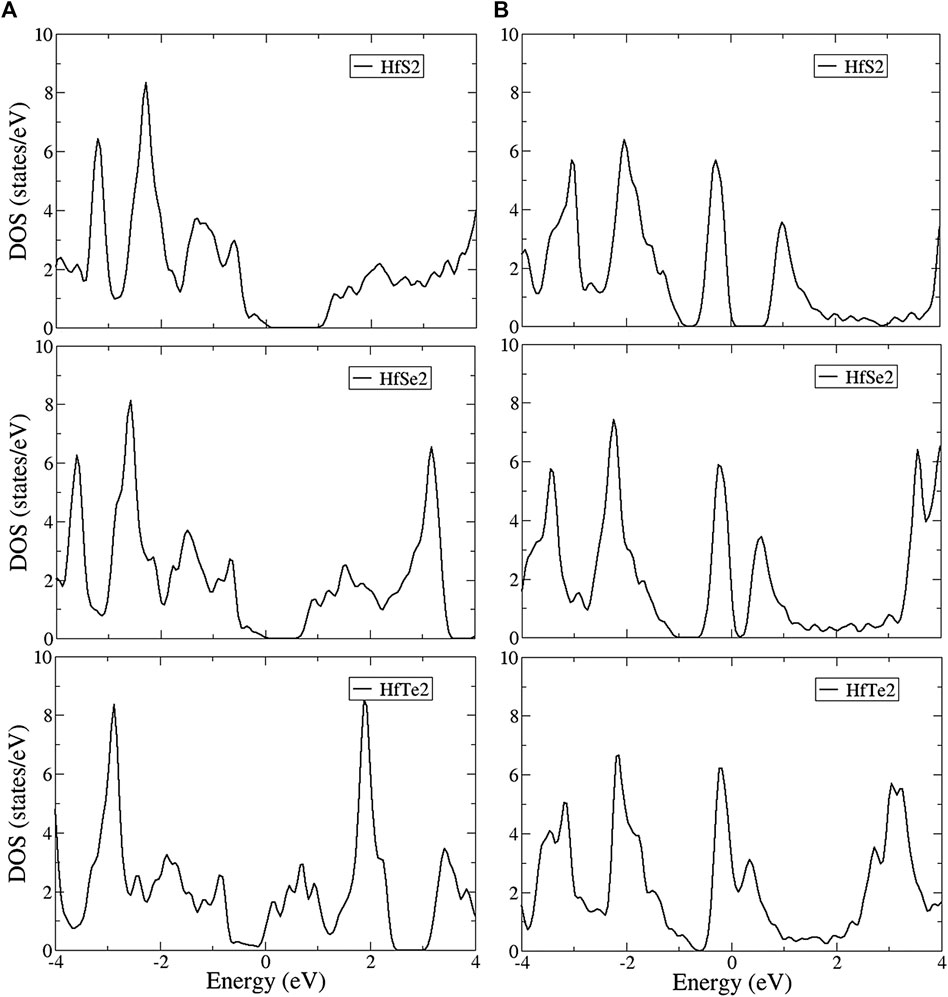
The density of states (DOS) is shown in Figure 5 for the T and H phases, which directly reflect the main features of the band structures. DOS is ranged from −4 to 4 eV and shows a pair of asymmetric peaks centered at the Fermi level, which characterizes the energy gap. The large energy difference between the valence and conduction peaks obviously demonstrates the asymmetry of the two bands. These structures originate from linear bands, parabolic bands near saddle points, and initial band-edge states of the parabolic bands. In the T phase structures shown in Figure 5A, DOS exhibits a logarithmic divergence at middle energy and shoulder structures at deeper and higher energy. Partially flat energy is exhibited in the valence bands of all structures and in the conduction bands of HfSe₂ and HfTe₂, while shoulder structures evidently appear in the conduction band of HfS₂. Moreover, the low DOS at the Fermi level illustrates the low free carrier density. In contrast, a linear energy dependence near the Fermi level is shown in the H phase structures (Figure 5B). The DOS of the H phase is much larger than that of the T phase at the Fermi level, indicating a higher free carrier density. At deeper and higher energy, DOS reveals peaks, as well as divergent and shoulder structures. Notice that the peak and shoulder structures correspond to the 3p_z, 4p_z, 5p_z, and (3p_x,3p_y), (4p_x,4p_y), (5p_x,5p_y) of HfS₂, HfSe₂, and HfTe₂, respectively, dominating energy bands as indicated in the orbital-projected DOS.

FIGURE 5

FIGURE 5. The density of states (DOS) in the (A) T and (B) H phase of monolayer HfX₂.

To further verify the various chemical bondings and examine the curvature effect, the orbital-projected DOS could be used as described in Figures 6 and 7. The figures show the local density of states with multi-orbital hybridization in the T and H phases. They show that the main contributions are due to two orbitals of the hafnium and two orbitals of the chalcogens, corresponding to the s, d orbitals of hafnium, and the s, p orbitals of chalcogens. With the T phase structures, the local density of states with multi-hybridization is shown in Figure 6, presenting the dominance of the multi-orbital hafnium and chalcogen atoms. At high energy, hafnium atoms are dominated by 5$d_{z^2}$ and 5$d_{x^2-y^2}$ orbitals, as clearly indicated in Figure 6A. But for low energy, DOS depends on the bondings of (3p_x,3p_y), (4p_x,4p_y) and (5p_x,5p_y) of HfS₂, HfSe₂ and HfTe₂, respectively (Figure 6B).

FIGURE 6

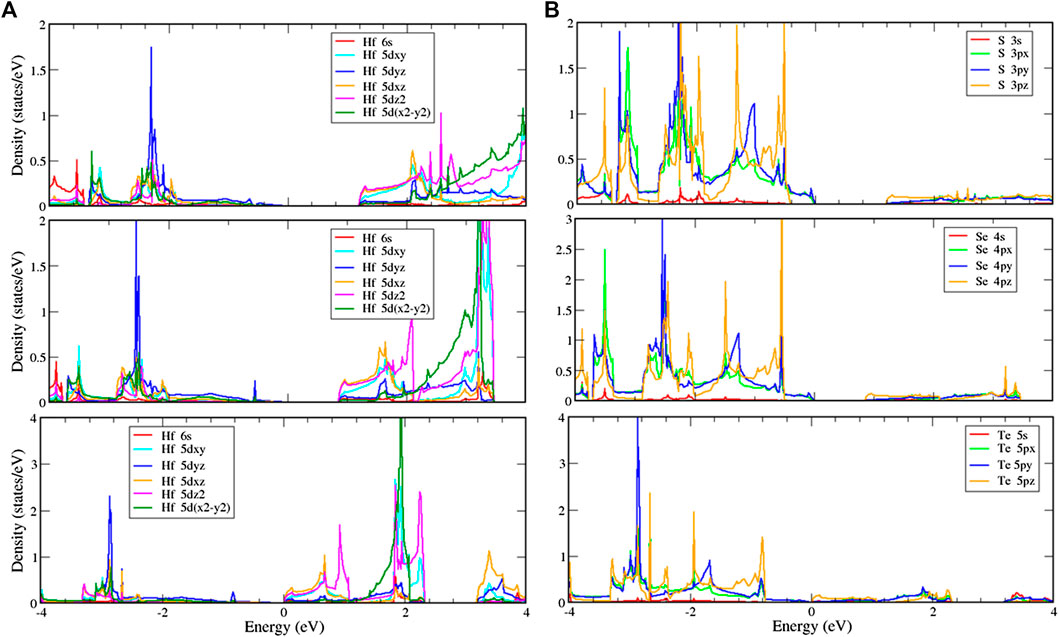
FIGURE 6. Local density of states (LDOS) of (A) hafnium and (B) chalcogen atoms with multi-orbital hybridization in the T phase.

Similar to the T phase, the H phase structures are shown in Figure 7 and indicate that the d-orbitals of hafnium and the p-orbitals of chalcogens, respectively, play essential roles in the conduction and valence bands. The 5$d_{z^2}$, 5d_xy, and 5$d_{x^2-y^2}$ orbitals dominate at high energy but exist with different features in each material (Figure 7A). HfS₂ is dominated by 5$d_{z^2}$ at high energy, while 5$d_{x^2-y^2}$mainly dominates in the conduction band of HfSe₂. HfTe₂ shows the dominance of all 5$d_{z^2}$, 5d_xy, and 5$d_{x^2-y^2}$ orbitals. With chalcogen atoms (Figure 7B), 3p_z, 4p_z, and 5p_z respectively, reveal a prominent dominance at low energy near the Fermi level and lower energy in HfS₂, HfSe₂, and HfTe₂. At middle energy in the valence band, they are respectively based on the (3p_x,3p_y), (4p_x,4p_y), and (5p_x,5p_y) orbitals. In summary, their contributions are comparable to each other in that the feature-rich energy bands are mainly determined by the d and p orbitals. There exist strong hybridizations of 5$d_{z^2}$, 5$d_{x^2-y^2}$ Hf-orbitals and (3p_x, 3p_y, 3p_z), (4p_x, 4p_y, 4p_z), (5p_x, 5p_y, 5p_z) chalcogen-orbitals. In addition, the p-orbitals of the chalcogens make significant contributions to the $\sigma$ bonding. These orbitals are evident for the multi-orbital hybridization in these materials.

FIGURE 7

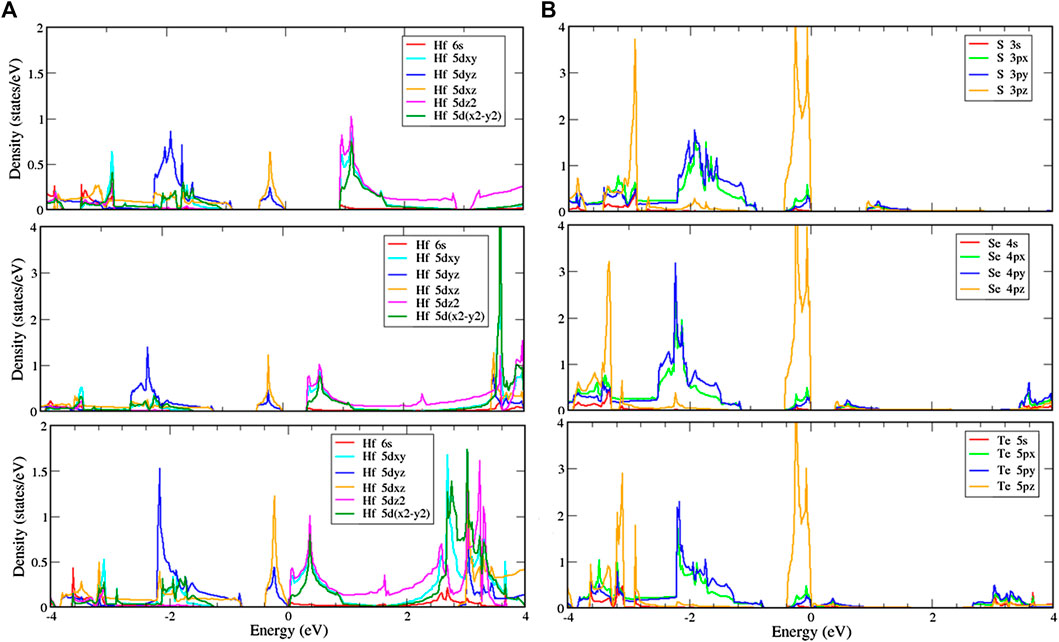
FIGURE 7. Local density of states (LDOS) of (A) hafnium and (B) chalcogen atoms with multi-orbital hybridization in the H phase.

Conclusion

The first-principles calculations are used to investigate the geometric and electronic properties of monolayer HfX₂ (X = S, Se, or Te). Our calculated band structures in the T and H phases can modulate their properties. All structures exist with a sharp buckle that shows height fluctuations at equilibrium. The d-orbitals and p-orbitals of the hafnium and chalcogen atoms, respectively, take part in the chemical bondings of Hf-X. As reported, both HfS₂ and HfSe₂ are semiconductors with an indirect middle-gap and narrow-gap, respectively, while HfTe₂ is a gapless semimetal. The energy gap trend suggests that the atomic species play a dominant role. A lot of asymmetric peaks and few symmetric ones due to the parabolic form are shown in the energy bands and density of states. The van Hove singularities mainly arise from the band-edge states in the DOS. The logarithmic divergence at middle energy and shoulder structures at lower and higher energy are exhibited in the DOS corresponding to the 3p_z, 4p_z, 5p_z and (3p_x,3p_y), (4p_x,4p_y), (5p_x,5p_y) of HfS₂, HfSe₂ and HfTe₂, respectively. In addition, these orbitals demonstrate multi-orbital hybridizations, as shown in the orbital-projected DOS. In summary, the electronic properties of the monolayer HfX₂ family are mainly determined by their geometry, chemical bondings, and the orbitals hybridization.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

TH: Conceptualization, Model building, Methodology, Software, Validation, Writing- Reviewing and Editing. DN: Model building, Data curation, Visualization, Original draft preparation. TN: Model building, Data curation, Visualization, Original draft. VD: Model building, Data curation, Visualization, Original draft preparation. NH: Model building, Data curation, Visualization, Original draft preparation. HP: Conceptualization, Model building, Methodology, Software, Validation, Reviewing and Editing, Supervision.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was financially supported by the Hierarchical Green Energy Materials (Hi-GEM) Research Center, from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) and the Ministry of Science and Technology (MOST 108–3017-F-006–003) in Taiwan.

References

Abdulsalam, M., and Joubert, D. P. (2016). Optical spectrum and excitons in bulk and monolayer MX₂ (M=Zr, Hf; X=S, Se). Phys. Status Solidi B 253 (4), 705–711. doi:10.1002/pssb.201552584

CrossRef Full Text | Google Scholar

Aminalragia-Giamini, S., Marquez-Velasco, J., Tsipas, P., Tsoutsou, D., Renaud, G., and Dimoulas, A. (2016). Molecular beam epitaxy of thin HfTe₂ semimetal films. 2D Mater. 4 (1). doi:10.1088/2053-1583/4/1/015001

CrossRef Full Text | Google Scholar

Aretouli, K. E., Tsipas, P., Tsoutsou, D., Marquez-Velasco, J., Xenogiannopoulou, E., Giamini, S. A., et al. (2015). Two-dimensional semiconductor HfSe₂ and MoSe₂/HfSe₂ van der Waals heterostructures by molecular beam epitaxy. Appl. Phys. Lett. 106 (14), 143105. doi:10.1063/1.4917422

CrossRef Full Text | Google Scholar

Balandin, A. A., Ghosh, S., Bao, W., Calizo, I., Teweldebrhan, D., Miao, F., et al. (2008). Superior thermal conductivity of single-layer graphene. Nano Lett. 8 (3), 902–907. doi:10.1021/nl0731872

CrossRef Full Text | Google Scholar

Bayliss, S. C., and Liang, W. Y. (1982). Symmetry dependence of optical transitions in group 4B transition metal dichalcogenides. J. Phys. C Solid State Phys. 15 (6), 1283–1296. doi:10.1088/0022-3719/15/6/021

CrossRef Full Text | Google Scholar

Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S., and Geim, A. K. (2009). The electronic properties of graphene. Rev. Mod. Phys. 81 (1), 109–162. doi:10.1103/revmodphys.81.109

CrossRef Full Text | Google Scholar

Cheng, C., Sun, J.-T., Chen, X.-R., and Meng, S. (2018). Hidden spin polarization in the 1 T -phase layered transition-metal dichalcogenides MX 2 ( M = Zr, Hf; X = S, Se, Te). Sci. Bull. 63 (2), 85–91. doi:10.1016/j.scib.2017.12.003

CrossRef Full Text | Google Scholar

Chung, H. C., Lee, M. H., Chang, C. P., and Lin, M. F. (2011). Exploration of edge-dependent optical selection rules for graphene nanoribbons. Optic Express 19 (23), 23350–23363. doi:10.1364/oe.19.023350

CrossRef Full Text | Google Scholar

Das, S., Robinson, J. A., Dubey, M., Terrones, H., and Terrones, M. (2015). Beyond graphene: progress in novel two-dimensional materials and van der Waals solids. Annu. Rev. Mater. Res. 45 (1), 1–27. doi:10.1146/annurev-matsci-070214-021034

CrossRef Full Text | Google Scholar

Ding, G., Gao, G. Y., Huang, Z., Zhang, W., and Yao, K. (2016). Thermoelectric properties of monolayer MSe₂ (M = Zr, Hf): low lattice thermal conductivity and a promising figure of merit. Nanotechnology 27 (37), 375703. doi:10.1088/0957-4484/27/37/375703

CrossRef Full Text | Google Scholar

Ernzerhof, M., and Scuseria, G. E. (1999). Assessment of the Perdew-Burke-Ernzerhof exchange-correlation functional. J. Chem. Phys. 110 (11), 5029–5036. doi:10.1063/1.478401

CrossRef Full Text | Google Scholar

Fiori, G., Bonaccorso, F., Iannaccone, G., Palacios, T., Neumaier, D., Seabaugh, A., et al. (2014). Electronics based on two-dimensional materials. Nat. Nanotechnol. 9 (10), 768–779. doi:10.1038/nnano.2014.207

CrossRef Full Text | Google Scholar

Greenaway, D. L., and Nitsche, R. (1965). Preparation and optical properties of group IV-VI2 chalcogenides having the CdI2 structure. J. Phys. Chem. Solid. 26 (9), 1445–1458. doi:10.1016/0022-3697(65)90043-0

CrossRef Full Text | Google Scholar

Guinea, F., Castro Neto, A. H., and Peres, N. M. R. (2006). Electronic states and Landau levels in graphene stacks. Phys. Rev. B 73 (24), 245426. doi:10.1103/physrevb.73.245426

CrossRef Full Text | Google Scholar

He, J., Hummer, K., and Franchini, C. (2014). Stacking effects on the electronic and optical properties of bilayer transition metal dichalcogenides MoS₂, MoSe₂, WS₂, and WSe₂. Phys. Rev. B 89 (7), 075409. doi:10.1103/physrevb.89.075409

CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136 (3B), B864–B871. doi:10.1103/physrev.136.b864

CrossRef Full Text | Google Scholar

Hu, J. Q., Shi, X. H., Wu, S. Q., Ho, K. M., and Zhu, Z. Z. (2019). Dependence of electronic and optical properties of MoS₂ multilayers on the interlayer coupling and Van Hove singularity. Nanoscale Res Lett. 14 (1), 288. doi:10.1186/s11671-019-3105-9

CrossRef Full Text | Google Scholar

Huang, Y. K., Chen, S. C., Ho, Y. H., Lin, C. Y., and Lin, M. F. (2014). Feature-rich magnetic quantization in sliding bilayer graphenes. Sci. Rep. 4, 7509. doi:10.1038/srep07509

CrossRef Full Text | Google Scholar

Hussain Reshak, A., and Auluck, S. (2005). Ab initio calculations of the electronic and optical properties of 1T-HfX₂ compounds. Phys. B Condens. Matter. 363 (1–4), 25–31. doi:10.1016/j.physb.2005.02.030

CrossRef Full Text | Google Scholar

Jiang, T., Liu, H., Huang, D., Zhang, S., Li, Y., Gong, X., et al. (2014). Valley and band structure engineering of folded MoS₂ bilayers. Nat. Nanotechnol. 9 (10), 825–829. doi:10.1038/nnano.2014.176

CrossRef Full Text | Google Scholar

Jiang, H. (2011). Structural and electronic properties of ZrX₂ and HfX₂ (X = S and Se) from first principles calculations. J. Chem. Phys. 134 (20), 204705. doi:10.1063/1.3594205

CrossRef Full Text | Google Scholar

Kanazawa, T., Amemiya, T., Ishikawa, A., Upadhyaya, V., Tsuruta, K., Tanaka, T., et al. (2016). Few-layer HfS₂ transistors. Sci. Rep. 6, 22277. doi:10.1038/srep22277

CrossRef Full Text | Google Scholar

Kang, M., Rathi, S., Lee, I., Lim, D., Wang, J., Li, L., et al. (2015). Electrical characterization of multilayer HfSe₂ field-effect transistors on SiO₂ substrate. Appl. Phys. Lett. 106 (14), 143108. doi:10.1063/1.4917458

CrossRef Full Text | Google Scholar

Kang, J., Zhang, L., and Wei, S.-H. (2016). A unified understanding of the thickness-dependent bandgap transition in hexagonal two-dimensional semiconductors. J. Phys. Chem. Lett. 7 (4), 597–602. doi:10.1021/acs.jpclett.5b02687

CrossRef Full Text | Google Scholar

Kaul, A. B. (2014). Two-dimensional layered materials: structure, properties, and prospects for device applications. J. Mater. Res. 29 (3), 348–361. doi:10.1557/jmr.2014.6

CrossRef Full Text | Google Scholar

Kim, S. J., Choi, K., Lee, B., Kim, Y., and Hong, B. H. (2015). Materials for flexible, stretchable electronics: graphene and 2D materials. Annu. Rev. Mater. Res. 45 (1), 63–84. doi:10.1146/annurev-matsci-070214-020901

CrossRef Full Text | Google Scholar

Kolobov, T. (2016). Two-dimensional transition-metal Dichalcogenides. Singapore: Springer.

Google Scholar

Kreis, C., Werth, S., Adelung, R., Kipp, L., Skibowski, M., Krasovskii, E. E., et al. (2003). Valence and conduction band states of HfS₂: from bulk to a single layer. Phys. Rev. B 68 (23), 235331. doi:10.1103/physrevb.68.235331

CrossRef Full Text | Google Scholar

Kresse, G., and Hafner, J. (1993). Ab initiomolecular dynamics for liquid metals. Phys. Rev. B 47 (1), 558–561. doi:10.1103/physrevb.47.558

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59 (3), 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Kumar, A., and Ahluwalia, P. K. (2012). Electronic structure of transition metal dichalcogenides monolayers 1H-MX₂ (M = Mo, W; X = S, Se, Te) from ab-initio theory: new direct band gap semiconductors. Eur. Phys. J. B 85 (6), 186. doi:10.1140/epjb/e2012-30070-x

CrossRef Full Text | Google Scholar

Lebègue, S., Björkman, T., Klintenberg, M., Nieminen, R. M., and Eriksson, O. (2013). Two-dimensional materials from data filtering and ab initio calculations. Phys. Rev. X 3 (3), 031002. doi:10.1103/physrevx.3.031002

CrossRef Full Text | Google Scholar

Lin, C.-Y., Wu, J.-Y., Ou, Y.-J., Chiu, Y.-H., and Lin, M.-F. (2015). Magneto-electronic properties of multilayer graphenes. Phys. Chem. Chem. Phys. 17 (39), 26008–26035. doi:10.1039/c5cp05013hhttps://pubs.rsc.org/en/content/articlelanding/2015/CP/C5CP05013H#!divAbstract

CrossRef Full Text | Google Scholar

Lin, Y.-K., Chen, R.-S., Chou, T.-C., Lee, Y.-H., Chen, Y.-F., Chen, K.-H., et al. (2016). Thickness-dependent binding energy shift in few-layer MoS₂ grown by chemical vapor deposition. ACS Appl. Mater. Interfaces. 8 (34), 22637–22646. doi:10.1021/acsami.6b06615

CrossRef Full Text | Google Scholar

Ma, R., Sheng, L., Shen, R., Liu, M., and Sheng, D. N. (2009). Quantum Hall effect in bilayer graphene: disorder effect and quantum phase transition. Phys. Rev. B 80 (20), 205101. doi:10.1103/physrevb.80.205101

CrossRef Full Text | Google Scholar

Mangelsen, S., Naumov, P. G., Barkalov, O. I., Medvedev, S. A., Schnelle, W., Bobnar, M., et al. (2017). Large nonsaturating magnetoresistance and pressure-induced phase transition in the layered semimetal HfTe₂. Phys. Rev. B 96 (20), 205148. doi:10.1103/physrevb.96.205148

CrossRef Full Text | Google Scholar

McDonnell, S. J., and Wallace, R. M. (2016). Atomically-thin layered films for device applications based upon 2D TMDC materials. Thin Solid Films 616, 482–501. doi:10.1016/j.tsf.2016.08.068

CrossRef Full Text | Google Scholar

Meng, L., Wang, Y., Zhang, L., Du, S., Wu, R., Li, L., et al. (2013). Buckled silicene formation on Ir(111). Nano Lett. 13 (2), 685–690. doi:10.1021/nl304347w

CrossRef Full Text | Google Scholar

Mirabelli, G., McGeough, C., Schmidt, M., McCarthy, E. K., Monaghan, S., Povey, I. M., et al. (2016). Air sensitivity of MoS₂, MoSe₂, MoTe₂, HfS₂, and HfSe₂. J. Appl. Phys. 120 (12), 125102. doi:10.1063/1.4963290

CrossRef Full Text | Google Scholar

Mleczko, M. J., Zhang, C. F., Lee, H. R., Kuo, H. H., Magyari-Kope, B., Moore, R. G., et al. (2017). HfSe₂ and ZrSe₂: two-dimensional semiconductors with native high-κ oxides. Sci. Adv. 3 (8), 1700481. doi:10.1126/sciadv.1700481

CrossRef Full Text | Google Scholar

Nakata, Y., Sugawara, K., Chainani, A., Yamauchi, K., Nakayama, K., Souma, S., et al. (2019). Dimensionality reduction and band quantization induced by potassium intercalation in 1T−HfTe₂. Phys. Rev. Mater. 3 (7), 071001. doi:10.1103/physrevmaterials.3.071001

CrossRef Full Text | Google Scholar

Nie, X.-R., Sun, B.-Q., Zhu, H., Zhang, M., Zhao, D.-H., Chen, L., et al. (2017). Impact of metal contacts on the performance of multilayer HfS₂ field-effect transistors. ACS Appl. Mater. Interfaces. 9 (32), 26996–27003. doi:10.1021/acsami.7b06160

CrossRef Full Text | Google Scholar

Novoselov, K. S., Mishchenko, A., Carvalho, A., and Castro Neto, A. H. (2016). 2D materials and van der Waals heterostructures Science 353 (6298), 9439. doi:10.1126/science.aac9439

CrossRef Full Text | Google Scholar

Perdew, J. P., and Wang, Y. (2018). Erratum: accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 98 (7), 079904. doi:10.1103/physrevb.98.079904

CrossRef Full Text | Google Scholar

Perdew, J. P., Chevary, J. A., Vosko, S. H., Jackson, K. A., Pederson, M. R., Singh, D. J., et al. (1993). Erratum: atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 48 (7), 4978. doi:10.1103/physrevb.48.4978.2

CrossRef Full Text | Google Scholar

Roubi, L., and Carlone, C. (1988). Resonance Raman spectrum ofHfS₂ and ZrS₂. Phys. Rev. B 37 (12), 6808–6812. doi:10.1103/physrevb.37.6808

CrossRef Full Text | Google Scholar

Salavati, M. (2018). Electronic and mechanical responses of two-dimensional HfS₂, HfSe₂, ZrS₂, and ZrSe₂ from first-principles. Front. Struct. Civ. Eng. 13 (2), 486–494. doi:10.1007/s11709-018-0491-5

CrossRef Full Text | Google Scholar

Setiyawati, I., Chiang, K.-R., Ho, H.-M., and Tang, Y.-H. (2019). Distinct electronic and transport properties between 1T-HfSe₂ and 1T-PtSe₂. Chin. J. Phys. 62, 151–160. doi:10.1016/j.cjph.2019.09.029

CrossRef Full Text | Google Scholar

Sun, X., and Wang, Z. (2017). Ab initio study of adsorption and diffusion of lithium on transition metal dichalcogenide monolayers. Beilstein J. Nanotechnol. 8, 2711–2718. doi:10.3762/bjnano.8.270

CrossRef Full Text | Google Scholar

Terashima, K., and Imai, I. (1987). Indirect absorption edge of ZrS₂ and HfS₂. Solid State Commun. 63 (4), 315–318. doi:10.1016/0038-1098(87)90916-1

CrossRef Full Text | Google Scholar

Toh, R. J., Sofer, Z., and Pumera, M. (2016). Catalytic properties of group 4 transition metal dichalcogenides (MX₂; M = Ti, Zr, Hf; X = S, Se, Te). J. Mater. Chem. 4 (47), 18322–18334. doi:10.1039/c6ta08089h

CrossRef Full Text | Google Scholar

Traving, M., Seydel, T., Kipp, L., Skibowski, M., Starrost, F., Krasovskii, E. E., et al. (2001). Combined photoemission and inverse photoemission study of HfS₂. Phys. Rev. B 63 (3), 035107. doi:10.1103/physrevb.63.035107

CrossRef Full Text | Google Scholar

Tsai, H.-S., Liou, J.-W., Setiyawati, I., Chiang, K.-R., Chen, C.-W., Chi, C.-C., et al. (2018). Photoluminescence characteristics of multilayer HfSe₂ synthesized on sapphire using ion implantation. Adv. Mater. Interfaces. 5 (8), 1701619. doi:10.1002/admi.201701619

CrossRef Full Text | Google Scholar

Wu, N., Zhao, X., Ma, X., Xin, Q., Liu, X., Wang, T., et al. (2017). Strain effect on the electronic properties of 1T-HfS₂ monolayer. Phys. E Low-dimens. Syst. Nanostruct. 93, 1–5. doi:10.1016/j.physe.2017.05.008

CrossRef Full Text | Google Scholar

Xiao, D., Liu, G. B., Feng, W., Xu, X., and Yao, W. (2012). Coupled spin and valley physics in monolayers of MoS₂ and other group-VI dichalcogenides. Phys. Rev. Lett. 108 (19), 196802. doi:10.1103/physrevlett.108.196802

CrossRef Full Text | Google Scholar

Xu, K., Wang, Z., Wang, F., Huang, Y., Wang, F., Yin, L., et al. (2015). Ultrasensitive phototransistors based on few-layered HfS₂. Adv. Mater. 27 (47), 7881–7887. doi:10.1002/adma.201503864

CrossRef Full Text | Google Scholar

Yan, P., Gao, G.-y., Ding, G.-q., and Qin, D. (2019). Bilayer MSe₂ (M = Zr, Hf) as promising two-dimensional thermoelectric materials: a first-principles study. RSC Adv. 9 (22), 12394–12403. doi:10.1039/c9ra00586b

CrossRef Full Text | Google Scholar

Yin, L., Xu, K., Wen, Y., Wang, Z., Huang, Y., Wang, F., et al. (2016). Ultrafast and ultrasensitive phototransistors based on few-layered HfSe₂. Appl. Phys. Lett. 109 (21), 213105. doi:10.1063/1.4968808

CrossRef Full Text | Google Scholar

Yue, R., Barton, A. T., Zhu, H., Azcatl, A., Pena, L. F., Wang, J., et al. (2015). HfSe₂ thin films: 2D transition metal dichalcogenides grown by molecular beam epitaxy. ACS Nano. 9 (1), 474–480. doi:10.1021/nn5056496

CrossRef Full Text | Google Scholar

Yun, W. S., Han, S. W., Hong, S. C., Kim, I. G., and Lee, J. D. (2012). Thickness and strain effects on electronic structures of transition metal dichalcogenides: 2H-MX₂ semiconductors (M = Mo, W; X = S, Se, Te). Phys. Rev. B 85 (3), 033305. doi:10.1103/physrevb.85.033305

CrossRef Full Text | Google Scholar

Zeng, H., and Cui, X. (2015). An optical spectroscopic study on two-dimensional group-VI transition metal dichalcogenides. Chem. Soc. Rev. 44 (9), 2629–2642. doi:10.1039/c4cs00265b

CrossRef Full Text | Google Scholar

Zeng, H., Dai, J., Yao, W., Xiao, D., and Cui, X. (2012). Valley polarization in MoS₂ monolayers by optical pumping. Nat. Nanotechnol. 7 (8), 490–493. doi:10.1038/nnano.2012.95

CrossRef Full Text | Google Scholar

Zhang, L., Zhang, Y., Camacho, J., Khodas, M., and Zaliznyak, I. (2011). The experimental observation of quantum Hall effect of l=3 chiral quasiparticles in trilayer graphene. Nat. Phys. 7 (12), 953–957. doi:10.1038/nphys2104

CrossRef Full Text | Google Scholar

Zhang, W, Huang, Z., Zhang, W., and Li, Y. (2014). Two-dimensional semiconductors with possible high room temperature mobility. Nano Res. 7 (12), 1731–1737. doi:10.1007/s12274-014-0532-x

CrossRef Full Text | Google Scholar

Zhao, Q., Guo, Y., Si, K., Ren, Z, Bai, J., and Xu, X. (2017). Elastic, electronic, and dielectric properties of bulk and monolayer ZrS₂, ZrSe₂, HfS₂, HfSe₂ from van der Waals density‐functional theory. Phys. Status Solidi (B) 254 (9), 1700033. doi:10.1002/pssb.201700033

CrossRef Full Text | Google Scholar

Zhou, J., Lin, J., Huang, X., Zhou, Y., Chen, Y., Xia, J., et al. (2018). A library of atomically thin metal chalcogenides. Nature 556 (7701), 355–359. doi:10.1038/s41586-018-0008-3

CrossRef Full Text | Google Scholar